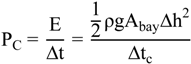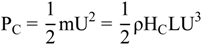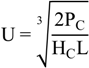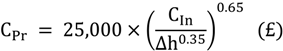1. Renewable Energy Reserves in Matsu
Since the global warming issue has become an important part of Taiwan’s energy policy, the current power structure with high-carbon emission has been examined critically, leading also to the extensive investigation into the total reserve of the renewable energy in Taiwan. A great deal of research has been devoted to studying the feasibility of deploying different kinds of renewable energy equipment on proper sites nationwide. Because Taiwan is a small island surrounded by oceans, the land utilization for deploying energy equipment is highly limited. Accordingly, we have to look for any possible deployment to the offshore area. The installation may include, for example, offshore wind energy, tidal energy, wave energy, and so on, which are all the targets we shall pursue.
For the aforementioned renewable energy, an extensive reserves assessment has been undertaken by Chen
et al. [
1] Their results showed that wind and solar energy reserves are the largest in Taiwan, with 29.9 kWh/person/day and 24.27 kWh/person/day, respectively. They also indicated that the total reserves of seven different kinds of renewable energy is 78.02 kWh/person/day, about 2.86 times the electricity produced in Taiwan in 2009 (
i.e., 27.32 kWh/person/day). Many studies also investigated the reserve of various individual renewable energies. For example, Chi [
2] assessed the solar energy reserve in Taiwan to be 236 TWh annually or 27.96 kWh/person/day. Yang [
3] analyzed the installed location and reserves of onshore and offshore wind power and found that they are 18.6 GW and 100.9 GW respectively, implying that onshore and offshore wind can generate 19.1 TWh and 294.7 TWh per year, accounting for 2.26 kWh/person/day and 34.9 kWh/person/day respectively. Lee [
4] studied the potential of biomass energy and found that it can generate 155.8 PJ heat every year.
All these studies demonstrated that the power reserves of renewable energy are more sufficient than the power demands in Taiwan. In this study, we focused the renewable energy reserve of Matsu, a tiny island in the Taiwan Strait close to mainland China. Since Matsu is separated from Taiwan by the 200-kilometer-wide Taiwan Strait, the weather and marine topography in Matsu are very different from those in Taiwan. As a result, the total reserves and characteristics of renewable energy in Matsu are expected to differ from Taiwan’s. After finishing an intensive investigation, we were able to summarize the total reserves of seven different kinds of Matsu’s renewable energy; the results are shown in
Table 1 [
5], where the reserves of renewable energy are the same as the energy presently available according to certain techniques and presented in a properly developed ratio.
As one can see from
Table 1, the reserves of offshore wind, hydro, and wave energy are too small to have economic value. The reserve of biomass is also limited due to the lack of usable areas and the issue of waste. The reserve of onshore wind energy is also small because of the lack of installable areas and an insufficient monsoon. Likewise, the solar energy reserve is relatively low since the installable area, such as rooftops or areas for industry, agriculture, and traffic, are too small to use. What can also be gleaned from the table is that the tidal energy reserve is the largest and is the only one with economic value.
Since renewable energies, especially wind and solar power, vary significantly with the season, we arranged four items of renewable energy variation and compared them with actual electric power consumption in Matsu, as shown in
Figure 1. From this figure, it can be observed that the reserve of tidal power is truly large enough to support the power need of this tiny island. If the reserved tidal power can be fully developed, the electric requirement of Matsu could be sufficiently met. Furthermore, tidal energy does not vary dramatically with the season and never vanishes at any point during the year. It can accordingly serve as a base load in the entire power supply structure. For these reasons, we studied the feasibility of the tidal energy in Matsu in depth and developed a conceptual design of the tidal power plant in Matsu.
Table 1.
Renewable energy reserves in Matsu by month.
Table 1.
Renewable energy reserves in Matsu by month.
| Unit: MWh | Solar | Onshore Wind | Offshore Wind | Biomass | Wave | Tidal | Hydro | Total Potential | Actual Consumption |
|---|
| Jan | 1245 | 76 | 0 | 103 | 0 | 11,712 | 0 | 13,136 | 4985 |
| Feb | 1416 | 64 | 0 | 103 | 0 | 10,639 | 0 | 12,221 | 4495 |
| Mar | 1957 | 23 | 0 | 103 | 0 | 12,023 | 0 | 14,106 | 5570 |
| Apr | 2068 | 45 | 0 | 103 | 0 | 11,555 | 0 | 13,771 | 5096 |
| May | 2813 | 35 | 0 | 103 | 0 | 11,459 | 0 | 14,411 | 5576 |
| Jun | 2708 | 91 | 0 | 103 | 0 | 11,063 | 0 | 13,965 | 5874 |
| Jul | 4001 | 163 | 0 | 103 | 0 | 11,696 | 0 | 15,963 | 5948 |
| Aug | 3694 | 70 | 0 | 103 | 0 | 12,248 | 0 | 16,115 | 6559 |
| Sep | 2655 | 63 | 0 | 103 | 0 | 12,311 | 0 | 15,132 | 6305 |
| Oct | 2076 | 114 | 0 | 103 | 0 | 12,373 | 0 | 14,666 | 5921 |
| Nov | 1460 | 104 | 0 | 103 | 0 | 11,815 | 0 | 13,482 | 5870 |
| Dec | 1520 | 51 | 0 | 103 | 0 | 11,956 | 0 | 13,630 | 5213 |
| Total | 27,613 | 900 | 0 | 1,237 | 0 | 140,851 | 0 | 170,600 | 67,411 |
We note that, as shown in
Figure 1, even though the tidal energy reserve is virtually two times the power consumption in Matsu, in reality not all of the reserved tidal power can be captured and by the water turbine. In fact, the total power generated is closely associated with turbine efficiency, tidal current characteristics, a turbine’s installed location, and the cost of construction. At the end of this paper, we will discuss these factors and assess the feasibility of a tidal power plant in Matsu.
Figure 1.
The variations of four renewable energies by month and the comparison with the power consumption in Matsu.
Figure 1.
The variations of four renewable energies by month and the comparison with the power consumption in Matsu.
2. Characteristics of Tidal Power Plants
There have been many different types of tidal power technology developed around the globe. The first economically profitable tidal power plant and the second largest one in the world is Rance Tidal Power Station [
6], which was built in 1967 in Brittany, France. With a 5 m tidal range, Rance River is bounded by a 750 m-long dam, including a 115 m-long gate and 332.5 m-long turbine sets. Rance Tidal Power Station is equipped with 24 Bulb turbines, whereby the generators are inside the cabin which make them generate electricity from both flow directions. The advantage of Bulb turbine is that it can withstand high flow rate and high rotating speed, but the huge cabin would block the water flow and cause some heat sink problem from generators [
7]. Each turbine’s installed capacity is 10 MW, and the total installed capacity of Rance power station is 240 MW, which can generate 500 GWh electricity every year.
Nowadays, the largest tidal power plant in the world is Sihwa Lake power plant [
8,
9], located in the Gyeonggi Province, Korea. Sihwa Lake was built in 1994 as an artificial lake originally providing clear water for inhabitants, and was rebuilt as tidal power plant in 2011 because of aquatic and environmental pollution. The average tidal range is 5.6 m in Sihwa Lake and the dam encloses a 39 km
2 area. The Sihwa power plant uses ten 25.4 MW Bulb turbines, whose rotor diameter is 7.5 m, and its total installed capacity is 254 MW to generate 552.7 GWh annually. According to a monitoring report [
10] in 2013, Sihwa Lake Power Plant generated 40 GWh per month from November 2012 to Mars 2013, and is expected to generate 480 GWh annually.
Located at the Bay of Fundy in Eastern Canada, the Annapolis Tidal Generation has the world’s highest tidal range. This tidal power plant was built in 1984. The tide at the site is semidiurnal, and its range averages above 6 m [
11,
12]. The installed capacity of the power plant is 20 MW, producing about 30 GWh electricity every year [
13,
14]. This power plant uses Straflo turbines [
7], which is characterized by a generator set that is not placed in the cabin after the rotors but fixed on the outside of the rotor; that is, although the Straflo turbine would greatly reduce the cabin volume, the energy loss would be significant due to friction.
These three tidal power plants are all characterized by their dam-type generation. They use dams to store tides of water to create a sea level difference, and release water to drive turbines to generate electricity. Since the water would be released at a certain time into a narrow sluice, the powerful kinetic energy would be released over a short period; hence, the advantage of dam-type generation is that the flow activates the turbines easily, and more energy can be captured. On the other hand, due to the fact that the power can only be generated at the time of water release, electricity is only generated four times a day.
3. Characteristics of Water Turbines
Currently, about 63 types of water turbines are in development [
15], and most of them belong to the lift-type turbine, which is characterized by the type of airfoil blade used. Characterized by the airfoil design, these turbines can operate at various flow speeds. In comparison with the drag-type turbine, the lift-type turbine can operate better in a free flow without dams to separate the water field, thereby having less impact on coastal ecosystems. In addition, since turbines can operate in regular tidal flow, the generation period is longer and is more convenient for electrical grid connection.
However, at the present time, there are only a few large-scale tidal power plants built in free flow, and many of them are still at the stage of prototype testing and construction planning. The most well-known installation is the dual horizontal axis turbines MCT (Marine Current Turbines) made by Siemens [
14,
16,
17], equipped with movable axis in vertical direction. The feature of a horizontal axis turbine is the rotor axis’s parallelism to the water flow, large rotor diameter, and high TSR (tip speed ratio). In 2003, a 300 kW MCT with a single rotor was tested in Lynmouth, Devon, UK. Later on, the 1.2 MW SeaGen with duel rotors was constructed and connected with electrical grid in 2008 in Strangford Lough, Northern Ireland. There are other horizontal axis turbines that have been tested, such as 1MW Hammerfest by Andritz Hydro turbine in Eday Island (2011) [
18] and 1 MW TGL (Tidal Generation Limited) in Orkney (2012) [
19]. Apart from that, the RTT (Rotech Tidal Turbine) and Open Centre Turbine use Venturi to accelerate water flow. By the shape of venture, water flow would be enhanced through turbine, and the capturing energy and output power would be increased. Correspondingly, these two 1 MW machines were tested in 2008 and 2009 by Lunar Energy and Open Hydro companies, respectively [
14,
16].
Uldolmok Tidal Power Plant [
8,
13,
20,
21] in Korea is the largest tidal plant in free flow. This power plant was equipped with 1 MW vertical helical blade turbines in 2009, generating 2.4 GWh electricity annually. The installed capacity was increased to 1.5 MW in 2011, and plans to increase to 90 MW in 2013. The plant was built in the Uldolmok Strait [
22], where the narrowest site is 250 meters wide with an average flow rate of 2.4 m/s, and the maximum tidal flow rate is up to 6.3 m/s.
Because the vertical helical blade turbine has been developing over a longer period of time, its operating information is more comprehensive than other types; moreover, its construction cost is relatively low. As a result, this study has chosen to focus on the helical blade turbine. Compared with horizontal and reciprocating turbines, the vertical axis turbine is characterized by the rotor’s axis being perpendicular to the flow direction, which makes the turbine unnecessary to modify yaw angle while flow direction changes so that the cost of the steering mechanism can be emitted. Since the starting torque is relatively low, the vertical turbine unit can be designed smaller; that is, turbine units can be combined to meet different demands in different situation.
Because the rotor’s axis is perpendicular to the flow direction, the greatest weakness of the straight blade vertical water turbine is its periodic force and torque variation from the attack angle changing with rotating azimuth angle, which might cause mechanical fatigue. To overcome this problem, there are two main solutions. Kobold turbine [
23] has designed passive variable blades to change the blade pitch angle for reducing the variation of attack angle. On the other hand, Gorlov [
24,
25,
26] uses helical shape blades that cover the turbine at each azimuth angle in order to force and torque superposition.
The helical turbine was patented by Alexander M. Gorlov in 1995–2001 [
24,
25,
26], and received the ASME Thomas A. Edison Patent Award in 2001. Gorlov published the first test report in 1998, and wrote articles about operating tests and market analysis in 2004 and 2010. Those articles include reports on the four tidal power tests in Cape Cod Canal, Massachusetts that took place from 1996 to 1998. The subsequent patent now belongs to GCK [
27] and Ocean Renewable Power Company (ORPC) [
28].
4. Dynamic Analyses of Helical Water Turbine
The basic theory of vertical axis water turbines originated from wind turbines [
29]. Traditionally, the Actuator Disk Theory [
30,
31,
32,
33,
34,
35] was brought up by Betz in 1919, using the actuator disk and streamtube assumption to estimate the turbine efficiency, and then extended to double multiple streamtube theory (DMS) later on. Another method for turbine analysis is the vortex method [
36,
37,
38,
39,
40], which estimates the blade vortex from the induction velocity by BEM (blade element momentum theory) and then keeps the circulation conservation to calculate the streak lines and wake flow. In recent years, computational fluid dynamic (CFD) has dominated the fluid dynamic analysis field. Using finite volume or finite element methods [
41,
42,
43], the CFD analysis has the advantages that it is more flexible for condition setting and more accurate than other methods, but it expends more hardware resources and requires a longer time in comparison [
44,
45,
46].
As a result, ANSYS Fluent was used as main solver in this research; this software uses finite volume methods and Reynolds Averaging to solve the continuity equation, momentum equation, and turbulence equation. The turbulence equation in this research used Shear-Stress Transport k-ω Model (SST k-ω) [
47,
48], which is considered very stable while being applied to airfoil and high-pressure gradient cases. In addition, the Pressure-Based Solver and the Pressure-Based Segregated Algorithm were used to solve those government equations.
Figure 2.
Model of helical turbine computing. (a) Schematic of turbine elements. (b) Dimension of whole computing domain.
Figure 2.
Model of helical turbine computing. (a) Schematic of turbine elements. (b) Dimension of whole computing domain.
4.1. Modelling Condition and Assumption
According to the original design [
24,
25,
26], the turbine has a 0.6096 m (D
G) diameter and 0.8636 m (H
G) height with three helical blades covering 120 degreed, respectively, and the turbine’s blade profile is NACA0020 with a chord length of 0.1778 m. This turbine analysis was divided into several parts: three helical blades, rotating axes, and upper and lower plates, as shown in
Figure 2 (a). The 3D model was illustrated in
Figure 2 (b): the upstream section is 6.5 D
G in length while the downstream is 15 D
G, and the height and width of model domain is 13 D
G. The helical turbine was simulated with rotating speed of 80 rpm (TSR = 3.65), and its wall boundaries are set to non-slip condition without deformation, heat transferring, and cavitation on the boundaries.
Furthermore, the flow was assumed through
x direction, whereas the turbine rotated about the
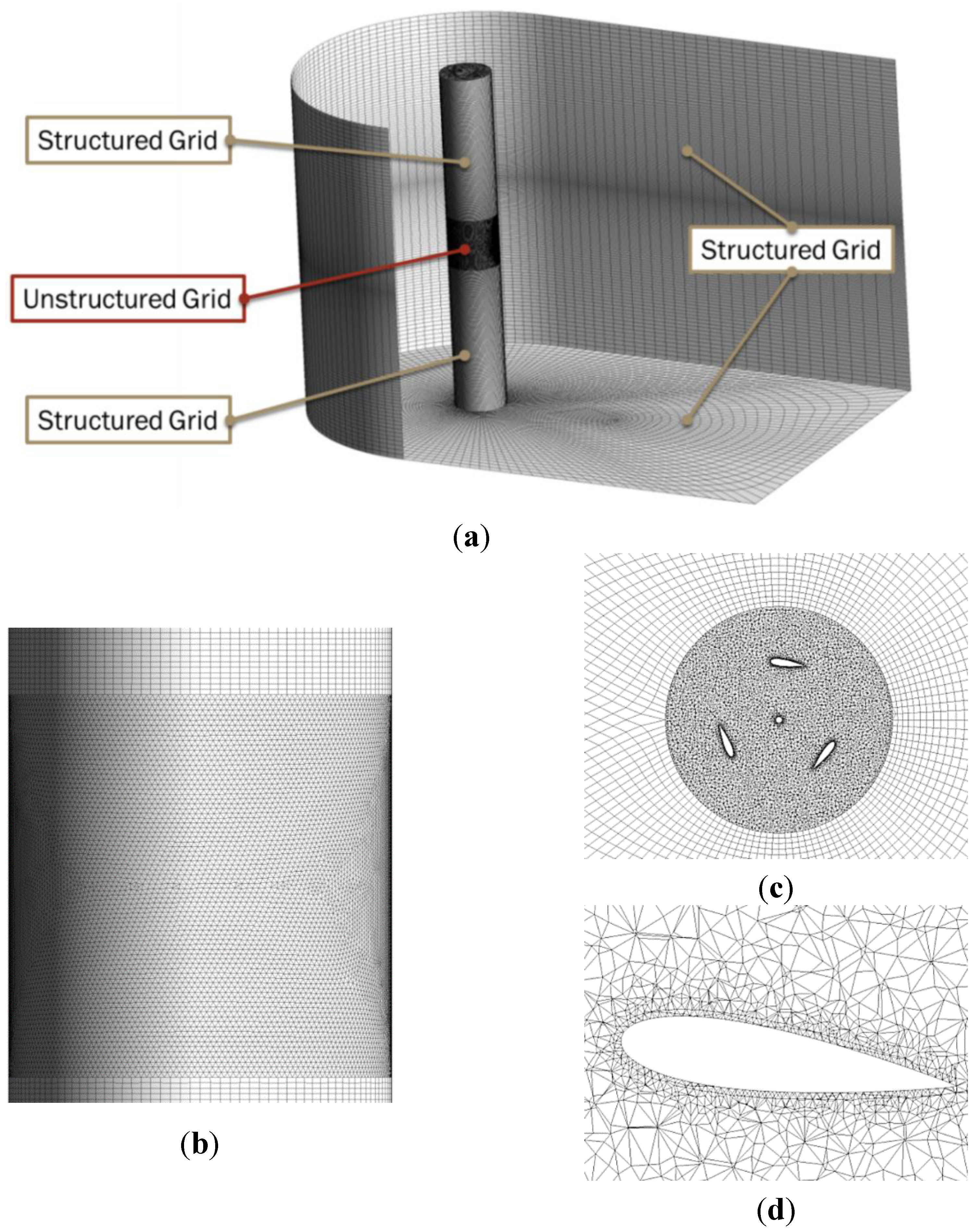
z direction. Both sides and upstream boundary condition were set to a flow rate of 1.4 m/s with constant turbulence kinetic energy (5%) and specific dissipation rate (3), and the downstream boundary kept mass conservation of the computing domain. In this model, water was under the assumption of incompressible fluid, and its density and viscosity were both assumed constant; however, its gravity term was also assumed nonexistent. Moreover, a cylinder interface outside the turbine was made to transfer data. The interface could keep the grid structure inside the cylinder while using the sliding mesh technique, and avoiding the huge resource waste from remeshing at each time step. The grids used in this model are shown in
Figure 3.
Figure 3.
Grids for calculation of helical blade turbines (a) Structured and unstructured grids according the complexity of domains. (b) Rotating grid interface. (c) Horizontal plane of rotating grid interface. (d) The blade grid.
Figure 3.
Grids for calculation of helical blade turbines (a) Structured and unstructured grids according the complexity of domains. (b) Rotating grid interface. (c) Horizontal plane of rotating grid interface. (d) The blade grid.
4.2. Force and Moment Distribution of Helical Turbine
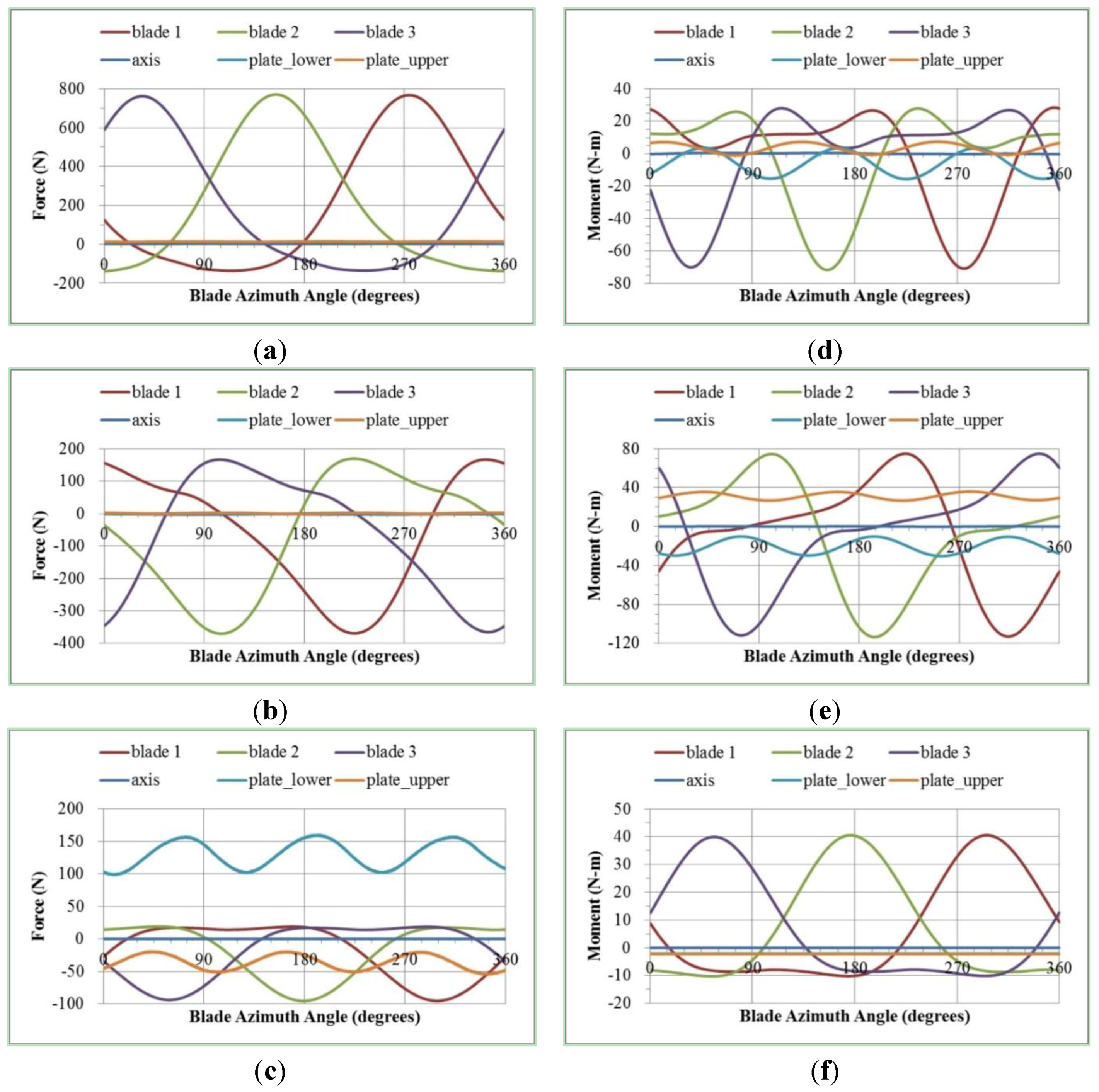
Figure 4 is the variation of force and moment distribution over elements, in which the turbine overall force averages about 617 N in
x direction and 186 N in
y direction, and the turbine overall moment is 13.2 N-m. One turbine can capture 147 W energy, and the power coefficient (Cp) is 22.3%. From the results shown in
Figure 4, it can be clearly found that the three turbine blades form three distinct waveforms during a cycle because they are the main components for capturing flow energy. Blade1 passes upstream when its azimuth angle is at 0°–90°, in which 0° is set to be in the y direction in
Figure 2. On the contrary, it passes downstream while it goes through 90°–180°. Since the blade geometry forms a concave curve downstream, blades take larger forces downstream than upstream.
Figure 4.
Variation of force and moment distribution at each element of helical blade turbine. (a) Force in x direction. (b) Force in y direction. (c) Force in z direction. (d) Moment about x axis. (e) Moment about y axis. (f) Moment about z axis.
Figure 4.
Variation of force and moment distribution at each element of helical blade turbine. (a) Force in x direction. (b) Force in y direction. (c) Force in z direction. (d) Moment about x axis. (e) Moment about y axis. (f) Moment about z axis.
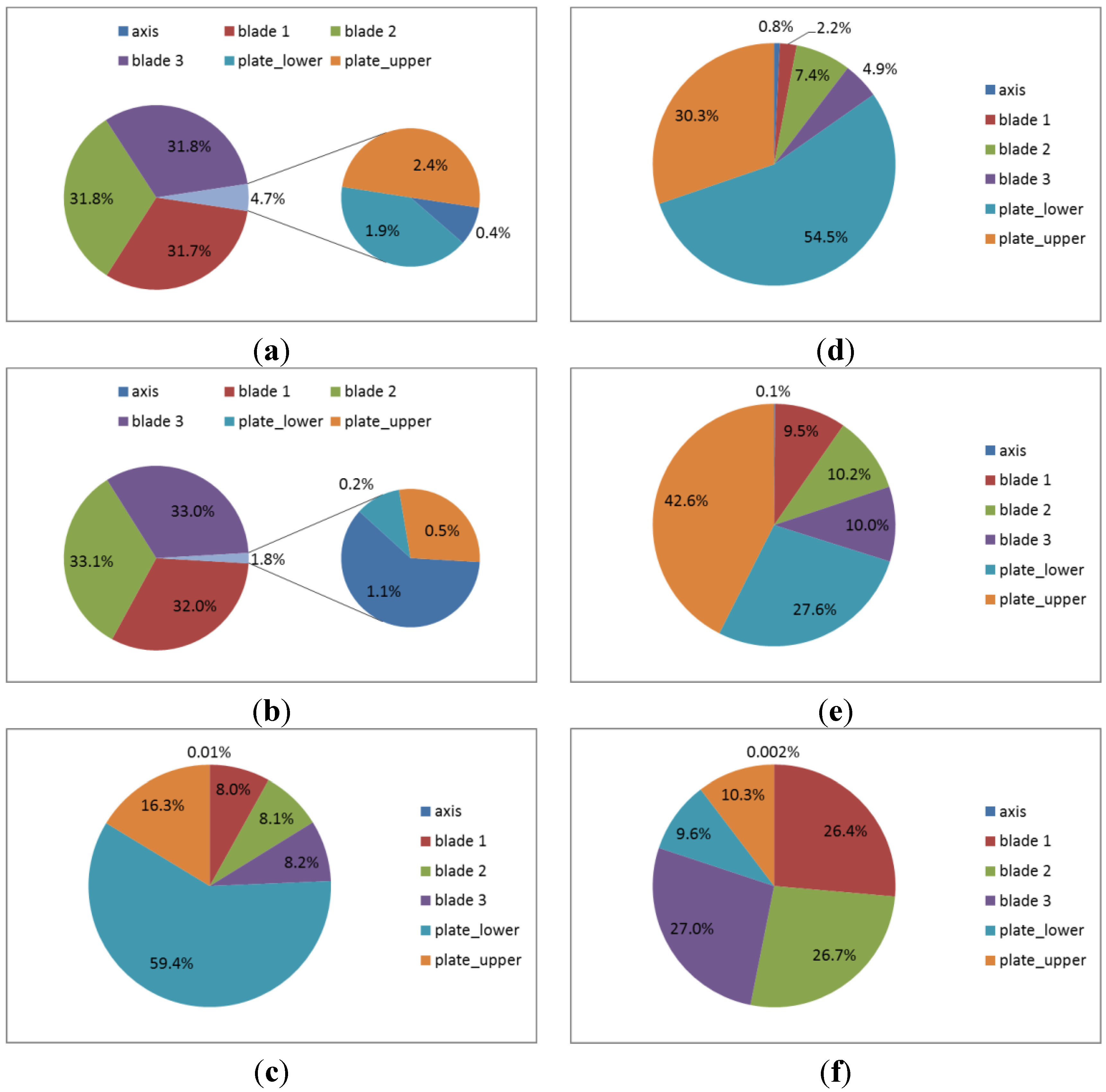
The force and moment distribution at each element of helical blade turbine is organized in
Figure 5. From force distribution of
x direction in
Figure 5(a), force distribution of
y direction in
Figure 5(b), and moment distribution about
z axis in
Figure 5(f), three helical blades sustain 80%–90% force and moment, and other elements take little distribution that would not affect the turbine performance. From force distribution of
z direction in
Figure 5(c), moment distribution about
x axis in
Figure 5(d), and moment distribution about
y axis in
Figure 5(e), the force and moment fraction of upper and lower is about 70%–80% due to the geometry, whereas the fraction of axis can still be ignored.
Figure 5.
Chart of force and moment distribution at each element of helical blade turbine. (a) Force in x direction. (b) Force in y direction. (c) Force in z direction. (d) Moment distribution about x axis. (e) Moment distribution about y axis. (f) Moment distribution about z axis.
Figure 5.
Chart of force and moment distribution at each element of helical blade turbine. (a) Force in x direction. (b) Force in y direction. (c) Force in z direction. (d) Moment distribution about x axis. (e) Moment distribution about y axis. (f) Moment distribution about z axis.
In comparison with a straight blade turbine in the same condition, which is described in
Table 2, the helical blade turbine’s force fluctuant ratio is lower at 81%, and its moment fluctuant ratio is lower at 121%; where the fluctuant ratio is the data’s range (difference between maximum and minimum) divided by the average value in a cycle. It is obvious that using a helical blade turbine design would make the blades take force uniformly, and effectively improve the problem of periodic force and moment variation in the traditional straight blade turbine; hence, occurrence of mechanical fatigue fracture would be avoided.
Table 2.
Simulation result comparison of helical blade turbine and straight blade turbine.
Table 2.
Simulation result comparison of helical blade turbine and straight blade turbine.
| Helical Blade Turbine | Straight Blade Turbine |
|---|
![Jmse 02 00506 i001]() | ![Jmse 02 00506 i002]() |
|---|
| Average | Fluctuant Ratio (%) | Average | Fluctuant Ratio (%) |
|---|
| Force (N) | 646.67 | 20% | 659.71 | 101% |
| Moment (N-m) | 40.05 | 77% | 15.78 | 198% |
| Power (W) | 146.76 | 50% | 116.34 | 327% |
4.3. The Dynamic Characteristics of the Helical Turbine
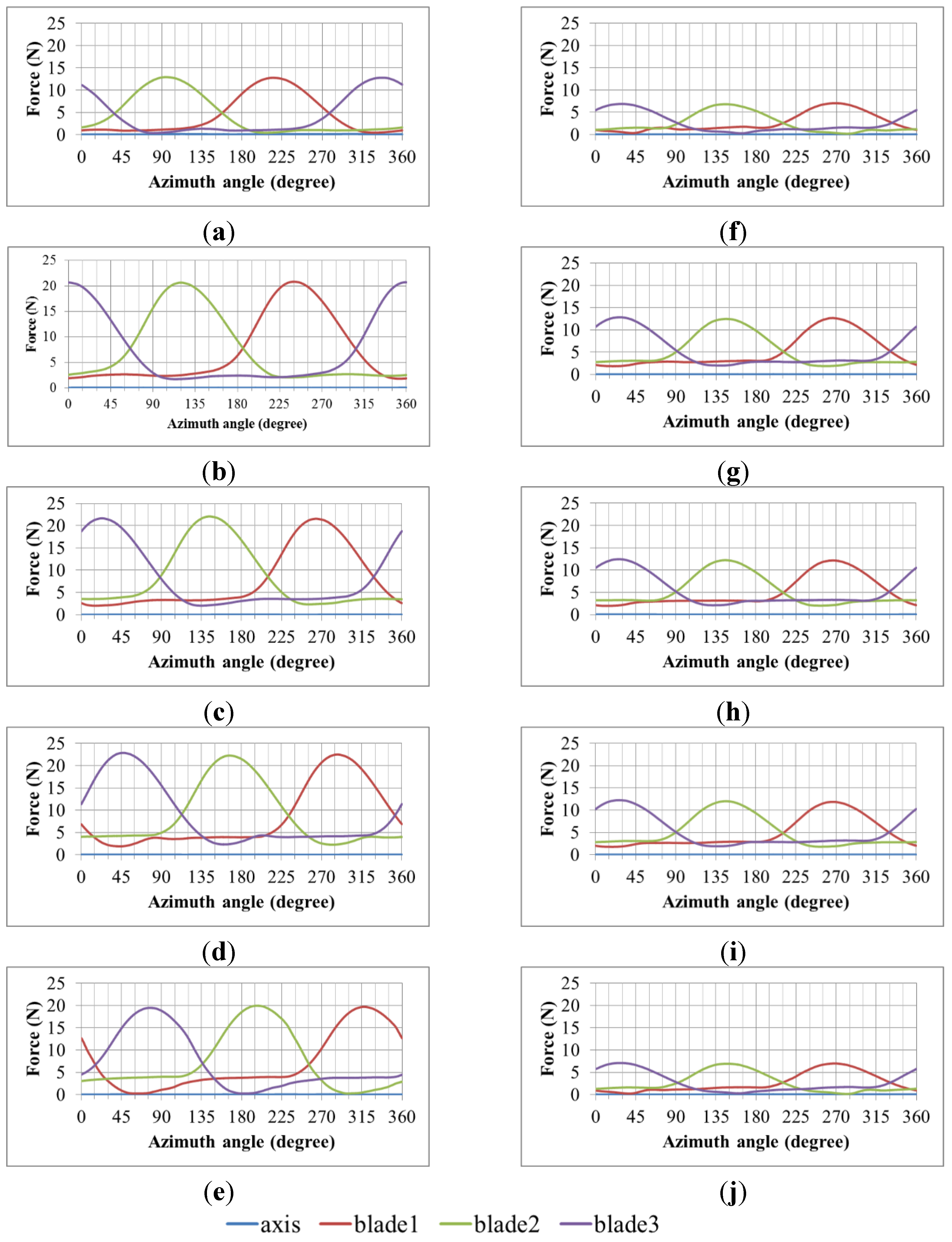
To further understand the dynamic phenomena of the helical blade turbine, the turbine was cut as five horizontal cross-sections in 0.4 m, 0.2 m, 0 m, –0.2 m, and –0.4 m, while the origin is set at the middle of turbine. In order to compare the cross-sectional force of turbine elements, all cross-sections are given 0.01 m thickness.
Figure 6 is the analysis result, showing the force variation of turbine cross-sections in a cycle. The left parts of
Figure 6 (from (a) to (e)) are the results of the helical blade turbine, and the black dashed lines indicates the blades cross-section at the same azimuth angle in different height; in contrast, the right parts of
Figure 6 (from (f) to (j)) are the results of the straight blade turbine.
By observing the force variation of the helical turbine at different heights, it has been found that every force distribution curve of blades are behind the above cross-section 30 degrees since helical blades are designed to 120 degrees. From the comparison with two turbines, the force distribution has the same trend when they are in the same azimuth angle at different heights. The blade takes the largest force in the middle section (z = 0 m), and the smaller while closing both sides (z = ±0.4 m) since the fluid energy is slowed by the vortex from the upper and lower plates. Furthermore, the force of the helical turbine closing lower plate (z = −0.4 m) is larger than those of the closing upper plate (z = +0.4 m) since the helical blade would lead the flow upward.
Conclusively, the helical blade turbine takes the force and moment more smoothly while operating, which can effectively improve the reliability and durability of the turbine. However, because of the helical turbine geometry, the moment about the x and y directions is increased and the flow through the turbine is driven upward. In addition, the blades of the helical turbine can be further modified from its previous design, in which the aspect ratio is obviously larger than the modern types, causing lower power efficiency.
Figure 6.
Force distribution of cross-sections. (a) Helical blade turbine at z = 0.4 m. (b) Helical blade turbine at z = 0.2 m. (c) Helical blade turbine at z = 0 m. (d) Helical blade turbine at z = −0.2 m. (e) Helical blade turbine at z = −0.4 m. (f) Straight blade turbine at z = 0.4 m. (g) Straight blade turbine at z = 0.2 m. (h) Straight blade turbine at z = 0 m. (i) Straight blade turbine at z = −0.2 m. (j) Straight blade turbine at z = −0.4 m.
Figure 6.
Force distribution of cross-sections. (a) Helical blade turbine at z = 0.4 m. (b) Helical blade turbine at z = 0.2 m. (c) Helical blade turbine at z = 0 m. (d) Helical blade turbine at z = −0.2 m. (e) Helical blade turbine at z = −0.4 m. (f) Straight blade turbine at z = 0.4 m. (g) Straight blade turbine at z = 0.2 m. (h) Straight blade turbine at z = 0 m. (i) Straight blade turbine at z = −0.2 m. (j) Straight blade turbine at z = −0.4 m.
6. Dynamic Analysis of Helical Turbine Sets
To fit the estuary depth in Matsu, turbine columns [
52] with four turbines should be designed. In order to further reduce the force and moment variation of the helical blade turbine, eight dual turbine sets were modelled (as in
Figure 10), which are the same phase and twins (symmetrical) helical turbines with 0°, 30°, 60°, and 90° angles offset respectively, to discuss each overall force and moment distribution in different cases.
Figure 10.
Schematic of dual helical turbine sets. (a) The same direction with 0° angle offset. (b) The symmetrical turbine with 0° angle offset. (c) The same direction with 30° angle offset. (d) The symmetrical turbine with 30° angle offset. (e) The same direction with 60° angle offset. (f) The symmetrical turbine with 60° angle offset. (g) The same direction with 90° angle offset. (h) The symmetrical turbine with 90° angle offset.
Figure 10.
Schematic of dual helical turbine sets. (a) The same direction with 0° angle offset. (b) The symmetrical turbine with 0° angle offset. (c) The same direction with 30° angle offset. (d) The symmetrical turbine with 30° angle offset. (e) The same direction with 60° angle offset. (f) The symmetrical turbine with 60° angle offset. (g) The same direction with 90° angle offset. (h) The symmetrical turbine with 90° angle offset.
6.1. Numerical Methodology
The overall force and moment of turbine sets can be calculated under the assumption that there would not be any interaction among the flow field of each turbine. Based on the CFD result of the helical blade turbine in the previous discussion, MATLAB software was applied for numerical linear superposition in different cases. The turbine sets schematic of two and four are shown as
Figure 11 and
Figure 12.
Figure 11.
Turbine sets schematic of dual turbines. (a) The same direction. (b) The symmetrical turbine sets.
Figure 11.
Turbine sets schematic of dual turbines. (a) The same direction. (b) The symmetrical turbine sets.
Figure 12.
Turbine sets schematic of turbine column. (a) The same direction. (b) The symmetrical turbine sets.
Figure 12.
Turbine sets schematic of turbine column. (a) The same direction. (b) The symmetrical turbine sets.
The coordinate system is dominated by the turbine above. In the case of turbine sets with the same direction, which are shown as
Figure 11(a) and
Figure 12(a), the force and torque are calculated by the following formula:
However, in the case of symmetrical turbine sets, which are shown as
Figure 11(b) and
Figure 12(b), the force and torque are calculated by the following equations:
6.2. Dynamic Characteristics of Dual Turbines
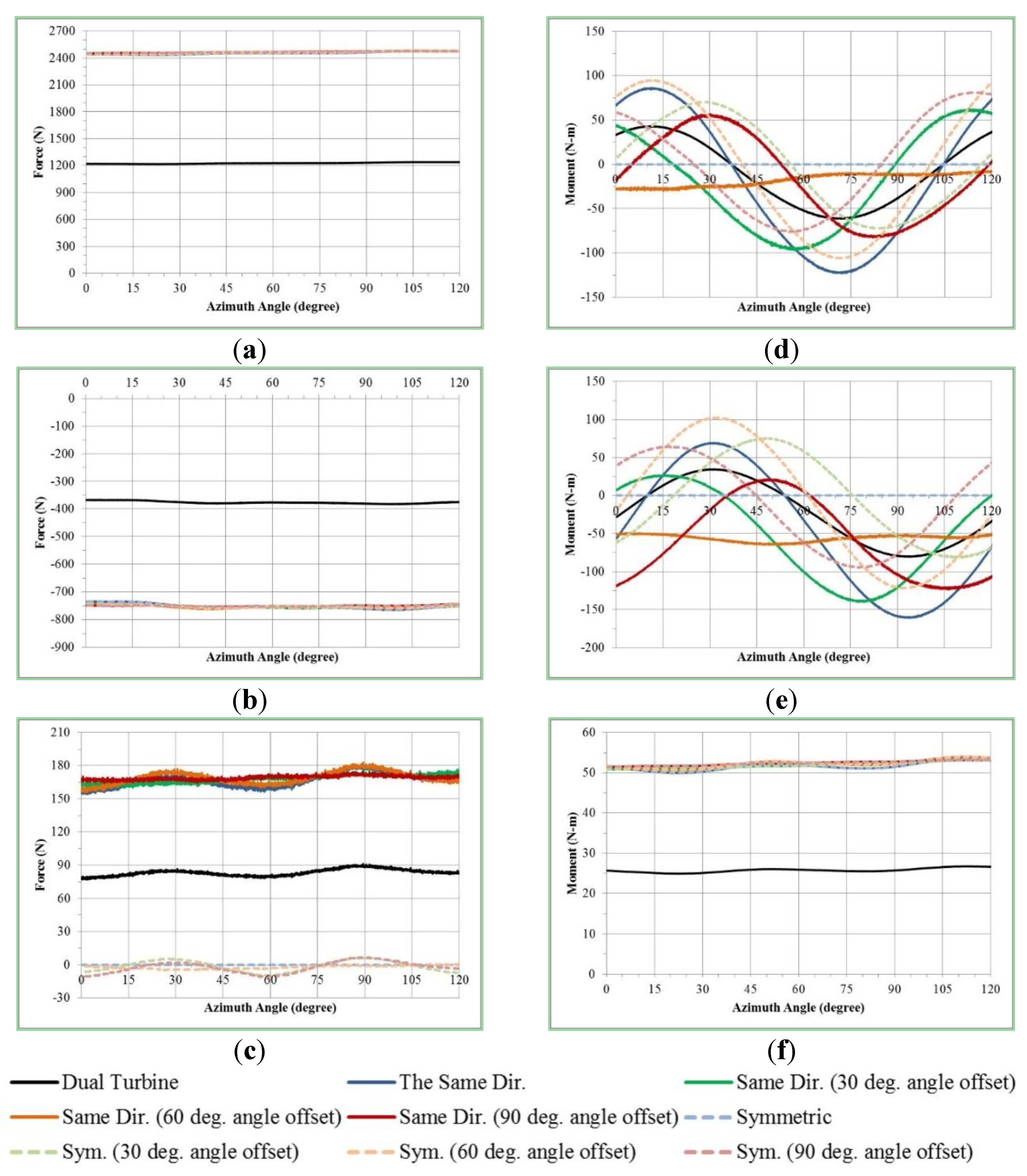
Figure 13 shows the force and moment variation of a dual turbine, where the black solid line is the single turbine data; the blue, green, orange, and red solid lines indicate the same direction turbine sets with 0°, 30°, 60°, and 90° angle offsets respectively; and the blue, green, orange, and red dashed lines represent the symmetrical turbine sets with 0°, 30°, 60°, and 90° angle offsets.
The force variation in
x direction is shown in
Figure 13(a); it is clear that the force fluctuant ratio of a turbine set with 60° angle offset is less significant than others because of the cancellation of wave peak and trough. Likewise, from
Figure 13(b) and (f), the force variation in
y direction and the moment variation about
z axis have the same trend become evident. The force variation in
z direction is shown in
Figure 13(c). The design of symmetrical turbine sets can effectively reduce overall force in
z direction; and those with 0° angle offset can even be completely destroyed; however, the range of force fluctuation is extremely large with the 60° angle offset. On the contrary, though the turbine sets of the same direction take a larger force, those with a 60° angle offset can effectively reduce range of force fluctuation in
z direction; however, those with 0° angle offset have great fluctuant ratio because it is completely superimposed on the peak–peak value.
Figure 13(d) and (e) shows the overall moment variation of dual turbine sets in
x and
y directions respectively, which is more complicated than others since the calculation uses the data of both force and moment. It can easily observed that the result of symmetrical turbine sets with zero angle offset is eliminated due to the geometry, analogous to the force in
x and
y direction. Furthermore, the turbine sets of the same direction with 30° angle offset has smaller fluctuant ratio.
Figure 13.
Overall force and moment results of turbine sets with two helical turbines. (a) Force in x direction. (b) Force in y direction. (c) Force in z direction. (d) Moment about x axis. (e) Moment about y axis. (f) Moment about z axis.
Figure 13.
Overall force and moment results of turbine sets with two helical turbines. (a) Force in x direction. (b) Force in y direction. (c) Force in z direction. (d) Moment about x axis. (e) Moment about y axis. (f) Moment about z axis.
To sum up, the fluctuation ratio of turbine sets with a 60° angle offset is minimum regardless of the overall force in x and y direction and moment about z axis ; however, the symmetrical turbine sets with 60° angle offset has large force fluctuation in z direction. The force in z direction and the moment about x and y direction of symmetrical turbine sets with 0° angle offset can be completely omitted. In addition, the force in z direction of the same phase turbine sets with a 60° angle offset has a smaller vibration, as does the moment about x and y direction of the same phase turbine sets with 30° angle offset. Considering the above factors, the same direction turbine sets with 60° angle offset was chosen as the dual turbine sets’ design so that the overall force is uniform without large vibration and the moment is more stable. Based on the combined result of two turbines, turbine sets of four turbines was designed in the following section.
6.3. Dynamic Characteristics of Turbine Column
From the optimization of dual turbine sets, two of the same direction turbines with 60° angle offset are used. Using Equation (1) to Equation (12), the overall force and moment of turbine column were evaluated, which is shown in
Figure 14. As has been optimized by dual turbine sets, all the overall force and moment fluctuant ratio of turbine sets of turbine column are less than 10%. Similarly, the force in
z direction and the moment about
x and
y direction of symmetrical turbine sets with 0° angle offset can be fully eliminated. Also, the symmetrical turbine sets with 60° angle offset take less force fluctuation in
z direction, and the same direction turbine sets with 60° angle offset have less moment fluctuation about
x and
y directions.
Table 4.
The force and moment variation of turbine sets.
Table 4.
The force and moment variation of turbine sets.
| Average (N) | Fluctuant Ratio (%) | | Average (N) | Fluctuant Ratio (%) |
|---|
| Fx | Single Turbine | 616.88 | 19.5% | Mx | Single Turbine | −4.21 | 1798.8% |
| Dual Turbine | 1233.76 | 2.3% | Dual Turbine | −8.41 | 1298.9% |
Turbine Column
(4 turbines) | 2467.52 | 2.3% | Turbine Column
(4 turbines) | 0.00 | N/A |
| Fy | Single Turbine | −185.61 | 62.3% | My | Single Turbine | −10.77 | 705.3% |
| Dual Turbine | −371.22 | 6.4% | Dual Turbine | −21.54 | 535.0% |
Turbine Column
(4 turbines) | −742.44 | 6.4% | Turbine Column
(4 turbines) | 0.00 | N/A |
| Fz | Single Turbine | 41.22 | 149.3% | Mz | Single Turbine | 13.16 | 67.2% |
| Dual Turbine | 82.45 | 20.6% | Dual Turbine | 26.33 | 9.0% |
Turbine Column
(4 turbines) | 0.00 | N/A | Turbine Column
(4 turbines) | 52.65 | 9.0% |
6.4. Dynamic Analysis Result of Turbine Sets
In the part of dual turbine sets, the same direction turbine sets with 60° angle offset has the best force and moment variation, and takes minimal fluctuant ratio of force and moment about the
z axis. Using this result, the turbine column with four turbines can be further analyzed. From the dual turbine result, the force in
x and
y directions and moment about
z axis of turbine sets with four turbines has little vibration. To further reduce the moment about
x and
y directions, using symmetrical turbine sets with 0° angle offset is the best choice. The force and moment data of final turbine column is shown in
Table 4. The fluctuant ratios of these are controlled below 9%, and the total power of one turbine column is 587.04 W.
Figure 14.
Overall force and moment result of turbine sets with four helical turbines, where the black solid line is the single turbine data, the blue, green, orange, and red solid lines indicates the same direction turbine sets with 0°, 30°, 60°, and 90° angle offsets respectively, and the blue, green, orange, and red dashed lines represents the symmetrical turbine sets with 0°, 30°, 60°, and 90° angle offset. (a) Force in x direction. (b) Force in y direction. (c) Force in z direction. (d) Moment about x axis. (e) Moment about y axis. (f) Moment about z axis.
Figure 14.
Overall force and moment result of turbine sets with four helical turbines, where the black solid line is the single turbine data, the blue, green, orange, and red solid lines indicates the same direction turbine sets with 0°, 30°, 60°, and 90° angle offsets respectively, and the blue, green, orange, and red dashed lines represents the symmetrical turbine sets with 0°, 30°, 60°, and 90° angle offset. (a) Force in x direction. (b) Force in y direction. (c) Force in z direction. (d) Moment about x axis. (e) Moment about y axis. (f) Moment about z axis.
7. Tidal Power Plant Design
From
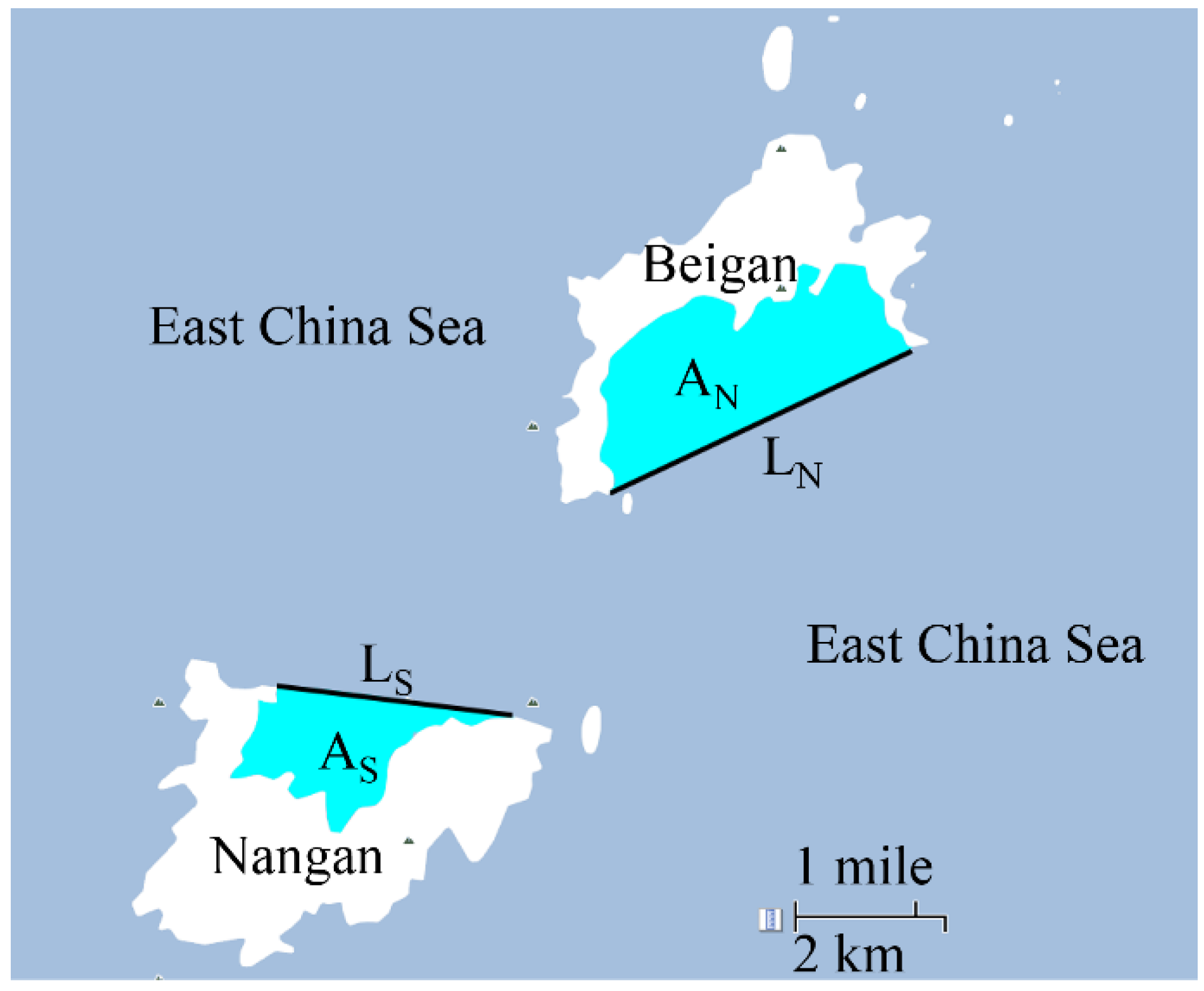
Figure 1, it becomes evident that tidal energy in Matsu has the most reserves and is the one most worth developing among renewable energies. However, full development is impossible due to several limitations. One limitation to be considered is cost, which includes turbine types, development area, and the power generating period.
In this section, tidal data in Matsu was used to estimate electricity while turbines were installed at two bays in Matsu. Google Map [
53] was used to measure the distance, and Google Planimeter [
54] was applied to measure the bay area as shown in
Figure 15. The bay distance between two capes is 4.35 km (L
N) in Beigan and 2.34 km (L
S) in Nangan, whereas the bay area is 6.14 km
2 (A
N) in Beigan and 2.75 km
2 (A
S) in Nangan. The tidal information was provided from the CWB (Central Weather Bureau) [
55] in Taiwan, and the annual tidal change in 2012 is illustrated in
Figure 16. It is worth noting that the tidal type in Matsu is semidiurnal, so there are two tides in a day. In both aspects of frequency and tidal height, the tides in Matsu are of high quality.
Figure 15.
Schematic of bay measurement in Matsu.
Figure 15.
Schematic of bay measurement in Matsu.
Figure 16.
The annual tidal change of Matsu in 2012.
Figure 16.
The annual tidal change of Matsu in 2012.
Figure 17.
Schematic of tidal energy estimation. (a) Electricity generation from water falling. (b) Electricity generation from water raising.
Figure 17.
Schematic of tidal energy estimation. (a) Electricity generation from water falling. (b) Electricity generation from water raising.
The method to estimate tidal energy is shown in
Figure 17, and there are two situations: electricity generation from water falling and from water raising. Assuming the tidal range was Δh and the bay area was A
bay, the tidal potential energy (E) was estimated from following formula:
where ρ is the water density and g is the gravity term which is 9.8 m/s. Then, the power from the tidal energy (P
C) was:
Assuming the tidal potential energy was totally transferred to kinetic energy, then the tidal current velocity (U) could be calculated as follows:
where the H
C stands for current height, L is the bay distance between two capes . In addition, Δt
c is the duration of water falling or raising (almost half tidal period).
According to seabed topography [
56] from Ocean Data Bank (ODB) of National Science Council (NSC), the current height was assumed to be 10 min Matsu, and the average tidal current velocity without dam is 1.06 m/s in Beigan and 0.99 m/s in Nangan.
Since the bay distance and current height would influence the tidal current velocity, the tidal velocity would be slowest without the dam. While the dam is built, the current is only allowed to pass from a narrow width so that it would be accelerated; that is, the bay distance would dominate the tidal current velocity. According to Equation 16, tidal velocities of several cases with different bay distances were estimated in
Table 5 with 5-meter current height assumption. As expected, the result shows that the tidal current velocity is higher with a shorter bay distance.
Nevertheless, considering present water turbine types would have better performance in the current velocity higher than 2 m/s, the sixth case, which was 1.00 km in Beigan and 0.50 km in Nangan, was chosen from
Table 5.
7.1. Tidal Power Plant Design with Helical Blade Turbines
If the bay is full of helical blade turbines, there are 1250 and 650 turbine columns constructed in Beigan and Nangan, respectively. While the power coefficient of the helical blade turbine is assumed constant (22.3%), the installed capacity (C
In) is 7.50 MW in Beigan and 1.35 MW in Nangan. Since the availability of the hydro power plant is 37% [
57], this power plant can generate 28.7 GWh electricity annually.
Table 5.
Tidal velocities with different sluice lengths in Matsu.
Table 5.
Tidal velocities with different sluice lengths in Matsu.
| Cases | Beigan | Nangan |
|---|
| Bay Distance (km) | Tidal Current Velocity (m/s) | Bay Distance (km)) | Tidal Current Velocity (m/s) |
|---|
| #1 | 3.50 | 1.43 | 2.00 | 1.32 |
| #2 | 3.00 | 1.51 | 1.50 | 1.45 |
| #3 | 2.50 | 1.60 | 1.25 | 1.54 |
| #4 | 2.00 | 1.72 | 1.00 | 1.66 |
| #5 | 1.50 | 1.90 | 0.75 | 1.83 |
| #6 | 1.00 | 2.17 | 0.50 | 2.09 |
| #7 | 0.50 | 2.74 | 0.25 | 2.64 |
In addition, according to the article by G. A. Aggidis
et al. [
58] in 2010, the cost of a hydro power plant (C
pr) can be shown as following:
If 125 turbine columns can be considered as one small power plant unit, the cost of power plant is estimated at 58.8 million NTD (about 2.0 million USD) in Beigan and 15.1 million (about 0.5 million USD) in Nangan. According to the electricity structure in Matsu, which is shown in
Table 1, the electricity demand is 67.4 GWh in 2011, and its 42.6% can be satisfied while building a tidal power plant with the helical blade turbines.
7.2. Tidal Power Plant Design with Other Turbines
Since the helical blade turbines cannot supply enough electricity to Matsu, two more ideas are brought out: designing a Matsu tidal power plant with a vertical axis turbine with variable pitch angles or a horizontal axis turbine.
(1) Vertical axis turbine with passive variable pitch angle
This turbine uses passive variable blades to change the blade pitch angle in order to achieve the best angle of attack. According to the airfoil characteristic, the variable pitch angle turbine keeps the airfoil at the position of the largest lift by adjusting the blade pitch angle, providing the maximum tangent force for maximum power production. This type of turbine is also called the Kobold turbine, which was developed by Ponte di Archimede Company in Italy, and completed its full-scale testing at the Strait of Messina, the southwestern of the Italy.
The advantage of this turbine is the low solidity design so that its power coefficient is 5% higher than that of the helical blade turbine, and the variable pitch angle design would further improve the efficiency by about 3%, bringing its overall power coefficient up to around 30%. Though the manufacture cost of the turbine might be about 20% more than a helical blade turbine, the cost of construction should be similar. If turbines with variable pitch angle are used, the tidal power plant can generate 38.6 GWh electricity annually, which would have covered 57% of consumption in Matsu for 2011.
(2) Horizontal axis turbine
This turbine type is different from those described above because the rotor axis runs parallel to the water flow. Since the power coefficient of the horizontal axis turbine is up to 40%, most tidal power plants use the horizontal axis turbine; however, the disadvantage is that the cost of the turbine and construction is higher than with vertical turbines. Another disadvantage is that the horizontal axis turbine can only generate electricity from flow in a specific direction; in other words, it can only generate electricity through one turbine group during water raising and another group during water falling. Hence, its cost is twice as high due to the necessary installation of two turbine groups with opposite directions. If the tidal power plant is to be equipped with horizontal axis turbines, then it is recommended that sluices 2 km long be constructed in Beigan and 1 km in Nangan, where half will be for water raising and the other for water falling. Since the sluice height is assumed to be about 5 m high, the tidal current velocity will be up to 2 m/s. On the other hand, the tidal power plant with a horizontal axis turbine is estimated to generate about 51.5 GWh electricity annually, and could have met 76% of the consumption demand for Matsu in 2011.
8. Conclusion and Discussion
From the 3D simulation, the helical blade turbine is proved better than the traditional straight blade turbine for the reason that it can significantly improve the force and moment vibration during operation. This turbine, made of three helical blades at 120°, can reduce the possibility of material fatigue so that is friendly to generating systems. Consequently, the turbine’s helical blades would lead the flow upward, causing upper blades to take more force than the lower ones, thus increasing the moment about x and y directions of the turbine. Using the CFD data, the solid mechanic properties of the helical blade turbine is further analyzed, and the result shows the turbine can be well supported by the structure steel.
In the comparison of force and moment fluctuation on the various turbine sets without hydrodynamic interactions, the same direction dual turbine with a 60° angle offset has the best performance with minimum forces fluctuation and minimum moment fluctuation about the z axis. Using this dual turbine set, the symmetrical turbine column with zero-angle offset well reduces the moment fluctuation about x and y direction. The force and moment fluctuant ratio of the final turbine set is less than 9%, and one turbine column can generate 587 W electricity in 1.4 m/s water flow.
To estimate the power that can be developed in Matsu, 1900 helical blade turbine sets are expected to be installed in Beigan and Nangan. From the 22.3% power coefficient of the helical blade turbine, the installed capacity of the tidal power plant in Matsu is 88.5 MW, which can generate 28.7 GWh annually and makes up 42.6% of electricity consumption in Matsu in 2011. The helical turbine concludes three twisted blades, and its advantage is that there is no necessity for starter motors; moreover, it operates smoothly with less fluctuation, and its simple mechanism causes low manufactory cost and easy maintenance. However, its low power coefficient cannot supply enough electricity to Matsu. As a result, we analyze two other cases. While designing a Matsu tidal power plant with a vertical axis turbine with variable pitch angles, 38.6GWh electricity would be generated; however, that with a horizontal axis turbine would be estimated for 51.5GWh electricity annually.
According to the survey undertaken for this study of seven renewable energy reserves in Matsu, tidal energy is the only renewable source that has enough reserves and economic potential. For this purpose, building a dam in Beigan and Nangan is recommended.