Development and Use of Tide Models in Alaska Supporting VDatum and Hydrographic Surveying
Abstract
:1. Introduction

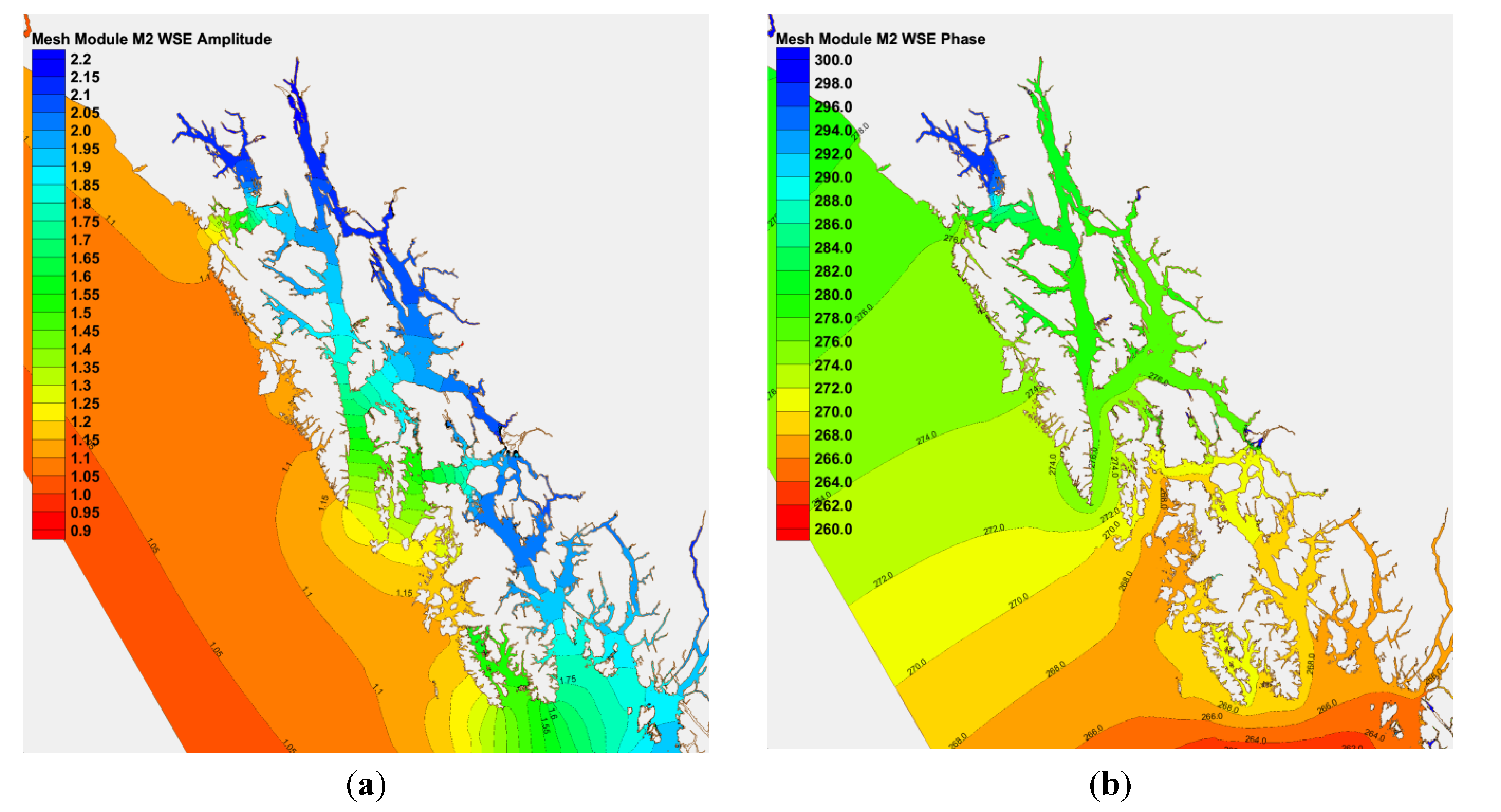
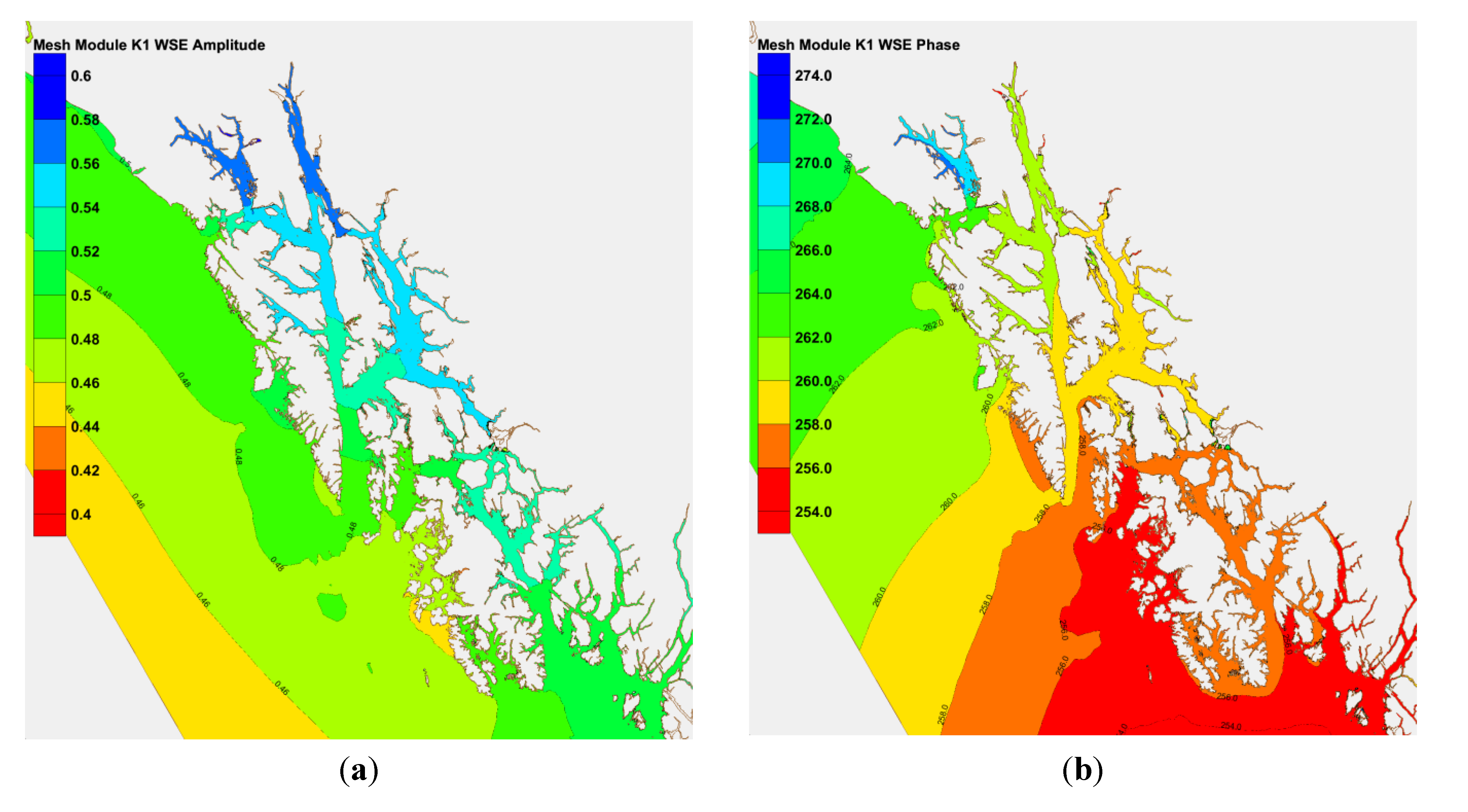
2. Tidal Modeling in SE Alaska
2.1. Model Development
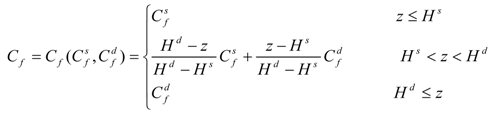
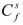 and
and 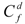 are constant bottom friction coefficients for water shallower than Hs and water deeper than Hd, respectively. Equation 1 provides a depth-dependent linear interpolated bottom friction for water depths between Hs and Hd. In this study, we use Cf = Cf (0.00375,0.00375), a constant over all depths, for the baseline study, and variable Cf scenarios are examined in sensitivity tests. The open boundary is forced by prescribed tidal information interpolated from Oregon State University’s Pacific Ocean basin scale tidal solution PO2009 [17]. The tidal forcing along the open boundary consisted of four semidiurnal constituents (M2, S2, N2 and K2), four diurnal constituents (K1, O1, P1 and Q1) and three shallow water components (M4, MS4 and MN4). The model has wetting and drying enabled, so as to cope with tidal flat scenarios.
are constant bottom friction coefficients for water shallower than Hs and water deeper than Hd, respectively. Equation 1 provides a depth-dependent linear interpolated bottom friction for water depths between Hs and Hd. In this study, we use Cf = Cf (0.00375,0.00375), a constant over all depths, for the baseline study, and variable Cf scenarios are examined in sensitivity tests. The open boundary is forced by prescribed tidal information interpolated from Oregon State University’s Pacific Ocean basin scale tidal solution PO2009 [17]. The tidal forcing along the open boundary consisted of four semidiurnal constituents (M2, S2, N2 and K2), four diurnal constituents (K1, O1, P1 and Q1) and three shallow water components (M4, MS4 and MN4). The model has wetting and drying enabled, so as to cope with tidal flat scenarios. 2.2. Model Validation

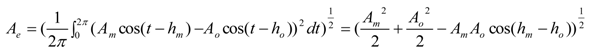
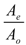 , will measure the relative model performance across the different tidal constituents. Mean RMSE and mean relative RMSE are the average RMSE and relative RMSE values over 43 tidal stations for one tidal constituent. The total mean RMSE (cm),
, will measure the relative model performance across the different tidal constituents. Mean RMSE and mean relative RMSE are the average RMSE and relative RMSE values over 43 tidal stations for one tidal constituent. The total mean RMSE (cm), 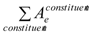 , measures the RMSE of all tidal constituents.
, measures the RMSE of all tidal constituents.| Amplitude error, MAE (cm) | Phase error, MAE (degree) | Mean RMSE (cm) | Mean relative RMSE (%) | |
|---|---|---|---|---|
| M2 | 8.29 | 2.93 | 9.47 | 5.5 |
| S2 | 3.81 | 2.61 | 3.68 | 6.6 |
| N2 | 1.63 | 3.53 | 2.14 | 6.3 |
| K2 | 1.14 | 11.80 | 2.56 | 16.4 |
| K1 | 2.96 | 4.71 | 3.90 | 7.9 |
| O1 | 2.41 | 5.56 | 2.91 | 9.7 |
| P1 | 0.62 | 6.03 | 1.35 | 8.3 |
| Q1 | 0.31 | 3.82 | 0.38 | 6.6 |
| M4 | 1.82 | 26.11 | 1.60 | 54.4 |
| Total | 28.7 |
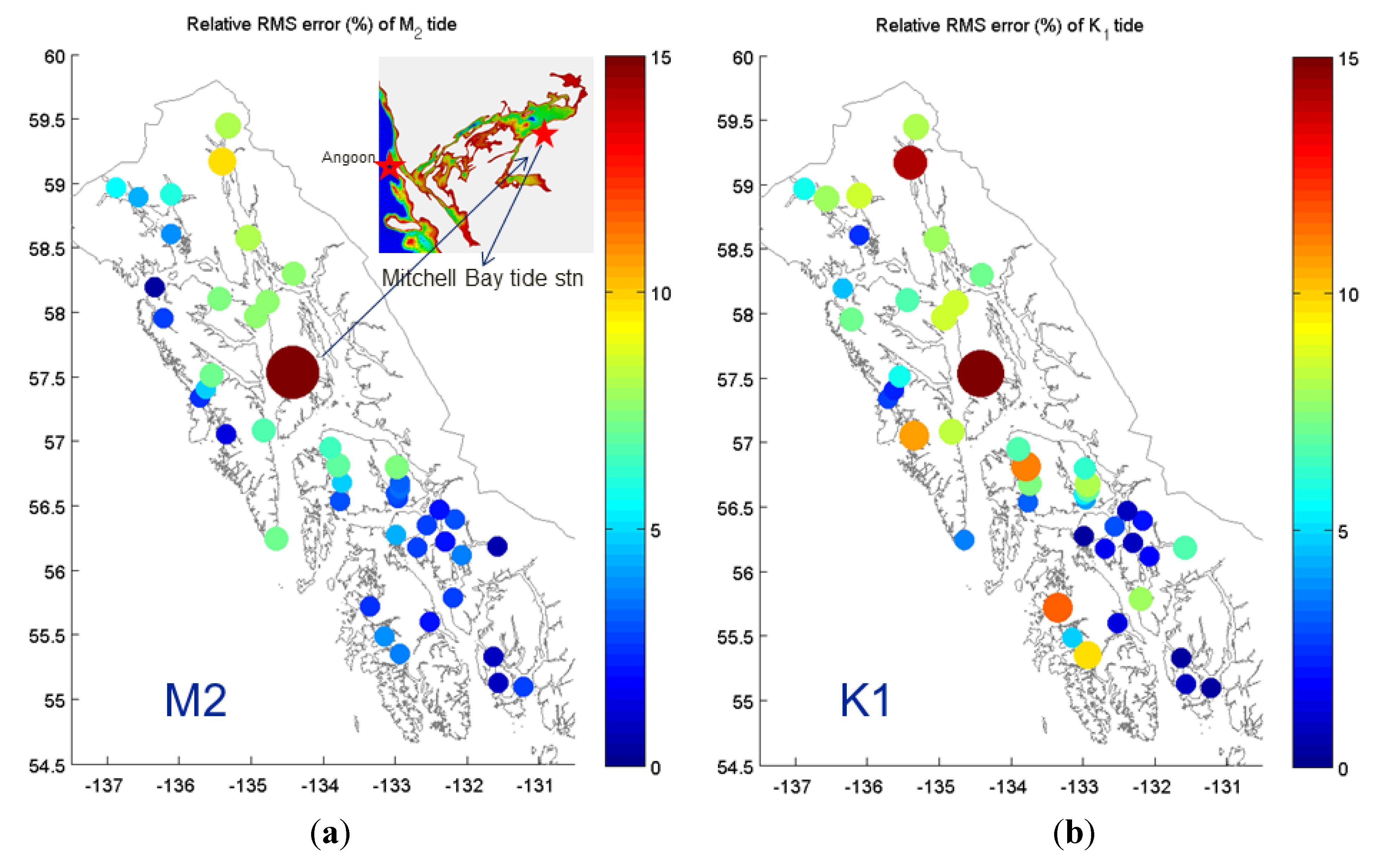
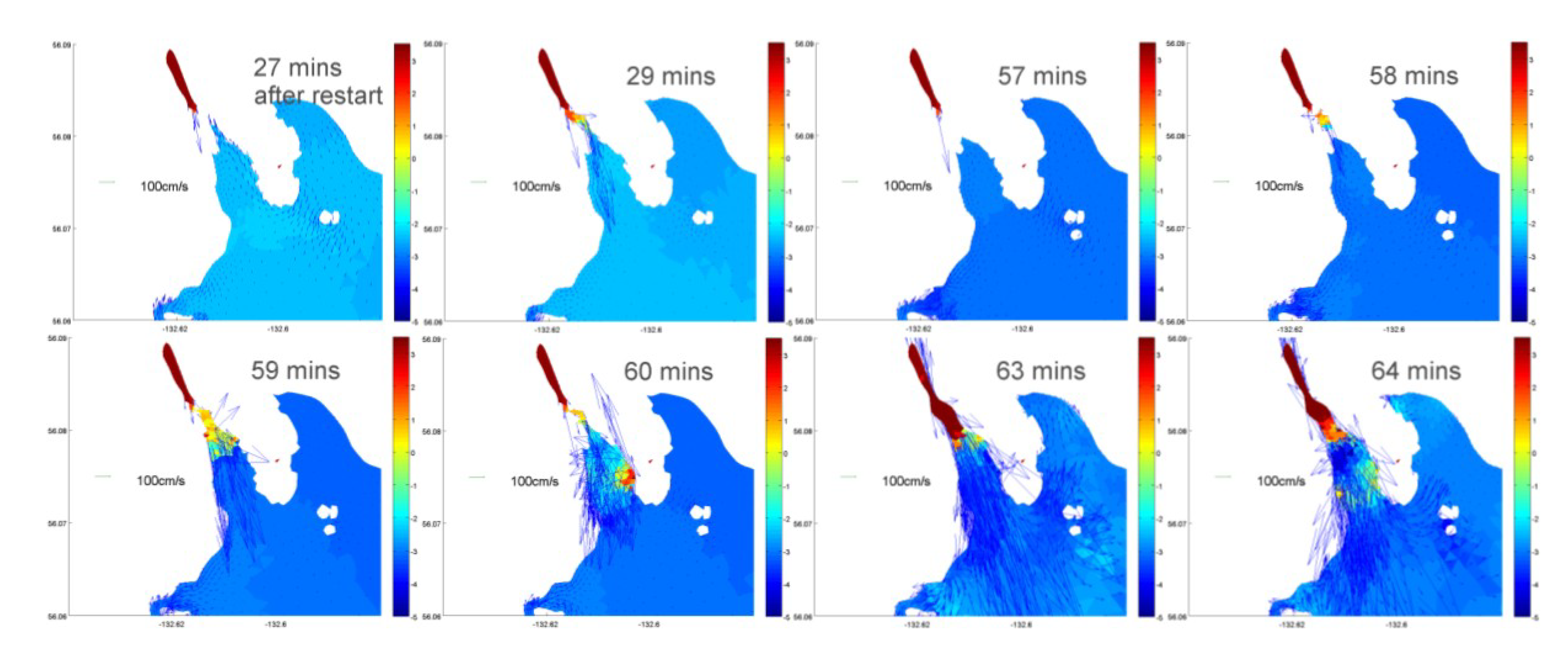
2.3. Discussion
3. Use of Existing Tide Model Outputs in Western Alaska to Support Hydrographic Surveys
3.1. Introduction
3.2. Methods and Results
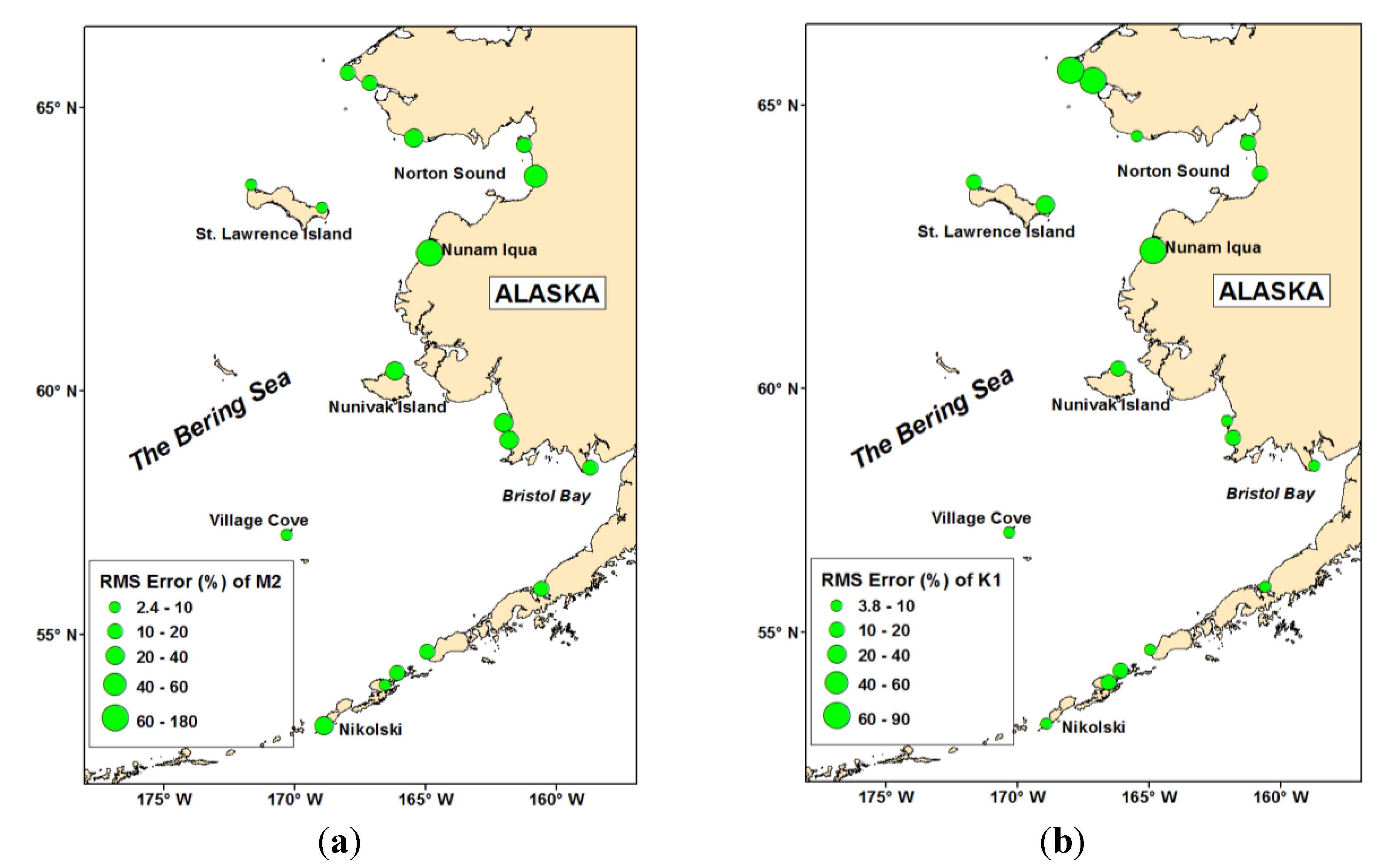
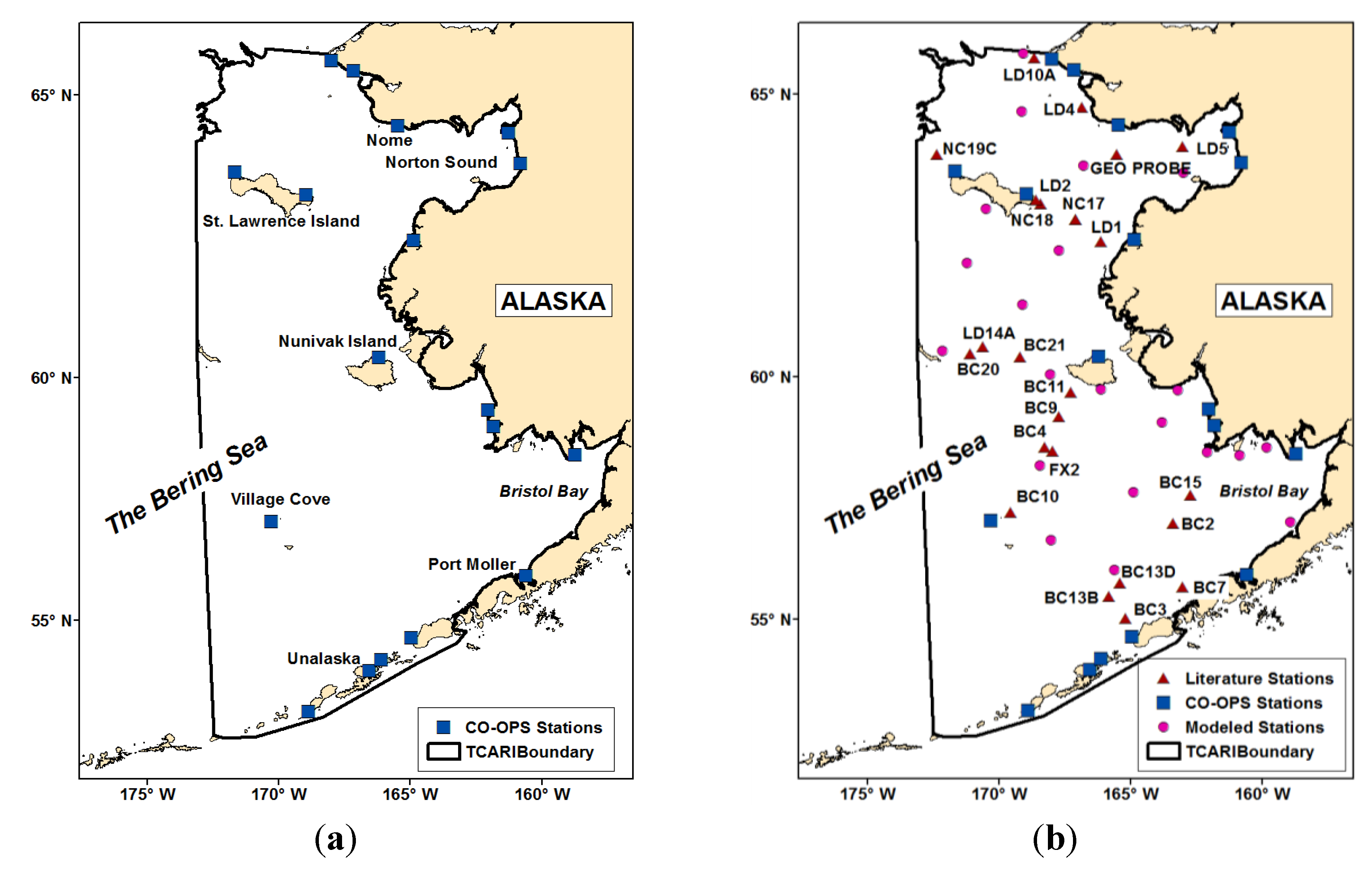
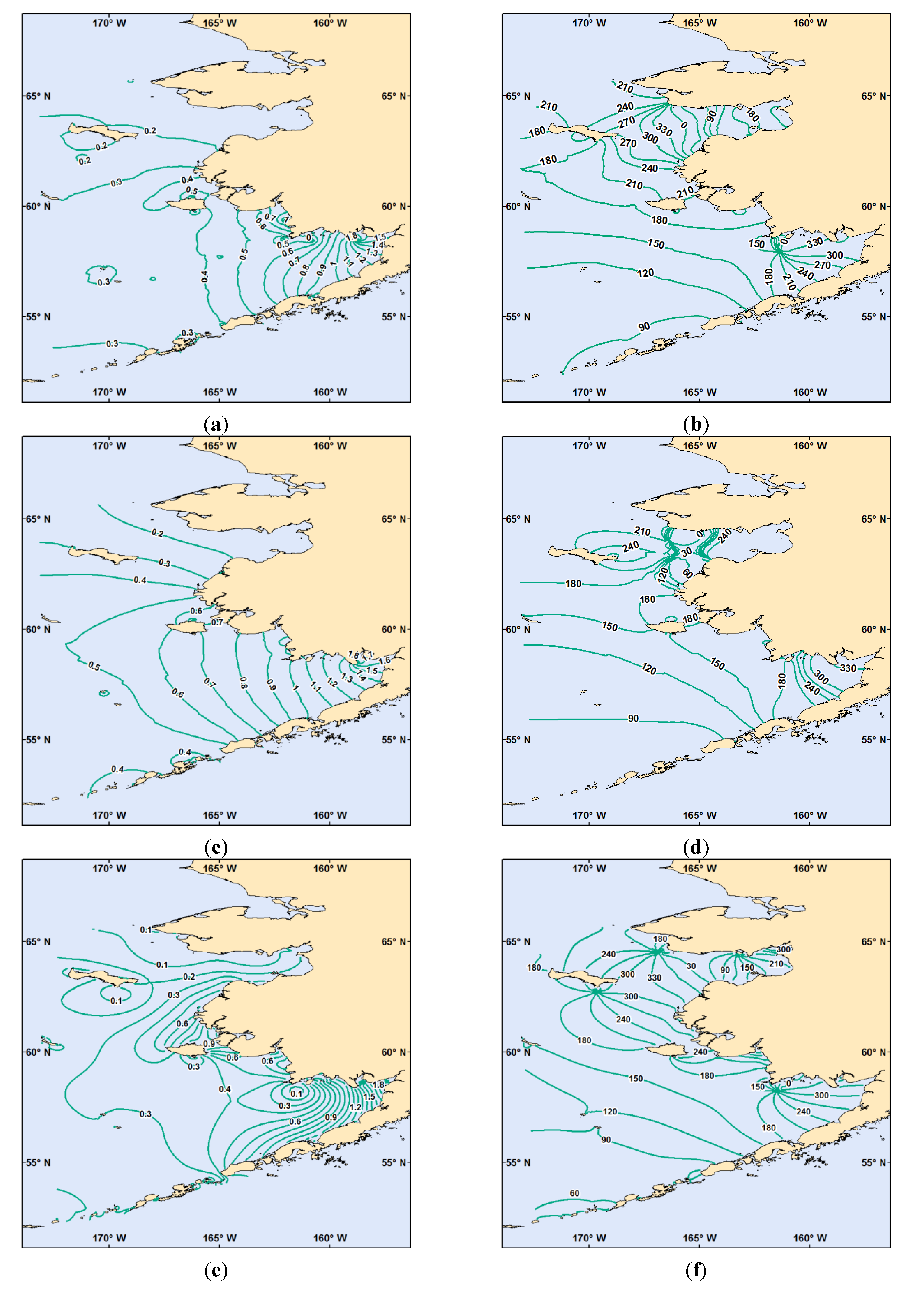
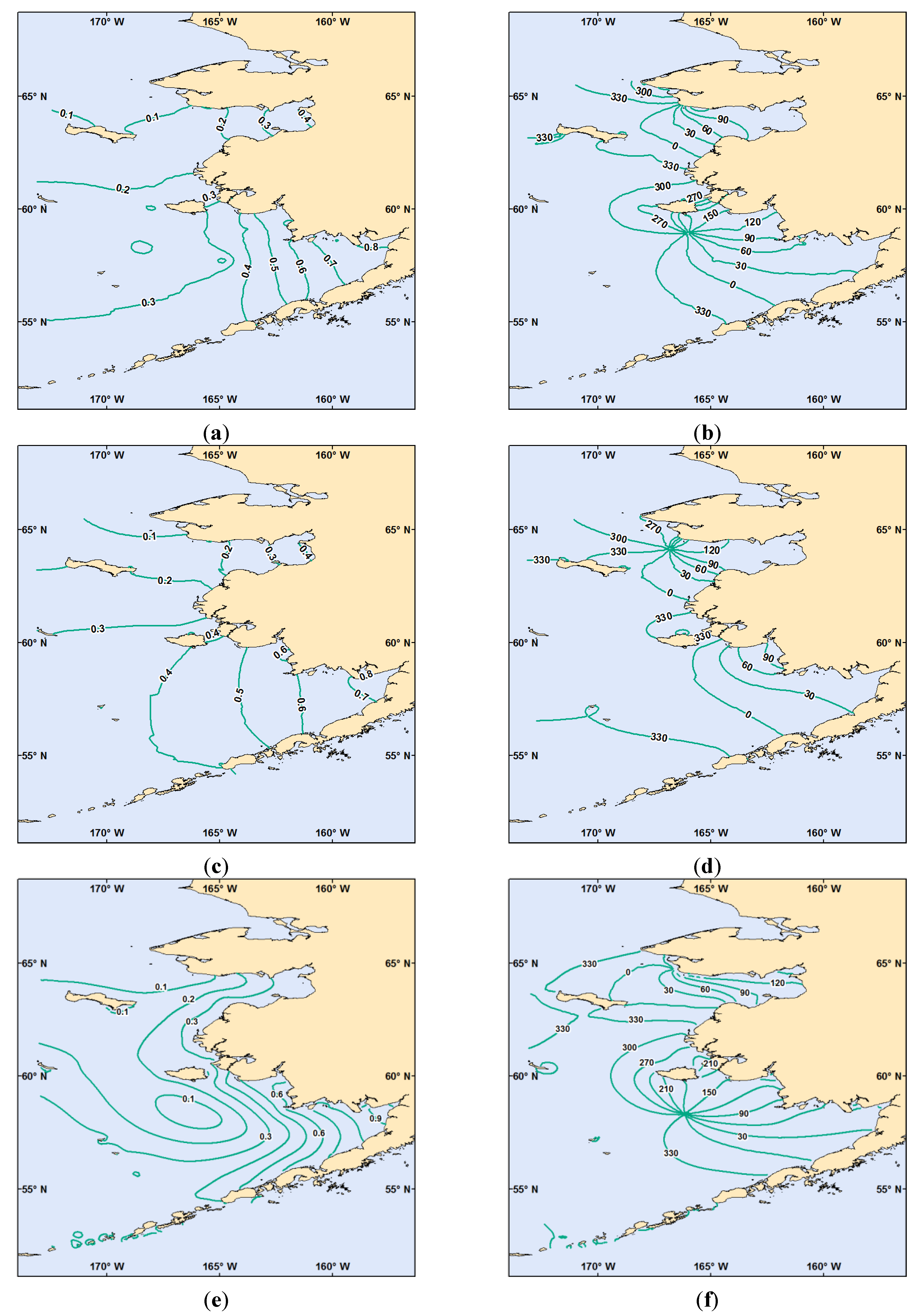
3.3. Discussion
| Station | Latitude (°N) | Longitude (°W) | Amplitude (cm) | Phase (°) | RMSE (cm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OBS | FM | TO | TOF | OBS | FM | TO | TOF | FM | TO | TOF | |||
| BC20 | 60.43 | 171.08 | 20.5 | 26.4 | 48.7 | 31.0 | 171.0 | 169.9 | 144.8 | 177.0 | 4.1 | 44.3 | 7.7 |
| BC3 | 55.02 | 165.17 | 41.9 | 42.7 | 52.0 | 39.8 | 89.0 | 84.5 | 79.3 | 89.5 | 2.4 | 22.3 | 1.5 |
| BC13B | 55.50 | 165.82 | 35.5 | 37.3 | 54.9 | 38.7 | 106.0 | 99.1 | 86.2 | 102.2 | 3.4 | 30.0 | 2.9 |
| BC13D | 55.78 | 165.38 | 39.0 | 41.0 | 59.8 | 40.6 | 109.0 | 109.3 | 91.6 | 108.8 | 1.4 | 33.7 | 1.1 |
| BC10 | 57.28 | 169.55 | 24.9 | 28.9 | 47.1 | 30.7 | 131.0 | 119.4 | 98.3 | 117.1 | 4.7 | 32.9 | 6.2 |
| BC4 | 58.62 | 168.23 | 33.4 | 35.7 | 57.7 | 35.1 | 151.0 | 145.0 | 121.3 | 151.8 | 3.0 | 46.4 | 1.2 |
| FX2 | 58.53 | 167.93 | 33.8 | 35.7 | 58.8 | 35.0 | 158.0 | 145.0 | 121.9 | 151.0 | 5.7 | 47.3 | 3.1 |
| BC9 | 59.22 | 167.70 | 36.7 | 38.1 | 59.8 | 36.1 | 164.0 | 157.3 | 135.8 | 169.9 | 3.3 | 53.0 | 2.7 |
| BC11 | 59.70 | 167.25 | 35.9 | 38.3 | 60.8 | 37.0 | 155.0 | 161.1 | 146.2 | 182.5 | 3.2 | 57.0 | 12.3 |
| BC21 | 60.38 | 169.18 | 30.9 | 36.8 | 51.8 | 35.6 | 189.0 | 186.2 | 152.8 | 185.2 | 4.3 | 51.6 | 3.7 |
| BC7 | 55.70 | 163.02 | 71.4 | 73.2 | 75.1 | 56.5 | 134.0 | 133.0 | 118.6 | 125.9 | 1.5 | 41.5 | 12.3 |
| BC2 | 57.07 | 163.37 | 45.2 | 43.6 | 82.5 | 56.1 | 157.0 | 157.9 | 141.0 | 147.3 | 1.2 | 69.3 | 9.7 |
| BC15 | 57.65 | 162.70 | 36.2 | 33.7 | 90.9 | 58.2 | 168.0 | 170.9 | 156.5 | 157.1 | 2.2 | 80.3 | 16.8 |
| LD1 | 62.50 | 166.12 | 46.1 | 44.2 | 30.3 | 22.9 | 328.0 | 325.0 | 76.3 | 327.0 | 2.2 | 17.7 | 16.4 |
| NC17 | 62.88 | 167.08 | 25.6 | 25.8 | 29.7 | 21.7 | 330.0 | 322.7 | 200.2 | 298.8 | 2.3 | 39.1 | 9.4 |
| NC18 | 63.15 | 168.38 | 22.4 | 20.2 | 30.4 | 21.1 | 324.0 | 314.9 | 246.7 | 272.3 | 2.8 | 34.7 | 13.5 |
| LD2 | 63.22 | 168.58 | 26.6 | 22.0 | 30.2 | 21.5 | 319.0 | 313.4 | 253.9 | 271.0 | 3.6 | 36.8 | 14.2 |
| LD4 | 64.78 | 166.83 | 4.9 | 3.8 | 16.9 | 12.9 | 138.0 | 162.7 | 191.8 | 219.4 | 1.5 | 15.4 | 9.2 |
| GEO PROBE | 64.00 | 165.50 | 13.0 | 11.4 | 18.4 | 14.4 | 44.0 | 32.5 | 35.4 | 15.6 | 2.1 | 5.7 | 4.8 |
| LD5 | 64.13 | 163.00 | 2.0 | 5.6 | 17.9 | 15.9 | 233.0 | 162.0 | 230.3 | 168.4 | 3.7 | 13.7 | 10.7 |
| LD14A | 60.57 | 170.60 | 21.9 | 27.8 | 48.8 | 31.3 | 180.0 | 177.0 | 149.0 | 181.1 | 4.3 | 45.5 | 6.6 |
| NC17C | 62.88 | 167.07 | 25.5 | 25.9 | 29.6 | 21.7 | 336.0 | 323.0 | 198.4 | 299.1 | 4.1 | 38.9 | 10.9 |
| NC19C | 64.00 | 172.33 | 23.5 | 25.2 | 28.5 | 20.3 | 172.0 | 181.9 | 201.7 | 200.4 | 3.2 | 36.8 | 7.9 |
| LD10A | 65.58 | 168.63 | 7.6 | 9.8 | 16.0 | 11.3 | 202.0 | 211.7 | 199.8 | 208.3 | 1.8 | 16.6 | 2.7 |
| Average | 3.0 | 37.9 | 7.8 | ||||||||||
| Station | Latitude (°N) | Longitude (°W) | Amplitude (cm) | Phase (°) | RMSE (cm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OBS | FM | TO | TOF | OBS | FM | TO | TOF | FM | TO | TOF | |||
| BC20 | 60.43 | 171.08 | 18.1 | 19.7 | 30.5 | 21.5 | 326.0 | 322.8 | 337.6 | 315.6 | 1.4 | 9.4 | 3.5 |
| BC3 | 55.02 | 165.17 | 40.9 | 42.2 | 42.8 | 36.5 | 319.0 | 315.6 | 322.3 | 323.7 | 2.0 | 2.2 | 3.8 |
| BC13B | 55.50 | 165.82 | 34.4 | 36.9 | 43.0 | 34.2 | 325.0 | 323.7 | 329.3 | 328.6 | 1.9 | 6.4 | 1.5 |
| BC13D | 55.78 | 165.38 | 33.4 | 35.9 | 44.6 | 34.6 | 327.0 | 327.9 | 334.0 | 333.0 | 1.8 | 8.6 | 2.7 |
| BC10 | 57.28 | 169.55 | 24.9 | 26.9 | 36.7 | 25.8 | 333.0 | 327.8 | 332.8 | 322.3 | 2.2 | 8.4 | 3.4 |
| BC4 | 58.62 | 168.23 | 12.4 | 12.4 | 38.1 | 20.8 | 303.0 | 301.1 | 339.7 | 310.4 | 0.3 | 20.6 | 6.1 |
| FX2 | 58.53 | 167.93 | 8.9 | 11.0 | 38.8 | 21.3 | 288.0 | 299.7 | 340.9 | 313.1 | 2.1 | 24.2 | 9.7 |
| BC9 | 59.22 | 167.70 | 9.7 | 10.8 | 37.9 | 22.7 | 258.0 | 255.1 | 342.9 | 290.8 | 0.9 | 27.1 | 10.9 |
| BC11 | 59.70 | 167.25 | 18.3 | 18.0 | 37.3 | 22.5 | 207.0 | 219.2 | 343.1 | 263.9 | 2.7 | 36.8 | 14.0 |
| BC21 | 60.38 | 169.18 | 16.6 | 18.2 | 31.4 | 20.5 | 297.0 | 296.6 | 336.7 | 298.5 | 1.1 | 15.2 | 2.8 |
| BC7 | 55.70 | 163.02 | 49.0 | 51.8 | 50.8 | 44.0 | 335.0 | 331.7 | 348.4 | 352.2 | 2.9 | 8.3 | 10.4 |
| BC2 | 57.07 | 163.37 | 28.3 | 27.9 | 52.4 | 43.1 | 13.0 | 13.7 | 3.9 | 19.0 | 0.3 | 17.6 | 10.8 |
| BC15 | 57.65 | 162.70 | 29.9 | 31.5 | 55.5 | 49.5 | 48.0 | 49.0 | 20.6 | 43.7 | 1.2 | 22.7 | 14.0 |
| LD1 | 62.50 | 166.12 | 31.7 | 30.9 | 20.6 | 17.9 | 324.0 | 333.6 | 16.6 | 356.5 | 3.8 | 17.8 | 13.6 |
| NC17 | 62.88 | 167.08 | 19.0 | 19.2 | 19.4 | 16.2 | 341.0 | 347.9 | 10.6 | 353.1 | 1.6 | 6.9 | 3.3 |
| NC18 | 63.15 | 168.38 | 8.9 | 11.7 | 17.3 | 13.6 | 356.0 | 358.6 | 358.8 | 349.5 | 2.0 | 6.0 | 3.4 |
| LD2 | 63.22 | 168.58 | 8.1 | 10.9 | 16.6 | 13.0 | 359.0 | 4.5 | 358.7 | 350.5 | 2.1 | 6.0 | 3.6 |
| LD4 | 64.78 | 166.83 | 4.2 | 0.9 | 9.9 | 7.9 | 222.0 | 7.4 | 264.4 | 320.1 | 3.5 | 5.2 | 6.7 |
| GEO PROBE | 64.00 | 165.50 | 14.0 | 13.3 | 16.7 | 16.0 | 71.0 | 63.4 | 118.4 | 74.6 | 1.4 | 8.9 | 1.6 |
| LD5 | 64.13 | 163.00 | 32.1 | 26.6 | 28.8 | 30.2 | 110.0 | 119.2 | 112.1 | 98.5 | 5.1 | 2.4 | 4.6 |
| LD14A | 60.57 | 170.60 | 17.2 | 18.9 | 30.2 | 20.8 | 322.0 | 318.2 | 337.8 | 312.7 | 1.5 | 10.2 | 3.4 |
| NC17C | 62.88 | 167.07 | 18.5 | 19.3 | 19.4 | 16.2 | 346.0 | 348.0 | 10.8 | 353.3 | 0.7 | 5.8 | 2.2 |
| NC19C | 64.00 | 172.33 | 9.9 | 11.4 | 14.3 | 10.9 | 328.0 | 329.7 | 326.9 | 334.5 | 1.1 | 3.1 | 1.1 |
| LD10A | 65.58 | 168.63 | 2.7 | 3.3 | 6.6 | 4.5 | 359.0 | 322.6 | 276.1 | 304.3 | 1.4 | 4.8 | 2.6 |
| Average | 1.9 | 11.9 | 5.8 | ||||||||||
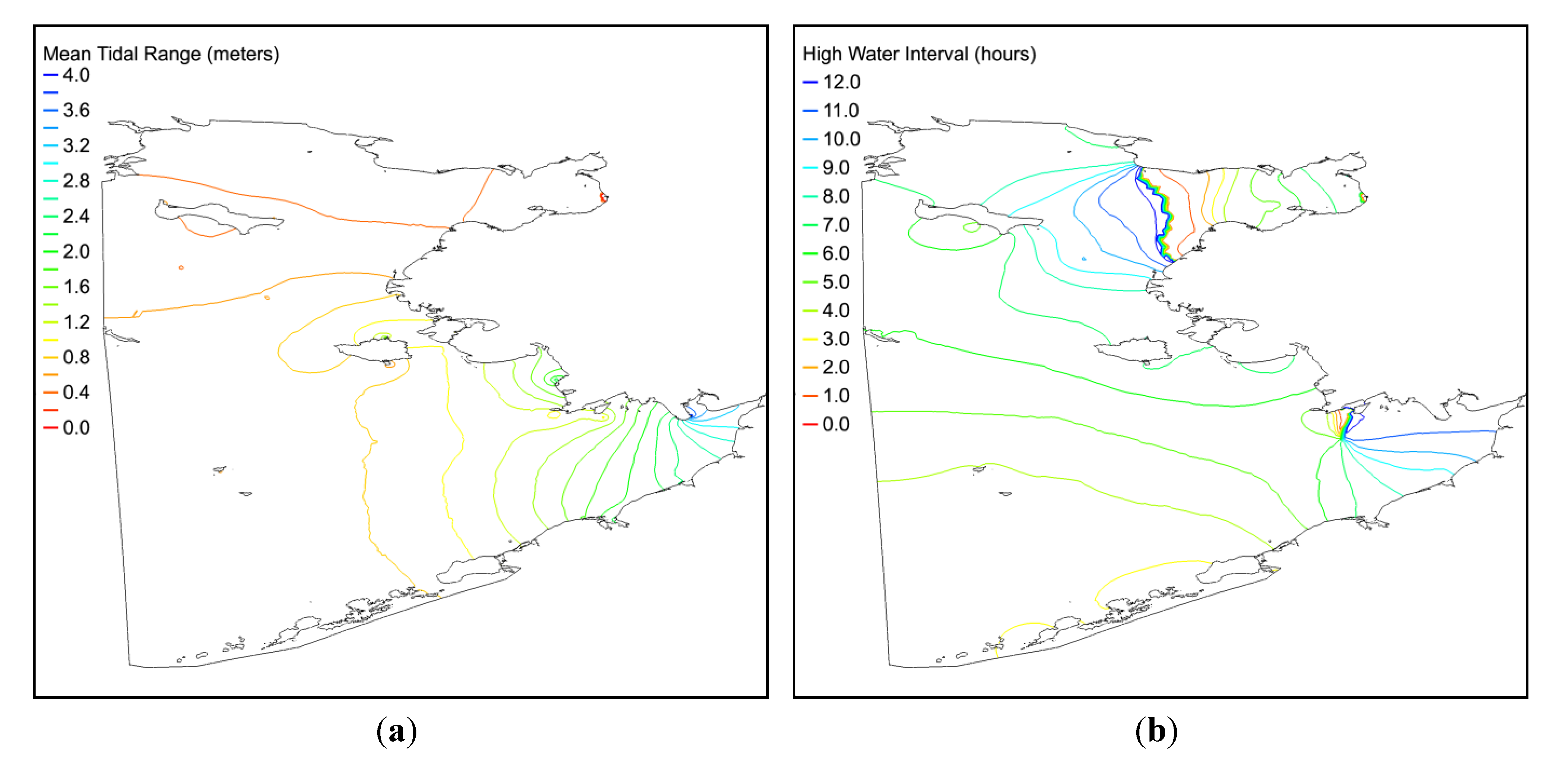
4. Summary and Future Work
Acknowledgments
Conflicts of Interest
References
- Parker, B.B.; Hess, K.W.; Milbert, D.G.; Gill, S. A national vertical datum transformation tool. Sea Technol. 2003, 44, 10–15. [Google Scholar]
- Vertical datum transformation. Available online: http://vdatum.noaa.gov/docs/standardprocedures.html (accessed on 18 Febuary 2014).
- Luettich, R.A., Jr.; Westerink, J.J.; Scheffner, N.W. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves Coasts and Estuaries, Report 1: Theory and Methodology of ADCIRC-2DDI and ADCIRC-3DL; Dredging Research Program Technical Report DRP-92-6; U.S. Army Engineers Waterways Experiment Station: Vicksburg, MS, USA, 1992; p. 137. [Google Scholar]
- Westerink, J.J.; Blain, C.A.; Luettich, R.A., Jr.; Scheffner, N.W. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves Coasts and Estuaries, Report 2: Users Manual for ADCIRC-2DDI; Dredging Research Program Technical Report DRP-92-6; U.S. Army Engineers Waterways Experiment Station: Vicksburg, MS, USA, 1994; p. 156. [Google Scholar]
- Foreman, M.G.G.; Crawford, W.R.; Cherniawsky, J.Y.; Henry, R.F.; Tarbotton, M.R. A high-resolution assimilating tidal model for the northeast Pacific Ocean. J. Geophys. Res. 2000, 105, 28629–28651. [Google Scholar] [CrossRef]
- Myers, E.P.; Baptista, A.M. Inversion for tides in the Eastern North Pacific Ocean. Adv. Water Resour. 2001, 24, 505–519. [Google Scholar] [CrossRef]
- Spargo, E.A.; Westerink, J.J.; Luettich, R.A.; Mark, D.J. ENPAC 2003: A Tidal Constituent Database for the Eastern North Pacific Ocean; Department of the Army Technical Note TR-04-12; U.S. Army Corps of Engineers: Washington, DC, USA, 2004. [Google Scholar]
- Hill, D.F.; Ciavola, S.J.; Etherington, L.; Klaar, M.J. Estimation of freshwater runoff into Glacier Bay, Alaska and incorporation into a tidal circulation model. Estuar. Coast. Shelf Sci. 2009, 82, 95–107. [Google Scholar] [CrossRef]
- Inazu, D.; Sato, T.; Miura, S.; Ohta, Y.; Nakamura, K. Accurate ocean tide modeling in southeast Alaska and large tidal dissipation around Glacier Bay. J. Oceanogr. 2009, 65, 335–347. [Google Scholar] [CrossRef]
- Egbert, G.D.; Bennett, A.F.; Foreman, M.G.G. TOPEX/POSEIDON tides estimated using a global inverse model. J. Geophys. Res. 1994, 99, 24821–24852. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Oceanic Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Carrère, L.; Lyard, F.; Cancet, M.; Guillot, A.; Roblou, L. FES2012: A New Global Tidal Model Taking Advantage of Nearly 20 Years of Altimetry. In Proceedings of the Meeting 20 Years of Altimetry, Venice, Italy, 24–29 September 2012.
- Myers, E.P.; Yang, Z.; Xu, J.; Hess, K.W.; Dhingra, E. Tide Modeling in Support of NOAA’s National VDatum Program. In Estuarine and Coastal Modeling, Proceedings of 11th International Conference on Estuarine and Coastal Modeling, Seattle, WA, USA, 4–6 November 2009; Spaulding, M.L., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2010; pp. 514–526. [Google Scholar]
- Liu, S.K.; Leendertse, J.J. Three-dimensional model of bering and chukchi sea. Coast. Eng. 1982, 18, 598–616. [Google Scholar]
- Kowalik, Z. Bering Sea Tides. In Dynamics of the Bering Sea; Loughlin, T.R., Ohtani, K., Eds.; University of Alaska Sea Grant: Fairbanks, AK, USA, 1999; pp. 93–127. [Google Scholar]
- Foreman, M.G.G.; Cummins, P.F.; Cherniawsky, J.Y.; Stabeno, P. Tidal energy in the Bering Sea. J. Mar. Res. 2006, 64, 797–818. [Google Scholar]
- OSU tidal data inversion. Available online: http://volkov.oce.orst.edu/tides (accessed on 18 Febuary 2014).
- NOAA NGDC. Integrated Models of Coastal Relief. Available online: http://www.ngdc.noaa.gov/mgg/coastal/coastal.html (accessed on 18 Febuary 2014).
- Amante, C.; Eakins, B.W. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; National Geophysical Data Center Marine Geology and Geophysics Division: Boulder, CO, USA, 2009; p. 19. [Google Scholar]
- Caldwell, R.J.; Eakins, B.W.; Taylor, L.A.; Carigna, K.S.; Collins, S. Digital Elevation Models of Southeast Alaska: Procedures, Data Sources and Analysis; National Geophysical Data Center Marine Geology and Geophysics Division: Boulder, CO, USA, 2010; p. 67. [Google Scholar]
- ADCIRC Related Publications. Available online: http://adcirc.org/home/documentation/adcirc-related-publications (accessed on 18 Febuary 2014).
- NOAA/NOS/CO-OPS—ODIN MAP. Available online: http://tidesandcurrents.noaa.gov/gmap3/index.shtml?type=TidePredictions®ion= (accessed on 18 Febuary 2014).
- Lefèvre, F.; le Provost, C.; Lyard, F.H. How can we improve a global ocean tide model at a regional scale? A test on the Yellow Sea and the East China Sea. J. Geophys. Res. 2000, 105, 8707–8726. [Google Scholar] [CrossRef]
- Foreman, M.G.G.; Henry, R.F.; Walters, R.A.; Ballantyne, V.A. A finite element model for tides and resonance along the north coast of British Columbia. J. Geophys. Res. 1993, 98, 2509–2531. [Google Scholar] [CrossRef]
- Egbert, G.D.; Ray, R.D. Semi-diurnal and diurnal tidal dissipation from Topex/Poseidon altimetry. Geophys. Res. Lett. 2003, 30, 1907. [Google Scholar] [CrossRef]
- Hess, K.W. Spatial interpolation of tidal data in irregularly-shaped coastal regions by numerical solution of Laplace’s equation. Estuar. Coast. Shelf Sci. 2002, 54, 175–192. [Google Scholar] [CrossRef]
- Hess, K.W. Water level simulation in bays by spatial interpolation of tidal constituents, residual water levels, and datums. Cont. Shelf Res. 2003, 23, 395–414. [Google Scholar] [CrossRef]
- Lindley, C.; Urizar, C.; Wolcott, D.; Yang, H.; Huang, L. Vertical Control and Tide Reducers in Tidal to Non-Tidal Transitional Areas. In Proceedings of the U.S. Hydro2013 Conference, The Hydrographic Society of America, New Orleans, LA, USA, 25–28 March 2013.
- Pearson, C.A.; Mofjeld, H.O.; Tripp, R.B. Tides of the Eastern Bering Sea Shelf. In The Eastern Bering Sea Shelf: Oceanography and Resources; Hood, D.W., Calder, J.A., Eds.; University of Washington Press: Seattle, WA, USA, 1981; pp. 111–130. [Google Scholar]
- Mofjeld, H.O. Observed Tides on the Northeastern Bering Sea Shelf. J. Geophys. Res. 1986, 91, 2593–2606. [Google Scholar] [CrossRef]
- C&GS. Manual of Harmonic Constant Reductions; U.S. Government Printing Office: Washington, DC, USA, 1952; p. 74. [Google Scholar]
- Shi, L.; Hess, K.W.; Myers, E.P. Spatial interpolation of tidal data using a multiple-order harmonic equation for unstructured grids. Int. J. Geosci. 2013, 10, 1425–1437. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shi, L.; Wang, J.; Myers, E.; Huang, L. Development and Use of Tide Models in Alaska Supporting VDatum and Hydrographic Surveying. J. Mar. Sci. Eng. 2014, 2, 171-193. https://doi.org/10.3390/jmse2010171
Shi L, Wang J, Myers E, Huang L. Development and Use of Tide Models in Alaska Supporting VDatum and Hydrographic Surveying. Journal of Marine Science and Engineering. 2014; 2(1):171-193. https://doi.org/10.3390/jmse2010171
Chicago/Turabian StyleShi, Lei, Jindong Wang, Edward Myers, and Lijuan Huang. 2014. "Development and Use of Tide Models in Alaska Supporting VDatum and Hydrographic Surveying" Journal of Marine Science and Engineering 2, no. 1: 171-193. https://doi.org/10.3390/jmse2010171




