Spontaneous Brillouin Scattering Spectrum and Coherent Brillouin Gain in Optical Fibers
Abstract
:1. Introduction
2. Results
2.1. The Scalar Model of Stimulated Brillouin Scattering
2.2. Langevin Noise Initiation
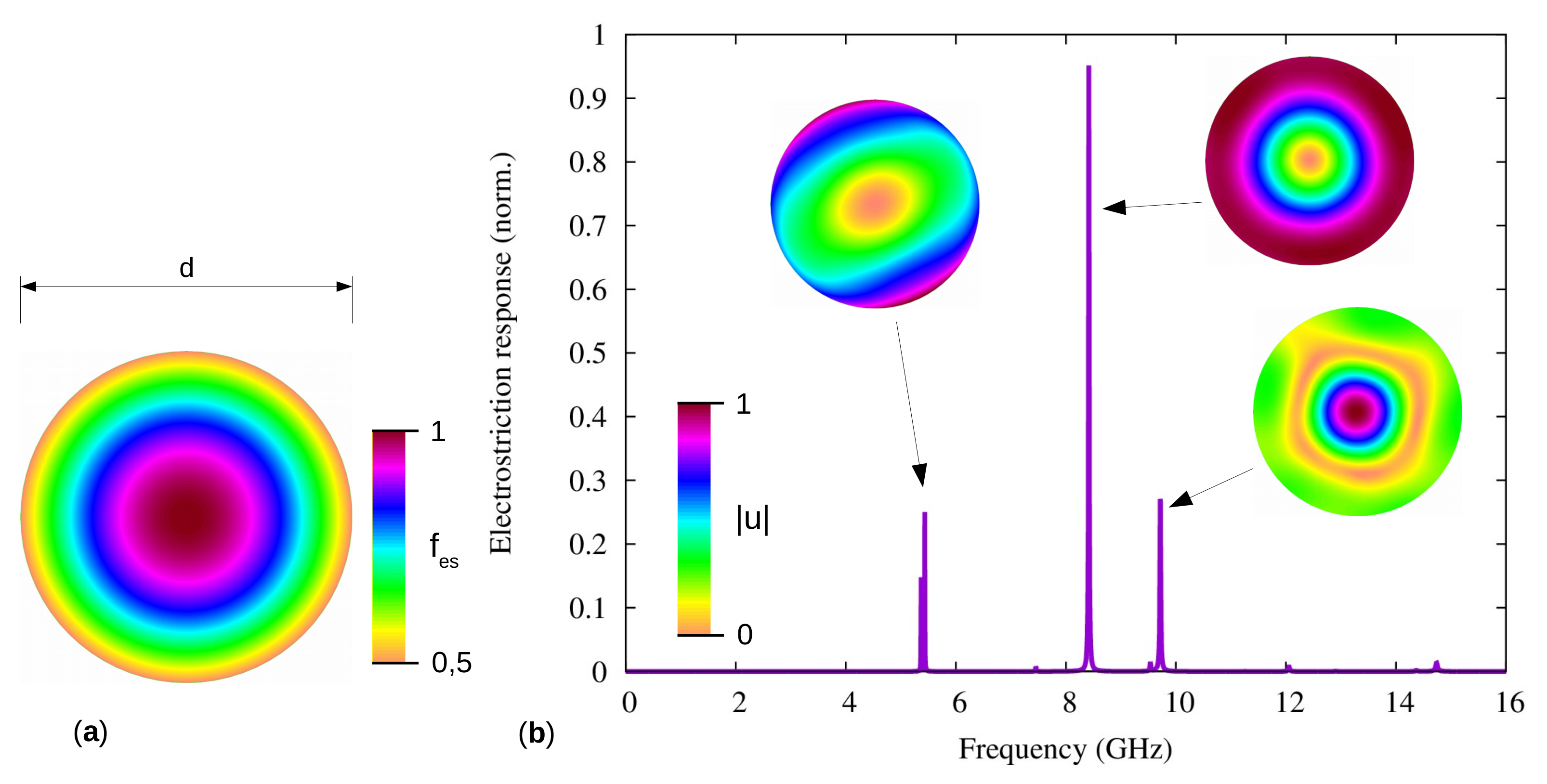
2.3. Elastodynamic Equation and Coherent Response
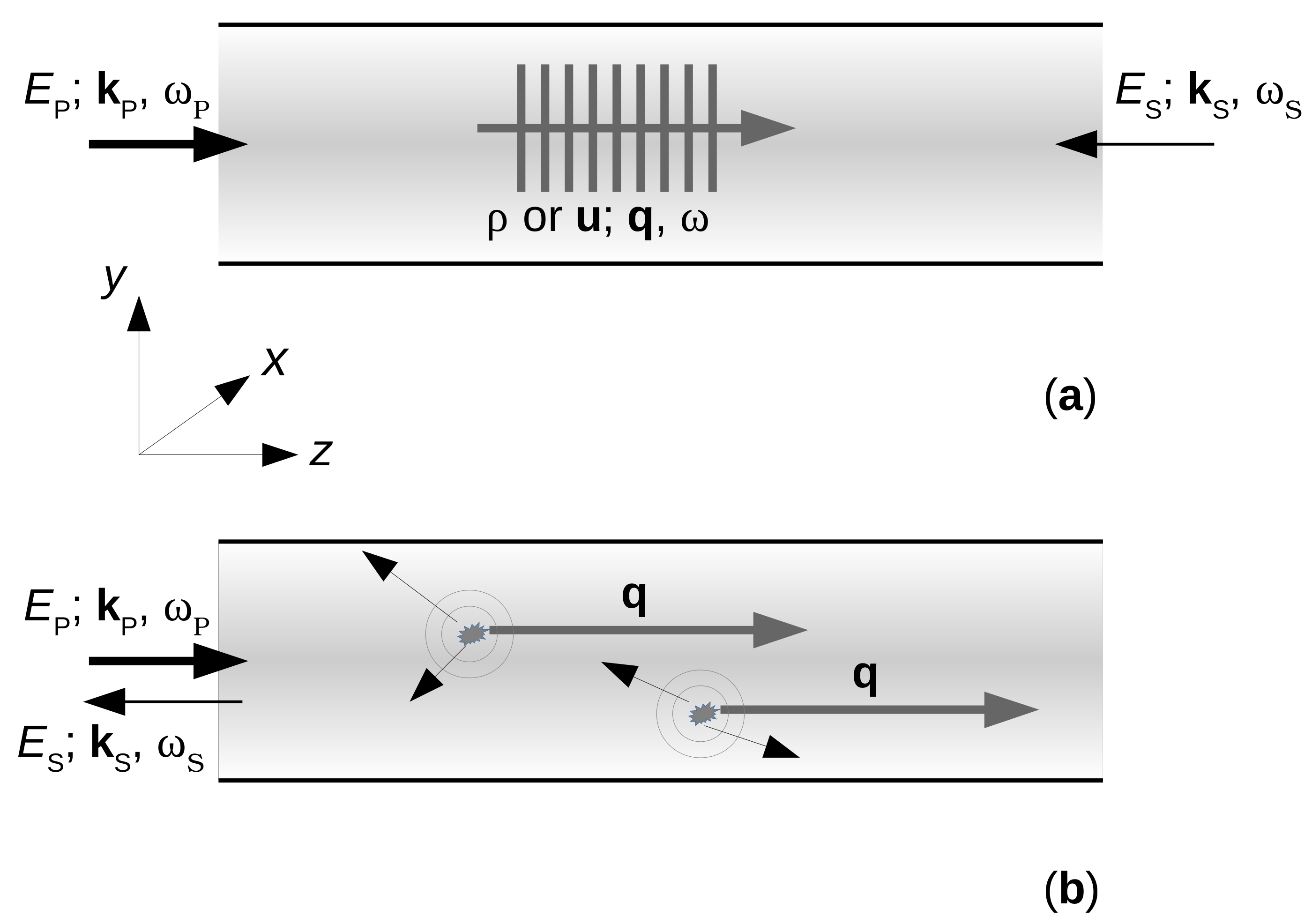
2.4. Spatial Noise Filtering
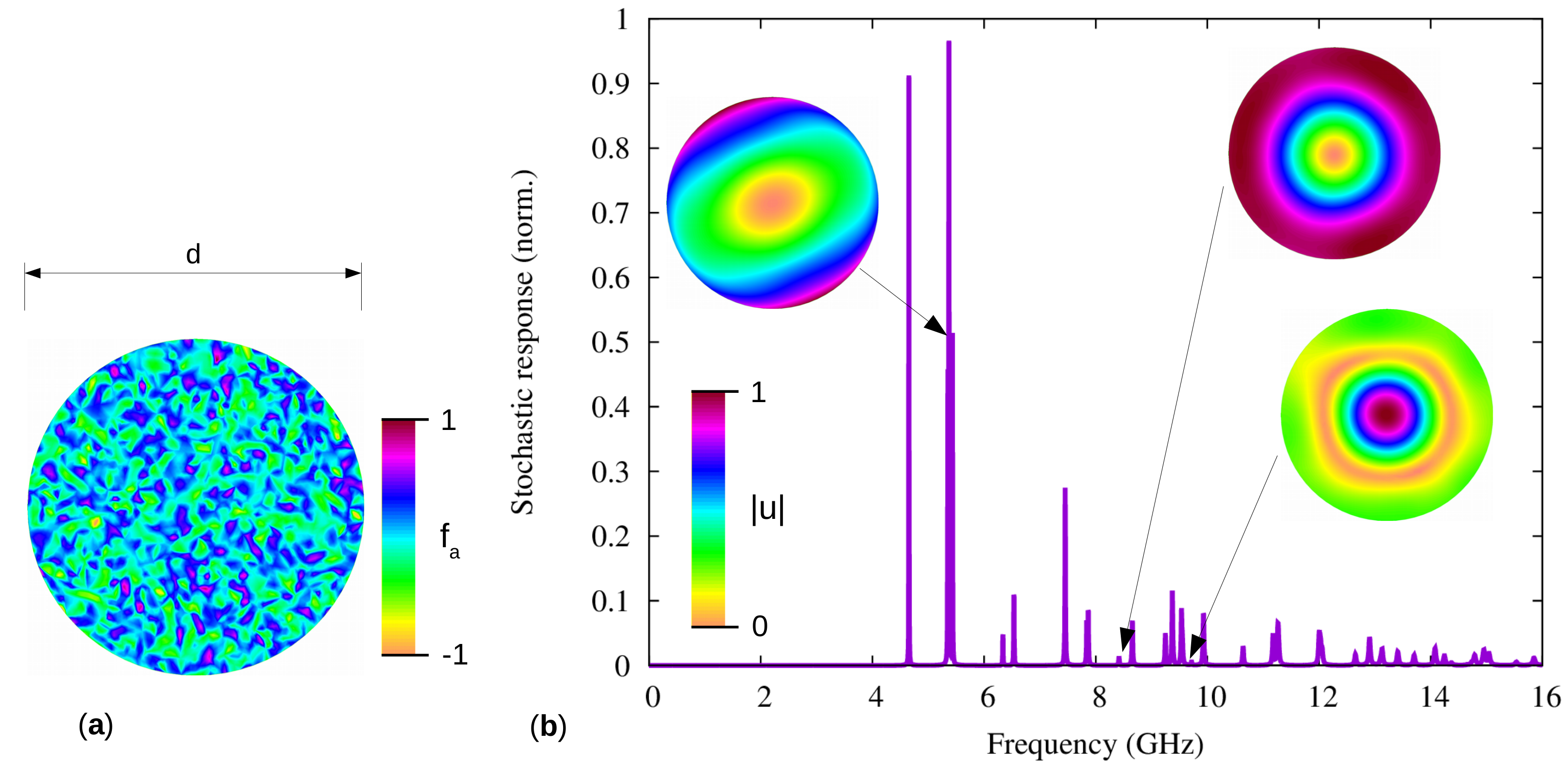
2.4.1. Discrete Spectrum of Guided Phonons
2.4.2. Continuum of Elastic Waves
3. Discussion
4. Methods
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| BLS | Brillouin light scattering |
| FT | Fourier transform |
| GAWBS | Guided acoustic wave Brillouin scattering |
| PSD | Power spectral density |
| SBS | Stimulated Brillouin Scattering |
References
- Brillouin, L. Diffusion de la lumière et des rayons X par un corps transparent homogène. Influence de l’agitation thermique. Ann. Phys. (Paris) 1922, 17, 21. [Google Scholar]
- Chiao, R.Y.; Townes, C.H.; Stoicheff, B.P. Stimulated Brillouin scattering and coherent generation of intense hypersonic waves. Phys. Rev. Lett. 1964, 12, 592–595. [Google Scholar] [CrossRef]
- Elser, D.; Andersen, U.; Korn, A.; Glöckl, O.; Lorenz, S.; Marquardt, C.; Leuchs, G. Reduction of guided acoustic wave Brillouin scattering in photonic crystal fibers. Phys. Rev. Lett. 2006, 97, 133901. [Google Scholar] [CrossRef] [PubMed]
- Thévenaz, L. Slow and fast light in optical fibres. Nat. Photonics 2008, 2, 474–481. [Google Scholar] [CrossRef] [Green Version]
- Kang, M.; Nazarkin, A.; Brenn, A.; Russell, P.S.J. Tightly trapped acoustic phonons in photonic crystal fibres as highly nonlinear artificial Raman oscillators. Nat. Phys. 2009, 5, 276. [Google Scholar] [CrossRef]
- Rakich, P.T.; Reinke, C.; Camacho, R.; Davids, P.; Wang, Z. Giant Enhancement of Stimulated Brillouin Scattering in the Subwavelength Limit. Phys. Rev. X 2012, 2, 011008. [Google Scholar] [CrossRef]
- Nikles, M.; Thévenaz, L.; Robert, P.A. Simple distributed fiber sensor based on Brillouin gain spectrum analysis. Opt. Lett. 1996, 21, 758–760. [Google Scholar] [CrossRef] [PubMed]
- Sancho, J.; Primerov, N.; Chin, S.; Antman, Y.; Zadok, A.; Sales, S.; Thévenaz, L. Tunable and reconfigurable multi-tap microwave photonic filter based on dynamic Brillouin gratings in fibers. Opt. Express 2012, 20, 6157–6162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Merklein, M.; Stiller, B.; Vu, K.; Madden, S.J.; Eggleton, B.J. A chip-integrated coherent photonic-phononic memory. Nat. Commun. 2017, 8, 574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Kroll, N.M. Excitation of hypersonic vibrations by means of photoelastic coupling of high-intensity light waves to elastic waves. J. Appl. Phys. 1965, 36, 34–43. [Google Scholar] [CrossRef]
- Tang, C. Saturation and spectral characteristics of the Stokes emission in the stimulated Brillouin process. J. Appl. Phys. 1966, 37, 2945–2955. [Google Scholar] [CrossRef]
- Boyd, R.W.; Rzaewski, K.; Narum, P. Noise initiation of stimulated Brillouin scattering. Phys. Rev. A 1990, 42, 5514. [Google Scholar] [CrossRef] [PubMed]
- Thomas, P.J.; Rowell, N.L.; van Driel, H.M.; Stegeman, G.I. Normal acoustic modes and Brillouin scattering in single-mode optical fibers. Phys. Rev. B 1979, 19, 4986–4998. [Google Scholar] [CrossRef]
- Dainese, P.; Russell, P.; Wiederhecker, G.; Joly, N.; Fragnito, H.; Laude, V.; Khelif, A. Raman-like light scattering from acoustic phonons in photonic crystal fiber. Opt. Express 2006, 14, 4141–4150. [Google Scholar] [CrossRef] [PubMed]
- Beugnot, J.C.; Sylvestre, T.; Maillotte, H.; Mélin, G.; Laude, V. Guided acoustic wave Brillouin scattering in photonic crystal fibers. Opt. Lett. 2007, 32, 17–19. [Google Scholar] [CrossRef] [PubMed]
- Dainese, P.; Russell, P.; Joly, N.; Knight, J.; Wiederhecker, G.; Fragnito, H.; Laude, V.; Khelif, A. Stimulated Brillouin scattering from multi-GHz-guided acoustic phonons in nanostructured photonic crystal fibres. Nat. Phys. 2006, 2, 388–392. [Google Scholar] [CrossRef]
- Kang, M.S.; Brenn, A.; Russell, P.S.J. All-Optical Control of Gigahertz Acoustic Resonances by Forward Stimulated Interpolarization Scattering in a Photonic Crystal Fiber. Phys. Rev. Lett. 2010, 105, 153901. [Google Scholar] [CrossRef] [PubMed]
- Beugnot, J.C.; Lebrun, S.; Pauliat, G.; Maillotte, H.; Laude, V.; Sylvestre, T. Brillouin light scattering from surface acoustic waves in a subwavelength-diameter optical fibre. Nat. Commun. 2014, 5, 5242. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beugnot, J.C.; Ahmad, R.; Rochette, M.; Laude, V.; Maillotte, H.; Sylvestre, T. Reduction and control of stimulated Brillouin scattering in polymer-coated chalcogenide optical microwires. Opt. Lett. 2014, 39, 482–485. [Google Scholar] [CrossRef] [PubMed]
- Van Laer, R.; Kuyken, B.; Van Thourhout, D.; Baets, R. Interaction between light and highly confined hypersound in a silicon photonic nanowire. Nat. Photonics 2015, 9, 199–203. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D.; Bell, J.; Kearsley, M.; Pitaevskii, L.; Lifshitz, E.; Sykes, J. Electrodynamics of Continuous Media; Elsevier: New York, NY, USA, 2013; Volume 8. [Google Scholar]
- Fabelinskii, I.L. Molecular Scattering of Light; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Stegeman, G.; Stoicheff, B. Spectrum of light scattering from thermal shear waves in liquids. Phys. Rev. Lett. 1968, 21, 202. [Google Scholar] [CrossRef]
- Beugnot, J.C.; Laude, V. Electrostriction and guidance of acoustic phonons in optical fibers. Phys. Rev. B 2012, 86, 224304. [Google Scholar] [CrossRef]
- Laude, V.; Beugnot, J.C. Lagrangian description of Brillouin scattering and electrostriction in nanoscale optical waveguides. New J. Phys. 2015, 17, 125003. [Google Scholar] [CrossRef] [Green Version]
- Laude, V.; Korotyaeva, M.E.; Beugnot, J.C. Generation of coherent acoustic beams in solids by mixing of counterpropagating, detuned optical beams. Appl. Opt. 2018, 57, C77–C82. [Google Scholar] [CrossRef] [PubMed]
- Florez, O.; Jarschel, P.F.; Espinel, Y.A.; Cordeiro, C.; Alegre, T.M.; Wiederhecker, G.S.; Dainese, P. Brillouin scattering self-cancellation. Nat. Commun. 2016, 7, 11759. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Godet, A.; Ndao, A.; Sylvestre, T.; Pecheur, V.; Lebrun, S.; Pauliat, G.; Beugnot, J.C.; Huy, K.P. Brillouin spectroscopy of optical microfibers and nanofibers. Optica 2017, 4, 1232–1238. [Google Scholar] [CrossRef]
- Poulton, C.G.; Pant, R.; Eggleton, B.J. Acoustic confinement and stimulated Brillouin scattering in integrated optical waveguides. J. Opt. Soc. Am. B 2013, 30, 2657–2664. [Google Scholar] [CrossRef]
- Hecht, F. New development in freefem++. J. Numer. Math. 2012, 20, 159–344. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laude, V.; Beugnot, J.-C. Spontaneous Brillouin Scattering Spectrum and Coherent Brillouin Gain in Optical Fibers. Appl. Sci. 2018, 8, 907. https://doi.org/10.3390/app8060907
Laude V, Beugnot J-C. Spontaneous Brillouin Scattering Spectrum and Coherent Brillouin Gain in Optical Fibers. Applied Sciences. 2018; 8(6):907. https://doi.org/10.3390/app8060907
Chicago/Turabian StyleLaude, Vincent, and Jean-Charles Beugnot. 2018. "Spontaneous Brillouin Scattering Spectrum and Coherent Brillouin Gain in Optical Fibers" Applied Sciences 8, no. 6: 907. https://doi.org/10.3390/app8060907




