Measurement of the Resonant Magneto-Optical Kerr Effect Using a Free Electron Laser
Abstract
:1. Introduction
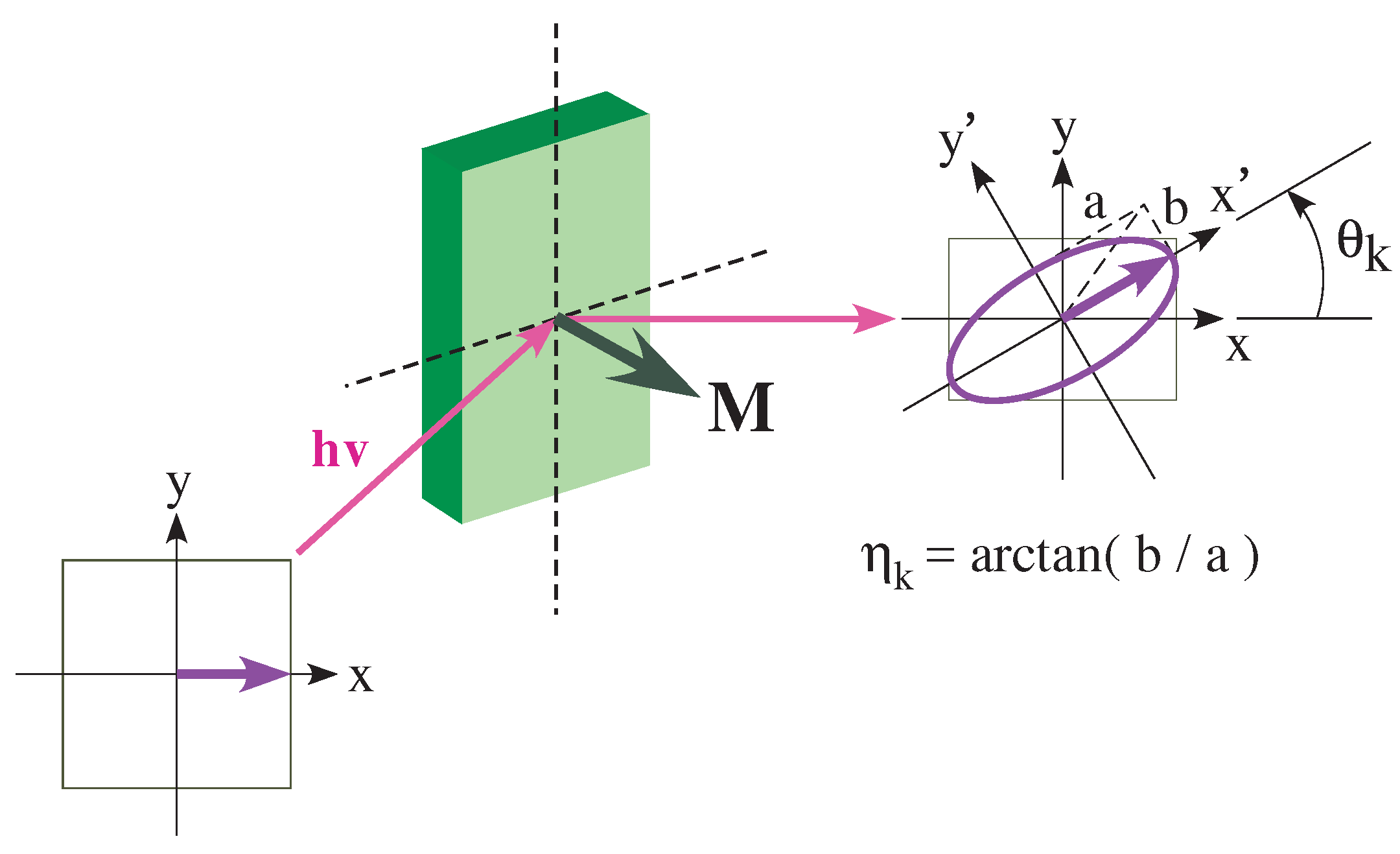
2. MOKE Phenomena
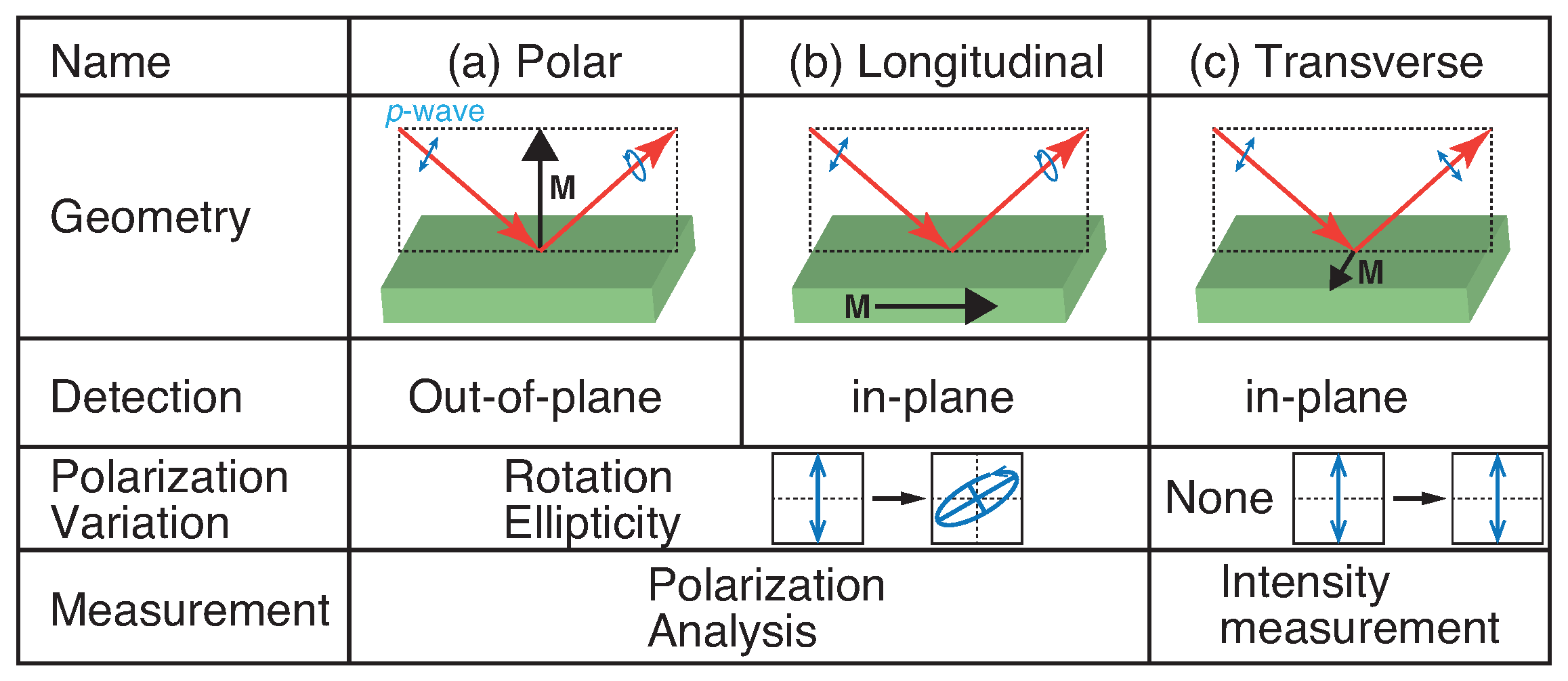
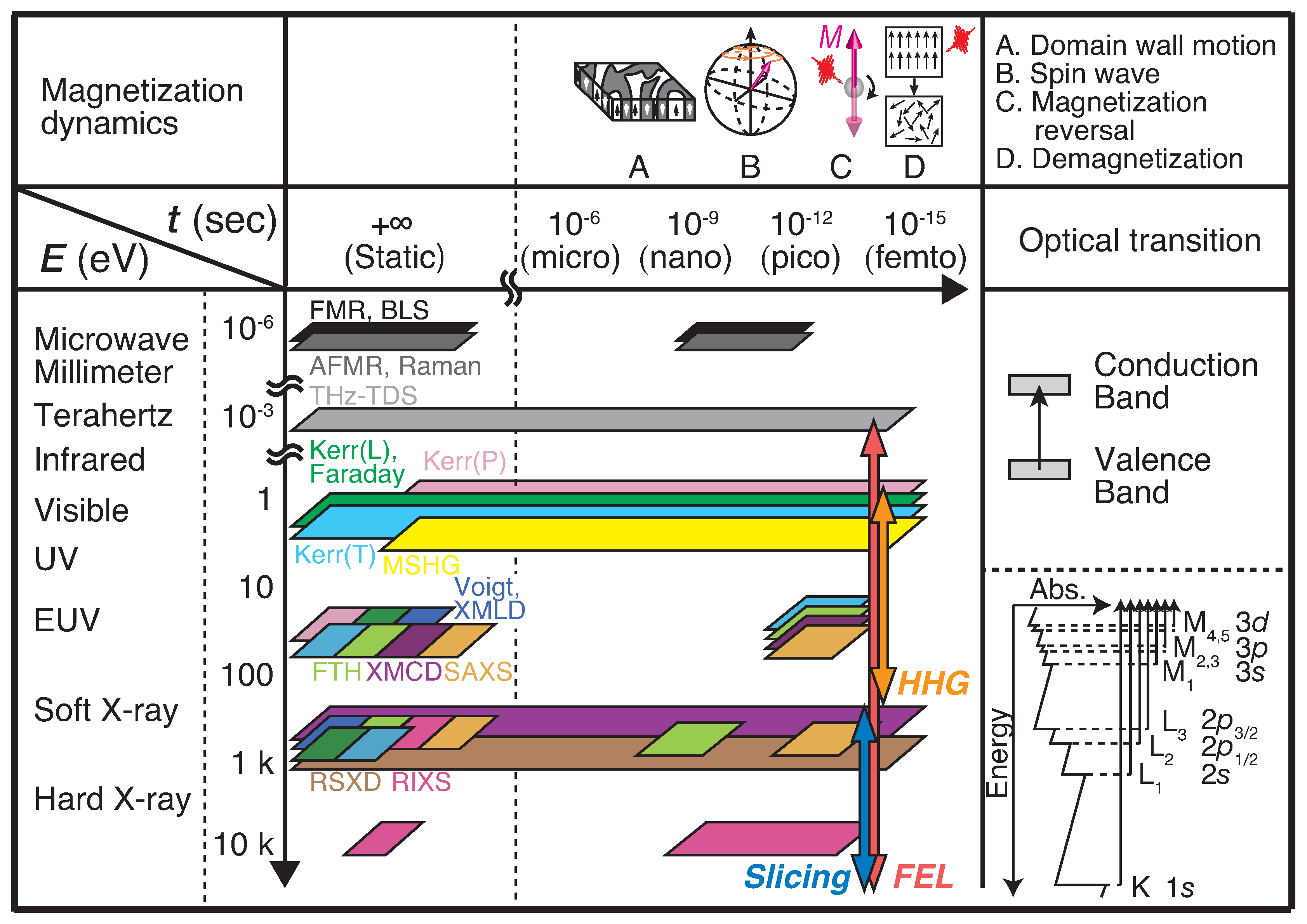
3. Techniques for Magnetization Dynamics Capture
Characteristics of the TR-RMOKE Technique
4. MOKE Measurement Scheme
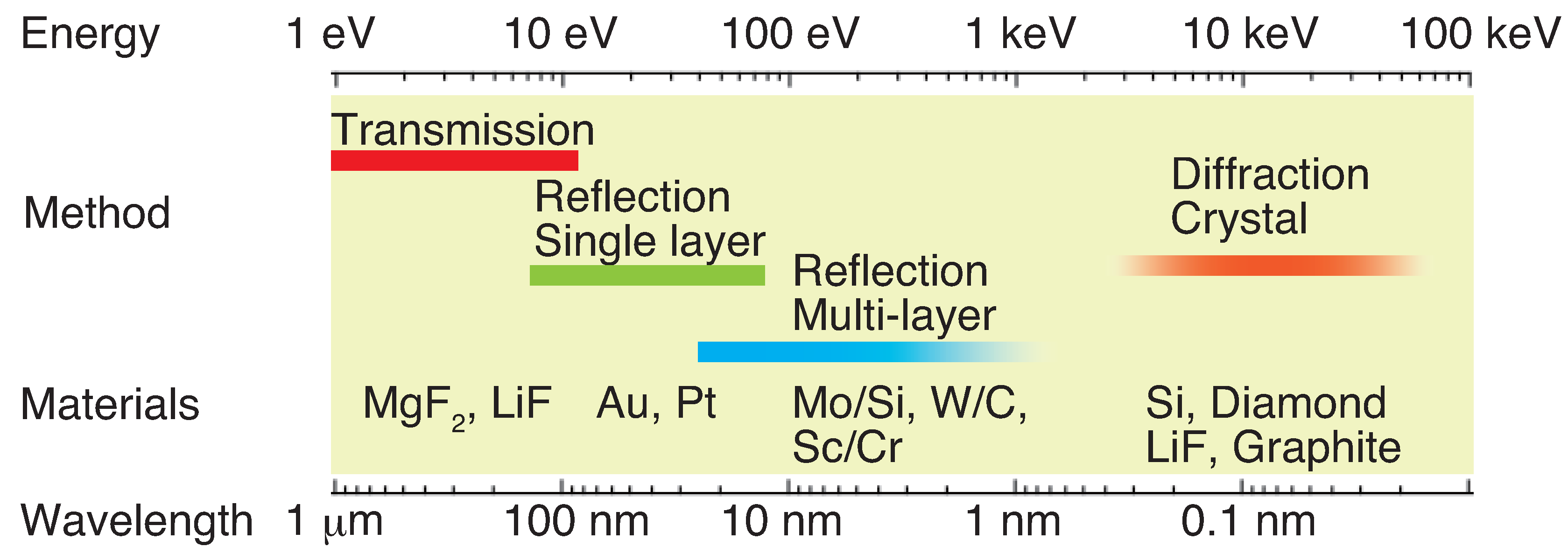
4.1. Visible MOKE
4.2. RMOKE
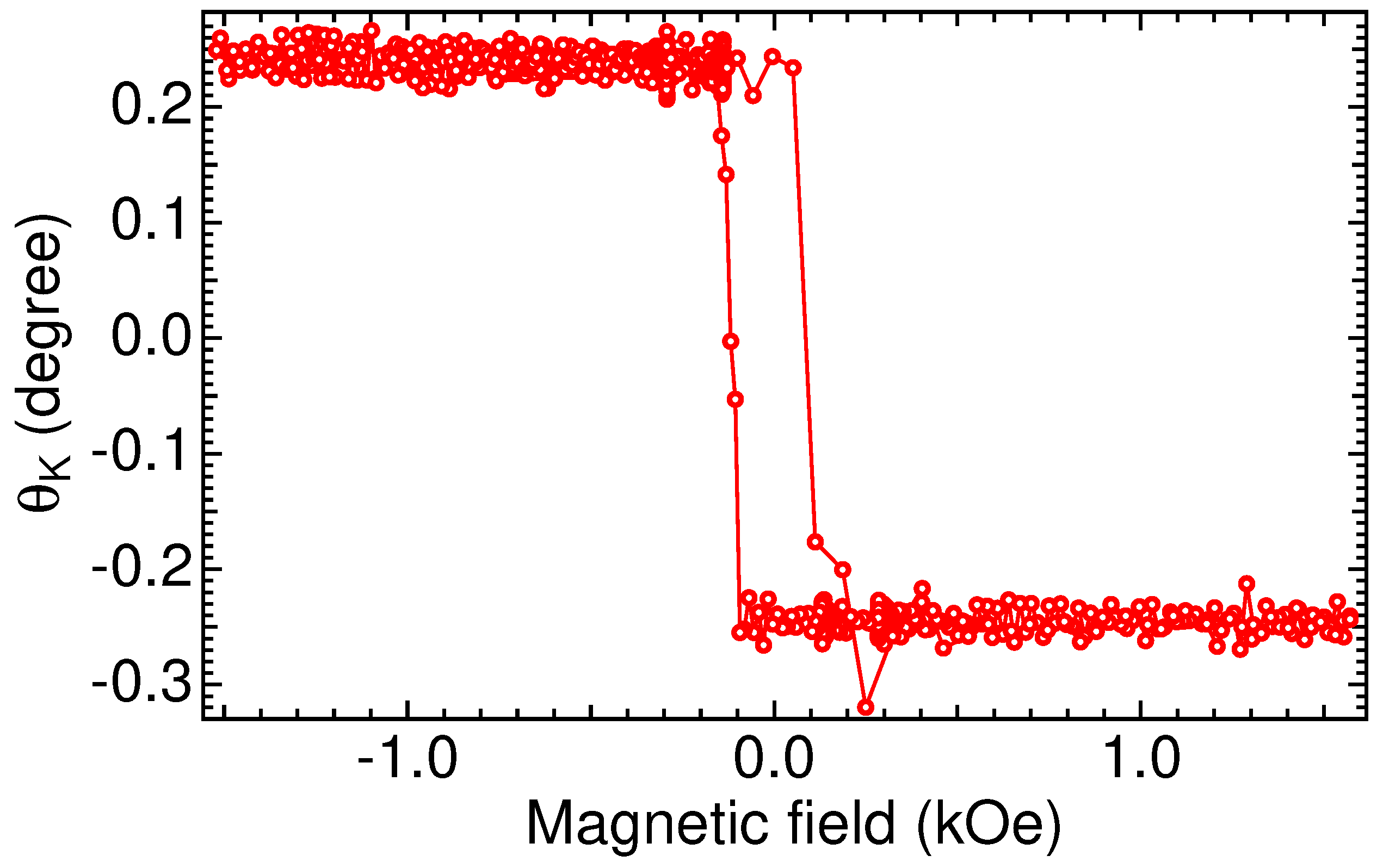
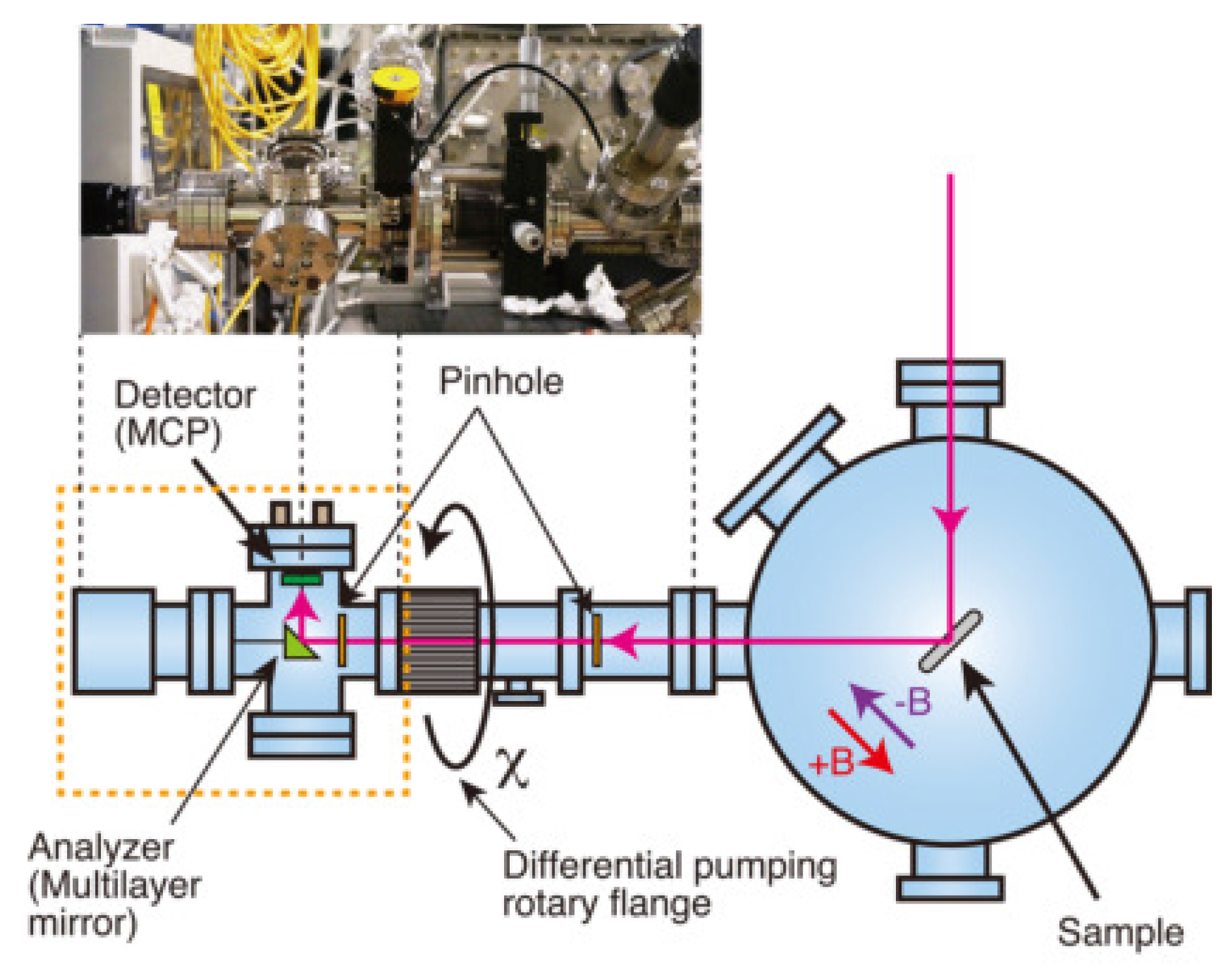
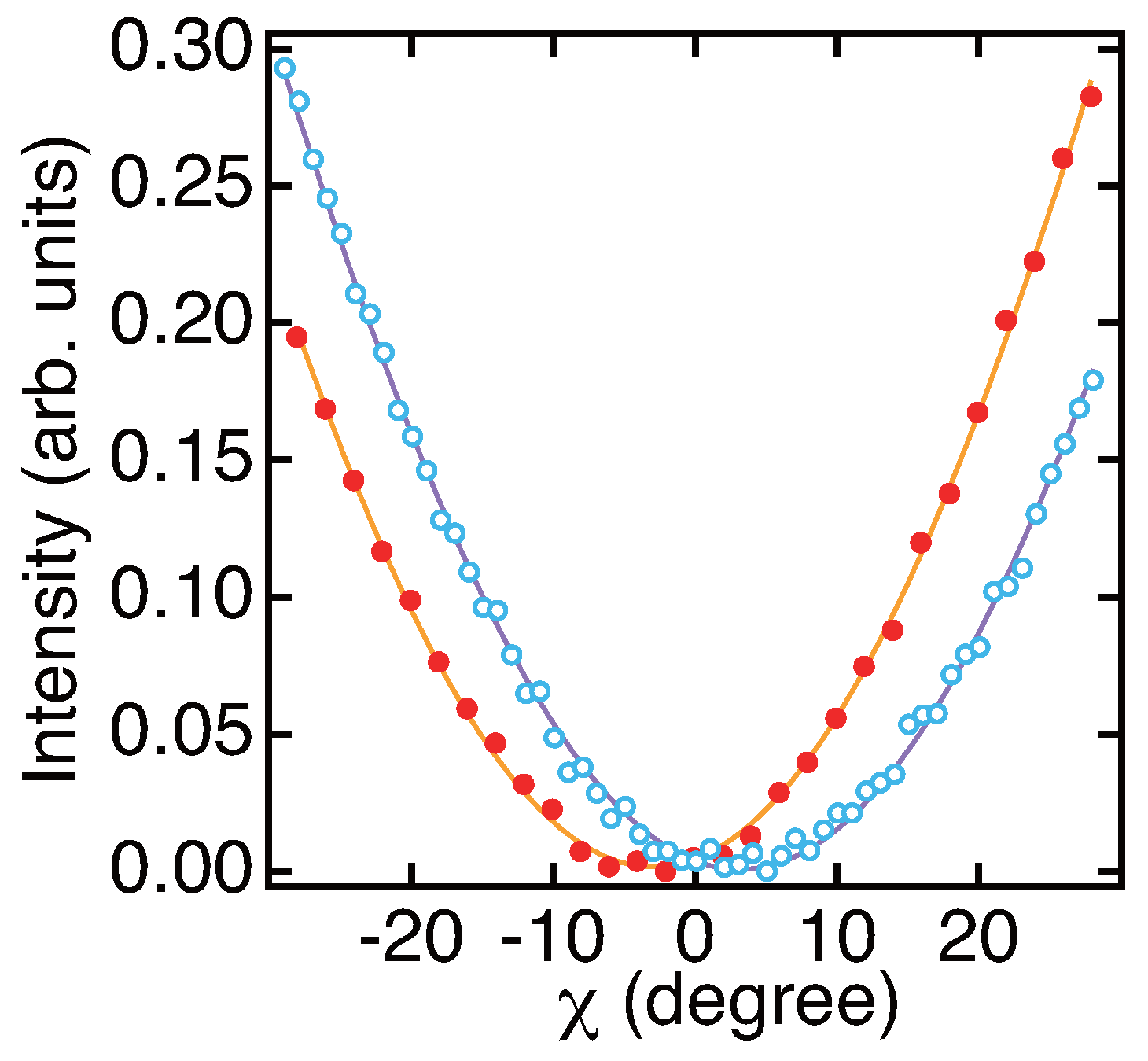
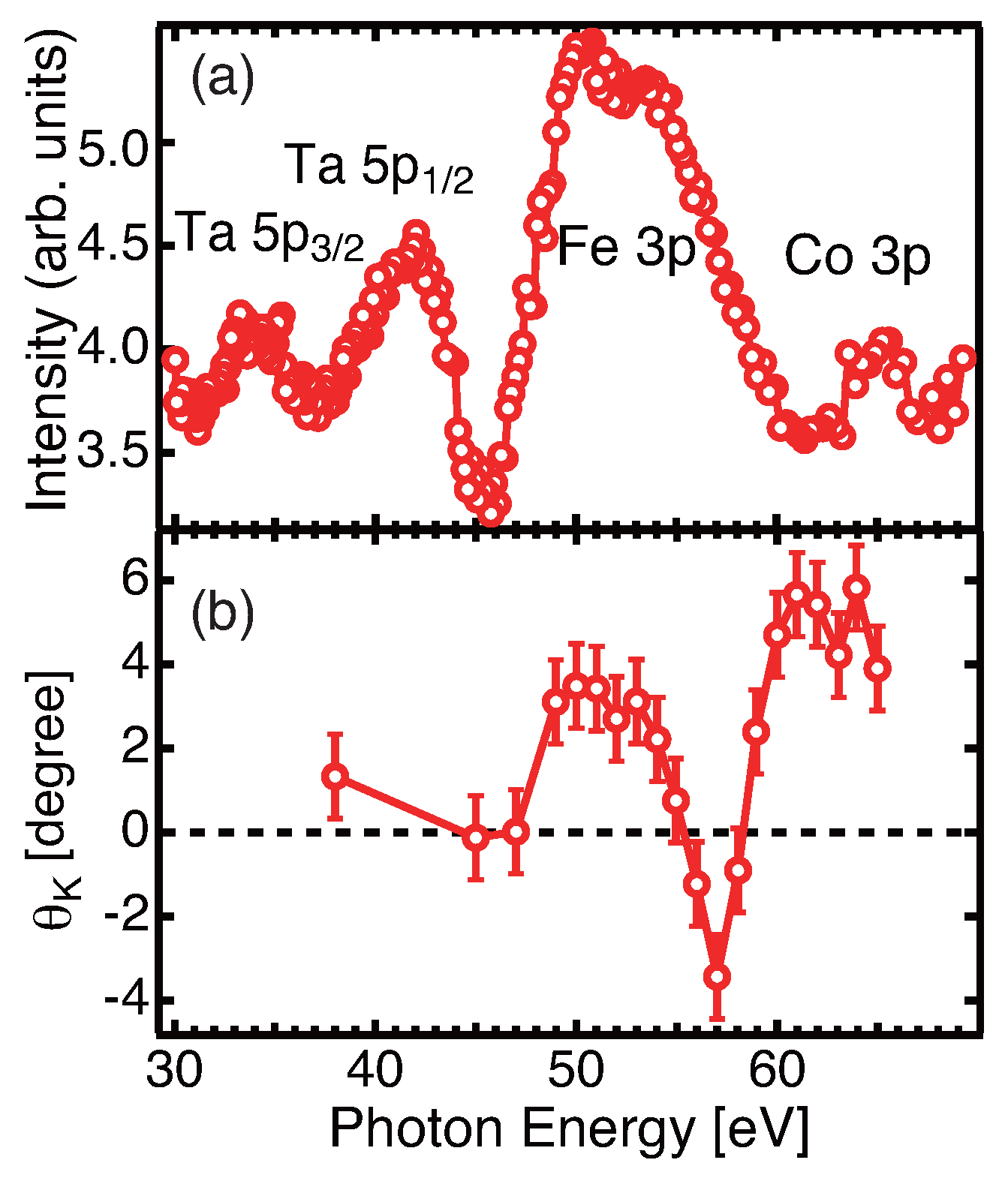
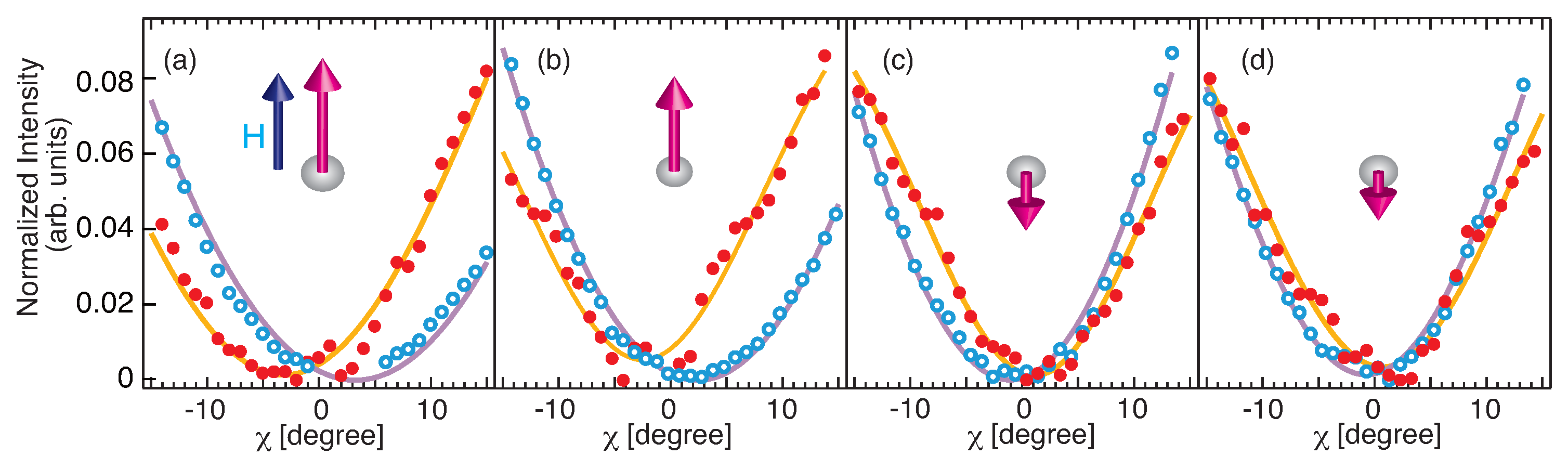
5. Static RMOKE Measurement
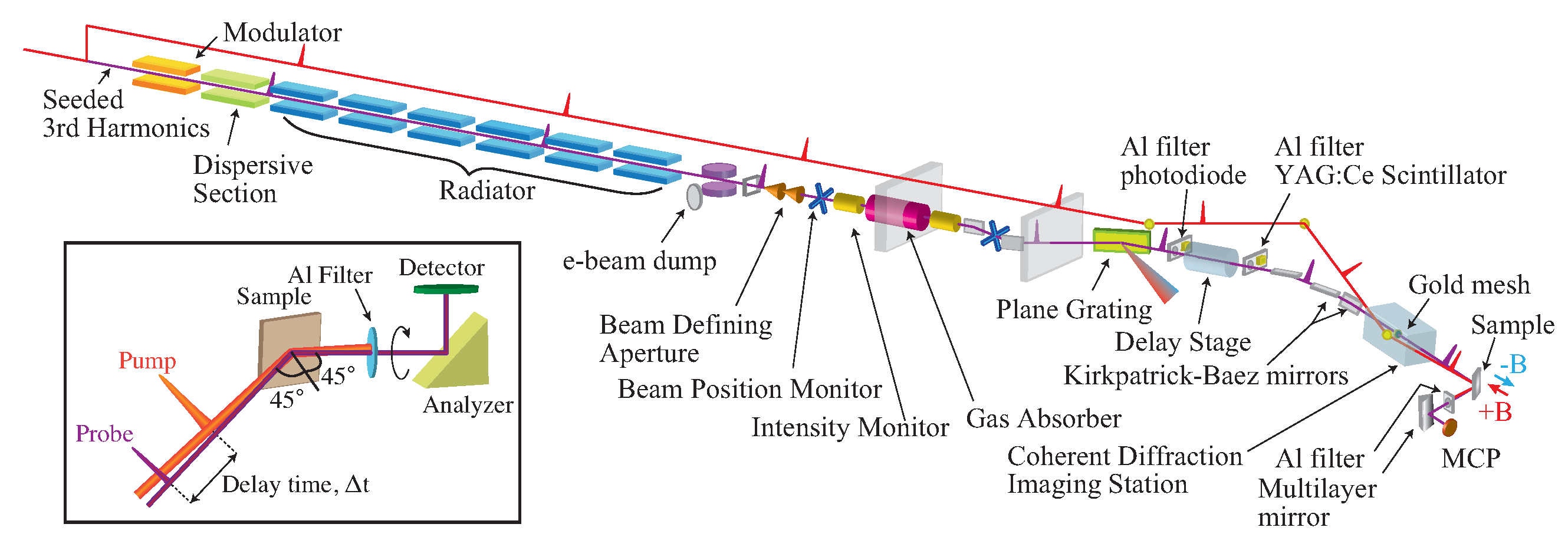
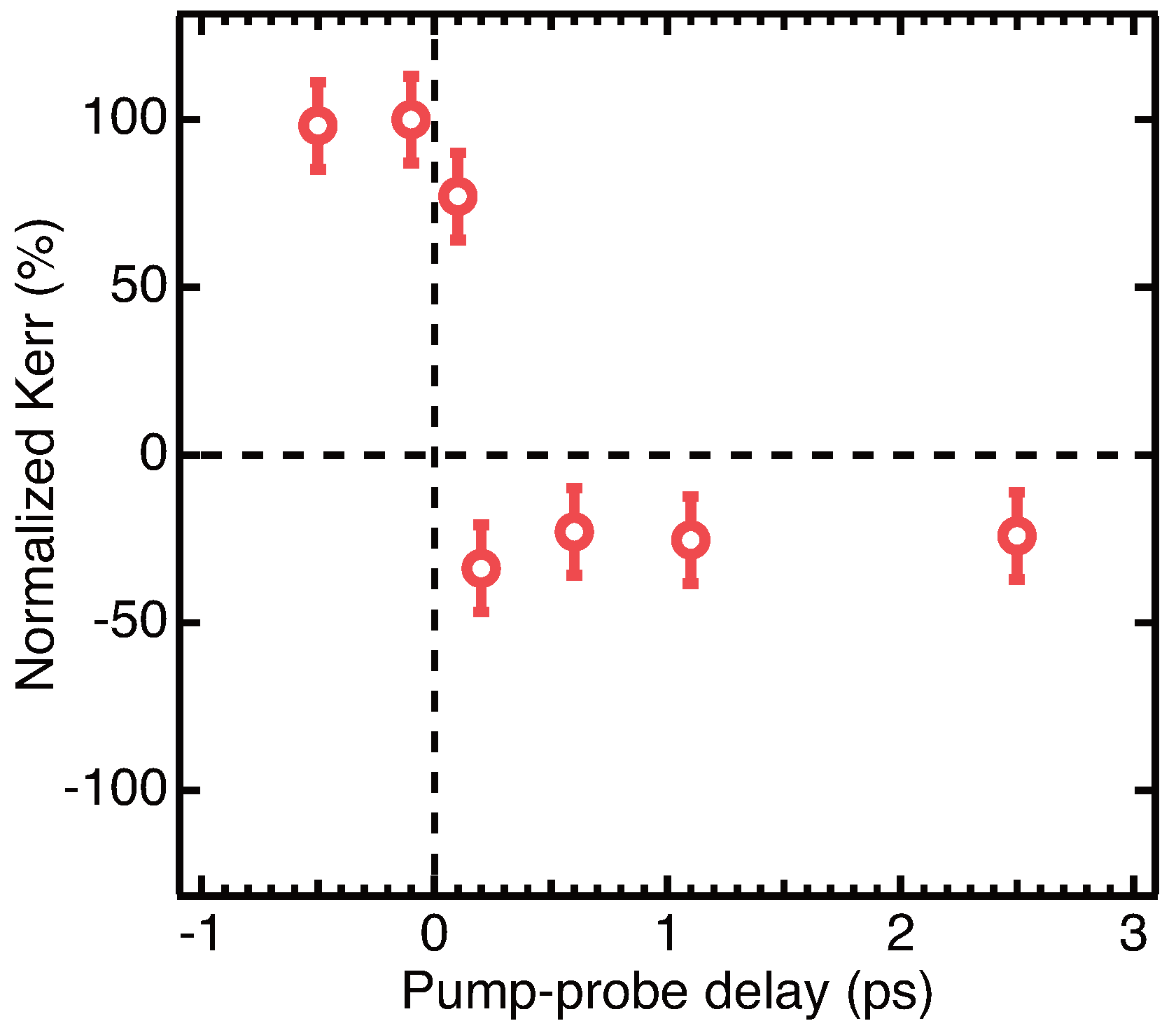
6. Demonstration of TR-RMOKE with a Soft X-ray FEL
7. Conclusions and Outlook
Acknowledgments
Conflicts of Interest
Abbreviations
| AFMR | Antiferromagnetic resonance |
| BLS | Brillouin light scattering |
| EUV | Extreme ultraviolet |
| FEL | Free electron laser |
| FMR | Ferromagnetic resonance |
| FTH | Fourier transform holography |
| HHG | High harmonic generation |
| L-RMOKE | Longitudinal resonant magneto-optical Kerr effect |
| MSHG | Magnetization-induced second harmonic generation |
| P-RMOKE | Polar resonant magneto-optical Kerr effect |
| RAE | Rotating analyzer ellipsometry |
| RMOKE | Resonant magneto-optical Kerr effect |
| RIXS | Resonant inelastic X-ray scattering |
| RSXD | Resonant soft X-ray diffraction |
| SAXS | Small angle X-ray scattering |
| SR | Synchrotron radiation |
| TFY | Total fluorescence yield |
| THz-TDS | Terahertz time domain spectroscopy |
| TR | Time-resolved |
| XMCD | X-ray magnetic circular dichroism |
| T-RMOKE | Transverse resonant magneto-optical Kerr effect |
| UV | Ultraviolet |
| XMCD | X-ray magnetic circular dichroism |
| XMLD | X-ray magnetic linear dichroism |
References
- Kirilyuk, A.; Kimel, A.V.; Rasing, T. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 2010, 82, 2731–2784. [Google Scholar] [CrossRef]
- Beaurepaire, E.; Merle, J.C.; Daunois, A.; Bigot, J.Y. Ultrafast spin dynamics in ferromagnetic nickel. Phys. Rev. Lett. 1996, 76, 4250–4253. [Google Scholar] [CrossRef] [PubMed]
- Radu, I.; Vahaplar, K.; Stamm, C.; Kachel, T.; Pontius, N.; Dürr, H.; Ostler, T.; Barker, J.; Evans, R.; Chantrell, R.; et al. Transient ferromagnetic-like state mediating ultrafast reversal of antiferromagnetically coupled spins. Nature 2011, 472, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Thiele, J.U.; Buess, M.; Back, C.H. Spin dynamics of the antiferromagnetic-to-ferromagnetic phase transition in FeRh on a sub-picosecond time scale. Appl. Phys. Lett. 2004, 85, 2857–2859. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Nakajima, M.; Suemoto, T. Coherent control of spin precession motion with impulsive magnetic fields of half-cycle terahertz radiation. Phys. Rev. Lett. 2010, 105, 237201. [Google Scholar] [CrossRef] [PubMed]
- Schellekens, A.; Koopmans, B. Comparing ultrafast demagnetization rates between competing models for finite temperature magnetism. Phys. Rev. Lett. 2013, 110, 217204. [Google Scholar] [CrossRef] [PubMed]
- Bigot, J.Y.; Vomir, M. Ultrafast magnetization dynamics of nanostructures. Annalen der Physik 2013, 525, 2–30. [Google Scholar] [CrossRef]
- Rudolf, D.; Chan, L.O.; Battiato, M.; Adam, R.; Shaw, J.M.; Turgut, E.; Maldonado, P.; Mathias, S.; Grychtol, P.; Nembach, H.T.; et al. Ultrafast magnetization enhancement in metallic multilayers driven by superdiffusive spin current. Nat. Commun. 2012, 3, 1037. [Google Scholar] [CrossRef] [PubMed]
- Dean, M.; Cao, Y.; Liu, X.; Wall, S.; Zhu, D.; Mankowsky, R.; Thampy, V.; Chen, X.; Vale, J.; Casa, D.; et al. Ultrafast energy-and momentum-resolved dynamics of magnetic correlations in the photo-doped Mott insulator Sr2IrO4. Nat. Mater. 2016, 15, 601–605. [Google Scholar] [CrossRef] [PubMed]
- Oppeneer, P. Magneto-optical Kerr spectra. Handb. Magn. Mater. 2001, 13, 229–422. [Google Scholar]
- Kortright, J.; Rice, M. Soft X-ray magneto-optic Kerr rotation and element-specific hysteresis measurement. Rev. Sci. Instrum. 1996, 67, 3353. [Google Scholar] [CrossRef]
- Mertins, H.C.; Valencia, S.; Abramsohn, D.; Gaupp, A.; Gudat, W.; Oppeneer, P.M. X-ray Kerr rotation and ellipticity spectra at the 2 p edges of Fe, Co, and Ni. Phys. Rev. B 2004, 69. [Google Scholar] [CrossRef]
- Chen, C.; Idzerda, Y.; Lin, H.J.; Smith, N.; Meigs, G.; Chaban, E.; Ho, G.; Pellegrin, E.; Sette, F. Experimental confirmation of the X-ray magnetic circular dichroism sum rules for iron and cobalt. Phys. Rev. Lett. 1995, 75, 152–155. [Google Scholar] [CrossRef] [PubMed]
- Stöhr, J.; Padmore, H.; Anders, S.; Stammler, T.; Scheinfein, M. Principles of X-ray magnetic dichroism spectromicroscopy. Surf. Rev. Lett. 1998, 5, 1297–1308. [Google Scholar] [CrossRef]
- Yamamoto, Sh.; Taguchi, M.; Someya, T.; Kubota, Y.; Ito, S.; Wadati, H.; Fujisawa, M.; Capotondi, F.; Pedersoli, E.; Manfredda, M.; et al. Ultrafast spin-switching of a ferrimagnetic alloy at room temperature traced by resonant magneto-optical Kerr effect using a seeded free electron laser. Revi. Sci. Instrum. 2015, 86. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Scheinfein, M. Combined three-axis surface magneto-optical Kerr effects in the study of surface and ultra-thin-film magnetism. J. Appl. Phys. 1993, 74, 6810–6823. [Google Scholar] [CrossRef]
- Strelniker, Y.M.; Bergman, D.J. Magneto-optical response of a periodic metallic nano-structure. In Proceedings of the SPIE 9574, International Society for Optics and Photonics, San Diego, CA, USA, 9 August 2015; p. 954705. [Google Scholar]
- Nozaki, T.; Shiota, Y.; Miwa, S.; Murakami, S.; Bonell, F.; Ishibashi, S.; Kubota, H.; Yakushiji, K.; Saruya, T.; Fukushima, A.; et al. Electric-field-induced ferromagnetic resonance excitation in an ultra-thin ferromagnetic metal layer. Nat. Phys. 2012, 8, 491–496. [Google Scholar] [CrossRef]
- Milano, J.; Steren, L.; Grimsditch, M. Effect of dipolar interaction on the antiferromagnetic resonance spectra of NiO. Phys. Rev. Lett. 2004, 93. [Google Scholar] [CrossRef] [PubMed]
- Hangyo, M.; Tani, M.; Nagashima, T. Terahertz time-domain spectroscopy of solids: A review. Int. J. Infrared Millim. Waves 2005, 26, 1661–1690. [Google Scholar] [CrossRef]
- Parchenko, S.; Satoh, T.; Yoshimine, I.; Stobiecki, F.; Maziewski, A.; Stupakiewicz, A. Non-thermal optical excitation of terahertz-spin precession in a magneto-optical insulator. Appl. Phys. Lett. 2016, 108. [Google Scholar] [CrossRef]
- Khorsand, A.; Savoini, M.; Kirilyuk, A.; Kimel, A.; Tsukamoto, A.; Itoh, A.; Rasing, T. Element-specific probing of ultrafast spin dynamics in multisublattice magnets with visible light. Phys. Rev. Lett. 2013, 110, 107205. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, Y.; Kaneko, Y.; He, J.; Yu, X.; Arima, T.; Tokura, Y. Magnetization-induced second harmonic generation in a polar ferromagnet. Phys. Rev. Lett. 2004, 92, 047401. [Google Scholar] [CrossRef] [PubMed]
- Regensburger, H.; Vollmer, R.; Kirschner, J. Time-resolved magnetization-induced second-harmonic generation from the Ni (110) surface. Phys. Rev. B 2000, 61, 14716–14722. [Google Scholar] [CrossRef]
- Mertins, H.C.; Oppeneer, P.; Kuneš, J.; Gaupp, A.; Abramsohn, D.; Schäfers, F. Observation of the X-ray magneto-optical Voigt effect. Phys. Rev. Lett. 2001, 87, 047401. [Google Scholar] [CrossRef] [PubMed]
- Höchst, H.; Rioux, D.; Zhao, D.; Huber, D.L. Magnetic linear dichroism effects in reflection spectroscopy: A case study at the Fe M 2, 3 edge. J. Appl. Phys. 1997, 81, 7584–7588. [Google Scholar] [CrossRef]
- Schwickert, M.; Guo, G.; Tomaz, M.; O’Brien, W.; Harp, G. X-ray magnetic linear dichroism in absorption at the L edge of metallic Co, Fe, Cr, and V. Phys. Rev. B 1998, 58, R4289. [Google Scholar] [CrossRef]
- Finazzi, M.; Duo, L.; Ciccacci, F. Magnetic properties of interfaces and multilayers based on thin antiferromagnetic oxide films. Surf. Sci. Rep. 2009, 64, 139–167. [Google Scholar] [CrossRef]
- Ament, L.J.; Van Veenendaal, M.; Devereaux, T.P.; Hill, J.P.; Van Den Brink, J. Resonant inelastic X-ray scattering studies of elementary excitations. Rev. Mod. Phys. 2011, 83, 705–767. [Google Scholar] [CrossRef]
- Fabbris, G.; Meyers, D.; Xu, L.; Katukuri, V.; Hozoi, L.; Liu, X.; Chen, Z.Y.; Okamoto, J.; Schmitt, T.; Uldry, A.; et al. Doping Dependence of Collective Spin and Orbital Excitations in the Spin-1 Quantum Antiferromagnet La2−xSrxNiO4 Observed by X Rays. Phys. Rev. Lett. 2017, 118, 156402. [Google Scholar] [CrossRef] [PubMed]
- Dean, M.; Springell, R.; Monney, C.; Zhou, K.; Pereiro, J.; Božović, I.; Dalla Piazza, B.; Rønnow, H.; Morenzoni, E.; Van Den Brink, J.; et al. Spin excitations in a single La2CuO4 layer. Nat. Mater. 2012, 11, 850–854. [Google Scholar] [CrossRef] [PubMed]
- Minola, M.; Di Castro, D.; Braicovich, L.; Brookes, N.; Innocenti, D.; Sala, M.M.; Tebano, A.; Balestrino, G.; Ghiringhelli, G. Magnetic and ligand field properties of copper at the interfaces of (CaCuO2)n/(SrTiO3)n superlattices. Phys. Rev. B 2012, 85, 235138. [Google Scholar] [CrossRef]
- Müller, L.; Gutt, C.; Pfau, B.; Schaffert, S.; Geilhufe, J.; Büttner, F.; Mohanty, J.; Flewett, S.; Treusch, R.; Düsterer, S.; et al. Breakdown of the X-ray resonant magnetic scattering signal during intense pulses of extreme ultraviolet free-electron-laser radiation. Phys. Rev. Lett. 2013, 110, 234801. [Google Scholar] [CrossRef] [PubMed]
- Yamasaki, Y.; Sudayama, T.; Okamoto, J.; Nakao, H.; Kubota, M.; Murakami, Y. Diffractometer for small angle resonant soft X-ray scattering under magnetic field. J. Phys. Conf. Ser. 2013, 425. [Google Scholar] [CrossRef]
- Günther, C.M.; Guehrs, E.; Schneider, M.; Pfau, B.; von Korff Schmising, C.; Geilhufe, J.; Schaffert, S.; Eisebitt, S. Experimental evaluations of signal-to-noise in spectro-holography via modified uniformly redundant arrays in the soft X-ray and extreme ultraviolet spectral regime. J. Opt. 2017, 19. [Google Scholar] [CrossRef]
- Eisebitt, S.; Lüning, J.; Schlotter, W.; Lörgen, M.; Hellwig, O.; Eberhardt, W.; Stöhr, J. Lensless imaging of magnetic nanostructures by X-ray spectro-holography. Nature 2004, 432, 885–888. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, A.; Chang, C.; Buchholz, M.; Trabant, C.; Schierle, E.; Schlappa, J.; Schmitz, D.; Ott, H.; Metcalf, P.; Tjeng, L.; et al. Analysis of charge and orbital order in Fe3O4 by Fe L2,3 resonant X-ray diffraction. Phys. Rev. B 2013, 88, 195110. [Google Scholar] [CrossRef]
- Chan, L.O.; Siemens, M.; Murnane, M.M.; Kapteyn, H.C.; Mathias, S.; Aeschlimann, M.; Grychtol, P.; Adam, R.; Schneider, C.M.; Shaw, J.M.; et al. Ultrafast demagnetization dynamics at the M edges of magnetic elements observed using a tabletop high-harmonic soft X-ray source. Phys. Rev. Lett. 2009, 103, 257402. [Google Scholar]
- Turgut, E.; Shaw, J.M.; Grychtol, P.; Nembach, H.T.; Rudolf, D.; Adam, R.; Aeschlimann, M.; Schneider, C.M.; Silva, T.J.; Murnane, M.M.; et al. Controlling the competition between optically induced ultrafast spin-flip scattering and spin transport in magnetic multilayers. Phys. Rev. Lett. 2013, 110, 197201. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, E.; Spezzani, C.; Fortuna, F.; Delaunay, R.; Vidal, F.; Nikolov, I.; Cinquegrana, P.; Diviacco, B.; Gauthier, D.; Penco, G.; et al. Element Selective Probe of the Ultra-Fast Magnetic Response to an Element Selective Excitation in Fe-Ni Compounds Using a Two-Color FEL Source. Photonics 2017, 4, 6. [Google Scholar] [CrossRef]
- Stamm, C.; Kachel, T.; Pontius, N.; Mitzner, R.; Quast, T.; Holldack, K.; Khan, S.; Lupulescu, C.; Aziz, E.; Wietstruk, M.; et al. Femtosecond modification of electron localization and transfer of angular momentum in nickel. Nat. Mater. 2007, 6, 740–743. [Google Scholar] [CrossRef] [PubMed]
- Willems, F.; Smeenk, C.; Zhavoronkov, N.; Kornilov, O.; Radu, I.; Schmidbauer, M.; Hanke, M.; von Korff Schmising, C.; Vrakking, M.; Eisebitt, S. Probing ultrafast spin dynamics with high-harmonic magnetic circular dichroism spectroscopy. Phys. Rev. B 2015, 92, 220405. [Google Scholar] [CrossRef]
- Higley, D.J.; Hirsch, K.; Dakovski, G.L.; Jal, E.; Yuan, E.; Liu, T.; Lutman, A.A.; MacArthur, J.P.; Arenholz, E.; Chen, Z.; et al. Femtosecond X-ray magnetic circular dichroism absorption spectroscopy at an X-ray free electron laser. Rev. Sci. Instrum. 2016, 87. [Google Scholar] [CrossRef] [PubMed]
- Pfau, B.; Schaffert, S.; Müller, L.; Gutt, C.; Al-Shemmary, A.; Büttner, F.; Delaunay, R.; Düsterer, S.; Flewett, S.; Frömter, R.; et al. Ultrafast optical demagnetization manipulates nanoscale spin structure in domain walls. Nat. Commun. 2012, 3, 1100. [Google Scholar] [CrossRef] [PubMed]
- Vodungbo, B.; Gautier, J.; Lambert, G.; Sardinha, A.B.; Lozano, M.; Sebban, S.; Ducousso, M.; Boutu, W.; Li, K.; Tudu, B.; et al. Laser-induced ultrafast demagnetization in the presence of a nanoscale magnetic domain network. Nat. Commun. 2012, 3, 999. [Google Scholar] [CrossRef] [PubMed]
- Graves, C.; Reid, A.; Wang, T.; Wu, B.; De Jong, S.; Vahaplar, K.; Radu, I.; Bernstein, D.; Messerschmidt, M.; Müller, L.; et al. Nanoscale spin reversal by non-local angular momentum transfer following ultrafast laser excitation in ferrimagnetic GdFeCo. Nat. Mater. 2013, 12, 293–298. [Google Scholar] [CrossRef] [PubMed]
- Büttner, F.; Moutafis, C.; Schneider, M.; Krüger, B.; Günther, C.; Geilhufe, J.; Schmising, C.v.K.; Mohanty, J.; Pfau, B.; Schaffert, S.; et al. Dynamics and inertia of skyrmionic spin structures. Nat. Phys. 2015, 11, 225–228. [Google Scholar] [CrossRef]
- Bukin, N.; McKeever, C.; Burgos-Parra, E.; Keatley, P.; Hicken, R.; Ogrin, F.; Beutier, G.; Dupraz, M.; Popescu, H.; Jaouen, N.; et al. Time-resolved imaging of magnetic vortex dynamics using holography with extended reference autocorrelation by linear differential operator. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Von Korff Schmising, C.; Pfau, B.; Schneider, M.; Günther, C.; Giovannella, M.; Perron, J.; Vodungbo, B.; Müller, L.; Capotondi, F.; Pedersoli, E.; et al. Imaging ultrafast demagnetization dynamics after a spatially localized optical excitation. Phys. Rev. Lett. 2014, 112, 217203. [Google Scholar] [CrossRef]
- Holldack, K.; Pontius, N.; Schierle, E.; Kachel, T.; Soltwisch, V.; Mitzner, R.; Quast, T.; Springholz, G.; Weschke, E. Ultrafast dynamics of antiferromagnetic order studied by femtosecond resonant soft X-ray diffraction. Appl. Phys. Lett. 2010, 97. [Google Scholar] [CrossRef]
- Pontius, N.; Kachel, T.; Schüßler-Langeheine, C.; Schlotter, W.; Beye, M.; Sorgenfrei, F.; Chang, C.; Foehlisch, A.; Wurth, W.; Metcalf, P.; et al. Time-resolved resonant soft X-ray diffraction with free-electron lasers: Femtosecond dynamics across the Verwey transition in magnetite. Appl. Phys. Lett. 2011, 98, 182504. [Google Scholar] [CrossRef]
- Först, M.; Caviglia, A.; Scherwitzl, R.; Mankowsky, R.; Zubko, P.; Khanna, V.; Bromberger, H.; Wilkins, S.; Chuang, Y.D.; Lee, W.; et al. Spatially resolved ultrafast magnetic dynamics initiated at a complex oxide heterointerface. Nat. Mater. 2015, 14, 883–888. [Google Scholar] [CrossRef] [PubMed]
- Henke, B.L.; Gullikson, E.; Davis, J.C. X-ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50–30,000 eV, Z = 1–92. At. Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Tsuyama, T.; Chakraverty, S.; Macke, S.; Pontius, N.; Schüßler-Langeheine, C.; Hwang, H.; Tokura, Y.; Wadati, H. Photoinduced Demagnetization and Insulator-to-Metal Transition in Ferromagnetic Insulating BaFeO3 Thin Films. Phys. Rev. Lett. 2016, 116, 256402. [Google Scholar] [CrossRef] [PubMed]
- Takubo, K.; Yamamoto, K.; Hirata, Y.; Yokoyama, Y.; Kubota, Y.; Yamamoto, Sh.; Yamamoto, S.; Matsuda, I.; Shin, S.; Seki, T.; et al. Capturing ultrafast magnetic dynamics by time-resolved soft x-ray magnetic circular dichroism. Appl. Phys. Lett. 2017, 110, 162401. [Google Scholar] [CrossRef]
- Yamamoto, Sh.; Taguchi, M.; Fujisawa, M.; Hobara, R.; Yamamoto, S.; Yaji, K.; Nakamura, T.; Fujikawa, K.; Yukawa, R.; Togashi, T.; et al. Observation of a giant Kerr rotation in a ferromagnetic transition metal by M-edge resonant magneto-optic Kerr effect. Phys. Rev. B 2014, 89, 064423. [Google Scholar] [CrossRef]
- Valencia, S.; Gaupp, A.; Gudat, W.; Mertins, H.C.; Oppeneer, P.; Abramsohn, D.; Schneider, C. Faraday rotation spectra at shallow core levels: 3p edges of Fe, Co, and Ni. New J. Phys. 2006, 8, 254. [Google Scholar] [CrossRef]
- Miyahara, T.; Park, S.Y.; Hanyu, T.; Hatano, T.; Moto, S.; Kagoshima, Y. Comparison between 3 p and 2 p magnetic circular dichroism in transition metals and alloys: Is the sum rule applicable to itinerant magnetic systems? Rev. Sci. Instrum. 1995, 66, 1558–1560. [Google Scholar] [CrossRef]
- Razdolski, I.; Alekhin, A.; Martens, U.; Bürstel, D.; Diesing, D.; Münzenberg, M.; Bovensiepen, U.; Melnikov, A. Analysis of the Time-Resolved Magneto-Optical Kerr Effect for Ultrafast Magnetization Dynamics in Ferromagnetic Thin Films. J. Phys. Condens. Matter 2017, 29, 174002. [Google Scholar] [CrossRef] [PubMed]
- Holldack, K.; Bahrdt, J.; Balzer, A.; Bovensiepen, U.; Brzhezinskaya, M.; Erko, A.; Eschenlohr, A.; Follath, R.; Firsov, A.; Frentrup, W.; et al. FemtoSpeX: A versatile optical pump–soft X-ray probe facility with 100 fs X-ray pulses of variable polarization. J. Synchrotron. Radiat. 2014, 21, 1090–1104. [Google Scholar] [CrossRef] [PubMed]
- Allaria, E.; Diviacco, B.; Callegari, C.; Finetti, P.; Mahieu, B.; Viefhaus, J.; Zangrando, M.; De Ninno, G.; Lambert, G.; Ferrari, E.; et al. Control of the polarization of a vacuum-ultraviolet, high-gain, free-electron laser. Phys. Rev. X 2014, 4, 041040. [Google Scholar] [CrossRef]
- Roussel, E.; Allaria, E.; Callegari, C.; Coreno, M.; Cucini, R.; Mitri, S.D.; Diviacco, B.; Ferrari, E.; Finetti, P.; Gauthier, D.; et al. Polarization Characterization of Soft X-ray Radiation at FERMI FEL-2. Photonics 2017, 4, 29. [Google Scholar] [CrossRef]
- Lutman, A.A.; MacArthur, J.P.; Ilchen, M.; Lindahl, A.O.; Buck, J.; Coffee, R.N.; Dakovski, G.L.; Dammann, L.; Ding, Y.; Dürr, H.A.; et al. Polarization control in an X-ray free-electron laser. Nat. Photonics 2016, 10, 468–472. [Google Scholar] [CrossRef]
- Vodungbo, B.; Sardinha, A.B.; Gautier, J.; Lambert, G.; Valentin, C.; Lozano, M.; Iaquaniello, G.; Delmotte, F.; Sebban, S.; Lüning, J.; et al. Polarization control of high order harmonics in the EUV photon energy range. Opt. Express 2011, 19, 4346–4356. [Google Scholar] [CrossRef] [PubMed]
- Lambert, G.; Vodungbo, B.; Gautier, J.; Mahieu, B.; Malka, V.; Sebban, S.; Zeitoun, P.; Luning, J.; Perron, J.; Andreev, A.; et al. Towards enabling femtosecond helicity-dependent spectroscopy with high-harmonic sources. Nat. Commun. 2015, 6. [Google Scholar] [CrossRef] [PubMed]
- Rasing, T.; Koerkamp, M.G.; Koopmans, B.; Berg, H.V. Giant nonlinear magneto-optical Kerr effects from Fe interfaces. J. Appl. Phys. 1996, 79, 6181–6185. [Google Scholar] [CrossRef]
- Williams, P.; Rose, A.; Wang, C. Rotating-polarizer polarimeter for accurate retardance measurement. Appl. Opt. 1997, 36, 6466–6472. [Google Scholar] [CrossRef] [PubMed]
- Aspnes, D.; Studna, A. High precision scanning ellipsometer. Appl. Opt. 1975, 14, 220–228. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, M.; Hirono, T. Control the light polarization. Jpn. Soc. Synchrotron Radiat. Res. 2006, 19, 444–453. [Google Scholar]
- Fujiwara, H. Spectroscopic Ellipsometry: Principles and Applications; John Wiley & Sons: Chichester, UK, 2007. [Google Scholar]
- Schäfers, F.; Mertins, H.C.; Gaupp, A.; Gudat, W.; Mertin, M.; Packe, I.; Schmolla, F.; Di Fonzo, S.; Soullié, G.; Jark, W.; et al. Soft-X-ray polarimeter with multilayer optics: Complete analysis of the polarization state of light. Appl. Opt. 1999, 38, 4074–4088. [Google Scholar] [CrossRef] [PubMed]
- Kimura, H.; Hirono, T.; Tamenori, Y.; Saitoh, Y.; Salashchenko, N.; Ishikawa, T. Transmission type Sc/Cr multilayer as a quarter-wave plate for near 400 eV. J. Electron. Spectrosc. Relat. Phenom. 2005, 144, 1079–1081. [Google Scholar] [CrossRef]
- Hirono, T.; Kimura, H.; Muro, T.; Saitoh, Y.; Ishikawa, T. Full polarization measurement of SR emitted from twin helical undulators with use of Sc/Cr multilayers at near 400 eV. J. Electron. Spectrosc. Relat. Phenom. 2005, 144, 1097–1099. [Google Scholar] [CrossRef]
- Namikawa, K.; Ando, M.; Nakajima, T.; Kawata, H. X-ray resonance magnetic scattering. J. Phys. Soc. Jpn. 1985, 54, 4099–4102. [Google Scholar] [CrossRef]
- De Bergevin, F.; Brunel, M. Diffraction of X-rays by magnetic materials. I. General formulae and measurements on ferro-and ferrimagnetic compounds. Acta Crystallogr. Sect. A 1981, 37, 314–324. [Google Scholar] [CrossRef]
- Igarashi, J.I.; Hirai, K. Magnetic circular dichroism at the K edge of nickel and iron. Phys. Rev. B 1994, 50, 17820. [Google Scholar] [CrossRef]
- Krinchik, G.; Gushchin, V. Investigation of Interband Transitions in Ferromagnetic Metals and Alloys by the Magneto-optical Method. Sov. Phys. JETP 1969, 29, 984. [Google Scholar]
- Kao, C.; Hastings, J.; Johnson, E.; Siddons, D.; Smith, G.; Prinz, G. Magnetic-resonance exchange scattering at the iron L II and L III edges. Phys. Rev. Lett. 1990, 65, 373. [Google Scholar] [CrossRef] [PubMed]
- Hannon, J.; Trammell, G.; Blume, M.; Gibbs, D. X-ray resonance exchange scattering. Phys. Rev. Lett. 1988, 61, 1245–1248. [Google Scholar] [CrossRef] [PubMed]
- Hillebrecht, F.; Kinoshita, T.; Spanke, D.; Dresselhaus, J.; Roth, C.; Rose, H.; Kisker, E. New magnetic linear dichroism in total photoelectron yield for magnetic domain imaging. Phys. Rev. Lett. 1995, 75, 2224–2227. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, T.; Rose, H.B.; Roth, C.; Spanke, D.; Hillebrecht, F.U.; Kisker, E. A new type of magnetic linear dichroism at Fe and Co M2,3 edges. J. Electron. Spectrosc. Relat. Phenom. 1996, 78, 237–240. [Google Scholar] [CrossRef]
- Grychtol, P.; Adam, R.; Kaiser, A.; Cramm, S.; Bürgler, D.; Schneider, C. Layer-selective studies of an anti-ferromagnetically coupled multilayer by resonant magnetic reflectivity in the extreme ultraviolet range. J. Electron. Spectrosc. Relat. Phenom. 2011, 184, 287–290. [Google Scholar] [CrossRef]
- Tesch, M.; Gilbert, M.; Mertins, H.C.; Bürgler, D.; Berges, U.; Schneider, C. X-ray magneto-optical polarization spectroscopy: An analysis from the visible region to the X-ray regime. Appl. Opt. 2013, 52, 4294–4310. [Google Scholar] [CrossRef] [PubMed]
- Kleibert, A.; Senz, V.; Bansmann, J.; Oppeneer, P. Thickness dependence and magnetocrystalline anisotropy of the X-ray transverse magneto-optical Kerr effect at the Co 2 p edges of ultra-thin Co films on W (110). Phys. Rev. B 2005, 72, 144404. [Google Scholar] [CrossRef]
- Pretorius, M.; Friedrich, J.; Ranck, A.; Schroeder, M.; Voss, J.; Wedemeier, V.; Spanke, D.; Knabben, D.; Rozhko, I.; Ohldag, H.; et al. Transverse magneto-optical Kerr effect of Fe at the Fe 3p threshold. Phys. Rev. B 1997, 55, 14133. [Google Scholar] [CrossRef]
- Hecker, M.; Oppeneer, P.M.; Valencia, S.; Mertins, H.C.; Schneider, C.M. Soft X-ray magnetic reflection spectroscopy at the 3p absorption edges of thin Fe films. J. Electron. Spectrosc. Relat. Phenom. 2005, 144, 881–884. [Google Scholar] [CrossRef]
- Zaharko, O.; Oppeneer, P.; Grimmer, H.; Horisberger, M.; Mertins, H.C.; Abramsohn, D.; Schäfers, F.; Bill, A.; Braun, H.B. Exchange coupling in Fe/NiO/Co film studied by soft X-ray resonant magnetic reflectivity. Phys. Rev. B 2002, 66, 134406. [Google Scholar] [CrossRef]
- Knabben, D.; Weber, N.; Raab, B.; Koop, T.; Hillebrecht, F.; Kisker, E.; Guo, G. Transverse magneto-optical Kerr effect of Fe at the 2p excitation threshold. J. Magn. Magn. Mater. 1998, 190, 349–356. [Google Scholar] [CrossRef]
- Mertins, H.C.; Abramsohn, D.; Gaupp, A.; Schäfers, F.; Gudat, W.; Zaharko, O.; Grimmer, H.; Oppeneer, P. Resonant magnetic reflection coefficients at the Fe 2 p edge obtained with linearly and circularly-polarized soft x rays. Phys. Rev. B 2002, 66, 184404. [Google Scholar] [CrossRef]
- Senz, V.; Kleibert, A.; Bansmann, J. Transverse magneto-optical Kerr effect in the soft X-ray regime of ultra-thin iron films and islands on W (110). Surf. Rev. Lett. 2002, 9, 913–919. [Google Scholar] [CrossRef]
- Kortright, J.; Kim, S.K.; Fullerton, E.; Jiang, J.; Bader, S. X-ray magneto-optic Kerr effect studies of spring magnet heterostructures. Nucl. Instrum. Methods Phys. Res. A 2001, 467, 1396–1403. [Google Scholar] [CrossRef]
- Sacchi, M.; Panaccione, G.; Vogel, J.; Mirone, A.; van der Laan, G. Magnetic dichroism in reflectivity and photoemission using linearly polarized light: 3 p core level of Ni (110). Phys. Rev. B 1998, 58, 3750–3754. [Google Scholar] [CrossRef]
- De Bergevin, F.; Brunel, M.; Gale, R.; Vettier, C.; Elkaim, E.; Bessière, M.; Lefebvre, S. X-ray resonant scattering in the ferromagnet CoPt. Phys. Rev. B 1992, 46, 10772. [Google Scholar] [CrossRef]
- Valencia, S.; Gaupp, A.; Gudat, W.; Abad, L.; Balcells, L.; Martinez, B. Surface degradation of magnetic properties in manganite thin films proved with magneto-optical techniques in reflection geometry. Appl. Phys. Lett. 2007, 90, 252509. [Google Scholar] [CrossRef]
- Kortright, J.B. Resonant soft X-ray and extreme ultraviolet magnetic scattering in nanostructured magnetic materials: Fundamentals and directions. J. Electron. Spectrosc. Relat. Phenom. 2013, 189, 178–186. [Google Scholar] [CrossRef]
- Kortright, J.; Rice, M.; Kim, S.K.; Walton, C.; Warwick, T. Optics for element-resolved soft X-ray magneto-optical studies. J. Magn. Magn. Mater. 1999, 191, 79–89. [Google Scholar] [CrossRef]
- Hellwig, O.; Kortright, J.; Takano, K.; Fullerton, E.E. Switching behavior of Fe-Pt/Ni-Fe exchange-spring films studied by resonant soft-X-ray magneto-optical Kerr effect. Phys. Rev. B 2000, 62, 11694. [Google Scholar] [CrossRef]
- Lee, K.S.; Kim, S.K.; Kortright, J. Atomic-scale depth selectivity of soft X-ray resonant Kerr effect. Appl. Phys. Lett. 2003, 83, 3764–3766. [Google Scholar] [CrossRef]
- Kim, S.K.; Lee, K.S.; Kortright, J.; Shin, S.C. Soft X-ray resonant Kerr rotation measurement and simulation of element-resolved and interface-sensitive magnetization reversals in a NiFe/FeMn/Co trilayer structure. Appl. Phys. Lett. 2005, 86, 102502. [Google Scholar] [CrossRef]
- Valencia, S.; Mertins, H.C.; Abramsohn, D.; Gaupp, A.; Gudat, W.; Oppeneer, P.M. Interference effects in the X-ray Kerr rotation spectrum at the Fe 2p edge. Phys. B Condensed Matter 2004, 345, 189–192. [Google Scholar] [CrossRef]
- Saito, K.; Igeta, M.; Ejima, T.; Hatano, T.; Watanabe, M. Faraday and Magnetic Kerr Rotation Measurements on Co and Ni Films Around M2, 3 Edges. Surf. Rev. Lett. 2002, 9, 943–947. [Google Scholar] [CrossRef]
- Erskine, J.; Stern, E. Calculation of the m 23 magneto-optical absorption spectrum of ferromagnetic nickel. Phys. Rev. B 1975, 12, 5016. [Google Scholar] [CrossRef]
- Capotondi, F.; Pedersoli, E.; Mahne, N.; Menk, R.; Passos, G.; Raimondi, L.; Svetina, C.; Sandrin, G.; Zangrando, M.; Kiskinova, M.; et al. Invited Article: Coherent imaging using seeded free-electron laser pulses with variable polarization: First results and research opportunities. Rev. Sci. Instrum. 2013, 84, 051301. [Google Scholar] [CrossRef] [PubMed]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.; Bassanese, S.; Biedron, S.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 2012, 6, 699–704. [Google Scholar] [CrossRef]
- Allaria, E.; Battistoni, A.; Bencivenga, F.; Borghes, R.; Callegari, C.; Capotondi, F.; Castronovo, D.; Cinquegrana, P.; Cocco, D.; Coreno, M.; et al. Tunability experiments at the FERMI@ Elettra free-electron laser. New J. Phys. 2012, 14, 113009. [Google Scholar] [CrossRef]
- Danailov, M.B.; Bencivenga, F.; Capotondi, F.; Casolari, F.; Cinquegrana, P.; Demidovich, A.; Giangrisostomi, E.; Kiskinova, M.P.; Kurdi, G.; Manfredda, M.; et al. Towards jitter-free pump-probe measurements at seeded free electron laser facilities. Opt. Express 2014, 22, 12869–12879. [Google Scholar] [CrossRef] [PubMed]
- Casolari, F.; Bencivenga, F.; Capotondi, F.; Giangrisostomi, E.; Manfredda, M.; Mincigrucci, R.; Pedersoli, E.; Principi, E.; Masciovecchio, C.; Kiskinova, M. Role of multilayer-like interference effects on the transient optical response of Si3N4 films pumped with free-electron laser pulses. Appl. Phys. Lett. 2014, 104, 191104. [Google Scholar] [CrossRef]
- Finetti, P.; Allaria, E.; Diviacco, B.; Callegari, C.; Mahieu, B.; Viefhaus, J.; Zangrando, M.; De Ninno, G.; Lambert, G.; Ferrari, E.; et al. Polarization measurement of free electron laser pulses in the VUV generated by the variable polarization source FERMI. In Proceedings of the SPIE 9210, International Society for Optics and Photonics, San Diego, CA, USA, 17 August 2014; p. 92100K. [Google Scholar]
- Stanciu, C.; Hansteen, F.; Kimel, A.; Kirilyuk, A.; Tsukamoto, A.; Itoh, A.; Rasing, T. All-optical magnetic recording with circularly-polarized light. Phys. Rev. Lett. 2007, 99, 047601. [Google Scholar] [CrossRef] [PubMed]
- Bigot, J.Y.; Vomir, M.; Beaurepaire, E. Coherent ultrafast magnetism induced by femtosecond laser pulses. Nat. Phys. 2009, 5, 515–520. [Google Scholar] [CrossRef]
- Mentink, J.; Hellsvik, J.; Afanasiev, D.; Ivanov, B.; Kirilyuk, A.; Kimel, A.; Eriksson, O.; Katsnelson, M.; Rasing, T. Ultrafast spin dynamics in multisublattice magnets. Phys. Rev. Lett. 2012, 108, 057202. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Hübner, W.; Lefkidis, G.; Bai, Y.; George, T.F. Paradigm of the time-resolved magneto-optical Kerr effect for femtosecond magnetism. Nat. Phys. 2009, 5, 499–502. [Google Scholar] [CrossRef]
- Carva, K.; Battiato, M.; Oppeneer, P.M. Is the controversy over femtosecond magneto-optics really solved? Nat. Phys. 2011, 7, 665. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamamoto, S.; Matsuda, I. Measurement of the Resonant Magneto-Optical Kerr Effect Using a Free Electron Laser. Appl. Sci. 2017, 7, 662. https://doi.org/10.3390/app7070662
Yamamoto S, Matsuda I. Measurement of the Resonant Magneto-Optical Kerr Effect Using a Free Electron Laser. Applied Sciences. 2017; 7(7):662. https://doi.org/10.3390/app7070662
Chicago/Turabian StyleYamamoto, Shingo, and Iwao Matsuda. 2017. "Measurement of the Resonant Magneto-Optical Kerr Effect Using a Free Electron Laser" Applied Sciences 7, no. 7: 662. https://doi.org/10.3390/app7070662




