Estimating Co-Contraction Activation of Trunk Muscles Using a Novel Musculoskeletal Model for Pregnant Women
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participant
2.2. Sitting Down and Standing Up Experiment
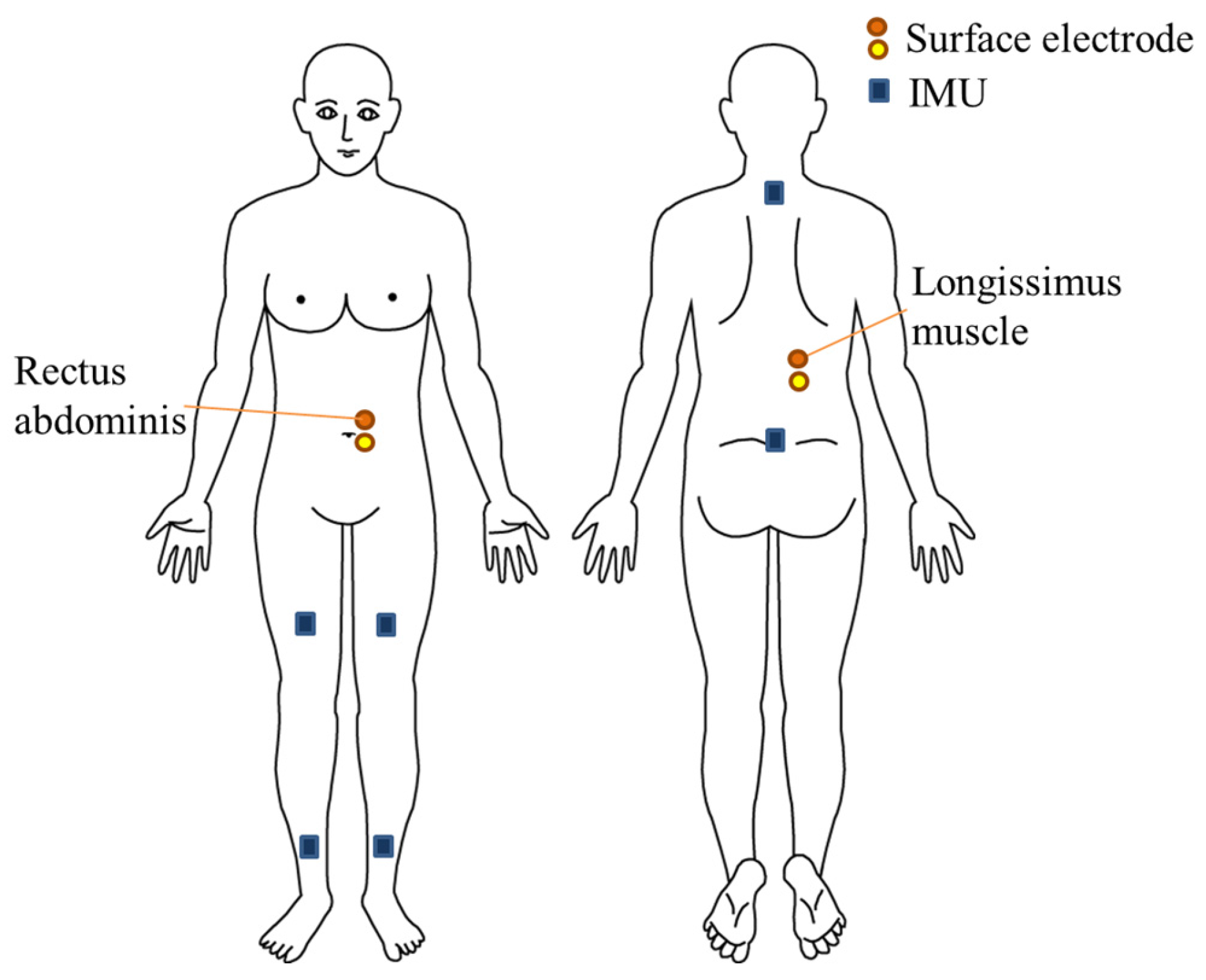
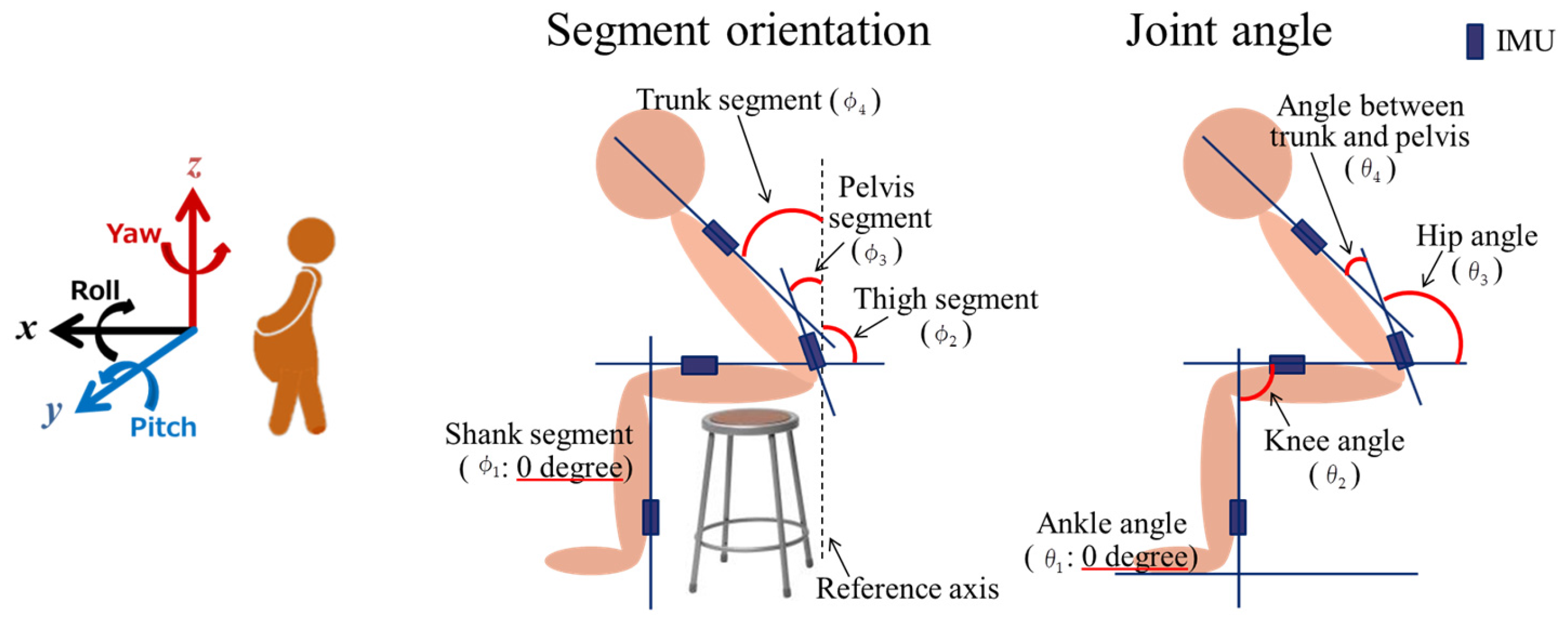
2.2.1. Motion Analysis
2.2.2. Electromyography
2.3. Proposal of Musculoskeletal Models for Pregnant Women
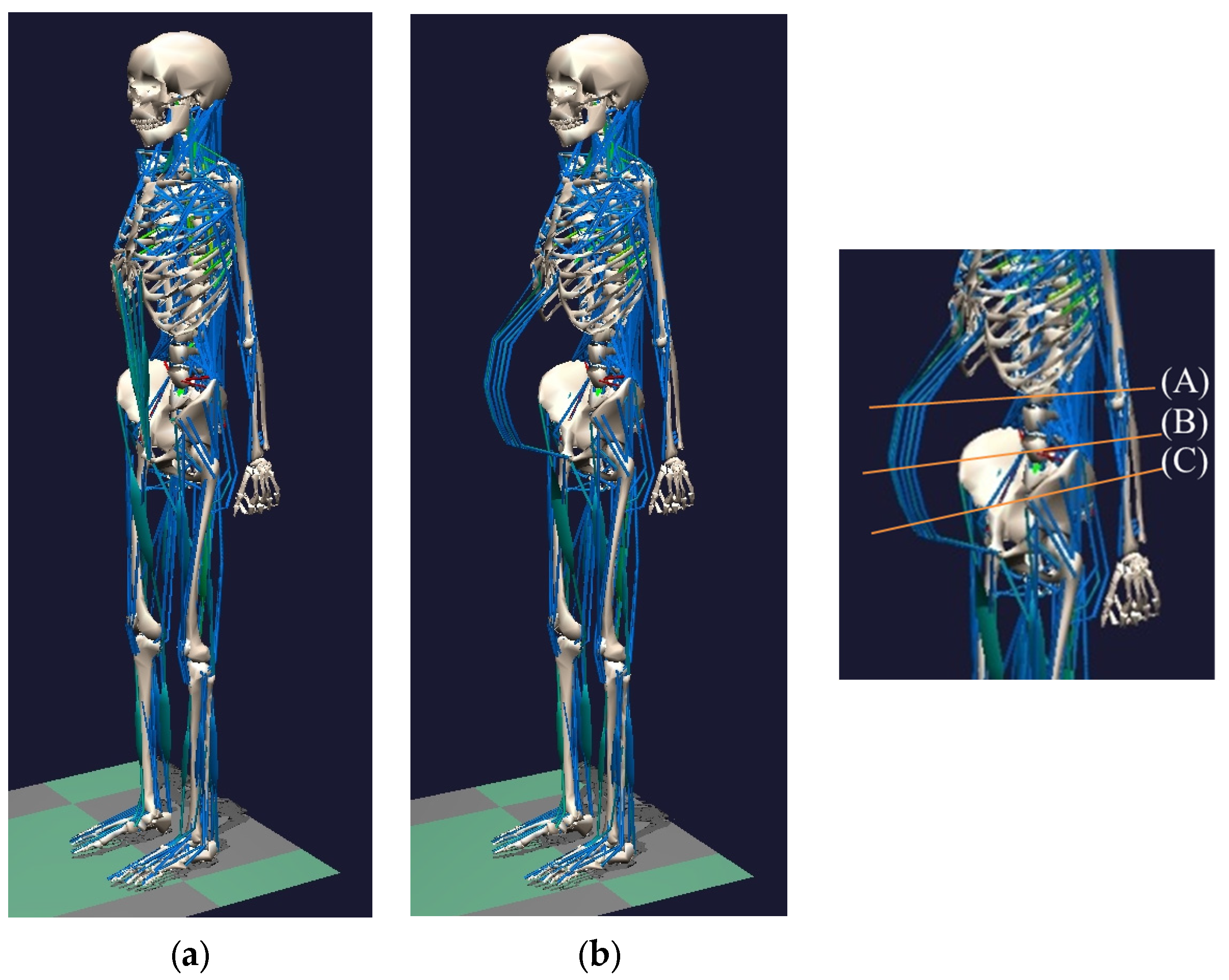
2.3.1. Changing the Skeletal Model
2.3.2. Changing the Muscular Model
2.3.3. Supplementing Body Weight during Pregnancy
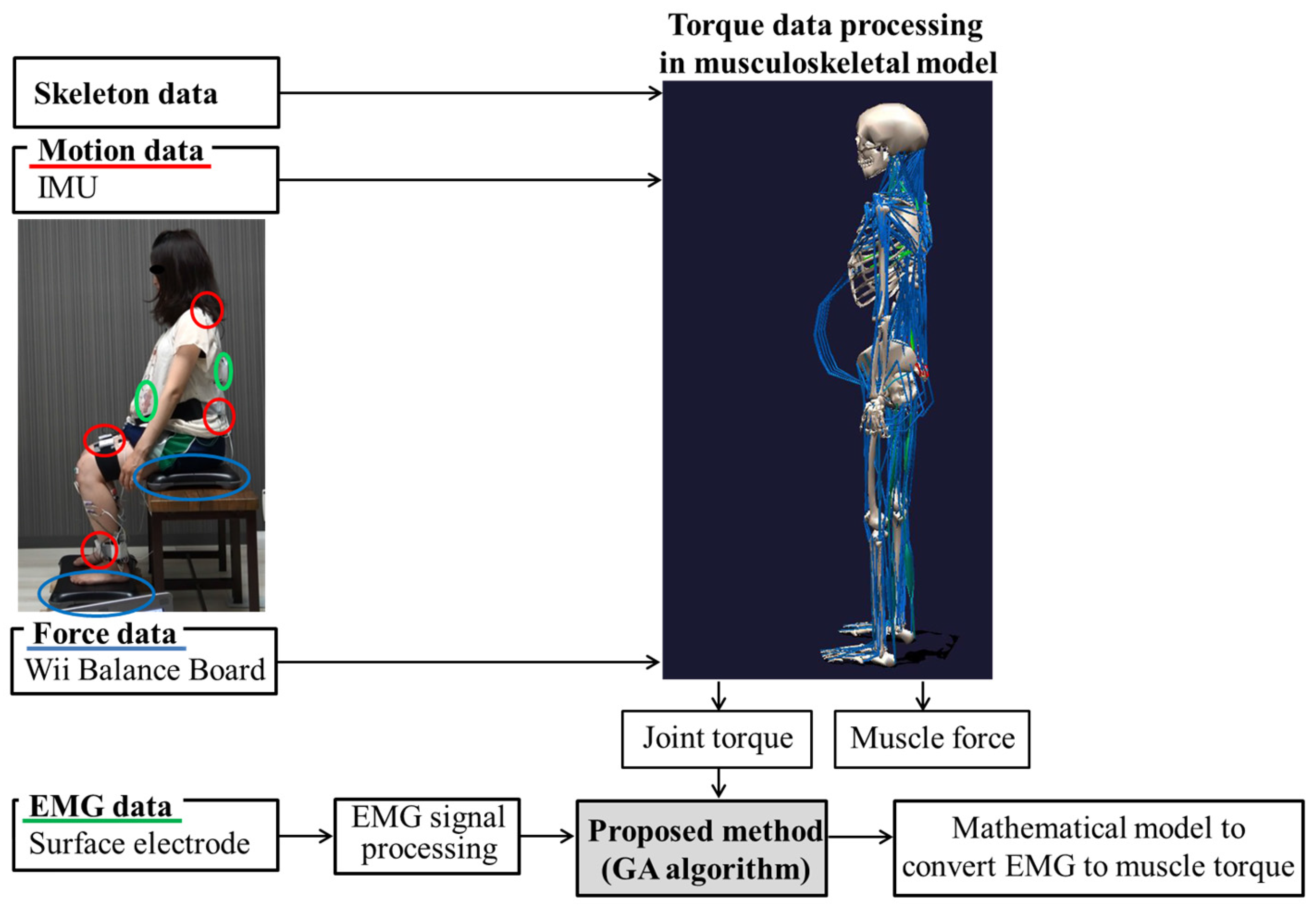
2.4. Measured Data Processing
2.5. Estimating Co-Contraction Activation Using a GA
3. Results and Discussion
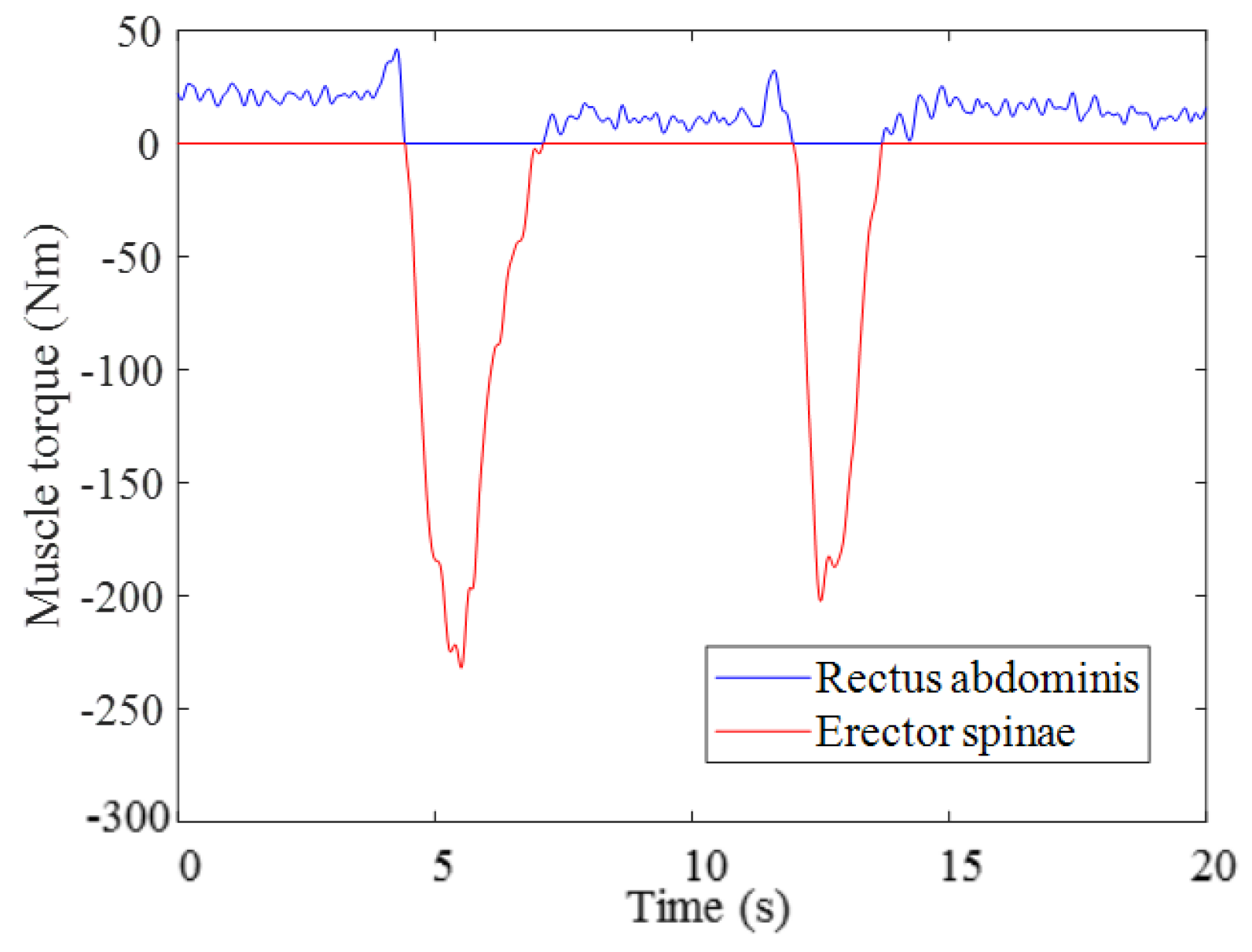
3.1. Result of Estimating Muscle Torque with the Proposed Musculoskeletal Model of a Pregnant Woman
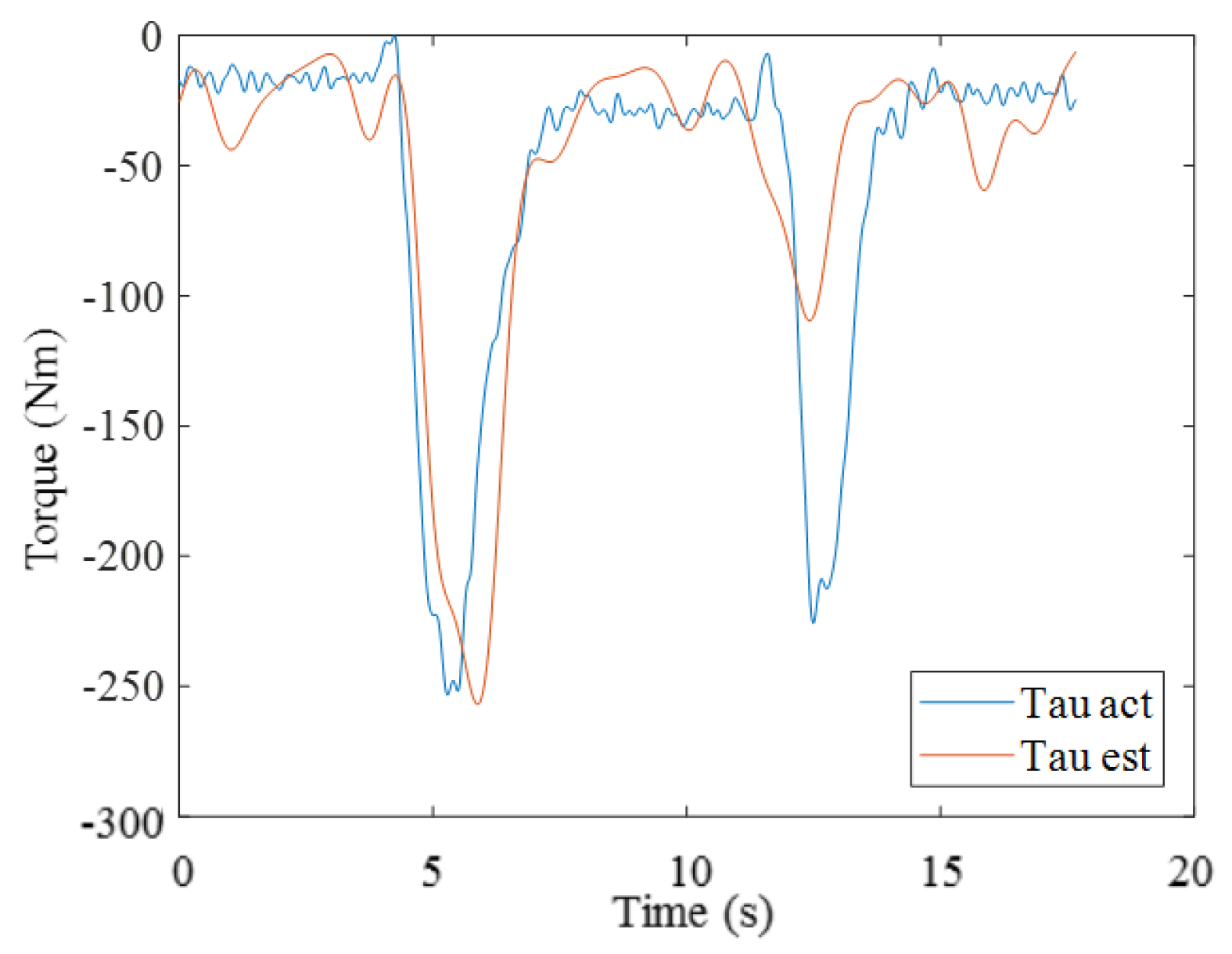
3.2. Results from Estimating Muscle Torque Using the GA
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Borg-Stein, J.; Dugan, S.A. Musculoskeletal disorders of pregnancy, delivery and postpartum. Phys. Med. Rehabil. Clin. N. Am. 2007, 18, 459–476. [Google Scholar] [CrossRef]
- Fast, A.; Weiss, L.; Ducommun, E.J.; Medina, E.; Butler, J.G. Low-back-pain in pregnancy—Abdominal muscles, sit-up performance, and back pain. Spine 1990, 15, 28–30. [Google Scholar] [CrossRef] [PubMed]
- Ho, S.S.; Yu, W.W.; Lao, T.T.; Chow, D.H.; Chung, J.W.; Li, Y. Effectiveness of maternity support belts in reducing low back pain during pregnancy: A review. J. Clin. Nurs. 2009, 18, 1523–1532. [Google Scholar] [CrossRef] [PubMed]
- Sneag, D.B.; Bendo, J.A. Pregnancy-related low back pain. Orthopedics 2007, 30, 839–845, quiz 846–7. [Google Scholar] [PubMed]
- Casagrande, D.; Gugala, Z.; Clark, S.M.; Lindsey, R.W. Low back pain and pelvic girdle pain in pregnancy. J. Am. Acad. Orthop. Surg. 2015, 23, 539–549. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.H.; Meijer, O.G.; Uegaki, K.; Mens, J.M.; van Dieen, J.H.; Wuisman, P.I.; Ostgaard, H.C. Pregnancy-related pelvic girdle pain (PPP), I: Terminology, clinical presentation, and prevalence. Eur. Spine J. 2004, 13, 575–589. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.H.; Meijer, O.G.; Bruijn, S.M.; Hu, H.; van Dieen, J.H.; Lamoth, C.J.; van Royen, B.J.; Beek, P.J. Gait in pregnancy-related pelvic girdle pain: Amplitudes, timing, and coordination of horizontal trunk rotations. Eur. Spine J. 2008, 17, 1160–1169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lund, T.; Nydegger, T.; Schlenzka, D.; Oxland, T.R. Three-dimensional motion patterns during active bending in patients with chronic low back pain. Spine 2002, 27, 1865–1874. [Google Scholar] [CrossRef] [PubMed]
- Al-Eisa, E.; Egan, D.; Deluzio, K.; Wassersug, R. Effects of pelvic asymmetry and low back pain on trunk kinematics during sitting: A comparison with standing. Spine 2006, 31, E135–E143. [Google Scholar] [CrossRef] [PubMed]
- Borg-Stein, J.; Dugan, S.A.; Gruber, J. Musculoskeletal aspects of pregnancy. Am. J. Phys. Med. Rehabil. 2005, 84, 180–192. [Google Scholar] [CrossRef] [PubMed]
- Doorenbosch, C.A.; Harlaar, J.; Roebroeck, M.E.; Lankhorst, G.J. Two strategies of transferring from sit-to-stand; the activation of monoarticular and biarticular muscles. J. Biomech. 1994, 27, 1299–1307. [Google Scholar] [CrossRef]
- Falconer, K.; Winter, D.A. Quantitative assessment of co-contraction at the ankle joint in walking. Electromyogr. Clin. Neurophysiol. 1985, 25, 135–149. [Google Scholar] [PubMed]
- Dounskaia, N. The internal model and the leading joint hypothesis: Implications for control of multi-joint movements. Exp. Brain Res. 2005, 166, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Langholz, J.B.; Westman, G.; Karlsteen, M. Musculoskeletal modelling in sports—Evaluation of different software tools with focus on swimming. Procedia Eng. 2016, 147, 281–287. [Google Scholar] [CrossRef]
- Blache, Y.; Begon, M. Influence of shoulder kinematic estimate on joint and muscle mechanics predicted by musculoskeletal model. IEEE Trans. Biomed. Eng. 2017. [Google Scholar] [CrossRef] [PubMed]
- Rajagopal, A.; Dembia, C.L.; DeMers, M.S.; Delp, D.D.; Hicks, J.L.; Delp, S.L. Full-body musculoskeletal model for muscle-driven simulation of human gait. IEEE Trans. Biomed. Eng. 2016, 63, 2068–2079. [Google Scholar] [CrossRef] [PubMed]
- Nakashima, M.; Komura, T. An analysis of muscle load on the erector spinae of a pregnant woman. J. Biomech. Sci. Eng. 2010, 5, 357–367. [Google Scholar] [CrossRef]
- Wagner, D.W.; Stepanyan, V.; Shippen, J.M.; DeMers, M.S.; Gibbons, R.S.; Andrews, B.J.; Creasey, G.H.; Beaupre, G.S. Consistency among musculoskeletal models: Caveat utilitor. Ann. Biomed. Eng. 2013, 41, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Cholewicki, J.; Mcgill, S.M. Emg assisted optimization—A hybrid approach for estimating muscle forces in an indeterminate biomechanical model. J. Biomech. 1994, 27, 1287–1289. [Google Scholar] [CrossRef]
- Gagnon, D.; Plamondon, A.; Lariviere, C. A biomechanical comparison between expert and novice manual materials handlers using a multi-joint emg-assisted optimization musculoskeletal model of the lumbar spine. J. Biomech. 2016, 49, 2938–2945. [Google Scholar] [CrossRef] [PubMed]
- Oyong, A.W.; Parasuraman, S.; Jauw, V.L. Robot assisted stroke rehabilitation: Estimation of muscle force /joint torque from EMG using GA. In Proceedings of the 2010 IEEE EMBS Conference on Biomedical Engineering and Sciences, Kuala Lumpur, Malaysia, 30 November–2 December 2010; pp. 341–347. [Google Scholar]
- Cheng, P.T.; Chen, C.L.; Wang, C.M.; Hong, W.H. Leg muscle activation patterns of sit-to-stand movement in stroke patients. Am. J. Phys. Med. Rehabil. 2004, 83, 10–16. [Google Scholar] [CrossRef] [PubMed]
- Ng, J.K.F.; Kippers, V.; Parnianpour, M.; Richardson, C.A. EMG activity normalization for trunk muscles in subjects with and without back pain. Med. Sci. Sport Exerc. 2002, 34, 1082–1086. [Google Scholar] [CrossRef]
- Shippen, J.; May, B. Bob—Biomechanics in matlab. In Proceedings of the 11th International Conference BIOMDOLE 2016, Druskininkai, Lithuania, 20–22 October 2016. [Google Scholar]
- Shippen, J.; May, B. Teaching Biomechanical Analysis Using Matlab/Simulink; Coventry University: Coventry, UK, 2013. [Google Scholar]
- Life and Welfare Technology Center. “Human Characteristics Database”, Human Characteristics Database. Available online: http://www.tech.nite.go.jp/human/indexeng.html (accessed on 6 June 2017).
- Matsuo, A.; Fukunaga, T.; Funato, K.; Asami, T.; Yamaguchi, T. Examination of mass and location of the center of gravity of segment of the body in Japanese women. Proc. Dep. Sports Sci. Coll. Arts Sci Univ. Tokyo 1990, 24, 37–54. [Google Scholar]
- Kioka, E.; Mori, Y. Basic study on designing maternity wear corresponding to change of body form in the later stage of pregnancy (Part 1): Experimental study on suitability of maternity dress. J. Home Econ. Jpn. 1994, 45, 137–146. [Google Scholar]
- Sunaga, Y.; Kanemura, N.; Anan, M.; Takahashi, M.; Shinkoda, K. Estimation of inertial parameters of the lower trunk in pregnant japanese women: A longitudinal comparative study and application to motion analysis. Appl. Ergon. 2016, 55, 173–182. [Google Scholar] [CrossRef] [PubMed]
- Madgwick, S.O.H.; Harrison, A.J.L.; Vaidyanathan, R. Estimation of imu and marg orientation using a gradient descent algorithm. Int. Conf. Rehabil. Robot. 2011. [Google Scholar] [CrossRef]
- Hall, H.; Cramer, H.; Sundberg, T.; Ward, L.; Adams, J.; Moore, C.; Sibbritt, D.; Lauche, R. Theeffectiveness of complementary manual therapies for pregnancy-related back and pelvic pain: A systematic review with meta-analysis. Medicine 2016, 95, e4723. [Google Scholar] [CrossRef] [PubMed]
- Goulart, F.R.; Valls-Sole, J. Patterned electromyographic activity in the sit-to-stand movement. Clin. Neurophysiol. 1999, 110, 1634–1640. [Google Scholar] [CrossRef]






| Age (years) | Duration of Pregnancy (weeks) | Height (cm) | Mass (at the Experiment) (kg) | Mass (before Pregnancy) (kg) | Experience of Childbirth |
|---|---|---|---|---|---|
| 24 | 36 | 153 | 50 | 41 | none |
| Spinal Level | Data from Previous Research [28] | Data from a Participant of This Study | ||
|---|---|---|---|---|
| Girth (m) (Measured Value) | Depth (m) (Measured Value) | Girth (m) (Measured Value) | Depth (m) (Calculated Value) | |
| L2 (A) † | 0.865 | 0.266 | 0.840 | 0.258 |
| L4 (B) | 0.936 | 0.289 | 0.905 | 0.279 |
| L5 (C) | 0.938 | 0.290 | 0.910 | 0.281 |
| Associated Model Parameters | RMSEl | RMSEv | ||||
|---|---|---|---|---|---|---|
| Trial 1 | x1 = 5008.0 | x2 = 1.8 | x3 = 1010.0 | x4 = 2.2 | 59.1027 | 69.0343 |
| x5 = 282.4 | x6 = 0.5 | x7 = 1092.2 | x8 = 75.7 | |||
| Trial 2 | x1 = 1560.2 | x2 = 2.1 | x3 = 1200.0 | x4 = 1.9 | 59.0246 | 39.0054 |
| x5 = −197.0 | x6 = 6.4 | x7 = 2550.1 | x8 = 1.4 | |||
| Trial 3 | x1 = 1666.3 | x2 = 2.0 | x3 = 2187.1 | x4 = 1.8 | 74.3103 | 57.0290 |
| x5 = 2180.7 | x6 = 1.2 | x7 = 2998.5 | x8 = 8.9 | |||
| Trial 4 | x1 = 302.5 | x2 = 2.0 | x3 = 1670.2 | x4 = 1.8 | 76.7090 | 54.4272 |
| x5 = 3980.9 | x6 = 7.2 | x7 = 2999.3 | x8 = 1.4 | |||
| Trial 5 | x1 = 613.1 | x2 = 2.0 | x3 = 826.6 | x4 = 2.0 | 66.0801 | 59.7488 |
| x5 = 1906.3 | x6 = 1.3 | x7 = −1397.6 | x8 = 3.4 | |||
| Trial 6 | x1 = 895.3 | x2 = 1.8 | x3 = 737.4 | x4 = 1.7 | 74.1615 | 58.9333 |
| x5 = 2006.8 | x6 = 1.7 | x7 = 1555.1 | x8 = 1.3 | |||
| Trial 7 | x1 = 5002.0 | x2 = 1.4 | x3 = 1012.0 | x4 = 2.1 | 60.4983 | 61.6914 |
| x5 = −801.5 | x6 = 1.1 | x7 = 1051.2 | x8 = 0.8 | |||
| Trial 8 | x1 = 787.4 | x2 = 2.0 | x3 = 539.7 | x4 = 2.0 | 72.2385 | 53.9310 |
| x5 = 1925.0 | x6 = 8.1 | x7 = 4619.7 | x8 = 1.6 | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morino, S.; Takahashi, M. Estimating Co-Contraction Activation of Trunk Muscles Using a Novel Musculoskeletal Model for Pregnant Women. Appl. Sci. 2017, 7, 1067. https://doi.org/10.3390/app7101067
Morino S, Takahashi M. Estimating Co-Contraction Activation of Trunk Muscles Using a Novel Musculoskeletal Model for Pregnant Women. Applied Sciences. 2017; 7(10):1067. https://doi.org/10.3390/app7101067
Chicago/Turabian StyleMorino, Saori, and Masaki Takahashi. 2017. "Estimating Co-Contraction Activation of Trunk Muscles Using a Novel Musculoskeletal Model for Pregnant Women" Applied Sciences 7, no. 10: 1067. https://doi.org/10.3390/app7101067





