Shift-Peristrophic Multiplexing for High Density Holographic Data Storage
Abstract
:1. Introduction
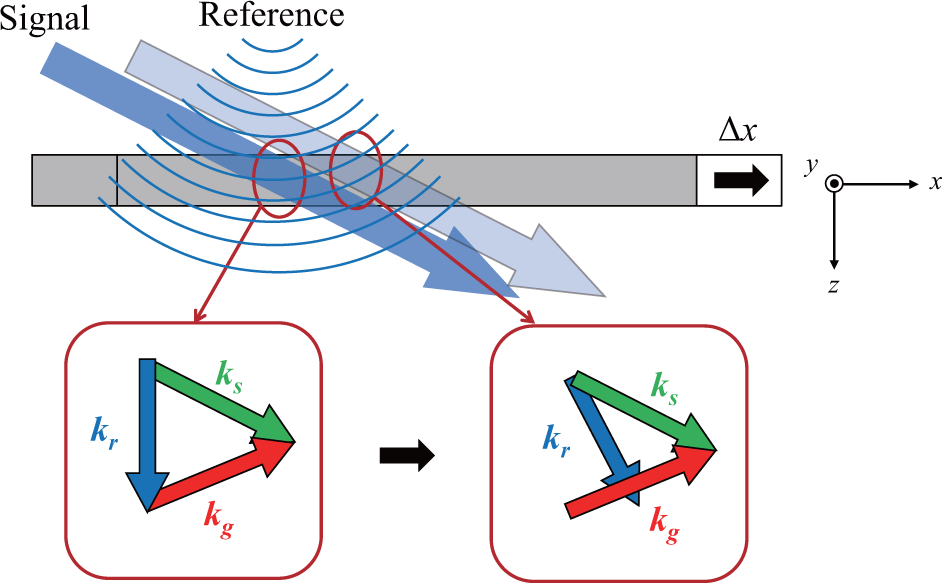
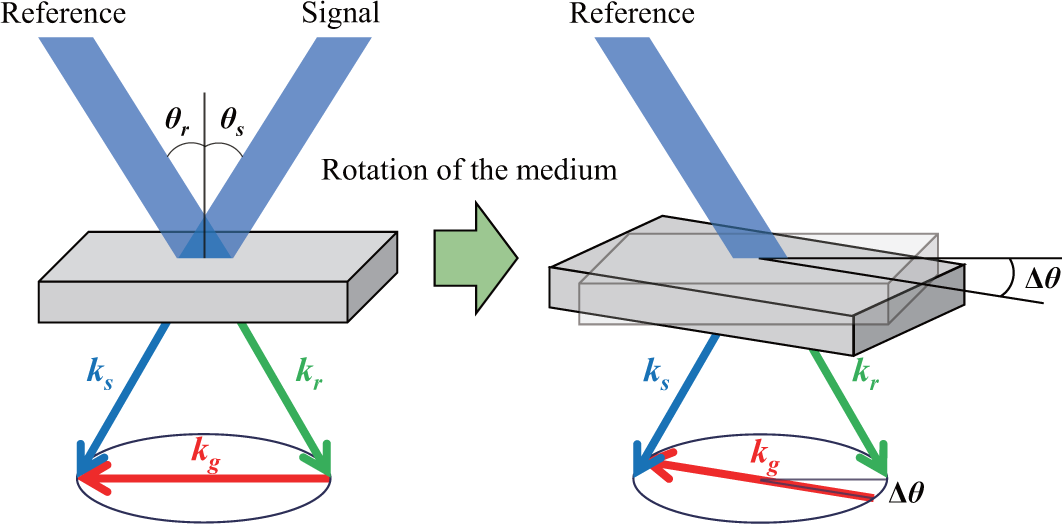
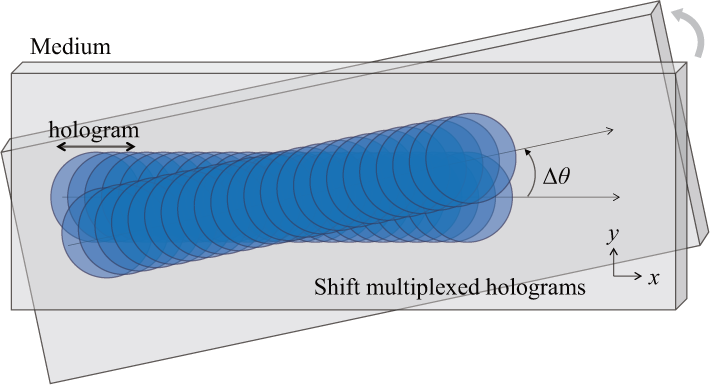
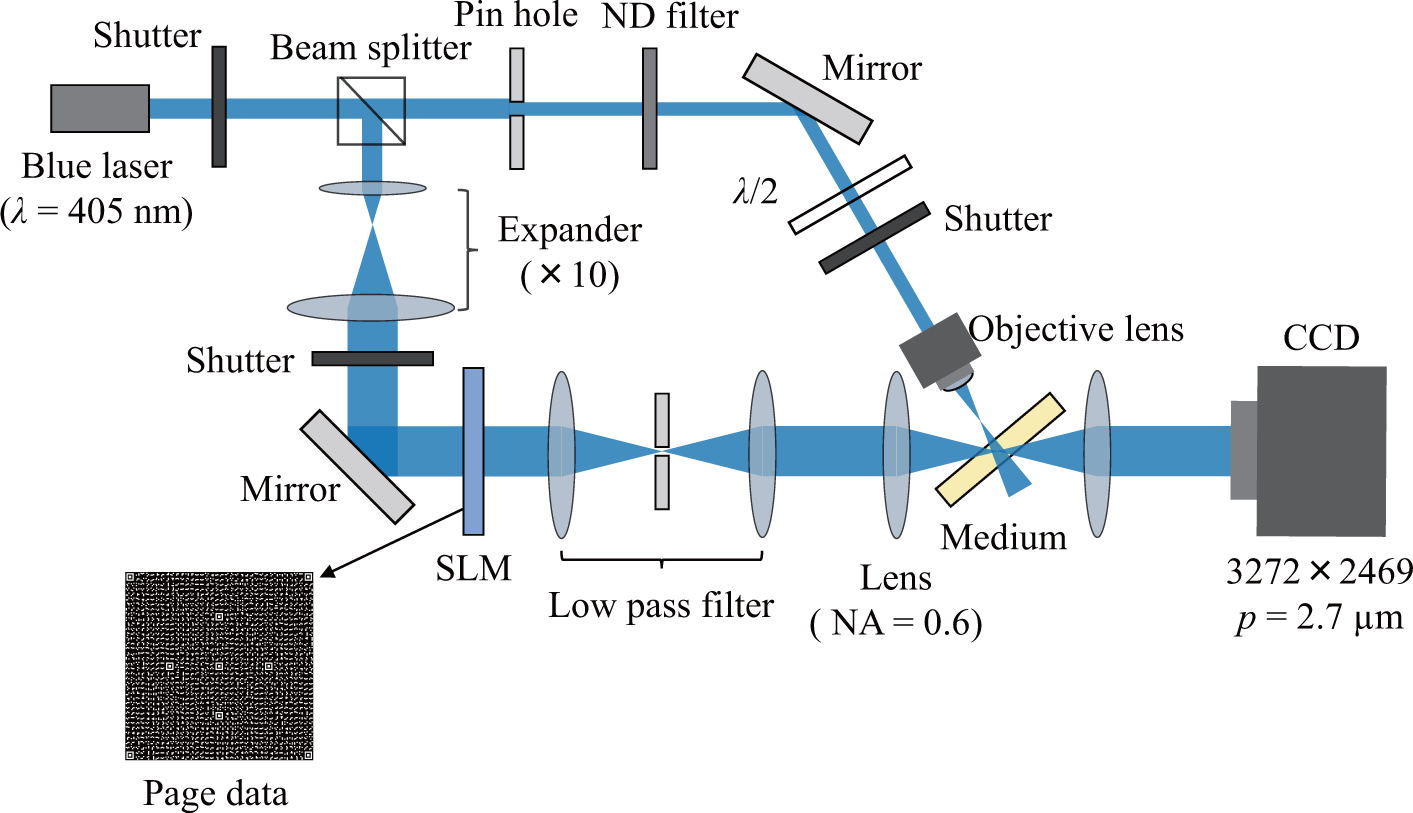
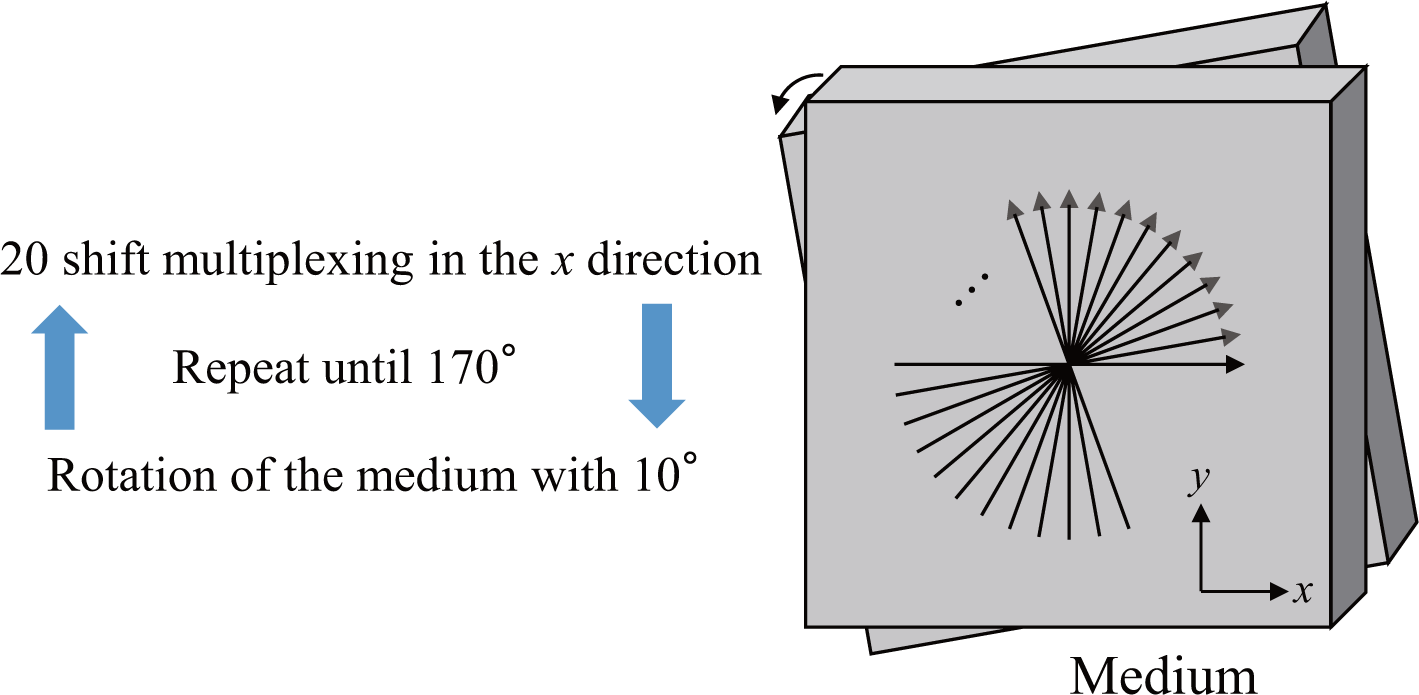
2. Recording Method
3. Experimental Evaluation
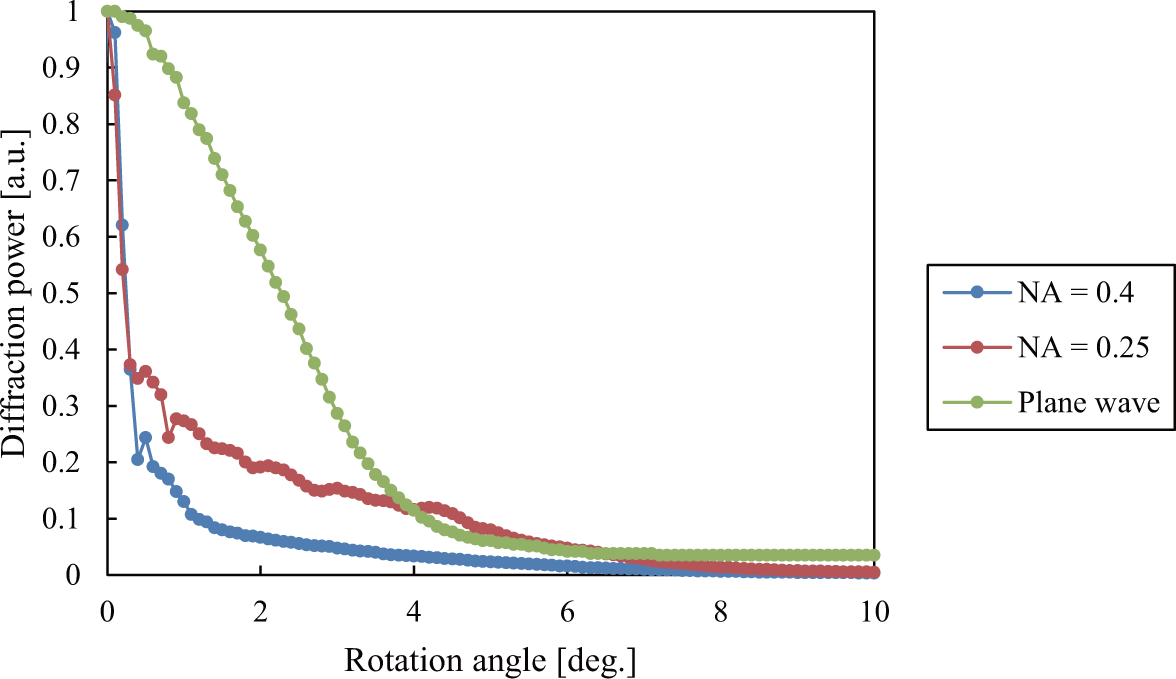
3.1. Evaluation of Basic Property
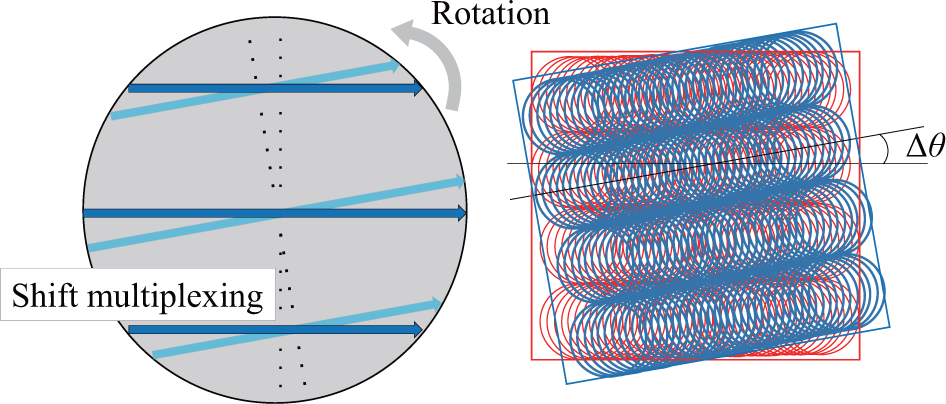
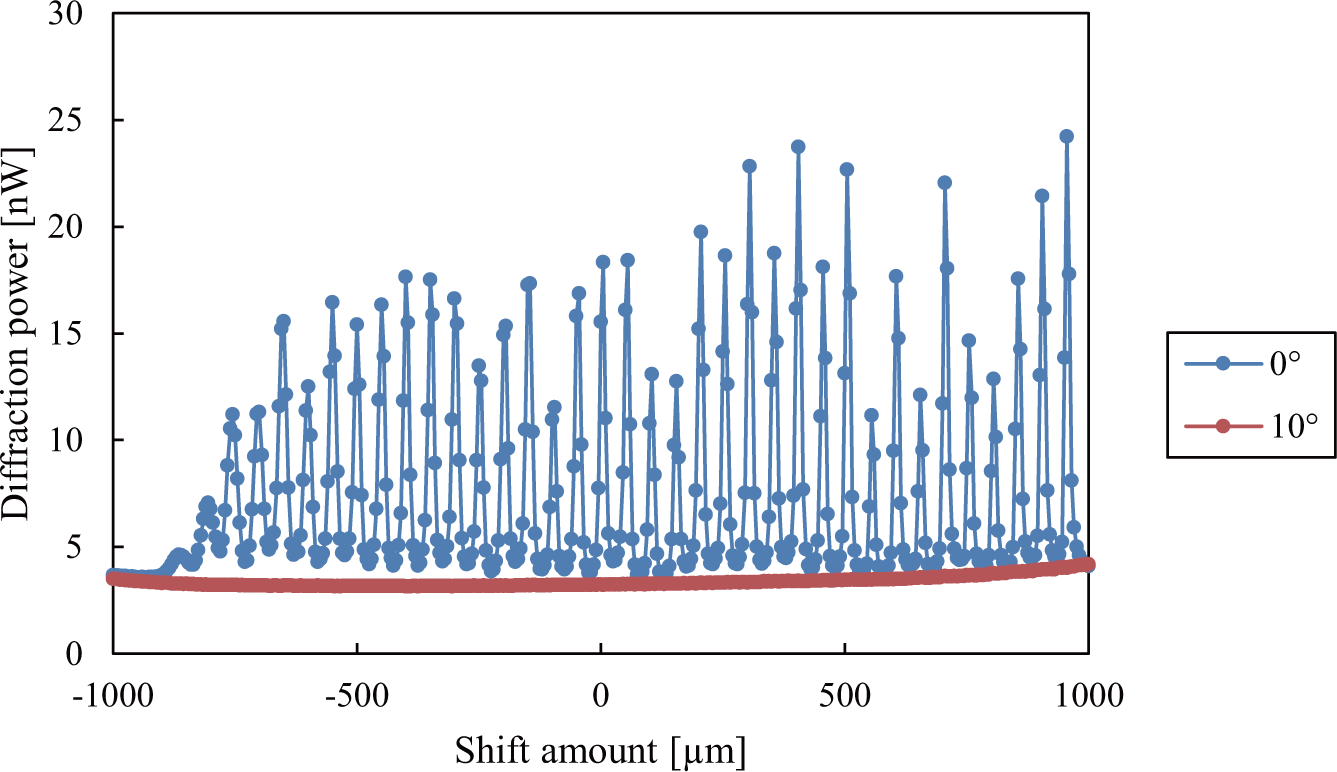
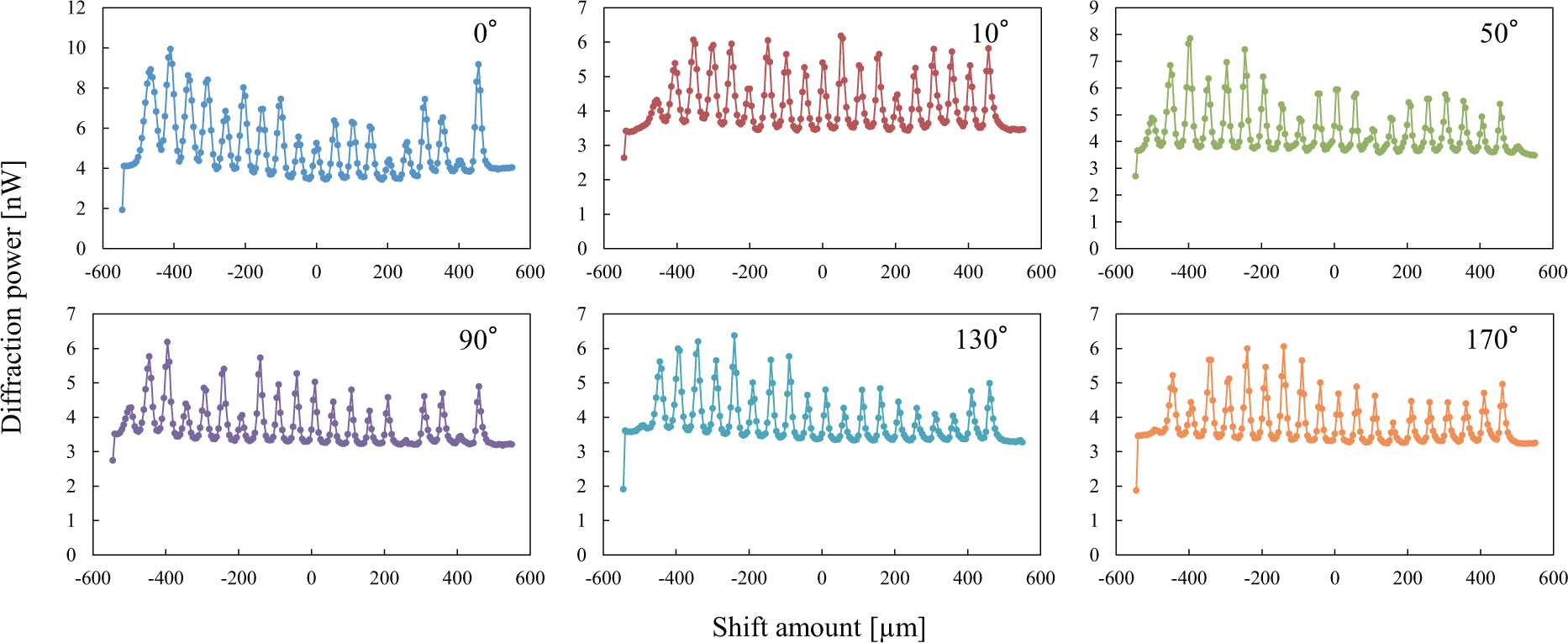
3.2. Evaluation of Shift-Peristrophic Multiplexing
4. Conclusions
Conflicts of Interest
References
- Hesselink, L.; Orlov, S.S.; Bashaw, M.C. Holographic data storage systems. Proc. IEEE. 2004, 92, 1231–1280. [Google Scholar]
- Coufal, H.J.; Psaltis, D.; Sincerbox, G. Hologr. Data Storage; Springer: Berlin, Germany, 2000. [Google Scholar]
- Curtis, K.; Dhar, L.; Hill, A.; Wilson, W.; Ayres, M. Materials for Holography. In Holographic Data Storage: From Theory to Practical Systems; Willey: New York, NY, USA, 2010; pp. 105–132. [Google Scholar]
- Lawrence, J.R.; O’Neill, F.T.; Sheridan, J.T. Photopolymer holographic recording material. Optik 2001, 112, 449–463. [Google Scholar]
- Ortuño, M.; Fernández, E.; Gallego, S.; Beléndez, A.; Pascual, I. New photopolymer holographic recording material with sustainable design. Opt. Express. 2007, 15, 12425–12435. [Google Scholar]
- Zhu, J.; Wang, G.; Hao, Y.; Xie, B.; Cheng, A.Y.S. Highly sensitive and spatially resolved polyvinyl alcohol/acrylamide photopolymer for real-time holographic applications. Opt. Express. 2010, 18, 18106–18112. [Google Scholar]
- Mok, F.H. Angle-multiplexed storage of 5000 holograms in lithium niobate. Opt. Lett. 1993, 18, 915–917. [Google Scholar]
- Staebler, D.L.; Burke, W.J.; Phillips, W.; Amodei, J.J. Multiple storage and erasure of fixed holograms in Fe-doped LiNbO3. Appl. Phys. Lett. 1975, 26, 182–184. [Google Scholar]
- Heanue, J.F.; Bashaw, M.C.; Hesselink, L. Volume holographic storage and retrieval of digital data. Science 1994, 265, 749–752. [Google Scholar]
- Rakuljic, G.A.; Leyva, V.; Yariv, A. Optical data storage by using orthogonal wavelength-multiplexed volume holograms. Opt. Lett. 1992, 20, 1471–1473. [Google Scholar]
- Campbell, S.; Yi, X.; Yeh, P. Hybrid sparse-wavelength angle-multiplexed optical data storage system. Opt. Lett. 1994, 24, 2161–2163. [Google Scholar]
- Denz, C.; Pauliat, G.; Roosen, G. Volume hologram multiplexing using a deterministic phase encoding method. Opt. Commun. 1991, 85, 171–176. [Google Scholar]
- Heanue, J.F.; Bashaw, M.C.; Hesselink, L. Recall of linear combinations of stored data pages based on phase-code multiplexing in volume holography. Opt. Lett. 1994, 19, 1079–1081. [Google Scholar]
- Curtis, K.; Pu, A.; Psaltis, D. Method for holographic storage using peristrophic multiplexing. Opt. Lett. 1994, 19, 993–994. [Google Scholar]
- Fernández, E.; García, C.; Pascual, I.; Ortuño, M.; Gallego, S.; Beléndez, A. Optimization of a thick polyvinyl alcohol-acrylamide photopolymer for data storage using a combination of angular and peristrophic holographic multiplexing. Appl. Opt. 2006, 45, 7661–7666. [Google Scholar]
- Fernández, E.; Ortuño, M.; Gallego, S.; García, C.; Beléndez, A.; Pascual, I. Comparison of peristrophic multiplexing and a combination of angular and peristrophic holographic multiplexing in a thick PVA/acrylamide photopolymer for data storage. Appl. Opt. 2007, 46, 5368–5373. [Google Scholar]
- Psaltis, D.; Levene, M.; Pu, A.; Barbastathis, G.; Curtis, K. Holographic storage using shift multiplexing. Opt. Lett. 1995, 20, 782–784. [Google Scholar]
- Steckman, G.J.; Pu, A.; Psaltis, D. Storage density of shift-multiplexed holographic memory. Appl. Opt. 2001, 40, 3387–3394. [Google Scholar]
- Anderson, K.; Curtis, K. Polytopic multiplexing. Opt. Lett. 2004, 29, 1402–1404. [Google Scholar]
- Jang, J.; Shin, D.; Park, Y. Holographic data storage by combined use of peristrophic, angular, and spatial multiplexing. Opt. Eng. 2000, 39, 2975–2981. [Google Scholar]
- Barbastathis, G.; Levene, M.; Psaltis, D. Shift multiplexing with spherical reference waves. Appl. Opt. 1996, 35, 2403–2417. [Google Scholar]
- Yoshida, S.; Kurata, H.; Ozawa, S.; Okubo, K.; Yamamoto, M.; Koga, S.; Tanaka, A. High-density holographic data storage using three-dimensional shift multiplexing with spherical reference wave. Jpn. J. Appl. Phys. 2013, 52. [Google Scholar] [CrossRef]
- Yoshida, S.; Matsubara, T.; Kurata, H.; Horiuchi, S.; Yamamoto, M. Multi-dimensional shift multiplexing technique with spherical reference waves. IEICE Trans. Electron. 2013, E96-C, 1520–1524. [Google Scholar]

| Wavelength λ | 405 nm |
| Focal length f | 60 mm |
| Medium thickness L (mm) | 1.5 |
| SLM pixel size Δ | 40 μm |
| CCD pixel size p | 2.7 μm |
| Incident angle of signal θs | 45° |
| Incident angle of signal θr | 15° |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ushiyama, Z.; Kurata, H.; Tsukamoto, Y.; Yoshida, S.; Yamamoto, M. Shift-Peristrophic Multiplexing for High Density Holographic Data Storage. Appl. Sci. 2014, 4, 148-157. https://doi.org/10.3390/app4020148
Ushiyama Z, Kurata H, Tsukamoto Y, Yoshida S, Yamamoto M. Shift-Peristrophic Multiplexing for High Density Holographic Data Storage. Applied Sciences. 2014; 4(2):148-157. https://doi.org/10.3390/app4020148
Chicago/Turabian StyleUshiyama, Zenta, Hiroyuki Kurata, Yu Tsukamoto, Shuhei Yoshida, and Manabu Yamamoto. 2014. "Shift-Peristrophic Multiplexing for High Density Holographic Data Storage" Applied Sciences 4, no. 2: 148-157. https://doi.org/10.3390/app4020148
APA StyleUshiyama, Z., Kurata, H., Tsukamoto, Y., Yoshida, S., & Yamamoto, M. (2014). Shift-Peristrophic Multiplexing for High Density Holographic Data Storage. Applied Sciences, 4(2), 148-157. https://doi.org/10.3390/app4020148




