Fluorinated and Non-Fluorinated Electro-Optic Copolymers: Determination of the Time and Temperature Stability of the Induced Electro-Optic Coefficient
Abstract
:1. Introduction
2. Electro-Optic Properties of Polymers
2.1. Second Order Nonlinear Susceptibility
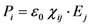
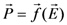
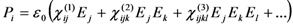
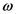 of the incident electromagnetic field, like in the case of the linear term χ(1), but the linear term responsible for the refractive index is modified by the presence of the static field:
of the incident electromagnetic field, like in the case of the linear term χ(1), but the linear term responsible for the refractive index is modified by the presence of the static field:
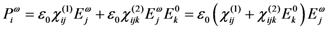
2.2. Electro-Optic Properties of a Single Molecule
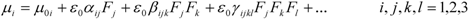
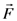 that is related to the macroscopic electric field
that is related to the macroscopic electric field 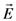 by the local field factor fω via the following relation:
by the local field factor fω via the following relation:
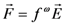
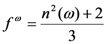
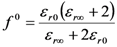
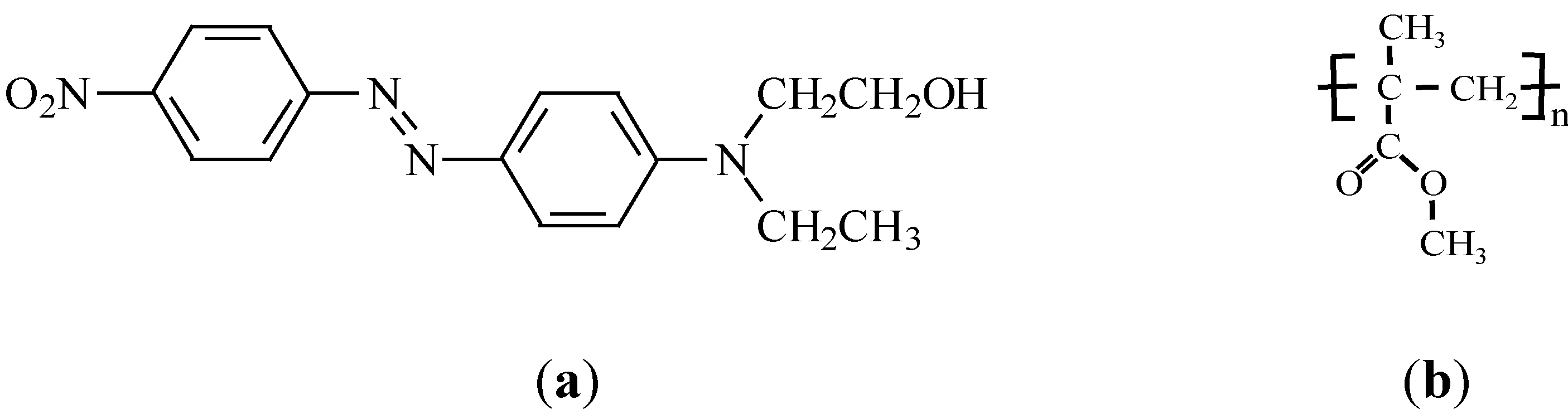
| Chromophore | λmax (nm, CHCl3) | μ0 (Debye) | β0 (10−30 esu) | β1.9μm (10−30 esu) | μ0β 1.9μm (10−48 esu) |
|---|---|---|---|---|---|
| DR1 | 480 (497) | 7.7 (8.7) | 40 | 5,046 | 580 |
2.3. Inducing of the Macroscopic Electro-Optic Properties
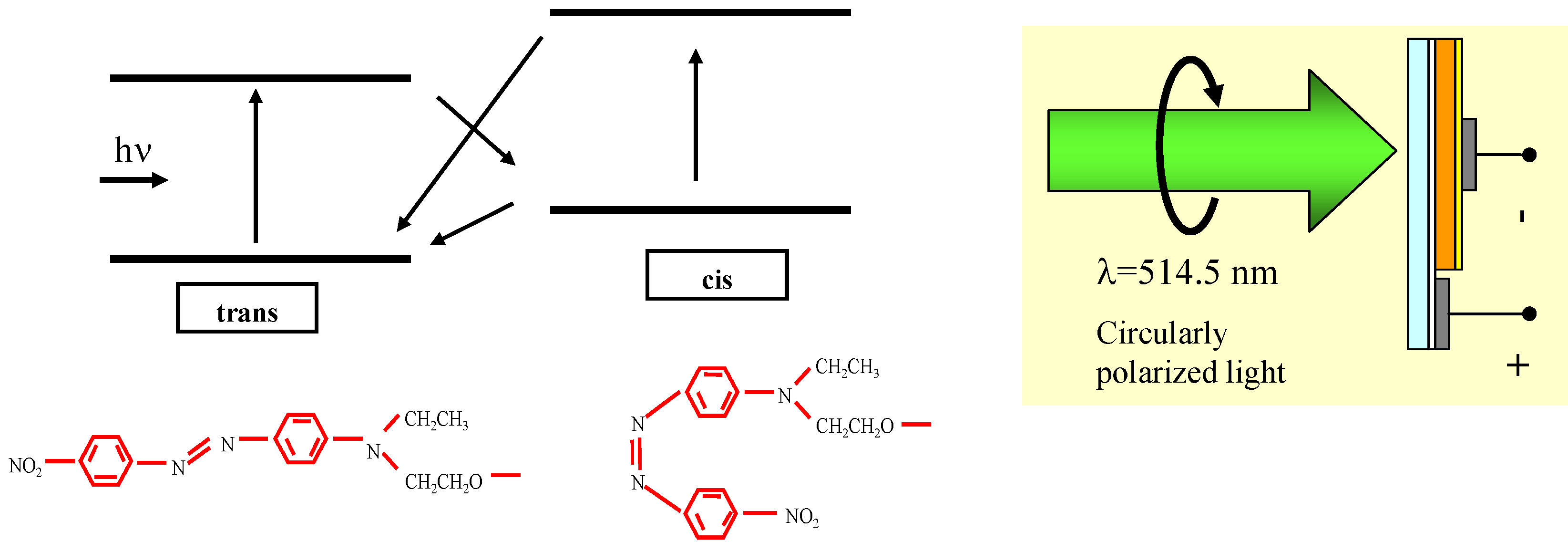
2.4. Steady-State Properties of the Induced Electo-Optic Coefficient
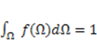 . In the following we consider that z is the direction of the poling field and 3 is the direction of the long axis of the molecule.
. In the following we consider that z is the direction of the poling field and 3 is the direction of the long axis of the molecule.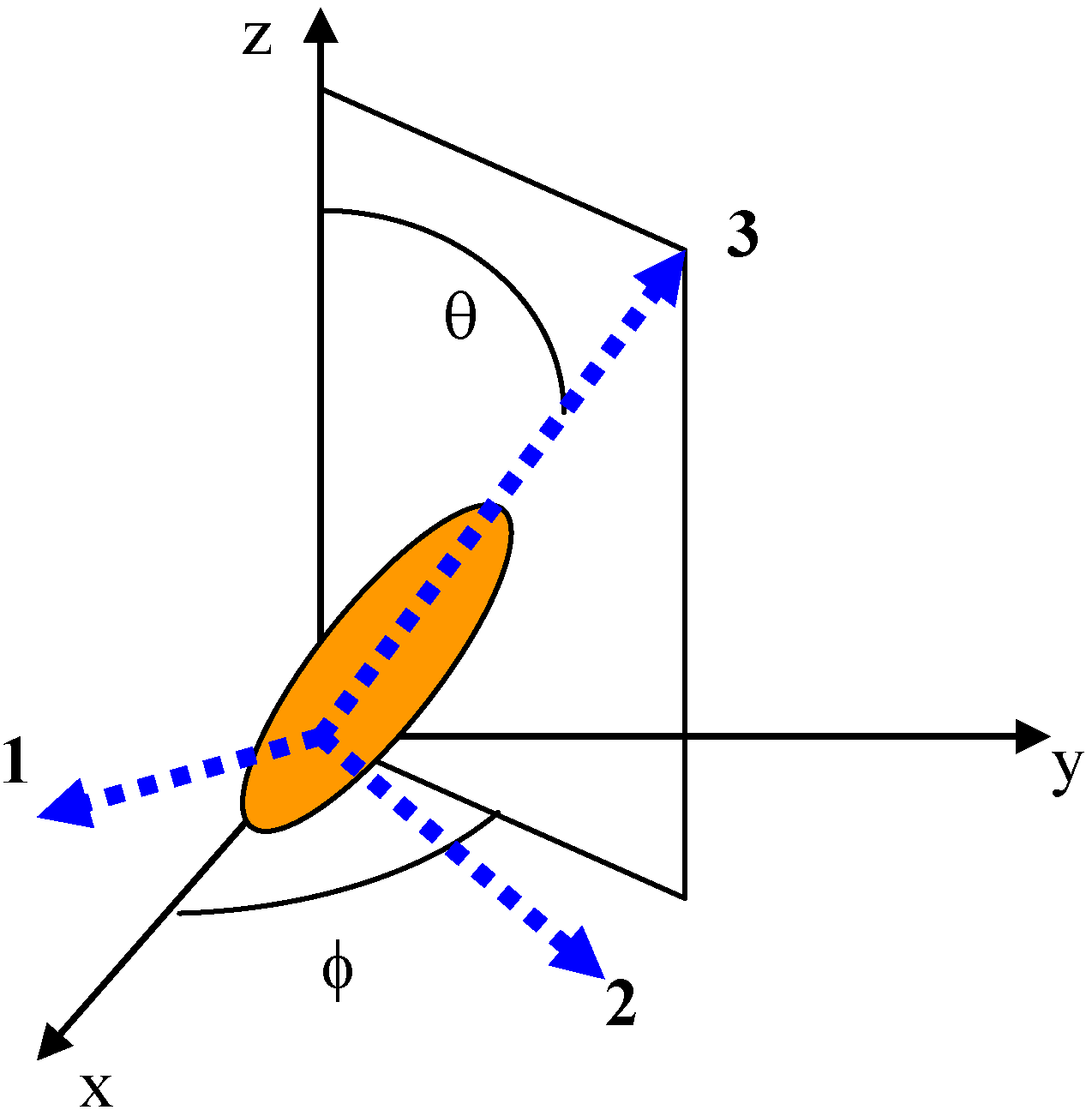
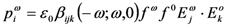
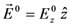 and by an optical field
and by an optical field 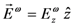 , both of them along the z direction, is:
, both of them along the z direction, is:
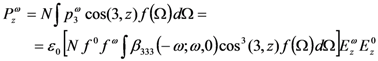
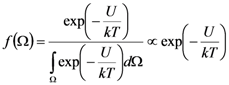
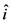 ,
, 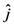 ) is the) cosine of the angle formed by the two directions
) is the) cosine of the angle formed by the two directions 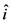 ,
, 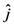 .
.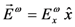 . In this case, the electro-optic susceptibility can be obtained by considering the induced polarization along the x direction:
. In this case, the electro-optic susceptibility can be obtained by considering the induced polarization along the x direction:
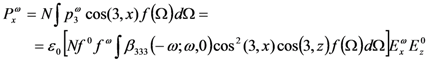
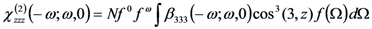
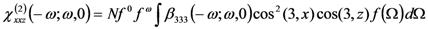
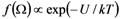 . The dipole interaction energy is given in the weak poling approximation by
. The dipole interaction energy is given in the weak poling approximation by 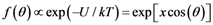 where
where 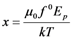 with
with 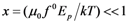 .
.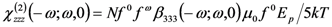
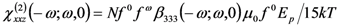
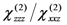 , that results in:
, that results in:
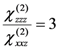
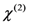 tensor [16], it is possible to apply the previous relations (15–16) to the electro-optic coefficient too.
tensor [16], it is possible to apply the previous relations (15–16) to the electro-optic coefficient too.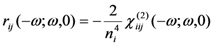
2.5. Transient Properties
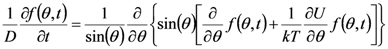
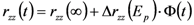
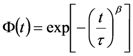
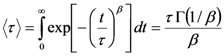
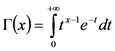 .
.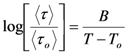
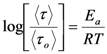
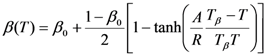
3. Measurement Techniques of the Electro-Optic Coefficient
3.1. Nonlinear Ellipsometry
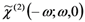 and
and 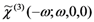 [42] complex susceptibilities. Moreover, it is sensitive to space distributions of charges trapped in the polymer films [1,16,43]. In order to be applied, the TMT needs to operate on samples in which the polymer film is sandwiched between two electrodes. In the case of polymers for χ(2) applications, the two electrodes are used either to pole the film or to apply a modulating voltage on the polymer film itself in order to measure the χ(2) values. As the TMT is based on the measurement of the electric field induced change of the optical phase difference experienced by the s (perpendicular to the incidence plane) and p (parallel to the incidence plane) components of a laser which propagates through the polymer film, at least one (reflection operation) of the electrodes must be transparent to the probe light.
[42] complex susceptibilities. Moreover, it is sensitive to space distributions of charges trapped in the polymer films [1,16,43]. In order to be applied, the TMT needs to operate on samples in which the polymer film is sandwiched between two electrodes. In the case of polymers for χ(2) applications, the two electrodes are used either to pole the film or to apply a modulating voltage on the polymer film itself in order to measure the χ(2) values. As the TMT is based on the measurement of the electric field induced change of the optical phase difference experienced by the s (perpendicular to the incidence plane) and p (parallel to the incidence plane) components of a laser which propagates through the polymer film, at least one (reflection operation) of the electrodes must be transparent to the probe light.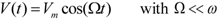
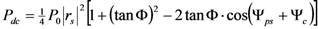
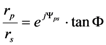
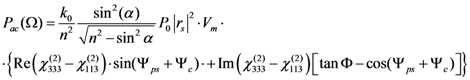
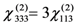 in the weak poling approximation.
in the weak poling approximation.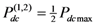 . Those conditions can be found when: Ψ = Ψps + Ψc = ± π/2.
. Those conditions can be found when: Ψ = Ψps + Ψc = ± π/2.
3.2. Second Harmonic Generation
 and
and  the internal refraction angles corresponding to ω and 2ω.
the internal refraction angles corresponding to ω and 2ω.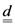 tensor components, the optical axes orientation with respect to the sample surface and the fundamental beam incidence angle α, where the d tensor is is related with the χ(2) tensor by the relation
tensor components, the optical axes orientation with respect to the sample surface and the fundamental beam incidence angle α, where the d tensor is is related with the χ(2) tensor by the relation
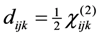
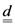 tensor corresponding to a poled polymer presents only two nonzero different components, d33 and d31 = d32 = d24 = d15. Depending on the polarization of both fundamental and generated beams, it is possible to retrieve separately the value of these components. The d31 component can be directly evaluated from SHG measurements obtained in the sωp2ω configuration, since in this case the expression of deff is given by:
tensor corresponding to a poled polymer presents only two nonzero different components, d33 and d31 = d32 = d24 = d15. Depending on the polarization of both fundamental and generated beams, it is possible to retrieve separately the value of these components. The d31 component can be directly evaluated from SHG measurements obtained in the sωp2ω configuration, since in this case the expression of deff is given by:
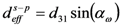
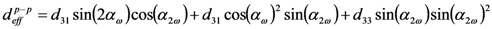
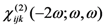 via the Equation (32). Then, in order to recover the electro-optic coefficient a modified expression of Equation (17) can be used [61,62]:
via the Equation (32). Then, in order to recover the electro-optic coefficient a modified expression of Equation (17) can be used [61,62]:
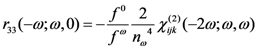
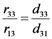 and, indirectly, verify if the assumption r33 ≈ 3r13, used in the nonlinear ellipsometric technique is valid. By continuously measuring the SHG signal, it is possible to perform faster measurements that can be usefully used in monitoring the time decay of the electro-optic coefficient as we will show later.
and, indirectly, verify if the assumption r33 ≈ 3r13, used in the nonlinear ellipsometric technique is valid. By continuously measuring the SHG signal, it is possible to perform faster measurements that can be usefully used in monitoring the time decay of the electro-optic coefficient as we will show later. 3.3. Temperature Scanning Technique
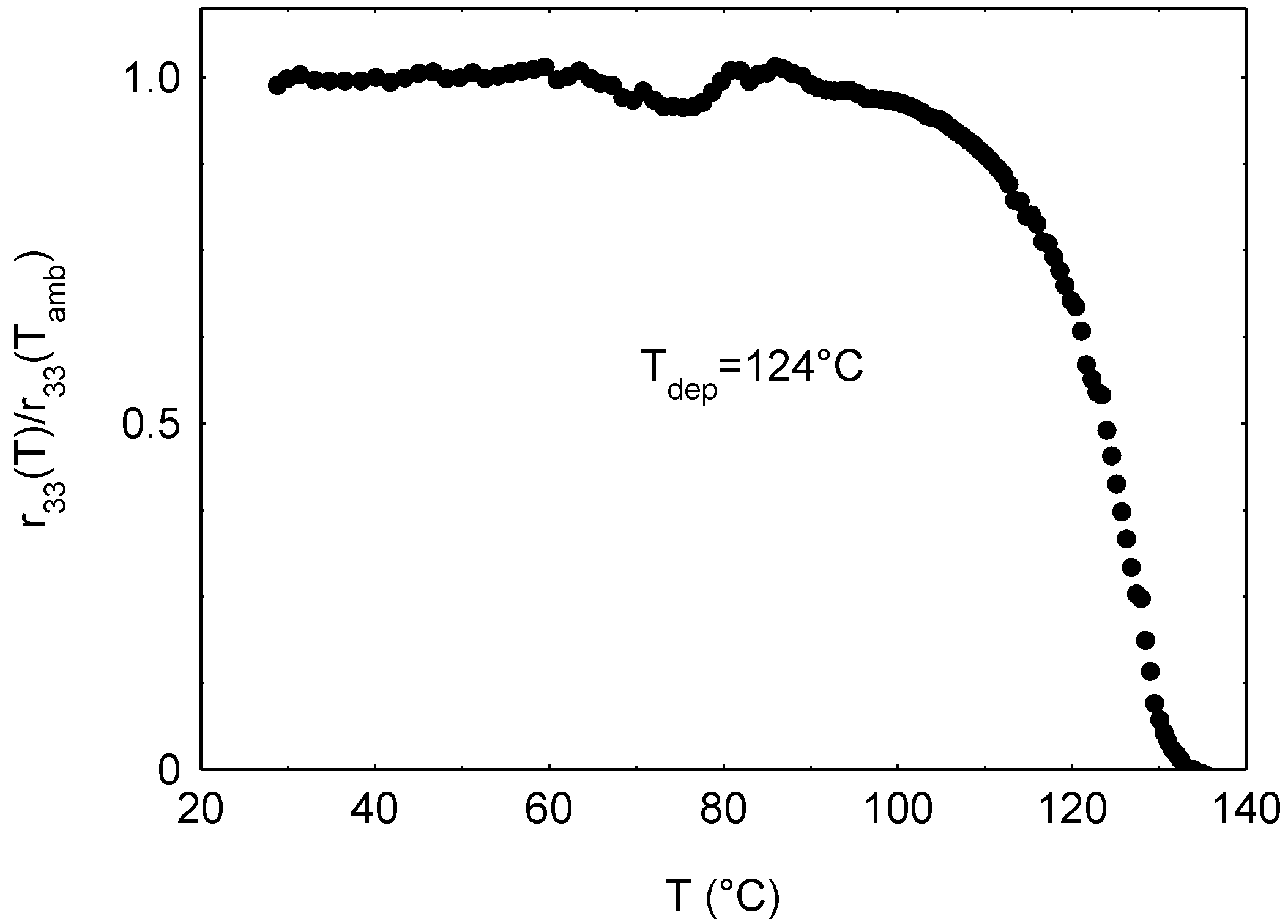
3.4. Isothermal Relaxation Measurements
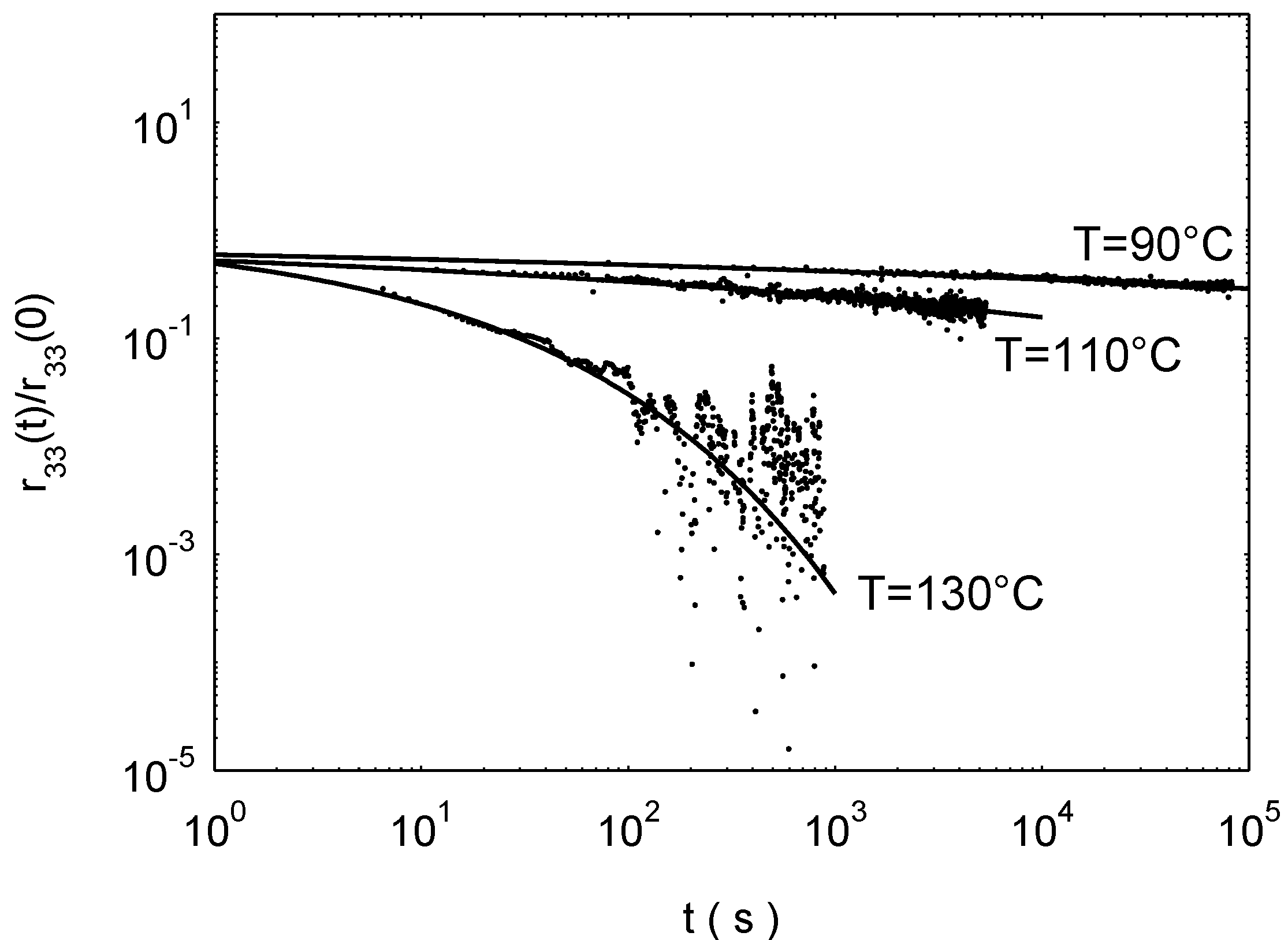
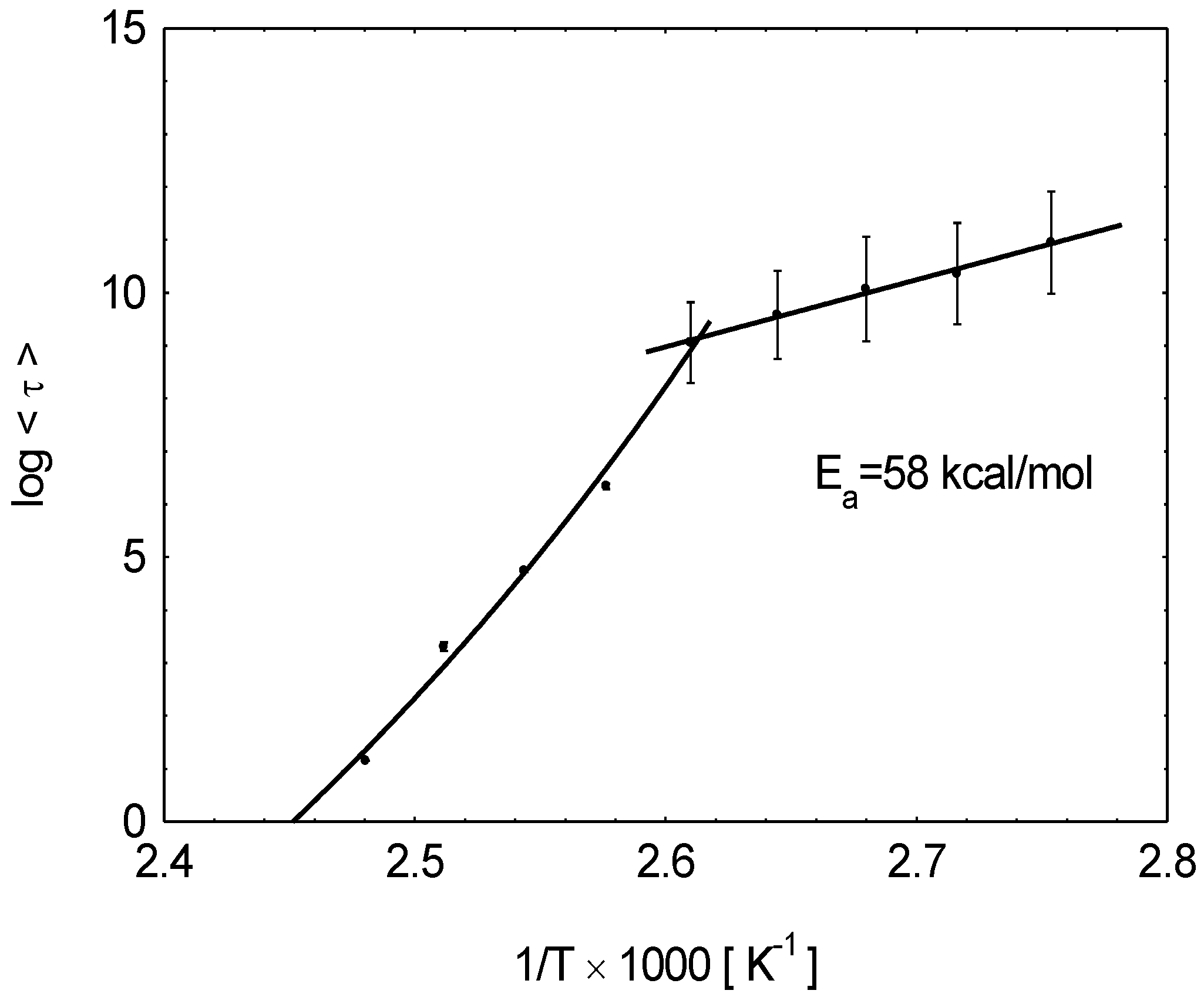
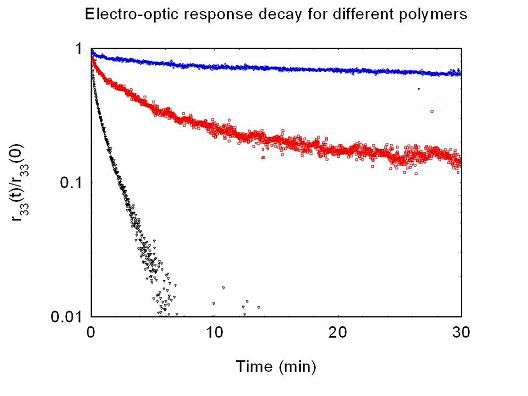
4. Stability of Some Fluorinated Polymers
4.1. HFIP-DR1AF
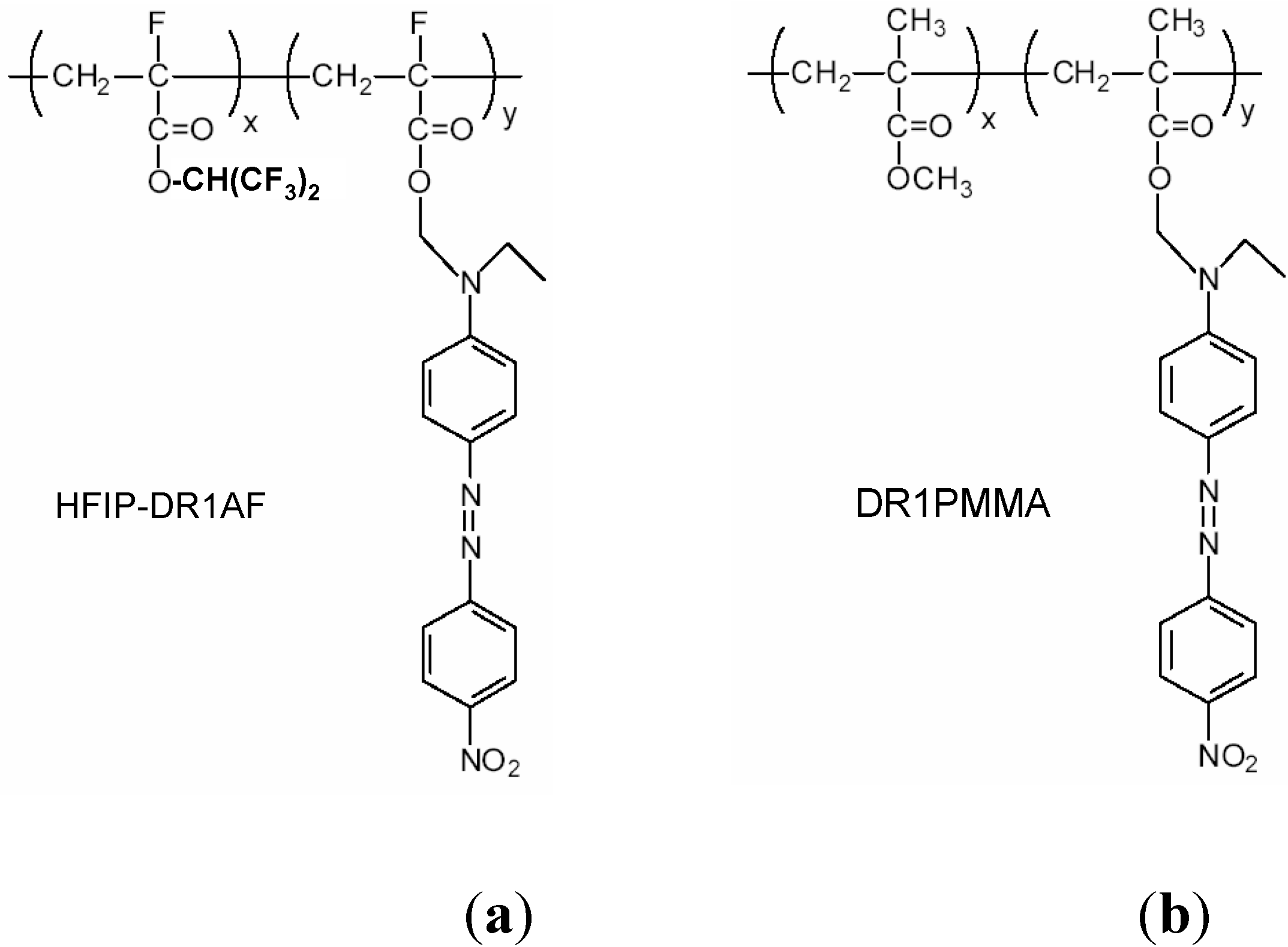
4.2. FATRIFE-DR1AF
4.3. ADAMANTANE-DR1AF
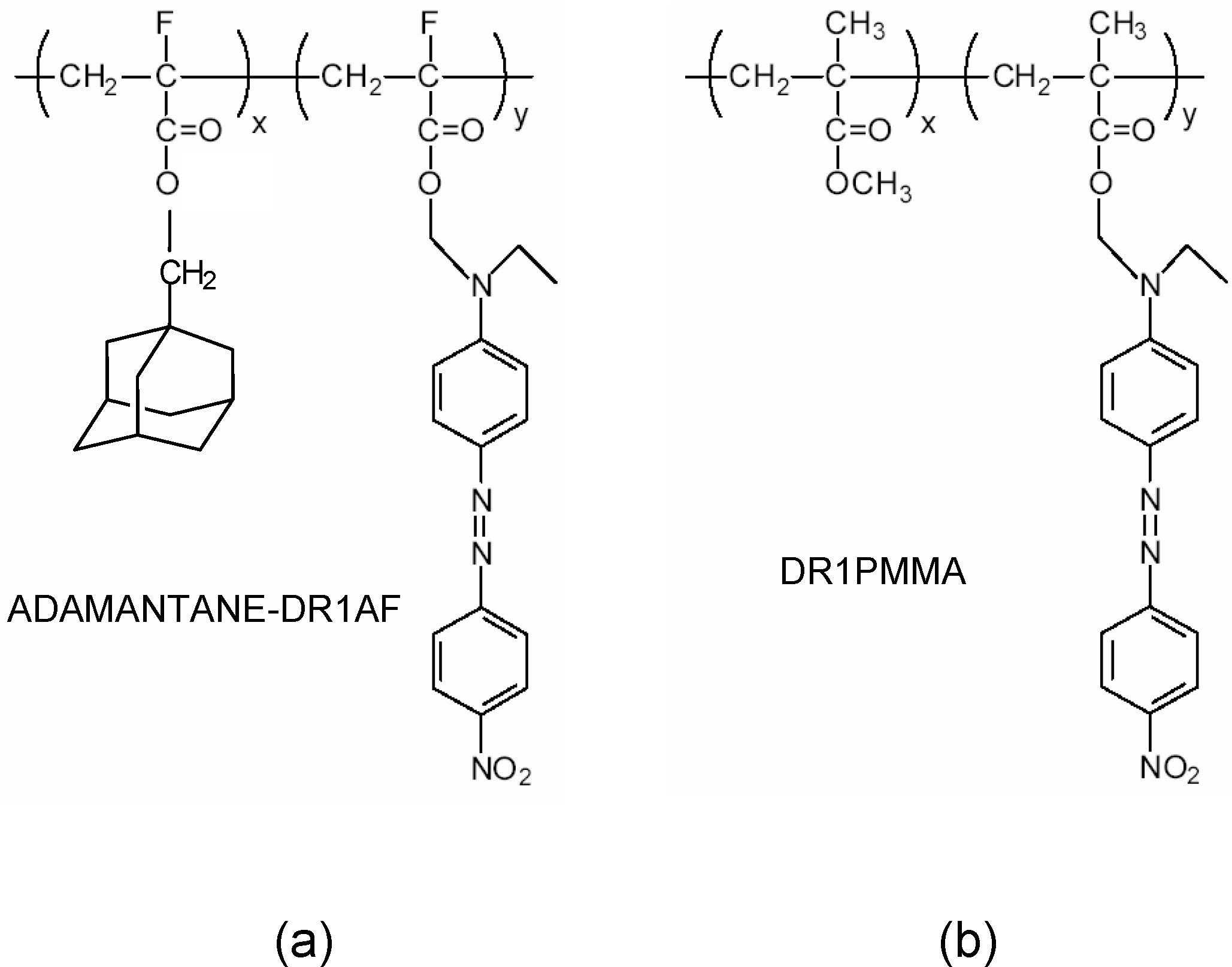
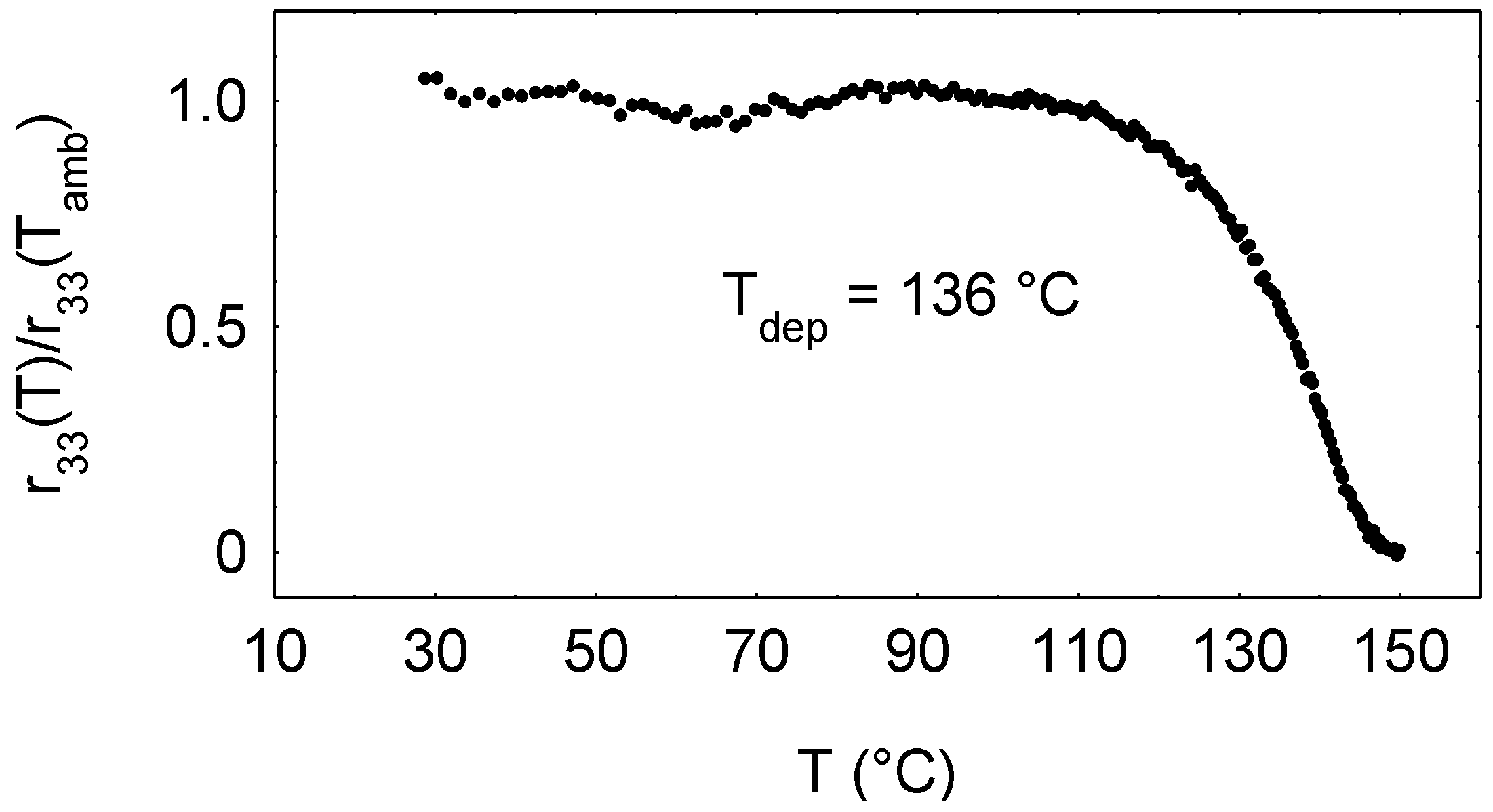
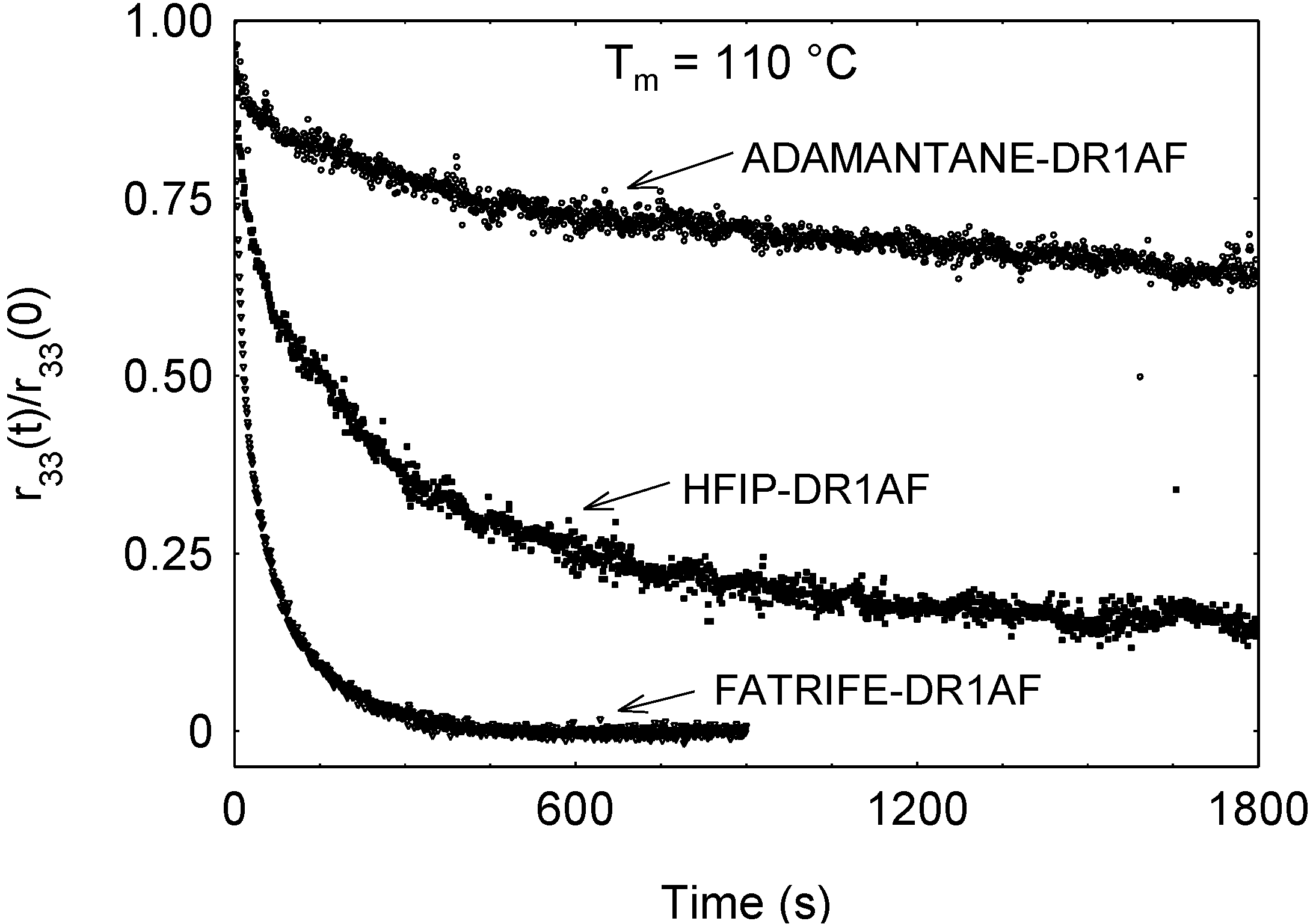
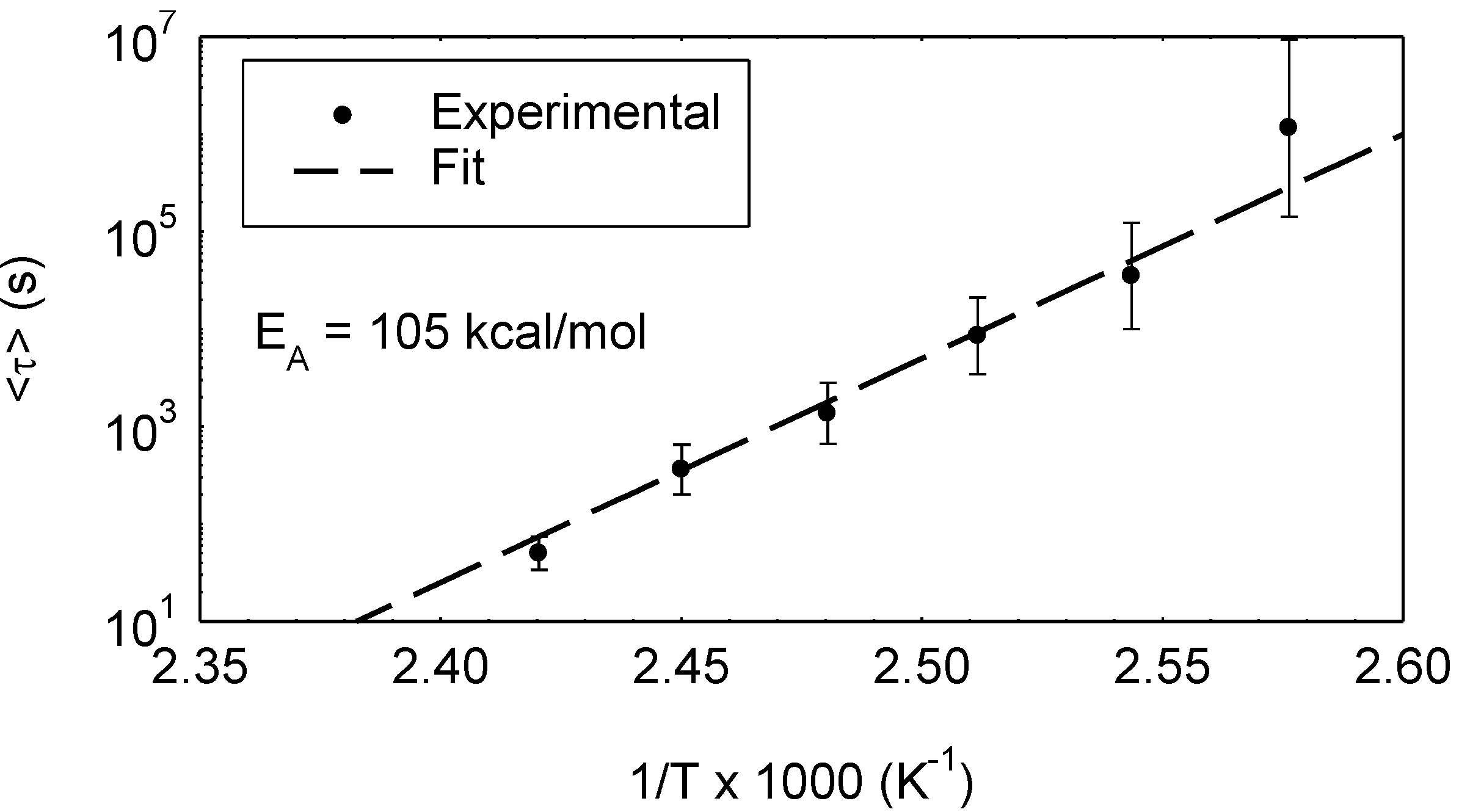
4.4. Polyimides-EHNT
4.5. Phenyltetraenic and AJL8 in Antrhracene Crosslinkable Matrix
4.6. FTC-EGDMA
5. Conclusions
Acknowledgments
References
- Zyss, J. Molecular Nonlinear Optics; Academic Press Inc.: San Diego, CA, USA, 1994. [Google Scholar]
- Rousseau, A.; Boutevin, B. Synthesis and characterization of organic materials for integrated optical devices. AIP Conf. Proc. 2003, 709, 214–232. [Google Scholar]
- Pyayt, A.L. Guiding light in electro-optic polymers. Polymers 2011, 3, 1591–1599. [Google Scholar] [CrossRef]
- Oh, M.-C.; Kim, K.-J.; Chu, W.-S.; Kim, J.-W.; Seo, J.-K.; Noh, Y.-O.; Lee, H.-J. Integrated photonic devices incorporating low-loss fluorinated polymer materials. Polymers 2011, 3, 975–997. [Google Scholar] [CrossRef]
- Lee, M.; Katz, H.E.; Erben, C.; Gill, D.M.; Gopalan, P.; Heber, J.D.; McGee, D.J. Broadband modulation of light by using an electro-optic polymer. Science 2002, 298, 1401–1403. [Google Scholar]
- Sun, H.; Chen, A.; Olbricht, B.C.; Davies, J.A.; Sullivan, P.A.; Liao, Y.; Dalton, L.R. Direct electron beam writing of electro-optic polymer microring resonators. Opt. Express 2008, 16, 6592–6599. [Google Scholar]
- Sun, H.; Chen, A.; Olbricht, B.C.; Davies, J.A.; Sullivan, P.A.; Liao, Y.; Dalton, L.R. Microring resonators fabricated by electron beam bleaching of chromophore doped polymers. Appl. Phys. Lett. 2008, 92, 193305:1–193305:3. [Google Scholar]
- Song, H.-C.; Oh, M.-C.; Ahn, S.-W.; Steier, W.H.; Fetterman, H.R.; Zhang, C. Flexible low-voltage electro-optic polymer modulators. Appl. Phys. Lett. 2003, 82, 4432–4434. [Google Scholar]
- Belardini, A.; Larciprete, M.C.; Cianci, E.; Foglietti, V.; Ratsimihety, A.; Rousseau, A.; Michelotti, F. Direct E-beam writing of electro-optic polymer channel waveguides. AIP Conf. Proc. 2003, 709, 427–428. [Google Scholar]
- Mori, Y.; Nakaya, K.; Piao, X.; Yamamoto, K.; Otomo, A.; Yokoyama, S. Large electro-optic activity and enhanced temporal stability of methacrylate-based crosslinking hyperbranched nonlinear optical polymer. J. Polym. Sci. A Polym. Chem. 2012, 50, 1254–1260. [Google Scholar] [CrossRef]
- Belardini, A.; Dominici, L.; Larciprete, M.C.; Michelotti, F.; Rousseau, A.; Ratsimihety, A. Enhanced stability of the second order optical properties of high-Tg fluorinated electro-optic copolymer. Appl. Phys. Lett. 2006, 89, 231110:1–231110:3. [Google Scholar]
- Pliška, T.; Cho, W.-R.; Meier, J.; Le Duff, A.-C.; Ricci, V.; Otomo, A.; Canva, M.; Stegeman, G.I.; Raimond, P.; Kajzar, F. Comparative study of nonlinear-optical polymers for guided-wave second-harmonic generation at telecommunication wavelengths. J. Opt. Soc. Am. B 2000, 17, 1554–1564. [Google Scholar] [CrossRef]
- Teng, C.C.; Man, H.T. Simple reflection technique for measuring the electro-optic coefficient of poled polymers. Appl. Phys. Lett. 1990, 56, 1734–1736. [Google Scholar] [CrossRef]
- Schildkraut, J.S. Determination of the electrooptic coefficient of a poled polymer film. Appl. Opt. 1990, 29, 2839–2841. [Google Scholar] [CrossRef]
- Michelotti, F.; Nicolao, G.; Tesi, F.; Bertolotti, M. On the measurement of the electro-optic properties of poled side-chain copolymer films with a modified Teng-Man technique. Chem. Phys. 1999, 245, 311–326. [Google Scholar] [CrossRef]
- Dominici, L.; Michelotti, F.; Whitelegg, S.; Campbell, A.; Bradley, D.D.C. Comparative study of space-charge effects in polymer light emitting diodes by means of reflection electro-optic and electroabsorption techniques. Phys. Rev. B 2004, 69, 054201:1–054201:10. [Google Scholar]
- Yariv, A. Optical Electronics, 4th ed.; Saunders College Publishing: Philadelphia, PA, USA, 1991. [Google Scholar]
- Maker, P.D.; Terhune, R.W.; Nisenhoff, M.; Savage, C.M. Effects of dispersion and focusing on the production of optical harmonics. Phys. Rev. Lett. 1962, 8, 21–22. [Google Scholar] [CrossRef]
- Jerphagnon, J.; Kurtz, S.K. Maker fringes: a detailed comparison of theory and experiment for isotropic and uniaxial crystals. J. Appl. Phys. 1970, 41, 1667–1681. [Google Scholar] [CrossRef]
- Herman, W.N.; Hayden, L.M. Maker fringes revisited: second-harmonic generation from birefringent or absorbing materials. J. Opt. Soc. Am. B 1995, 12, 416–427. [Google Scholar] [CrossRef]
- Bloembergen, N. Nonlinear Optics, 4th ed.; World Scientific Publication Co. Pte. Ltd.: River Edge, NJ, USA, 1996. [Google Scholar]
- Fazio, E.; Ramadan, W.; Belardini, A.; Bosco, A.; Bertolotti, M.; Petris, A.; Vlad, V.I. (2+1)D vortex soliton-like propagation in photorefractive Bi12SiO20 crystals. Phys. Rev. E 2003, 67, 026611:1–026611:8. [Google Scholar]
- Singer, K.D.; Kuzyk, M.G.; Sohn, J.E. Second-order nonlinear-optical processes in orientationally ordered materials: relationship between molecular and macroscopic properties. J. Opt. Soc. Am. B 1987, 4, 968–976. [Google Scholar] [CrossRef]
- Harper, A.W.; Sun, S.; Dalton, L.R.; Garner, S.M.; Chen, A.; Kalluri, S.; Steier, W.H.; Robinson, B.H. Translating microscopic optical nonlinearity into macroscopic optical nonlinearity: the role of chromophore chromophore electrostatic interactions. J. Opt. Soc. Am. B 1998, 15, 329–337. [Google Scholar] [CrossRef]
- Cheng, L.T.; Tam, W.; Stevenson, S.H.; Meredith, G.R.; Rikken, G.; Marder, S.R. Experimental investigations of organic molecular nonlinear optical polarizabilities. 1. Methods and results on benzene and stilbene derivatives. J. Phys. Chem. 1991, 95, 10631–10643. [Google Scholar]
- Cheng, L.T.; Tam, W.; Stevenson, S.H.; Meredith, G.R.; Rikken, G.; Marder, S.R. Experimental investigations of organic molecular nonlinear optical polarizabilities. 2. A study of conjugation dependences. J. Phys. Chem. 1991, 95, 10643–10652. [Google Scholar] [CrossRef]
- Dalton, L.R.; Steier, W.H.; Robinson, B.H.; Zhang, C.; Ren, A.; Garner, S.; Chen, A.; Londergan, T.; Irwin, L.; Carlson, B.; Fifield, L.; Phelan, G.; Kincaid, C.; Amend, J.; Jen, A. From molecules to opto-chips: Organic electro-optic materials. J. Mater. Chem. 1999, 9, 1905–1920. [Google Scholar] [CrossRef]
- Dalton, L.; Harper, A.; Ren, A.; Wang, F.; Todorova, G.; Chen, J.; Zhang, C.; Lee, M. Polymeric electro-optic modulators: From chromophore design to integration with semiconductor very large scale integration electronics and silica fiber optics. Ind. Eng. Chem. Res. 1999, 38, 8–33. [Google Scholar] [CrossRef]
- Moylan, C.R.; Twieg, R.J.; Lee, V.Y.; Swanson, S.A.; Betterton, K.M.; Miller, R.D. Nonlinear optical chromophores with large hyperpolarizabilities and enhanced thermal stabilities. J. Am. Chem. Soc. 1993, 115, 12599–12600. [Google Scholar] [CrossRef]
- Skinner, I.M.; Garth, S.J. Reconciliation of esu and mksa units in nonlinear optics. Am. J. Phys. 1990, 58, 177–181. [Google Scholar] [CrossRef]
- Blanchard, D.M.; Mitchell, G.R. A comparison of photoinduced poling and thermal poling of azo-dye-doped polymer films for second order nonlinear optical applications. Appl. Phys. Lett. 1993, 63, 2038–2040. [Google Scholar] [CrossRef]
- Bauer-Gogonea, S.; Bauer, S.; Wirges, W.; Gerhard-Multhaupt, R. Pyroelectrical investigation of the dipole orientation in nonlinear optical polymers during and after photoinduced poling. J. Appl. Phys. 1994, 76, 2627–2635. [Google Scholar] [CrossRef]
- Wu, J.W. Birefringent and electro-optic effects in poled polymer films: Steady-state and transient properties. J. Opt. Soc. Am. B 1991, 8, 142–152. [Google Scholar] [CrossRef]
- Michelotti, F.; Toussaere, E. Pulse poling of side-chain and crosslinkable copolymers. J. Appl. Phys. 1997, 82, 5728–5744. [Google Scholar] [CrossRef]
- Brasselet, S.; Zyss, J. Multipolar molecules and multipolar fields: Probing and controlling the tensorial nature of nonlinear molecular media. J. Opt. Soc. Am. B 1998, 15, 257–288. [Google Scholar] [CrossRef]
- Quatela, A.; De Matteis, F.; Casalboni, M.; Stella, F.; Colombo, M.; Zaopo, A. Order relaxation of a poled azo dye in a high Tg, fully aromatic polyimide. J. Appl. Phys. 2007, 101, 023116:1–023116:6. [Google Scholar]
- Scher, H.; Shlesinger, M.F.; Bendler, J.T. Time scale invariance in transport and relaxation. Phys. Today 1991, 44, 26–34. [Google Scholar] [CrossRef]
- Williams, G.; Watts, D.C. Non-symmetrical dielectric relaxation behaviour arising from a simple empirical decay function. Trans. Faraday Soc. 1970, 66, 80–85. [Google Scholar] [CrossRef]
- Ghebremichael, F.; Kuzyk, M.G. Optical second-harmonic generation as a probe of the temperature dependence of the distribution of sites in a poly(methyl methacrylate) polymer doped with disperse red 1 azo dye. J. Appl. Phys. 1995, 77, 2896–2901. [Google Scholar] [CrossRef]
- Michelotti, F.; Taggi, V.; Bertolotti, M.; Gabler, T.; Hörhold, H.H.; Bräuer, A. Reflection electro-optical measurements on electroluminescent polymer films: A good tool for investigating charge injection and space charge effects. J. Appl. Phys. 1998, 83, 7886–7895. [Google Scholar]
- Michelotti, F.; Bussi, S.; Dominici, L.; Bertolotti, M.; Bao, Z. Space charge effects in polymer-based light-emitting diodes studied by means of a polarization sensitive electroreflectance technique. J. Appl. Phys. 2002, 91, 5521–5532. [Google Scholar] [CrossRef]
- Miniewicz, A.; Michelotti, F.; Belardini, A. Photoconducting polymer-liquid crystal structure studied by electroreflectance. J. Appl. Phys. 2004, 95, 1141–1147. [Google Scholar] [CrossRef]
- Michelotti, F.; Dominici, L.; Belardini, A. Charge injection and trapping contributions to the electro-optic response of mesoscopic polymer systems. AIP Conf. Proc. 2003, 709, 233–251. [Google Scholar]
- Jespersen, K.G.; Pedersen, T.G.; Johansen, P.M. Electro-optic response of chromophores in a viscoelastic polymer matrix to a combined dc and ac poling field. J. Opt. Soc. Am. B 2003, 20, 2179–2188. [Google Scholar]
- Nagtegaele, P.; Brasselet, E.; Zyss, J. Anisotropy and dispersion of a Pockels tensor: A benchmark for electro-optic organic thin-film assessment. J. Opt. Soc. Am. B 2003, 20, 1932–1936. [Google Scholar] [CrossRef]
- Michelotti, F.; Belardini, A.; Larciprete, M.C.; Bertolotti, M.; Rousseau, A.; Ratsimihety, A.; Schoer, G.; Mueller, J. Measurement of the electro-optic properties of poled polymers at λ = 1.55μm by means of sandwich structures with zinc oxide transparent electrode. Appl. Phys. Lett. 2003, 83, 4477–4479. [Google Scholar]
- Park, D.H.; Lee, C.H.; Herman, W.N. Analysis of multiple reflection effects in reflective measurements of electro-optic coefficients of poled polymers in multilayer structures. Opt. Express 2006, 14, 8866–8884. [Google Scholar] [CrossRef]
- Hou, A.; Liu, H.; Sun, J.; Zhang, D.; Yi, M. Measurement of the electro-optic coefficient of polymer thin films with better spatial resolution. Optics & Laser Tech. 2007, 39, 411–414. [Google Scholar]
- Park, D.H.; Luo, J.; Jen, A.K.-Y.; Herman, W.N. Simplified reflection Fabry-Perot method for determination of electro-optic coefficients of poled polymer thin films. Polymers 2011, 3, 1310–1324. [Google Scholar] [CrossRef]
- Michelotti, F.; Belardini, A.; Rousseau, A.; Ratsimihety, A.; Schoer, G.; Muller, J. Use of sandwich structures with ZnO:Al transparent electrodes for the measurement of the electro-optic properties of standard and fluorinated poled copolymers at λ = 1.55 μm. J. Non-Crystalline Solids 2006, 352, 2339–2342. [Google Scholar] [CrossRef]
- Michelotti, F.; Canali, R.; Dominici, L.; Belardini, A.; Menchini, F.; Schoer, G.; Muller, J. Second order optical nonlinearity of ZnO/ZnO:Al bilayers deposited on glass by low temperature radio frequency sputtering. Appl. Phys. Lett. 2007, 90, 181110:1–181110:3. [Google Scholar]
- Franken, P.A.; Hill, A.E.; Peters, C.W.; Weinreich, G. Generation of optical harmonics. Phys. Rev. Lett. 1961, 7, 118–119. [Google Scholar] [CrossRef]
- Cattaneo, S.; Kauranen, M. Determination of second-order susceptibility components of thin films by two-beam second-harmonic generation. Opt. Lett. 2003, 28, 1445–1447. [Google Scholar] [CrossRef]
- Larciprete, M.C.; Bovino, F.A.; Giardina, M.; Belardini, A.; Centini, M.; Sibilia, C.; Bertolotti, M.; Passaseo, A.; Tasco, V. Mapping the nonlinear optical susceptibility by noncollinear second-harmonic generation. Opt. Lett. 2009, 34, 2189–2191. [Google Scholar] [CrossRef]
- Verbiest, T.; Kauranen, M.; Van Rompaey, Y.; Persoonson, A. Optical activity of anisotropic achiral surfaces. Phys. Rev. Lett. 1996, 77, 1456–1459. [Google Scholar] [CrossRef]
- Belardini, A.; Larciprete, M.C.; Centini, M.; Fazio, E.; Sibilia, C.; Chiappe, D.; Martella, C.; Toma, A.; Giordano, M.; Buatier de Mongeot, F. Circular dichroism in the optical second-harmonic emission of curved gold metal nanowires. Phys. Rev. Lett. 2011, 107, 257401:1–257401:5. [Google Scholar]
- Verbiest, T.; Clays, K.; Rodriguez, V. Second-Order Nonlinear Optical Characterization Techniques. CRC Press: NY, USA, 2009. [Google Scholar]
- Belardini, A.; Pannone, F.; Leahu, G.; Larciprete, M.C.; Centini, M.; Sibilia, C.; Martella, C.; Giordano, M.; Chiappe, D.; Buatier de Mongeot, F. Evidence of anomalous refraction of self-assembled curved gold nanowires. Appl. Phys. Lett. 2012, 100, 251109:1–251109:5. [Google Scholar]
- Palazzesi, C.; Stella, F.; de Matteis, F.; Casalboni, M. In-plane poling characterization of organic electro-optical polymer. J. Appl. Phys. 2010, 107, 113101:1–113101:5. [Google Scholar]
- Park, D.H.; Herman, W.N. Closed-form Maker fringe formulas for poled polymer thin films in multilayer structures. Opt. Express 2012, 20, 173–185. [Google Scholar] [CrossRef]
- Large, M.J.; Kajzar, F.; Raimond, P. Modulation of second harmonic generation in photochromic materials by the application of electric fields and low intensity light. Appl. Phys. Lett. 1998, 73, 3635–3637. [Google Scholar] [CrossRef]
- Belardini, A.; Larciprete, M.C.; Passeri, D.; Michelotti, F.; Ratsimihety, A.; Rousseau, A.; Menchini, F.; Nichelatti, E. Concentration dependence of the optical nonlinearity in extremely doped fluorinated organic copolymers. J. Appl. Phys. 2005, 98, 093521:1–093521:8. [Google Scholar]
- Ahn, S.-W.; Steier, W.H.; Kuo, Y.-H.; Oh, M.-C.; Lee, H.-J.; Zhang, C.; Fetterman, H.R. Integration of electro-optic polymer modulators with low-loss fluorinated polymer waveguides. Opt. Lett. 2002, 27, 2109–2111. [Google Scholar] [CrossRef]
- Belardini, A.; Michelotti, F.; Rousseau, A.; Ratsimihety, A. Temperature stability of the electro-optic response of highly fluorinated side chain organic copolymers. Ferroelectrics 2007, 352, 35–41. [Google Scholar] [CrossRef]
- He, M.; Zhou, Y.; Dai, J.; Liu, R.; Cui, Y.; Zhang, T. Synthesis and nonlinear optical properties of soluble fluorinated polyimides containing hetarylazo chromophores with large hyperpolarizability. Polymer 2009, 50, 3924–3931. [Google Scholar] [CrossRef]
- Shi, Z.; Luo, J.; Huang, S.; Polishak, B.M.; Zhou, X.-H.; Liff, S.; Younkin, T.R.; Block, B.A.; Jen, A.K.-J. Achieving excellent electro-optic activity and thermal stability in poled polymers through an expeditious crosslinking process. J. Mater. Chem. 2012, 22, 951–959. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Belardini, A. Fluorinated and Non-Fluorinated Electro-Optic Copolymers: Determination of the Time and Temperature Stability of the Induced Electro-Optic Coefficient. Appl. Sci. 2012, 2, 682-708. https://doi.org/10.3390/app2040682
Belardini A. Fluorinated and Non-Fluorinated Electro-Optic Copolymers: Determination of the Time and Temperature Stability of the Induced Electro-Optic Coefficient. Applied Sciences. 2012; 2(4):682-708. https://doi.org/10.3390/app2040682
Chicago/Turabian StyleBelardini, Alessandro. 2012. "Fluorinated and Non-Fluorinated Electro-Optic Copolymers: Determination of the Time and Temperature Stability of the Induced Electro-Optic Coefficient" Applied Sciences 2, no. 4: 682-708. https://doi.org/10.3390/app2040682