1. Introduction
The jet formation process of shaped charges, including both linear and conical, has been a major research area for over a half century and has been aimed at the increase in penetration capability for many different applications. However, due to a few numbers of applications for military purposes and a multi-dimensional complex geometry, a comparatively small amount of study has been done in the field of linear shaped charges.
There have been few publications about the motion of the LSC liner since the initiation of the Birkhoff theory [
1] including the development of a numerical simulation code, LESCA, specifically designed for LSCs applications which involve a combination of numerical approaches and a series of analytical approximations [
2]. Traditionally, the jet formation process of LSCs has been assumed to be the same process as that of CSCs based on the Birkhoff theory. The jet is created by a gradual collapse of the liner caused by the detonation of a high explosive charge. The jet is then elongated due to the velocity gradient between the tip and base of the jet [
3]. However, in case of the LSC, the initiation point is not along the top of the liner as in the case of a CSC. Due to this, it is anticipated that the jet formation process of a LSC is somewhat different from that of a CSC. The laterally long high explosive charge along the length of LSC has to be initiated from one end in common practices, creating a gradual flat liner collapse in a side direction [
4,
5]. Because a LSC liner consists of two flat metallic components instead of a curved liner as in CSCs, different jetting properties during penetration would be present and a more detailed investigation regarding the jet formation or behavior is necessary to understand the penetration performance of LSCs.
The main objective in this series of preliminary simulations is to identify both the jetting behavior during the detonation of a LSC and specific flight formation of the jet before impacting a target. During the course of the project, a preliminary computational study of LSC jet impacts on a mild steel target is investigated and the impact formation to the target is identified as well. The impact configurations are changed by varying the standoff distance, and a series of hydrocode simulations using AUTODYN® is completed to validate the results.
2. Numerical Modeling I
A series of computer simulations is run to identify a general trend of damage and other related behaviors on the surface of a mild steel target under the impact of a LSC jet.
By studying the parameters of the linear shaped charge jet impact onto the target surface, including the penetration depth, several effects can be studied. Firstly, the overall extent of the damage profile generated from the LSC jet impact after flight of a certain standoff distance can be more effectively analyzed. The accuracy of the simulation parameters can also be examined allowing a further detailed investigation later by comparing the simulation results to the actual testing results and the numerical parameters can be re-adjusted to improve the accuracy of the simulation results. Because of the identification of the damage profile on the surface of the mild steel target and the flight pattern of the jetting is more important than the study of jet formation after the liner collapse in this section, the investigation focuses on the damage profile after the impact and jetting pattern during flight. The computer simulation software used during this analysis is AUTODYN®.
In order to investigate the jet penetration formation into a mild steel target, a commercially manufactured 1,200 gr/ft LSC and a mild steel target are modeled and simulated. The 1,200 gr/ft LSC is created based on the manufacturer specifications for accuracy. The LSC and target are built using the SPH and Lagrangian solvers [
6] respectively totaling 2.7 million cells in a single model.
The LSC and target are set to maintain the optimum standoff distance (OSD) between the LSC base and the target surface as described by the manufacturer. The material properties of the models can be seen in
Table 1.
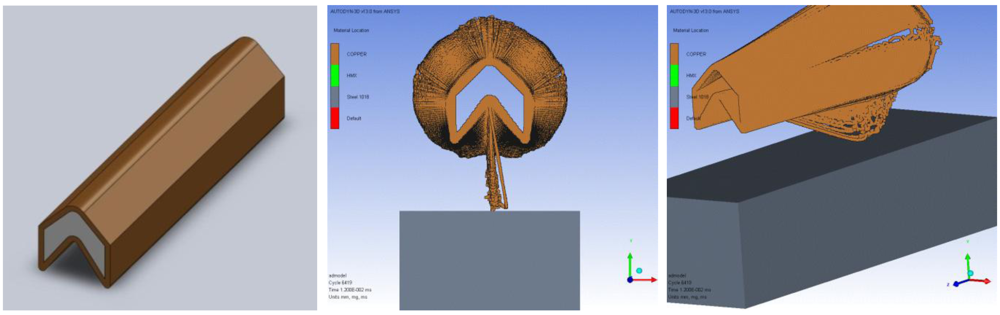
Figure 1 shows the externally drawn 1,200 gr/ft LSC before being imported into AUTODYN
® and the LSC 12 µs after detonation.
Table 1.
Material properties of the simulation model template [
6].
Table 1.
Material properties of the simulation model template [6].
| Material Name–Copper (LSC) | Material Name–1018 Steel (mild steel target) |
| Equation of State | Tillotson | Equation of State | Linear |
| Reference density | 8.90000E+00 (g/cm3) | Reference density | 7.87000E+00 (g/cm3) |
| Parameter A | 1.39000E+08 (kPa) | Bulk Modulus | 1.40000E+08 (kPa) |
| Parameter B | 1.10000E+08 (kPa) | Reference Temperature | 2.93000E+02 (K) |
| Parameter a | 5.00000E−01 (none) | Specific Heat | 4.86000E+02 (J/kgK) |
| Parameter b | 1.50000E+00 (none) | Thermal Conductivity | 5.19000E+01 (J/mKs) |
| Parameter alpha | 5.00000E+00 (none) | Strength | Johnson Cook |
| Parameter beta | 5.00000E+00 (none) | Shear Modulus | 8.00000E+07 (kPa) |
| Parameter e0 | 3.25000E+07 (J/kg) | Yield Stress | 2.20000E+05 (kPa) |
| Parameter es | 1.38000E+06 (J/kg) | Melting Temperature | 1.72189E+03 (K) |
| Parameter esd | 6.90000E+06 (J/kg) | Ref. Strain Rate (/s) | 1.00000E+00 (none) |
| Reference Temperature | 3.00000E+02 (K) | Strain Rate Correction | 1st Order |
| Specific Heat | 3.83000E+02 (J/kgK) | Erosion | Geometric Strain |
| Thermal Conductivity | 0.00000E+00 (J/mKs) | Erosion Strain | 7.50000E−01 (none) |
| | Type of Geometric Strain | Instantaneous |
| Material Name–HMX (explosives) |
| Equation of State | JWL |
| Reference density | 1.89100E+00 (g/cm3) |
| Parameter A | 7.78280E+08 (kPa) |
| Parameter B | 7.07140E+06 (kPa) |
| Parameter R1 | 4.20000E+00 (none) |
| Parameter R2 | 1.00000E+00 (none) |
| Parameter W | 3.00000E−01 (none) |
| C-J Detonation velocity | 9.11000E+03 (m/s) |
| C-J Energy/unit volume | 1.05000E+07 (kJ/m3) |
| C-J Pressure | 4.20000E+07 (kPa) |
| Auto-convert to Ideal Gas | Yes |
Figure 1.
1,200 gr/ft. Linear Shaped Charge (LSC) drawn before being imported into AUTODYN®, LSC detonation at OSD 12 µsafter detonation from left to right.
Figure 1.
1,200 gr/ft. Linear Shaped Charge (LSC) drawn before being imported into AUTODYN®, LSC detonation at OSD 12 µsafter detonation from left to right.
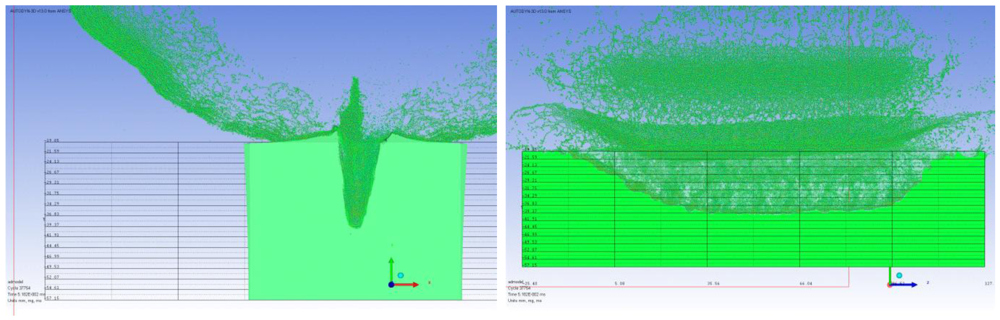
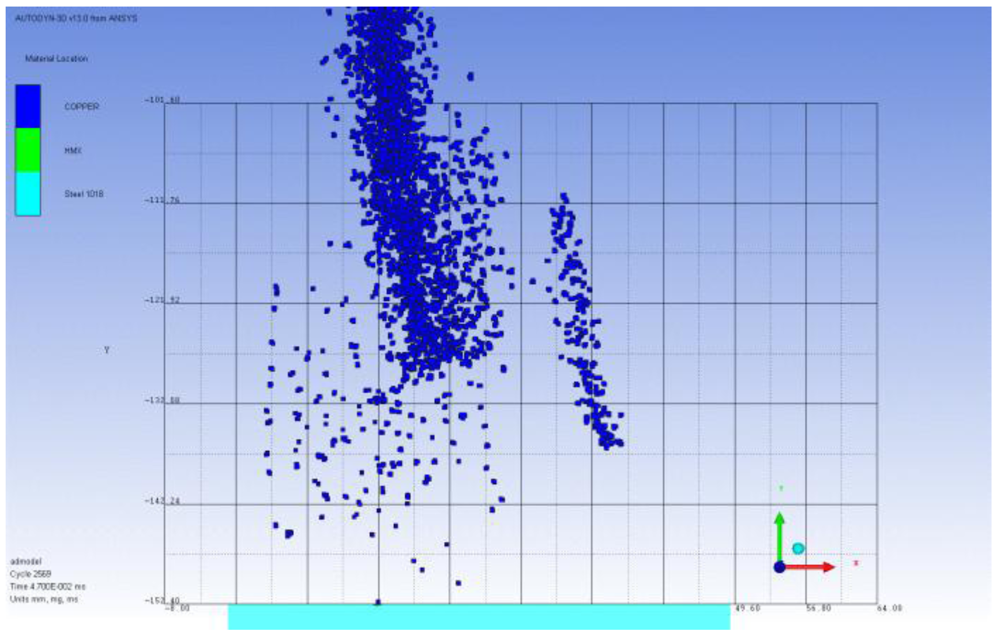
The OSD model is created in order to validate the penetration depth into the mild steel target. It is then compared to the penetration profile created in a target from previous experimental data. This is a vital model in the validation of the model set-up since there are several comparable data sets available and the outcome of the shot is well-known. For this model the LSC is detonated with a plane wave at 0.75 inches (1.905 cm, OSD) above the target. The front and side profiles of the pentration can be seen in
Figure 2,
Figure 3 and
Figure 4.
Figure 2.
Simulation results (front and side view of penetration profile at optimum standoff distance (OSD)).
Figure 2.
Simulation results (front and side view of penetration profile at optimum standoff distance (OSD)).
Figure 3.
A general cutting formation (a mild steel target was dissected to reveal the penetration profile).
Figure 3.
A general cutting formation (a mild steel target was dissected to reveal the penetration profile).
Figure 4.
Top view of target at OSD (left: simulation result, right: a general testing result).
Figure 4.
Top view of target at OSD (left: simulation result, right: a general testing result).
The penetration depth from the simulation result was around 20.32 mm at the deepest point, and the testing result shows around 26.2 mm. The penetration depth is not exactly matching in two cases, but the jet remnant over the penetration in
Figure 2 may create more penetration afterward getting close to the testing result. In general, the jet entrance width on the surface of the target, skewed jet marks near the main penetration and penetration profile inside the target are almost identical to the experimental results. From the figures above, the model is able to validate the level of accuracy of the template for further investigation.
3. Numerical Modeling II
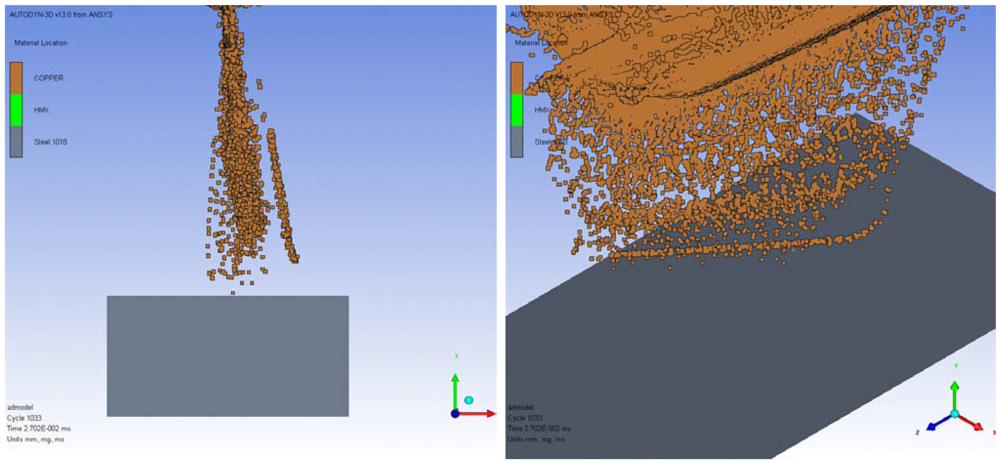
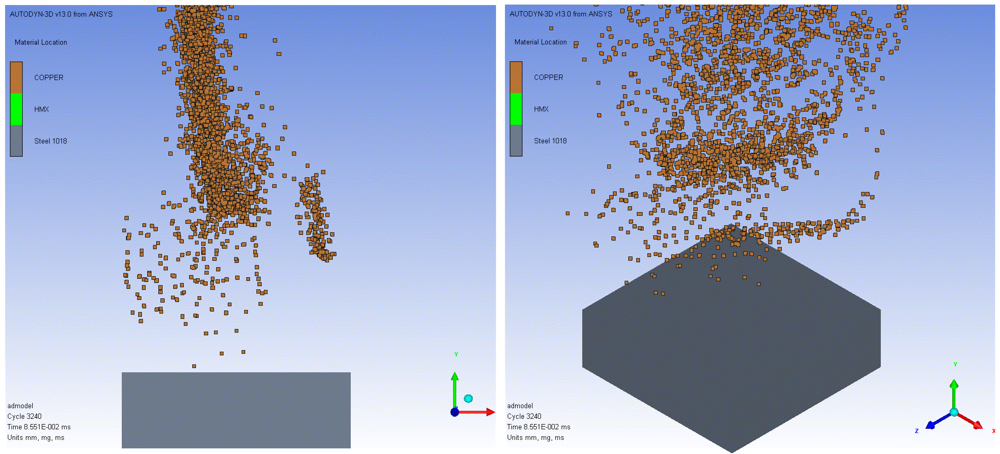
Another important model created is the simulation of a LSC being shot without a target below. The model ran long enough for the tip of the jet to travel 12 inches (30.48 cm). The main purpose of this model is to simulate and analyze the jet break-up process over the surface of target when the LSC is subjected to large standoff distances. Because the large standoff distance in the operation of LSCs would significantly reduce the focusing of the elongated jet, the study of the jet behavior during the flight to the target is an important issue providing the essential information in determination of the effective standoff distance or optimum jet properties. A free shot LSC is simulated using the previously built template model of the 1,200 gr/ft LSC.
Figure 5,
Figure 6 and
Figure 7 show the jet after traveling 3, 6, and 12 inches (7.62, 15.24, 30.48 cm respectively). Two figures at each distance show the front and isometric views of the jet. The target is placed at the appropriate distance below the base of the LSC as a reference.
Figure 5.
Front and isometric view after jet traveling 3 inches (7.63 cm).
Figure 5.
Front and isometric view after jet traveling 3 inches (7.63 cm).
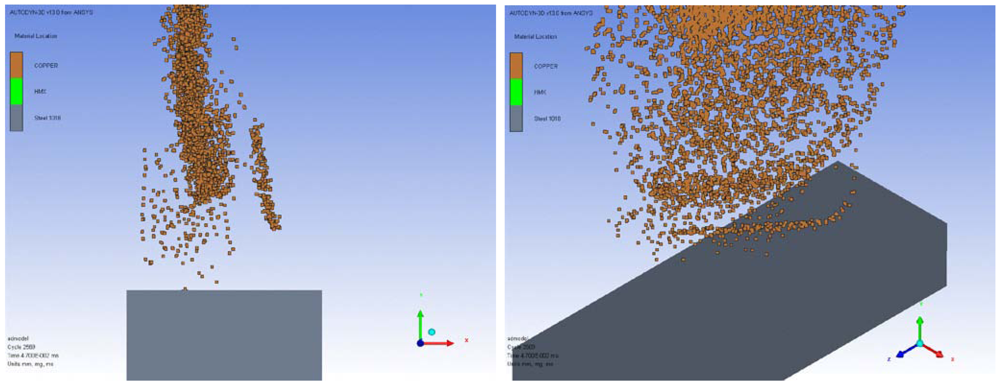
Figure 6.
Front and isometric view after jet traveling 6 inches (15.24 cm).
Figure 6.
Front and isometric view after jet traveling 6 inches (15.24 cm).
Figure 7.
Front and isometric view after jet traveling 12 inches (30.48 cm).
Figure 7.
Front and isometric view after jet traveling 12 inches (30.48 cm).
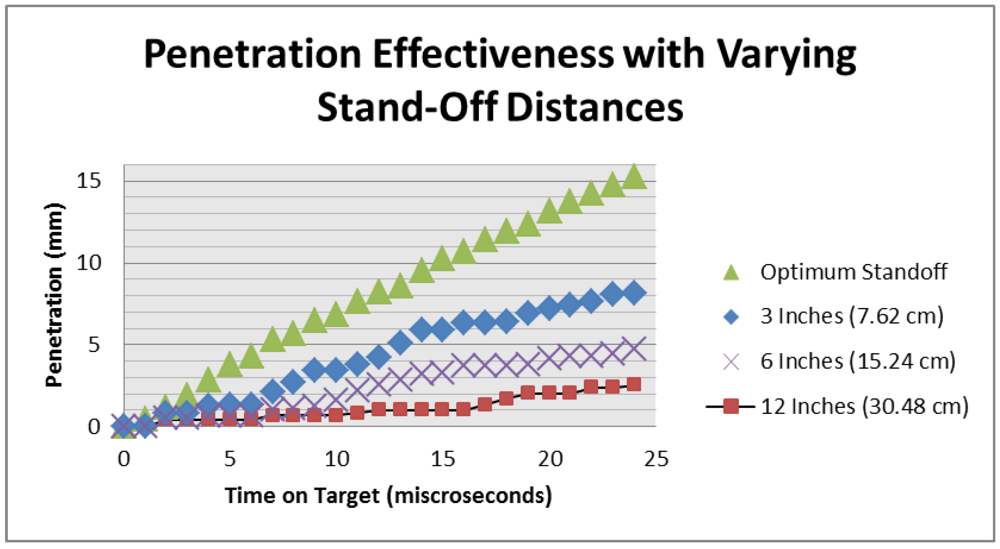
Due to the extended model run time, a complete penetration profile is not able to be obtained for each of the four models. Instead, an analysis method is devised that consists of looking at the change in penetration into the target every microsecond over a 24 µs period. The zero time is considered to be when a part of the jet initially makes contact with the target. The penetration profile is then analyzed at every microsecond afterward for 24 µs to determine the penetration efficiency at the given standoff distance. Penetration profiles are analyzed for 0.75, 3, 6, and 12 inches (1.905, 7.62, 15.24, 30.48 cm respectively) standoff distances. The penetration into the target created by the jets formed by the different standoff distances can be seen in
Figure 8. The points are recorded from the deepest point of penetration into the target viewed from a side penetration profile such as in
Figure 2.
Figure 8.
Penetration effectiveness at different standoff distances.
Figure 8.
Penetration effectiveness at different standoff distances.
This graph illustrates the penetration of the LSC jet into the mild steel target over a period of 24 µs after the initial contact between the jet and the target. As shown, the penetration into the target decreases significantly as standoff distance increases. This is due to two different reasons. Firstly, break-up of the jet during the flight shortens the solid length of jet as it travels across the increased distance. This effect is one of the dominant factors that control the penetration capability in shaped charges. The second reason for such penetration reduction is the jet spreading over a wide area during flight as shown in
Figure 5,
Figure 6 and
Figure 7. This effect of the jet spreading is not significant in the application of CSCs due to the single axis of jet production during the liner collapse. LSCs, however, are under the linear jet (two dimensional) focusing regime due to the linearly long shape during the liner collapse creating a less coherent jet. This mechanism acts as a drive of the jet spreading over a wide range at large standoff distances as it can be seen in
Figure 5,
Figure 6 and
Figure 7.
Table 2 and
Figure 9 show the jet width at varying standoff distances.
Table 2.
Jet width under different standoff distances.
Table 2.
Jet width under different standoff distances.
| Standoff (inches) | Min. Value | Max Value | Jet Width (mm) | Jet Width (inches) |
|---|
| 0.75 | 9.9271 | 15.8230 | 5.8959 | 0.2321 |
| 3.00 | 6.7410 | 25.7200 | 18.9790 | 0.7472 |
| 6.00 | 2.3565 | 38.1730 | 35.8165 | 1.4101 |
| 12.00 | −6.7842 | 62.8020 | 69.5862 | 2.7396 |
Figure 9.
Jet width at different standoff distance.
Figure 9.
Jet width at different standoff distance.
As is clearly shown in
Figure 9, the LSC jet spreads widely apart as it travels long distances. This occurrence follows a linear fashion in the entire range of standoff distances. For an engineering application investigating the penetration capability of LSCs, the width of the LSCs jet does not generate valuable information and more related information is necessary.
Figure 10 shows the jet velocity component variation collected from the simulation along the width of the spread jet.
Figure 10.
%Y-velocity distribution along the jet width in large standoff distance.
Figure 10.
%Y-velocity distribution along the jet width in large standoff distance.
The x-direction of the jet (cross-sectional) is split into 10 pieces each approximately 7.2 mm in width as seen in
Figure 11. The x-axis in the jet runs from −36 mm to 36 mm in order to compensate for the large jet width at the 12 inches (30.48 cm) standoff distance. In order for a fair comparison for each standoff distance, this is kept throughout even though the jet width is much narrower at the shorter standoff distances. The y-axis shows the bottom 2 inches (50.8 mm) of the jet. This is also consistent with all of the models except the optimum standoff model. In this case, because the jet has not moved 2 inches (50.8 mm), the y-axis is set for the bottom 0.75 inches (19.05 mm). Note that the y-axis is not important for the analysis. It is merely to help illustrate the bottom 2 inches (50.8 cm) of the jet to put in perspective the concentration of the jet from model to model.
Figure 11.
Cross sectional area of the jet split into 10 separate pieces for analysis.
Figure 11.
Cross sectional area of the jet split into 10 separate pieces for analysis.
In each section, particles in the x-axis are picked at random. The magnitude of the y-velocity is then divided by the absolute velocity (
Figure 10). By dividing the magnitude of the y-velocity by the absolute velocity, the fractional component of the absolute velocity that was the y-velocity is found. Five particles are picked, the percentage of the absolute velocity that is the y-velocity is recorded, and these numbers are averaged to show an average percentage for each section. The graph shows the average percentage on the y-axis and the distance from the center of the jet on the x-axis (
Figure 10). Note that the ‘center’ is only really the center of the jet for the 12 inches (30.48 cm) standoff distance. The axes are kept unchanged for consistency in comparing the models. Due to the fact that in all of the graphs there is at least one section that has zero particles in it, these data points are left out since it would skew the graph. This also helps illustrate the jet width as the standoff increases. As the graph shows, the shorter the standoff distance becomes the more narrow the jet becomes. This is illustrated with the optimum standoff model only having two useful data points whereas the 12 inches (30.48 cm) standoff model has 9 useful data points.
Due to the jet spreading during the flight at large standoff distances, the center of the jet offsets from the true center of the LSC (or jet width). However, the graph is able to illustrate the center of the jet width by the peak point of each curve (i.e., the center or mid-point of the jet width in 12 inches (30.48 cm) standoff distance curve is located near +8 mm). The reason for the jet spreading during the flight in the simulation is not clearly known at this point. However, it is believed that the local unbalanced cell configurations in between the left and right wing of LSCs in the SPH model generates a miniscule time mismatch during the liner collapse, which separates the jet. In reality, this happens quite often due to the low level of manufacturing precision and the multi-dimensional axis of the jet formation as we described earlier.
In general, the entire curve shows a similar trend of the peak y-velocity (vertical jet velocity) ratio near the center of the jet width and low y-velocity ratio near the edge of the jet width. This means the downward jet velocity toward the target is larger near the center of the jet width and the other velocity components are larger near the edge of the jet width. This is a reasonable and expected result and is one of the main contributing factors to the limited cutting performances at larger standoff distances.
Another investigation is done to understand the cutting performances of LSC jets at different standoff distances as follows. In this analysis, the penetration profiles are revealed to show the effect at large standoff distance.
Figure 12,
Figure 13 and
Figure 14 show the penetration profiles created and a detailed description follows each figure.
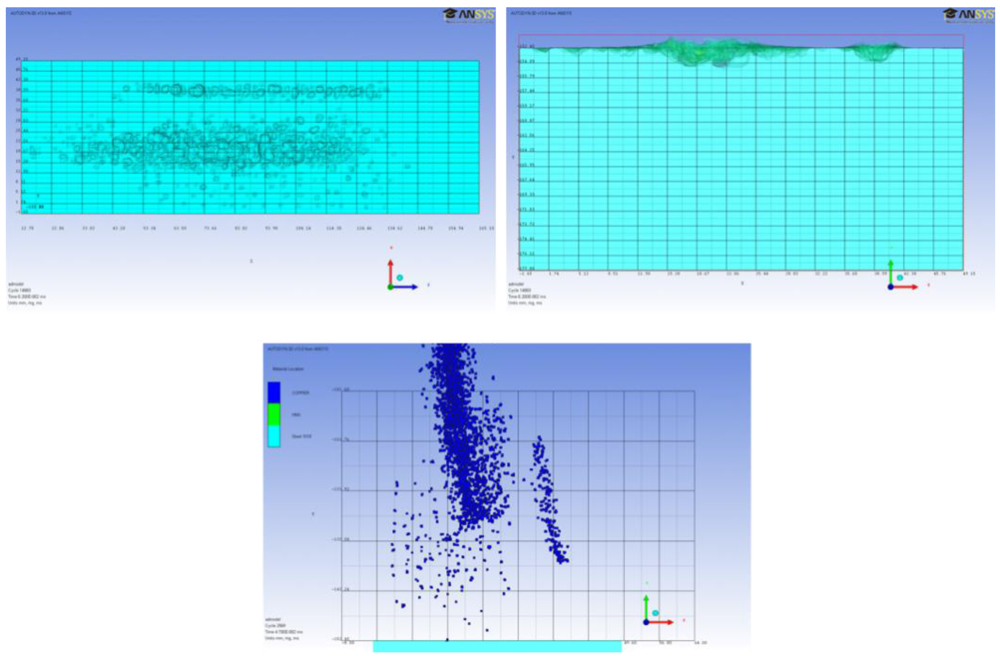
Figure 12.
The penetration profile can be seen on the top of the target and in a cross section of the target at the optimum standoff distance(1.905 cm) after 15 µs (left and right pictures respectively).
Figure 12.
The penetration profile can be seen on the top of the target and in a cross section of the target at the optimum standoff distance(1.905 cm) after 15 µs (left and right pictures respectively).
Figure 13.
The penetration profile can be seen on the top of the target and in a cross section of the target at a 3 inches (7.62 cm) standoff distance after 15 µs (top left and top right pictures respectively). The bottom picture above shows the jet spreading due to the distance traveled by the jet.
Figure 13.
The penetration profile can be seen on the top of the target and in a cross section of the target at a 3 inches (7.62 cm) standoff distance after 15 µs (top left and top right pictures respectively). The bottom picture above shows the jet spreading due to the distance traveled by the jet.
Figure 14.
The penetration profile can be seen on the top of the target and in a cross section of the target at a 6 inches (15.24 cm) standoff distance after 15 µs (top left and top right pictures respectively). The bottom picture above shows the jet spreading due to the distance traveled by the jet.
Figure 14.
The penetration profile can be seen on the top of the target and in a cross section of the target at a 6 inches (15.24 cm) standoff distance after 15 µs (top left and top right pictures respectively). The bottom picture above shows the jet spreading due to the distance traveled by the jet.
As seen in
Figure 12, the LSC placed at the OSD clearly shows the maximum penetration capability. There is no significant spreading of the jet over the penetration surface and the target shows a clean cut.
Figure 13 shows a reduction in penetration depth due to the 3 inches (7.72 cm) travel distance. A portion of the jet particles are skewed to the right side and a large jet entrance compared to the OSD models shows a reduction in the penetration depth.
There is significant reduction in penetration depth and wide spreading of the jet during impact shown in
Figure 14. There is minimum effective penetration and several large indentations are left after the jet impact. This results in poor penetration.
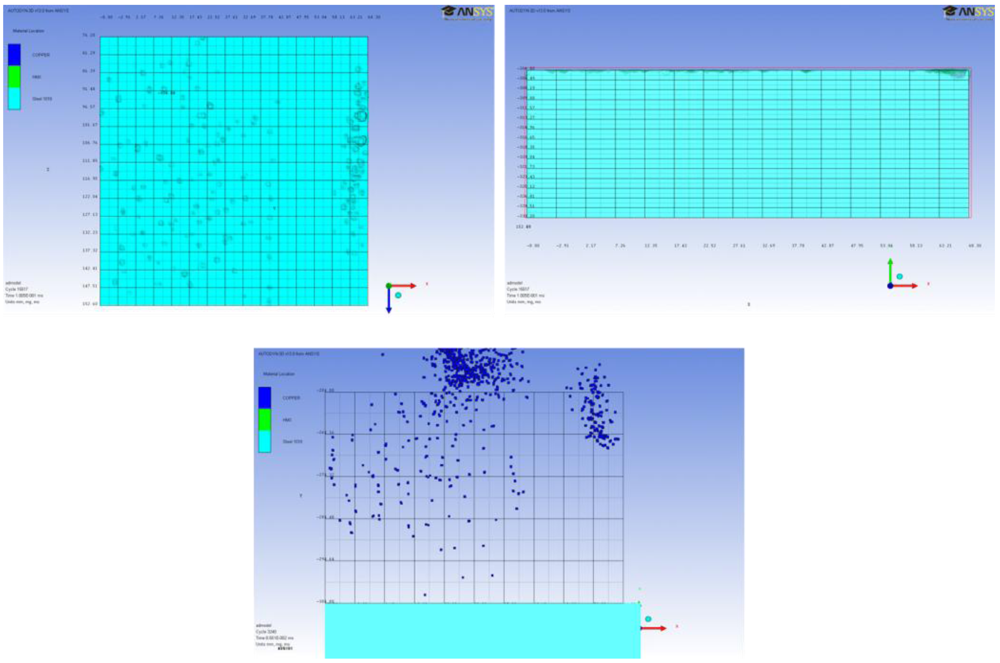
There is no penetration at the 12 inches (30.48 cm) standoff distance but numerous small indentations as seen in
Figure 15. The LSC jet spread too much resulting in no effective penetration to the target.
Figure 15.
The penetration profile can be seen on the top of the target and in a cross section of the target at a 12 inches (30.48 cm) standoff distance after 15 µs (top left and top right pictures respectively). The bottom picture above shows the jet spreading due to the distance traveled by the jet.
Figure 15.
The penetration profile can be seen on the top of the target and in a cross section of the target at a 12 inches (30.48 cm) standoff distance after 15 µs (top left and top right pictures respectively). The bottom picture above shows the jet spreading due to the distance traveled by the jet.
In general, we are able to understand the penetration capability under different standoff distances based on the visual investigation of the penetration profile. It is concluded that any effective penetration only occurs below the 3 inches (7.62 cm) standoff distance.