Improvement of the Dynamic and Seismic Behaviour of Rigid Block-like Structures by a Hysteretic Mass Damper Coupled with an Inerter
Abstract
:1. Introduction
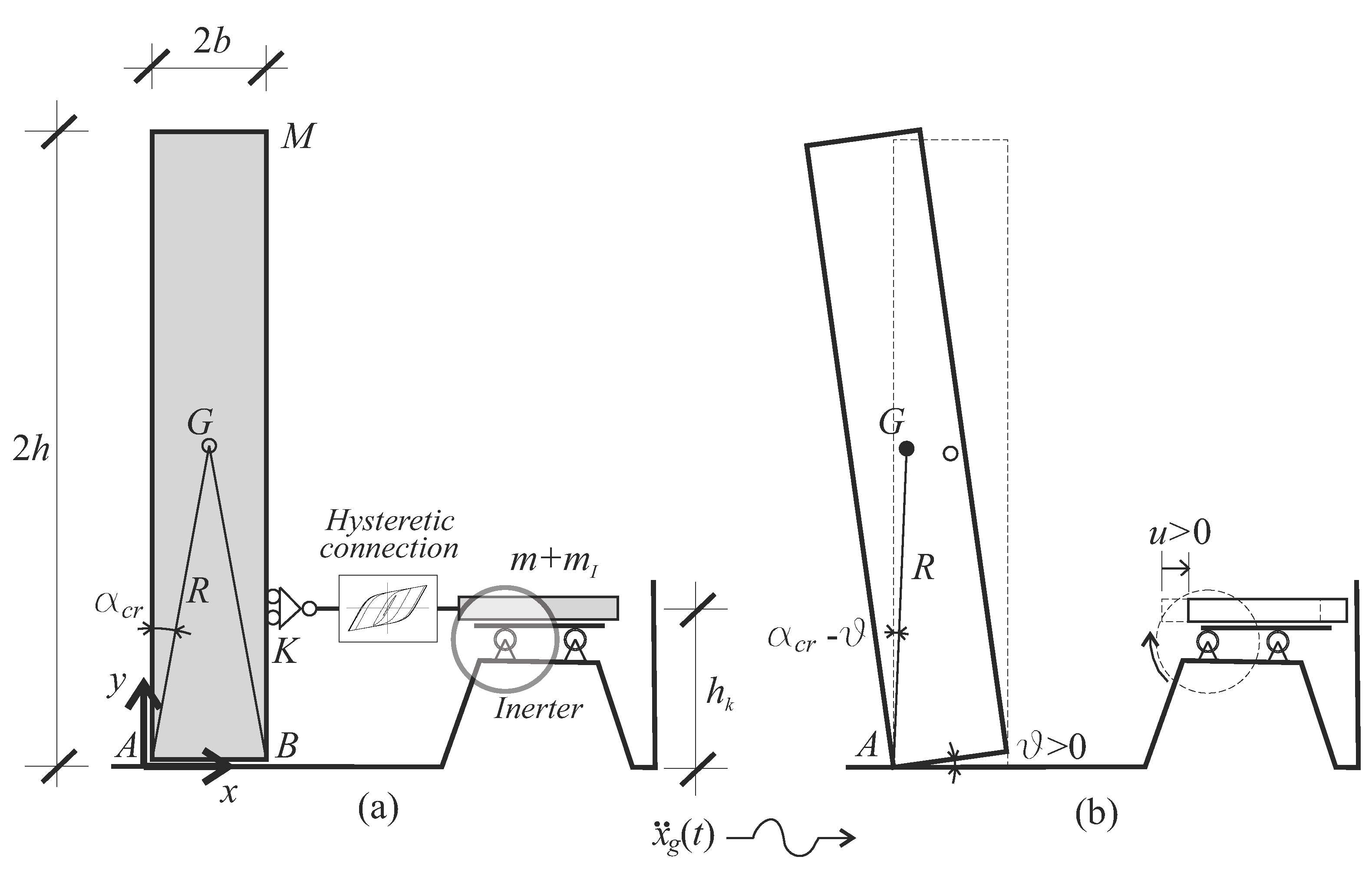
2. Mechanical Model of the Coupled System
2.1. Equations of Motion
2.1.1. Rocking Phase
2.1.2. Full-Contact Phase
2.2. Interter Device
2.3. Uplift, Impact, and Failure Conditions
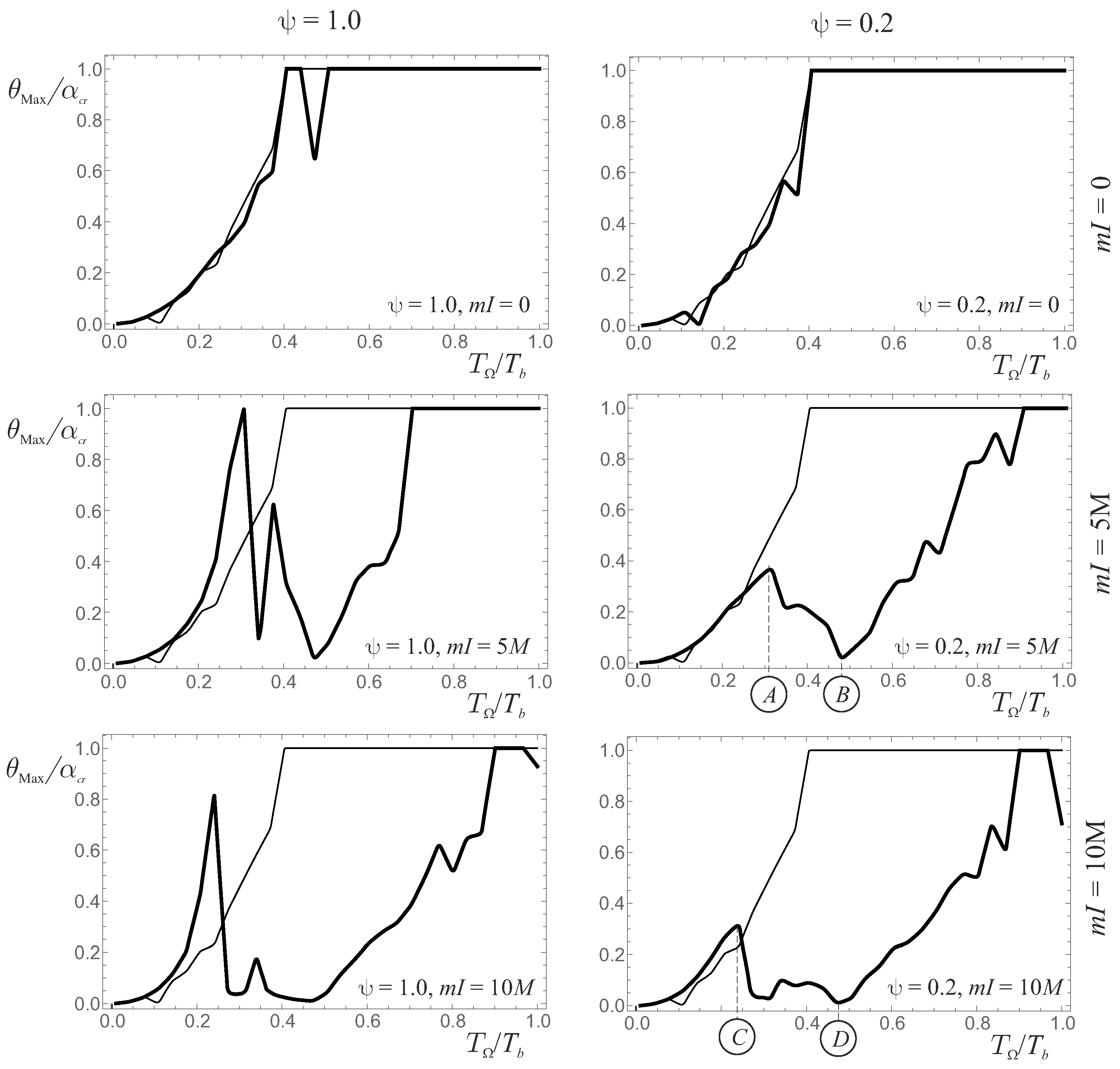
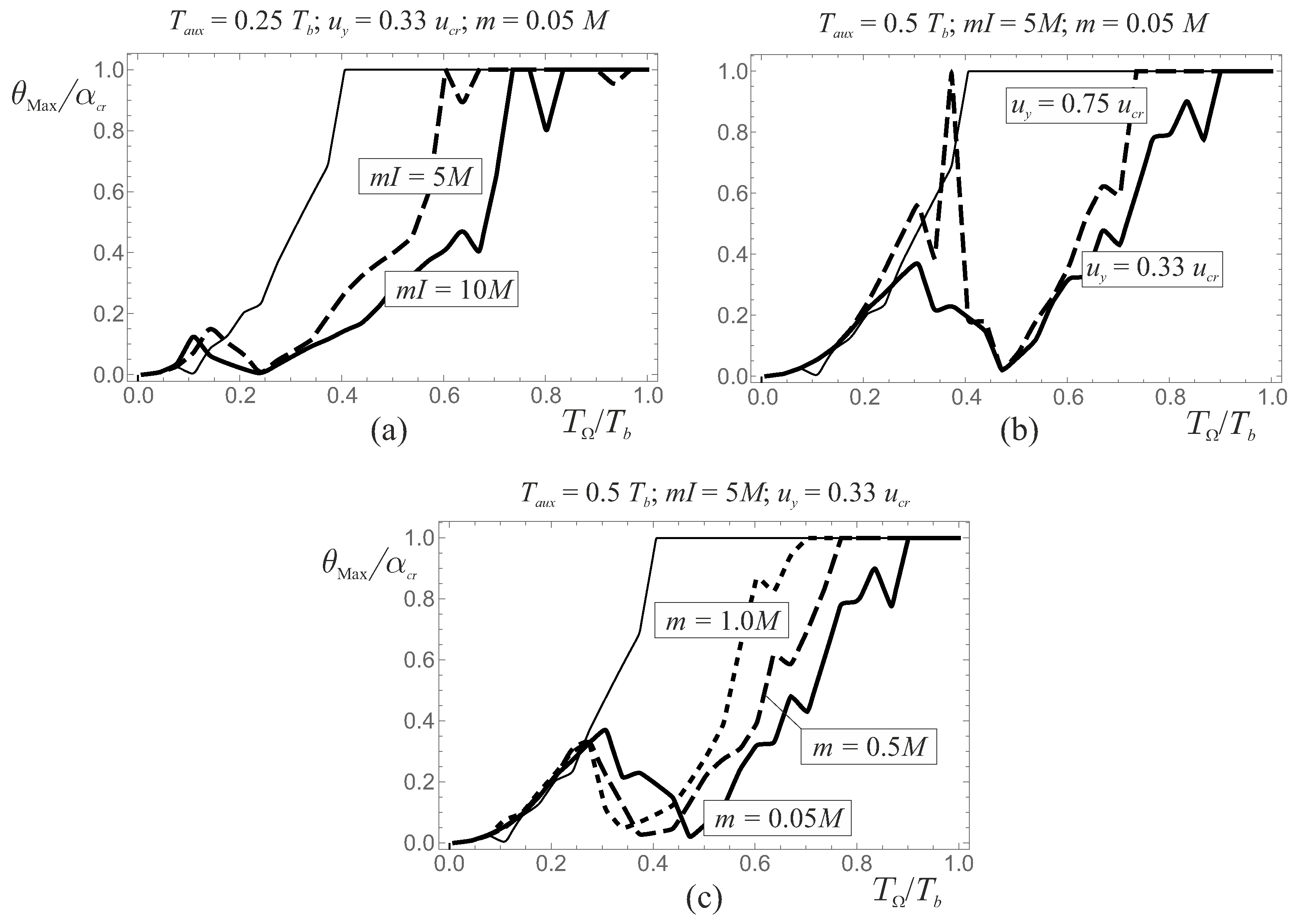
3. Harmonic Analyses
3.1. Modal Analysis of the Linearised Coupled System
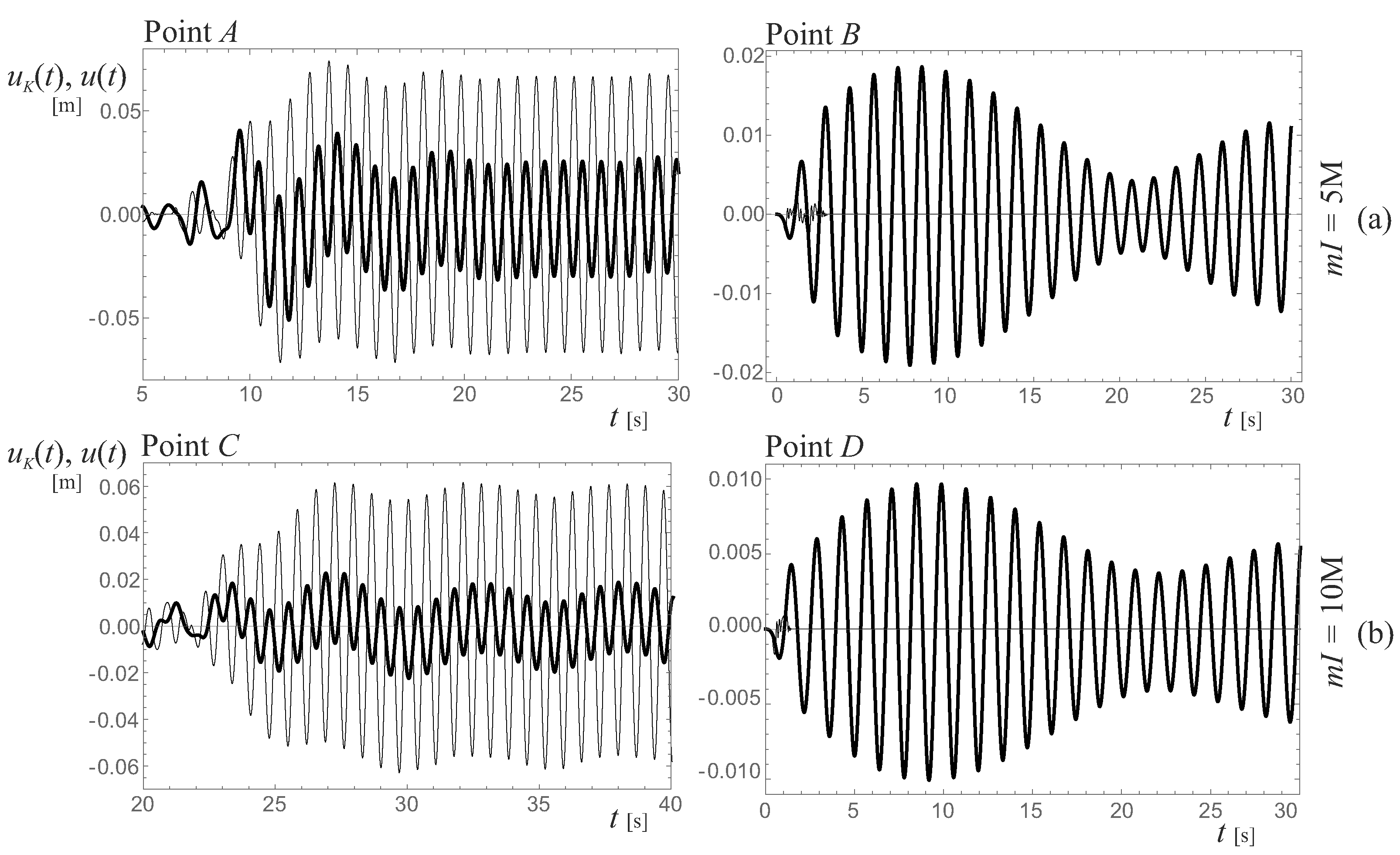
3.2. Frequency–Response Curves
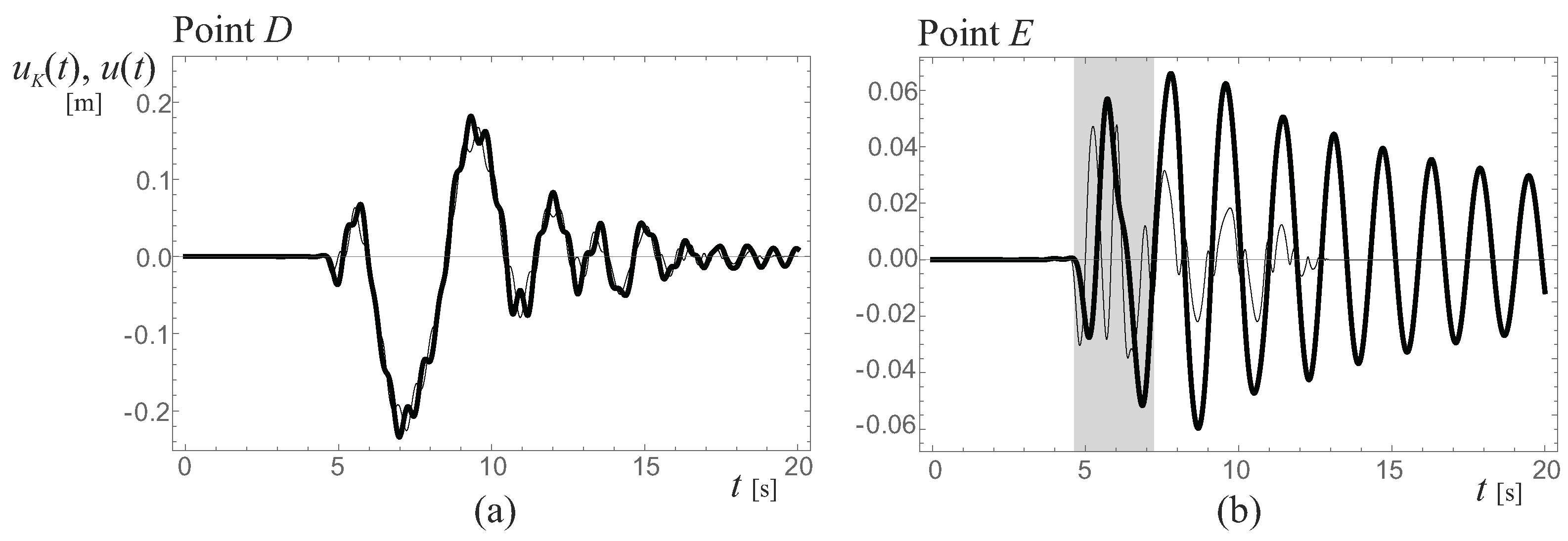
4. Seismic Analysis
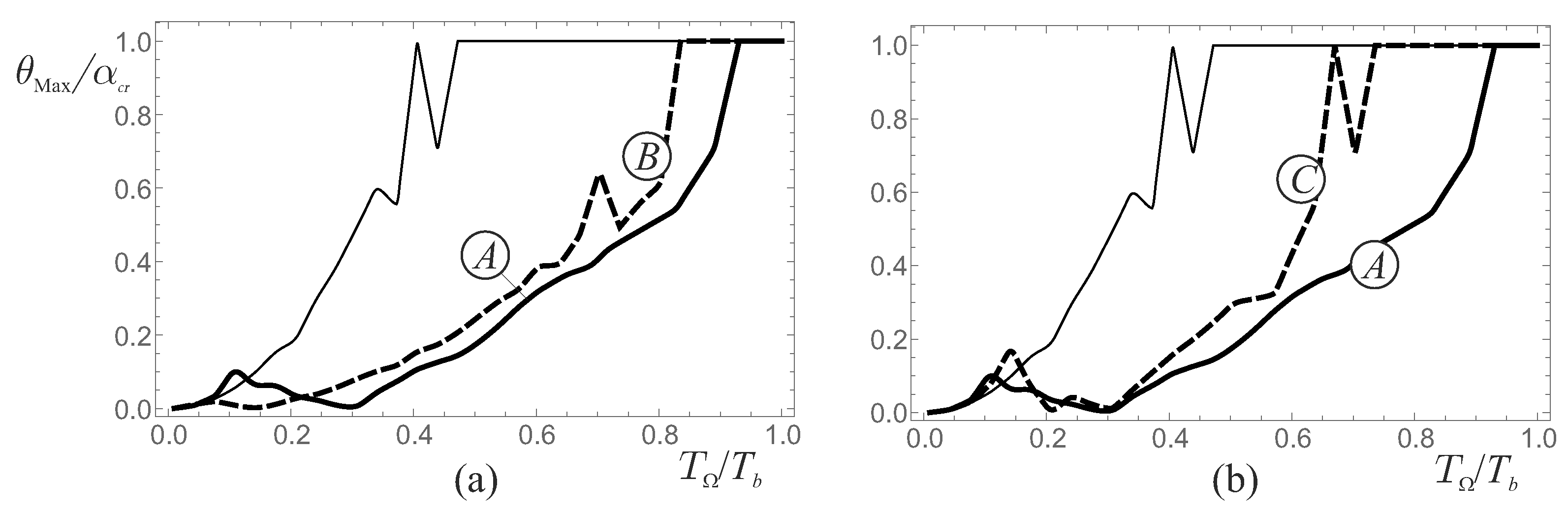
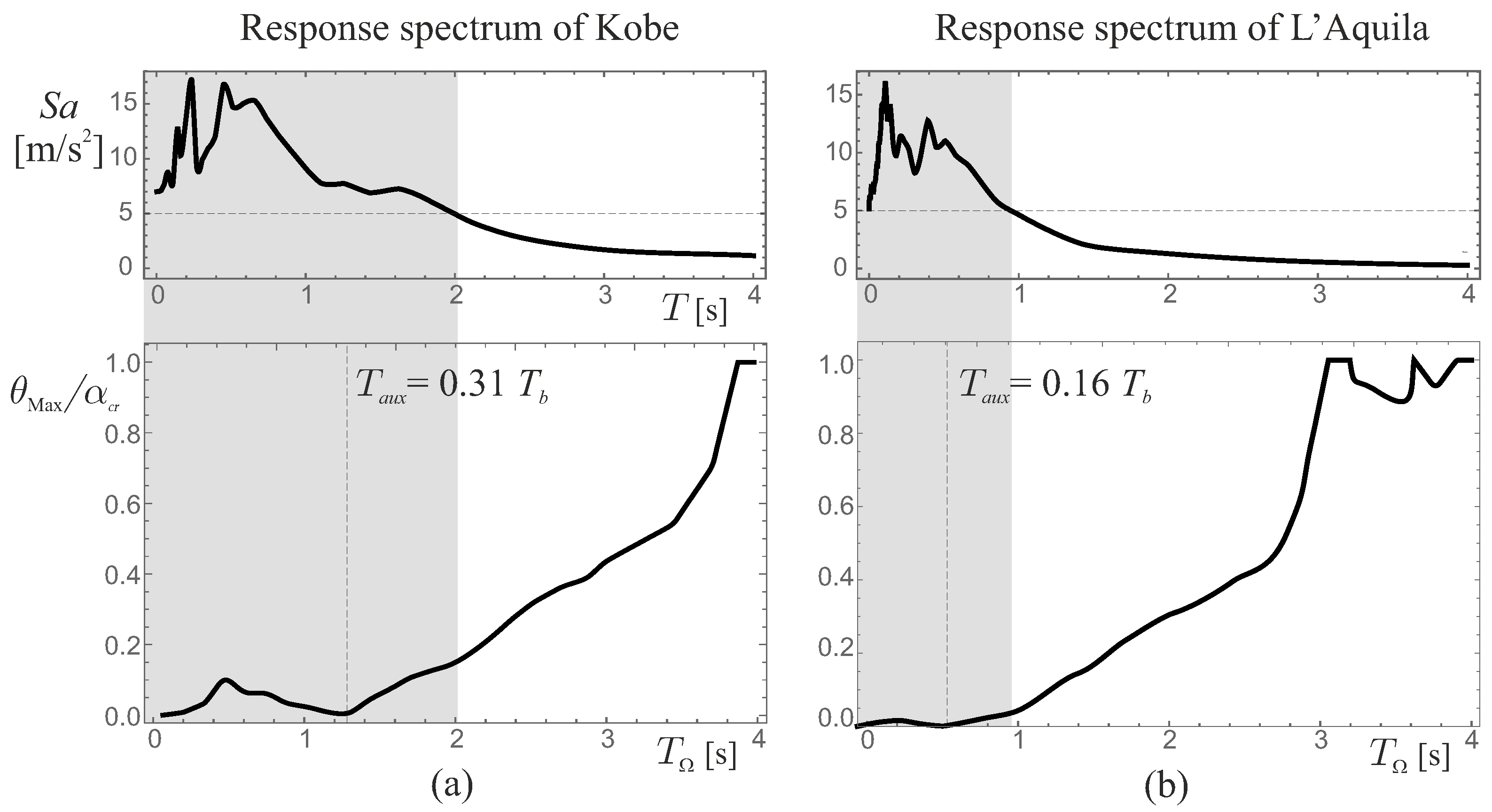
- If the rotation of the stand-alone rigid block does not reach , assumes maximum values slightly higher than unity when the rotation of the coupled system reaches ;
- If the rotation of the stand-alone rigid block reaches , acquires the unitary value when the rotation of the coupled system reaches .
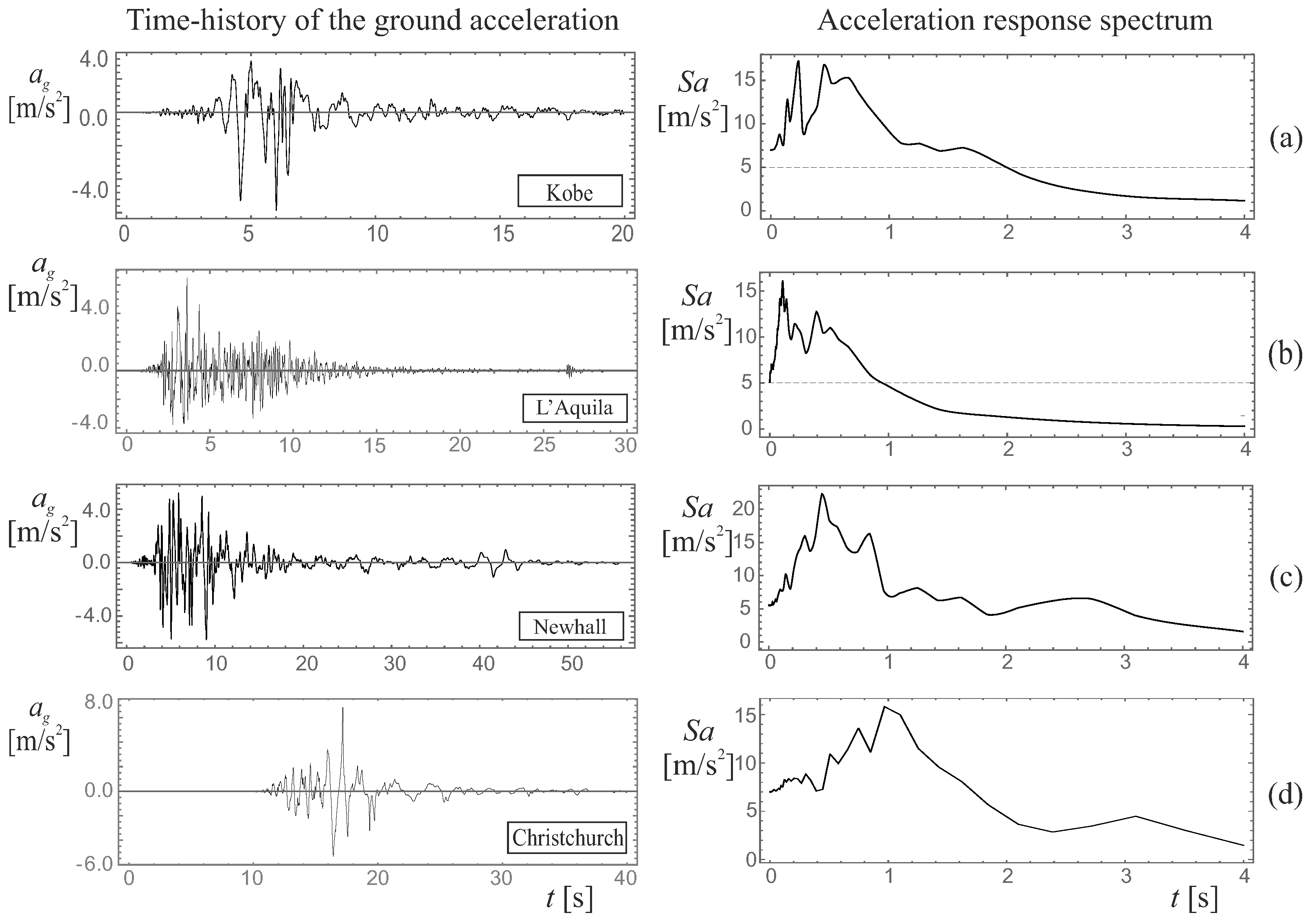
4.1. Seismic Records
- (a)
- Kobe, Takarazuka-000 station, ground motion recorded during the 1995 Japan earthquake;
- (b)
- L’Aquila, IT.AQV.HNE.D.20090406.013240.X.ACC station, ground motion recorded during the 2009 Italian earthquake;
- (c)
- Newhall, Newhall-360 station, ground motion recorded during the 1994 Northridge, California earthquake;
- (d)
- Christchurch, REHS ground 2011 Christchurch New Zealand.
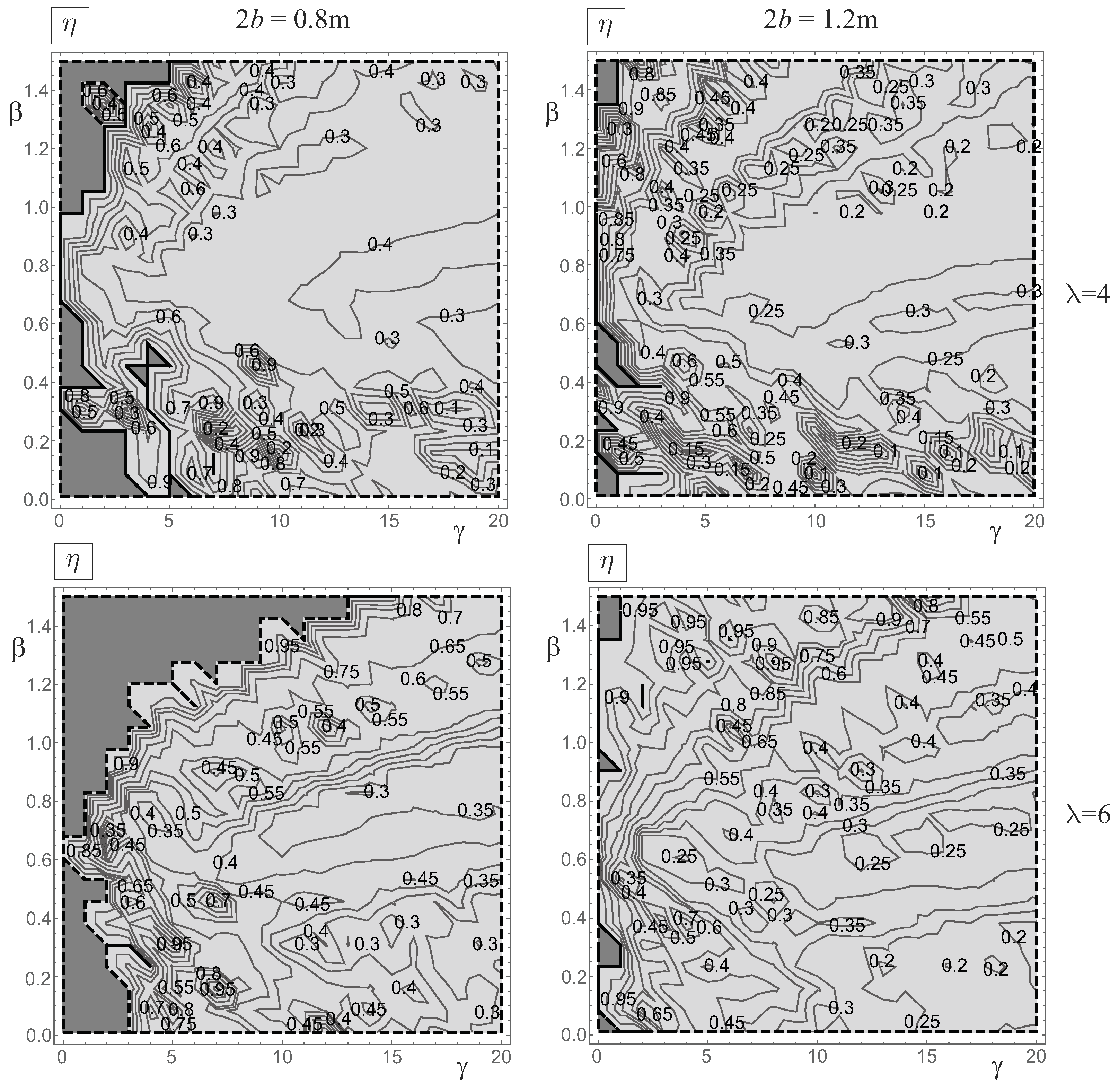
4.2. Gain Coefficients, Surfaces, and Maps
- (1)
- for the rigid block with and ;
- (2)
- for the rigid block with and ;
- (3)
- for the rigid block with and ;
- (4)
- for the rigid block with and .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akif Bülbül, M.; Harirchian, E.; Fatih Işık, M.; Ehsan Aghakouchaki Hosseini, S.; Işık, E. A Hybrid ANN-GA Model for an Automated Rapid Vulnerability Assessment of Existing RC Buildings. Appl. Sci. 2022, 12, 5138. [Google Scholar] [CrossRef]
- Harirchian, E.; Ehsan Aghakouchaki Hosseini, S.; Jadhav, K.; Kumari, V.; Rasulzade, S.; Işık, E.; Wasif, M.; Lahmer, T. A review on application of soft computing techniques for the rapid visual safety evaluation and damage classification of existing buildings. J. Build. Eng. 2021, 43, 102536. [Google Scholar] [CrossRef]
- Simoneschi, G.; Olivieri, C.; de Leo, A.; Di Egidio, A. Pole placement method to control the rocking motion of rigid blocks. Eng. Struct. 2018, 167, 39–47. [Google Scholar] [CrossRef]
- Di Egidio, A.; Contento, A.; Olivieri, C.; de Leo, A. Protection from overturning of rigid block-like objects with Linear Quadratic Regulator active control. Struct. Control Health Monit. 2020, 27, e2598. [Google Scholar] [CrossRef]
- Di Egidio, A.; de Leo, A.; Simoneschi, G. Effectiveness of mass-damper dynamic absorber on rocking block under one-sine pulse ground motion. Int. J. Non-Linear Mech. 2016, 98, 154–162. [Google Scholar] [CrossRef]
- Simoneschi, G.; de Leo, A.; Di Egidio, A. Effectiveness of oscillating mass damper system in the protection of rigid blocks under impulsive excitation. Eng. Struct. 2017, 137, 285–295. [Google Scholar] [CrossRef]
- Brzeski, P.; Kapitaniak, T.; Perlikowski, P. The Use of Tuned Mass Absorber to Prevent Overturning of the Rigid Block During Earthquake. Int. J. Struct. Stab. Dyn. 2016, 16, 1550075. [Google Scholar] [CrossRef]
- Thiers-Moggia, R.; Málaga-Chuquitaype, C. Seismic protection of rocking structures with inerters. Earthq. Eng. Struct. Dyn. 2019, 48, 528–547. [Google Scholar] [CrossRef] [Green Version]
- Thiers-Moggia, R.; Málaga-Chuquitaype, C. Seismic control of flexible rocking structures using inerters. Earthq. Eng. Struct. Dyn. 2020, 49, 1519–1538. [Google Scholar] [CrossRef]
- Thiers-Moggia, R.; Málaga-Chuquitaype, C. Dynamic response of post-tensioned rocking structures with inerters. Int. J. Mech. Sci. 2020, 187, 1–15. [Google Scholar] [CrossRef]
- Pietrosanti, D.; De Angelis, M.; Giaralis, A. Experimental study and numerical modeling of nonlinear dynamic response of SDOF system equipped with tuned mass damper inerter (TMDI) tested on shaking table under harmonic excitation. Int. J. Mech. Sci. 2020, 184, 105762. [Google Scholar] [CrossRef]
- Pietrosanti, D.; De Angelis, M.; Giaralis, A. Experimental seismic performance assessment and numerical modelling of nonlinear inerter vibration absorber (IVA)-equipped base isolated structures tested on shaking table. Earthq. Eng. Struct. Dyn. 2021, 50, 2732–2753. [Google Scholar] [CrossRef]
- Rana, R.; Soong, T. Parametric analysis and simplified design of tuned mass damper. Eng. Struct. 1998, 20, 193–204. [Google Scholar] [CrossRef]
- Engle, T.; Mahmoud, H.; Chulahwat, A. Hybrid tuned mass damper and isolation floor slab system optimized for vibration control. J. Earthq. Eng. 2015, 19, 1197–1221. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Earthquake-resilient design of base isolated buildings with TMD at basement: Application to a case study. Soil Dyn. Earthq. Eng. 2018, 113, 503–521. [Google Scholar] [CrossRef]
- Xiang, P.; Nishitani, A. Optimum design for more effective tuned mass damper system and its application to base isolated buildings. Struct. Control. Health Monit. 2014, 21, 98–114. [Google Scholar] [CrossRef]
- Marian, L.; Giaralis, A. Optimal design of a novel tuned mass-damper-inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probabilistic Eng. Mech. 2014, 38, 156–164. [Google Scholar] [CrossRef]
- Brzeski, P.; Kapitaniak, T.; Perlikowski, P. Novel type of tuned mass damper with inerter which enables changes of inertance. J. Sound Vib. 2015, 349, 56–66. [Google Scholar] [CrossRef]
- Pietrosanti, D.; De Angelis, M.; Basili, M. A generalized 2-DOF model for optimal design of MDOF structures controlled by Tuned Mass Damper Inerter (TMDI). Int. J. Mech. Sci. 2020, 185, 105849. [Google Scholar] [CrossRef]
- Pietrosanti, D.; De Angelis, M.; Basili, M. Optimal design and performance evaluation of systems with Tuned Mass Damper Inerter (TMDI). Earthq. Eng. Struct. Dyn. 2017, 46, 1367–1388. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI). Earthq. Eng. Struct. Dyn. 2018, 47, 1169–1192. [Google Scholar] [CrossRef]
- Vestroni, F.; Casini, P. Mitigation of structural vibrations by hysteretic oscillators in internal resonance. Nonlinear Dyn. 2020, 99, 505–518. [Google Scholar] [CrossRef]
- Wen, Y.K. Method for random vibration of hysteretic systems. J. Eng. Mech. 1976, 102, 249–263. [Google Scholar] [CrossRef]
- Housner, G. The behavior of inverted pendulum structures during earthquakes. Bull. Seismol. Soc. Am. 1963, 53, 404–417. [Google Scholar] [CrossRef]
- Kounadis, A.N. Parametric study in rocking instability of a rigid block under harmonic ground pulse: A unified approach. Soil Dyn. Earthq. Eng. 2013, 45, 125–143. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, H.; Bockstedte, A.; Foliente, G.; Paevere, P. Parameter Analysis of the Differential Model of Hysteresis. J. Eng. Mech. 2004, 71, 342–349. [Google Scholar] [CrossRef]
- Constantinou, M.; Adnane, M. Dynamics of Soil-Base-Isolated Structure Systems: Evaluation of Two Models for Yielding Systems; Report to NSAF; Department of Civil Engineering, Drexel University: Philadelphia, PA, USA, 1987. [Google Scholar]
- Makris, N.; Kampas, G. Seismic Protection of Structures with Supplemental Rotational Inertia. J. Eng. Mech. 2016, 142, 04016089. [Google Scholar] [CrossRef]
- Cheng, F.Y. Matrix Analysis of Structural Dynamics—Applications and Earthquake Engineering; Marcel Dekker, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Vaiana, N.; Rosati, L. Classification and unified phenomenological modeling of complex uniaxial rate-independent hysteretic responses. Mech. Syst. Signal Process. 2023, 182, 109539. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Rosati, L. A generalized class of uniaxial rate-independent models for simulating asymmetric mechanical hysteresis phenomena. Mech. Syst. Signal Process. 2021, 146, 106984. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Egidio, A.; Contento, A. Improvement of the Dynamic and Seismic Behaviour of Rigid Block-like Structures by a Hysteretic Mass Damper Coupled with an Inerter. Appl. Sci. 2022, 12, 11527. https://doi.org/10.3390/app122211527
Di Egidio A, Contento A. Improvement of the Dynamic and Seismic Behaviour of Rigid Block-like Structures by a Hysteretic Mass Damper Coupled with an Inerter. Applied Sciences. 2022; 12(22):11527. https://doi.org/10.3390/app122211527
Chicago/Turabian StyleDi Egidio, Angelo, and Alessandro Contento. 2022. "Improvement of the Dynamic and Seismic Behaviour of Rigid Block-like Structures by a Hysteretic Mass Damper Coupled with an Inerter" Applied Sciences 12, no. 22: 11527. https://doi.org/10.3390/app122211527





