Experimental Dynamic Response of a Multi-Story Frame Structure Equipped with Non-Conventional TMD Implemented via Inter-Story Isolation
Abstract
:1. Introduction
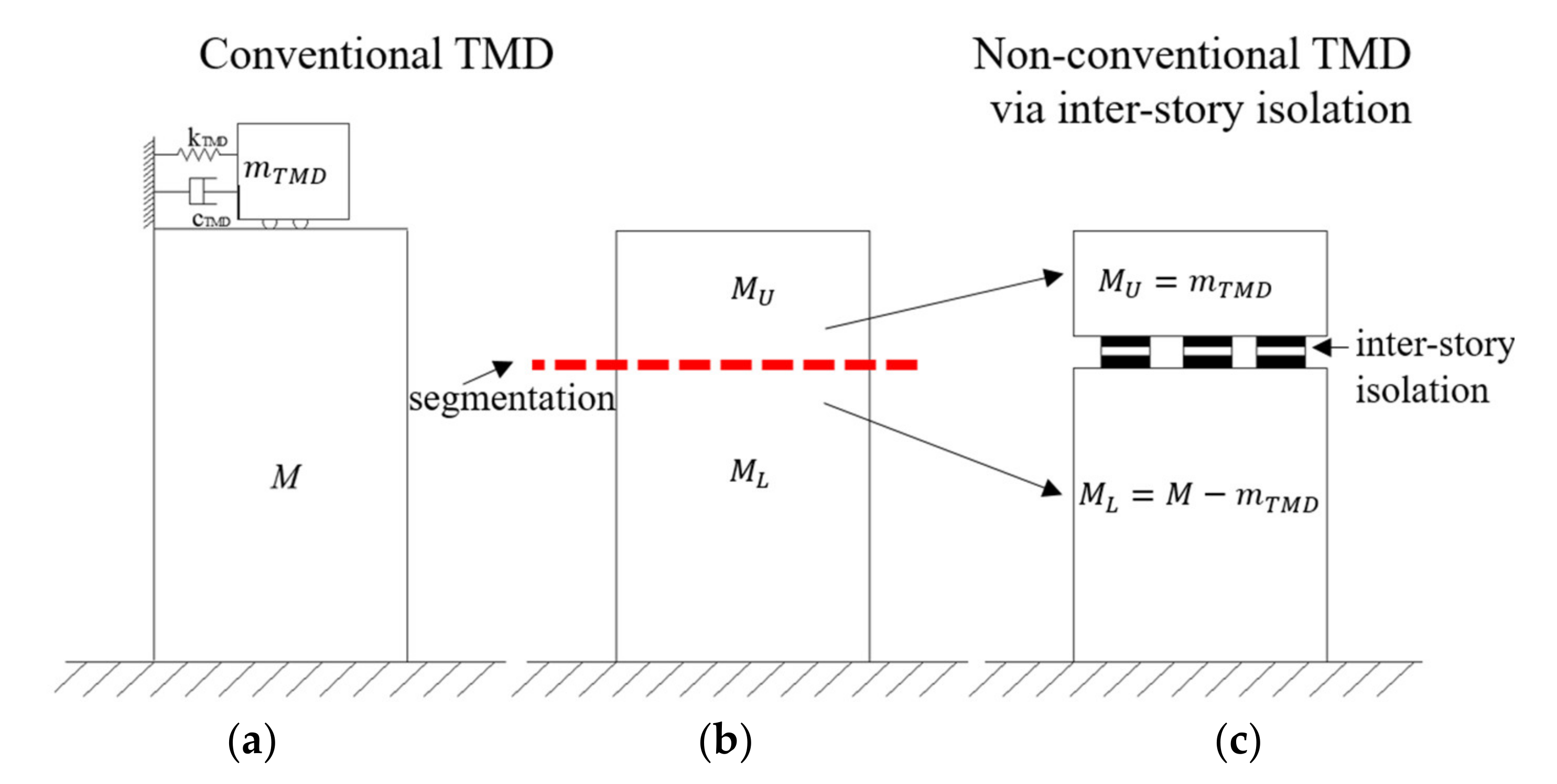
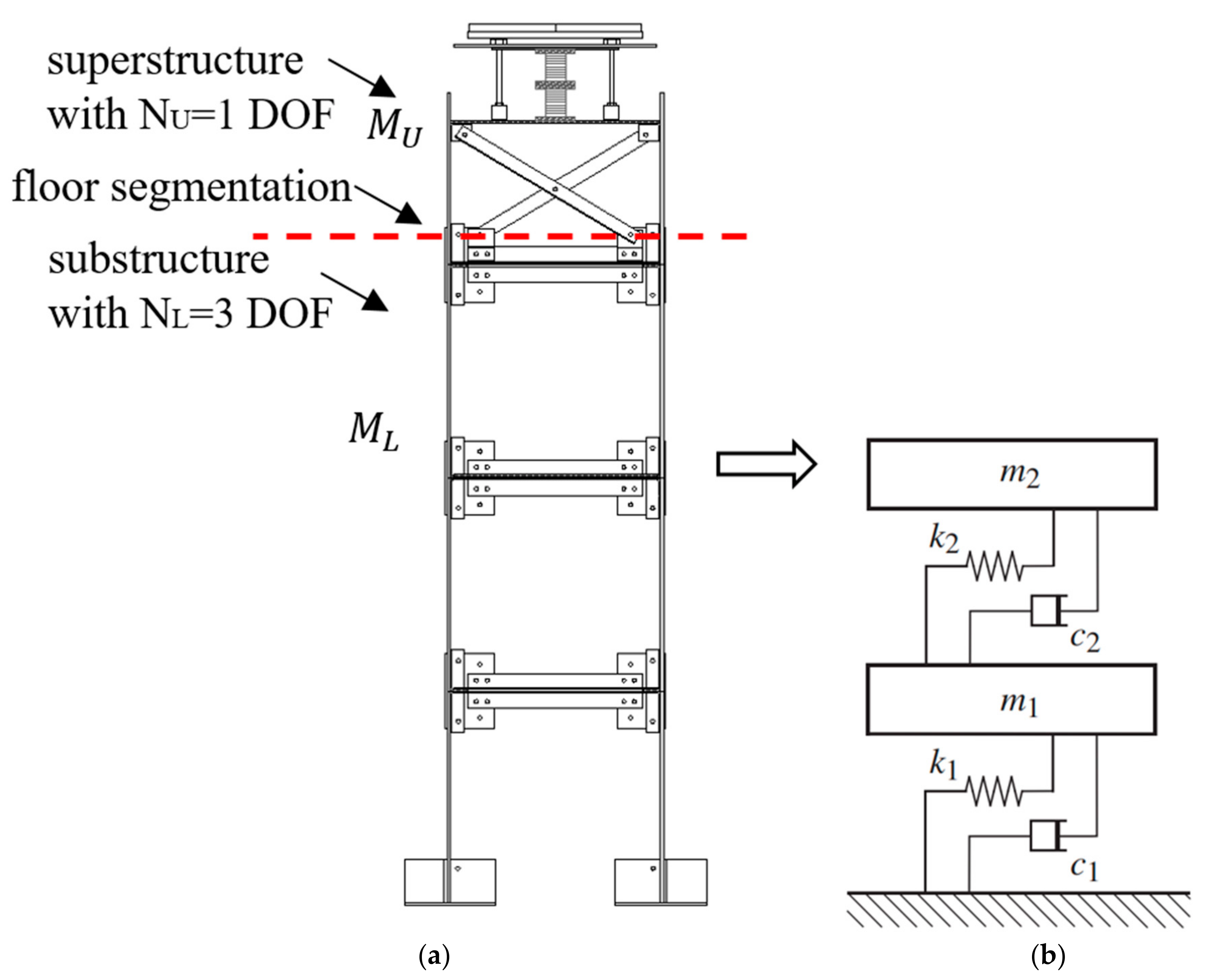
2. Description of the Physical Models
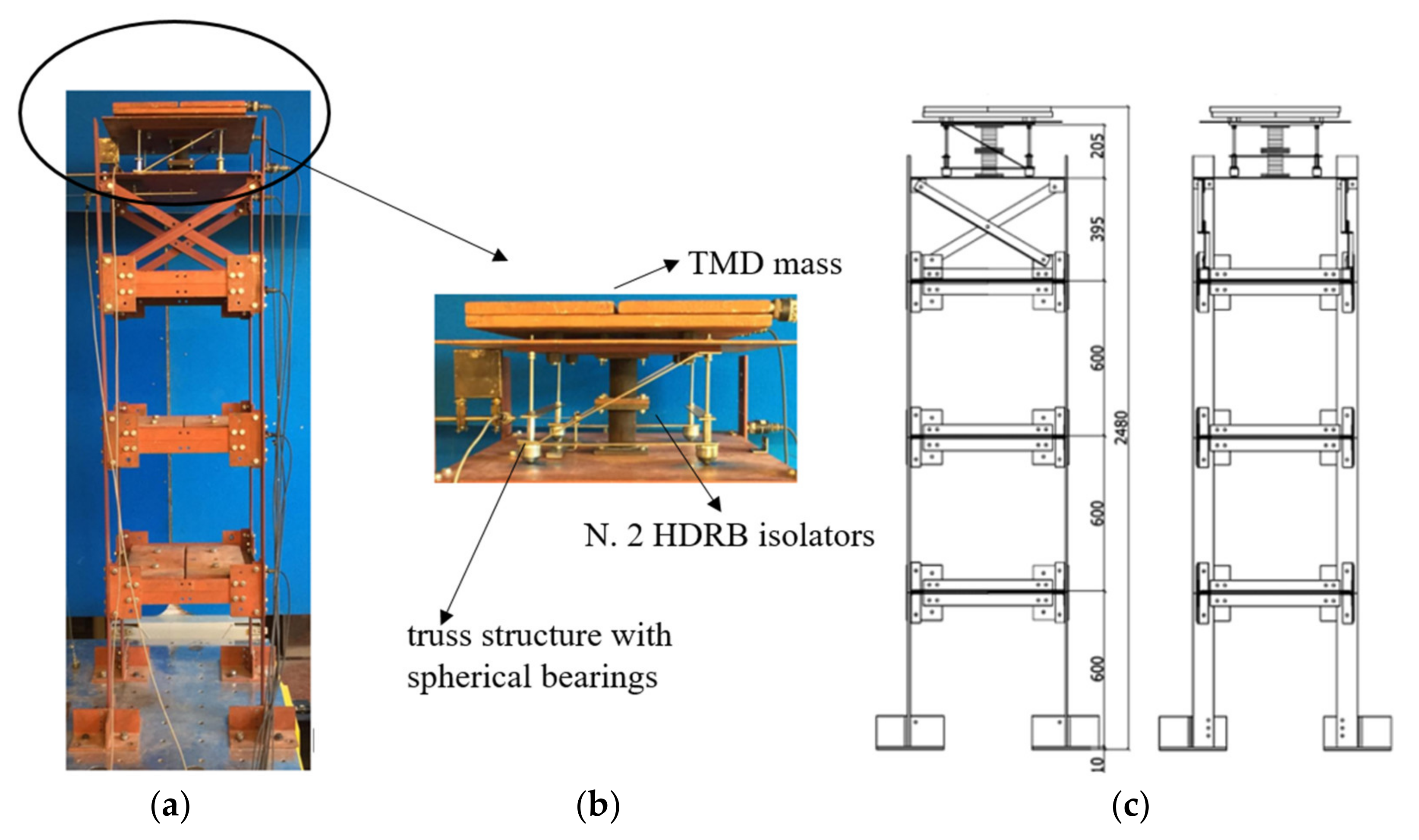
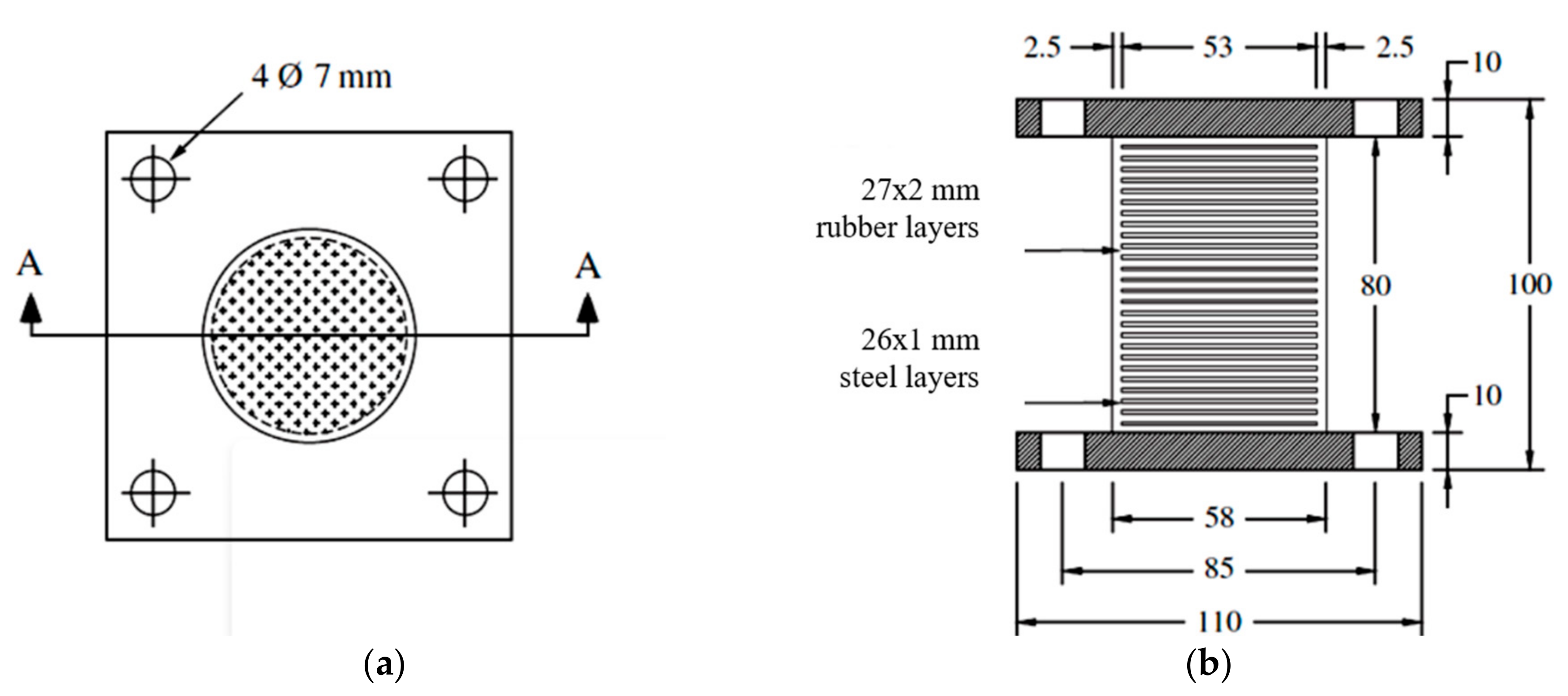
3. Non-Conventional TMD Design
4. Experimentation
4.1. Experimental Set-Up
4.2. Input Signals
5. Experimental Results
5.1. Dynamic Tests
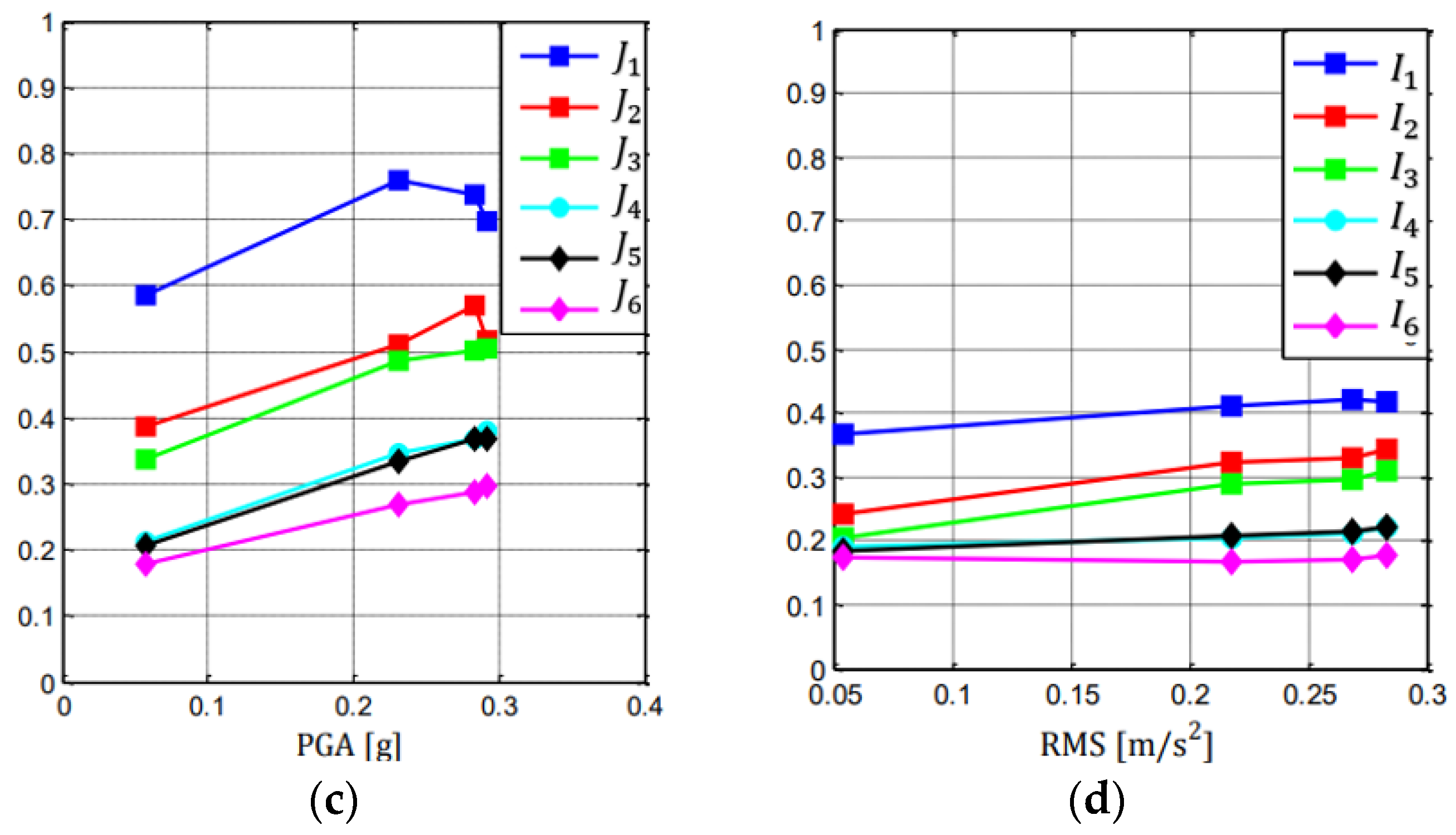
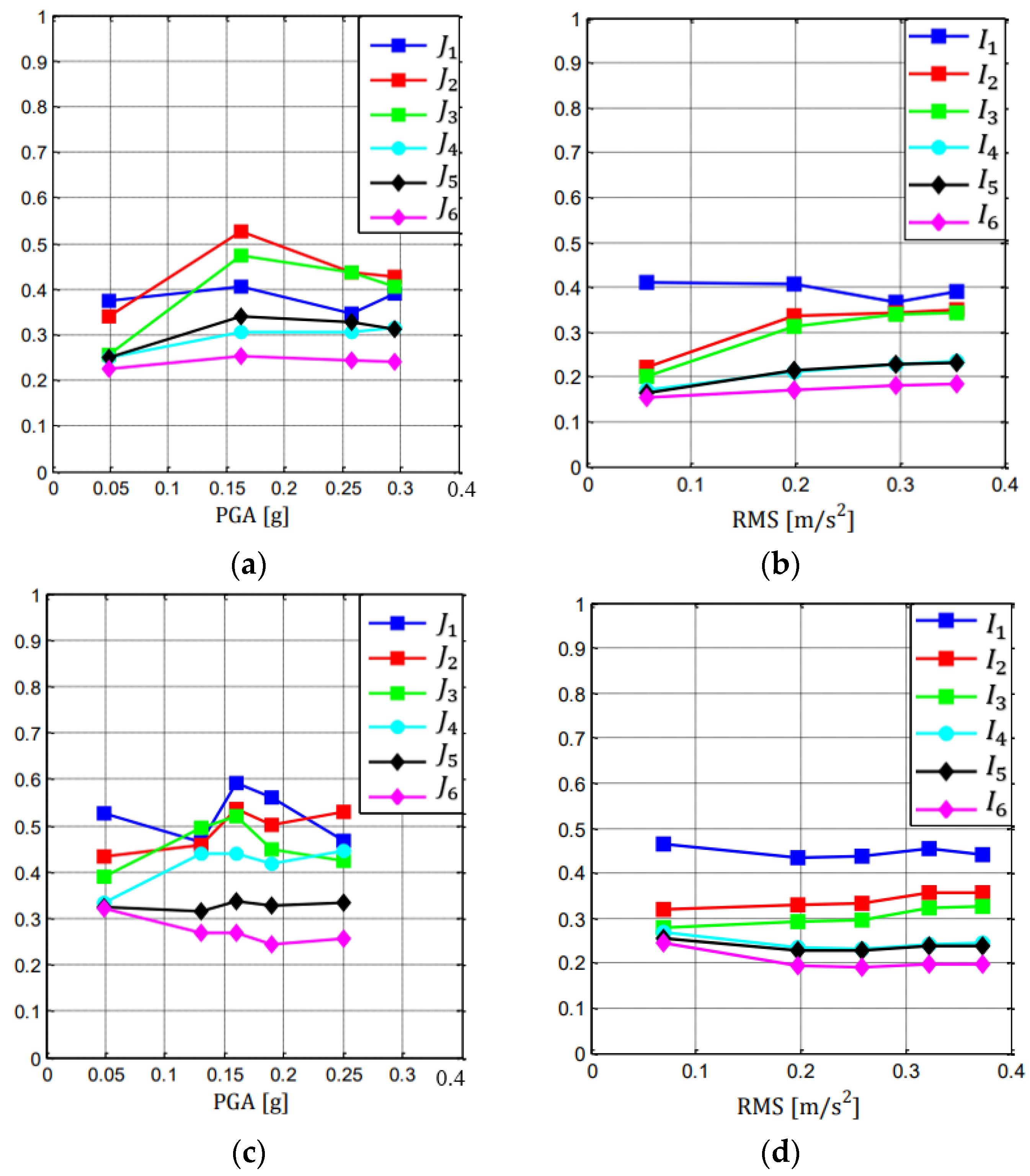
5.2. Seismic Effectiveness
5.3. Further Considerations on the TMD Effectiveness
6. Conclusions
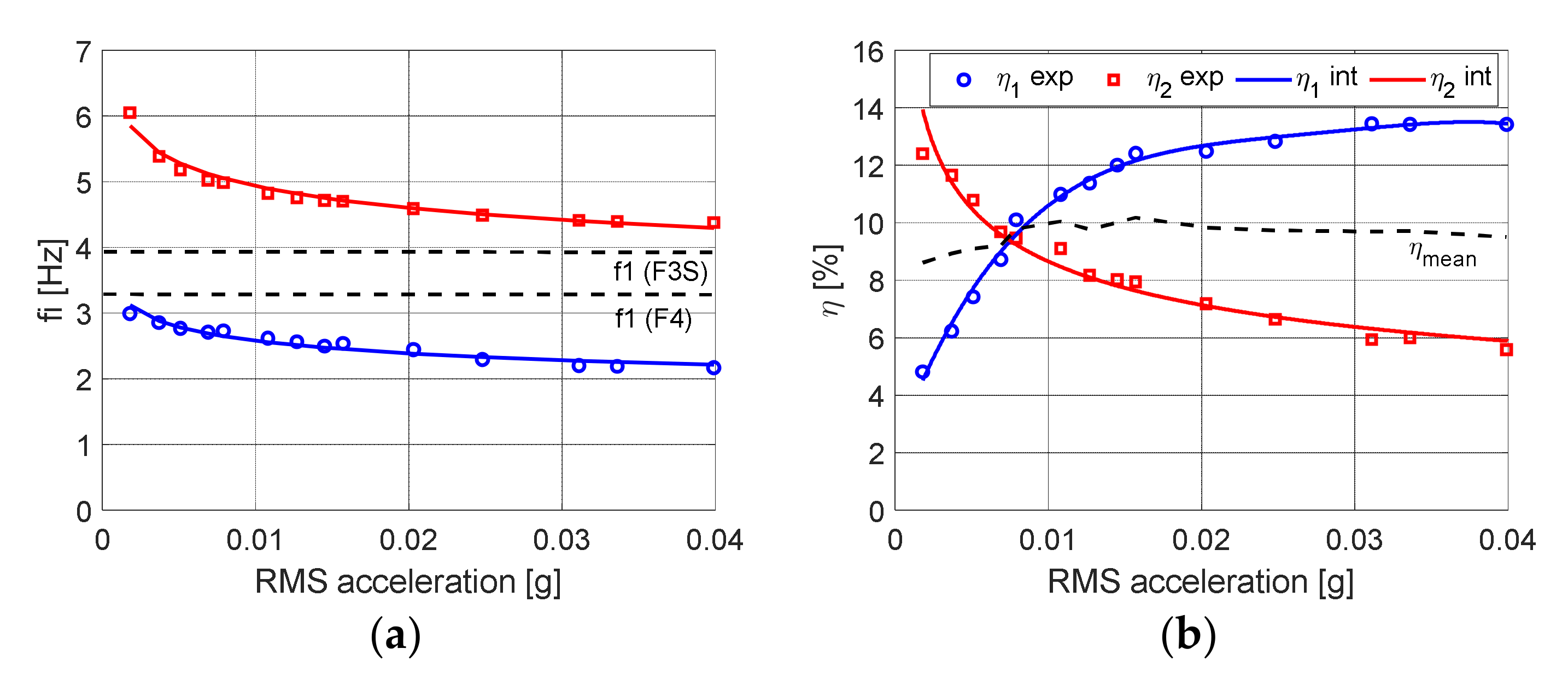
- From white noise tests, the dynamical characterization of the models tested was conducted by observation of PFRFs. For each configuration, structural identification was carried out. A dynamic behavior for the F4 and F3S configurations emerged that was almost linear. For the FTMD configuration, a softening behavior due to the nonlinearity introduced by the HDRB isolators emerged by increasing the excitation. The first two frequencies decreased with the input intensity, however they maintained a difference between each other, that was almost constant by increasing the excitation. Instead, the first two damping factors showed a rapid exchange between them that was almost constant in the mean value. The high dissipative capabilities induced by the HDRB isolators were highlighted.
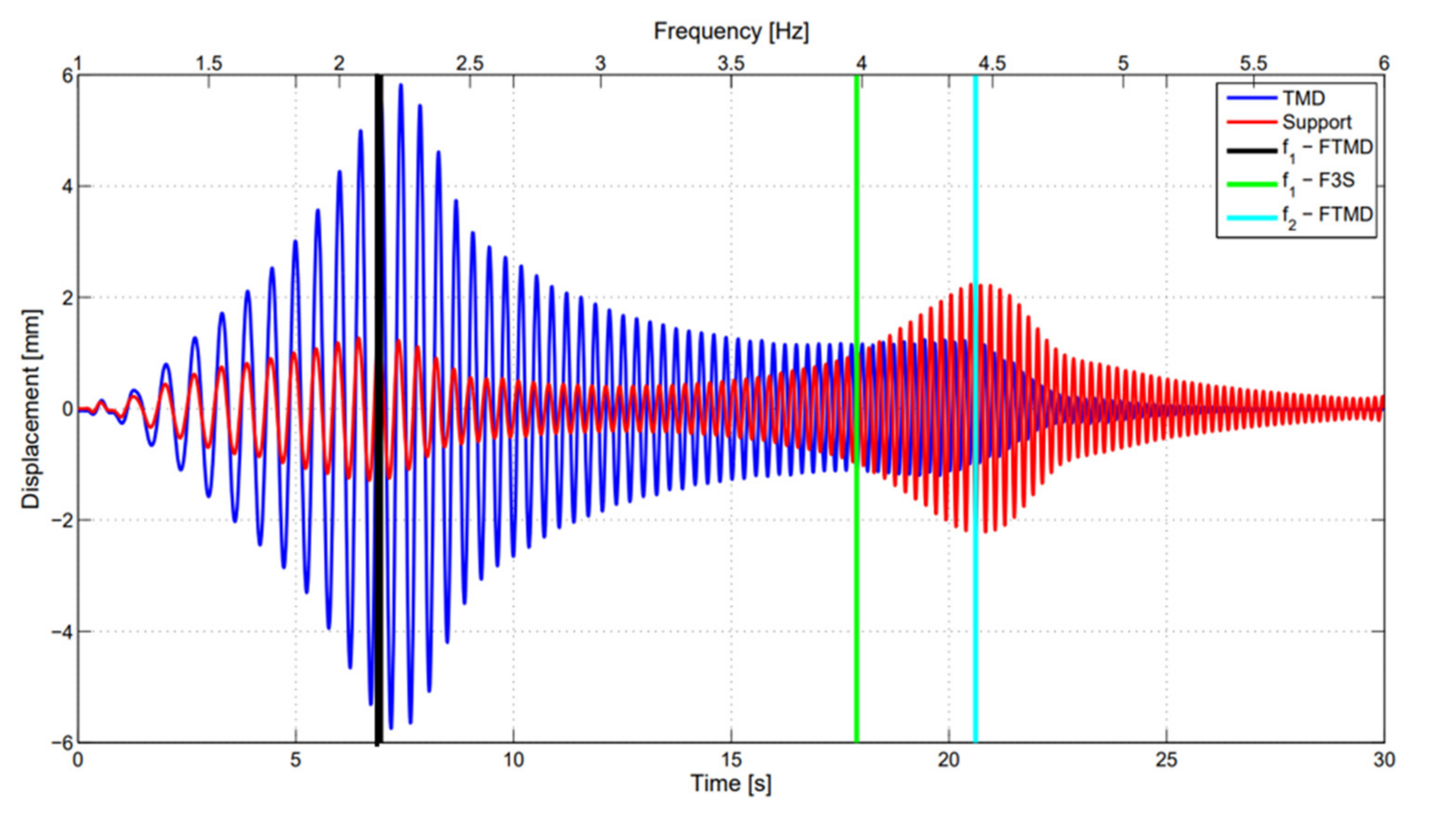
- Sine sweep tests confirmed the main resonances observed for the controlled structure as well as the response nonlinearities, highlighted through different amplification values at increasing and decreasing tests.
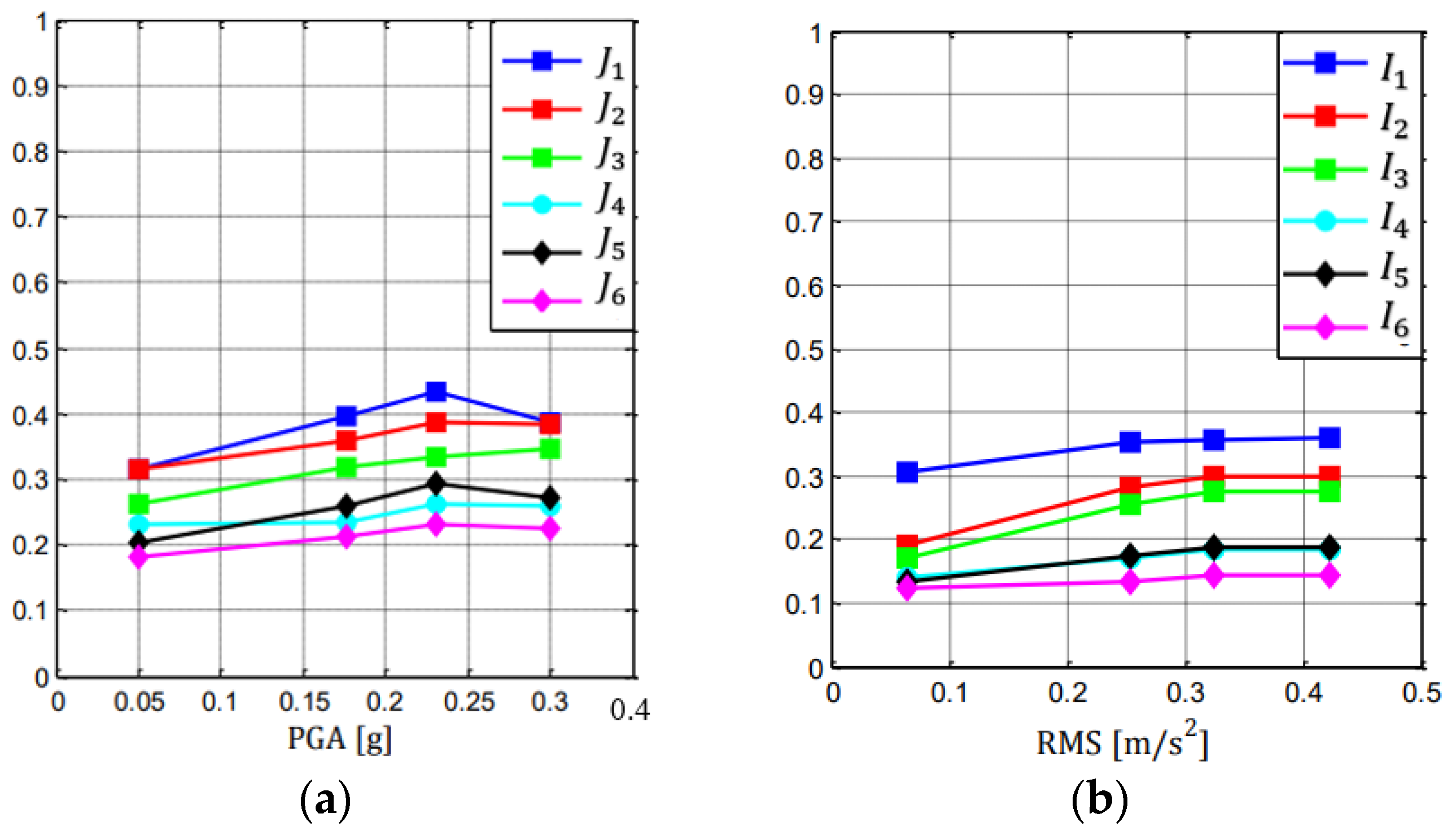
- The effectiveness of the control strategy was proven from seismic tests, in addition to what was evidenced by white noise and sine sweep tests. Implementing inter-story isolation to realize a non-conventional TMD, all responses were strongly reduced in terms of peaks and RMS values in a wide range of intensities. Adding a non-conventional TMD in an original uncontrolled structure was demonstrated to be effective as well, producing large response reductions in all the ranges of intensities considered.
- With respect to a non-segmented structure, the implementation of inter-story isolation and realization of a non-conventional TMD produced a great attenuation of the dynamic structural response at all the frequencies, proving that it is a smart control strategy useful to enhance structural vibration mitigation.
- With respect to a three-story structure, the introduction of a TMD with a high mass ratio produced its control action mainly around the first mode, with a great attenuation of the dynamic response in a wide range of frequencies centered on the first uncontrolled mode.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soong, T.T.; Dargush, G.F. Passive Energy Dissipation Systems in Structural Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Reggio, A.; De Angelis, M. Optimization of a non-conventional TMD implemented via inter-storey isolation. In Proceedings of the 9th International Conference on Structural Dynamics, Eurodyn, Porto, Portugal, 30 June–2 July 2014. [Google Scholar]
- Reggio, A.; De Angelis, M. Optimal energy-based seismic design of non-conventional Tuned Mass Damper (TMD) implemented via inter-story isolation. Earthq. Eng. Struct. Dyn. 2015, 44, 1623–1642. [Google Scholar] [CrossRef]
- Feng, M.Q.; Mita, A. Vibration control of tall buildings using mega subconfiguration. J. Eng. Mech. 1995, 121, 1082–1088. [Google Scholar] [CrossRef]
- Limazie, T.; Zhang, X.; Wang, X. Vibration control parameters investigation of the mega-sub controlled structure system (MSCSS). Earthq. Struct. 2013, 5, 225–237. [Google Scholar] [CrossRef]
- Villaverde, R.; Aguirre, M.; Hamilton, C. Aseismic roof isolation system built with steel oval elements. Earthq. Spectra. 2005, 21, 225–241. [Google Scholar] [CrossRef]
- Pagliaro, S.; Di Egidio, A. Archetype Dynamically Equivalent 3-DOF Model to Evaluate Seismic Performances of Intermediate Discontinuity in Frame Structures. J. Eng. Mech. 2022, 148, 04022004. [Google Scholar] [CrossRef]
- Fabrizio, C.; Di Egidio, A.; de Leo, A.M. Top disconnection versus base disconnection in structures subjected to harmonic base excitation. Eng. Struct. 2017, 152, 660–670. [Google Scholar] [CrossRef]
- Faiella, D.; Mele, E. Insights into inter-story isolation design through the analysis of two case studies. Eng. Struct. 2020, 215, 11066. [Google Scholar] [CrossRef]
- Faiella, D.; Calderoni, B.; Mele, E. Seismic Retrofit of Existing Masonry Buildings through Inter-story Isolation System: A Case Study and General Design Criteria. J. Earthq. Eng. 2022, 26, 2051–2087. [Google Scholar] [CrossRef]
- Basili, M.; De Angelis, M. Investigation on the optimal properties of semi active control devices with continuous control for equipment isolation. Scalable Comput. 2014, 15, 331–343. [Google Scholar] [CrossRef]
- Pietrosanti, D.; De Angelis, M.; Basili, M. Optimal design and performance evaluation of systems with Tuned Mass Damper Inerter. (TMDI). Earthq. Eng. Struct. Dyn. 2017, 46, 1367–1388. [Google Scholar] [CrossRef]
- Pietrosanti, D.; De Angelis, M.; Basili, M. A generalized 2-DOF model for optimal design of MDOF structures controlled by Tuned Mass Damper Inerter (TMDI). Int. J. Mech. Sci. 2020, 185, 105849. [Google Scholar] [CrossRef]
- De Angelis, M.; Giaralis, A.; Petrini, F.; Pietrosanti, D. Optimal tuning and assessment of inertial dampers with grounded inerter for vibration control of seismically excited base-isolated systems. Eng. Struct. 2019, 196, 109250. [Google Scholar] [CrossRef]
- Liang, Q.; Li, L.; Yang, Q. Seismic analysis of the tuned-inerter-damper enhanced mega-sub structure system. Struct. Contol. Health Monit. 2020, 28, 2658. [Google Scholar] [CrossRef]
- Wang, Z.; Giaralis, A. Top-Story Softening for Enhanced Mitigation of Vortex Shedding-Induced Vibrations in Wind-Excited Tuned Mass Damper Inerter-Equipped Tall Buildings. J. Struct. Eng. 2021, 147, 04020283. [Google Scholar] [CrossRef]
- Saha, A.; Mishra, S.K. Amplification of seismic demands in inter-storey-isolated buildings subjected to near fault pulse type ground motions. Soil Dyn. Earthq. Eng. 2021, 147, 106771. [Google Scholar] [CrossRef]
- Saha, A.; Mishra, S.K. Implications of inter-storey-isolation (ISI) on seismic fragility, loss and resilience of buildings subjected to near fault ground motions. Bull. Earthq. Eng. 2022, 20, 899–939. [Google Scholar] [CrossRef]
- Villaverde, R.; Mosqueda, G. Aseismic roof isolation system: Analytic and shake table studies. Earthq. Eng. Struct. Dyn. 1999, 28, 217–234. [Google Scholar] [CrossRef]
- De Angelis, M.; Perno, S.; Reggio, A. Dynamic response and optimal design of structures with large mass ratio TMD. Earthq. Eng. Struct. Dyn. 2012, 41, 41–60. [Google Scholar] [CrossRef]
- Shi, S.; Du, D.; Xu, W.; Wang, S. Theoretical and experimental study on an innovative seismic retrofit solution for old brick masonry buildings. Eng. Struct. 2020, 225, 111296. [Google Scholar] [CrossRef]
- Tronci, E.M.; De Angelis, M.; Betti, R.; Altomare, V. Vibration-based structural health monitoring of a RC-masonry tower equipped with non-conventional TMD. Eng. Struct. 2020, 224, 111212. [Google Scholar] [CrossRef]
- Basili, M.; De Angelis, M. Preliminary experimental results of shaking table tests on mdof structure equipped with non-conventional tmd. Lect. Notes Mech. Eng. 2020, 223–232. [Google Scholar] [CrossRef]
- Luş, H.; Betti, R.; Yu, J.; De Angelis, M. Investigation of a system identification methodology in the context of the ASCE benchmark problem. J. Eng. Mech. 2004, 130, 71–78. [Google Scholar] [CrossRef]
- Luş, H.; Betti, R.W.; Longman, R.W. Identification of linear structural systems using earthquake-induced vibration data. Earthq. Eng. Struct. Dyn. 1999, 28, 1449–1467. [Google Scholar] [CrossRef]
- Miranda, J.C. Discussion of system intrinsic parameters of tuned mass dampers used for seismic response reduction. Struct. Control Health Monit. 2016, 23, 349–368. [Google Scholar] [CrossRef]


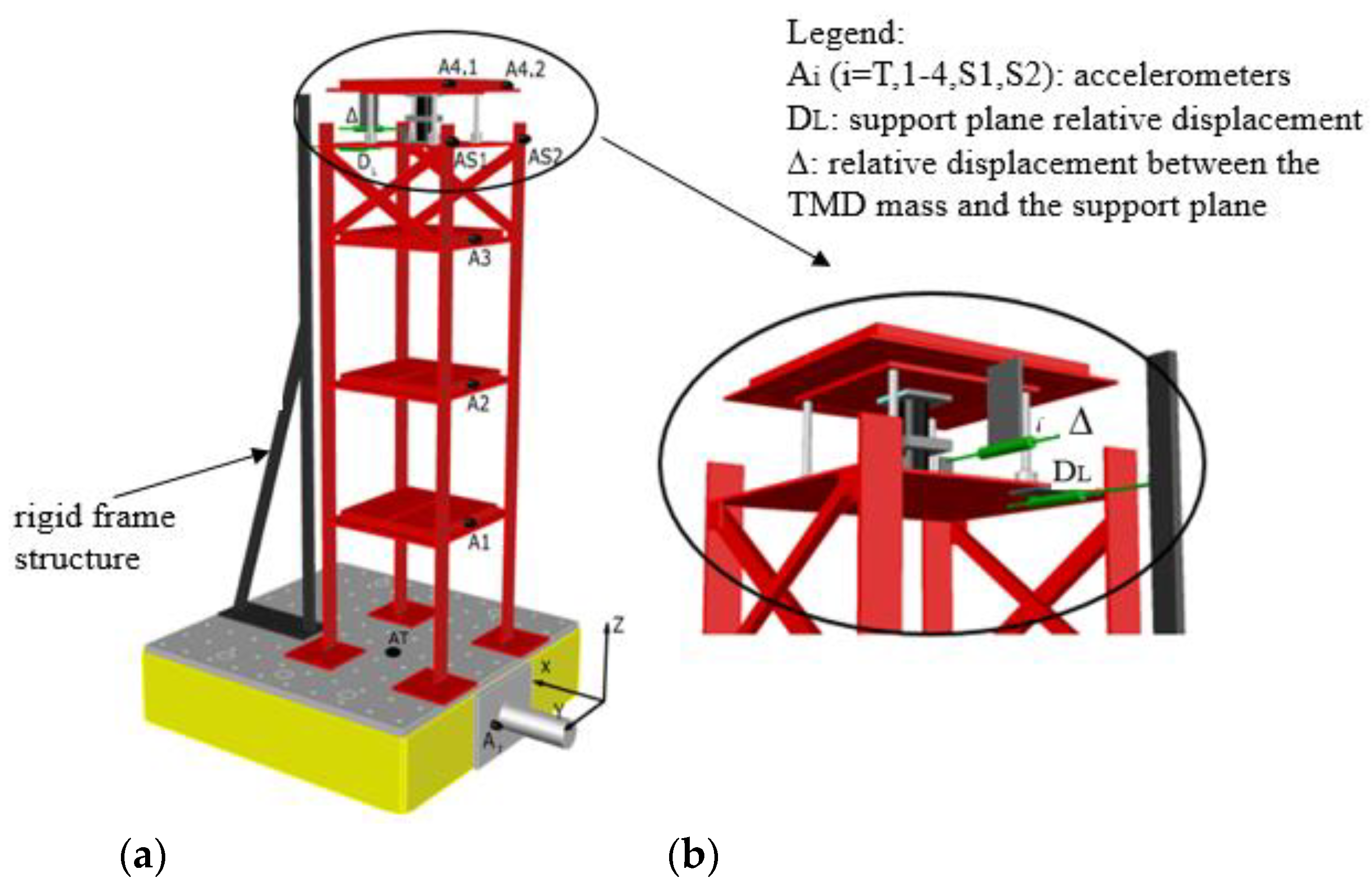







| Configurations |
 |
| Description | Type of Signal |
|---|---|
| White noise (WN) tests. Range of frequencies investigated 1–25 Hz, range of acceleration investigated with RMS values 0.002–0.04 g. | 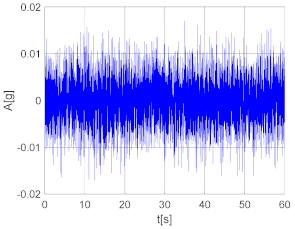 |
| Sine sweep (SS) tests at increasing and decreasing frequency (in the figure increasing sine sweep). Range of frequencies investigated 1–25 Hz at rate 1 Hz/s, base acceleration 100–500 mm/s2, signal duration 300 s. |  |
| Natural earthquake (NE) signals considered: Kobe, Northridge, El Centro (in the figure), Hachinohe. Range of amplitude considered reported in Table 3. | 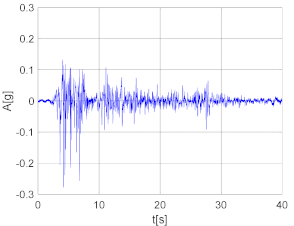 |
| Earthquake | PGA (g) | RMS (m/s2) |
|---|---|---|
| Kobe | 0.05 | 0.07 |
| 0.18 | 0.25 | |
| 0.23 | 0.32 | |
| 0.3 | 0.42 | |
| Northridge | 0.06 | 0.05 |
| 0.23 | 0.22 | |
| 0.28 | 0.27 | |
| 0.29 | 0.28 | |
| El Centro | 0.05 | 0.06 |
| 0.16 | 0.2 | |
| 0.26 | 0.3 | |
| 0.3 | 0.35 | |
| Hachinohe | 0.05 | 0.07 |
| 0.13 | 0.2 | |
| 0.16 | 0.26 | |
| 0.19 | 0.32 | |
| 0.25 | 0.37 |
| Frequencies (Hz) | ||||||
|---|---|---|---|---|---|---|
| Mode | ||||||
| RMS (g) | 1 | 2 | 3 | 4 | 5 | 6 |
| 0.002 | 2.995 | 6.053 | 12.173 | 17.159 | 17.772 | 20.927 |
| 0.005 | 2.766 | 5.182 | 12.051 | 17.122 | 17.727 | 20.889 |
| 0.010 | 2.618 | 4.822 | 11.966 | 17.018 | 17.627 | 20.782 |
| 0.020 | 2.446 | 4.592 | 11.905 | 16.931 | 17.549 | 20.696 |
| 0.040 | 2.168 | 4.380 | 11.818 | 16.768 | 17.450 | 20.579 |
| Damping Factors (%) | ||||||
| Mode | ||||||
| RMS [g] | 1 | 2 | 3 | 4 | 5 | 6 |
| 0.002 | 4.814 | 12.406 | 1.038 | 0.516 | 0.474 | 0.413 |
| 0.005 | 7.420 | 10.790 | 0.830 | 0.590 | 0.540 | 0.420 |
| 0.010 | 10.991 | 9.105 | 0.775 | 0.653 | 0.556 | 0.457 |
| 0.020 | 12.487 | 7.187 | 0.786 | 0.802 | 0.607 | 0.560 |
| 0.040 | 13.420 | 5.580 | 0.850 | 1.060 | 0.670 | 0.680 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basili, M.; Angelis, M.D. Experimental Dynamic Response of a Multi-Story Frame Structure Equipped with Non-Conventional TMD Implemented via Inter-Story Isolation. Appl. Sci. 2022, 12, 9153. https://doi.org/10.3390/app12189153
Basili M, Angelis MD. Experimental Dynamic Response of a Multi-Story Frame Structure Equipped with Non-Conventional TMD Implemented via Inter-Story Isolation. Applied Sciences. 2022; 12(18):9153. https://doi.org/10.3390/app12189153
Chicago/Turabian StyleBasili, Michela, and Maurizio De Angelis. 2022. "Experimental Dynamic Response of a Multi-Story Frame Structure Equipped with Non-Conventional TMD Implemented via Inter-Story Isolation" Applied Sciences 12, no. 18: 9153. https://doi.org/10.3390/app12189153





