3.1. Time Series and Multiple Linear Regression Analyses of CREST-SAFE Data
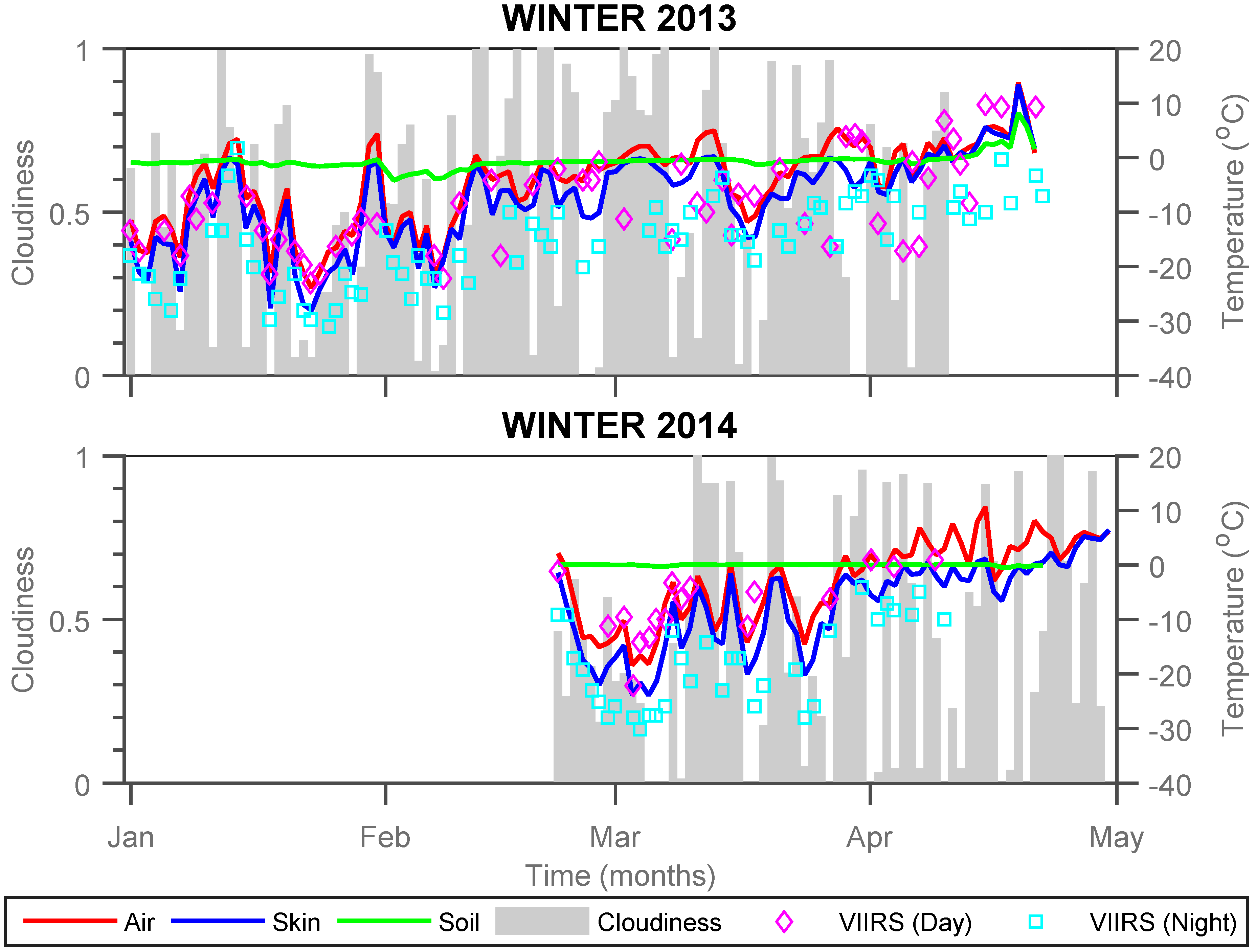
T-skin, T-soil, and T-air hourly data from the CREST-SAFE station were averaged daily for the two years (2013 and 2014) to study their behavior throughout the winter months (
Figure 2). VIIRS LSTs (daytime and nighttime overpasses) were included in the figure as well. However, it should be noted that the T-skin and T-air values used in
Section 3.2 for the
in situ temperature
vs. RS LST comparisons were not daily averages. Instead, these were collocated and matched temporally with the satellite overpass over Caribou. Additionally, average hourly cloudiness data acquired from the NWS website were averaged daily and included as a bar graph in the same figure.
Figure 2.
Daily T-skin, T-soil, T-air (at 2 m from soil surface), cloudiness, and VIIRS LST (daytime and nighttime overpasses) for the winters of 2013 and 2014.
Figure 2.
Daily T-skin, T-soil, T-air (at 2 m from soil surface), cloudiness, and VIIRS LST (daytime and nighttime overpasses) for the winters of 2013 and 2014.
The analysis indicates that T-air is warmer than T-skin throughout all winter months. However, the magnitude of the T-air minus T-skin difference (T-diff) is in the order of 1–3 °C between the months of December and February and increases to 5–8 °C at the beginning of March. Both temperatures display the same trends (peaks and valleys) because T-air affects T-skin directly, even though the latter’s fluctuations are not as drastic [
21]. The record shows that the winter of 2013 was the coldest of the two (hourly lows of −26 °C and −36 °C in late January for T-air and T-skin, respectively). Nevertheless, it cannot be ruled out that it is possible for T-air to be colder than T-skin at particular hours throughout a winter day (
Section 3.3). T-soil does not fluctuate as radically (mainly remains around 0 °C) as T-skin and T-air throughout all winter months nor does it follow the same behavioral pattern. This makes sense since the soil surface is constantly covered by various snow layers isothermal at 0 °C, unlike the snow layers at the surface of the snowpack. The reason for all temperatures sharing the same behavior after mid-April in 2013 is due to the fact that a very thin snow layer (approximately 1 cm) remained and the Apogee Infrared Radiometer might have been reading the thermal energy produced by the soil directly instead of the snow surface’s thermal energy. However, for winter 2014, the snowpack depth was still 10cm in mid-April and remained until 22 April 2014. The highest accumulated daily snowpack depths were 25 cm and 45 cm for 2013 (late February) and 2014 (mid-March), respectively. VIIRS LST readings deviate significantly from T-skin, T-soil, and T-air daily averages. Particularly for the nighttime overpasses, corroborating the importance of temporal matching.
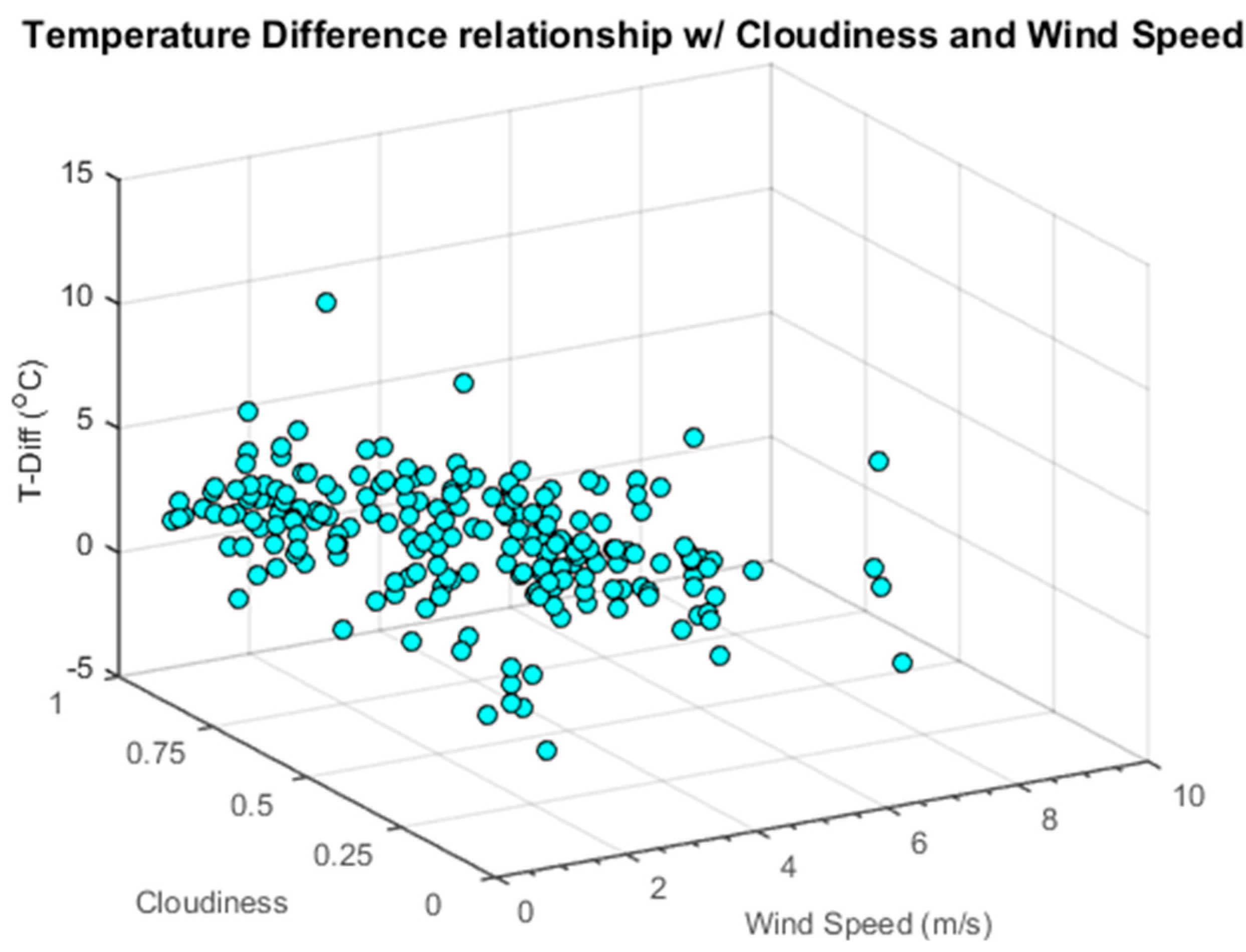
Figure 3 illustrates the relationship between cloud cover, wind speed, and T-diff with a 3D scatterplot. A multiple linear regression analysis with linear coefficients was performed using cloud cover and wind speed as independent variables (inputs) and T-diff as the dependent variable (output). The results are illustrated in
Table 1 (coefficient estimate, Standard Error (SE) of the coefficient, t-value, and p-value). The coefficient estimates for cloudiness (−3.5653) and wind speed (−0.18729) show that both parameters affect T-diff inversely, and that cloudiness has more effect on T-diff. The coefficient estimate results indicate that a 10% (0.35653) change in sky cover will have close to twice the impact of a 1 m/s (0.18729) change in wind speed on T-diff. The fact that T-diff is lower when there are more clouds could indicate that T-skin is less heated by the radiative effect of the sun which, in turn, will make the snow surface temperature try to reach equilibrium with T-air directly (especially with the wind blowing), thus reducing T-diff. Furthermore, higher wind speeds will “renew” the snow surface by blowing away the snow layer at the top of the snowpack and replacing it with new snow whose temperature is closer to T-air. This phenomenon tends to make T-skin closer to T-air, decreasing T-diff as well. Lower SE values for wind speed (0.075) rather than cloudiness (0.34936) are indicative of the regression’s capability of estimating the former with much better accuracy. This also demonstrates the unpredictability of cloudiness when compared to wind speed. These uncertainties can perhaps be attributed to instrument errors due to the fact that the ASOS algorithm can misinterpret sky cover with false cloud “hits” by the backscattered signals since the ceilometer pulses are sent kilometers away skyward and will be affected by atmospheric effects, airplanes, and any living object flying over the instrument. P-values lower than 0.05 for cloudiness and wind speed indicate that there is a 95% probability that both have significant effect on T-diff. The P-values close to zero for cloudiness confirm that it affects T-diff more than wind speed, as was stated by the coefficient estimates. However, the p-value of 0.013 for wind speed indicates that wind speed does have an effect on T-diff, albeit not as drastic as the effect of sky cover. An RSME value of 1.70 °C shows that there is close to 20% error in the model’s T-diff estimation, since it varied commonly from 0–10 °C for 2013 and 2014 at CREST-SAFE. While an R
2 linear correlation coefficient value of 0.37 indicates that the relationship between these three variables is non-linear and suggestive that other parameters (e.g., snowpack temperature) might be affecting T-diff as well.
Figure 3.
Average daily cloudiness, wind speed and T-diff relationship at CREST-SAFE for winters 2013 and 2014.
Figure 3.
Average daily cloudiness, wind speed and T-diff relationship at CREST-SAFE for winters 2013 and 2014.
Table 1.
Cloudiness, wind speed, and T-diff multiple linear regression analyses results for CREST-SAFE data for the winter of 2013 and 2014.
Table 1.
Cloudiness, wind speed, and T-diff multiple linear regression analyses results for CREST-SAFE data for the winter of 2013 and 2014.
| Multiple Linear Regression Analysis Results |
|---|
| -- | Coefficient | SE | tStat | pValue |
| Intercept | 5.6915 | 0.2627 | 21.665 | 1.3889 × 10−54 |
| Cloudiness | −3.5653 | 0.34936 | −10.205 | 5.5022 × 10−20 |
| Wind Speed | −0.18729 | 0.075131 | −2.4928 | 0.013477 |
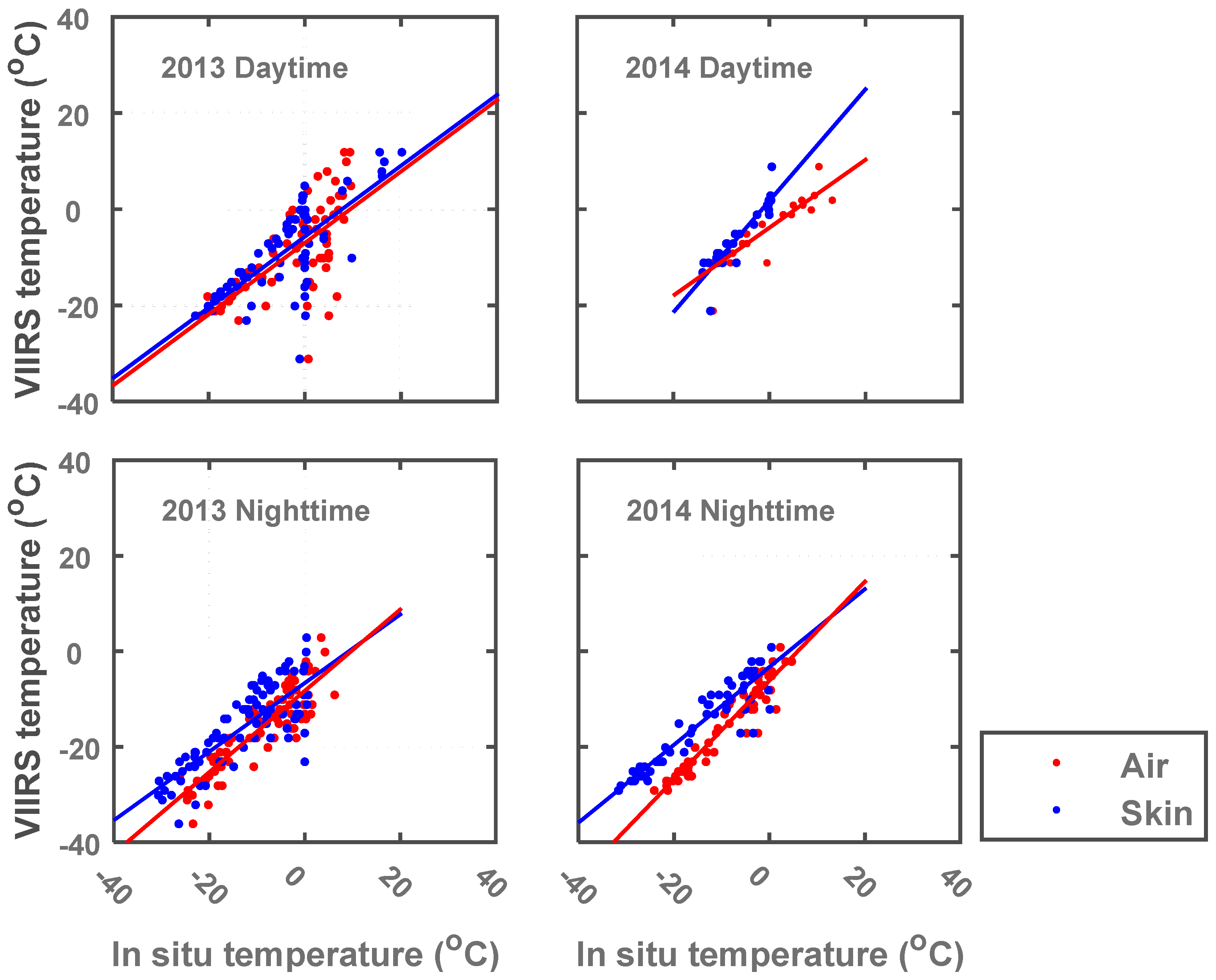
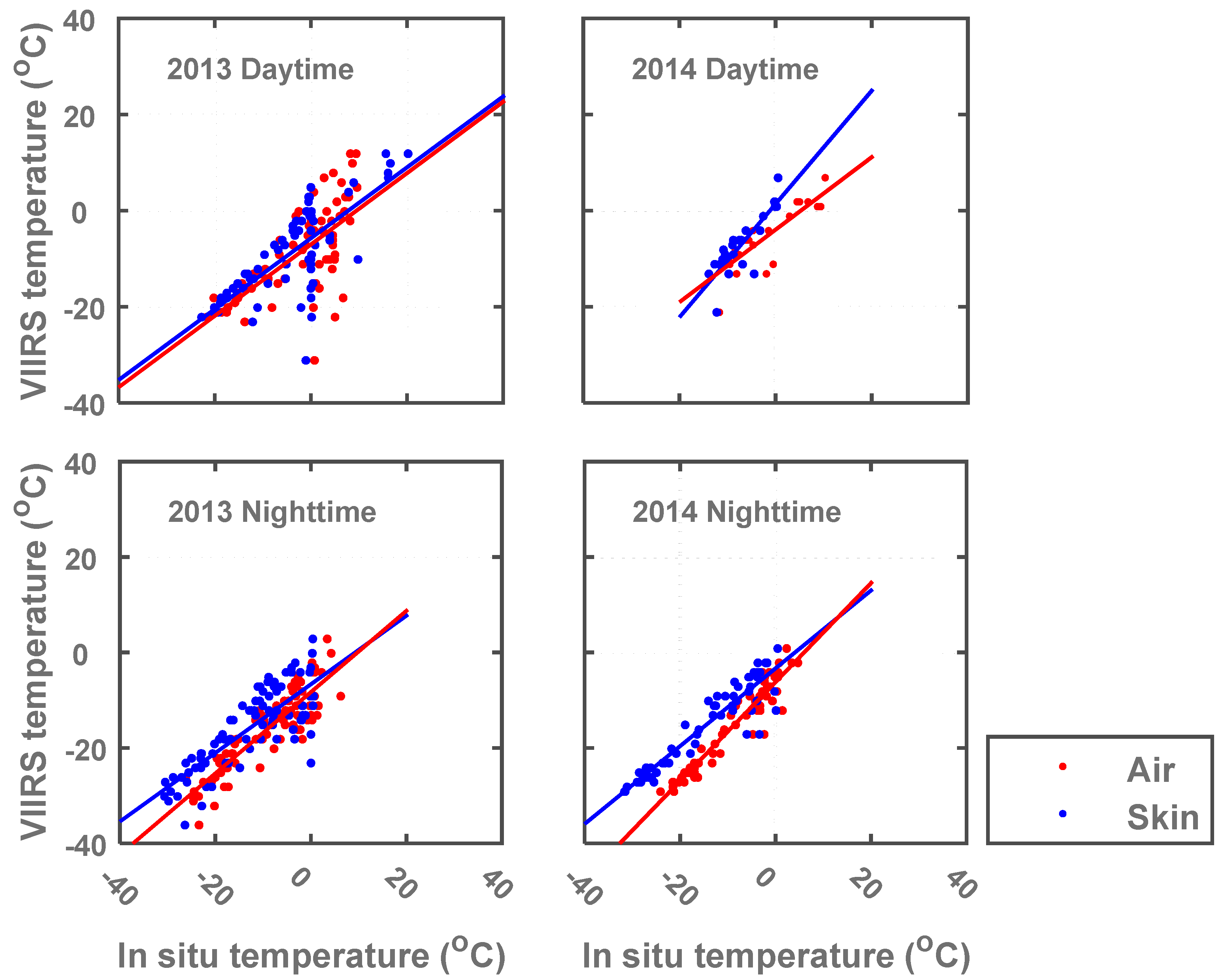
3.2. Satellite RS LST vs. In Situ T-skin and T-air
CREST-SAFE
in situ T-skin and T-air (abscissas)
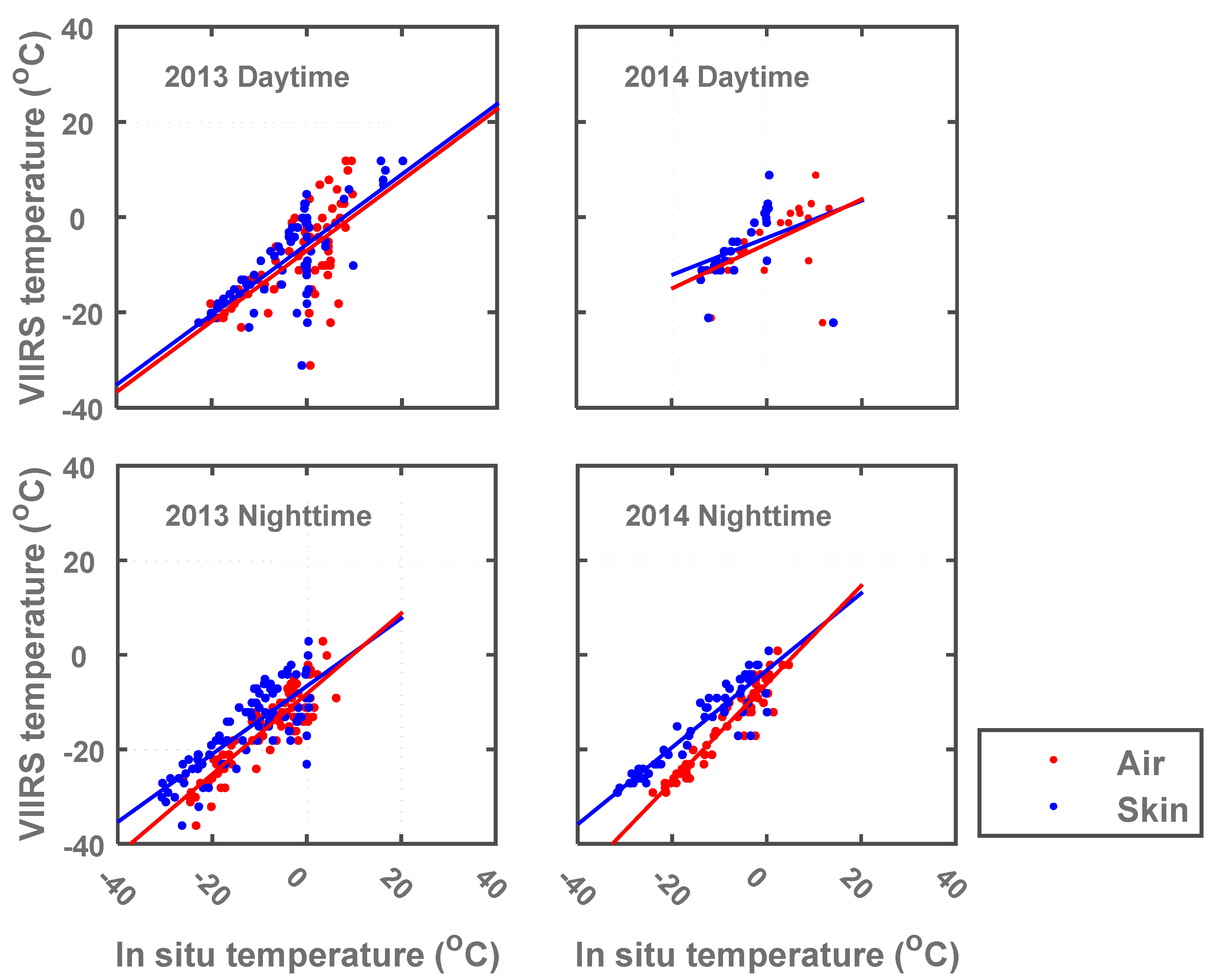
vs. VIIRS LST (ordinates) daytime and nighttime scatterplots (
Figure 4) were created to obtain the R and R
2 linear correlation coefficient values (
Table 2) as well as the Mean Absolute Difference (MAD) and biases for both years.
Table 2.
R2 correlation coefficient values between VIIRS LST, T-skin, and T-air at CREST-SAFE for winters 2013 and 2014 daytime and nighttime views.
Table 2.
R2 correlation coefficient values between VIIRS LST, T-skin, and T-air at CREST-SAFE for winters 2013 and 2014 daytime and nighttime views.
| T. | 2013 Daytime | 2013 Nighttime | 2014 Daytime | 2014 Nighttime |
|---|
| R | R2 | MAD (°C) | Bias (°C) | R | R2 | MAD (°C) | Bias (°C) | R | R2 | MAD (°C) | Bias (°C) | R | R2 | MAD (°C) | Bias (°C) |
|---|
| Air | 0.71 | 0.51 | 6.6 | −5.76 | 0.87 | 0.76 | 6.6 | −6.66 | 0.80 | 0.64 | 6.4 | −6.11 | 0.95 | 0.90 | 7.1 | −7.07 |
| Skin | 0.82 | 0.67 | 5.0 | −4.35 | 0.81 | 0.66 | 4.0 | −2.70 | 0.62 | 0.38 | 4.6 | −2.68 | 0.93 | 0.86 | 2.6 | −1.31 |
R and R
2 linear correlation coefficient values between VIIRS LST and
in situ T-air daytime data vary from 0.71–0.80 and 0.51–0.64, respectively. R and R
2 correlation values for daytime VIIRS LST and
in situ T-skin range from 0.62–0.82 and 0.38–0.67. These correlation values drop drastically for T-soil and vary from 0.26–0.57 and 0.07–0.32. Nighttime R and R
2 linear correlation coefficient values are generally higher for all temperatures (T-skin and T-air) with few exceptions. This is mostly because the atmospheric water vapor is less and LST behaves almost homogeneously at night. Therefore, the ground temperature measurements during nighttime are more representative of the LST at the satellite pixel scale than those during daytime [
7]. For T-air, the correlation values fluctuate between 0.87–0.95 and 0.76–0.90, respectively. The correlations values range from 0.81–0.93 and 0.66–0.86 for T-skin. Results indicate that a higher correlation exists between T-air and the RS LST. VIIRS LST readings have a lower correlation with the T-skin values observed at CREST-SAFE. However, it should be noted that these values improved from one winter (2013) to the next (2014) for T-air and T-skin. This might be indicative of the continuous and ongoing improvements done to the VIIRS LST product. T-soil does not change much over time (remains around 0ºC), making it almost constant and naturally very different from RS LST, T-air, and T-skin. MAD daytime T-air values vary barely, ranging from 6.4–6.6 °C. Daytime MAD values for T-skin range from 4.6–5.0 °C. Nighttime MAD values for T-air and T-skin vary from 6.6–7.1 °C and 2.6–4.0 °C, respectively. VIIRS daytime biases vary from −6.11 °C to −5.76 °C and −4.35 °C to −2.68 °C for T-air and T-skin, respectively. Nighttime biases vary from −7.07 °C to −6.66 °C and −2.70 °C to −1.31 °C for T-air and T-skin, respectively. We can say that the evaluation results for nighttime are better than those during daytime, especially in terms of R and R
2 values and, to some extent, MAD, and biases. The cold biases for all temperatures and satellite overpasses indicate that the VIIRS LST algorithm underestimates the LST for snow-covered surfaces.
Figure 4.
CREST-SAFE in situ T-skin and T-air correlation with satellite VIIRS LST daytime and nighttime data for winters 2013 and 2014.
Figure 4.
CREST-SAFE in situ T-skin and T-air correlation with satellite VIIRS LST daytime and nighttime data for winters 2013 and 2014.
While simpler to explain why the RS
vs. in situ correlations are higher during nighttime, the reason for discrepancies between T-air and T-skin are less trivial. Foremost, as it was previously stated in
Section 3.1, cloud cover and wind speed play an important role in the behavioral patterns of T-air and T-skin. Generally, if there is no (or weak) advection and no clouds, T-diff is mostly driven by the radiative cooling of the land surface because the radiative heating by the sun is quite small compared to it. On the other hand, the presence of clouds provides a substantial downward thermal flux that heats the surface and, to a lesser extent, the air; therefore reducing T-diff [
22,
23]. This accounts partially for
in situ T-skin having lower correlation values with VIIRS LST, because changes in T-skin happen at a slower pace (unlike bare soil) than they do for T-air.
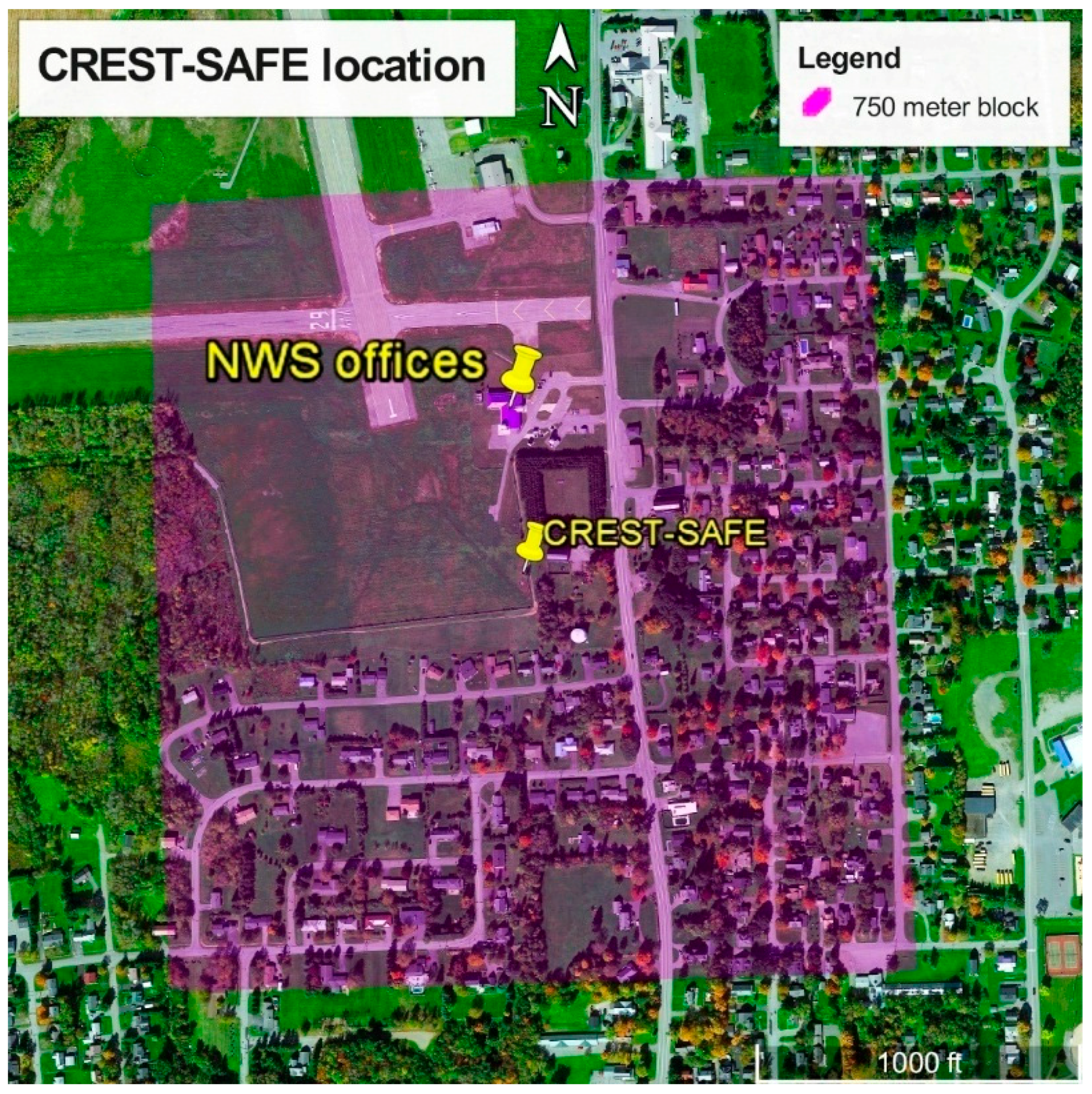
Another remark is that the low correlation values between VIIRS LST and
in situ T-skin can be attributed to the fact that VIIRS characterizes the brightness temperature of the vegetation (whose temperature is closer to T-air) that is abundant in the vicinity of the field experiment, as seen by a 750 m block around the site—not to be confused with the satellite swath—in
Figure 5 (approximately 45% grassland, 35% residential homes, 15% paved roads, 5% forest cover). Satellite radiometry is applied to large areas (750 m in this study) which often consist of various land and vegetation types. A low spatial resolution will undoubtedly include some vegetation (forest cover) in the region and divert the RS LST from its true point value. Moreover, meteorological conditions for snow accumulation and melt on forest floors differ from those in clearings because of the influence of the canopy [
24]. Additionally, snow becomes patchy while melting, giving a heterogeneous surface with large contrasts in characteristics such as albedo (
i.e., reflectance, TB) [
25]. Hence, the combination of above freezing temperatures during daytime with below freezing temperatures at night cause multiple freezing and melting events within the snowpack during the melting period (late winter). Daytime solar radiation causes snowmelt in the uppermost layer that produces higher water content in the superior layers of the snow pack. These events cause a large diurnal variation in the RS TB that is difficult to reproduce using satellite retrievals [
26]. When comparing satellite RS and
in situ point-wise data, the primary issue is whether the surface properties at the site are representative for land surface properties within the instrument Field Of View (FOV). The temperature of vegetation canopy is usually closer to the T-air than to the land surface temperature. Therefore, for forested areas covered with snow in winter, the VIIRS LST is better correlated with T-air [
27,
28].
Furthermore, when discussing the radiative properties of the snow surface, while not uniform, the IR emissivity of snow is understood enough to compensate for its effects in the remote sensing of T-skin. At near-normal viewing angles, the RS TB can be as much as 1.5 ºC lower than the thermodynamic temperature at wavelengths around 13 µm [
29]. At the shorter IR wavelength window (3.5–4 µm), uncertainty in emissivity does not translate into uncertainty in temperature because of the nonlinear nature of Planck’s function, but at longer wavelengths it does. Fortunately, the highest and unreliable uncertainties in emissivity are beyond the 10.5–12.5 µm atmospheric window that the VIIRS LST SW algorithm uses for retrievals. However, studies indicate that snow grains are independent scatterers, and that emissivity decreases with grain size and the presence of liquid water in the snow [
30,
31]. Nonetheless, T-skin measurements have been used in few climate or hydrologic studies. Results have shown that the differences between RS LST and T-skin have not been due to emissivity as much as: orographic effects, topography, topographic shadowing, and snow deposition [
32,
33,
34,
35].
Figure 5.
CREST-SAFE land cover 750-m block.
Figure 5.
CREST-SAFE land cover 750-m block.
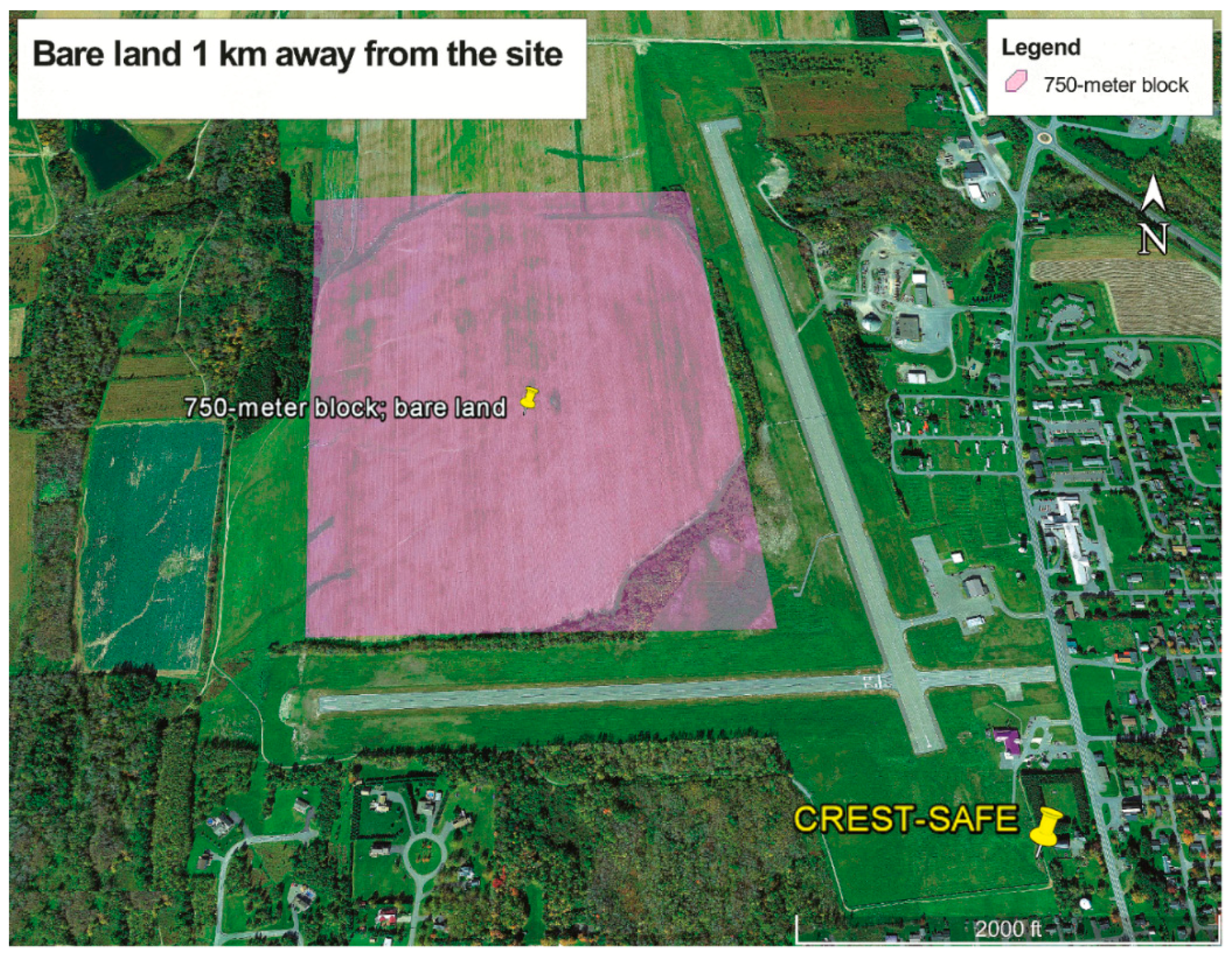
For this particular reason, two additional pixels (one bare land, one forest cover/vegetation) were considered in this study to check whether the T-air and T-skin data observed at CREST-SAFE is representative of other areas that surround the site in Caribou with different land cover.
Figure 6 illustrates a 750-m block of bare land 1 km away from CREST-SAFE,
Figure 7 displays the CREST-SAFE
in situ T-skin and T-air
vs. VIIRS LST daytime and nighttime for the bare land pixel scatterplots, and
Table 3 contains the R and R
2 linear correlation coefficient values, MADs, and biases for the scatterplots for both years.
Table 3.
R and R2 correlation coefficient values, MAD, and biases between VIIRS LST daytime and nighttime views for the bare land pixel, T-skin, and T-air at CREST-SAFE for winters 2013 and 2014.
Table 3.
R and R2 correlation coefficient values, MAD, and biases between VIIRS LST daytime and nighttime views for the bare land pixel, T-skin, and T-air at CREST-SAFE for winters 2013 and 2014.
| T. | 2013 Daytime | 2013 Nighttime | 2014 Daytime | 2014 Nighttime |
|---|
| R | R2 | MAD (°C) | Bias (°C) | R | R2 | MAD (°C) | Bias (°C) | R | R2 | MAD (°C) | Bias (°C) | R | R2 | MAD (°C) | Bias (°C) |
|---|
| Air | 0.62 | 0.38 | 7.31 | −6.45 | 0.84 | 0.70 | 7.16 | −7.16 | 0.86 | 0.74 | 6.00 | −5.70 | 0.96 | 0.91 | 6.75 | −6.75 |
| Skin | 0.70 | 0.50 | 5.73 | −4.98 | 0.77 | 0.60 | 4.50 | −3.15 | 0.87 | 0.75 | 4.37 | −2.16 | 0.95 | 0.90 | 2.17 | −0.58 |
Figure 6.
750 m block of bare land 1km away from CREST-SAFE.
Figure 6.
750 m block of bare land 1km away from CREST-SAFE.
Figure 7.
CREST-SAFE in situ T-skin and T-air vs. satellite VIIRS LST daytime and nighttime data for the bare land pixel scatterplots for winters 2013 and 2014.
Figure 7.
CREST-SAFE in situ T-skin and T-air vs. satellite VIIRS LST daytime and nighttime data for the bare land pixel scatterplots for winters 2013 and 2014.
R and R2 linear correlation coefficient values between VIIRS LST for the bare land pixel and in situ T-air daytime data vary from 0.62–0.86 and 0.38–0.74, respectively. R and R2 correlation values for daytime VIIRS LST and in situ T-skin range from 0.70–0.87 and 0.50–0.75.R and R2 nighttime correlation values for T-air fluctuate between 0.84–0.96 and 0.70–0.91, respectively. These correlations values range from 0.77–0.95 and 0.60–0.90 for T-skin. MAD daytime T-air values vary from 6.0–7.31 °C. Daytime MAD values for T-skin range from 4.37–5.73 °C. Nighttime MAD values for T-air and T-skin vary from 6.75–7.16 °C and 2.17–4.50 °C, respectively. VIIRS daytime biases vary from −6.45 °C to −5.70 °C and −4.98 °C to −2.16 °C for T-air and T-skin, respectively. Nighttime biases vary from −7.16 °C to −6.75 °C and −3.15 °C to −0.58 °C for T-air and T-skin, respectively. When comparing these values with those obtained by matching CREST-SAFE in situ vs. VIIRS LST from the CREST-SAFE pixel, it can be seen that the two pixels display very similar results, regardless of the differences in land cover.
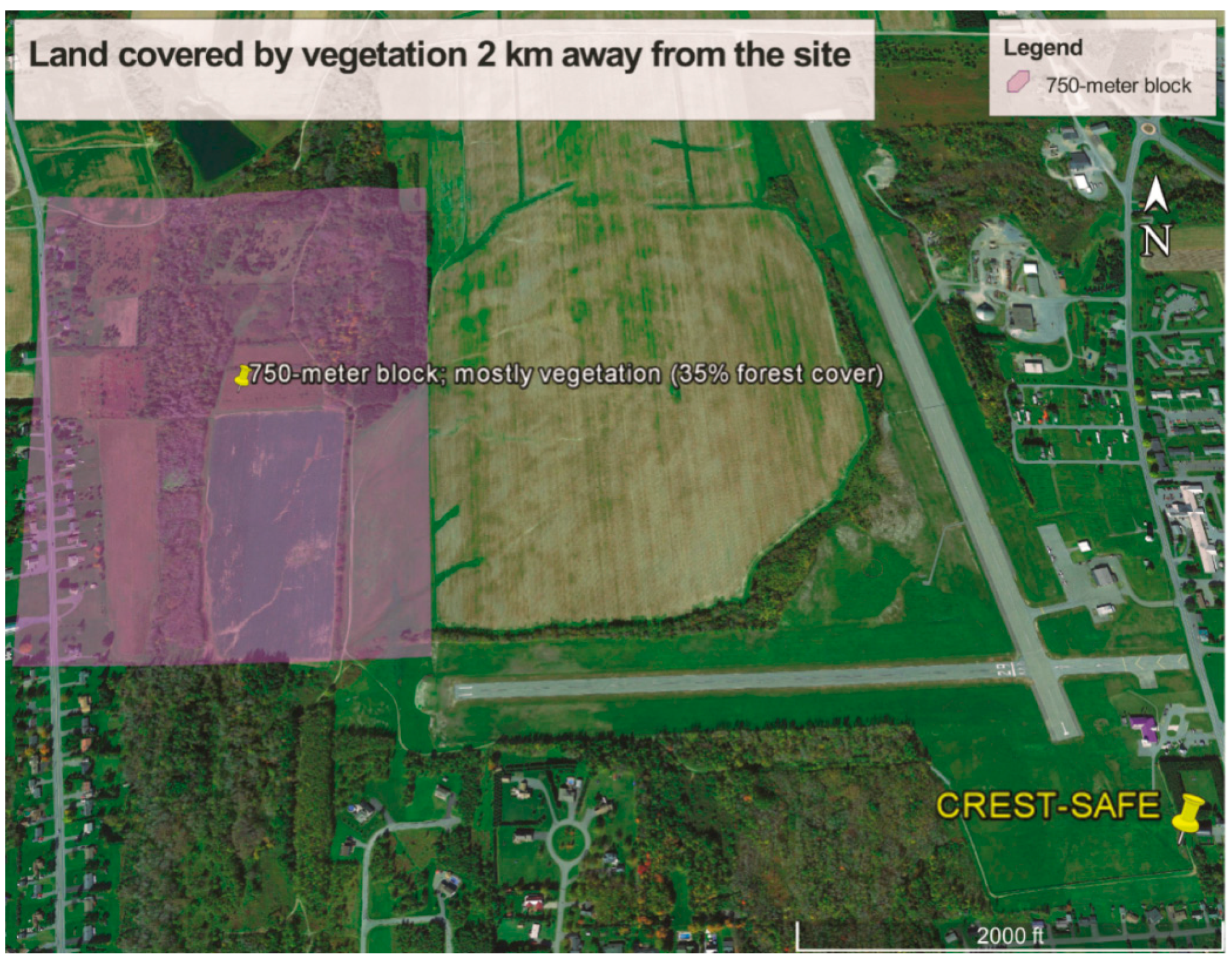
In
Figure 8, a 750 m block of land covered by forest and vegetation 2 km away from CREST-SAFE is illustrated. There are VIIRS LST satellite pixels in Caribou that have 100% forest cover but these are more than 10km away from the site, which would render the CREST-SAFE
in situ temperatures useless for a comparison.
Figure 9 displays the CREST-SAFE
in situ T-skin and T-air
vs. VIIRS LST daytime and nighttime for forest/vegetation covered pixel scatterplots, and
Table 4 shows the R and R
2 linear correlation coefficient values, MADs, and biases for the scatterplots for both years.
Figure 8.
750 m block of land covered by forest and vegetation 2 km away from CREST-SAFE.
Figure 8.
750 m block of land covered by forest and vegetation 2 km away from CREST-SAFE.
R and R2 linear correlation coefficient values between VIIRS LST for forest/vegetation covered pixel and in situ T-air daytime data vary from 0.67–0.89 and 0.45–0.80, respectively. R and R2 correlation values for daytime VIIRS LST and in situ T-skin range from 0.74–0.91 and 0.55–0.82. R and R2 nighttime correlation values for T-air fluctuate between 0.86–0.96 and 0.74–0.91, respectively. These correlations values range from 0.80–0.93 and 0.64–0.87 for T-skin. MAD daytime T-air values vary from 5.00–7.22 °C. Daytime MAD values for T-skin range from 3.36–5.30 °C. Nighttime MAD values for T-air and T-skin vary from 6.46–6.99 °C and 2.34–4.50 °C, respectively. VIIRS daytime biases vary from −6.53 °C to −4.62°C and −4.74 °C to −0.91 °C for T-air and T-skin, respectively. Nighttime biases vary from −6.99 °C to −6.46 °C and −3.13 °C to −0.57 °C for T-air and T-skin, respectively.
Table 4.
R and R2 correlation coefficient values, MAD, and biases between VIIRS LST daytime and nighttime views for the forest/vegetation covered pixel and T-skin and T-air at CREST-SAFE for winters 2013 and 2014.
Table 4.
R and R2 correlation coefficient values, MAD, and biases between VIIRS LST daytime and nighttime views for the forest/vegetation covered pixel and T-skin and T-air at CREST-SAFE for winters 2013 and 2014.
| T. | 2013 Daytime | 2013 Nighttime | 2014 Daytime | 2014 Nighttime |
|---|
| R | R2 | MAD (°C) | Bias (°C) | R | R2 | MAD (°C) | Bias (°C) | R | R2 | MAD (°C) | Bias (°C) | R | R2 | MAD (°C) | Bias (°C) |
|---|
| Air | 0.67 | 0.45 | 7.22 | −6.53 | 0.86 | 0.74 | 6.99 | −6.99 | 0.89 | 0.80 | 5.00 | −4.62 | 0.96 | 0.91 | 6.46 | −6.46 |
| Skin | 0.74 | 0.55 | 5.30 | −4.74 | 0.80 | 0.64 | 4.50 | −3.13 | 0.91 | 0.82 | 3.36 | −0.91 | 0.93 | 0.87 | 2.34 | −0.57 |
Figure 9.
CREST-SAFE in situ T-skin and T-air vs. satellite VIIRS LST daytime and nighttime data for the forest/vegetation covered pixel scatterplots for winters 2013 and 2014.
Figure 9.
CREST-SAFE in situ T-skin and T-air vs. satellite VIIRS LST daytime and nighttime data for the forest/vegetation covered pixel scatterplots for winters 2013 and 2014.
The similar linear correlation coefficients, MADs, and biases displayed by three pixels with evident different land covers lead to the notion that the CREST-SAFE T-air and T-skin might be representative of the county of Caribou, ME. However, when compared to the CREST-SAFE pixel, the bare land pixel showed small improvement in VIIRS LST’s estimation of T-skin and T-air. There was also some improvement in VIIRS LST’s estimation of the
in situ observations when comparing the forest/vegetation covered pixel with the CREST-SAFE pixel, although it was not as effective as the RS LST estimations for the bare land pixel. The small improvement shown by the bare land and forest/vegetation covered pixels was expected due to the surface homogeneity in the bare land and forest/vegetation covered pixels, when compared to the CREST-SAFE pixel. However, it is not significant enough to establish that VIIRS LST is affected by land cover in the region under study. Instead, it can be established that the differences between RS LST and
in situ observations are due to the unpredictability in both the physical and radiative properties of the snow and its surface, as stated previously, sky cover, and wind speed. These findings lead to the proposition of empirical formulas (
Section 3.4) to derive T-skin and T-air from RS LST to improve the understanding of VIIRS LSTs.
3.3. CREST-SAFE Diurnal Cycle Analysis
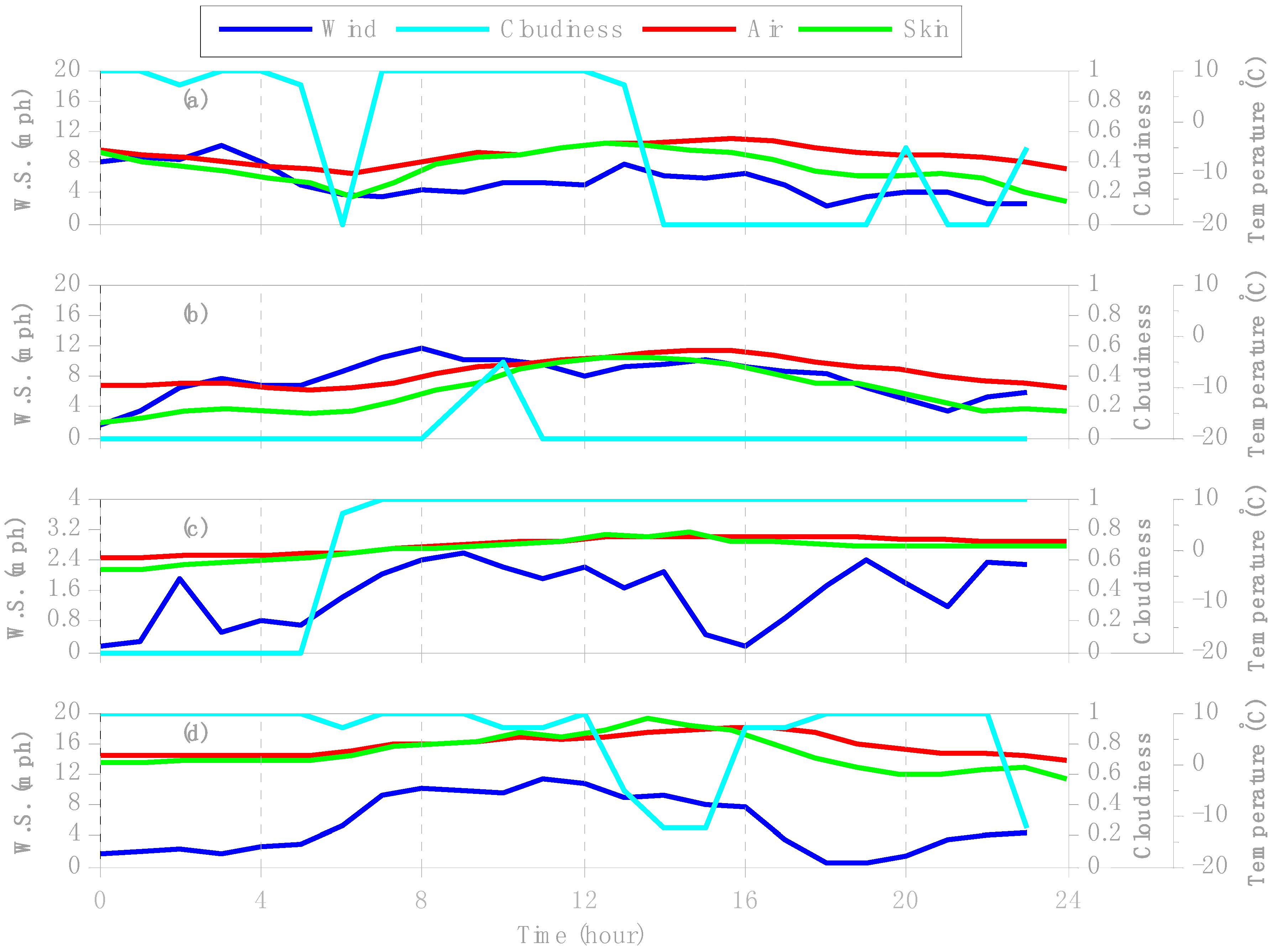
CREST-SAFE hourly data from eight days of winter 2013 were selected (
Figure 10a–d and
Figure 11a–d) to study T-diff throughout the diurnal cycle and further examine the consistency between
in situ T-skin and VIIRS LST. Hourly wind speed and cloud coverage were taken into account to try to explain these disparities.
Figure 10.
Snow surface and near-surface air temperature hourly values at the CREST-SAFE station in Caribou, ME for the days of 22–23 January (a,b) and 15–16 February (c,d) of winter 2013.
Figure 10.
Snow surface and near-surface air temperature hourly values at the CREST-SAFE station in Caribou, ME for the days of 22–23 January (a,b) and 15–16 February (c,d) of winter 2013.
Figure 11.
Snow surface and near-surface air temperature hourly values at the CREST-SAFE station in Caribou, ME for the days of 15–16 March (a,b) and 9–10 April (c,d) of winter 2013.
Figure 11.
Snow surface and near-surface air temperature hourly values at the CREST-SAFE station in Caribou, ME for the days of 15–16 March (a,b) and 9–10 April (c,d) of winter 2013.
Figure 10 illustrates the coldest days of January (lowest temperature values recorded for the whole winter) and two days of mid-February to examine early winter. The lowest recorded temperature (−36 °C) happened on 23 January under non-cloudy conditions with a low daily average wind speed of 5.15 ft/s. January and February temperatures peaked sometime between 12:00–2:00 p.m. LT and showcased the largest T-diff from 2:00–6:00 a.m. LT and 3:00–7:00 p.m. LT, respectively. Since S-NPP’s ascension/descend over Caribou, ME happens sometime within these particular hours (1:00–3:00 p.m./a.m. LT), it seems rational to partially attribute the difference in correlation coefficient values between VIIRS LST
vs. T-skin and VIIRS LST
vs. T-air to this issue. Furthermore, T-air exhibits less fluctuation throughout a winter day, making it more accurate to estimate RS LST using it as input rather than T-skin [
36].
In contrast, T-skin is affected because the seasonal snowpack grows in layered structure, causing heterogeneity, with each layer having different physical and mechanical characteristics. Then, the snowpack gets stratified because of successive snow events throughout the winter season. Hence, each snow event encounters a different set of meteorological parameters at the time of its occurrence and afterward. The snow continuously interacts with the environment and exchanges energy with the atmosphere above it and the ground below. These energy exchange processes set up the temperature distribution within the snowpack, which in turn is responsible for its metamorphic changes with time [
37,
38]. Moreover,
Figure 10a shows that under low wind speed and non-cloudy conditions, T-diff is large. Mostly leading to the understanding that the low VIIRS LST and T-skin correlation values can be credited in some measure not only to the clouds’ downward thermal flux but to wind speed, as well. This can be seen in
Figure 10b, revealing that a day with high wind speed conditions and close to no cloud coverage can have a small T-diff. It can also be inferred from
Figure 10c,d that the T-diff is smaller for a cloudy day, even under low wind speed conditions.
In
Figure 11, late winter behavior was studied analyzing two days of mid-March and two days of early April.
Figure 11a,b display the first time T-skin is similar to T-air under both cloudy and non-cloudy conditions. The daily temperature peak moves to sometime between 2:00–3:00 p.m. LT (still within S-NPP’s ascension/descend over the area). The two days of early April were selected because these were the last days when the National Environmental Satellite, Data, and Information Service (NESDIS) recorded cloud cover data for Caribou, ME. Data from early April (
Figure 11c,d) showcase the first time when T-skin is higher than T-air around 11:00 a.m.–1:00 p.m. LT. Hourly temperatures rise by approximately 10 °C when compared to mid-March, the peak is less significant, and moves closer to 3 p.m. LT. T-skin and T-air values are almost similar throughout a whole day. The diurnal cycle clearly explains why VIIRS LST data will be higher correlated with the months of March and April for T-skin and T-air CREST-SAFE data. The opposite can be said for the cold winter months of January and February. This also clarifies why RS LST
vs. in situ correlations are higher for winter 2014, since the CREST-SAFE 2014 data was recorded from late February onwards. CREST-SAFE 2013 data started logging from 1 January 2013. Lastly, CREST-SAFE hourly data indicates that both wind speed and cloud cover affect T-air and T-skin throughout the diurnal cycle.
3.4. Derivation of Empirical Formulas to Obtain In Situ T-Skin (under Dry and Wet Snow Conditions) from RS LST
This section proposes derived empirical formulas to estimate T-skin using VIIRS LST retrievals under clear-sky conditions. In order to derive these empirical formulas, CREST-SAFE
in situ T-skin observations were sub-divided into two different groups. The recorded
in situ temperatures that happened during daytime are to be considered wet snow observations due to possible snow melting at the top layer of the snowpack with the incoming solar radiation, changing the dielectric properties of the snow, and affecting its emissivity and the VIIRS radiative transfer signal. Inversely, T-skin measurements logged during nighttime were regarded as dry snow due to snow refreezing in the evening creating a more homogeneous snow surface. All the observations used to develop the formulas were under clear-sky conditions.
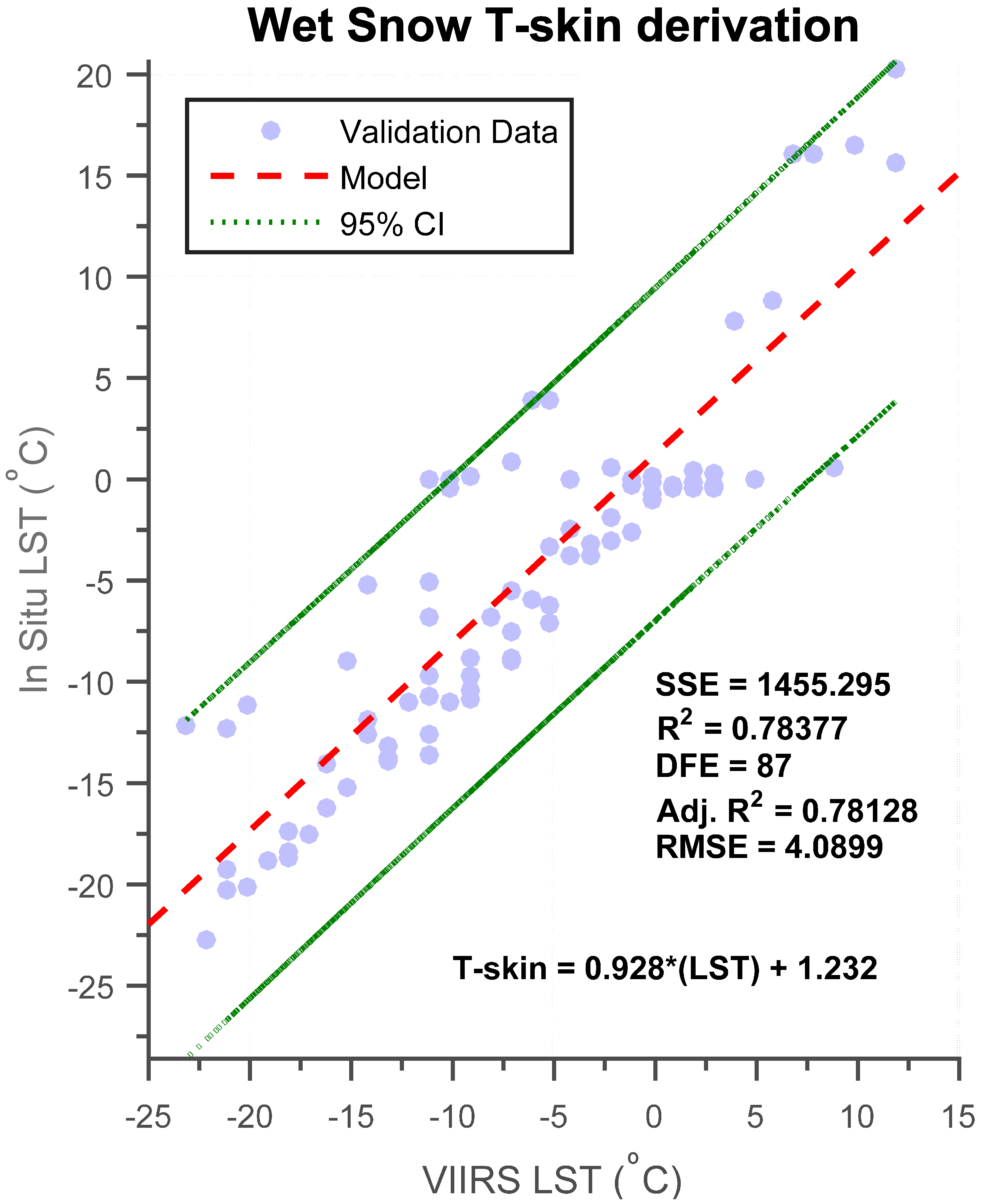
Figure 12 illustrates the validation data used to derive T-skin using RS LST under wet snow conditions (daytime) based on the linear regression model (Equation (2)) that was created, and the 95% upper and lower Confidence Intervals (CIs) for said model. The Sum of Square Errors (SSE) and degrees of freedom are 1455.3 °C
2 and 87, respectively. All but two observations are within the 95% confidence intervals. More importantly, R
2, Adjusted R
2, and RMSE are 0.783, 0.781, and 4.09 °C, respectively. All metrics indicating that the numerical predictions by the model are satisfactory.
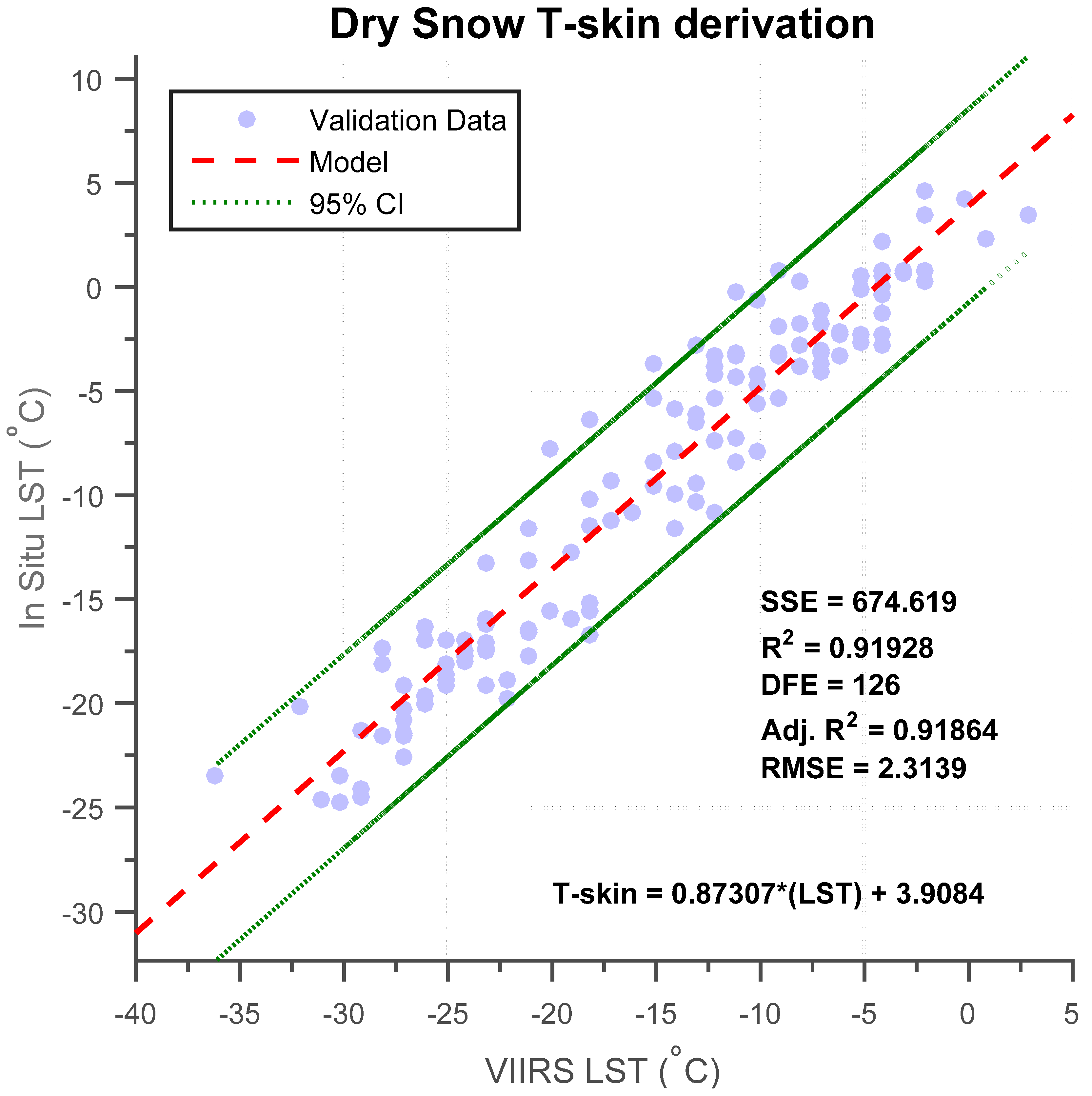
Figure 13 displays the validation data used to derive T-skin using RS LST under dry snow conditions (nighttime) based on the linear regression model (Equation (3)) that was created, and the 95% upper and lower confidence intervals (CIs) for the model. The Sum of Square Errors (SSE) and degrees of freedom are 674.62 °C
2 and 126, respectively. All but four observations are within the 95% confidence intervals. Furthermore, R
2, Adjusted R
2, and RMSE are 0.919, 0.918, and 2.31 °C, respectively. As expected, all metrics indicate that the numerical predictions by the model are highly satisfactory. Additionally, when compared to the wet snow model, it is confirmed that VIIRS makes better LST estimates during nighttime.
In light of the good accuracy provided by the linear regression models, the idea of producing an additional formula to correct RS LST with sky cover was developed. The developmental details are presented in
Section 3.5.
Figure 12.
T-skin derived empirical formula based on linear regression model between clear-sky VIIRS LST daytime (wet snow) views with respective in situ temperatures at CREST-SAFE.
Figure 12.
T-skin derived empirical formula based on linear regression model between clear-sky VIIRS LST daytime (wet snow) views with respective in situ temperatures at CREST-SAFE.
Figure 13.
T-skin derived empirical formula based on linear regression model between clear-sky VIIRS LST nighttime (dry snow) views with respective in situ temperatures at CREST-SAFE.
Figure 13.
T-skin derived empirical formula based on linear regression model between clear-sky VIIRS LST nighttime (dry snow) views with respective in situ temperatures at CREST-SAFE.
3.5. Derivation of Empirical Formula to correct RS LST using Cloud Cover to Obtain In Situ LST
The good accuracy for numerical predictions provided by the linear regression models in
Section 3.4 led to the idea of using the developed empirical formulas inversely by utilizing the
in situ T-skin from CREST-SAFE to obtain what were named
in situ wet and dry snow LSTs, and compare them with the actual VIIRS LSTs via a relation with cloudiness. These wet and dry snow LSTs would ideally be the RS LST (daytime and nighttime, respectively) under clear-sky conditions, since the empirical formulas were created using clear-sky observations only.
Figure 14 illustrates the VIIRS LST daytime and nighttime retrievals, the derived wet and dry snow LSTs, and the cloud cover in the background. The wet and dry snow LSTs were created using T-skin observations that matched temporally with all VIIRS LST (cloud-contaminated and clear-sky).
Figure 14.
VIIRS LST daytime and nighttime views and inversely retrieved LSTs (wet and dry snow conditions) using the empirical formulas derived from the linear regression models in
Section 3.4. Sky cover in the background.
Figure 14.
VIIRS LST daytime and nighttime views and inversely retrieved LSTs (wet and dry snow conditions) using the empirical formulas derived from the linear regression models in
Section 3.4. Sky cover in the background.
A multiple linear regression analysis with linear correlation coefficients was used to correlate derived
in situ LSTs (output) with RS LST and cloudiness as predictor variables. It should be mentioned that other correlation coefficient combinations were used, but few showed improvements in the model and these were minimal.
Figure 15 illustrates a three-dimensional scatterplot with its representative multiple linear regression model (Equation (4)) in mesh-grid form. DFE, R
2, Adjusted R
2, and RMSE are 163, 0.547, 0.538, and 7.128 °C, respectively. Metrics indicate that the linear regression model can estimate
in situ LST with reasonable accuracy. However, it is clear that cloudiness variability affects the predictions considerably.
Table 5 shows the multiple linear regression results.
Table 5.
Multiple linear regression model results for in situ LST estimation using RS LST and cloudiness as predictor variables.
Table 5.
Multiple linear regression model results for in situ LST estimation using RS LST and cloudiness as predictor variables.
| Multiple Linear Regression Analysis Results |
|---|
| -- | Coefficient | SE | tStat | pValue |
| Intercept | −9.3982 | 1.2799 | −7.3427 | 9.4521 × 10−12 |
| RS LST | 0.5376 | 1.5978 | 4.4601 | 1.5197 × 10−5 |
| Cloudiness | 7.1266 | 0.0665 | 8.0737 | 1.4251 × 10−13 |
Figure 15.
Three-dimensional scatterplot of in situ LST, VIIRS LST, and cloudiness with linear regression model in mesh-grid form to estimate in situ LST with RS LST and cloudiness as predictor variables.
Figure 15.
Three-dimensional scatterplot of in situ LST, VIIRS LST, and cloudiness with linear regression model in mesh-grid form to estimate in situ LST with RS LST and cloudiness as predictor variables.
The coefficient estimates for RS LST (0.5376) and cloudiness (7.1266) highlight again how RS LST underestimates in situ LST for the region under study. The coefficient estimate results indicate that a 30% change in sky cover will result in a 2 °C change between in situ LST and RS LST. Low SE values are indicative of the regression’s capability of estimating both input variables with reasonable accuracy. Lower p-values for cloudiness indicate that there is a 95% probability that it has significant effect on estimating in situ LST using RS LST. The RSME value of 7.13 °C shows that there is error in the model’s in situ estimation due to cloud variability. Lastly, it should be noted that these proposed equations might not apply elsewhere, but are a step in the right direction for the improvement of VIIRS LST retrievals. If anything, these equations still provide user-friendly, preliminary means to estimate T-skin using RS LST retrievals, as well as an empirical formula to correct the RS LST for cloud contamination.