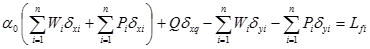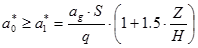1. Introduction
The Italian earthquakes of Umbria and Marche in 1997 [
1] and Abruzzo in 2009 [
2], have highlighted the need for an extensive monitoring and safety assessment of historic Italian construction heritage. Following the debate developed in the scientific community, new Italian Technical Recommendations for buildings have been drawn up: first after 2003 [
3,
4] and later, after 2008 [
5,
6]. As is known, ancient masonry buildings, although perfectly able to bear vertical loads, usually are not adequate to sustain the horizontal forces produced by earthquakes. So, they are particularly prone to severe damage under seismic loading. In addition, historic built heritage represents an economic concern especially in contexts where tourism has become one of the major sources of wealth. Therefore, preserving historic constructions is a cultural requirement and an economic and developmental demand [
7].
The structural analysis of a new masonry building is a relatively simple task, whereas the assessment of the seismic vulnerability of an ancient masonry building is a challenging task, because of several uncertainties affecting the geometrical and the mechanical characteristics of the structural elements [
8]. Each masonry building is characterized by its own history and the actual configuration is the result of fusions, additions and replacements of many structural elements. Thus, a correct structural analysis of an historic building requires a deep knowledge of: (a) the building history and its evolution; (b) the geometry; (c) the structural details; (d) the cracking pattern and the damage map; and (e) the masonry construction techniques [
9,
10].
The characterization of the material properties is required to develop a proper structural analysis. This knowledge can be achieved combining
in-situand laboratory experimental tests. Due to the difficulties in obtaining all information to be used for a proper definition of a numerical model, in some cases it is necessary to perform simplified, often iterative, procedures for evaluation of the static and the seismic reliability. Hence, the structural engineers should be able to address the relevant aspects of the problem and provide guidance in analyses and experiments [
11].
Maintenance of historic buildings has become a relevant scientific issue that has attracted the interest of researchers all over the world as demonstrated by the growing number of researches presented in recent decades. These studies represent a wide state-of-the-art of the engineering approach for evaluation of safety of historic buildings. Among the various researches in this field there is the work of Lourenço
et al. [
12]. The authors discuss the case of the Monastery of Jerónimos in Lisbon (Portugal) and show that it is possible to understand the behavior and the damage of a complex historic construction providing valuable information in designing
in-situtests and monitoring. The relevance of proper numerical strategies has been pointed out by Cardoso
et al. [
13,
14]. These authors discuss the aseismic provisions included in old masonry buildings in downtown Lisbon, after the Lisbon earthquake in 1755. They propose an iterative method for the seismic assessment in which the damage to the structural elements or connections is identified and the stiffness of the structural model is changed accordingly. Each iteration comprises a linear elastic analysis, so the procedure is useful for current design practice. Betti and Vignoli [
15] discussed the seismic vulnerability of the Basilica of Santa Maria of Impruneta (Italy), and proposed the combination of a finite element model of the building with a simplified approach based on the kinematic theorem of limit analysis. The results suggest that the comparison between different techniques of analysis is mandatory to cover the unknowns affecting the mechanic properties of the materials. Relevance of a wide spread analysis approach has been pointed out also by Mallardo
et al. [
16]. The authors discuss the seismic behavior of a Renaissance Palace in Ferrara (Italy). Firstly, a 3D nonlinear model of the Palace is considered in order to understand the large-scale structural performance. Next, a detailed study of the main façade of the Palace is presented, by means of three reduced 2D nonlinear models. The authors show that the use of different modeling strategies allows a critical evaluation of the seismic vulnerability of the main elements. An integrated multilevel approach that combines laboratory and non-destructive testing methods with monitoring systems has been recently presented by Anzani
et al. [
17] to evaluate the state of conservation of historic structures. They discussed the cases of some damaged towers in Italy and suggested an investigation procedure to be adopted for safety assessment of historic towers.
This paper presents an evaluation of the seismic vulnerability of the Vicarious Palace (Palazzo del Vicario) in Pescia, a small town near Florence. In the first part, the geometrical and mechanical descriptions of the building are presented, together with a brief report of its history. Then, the seismic assessment approach is illustrated.
Firstly, a structural analysis of the Palace was made using a finite element model. Specific assumptions of the material properties and the nonlinear behavior of the masonry were considered. Static analysis under vertical loads (dead and live loads), and pushover analyses were performed, according to the Italian Technical Recommendations [
3,
4]. Next, a simplified approach based on the kinematic theorem of limit analysis was applied. With reference to the failure mechanisms activated in similar buildings during past earthquakes [
18,
19], some macro-elements were individuated and analyzed.
The results provide a description of the building response under seismic loading and offer a representative case which is fruitful in extending the comprehension of the structural behavior of this building typology.
3. 3. Finite Element Model
The structural analysis of the Palace was approached by a 3D finite element model based on the concepts of homogenized material and smeared crack modeling using the ANSYS code v.11.0 [
25]. The masonry walls were discretized with
Solid65 elements (isoparametric three-dimensional eight node elements), whereas the ground floor vaults were discretized with
Shell63 elements (isoparametric two-dimensional four node elements). The wooden floors and timber roof were not considered in the model and their own weights were applied on the bearing walls by means of vertical concentrated loads.
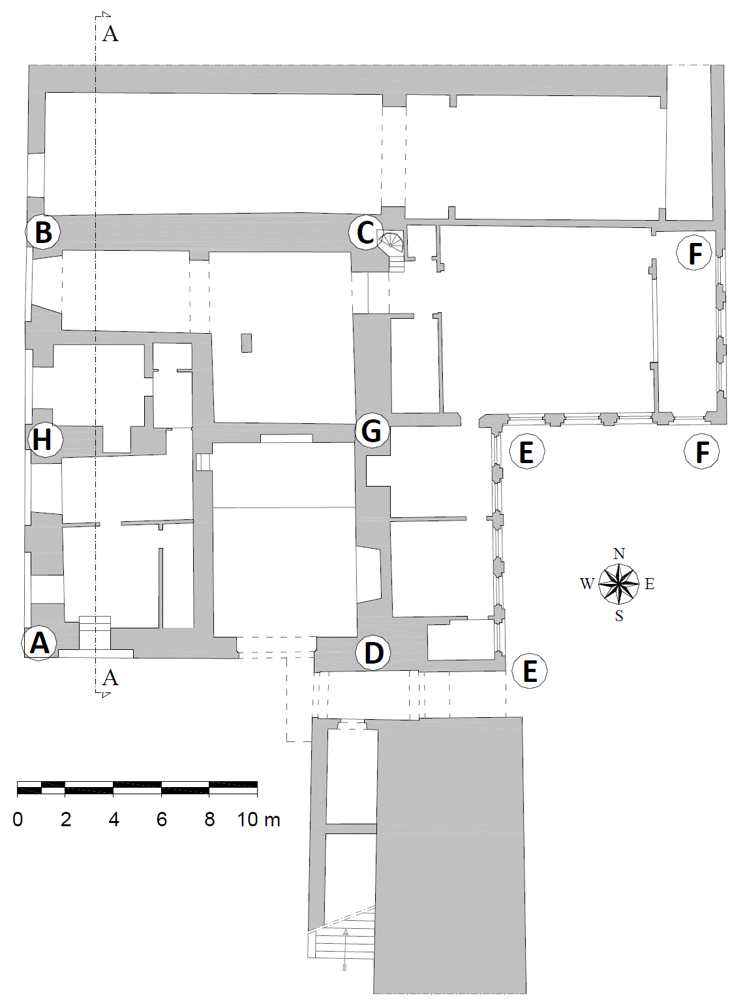
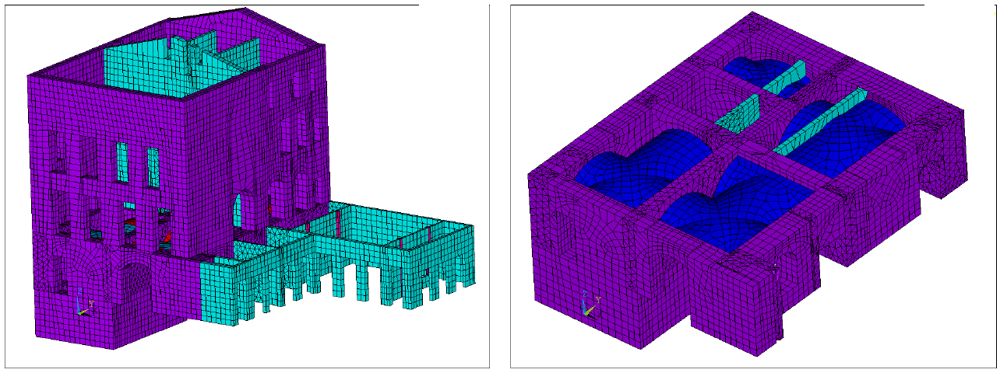
An in-situ survey of the building was made to accurately reproduce the geometry, the structural details and the irregularities of the Palace. This investigation consisted of a geometrical relief aimed at characterizing the masonry texture and to check up the quality of wall-to-wall, wall-to-floors and wall-to-roof connections. The 3D model is represented in Figure 7. It consists of 37,402 nodes, 36,557 Solid65 elements and 813 Shell63 elements, corresponding to 108,399 DOFs.
The nonlinear behavior of the masonry was represented by combining plasticity with a smeared crack approach. The perfectly-elastic plastic behavior with the Drucker-Prager (DP) yield surface was used to reproduce the plasticity properties, whereas the Willam-Warnke (WW) failure surface was considered for model crush and cracking [
26].
Both DP and WW models were been extensively used to simulate the inelastic behavior of masonry. Discussing the homogenization approach for masonry, Zucchini and Lourenco [
27] adopted the DP model to simulate the plastic deformation in masonry cells. They showed that it is possible to account for degradation of masonry mechanical properties in compression. Cerioni
et al. [
28] adopted the DP criterion to investigate the seismic behavior of the Parma Cathedral Bell-Tower. The WW criterion was used by Adam
et al. [
29] for model cracking and crushing capabilities of masonry materials; comparison between numerical and experimental results shows good agreement. Chiostrini
et al. [
23] combined the DP and the WW criteria to reproduce the results of several diagonal tests on masonry specimens, obtaining good agreement with experimental values. Betti and Vignoli combine the DP and the WW criteria to discuss the seismic vulnerability of a masonry church [
15,
30].
Figure 7.
Figure 7. Finite element model of the Vicarious Palace.
Figure 7.
Figure 7. Finite element model of the Vicarious Palace.
The cohesion
c and the internal friction angle
φ are the two material parameters required to define the DP yield surface. The Willam-Warnke (WW) failure surface is defined by two material constants,
i.e. the uniaxial compressive strength
fcWWand the uniaxial tensile strength
ftWW of the masonry. A proper selection of these values allows the introduction of a cut-off to the tensile strength and an upper limit to the biaxial compressive strength. So, the model reproduces effectively the small tensile strength of the masonry, the plasticity behavior in regime of average compression and the crushing phenomenon for high compressive stresses.
Table 2 collates the values of the nonlinear material parameters.
Table 2.
Table 2. Constitutive parameters of the masonries adopted for nonlinear FEM analyses (DP = plasticity criterion and WW = failure surface).
Table 2.
Table 2. Constitutive parameters of the masonries adopted for nonlinear FEM analyses (DP = plasticity criterion and WW = failure surface).
| DP yield surface |
|---|
| c (N/mm2) | Cohesion | 0.09 |
| φ (°) | Friction angle | 38° |
| δ (°) | Dilatancy angle | 15° |
| WW failure surface |
| fcWW (N/mm2) | Uniaxial compressive strength | 4.00 |
| ftWW (N/mm2) | Uniaxial tensile strength | 0.12 |
| βc(-) | Shear transfer coefficient for closed cracks | 0.75 |
| βt(-) | Shear transfer coefficient for open cracks | 0.25 |
Firstly, the 3D model was used to evaluate the stresses in the masonry walls produced by the vertical loads i.e.,: the dead weights, the live floor loads (2.0 kN/m2) and the snow load on the roof (1.1 kN/m2). The whole structure was analyzed in the nonlinear range to identify the weak points of possible failure, assuming fixed base restraint conditions.
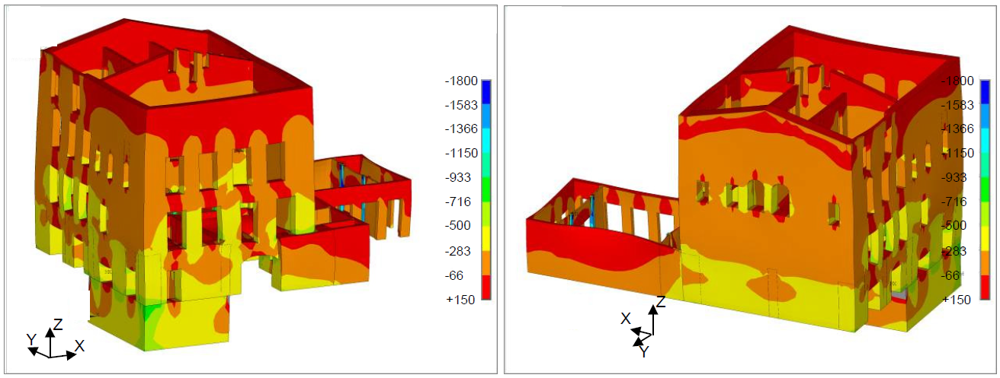
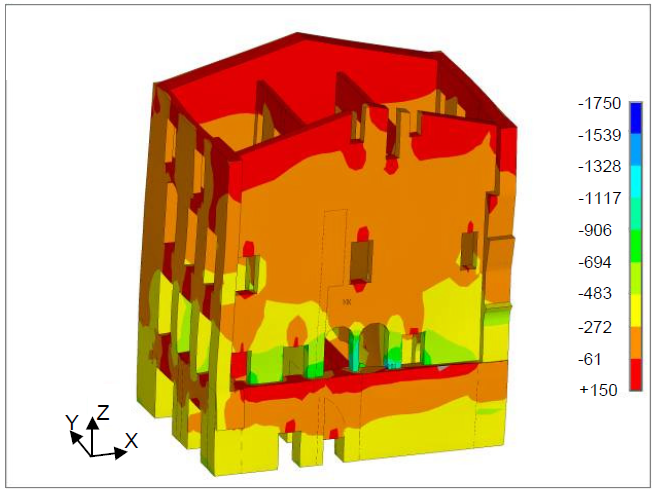
Results in terms of vertical stresses are reported in Figures 8 and 9. The average compressive stress at the base of the walls is about 0.5 N/mm2 with small tensile stresses located on the top surface of the walls. These tensile stresses are produced by the local numerical effect depending on the concentrated loads of the roof. The maximum compressive stress (about 1.7 N/mm2) is reached in a column close to an arch opening in the internal wall (Figure 9). Even if this value is high it is much less than the crushing limit of the masonry (local sandstone). Results of the analysis illustrate that the Palace is adequate to withstand the vertical loads under exercise conditions. This is a common result for this typology of buildings designed by skilled manufacturers.
Figure 8.
Figure 8. Static analysis: vertical compressive stresses (units are kN/m2).
Figure 8.
Figure 8. Static analysis: vertical compressive stresses (units are kN/m2).
Figure 9.
Figure 9. Static analysis: vertical compressive stresses, detail of the internal wall (units are kN/m2).
Figure 9.
Figure 9. Static analysis: vertical compressive stresses, detail of the internal wall (units are kN/m2).
4. Seismic Analysis
4.1. Kinematic Analysis
The main assumptions of the kinematic method are: (a) masonry is a no-tension material (although this hypothesis may be considered conservative, only very small tension forces are transferred across the mortar joints); (b) masonry has infinite compressive strength (this hypothesis is not conservative, but in most cases collapse of masonry is due to cracks opening rather than to compression failure); and (c) structures are considered as assemblages of macro-elements (rigid bodies). The assessment of these macro-elements is based on structural geometry, shape (
i.e., whole façades), details (
i.e., the quality of existing connections between walls), and by examining collapses and damages consequent to past earthquakes in similar buildings [
11,
31].
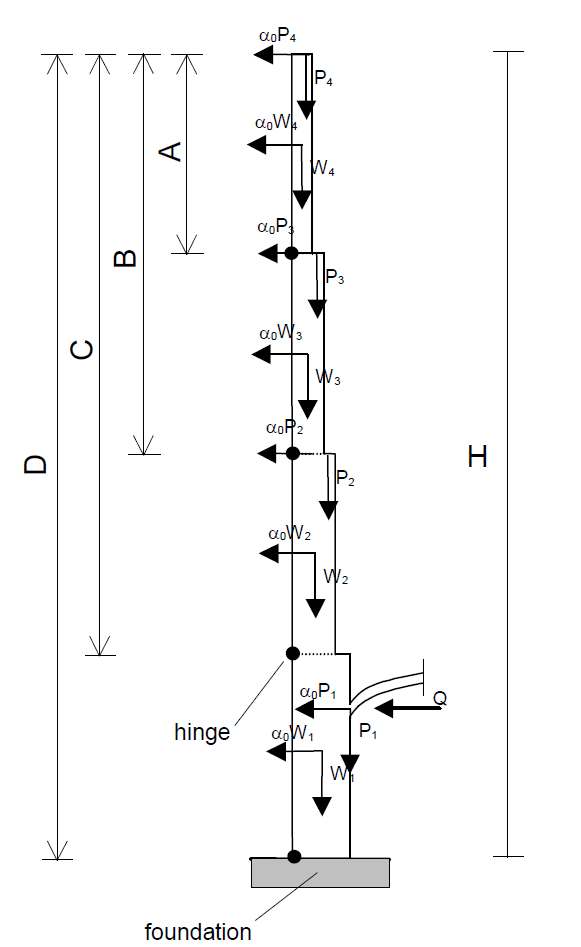
Each allowable mechanism has a single degree of freedom and it is characterized by the formation of linear hinges among the single macro-elements. The seismic loads are assumed to be static horizontal forces amplified by a kinematic multiplier α ; the gravity loads are stabilization forces. Given an allowable mechanism, the corresponding kinematic multiplier at collapse α 0 is evaluated by the Virtual Work Theorem (V.W.T.).
The mechanisms considered in this study concern partial and global overturns of the main façades,
and the collapse multipliers
α 0 are evaluated according to Eq. (1) (see the general scheme reported in
Figure 10; A, B, C and D identify different mechanisms):
Figure 10.
Out-of-plane mechanisms; Pi are the vault or the floor vertical loads; Wi are the own weights of the walls; α 0Pi and α 0Wi are the seismic loads.
Figure 10.
Out-of-plane mechanisms; Pi are the vault or the floor vertical loads; Wi are the own weights of the walls; α 0Pi and α 0Wi are the seismic loads.
In Equation (1) Wi are the dead weights of the elements involved in the mechanism; Pi are the weights transmitted at the selected macro-element by vault, floors or roof; δxi are the horizontal virtual displacements of the points of application of Wi and Pi; δyi are the vertical virtual displacements of the points of application of Wiand Pi; Q is the static drift of the vault; δxq is the corresponding horizontal virtual displacement and Lfi is the virtual work of the internal forces, here assumed equal to zero. After the evaluation of the collapse multiplier α 0, the corresponding seismic spectral acceleration a0* is given by:
where
M* is the effective participating mass and
g is the gravity acceleration. According to [
3] the analyzed
mechanism will not be possible under design earthquake if:
where agS is the design elastic spectral acceleration at T = 0, q is
the behavior factor (assumed equal to 2.0), Z is the height to the ground of the linear hinge of the mechanism and H is the total height of the façade. Each macro-element, i.e., each masonry façade, was analyzed considering first the overturning of the last floor only (the fourth floor, case A), then the overturning of the fourth and the third floor (case B), until in the last case where the overturning of the whole façade was analyzed (case D). The results are summarized in Table 3. The more vulnerable walls are the DA, the AH and the HB in which the vulnerability indexes a1*/a0* are higher. In all cases the overturning minimum collapse multipliers are obtained when the whole façade mechanism is considered; this suggests proper strengthening techniques.
Table 3.
Table 3. Vulnerability indexes obtained with kinematic analysis (α 0 = collapse multipliers; a0*= seismic spectral accelerations corresponding to α 0; a1*= seismic spectral accelerations demanded for ultimate limit state).
Table 3.
Table 3. Vulnerability indexes obtained with kinematic analysis (α 0 = collapse multipliers; a0*= seismic spectral accelerations corresponding to α 0; a1*= seismic spectral accelerations demanded for ultimate limit state).
| Wall | Mechanism | α0 | a0* (m/s2) | (m/s2) | | Check (a0*≥ a1*) |
|---|
| 1-DA | A | 0.48 | 4.75 | 2.62 | 0.55 | YES |
| B | 0.08 | 0.78 | 1.99 | 2.55 | NO |
| C | 0.06 | 0.60 | 1.62 | 2.70 | NO |
| D | 0.03 | 0.33 | 1.10 | 3.33 | NO |
| 2a-AH | A | 0.36 | 3.52 | 2.60 | 0.74 | YES |
| B | 0.09 | 0.84 | 2.01 | 2.39 | NO |
| C | 0.06 | 0.56 | 1.58 | 2.82 | NO |
| D | 0.03 | 0.27 | 1.10 | 4.07 | NO |
| 2b-HB | A | 0.08 | 0.81 | 2.37 | 2.93 | NO |
| B | 0.06 | 0.62 | 1.94 | 3.13 | NO |
| C | 0.05 | 0.49 | 1.53 | 3.12 | NO |
| D | 0.04 | 0.36 | 1.10 | 3.06 | NO |
| 3a-DG | A | 0.44 | 4.32 | 2.60 | 0.60 | YES |
| B | 0.11 | 1.12 | 2.02 | 1.80 | NO |
| C | 0.08 | 0.83 | 1.60 | 1.93 | NO |
| D | 0.05 | 0.47 | 1.10 | 2.34 | NO |
| 3b-GC | A | 0.15 | 1.49 | 2.46 | 1.65 | NO |
| B | 0.12 | 1.13 | 2.00 | 1.77 | NO |
| C | 0.09 | 0.91 | 1.55 | 1.70 | NO |
| D | 0.08 | 0.83 | 1.10 | 1.33 | NO |
| 4-BC | A | 0.22 | 2.14 | 2.46 | 1.15 | NO |
| B | 0.10 | 1.00 | 2.05 | 2.05 | NO |
| C | 0.07 | 0.70 | 1.55 | 2.21 | NO |
| D | 0.07 | 0.70 | 1.10 | 1.57 | NO |
4.2. Pushover Analysis
The seismic behavior of the Palace was also investigated by a non linear static analysis. The FE model was subject to constant gravity loads and, subsequently, to monotonically increasing horizontal forces (pushover analysis [
32,
33]). Specifically, the effects of the seismic action were evaluated by applying two systems of horizontal forces, not acting simultaneously, perpendicular to one another. The distribution of these forces is directly proportional to the masses by the displacements of the first modal shape in the pertinent direction (modal load).
Soon after its introduction in the late seventies, the pushover analysis became very attractive in earthquake engineering due to its relative simplicity (e.g., it requires quite simple material models, which do not account for progressive damage accumulation) and its reduced computational effort, compared with nonlinear dynamic analysis. Nevertheless, the method is not devoid of disadvantages and critical points, as highlighted by the scientific community. A comprehensive review of criticisms, advantages and disadvantages, together with the theoretical basis of the method, is reported in [
34,
35]. In this study a conventional pushover is performed,
i.e., distribution of the horizontal forces does not change with progressive structural degradation occurring during an earthquake. This means that the analysis does not account for the progressive changes in modal frequencies due to crushing and cracking phenomena. This is a critical point for the application of conventional pushover to historic masonry buildings, because it is predictable that damaging of the building leads to a period elongation. Therefore, different spectral amplifications and modal load distributions should be considered [
36,
37]. The hypothesis of invariance of the distribution of the horizontal loads could cause an overestimation of the building seismic capacity, especially when non uniform damage or high level of cracking are expected. Yet, also in its conventional form pushover provides an efficient alternative method to expensive computational inelastic dynamic analyses and offers effective information on the damage state.
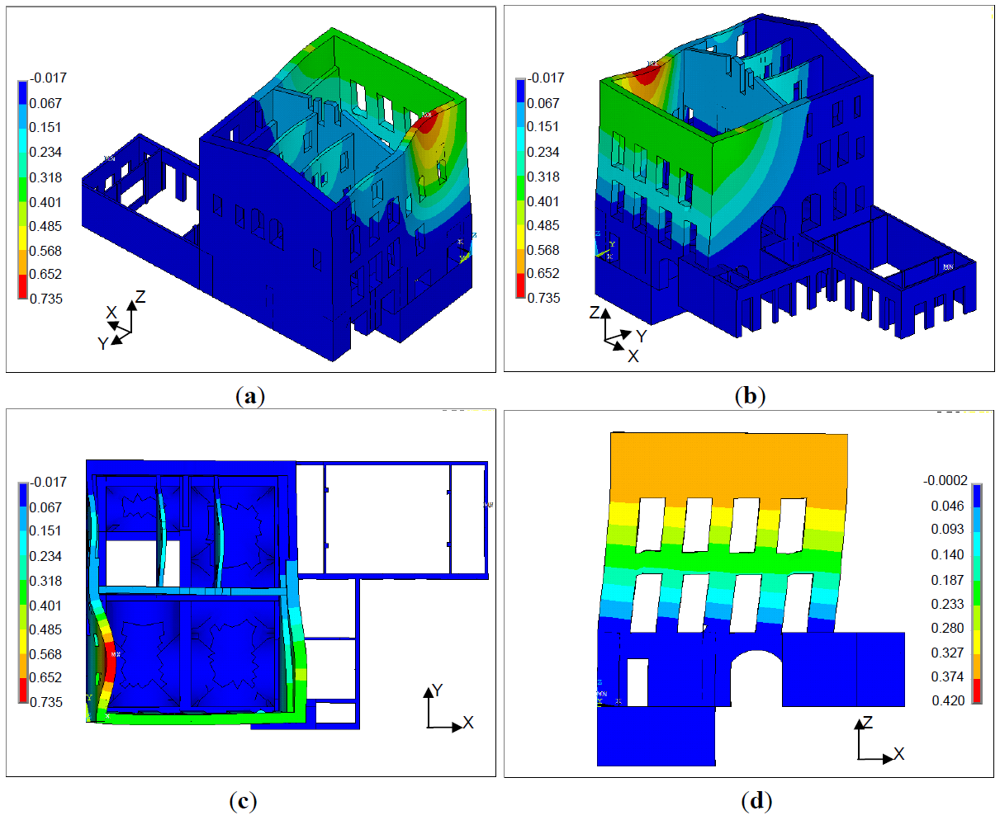
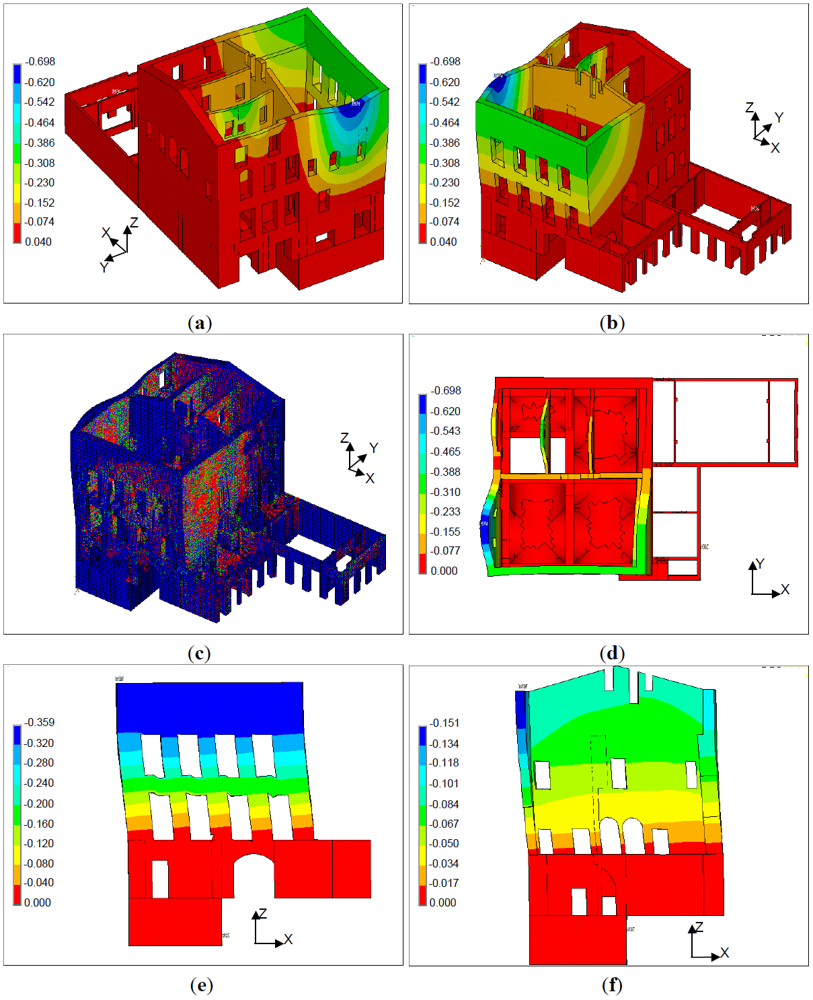
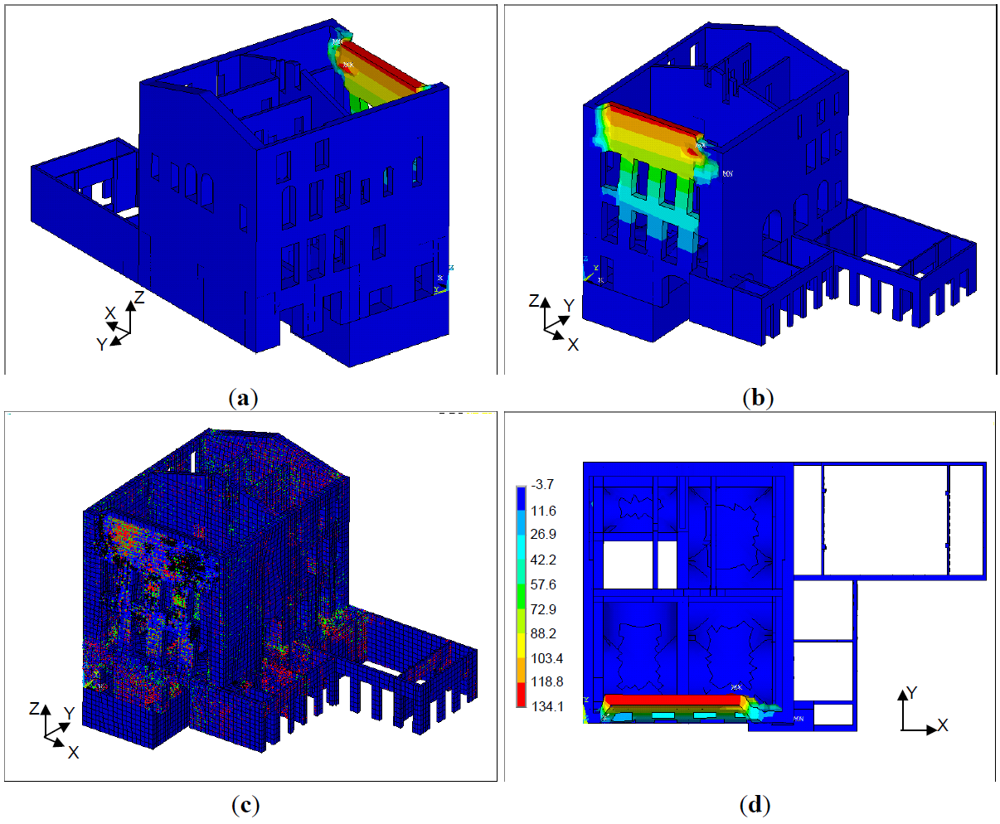
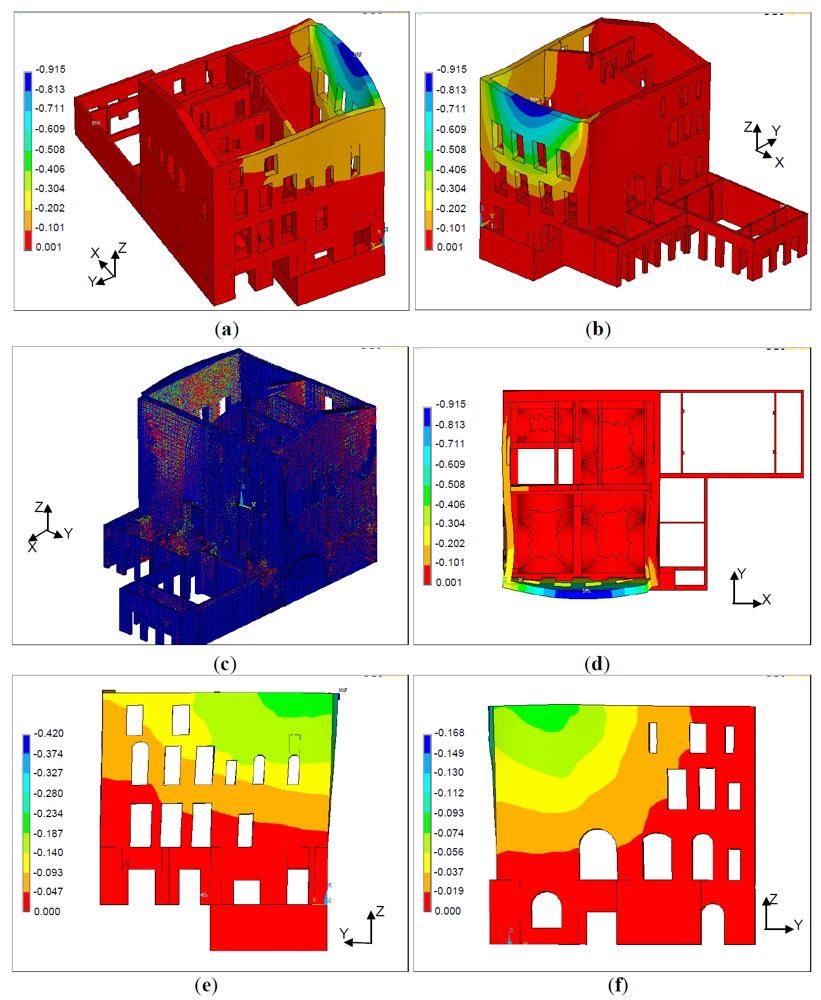
Results of pushover analysis in terms of displacements and crack and crushing patterns are reported in Figures 11 to 14. Figures 11 and 12 report the final configuration of the Palace for seismic loading acting in the transversal direction (+X and –X). In both cases there is a remarkable out-of-plane deformation of the wall AH, that confirms the results obtained with the kinematic analysis. Figures 13 and 14 show the Palace configuration for seismic loading acting in the longitudinal direction (+Y and –Y). Again it is possible to find a good agreement in terms of failure process between pushover and kinematic analysis, both confirming the overturning of the wall DA.
Figure 11.
Figure 11. Pushover analysis results (+X direction): (a), (b), (c) and (d) horizontal displacement in X direction (units are m).
Figure 11.
Figure 11. Pushover analysis results (+X direction): (a), (b), (c) and (d) horizontal displacement in X direction (units are m).
Figure 12.
Figure 12. Pushover analysis results (–X direction): (a), (b), (d), (e) and (f) horizontal displacement in X direction (units are m), (c) final cracking and crushing patterns.
Figure 12.
Figure 12. Pushover analysis results (–X direction): (a), (b), (d), (e) and (f) horizontal displacement in X direction (units are m), (c) final cracking and crushing patterns.
Figure 13.
Figure 13. Pushover analysis results (+Y direction): (a), (b) and (d) horizontal displacement in Y direction (units are m), (c) final cracking and crushing patterns.
Figure 13.
Figure 13. Pushover analysis results (+Y direction): (a), (b) and (d) horizontal displacement in Y direction (units are m), (c) final cracking and crushing patterns.
Figure 14.
Figure 14. Pushover analysis results (−Y direction): (a), (b), (d), (e) and (f) horizontal displacement in Y direction (units are m), (c) final cracking and crushing patterns.
Figure 14.
Figure 14. Pushover analysis results (−Y direction): (a), (b), (d), (e) and (f) horizontal displacement in Y direction (units are m), (c) final cracking and crushing patterns.
In case of seismic loading acting in the transversal direction (+X and –X) the analyses stop at a horizontal load corresponding to about 28–30% of the overall weight of the Palace; in case of seismic loading acting in the longitudinal direction (+Y and –Y) the analyses stop at a horizontal load corresponding to about 35–37% of the overall weight of the Palace.
Results obtained by analyses agree well with those obtained by the macro-element approach. The vulnerability of the Palace is mostly due to the absence of adequate connections between the opposite walls of the building due to the typology of the floors and the roof made of wooden beams. This has been already highlighted by other authors [
38]. Absence of effective connections between structural components leads to overturning collapses of the perimeter walls under seismic loading due to the lack of box-behavior. Results suggest a proper strategy to improve the strength of the Palace against horizontal loads. A traditional retrofitting by means of steel chains and the creation of effective connections between wooden floors and masonry walls will prevent overturning of the façades [
39].