A Combined Experimental-Numerical Approach for Investigating Texture Evolution of NiTi Shape Memory Alloy under Uniaxial Compression
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
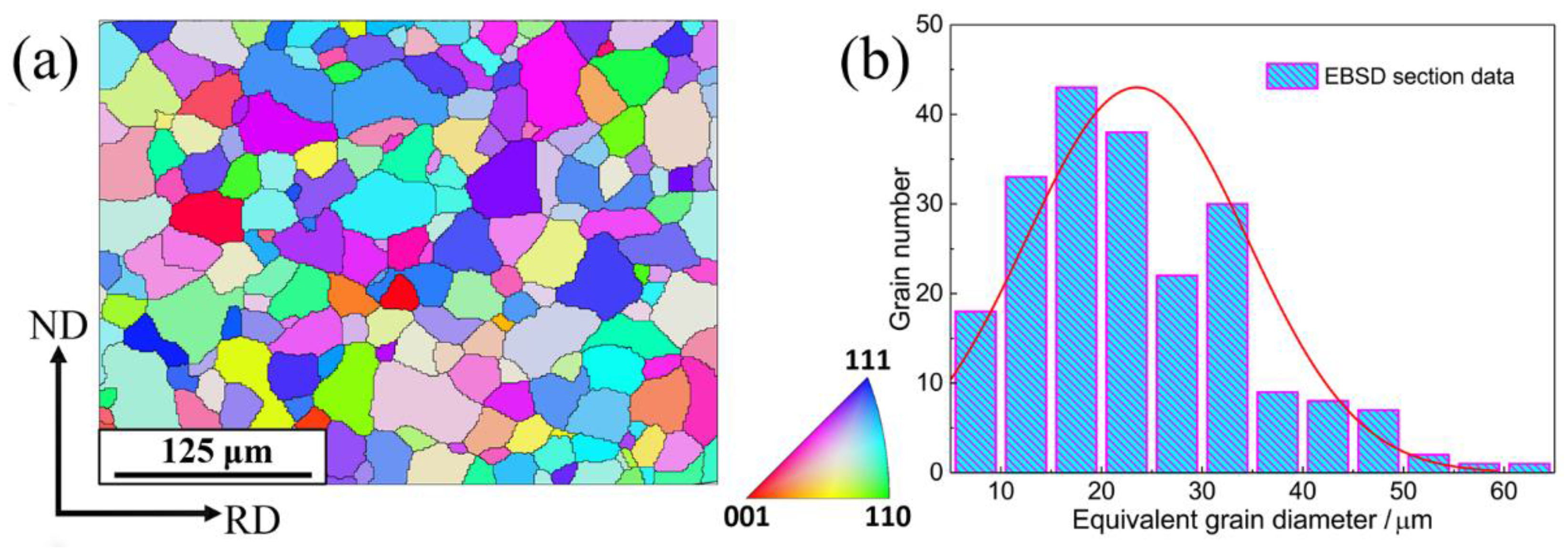
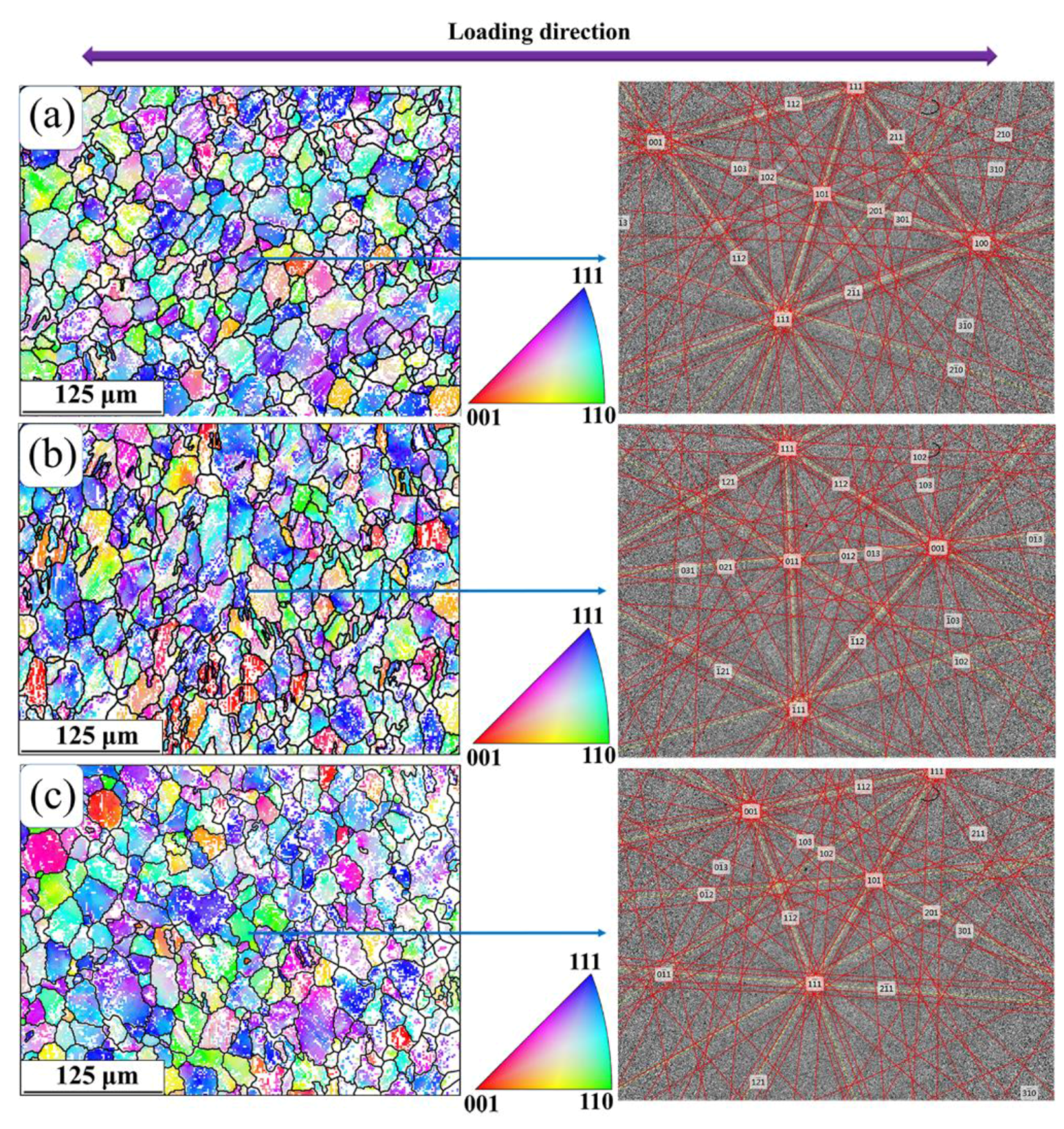
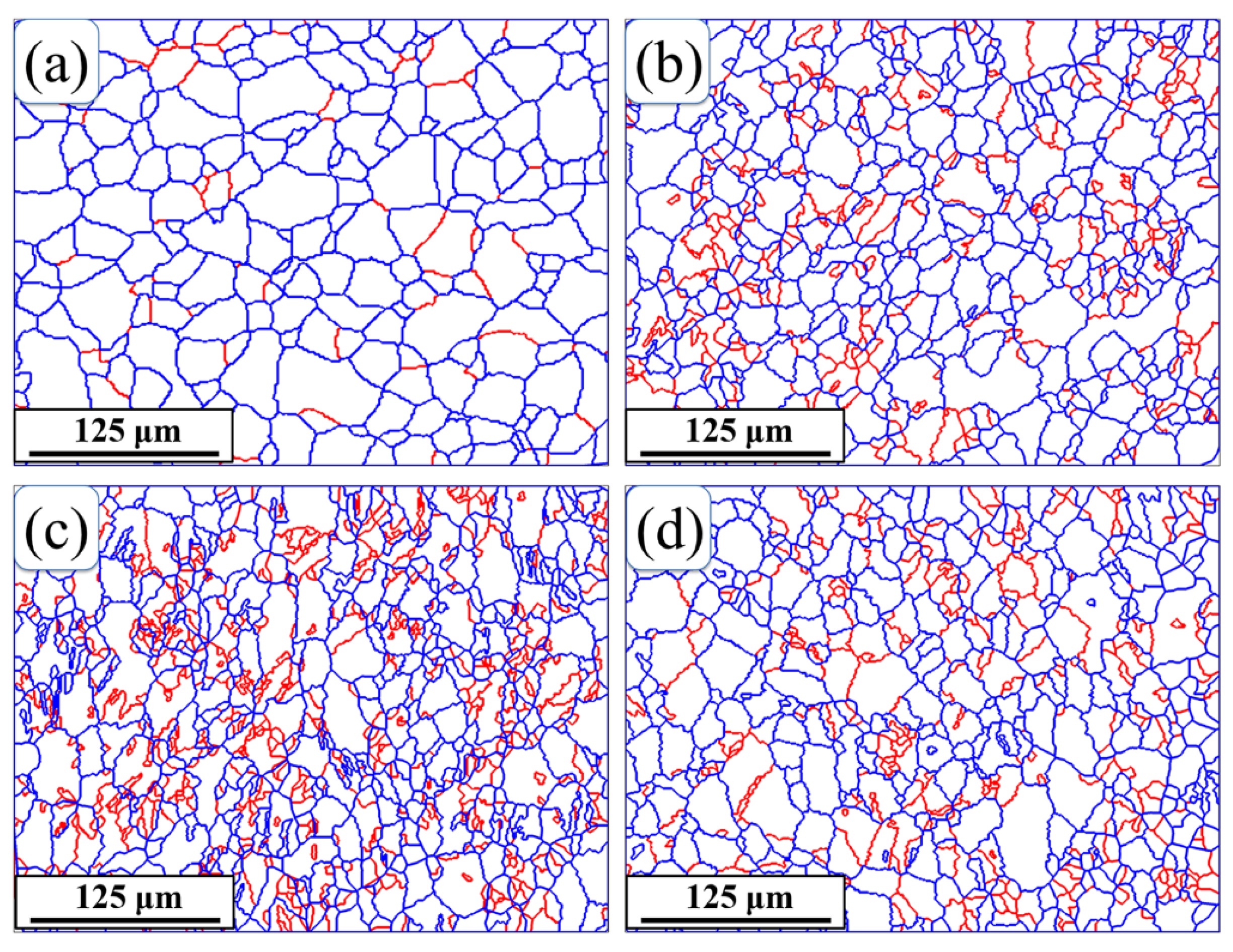
3.1. Investigation on Microstructure Evolution
3.2. Investigation on Texture Evolution Based on CPFEM
3.2.1. Crystal Plasticity Constitutive Model
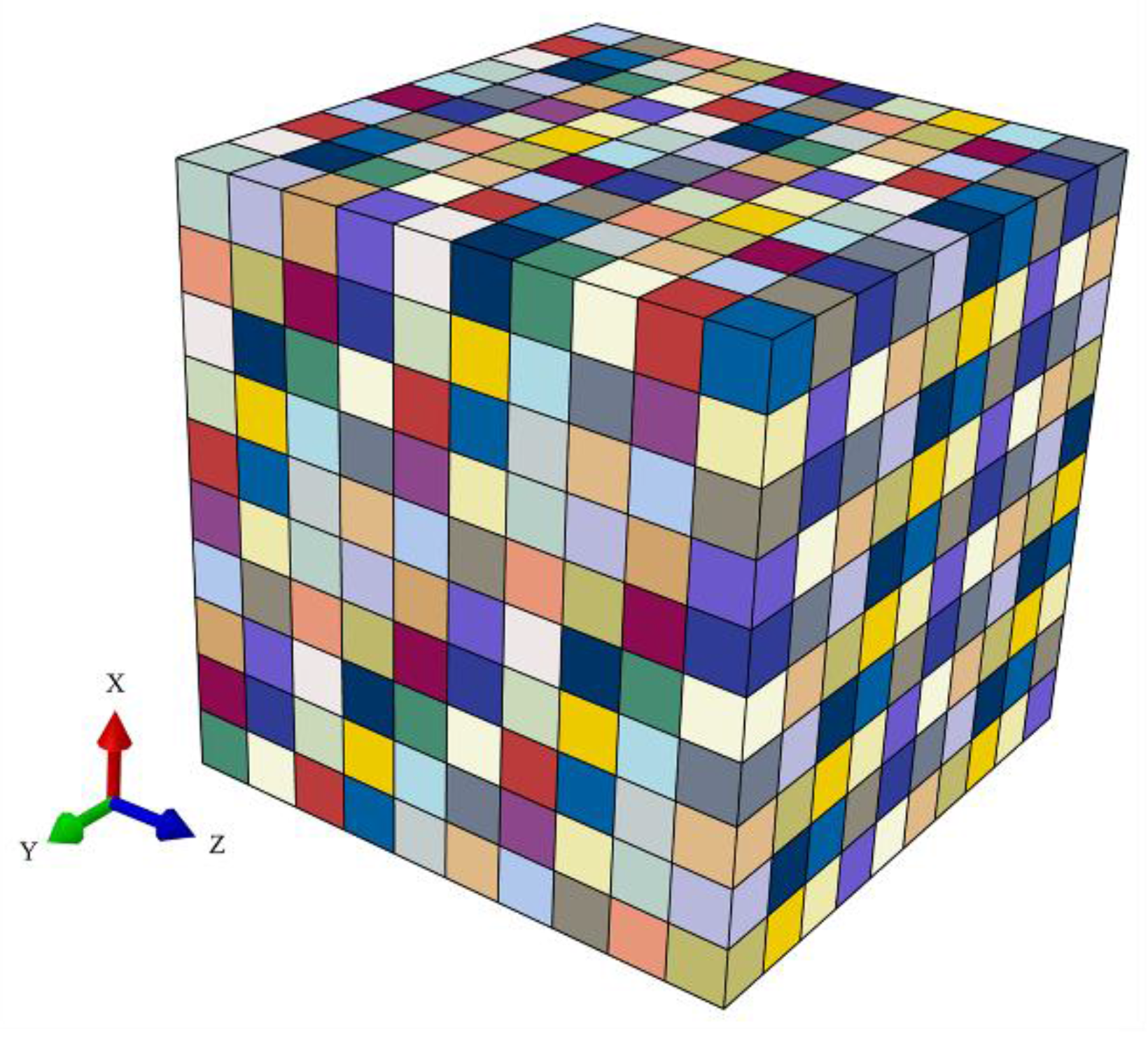
3.2.2. Establishment of RVE Model
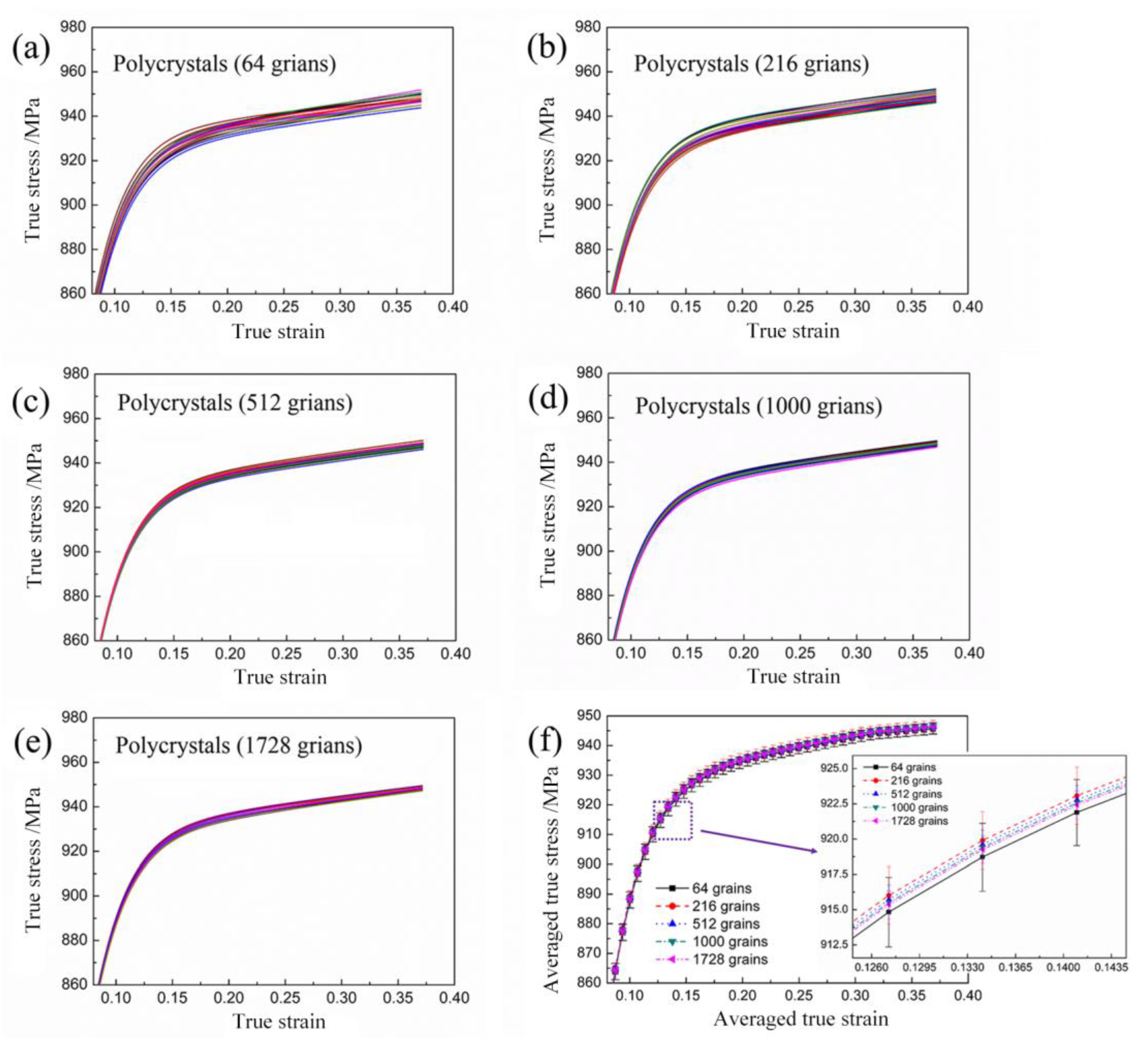
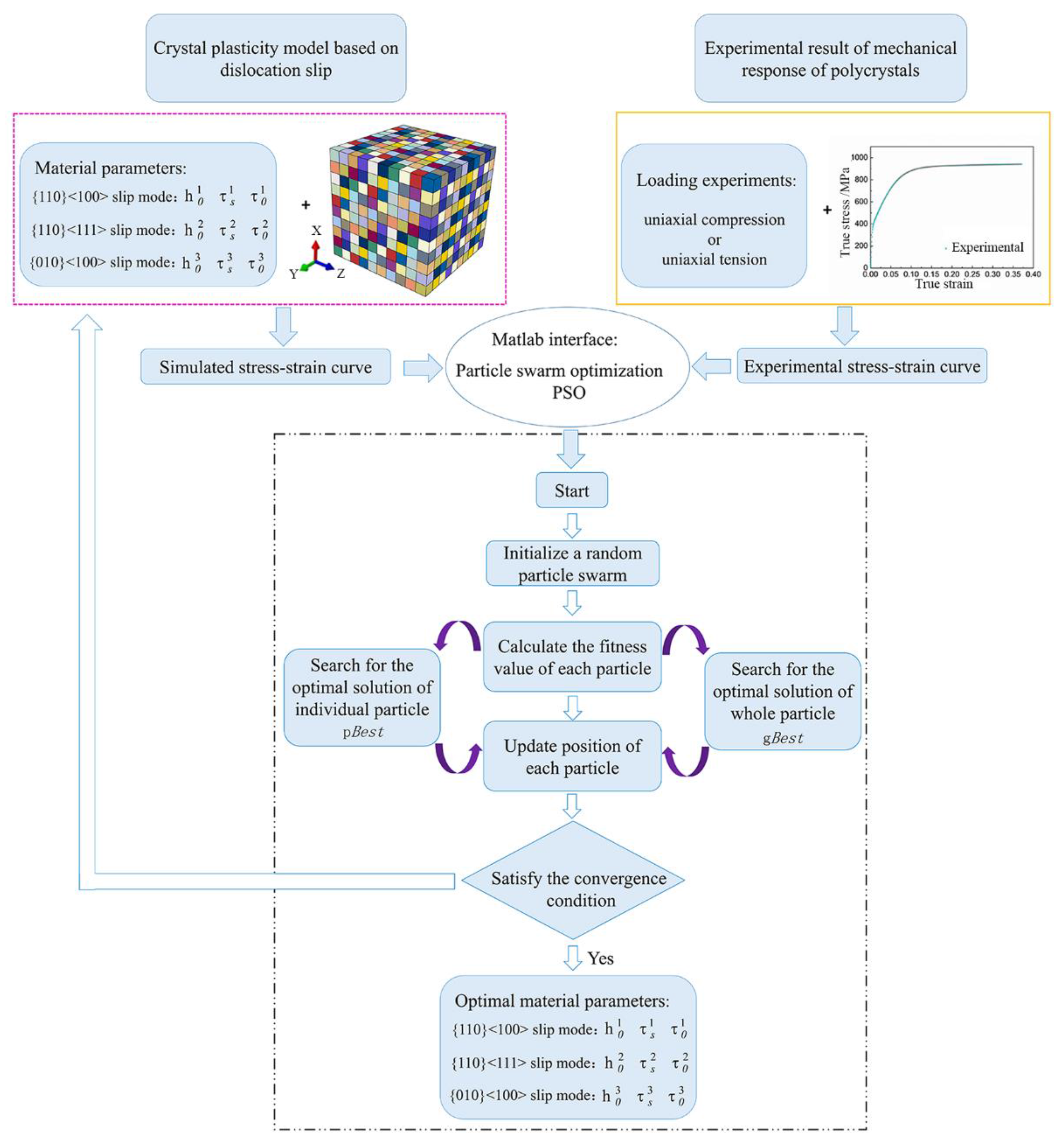
3.2.3. Parameters Calibration
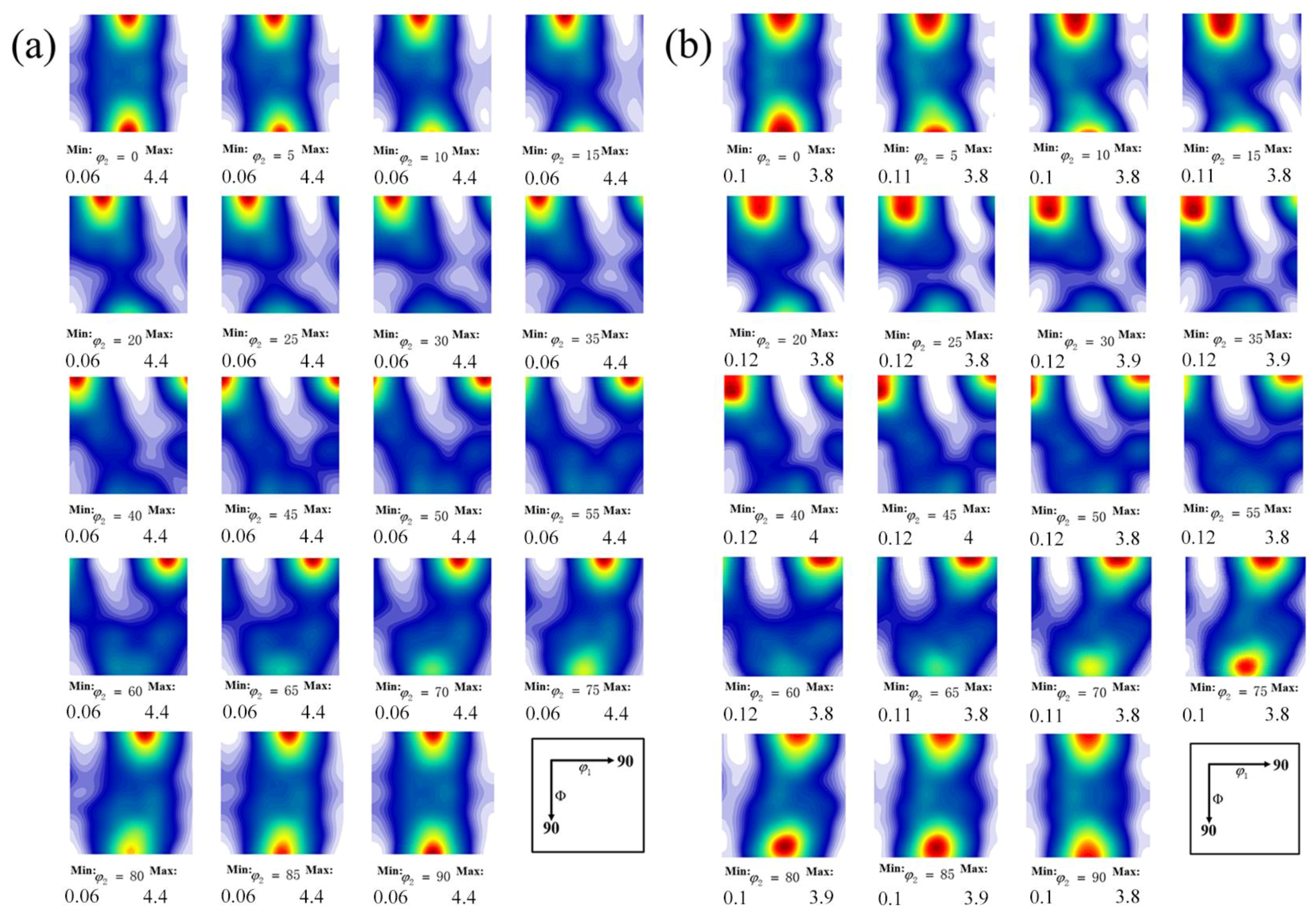
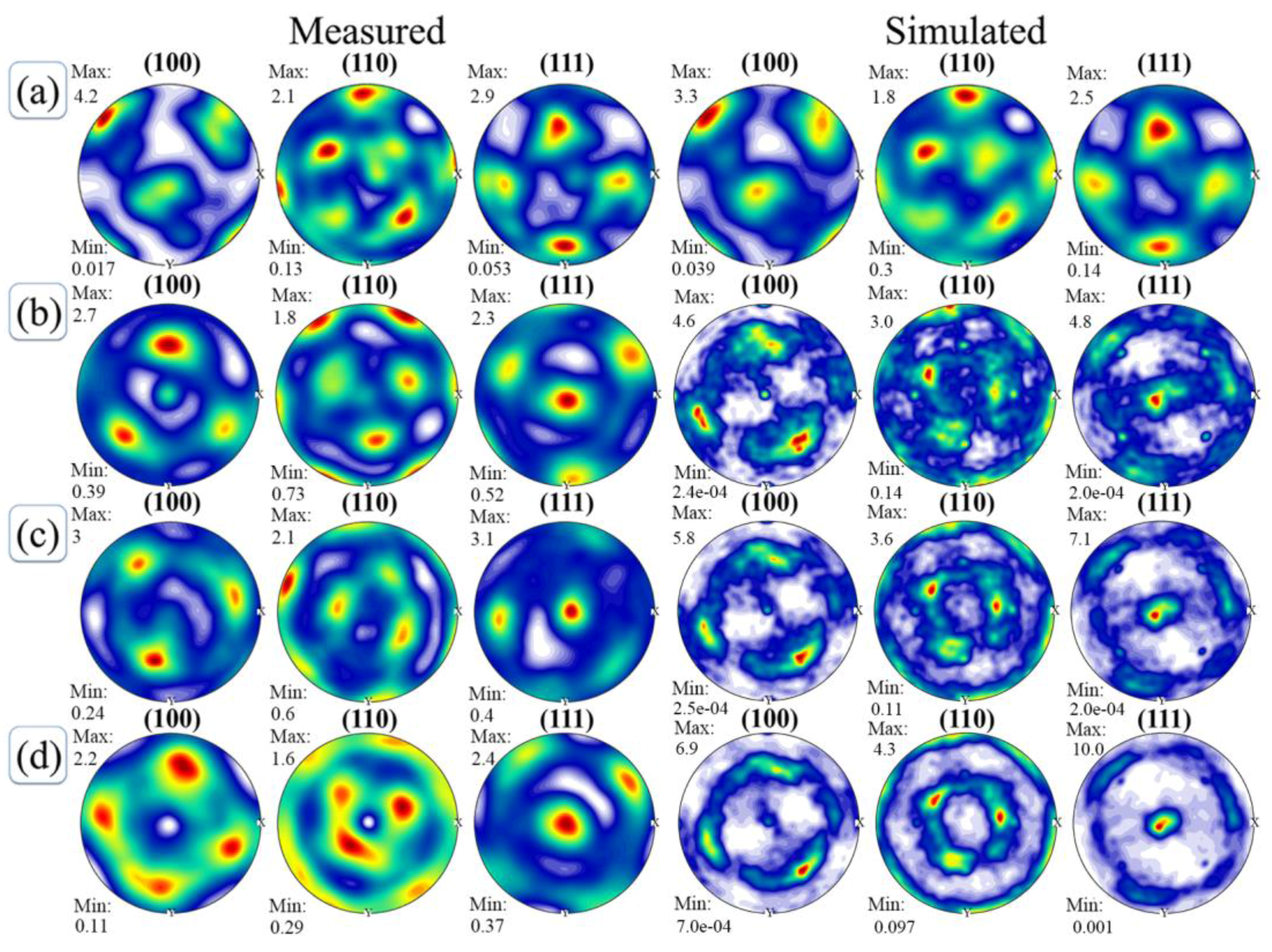
3.2.4. Texture Evolution of NiTi SMA under Uniaxial Compression
4. Conclusions
- (1)
- TEM observation demonstrates that dislocation slip rather than deformation twinning is responsible for plastic deformation mechanisms of B2 austenite NiTi SMA at 673 K (400 °C). EBSD experiment demonstrates the heterogeneous microstructure evolution during uniaxial compression, where subgrain substructures are formed and distributed within individual grains.
- (2)
- Based on the experimental observations, {110}<100>, {010}<100> and {110}<111> slip systems are introduced into the single-crystal constitutive equations in order to accommodate plastic deformation of NiTi SMA. Particle swarm optimization (PSO) algorithm is used to identify crystal plasticity parameters from experimental results of NiTi SMA. The validity of the fitted material parameters is well confirmed based on the fact that the simulated stress-strain curve on the basis of constructed Voxel RVE model is in good agreement with the experimental result.
- (3)
- CPFEM based on the constructed RVE model is able to accurately predict texture evolution of NiTi SMA during uniaxial compression deformation. The simulation results are in good agreement with the experimental ones. With the progression of plastic deformation, a crystallographic plane of NiTi SMA gradually rotates to be vertical to the loading direction, which lays the foundation for forming the <111> fiber texture.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vojtěch, D.; Michalcova, A.; Čapek, J.; Marek, I.; Dragounova, L. Structural and mechanical stability of the nano-crystalline Ni–Ti (50.9 at.% ni) shape memory alloy during short-term heat treatments. Intermetallics 2014, 49, 7–13. [Google Scholar] [CrossRef]
- Sharifi, E.M.; Karimzadeh, F.; Kermanpur, A. The effect of cold rolling and annealing on microstructure and tensile properties of the nanostructured Ni 50 Ti 50 shape memory alloy. Mater. Sci. Eng. A Struct. Mater. 2014, 607, 33–37. [Google Scholar] [CrossRef]
- Delobelle, V.; Chagnon, G.; Favier, D.; Alonso, T. Study of electropulse heat treatment of cold worked NiTi wire: From uniform to localised tensile behaviour. J. Mater. Process. Technol. 2016, 227, 244–250. [Google Scholar] [CrossRef]
- Hu, L.; Jiang, S.H.; Zhang, Y.Q.; Zhao, Y.N.; Liu, S.W.; Zhao, C.Z. Multiple plastic deformation mechanisms of NiTi shape memory alloy based on local canning compression at various temperatures. Intermetallics 2016, 70, 45–52. [Google Scholar] [CrossRef]
- Benafan, O.; Noebe, R.; Padula, S.; Garg, A.; Clausen, B.; Vogel, S.; Vaidyanathan, R. Temperature dependent deformation of the B2 austenite phase of a NiTi shape memory alloy. Int. J. Plast. 2013, 51, 103–121. [Google Scholar] [CrossRef]
- Duerig, T. Some unsolved aspects of Nitinol. Mater. Sci. Eng. A Struct. Mater. 2006, 438, 69–74. [Google Scholar] [CrossRef]
- Lin, Y.S.; Cak, M.; Paidar, V.; Vitek, V. Why is the slip direction different in different B2 alloys? Acta Mater. 2012, 60, 881–888. [Google Scholar] [CrossRef]
- Manchiraju, S.; Anderson, P.M. Coupling between martensitic phase transformations and plasticity: A microstructure-based finite element model. Int. J. Plast. 2010, 26, 1508–1526. [Google Scholar] [CrossRef]
- Yu, C.; Kang, G.; Kan, Q. A micromechanical constitutive model for anisotropic cyclic deformation of super-elastic niti shape memory alloy single crystals. J. Mech. Phys. Solids 2015, 82, 97–136. [Google Scholar] [CrossRef]
- Pelton, A.; Huang, G.; Moine, P.; Sinclair, R. Effects of thermal cycling on microstructure and properties in Nitinol. Mater. Sci. Eng. A Struct. Mater. 2012, 532, 130–138. [Google Scholar] [CrossRef]
- Ezaz, T.; Wang, J.; Sehitoglu, H.; Maier, H. Plastic deformation of NiTi shape memory alloys. Acta Mater. 2013, 61, 67–78. [Google Scholar] [CrossRef]
- Ezaz, T.; Sehitoglu, H.; Maier, H.J. Energetics of (114) twinning in B2 NiTi under coupled shear and shuffle. Acta Mater. 2012, 60, 339–348. [Google Scholar] [CrossRef]
- Zaki, W.; Moumni, Z. A three-dimensional model of the thermomechanical behavior of shape memory alloys. J. Mech. Phys. Solids 2007, 55, 2455–2490. [Google Scholar] [CrossRef]
- Auricchio, F.; Reali, A.; Stefanelli, U. A three-dimensional model describing stress-induced solid phase transformation with permanent inelasticity. Int. J. Plast. 2007, 23, 207–226. [Google Scholar] [CrossRef]
- Yu, C.; Kang, G.; Song, D.; Kan, Q. Micromechanical constitutive model considering plasticity for super-elastic NiTi shape memory alloy. Comput. Mater. Sci. 2012, 56, 1–5. [Google Scholar] [CrossRef]
- Suwas, S.; Ray, R.K. Crystallographic Texture of Materials; Springer: London, UK, 2014; pp. 11–38. [Google Scholar]
- Hill, R.; Rice, J. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Huang, Y.G. A User-Material Subroutine Incroporating Single Crystal Plasticity in the Abaqus Finite Element Program; Harvard University: Cambridge, MA, USA, 1991. [Google Scholar]
- Abdolvand, H.; Daymond, M.R.; Mareau, C. Incorporation of twinning into a crystal plasticity finite element model: Evolution of lattice strains and texture in zircaloy-2. Int. J. Plast. 2011, 27, 1721–1738. [Google Scholar] [CrossRef]
- Jiang, S.H.; Zhang, Y.Q.; Zhao, Y.N.; Tang, M.; Yi, W.L. Constitutive behavior of Ni-Ti shape memory alloy under hot compression. J. Cent. South Univ. Technol. 2013, 20, 24–29. [Google Scholar] [CrossRef]
- Cailletaud, G. A micromechanical approach to inelastic behaviour of metals. Int. J. Plast. 1992, 8, 55–73. [Google Scholar] [CrossRef]
- Diard, O.; Leclercq, S.; Rousselier, G.; Cailletaud, G. Evaluation of finite element based analysis of 3D multicrystalline aggregates plasticity: Application to crystal plasticity model identification and the study of stress and strain fields near grain boundaries. Int. J. Plast. 2005, 21, 691–722. [Google Scholar] [CrossRef]
- Lv, L.; Zhen, L. Crystal plasticity simulation of polycrystalline aluminum and the effect of mesh refinement on mechanical responses. Mater. Sci. Eng. A Struct. Mater. 2011, 528, 6673–6679. [Google Scholar] [CrossRef]
- Zhang, K.S.; Ju, J.W.; Li, Z.; Bai, Y.L.; Brocks, W. Micromechanics based fatigue life prediction of a polycrystalline metal applying crystal plasticity. Mech. Mater. 2015, 85, 16–37. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, X.; Wang, Y.; Hu, X.; Zbib, H.M. A mechanism-based model for deformation twinning in polycrystalline FCC steel. Mater. Sci. Eng. A Struct. Mater. 2014, 607, 206–218. [Google Scholar] [CrossRef]
- Lee, M.G.; Wang, J.; Anderson, P.M. Texture evolution maps for upset deformation of body-centered cubic metals. Mater. Sci. Eng. A Struct. Mater. 2007, 463, 263–270. [Google Scholar] [CrossRef]
- Xie, C.; Ghosh, S.; Groeber, M. Modeling cyclic deformation of HSLA steels using crystal plasticity. J. Eng. Mater. Technol. Trans. ASME 2004, 126, 339–352. [Google Scholar] [CrossRef]
- Cheng, J.; Ghosh, S. A crystal plasticity FE model for deformation with twin nucleation in magnesium alloys. Int. J. Plast. 2015, 67, 148–170. [Google Scholar] [CrossRef]
- Hasija, V.; Ghosh, S.; Mills, M.J.; Joseph, D.S. Deformation and creep modeling in polycrystalline Ti-6Al alloys. Acta Mater. 2003, 51, 4533–4549. [Google Scholar] [CrossRef]
- Esmin, A.A.; Coelho, R.A.; Matwin, S. A review on particle swarm optimization algorithm and its variants to clustering high-dimensional data. Artif. Intell. Rev. 2015, 44, 23–45. [Google Scholar] [CrossRef]


| Slip Mode | q | n | ||||
|---|---|---|---|---|---|---|
| {110}<100> slip system | 1283.29 MPa | 354.59 MPa | 134.53 MPa | 0.001 s−1 | 1.40 | 20 |
| {010}<100> slip system | 5191.62 MPa | 505.90 MPa | 489.93 MPa | 0.001 s−1 | 1.40 | 20 |
| {110}<111> slip system | 3574.64 MPa | 390.27 MPa | 239.58 MPa | 0.001 s−1 | 1.40 | 20 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, L.; Jiang, S.; Zhang, Y. A Combined Experimental-Numerical Approach for Investigating Texture Evolution of NiTi Shape Memory Alloy under Uniaxial Compression. Metals 2017, 7, 356. https://doi.org/10.3390/met7090356
Hu L, Jiang S, Zhang Y. A Combined Experimental-Numerical Approach for Investigating Texture Evolution of NiTi Shape Memory Alloy under Uniaxial Compression. Metals. 2017; 7(9):356. https://doi.org/10.3390/met7090356
Chicago/Turabian StyleHu, Li, Shuyong Jiang, and Yanqiu Zhang. 2017. "A Combined Experimental-Numerical Approach for Investigating Texture Evolution of NiTi Shape Memory Alloy under Uniaxial Compression" Metals 7, no. 9: 356. https://doi.org/10.3390/met7090356




