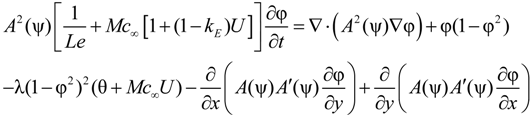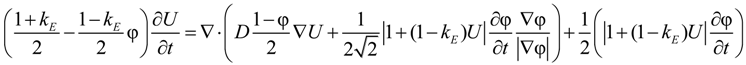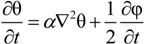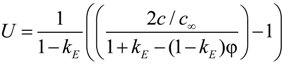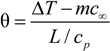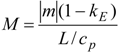1. Introduction
Dendritic solidification is a subject of enduring interest within the scientific community, both because dendrites are a prime example of spontaneous pattern formation and due to their pervasive influence on the engineering properties of metals. One long-standing problem with regard to the dendritic solidification of metals has been that of spontaneous grain refinement in undercooled pure melts, first reported to occur in Ni by Walker [
1] in 1959. At a well defined undercooling, Δ
T* = 140–150 K, Walker observed an abrupt transition from a coarse columnar grain structure to a fine equiaxed structure, with a reduction in grain size of at least one order of magnitude. Similar behavior was found in Co, with a value for Δ
T* of ≈180 K. This effect has subsequently been identified in other pure metals [
2,
3,
4] and in a range of alloy systems [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14], in which a more complex evolutionary sequence is often observed as the undercooling is increased. At low undercooling an initially columnar growth pattern is observed which gives way to an equiaxed grain structure as the undercooling is increased beyond a critical value, Δ
T1*. At yet higher undercooling a second region of columnar growth is observed which, in most of systems, is replaced by a second region of equiaxed growth at still higher undercooling, with the critical undercooling for this second grain refinement transition being Δ
T2*.
In many of the systems in which spontaneous grain refinement is observed simultaneous measurement of the dendrite growth velocity has also been undertaken. As first demonstrated by Willnecker
et al. [
2] in levitation melted Ni, such measurements reveal an apparent correlation between the velocity-undercooling relationship and grain refinement. Below Δ
T*, growth velocity can be adequately represented by current dendrite growth models, with
V ∝ Δ
Tβ, β > 1. Above Δ
T* the velocity-undercooling relationship is approximately linear. In alloy systems this transition is usually observed to occur coincident with the Δ
T2* transition. In most cases the transition to a grain refined microstructure at the lower undercooling, Δ
T1*, does not appear to have any obvious signature in the velocity undercooling curve. Moreover, differences between the as-solidified microstructures of the two grain refined regions indicate that there may be subtle differences in the underlying grain refinement mechanism. In the grain refined structures, found at high undercooling, the solute segregation pattern is spheroidal about a small dendrite fragment, whereas in grain refined materials formed at low undercooling some of the grains appear to contain small, but well developed, equiaxed dendritic structures [
15].
The origins of the effect are controversial. Early theories suggested a range of mechanisms which included nucleation ahead of the solidification front induced by the pressure pulse associated with solidification [
1], recrystallisation, either during or immediately after solidification [
16,
17], or the role of minor solute additions [
18,
19,
20]. However, more recent theories regarding the origin of this phenomenon tend to invoke fragmentation of the primary crystal, either during [
21,
22] or immediately after [
23,
24] recalescence. Such fragmentation might be aided by flow in the melt [
25], with many samples being subject to significant electromagnetic stirring [
26] due to the heating/levitation fields used in containerless processing of undercooled melts. We have argued previously that the occurrence of a discontinuity in the velocity-undercooling curve [
2,
27] coincident with the onset of grain refinement would tend to suggest the former of these possibilities is more likely, as would an apparent change in the morphology of the growth front revealed by high-speed imaging [
28]. Specifically, we have suggested that a tip-splitting instability at the dendrite tip leads to the growth of an unstable “dendritic seaweed” structure, which subsequently remelts to give the observed grain-refinement. Phase-field modeling of the thermally controlled solidification of a pure material at high undercooling [
29] appear to support this suggestion, as does the observation, in deeply undercooled ultra-high purity Cu, of a “frozen in” seaweed morphology [
30] above some critical undercooling. Moreover, above this critical undercooling a discontinuity in the velocity-undercooling curve was observed identical in character to that found in materials that display spontaneous grain refinement. Such a “seaweed” morphology might come about due to a competition between differently directed capillary and kinetic anisotropies. Microstructure selection maps (in undercooling-anisotropy space) produced by Brener
et al. [
31] using solvability theory indicate a range of such transitions should occur, while simulations by Haxhimali
et al. [
32] have suggested that many common metals may lay close to the dendritic–“seaweed” transition. One such transition has been observed directly as a function of composition in Al-Zn alloys by Dantzig
et al. [
33]. A range of undercooling mediated growth direction transitions have also been observed by Castle
et al. [
34] in Cu-10at.% Ni alloy, in which 4-, 6- and 8-fold symmetric dendrites are observed as the undercooling is progressively increased, with 4-fold symmetry finally being recovered at the highest undercoolings achieved, providing strong evidence for velocity mediated transitions in the growth direction. In some samples ‘dendritic seaweed’ was observed as an intermediate structure between these transitions.
However, the dendritic fragmentation model of Schwarz
et al. [
23,
24] is perhaps still the most widely accepted model for spontaneous grain refinement. The model postulates that two characteristic timescales can be defined for dendritic growth from an undercooled melt. The first is the breakup time, τ
bu, which is the time required for fragmentation of the side branches due to remelting and Rayleigh instability and is a monotonic function of the dendrite trunk radius, with small radii giving short breakup times. If, as seems likely from observations of dendritic growth in transparent systems such as xenon [
35], dendrites are self-similar when scaled by the tip radius, ρ, this is equivalent to τ
bu being a monotonic function of ρ. The second timescale is the plateau time, τ
pl, which is the time the melt remains at, or around, the melting temperature during recalescence and is determined by the macroscopic heat extraction rate. The theory postulates that grain refinement occurs when τ
bu < τ
pl, which corresponds to the tip radius being below some critical value, ρ*, determined by the heat extraction rate. Consequently, if it is assumed that ρ varies with undercooling as predicted by marginal stability theory [
36,
37] the model appears to offer a natural explanation for there being a single grain refinement transition in pure materials and two transitions in alloy systems (see
Figure 1). However, in this model the transition in the velocity-undercooling curve coincident with the onset of grain refinement is assumed to be fortuitous, which seems unlikely given the number of different systems in which it has been observed. Questions have also been raised over the proposed break-up model, with a reworking of the stability analysis [
38] showing that the postulated re-melting is much less likely to occur within an array of dendrites than would be the case for an isolated dendrite. In deed, once the fraction solid within the array exceeds 35% it was shown that remelting could not occur, which would tend to rule out such a mechanism being responsible for spontaneous grain refinement in most systems, as the observed undercooling at which the transition occurs would give a solid fraction in excess of this.
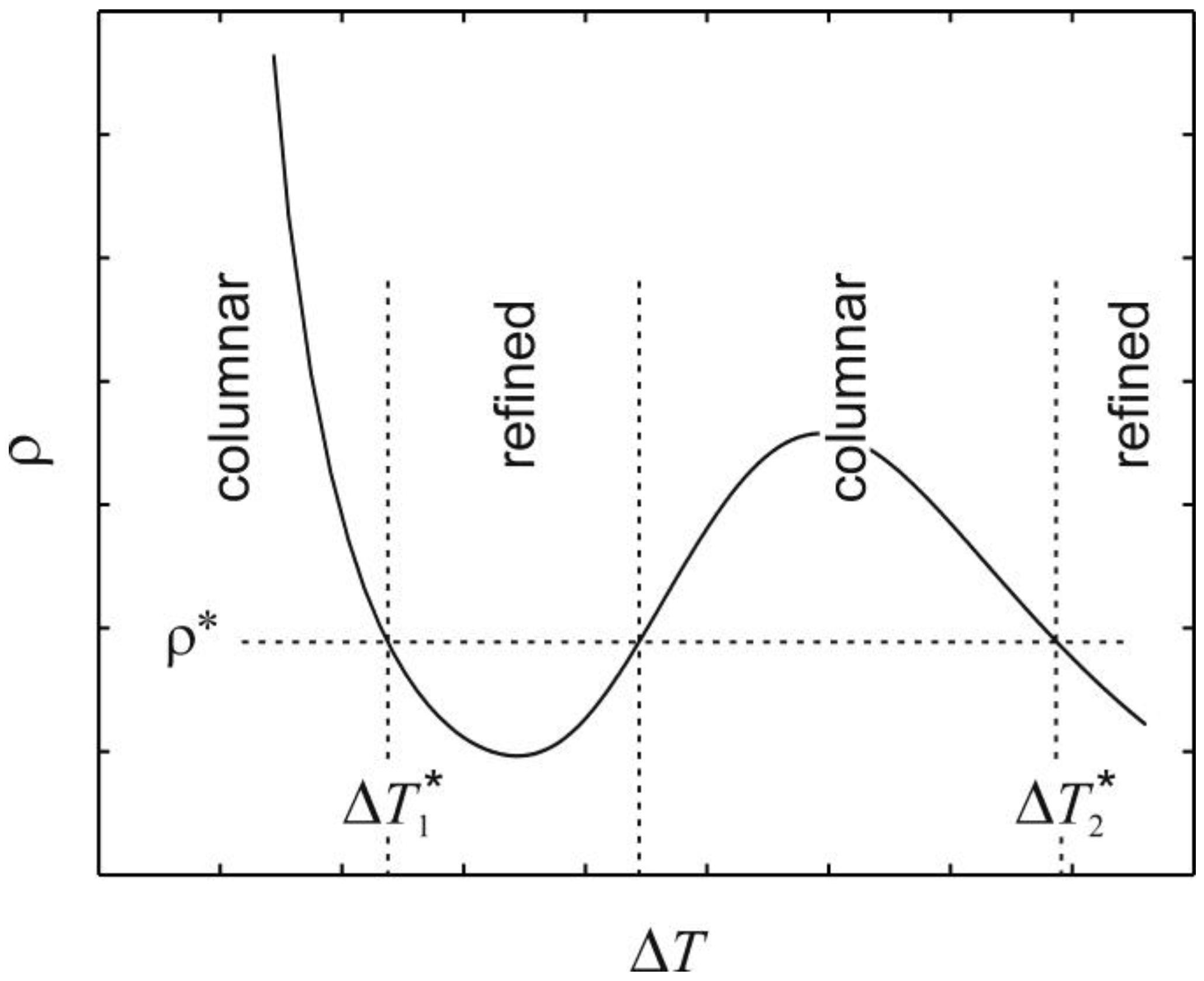
The dependence of the dendrite tip radius upon undercooling as predicted by marginal stability theory for alloy systems, with its characteristic local minimum followed by a local maximum, has very much been a cornerstone of rapid solidification theory for the past 20 years. However, since the advent of microscopic solvability theory [
39,
40] there can be considered to be no theoretical basis for marginal stability theory and the experimental evidence in support of the existence of either a local minimum, or a local maximum, in the tip radius is scant. Transparent analogue casting alloys, such as succinonitrile-acetone, in which direct measurement of the dendrite tip radius is possible [
41], can only be undercooled by very small amounts so that the predicted undercooling range in which a local minimum might be observed is not accessible. In metallic systems only an indirect estimate of the tip radius is possible, generally by assuming that some characteristic microstructural length-scale, such as the grain size or dendrite trunk radius, where observable, scales as a constant multiple of the tip radius. However, although there is plentiful evidence of an initial decrease in microstructural length scale in the low undercooling region, it has proved almost impossible to make a continuous extension of such an analysis into the high undercooling regime where the presence of a local minimum might be inferred.
Figure 1.
Schematic illustration of the dendrite tip radius, ρ, as a function of undercooling, Δ
T, in an alloy system, according to the model of Lipton, Kurz and Trivedi [
37]. Also shown is how this relates to the grain refinement in the model of Schwarz
et al. [
23]. It is assumed that for a particular macroscopic heat extraction rate there will be a critical radius, ρ*, below which remelting of the dendrite will occur. If the form of the radius curve obtained from [
37] is correct this would lead to two grain refinement transitions.
Recently though it has become possible to use quantitative phase-field modeling to simulate the growth of dendrites under coupled thermo-solutal control [
42,
43], breaking the previous reliance on marginal stability models for estimating the tip radius in alloy systems where growth is sufficiently rapid that the isothermal approximation is no longer valid. Such coupled thermo-solutal simulations are extremely computationally challenging due to the severe multi-scale nature of the problem and it is only with the application of advanced numerical techniques such as adaptive meshing, implicit time-stepping and efficient multigrid solvers [
44] that investigations into dendritic growth in undercooled alloy systems have become feasible over significant regions of the available parameters space, including at high Lewis number [
45] (Lewis number,
Le, is the ratio of the thermal to solutal diffusivity, α/
D). In fact, such studies appear to indicate that, although the occurrence of a local minimum in ρ as the undercooling is increased is indeed ubiquitous in the solidification of alloy systems, as predicted by marginal stability theory, a subsequent local maximum in ρ at yet higher undercooling is not [
46]. In fact, in a systematic study of the calculated radius-undercooling behavior of alloy systems as a function of alloy concentration, partitioning strength and Lewis number [
47] were unable to identify any part of the studied parameter space in which a maximum in ρ could be observed as the undercooling was increased.
These calculations of the dendrite tip radius in undercooled alloy systems present a potentially serious problem for the accepted model of spontaneous grain refinement in alloy systems. If the radius does not display a local maximum as the undercooling is increased, then it is difficult to reconcile how a break-up time that scales monotonically with tip radius can predict two region of grain refined microstructure, nor indeed why the growth of grain refined structures above Δ
T1* should give way to columnar growth as the undercooling is increased. However, these calculations also revealed that the tip selection parameter, σ*, did show this pattern of local minimum followed by local maximum as the undercooling were increased. In fact, qualitatively, the similarities between the behavior of σ* as predicted by the phase-field model and the form of the curve shown in
Figure 1 are remarkable. Here, and as in a recent presentation at the MCWASP XIII Conference [
48], we explore whether this behavior observed in σ* has any bearing on the phenomenon of spontaneous grain refinement.
2. Description of the Model
The model adopted here is based upon that of [
42] in which, following non-dimensionalization against characteristic length and time scales,
W0 and τ
0, the evolution of the phase-field, φ, and the dimensionless concentration and temperature fields
U and θ are given by
where, for 4-fold growth,
A(ψ) = 1 + εcos(4ψ),
d0 is the chemical capillary length,
kE is the partition coefficient
L and
cp are the latent and specific heats respectively and λ is a coupling parameter given by λ =
D/
a2 =
a1W0/
d0 with
a1 and
a2 taking the values 5√2/8 and 0.6267 respectively [
49].
U and θ are related to physical concentration,
c, and temperature,
T, via
and
where
m is the slope of the liquidus line, which has dimensionless form
The governing equations are discretized using a finite difference approximation based upon a quadrilateral, non-uniform, locally-refined mesh with equal grid spacing in both directions. This allows the application of standard second order central difference stencils for the calculation of first and second differentials, while a compact 9-point scheme has been used for Laplacian terms, in order to reduce the mesh induced [
50] anisotropy. To ensure sufficient mesh resolution around the interface region and to handle the extreme multi-scale nature of the problem at high Lewis number local mesh refinement (coarsening) is employed when the weighted sum of the gradients of φ,
U and θ exceeds (falls below) some predefined value.
It has been shown elsewhere that if explicit temporal discretization schemes are used for this problem the maximum stable time-step is given by Δ
t ≤
Ch2, where
h is the mesh spacing on the finest level and
C =
C(λ,
Le, Δ
T), with
C varying from ≈0.3 at
Le = 1 to
C ≤ 0.001 at
Le = 500 [
51], leading to unfeasibly small time-steps at high Lewis number. Consequently, an implicit temporal discretization is employed here based on the second order Backward Difference Formula with variable time-step.
When using implicit time discretization methods it is necessary to solve a very large, but sparse, system of non-linear algebraic equations at each time-step. Multigrid methods are among the fastest available solvers for such systems and in this work we apply the non‑linear generalization known as FAS (full approximation scheme [
52]). The local adaptivity is accommodated via the multilevel algorithm originally proposed by Brandt [
53]. The interpolation operator is bilinear while injection is used for the restriction operator. For smoothing the error we use a fully-coupled nonlinear weighted Gauss-Seidel iteration where the number of pre- and post-smoothing operations required for optimal convergence is determined empirically [
50]. Full details of the numerical scheme are given in [
44,
50,
54].
3. Results
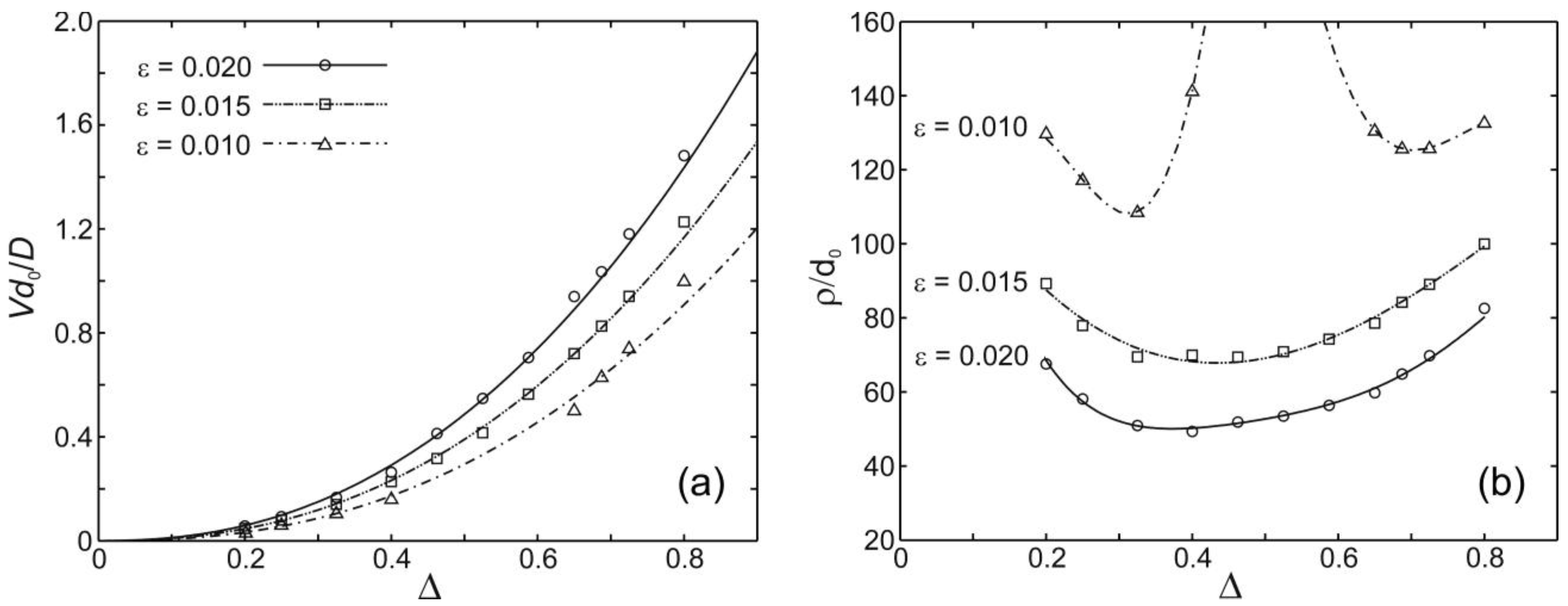
Figure 2 shows the variation of (a) the dendrite tip velocity,
V, and (b) the equivalent parabolic [
43] tip radius, ρ, as a function of the dimensionless undercooling, Δ, for three values of the anisotropy parameter ε, namely 0.020, 0.015 and 0.010.
Figure 3 shows the effective radius selection parameter, σ*, calculated using the methodology described in [
43]. Except for the anisotropy parameter all three sets of simulations were run under identical conditions with
Mc∞ = 0.05,
Le = 200, λ = 1 and
kE = 0.3. All simulations are run on a domain of Ω = [−1600:1600]
2 using a maximum of 12 levels of refinement, giving a minimum mesh size,
h, of 0.78. This is equivalent, were a uniform mesh to have been used, of a mesh size which is 2
12 × 2
12. For each parameter set simulations were run over the undercooling range Δ = 0.2–0.8. Below Δ = 0.2 growth is very slow leading to excessive computation times while above Δ = 0.8 the requirement that
W0V/
D << 1 is not satisfied.
At ε = 0.020 the results are as previously reported, with the velocity increasing monotonically with undercooling and displaying, to a very good approximation, a power-law dependence with exponent ≈2.3. The radius displays a minimum at intermediate undercooling and subsequently increases at high undercooling. This results in an operating point parameter, σ*, which initially decreases with increasing undercooling, before passing through a local minimum to increase with undercooling. At yet higher undercooling σ* passes through a local maximum so at the highest undercoolings studied σ* is decreasing rapidly with increasing undercooling. We have previously argued [
47] that this behavior can be rationalized if the competition between solutal and thermal control of dendritic growth is manifest not in the tip radius, as for instance is evident in marginal stability models of dendrite growth [
37], but in the operating point parameter, σ*. We also note that in the limit Δ→0, we find σ* ≈ 0.07, in good agreement with [
43].
Figure 2.
(a) The dendrite growth velocity (b) and tip radius as predicted by the phase-field model as a function of undercooling and anisotropy strength.
Figure 3.
Calculated operating point parameter, σ*, as predicted by the phase field model as a function of undercooling and anisotropy strength. At ε = 0.01 stable dendritic growth is not observed in the undercooling range 0.4625 ≤ Δ ≤ 0.5875. Instead a tip-splitting instability leads to the growth of ‘dendritic-seaweed’. It is suggested that remelting of this seaweed structure gives rise to the grain-refined microstructures observed at low undercoolings.
If we now consider reducing the anisotropy strength from ε = 0.020 to ε = 0.015 the effect on the radius and velocity is broadly in line with what we might expect. The radius follows the same trend as at the higher anisotropy level, but with a larger radius being observed at all undercoolings. This is to be expected as σ* is a monotonically decreasing function of ε. The velocity is correspondingly reduced, in line with the expectation that the Peclet number is only very weakly dependent upon ε. σ* is reduced at all undercoolings and, like the tip radius, displays the same general form as at the higher anisotropy level, although in this case we note that the difference between the minimum and maximum values is also significantly reduced.
Finally we consider a further reduction in the anisotropy strength to ε = 0.010, wherein a significant change in behavior is observed. If we consider the behavior of σ* first we observe that, in line with expectation, the value for Δ→0 is reduced, and as with the curves for ε = 0.020 and 0.015, the value of σ* initially decreases as Δ is increased. However, for undercooling between Δ = 0.4625 and 0.5875 stable dendritic growth was not observed, with the solid nuclei used to seed solidification initially developing a preferred four-fold growth morphology but then experiencing a bifurcation at the tip which ultimately leads to a tip-splitting instability in the growing crystal (doublon formation), mediating a transition from a dendritic to ‘dendritic seaweed’ morphology. As a consequence of this tip splitting instability, in the undercooling range Δ = 0.4625–0.5875 neither a value for ρ nor σ* could be obtained. At undercoolings above Δ = 0.5875 stable dendritic growth is once again established. From the values of σ* either side of this undercooling range it appears that this growth instability is consistent with a collapse to zero in the value of σ*. For undercoolings either side of this unstable range the measured tip radius appears to be abnormally large, which is also consistent with the hypothesized collapse of σ*, with small σ* giving rise to large values of ρ. In the unstable growth regime we have not attempted to determine a characteristic growth velocity as the instantaneous growth rate is subject to significant fluctuations as the morphology of the tip changes. However, once stable dendritic growth is re-established in the high undercooling regime, we note that the measured velocities are consistent with a power-law relationship with the same exponent as in the low undercooling regime.
4. Discussion
The breakdown of dendritic growth in phase-field simulations of solidification at high undercooling has been noted by a number of groups and has generally been attributed to a competition between capillary and kinetic anisotropies, with capillary effects dominating at low undercooling and kinetic effects dominating at high undercooling. In the case where these anisotropies are oppositely directed, doublon or dendritic seaweed morphologies, which are characteristic of growth at low anisotropy, may be observed when the competing effects are of similar magnitude. However, we do not believe that this is the case here. Firstly, the model has been constructed in the thin-interface limit, wherein the choice of parameters adopted here should eliminate all kinetics from the model and, secondly, the stable dendritic growth observed in the high undercooling regime has the same orientation as in the low undercooling regime (i.e., in both cases the dendrite arms are oriented towards the sides of the computational domain, which is the direction of the applied capillary anisotropy). This is inconsistent with an oppositely directed kinetic anisotropy which, if present, would result in growth directed towards the corners of the computational domain. By setting ε = 0 the model has also been tested at all undercoolings considered here to determine whether there are effects resulting from mesh induced anisotropy, and this appears not to be the case.
For the ε = 0.010 case given in
Figure 3, the maximum in σ* observed at higher anisotropies is quite poorly developed, possibly by virtue of being shifted to somewhat higher undercooling than for the higher anisotropy simulations. Therefore, in the particular case considered here a second region of dendritic seaweed growth was not observed at higher undercoolings within the undercooling range considered. This may be an artifact of the rather low Lewis number (
Le = 200) used in these simulations. In most metals
Le is typically of the order 10
4 while in [
47] we report that increasing the Lewis results in a more pronounced maximum in σ* and a steeper decline at high undercooling. It is currently a matter for investigation as to whether or not such simulations do result in a second region of doublon formation, although the simulations become much more computationally intensive as the Lewis number is increased due to the multi-scale nature of the problem.
Finally, we illustrate how the formation of doublons or dendritic seaweed might give rise to grain refined microstructures. An example of a dendritic seaweed morphology is shown in
Figure 4a. We assume that immediately following rapid growth of the seaweed the system temperature reaches a value close to the equilibrium liquidus and partial remelting of the solid takes place. The remelted solid then solidifies slowly as heat is lost at a rate imposed by the external conditions (which in undercooling, as opposed to rapid quenching, experiments might be quite slow).
Figure 4b illustrates the kind of morphology that might result. Here we have used the phase field model to remelt and then solidify the region of seaweed in
Figure 4a shown within the white box. We have assumed that recalescence brings the system back up to the liquidus temperature for a period corresponding to ≈0.2 ms followed by re-solidification which we have arbitrarily stopped at a solid fraction of 77% so that the locations of the residual liquid channels, which will upon completion of solidification become grain boundaries, can easily be observed. It can be seen from the figure that a large number of small grains would in deed be produced by the remelting process, with the result that a structure very like that observed in spontaneous grain refinement is formed. In contrast, when a normal dendritic morphology is subject to remelting the usual sequence is for the side arms to melt off leaving the continuous primary trunk intact, which does not lead to a grain refined structure. One expected consequence of this would be that grains arising from neighbouring seaweed branches would have similar, but not identical crystallographic orientations, which in the as-solidified sample would lead to a high density of low-angle grain boundaries (LAGB). Recent analysis of undercooled Co-Pd [
55] and Ni-Pd [
54,
56] alloys by Xu
et al. found just such evidence for a high density of LAGB’s, although they took this as being evidence for a recrystallisation mechanism for grain refinement, rather than remelting, on the assumption that the underlying structure preceding remelting was dendritic. However, their result would be consistent with a remelting model if the original solidification structure prior to remelting were seaweed, rather than conventional dendrites. We therefore conclude that a switch to a doublon or dendritic seaweed morphology due to the collapse to zero of σ* as identified here, followed by post-recalescence remelting, presents a plausible explanation for grain refinement at low undercooling, and possibly at high undercooling as well, although this remains subject to further simulation.
Figure 4.
(a) Phase-field simulation illustrating how remelting of a dendritic seaweed structure (a) can give rise (b) to a grain refined structure.