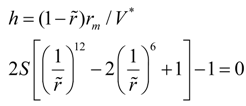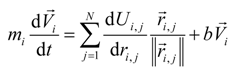1. Introduction
Friction is an important component of the physical processes in nature and technology. It is, however, difficult and inconsistent in demonstrations: On the one hand it is impossible to walk without friction and on the other hand about a third of produced energy is lost on friction.
An uncircumscribed field of action in chemistry, biology and physics was discovered in 1985 together with discover the new form of carbon, named fullerene. Later, a set of materials with great potential importance in tribology was discovered, such as the nanotube, the fullerene and fullerene-like nano-onions and others. According to the Stribeck curve [
1] there are three categories of lubrication: boundary lubrication, mixed lubrication and hydrodynamic lubrication. Nanotechnologies adopt well in boundary and mixed lubrication. A group of researchers studied molecular monolayer thickness lubricating film. Combination of rolling and sliding molecular friction mechanism is a principal question in friction the decrease of loses [
2]. In addition it was found that the addition of fullerene-containing materials to lubricating oils improves the antiwear [
3] and the antifriction [
1] properties.
The hydrodynamic theory of lubrication, the main points of which were formulated over a century ago, uncovered one of the most efficient ways to decrease friction losses in the bearing. Those basics are permanent and simple [
4,
5], but modern science of new materials seems to decrease average friction losses. Perhaps the mechanism of fluid friction can be demonstrated not only by liquids, but also by ultrafine particles with a set of specific physical properties and it will allow researchers to discover additional methods of friction reduction.
This paper presents a theoretical study of the motion of microscopic particles of a lubricating layer of about 10 molecules thick in the journal bearing. The main objective is to define the basic parameters of a computational experiment which will provide satisfactory convergence of the result. The problem is solved by known methods of molecular dynamics [
6], which allow us to simulate the motion of 10
3–10
6 particles during a 10
−6–10
−9 s in this stage of computer technology development. These restrictions prevent us from studying the macroscopic objects in the usual time slots, but help to clarify many important physical laws.
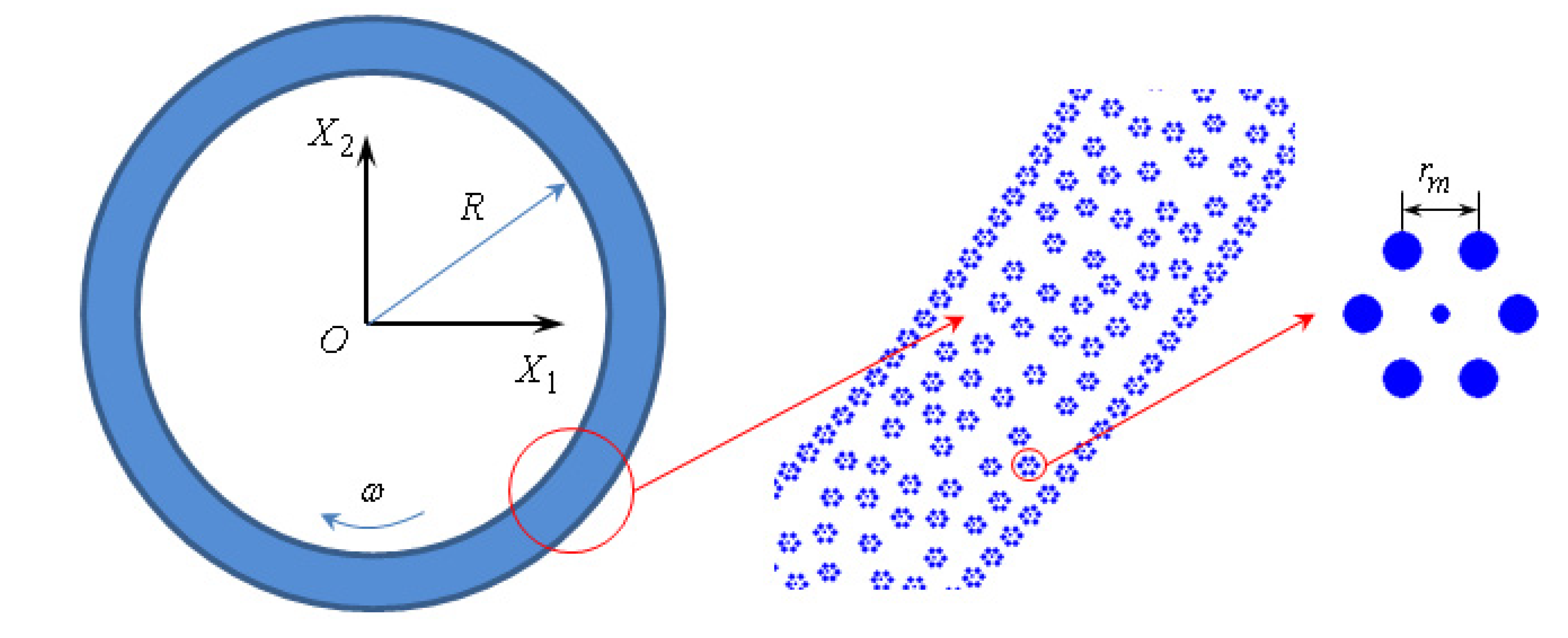
2. Molecular Model of Fullerene-Like Lubricant and Journal Bearing
The two-dimensional model of the molecule of fullerene-based lubricant is formed as a hexagon with a radius of the circumscribed circle of 3.5 A, which corresponds to the radius of the fullerene C
60. At the vertices of the hexagon there are atoms that are similar in physical properties to carbon atoms. The central atom compensates stiffness and mass of the volumetric fullerene molecule C
60 in its 2nd model. Such a two-dimensional model was used in the study of the motion of a monolayer fullerene lubricant between the parallel walls [
7].
According to the molecular dynamics approaches, it is assumed that the interaction of any two atoms is determined only by the distance between them, and that the superposition principle holds true for interaction of many atoms [
6]. This dual atomic interaction can be conveniently described by the potential of Lennard-Jones [
6]:
Where
ri,j—the distance between
i-th and
j-th atoms, m;
ξ—characteristic energy that determines the depth of the potential well, J;
σ—characteristic length that determines the distance with zero energy, m.
The state with the lowest energy corresponds to the distance between the atoms rm = 21/6σ. This is evident from the Equation (1).
The movement of the set of atoms in the molecule as a result of intramolecular and intermolecular interaction is determined by many of the classical equations of motion:
where
mi—the mass of the atom, kg;
The solution of the set of Equation (2) is convenient to carry out by the method of finite differences. The derivative of the left-hand side of the Equation (2) is approximated by the difference analogue of finite difference schemes [
6], the derivative of the right-hand side of Equation (2) can be determined analytically.
Under the terms of the hydrodynamic lubrication theory, in order to create the effect of hydrodynamic lubrication the lubricant is required to have the property of viscous internal friction and the ability to “stick” to the surface of the bearing [
5]. The presence of the inner friction in the lubricant moving according to Equation (2) will be determined by numerical experiment and fulfillment of an adhesion condition is guaranteed because the surface of the bush and the trunnion are modeled as a set of closely spaced molecules of lubricant (
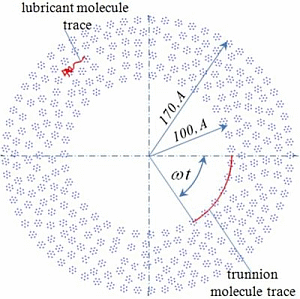
Figure 1). The central atoms of the molecules on the trunnion and on the bush are rigidly fixed, the movement of the other atoms in the molecules on the trunnion and on the bush is determined by solving the equations of motion (2). Thus, the bearing represents as a set of “adhered” lubricant molecules on its surface. The lubricating layer is formed by plurality of molecules in the gap between the trunnion and the bush, the initial position is randomly selected (
Figure 1). Initial velocity of the molecules of lubricant can be determined from the thermodynamic connection between temperature and the kinetic energy of the molecules [
6].
Figure 1.
Two-dimensional model of journal bearing lubricated with fullerene.
Figure 1.
Two-dimensional model of journal bearing lubricated with fullerene.
3. Research of the Convergence of the Numerical Solutions
The movement of all molecules or atoms except the central atoms of molecules on surfaces of the trunnion and the bearing bush is determined by numerically solving of the set of the Equation (2). At each point of time, acceleration, speed and position are defined for each atom. To obtain the correct result it is necessary that during the step Δ
t =
h the calculated atom should not have time to approach too close to another atom, as in this case their potential energy may rise, resulting in a sharp increase of atoms’ velocity in the next step and subsequent “explosion” of the molecules. Therefore, depending on the geometric and kinematic parameters of the bearing and the physical properties of the lubricant, it is necessary to determine size of the time step in advance. Such evaluation can be made by means of the apparatus of the similarity theory and dimensional analysis [
5].
It is convenient to consider the case of one-dimensional motion of two atoms along a straight line. This assumes a situation in which the atoms move in opposite directions and at the time
t0 the distance between them is equilibrium
r =
rm, and the modules of their velocities are equal to some characteristic velocity
V* = ω
R. This value corresponds to the circumferential velocity of the molecules on the surface of the trunnion with radius
R (
Figure 1). It is required to determine the period of time enough to stop the atoms fully. Since the interaction of atoms is potential, the law of conservation of mechanical energy in dimensionless variables takes the form:
Where
![Lubricants 02 00001 i005]()
—dimensionless velocity of atoms;
![Lubricants 02 00001 i006]()
—dimensionless criterion of the energy balance of atoms;
![Lubricants 02 00001 i007]()
—dimensionless distance between atoms.
It is further assumed that from time
t0 to time of atoms stop is one time step Δ
t =
h and during this period of time the value of acceleration is constant and the speed decreases linearly from the value
V* to zero. The value of the time step can be found by a joint decision of the two equations:
The Equation (4) shows that the value of the characteristic length σ does not affect the convergence of numerical solutions. Graphically the dependence of the time step on the dimensionless energy balance criterion is presented in
Figure 2.
The proposed procedure allows identifying only the necessary conditions of correct solutions and helps to assess the computational complexity of the problem in advance, for example, an approximate value of time needed for a calculation.
Figure 2.
The dependence of the time step h on the criteria S for different values of the properties ξ/m, (1) −ξ/m = 2.3, J/kg; (2) −ξ/m = 0.23, J/kg; (3) −ξ/m = 23, J/kg.
Figure 2.
The dependence of the time step h on the criteria S for different values of the properties ξ/m, (1) −ξ/m = 2.3, J/kg; (2) −ξ/m = 0.23, J/kg; (3) −ξ/m = 23, J/kg.
4. Fullerene-Based Journal Bearing Simulation
The character model with fullerene-bearing lubricant was investigated using a program developed by the authors in the environment “GNU-Octave” [
8]. The program is based on an algorithm described in Chapter 2 of the present article. A series of numerical experiments with the use of Euler circuits, Euler-Cromer [
6] and Adams-Bashforth [
5] showed the best convergence and stability of solutions to the Euler-Cromer scheme. Perhaps this is due to the fact that the motion of each atom is essentially a forced oscillation nearly the equilibrium state. Euler-Cromer scheme works well exactly in the problems of oscillations.
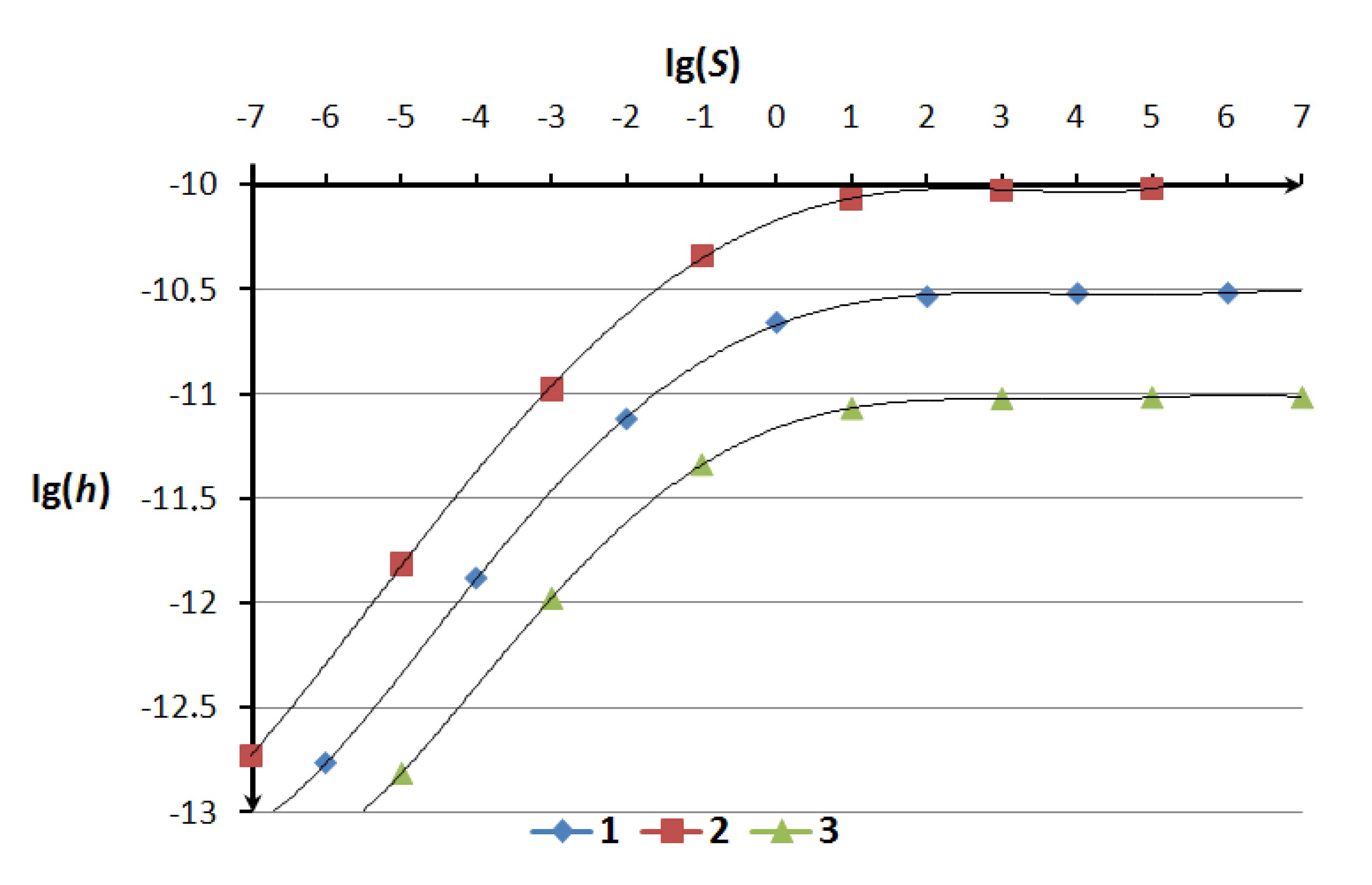
The flow chart of the simulation program is presented on
Figure 3.
Block 1 “Input data” represents input source data, such as journal bearing sizes, trunnion position and its angular velocity, number of molecules and their properties, process duration and others.
Block 2 “Initial conditions” is a subprogram which determines initial position and velocity of all molecules.
Block 3 “Time event loop” is the FOR-loop of I = 1…N, where N—is predefined in “Block 1” number of time steps.
Block 4 “Contact detecting” is a subprogram which determines the intramolecular interaction condition by means of comparison the distance between each pair of molecules and predefined no-acting distance (a multiple of rm as usual) and summary force of intramolecular interaction on each acting atom.
Block 5 “Inner reactions” is a subprogram which determines intermolecular interaction forces of atoms motion.
Block 6 “Atoms event loop” is the double FOR-loop with outer cycle of ci = 1…Ng and inner cycle of bi = 1…ng, where Ng and ng—are predefined in “Block 1” number of molecules of fullerenes and number of atoms in each molecule respectively.
Block 7 “Equations of motion solver” represents equations of motion (2) solver by various algorithms.
Block 8 “Output data” represents the results in matrix and graphics.
Figure 3.
The flow chart.
Figure 3.
The flow chart.
The first set of numerical experiments was carried out to study of the convergence of solutions depending on the size of the time step and validation of an approximate estimate of step by the criterion of the energy balance and the Equation (4). We examined the journal bearing with the following characteristics: The radius of trunnion is
R = 100 A; angular velocity ω = 10
7 rad/s; the mass of the lubricant atom is
ma = 12 Da; the mass of the lubricant molecule
mm = 60
ma; radius of the lubricant molecule
r = 3.5 A; parameters of the potential Lennard Jones [
9] ξ = 275/
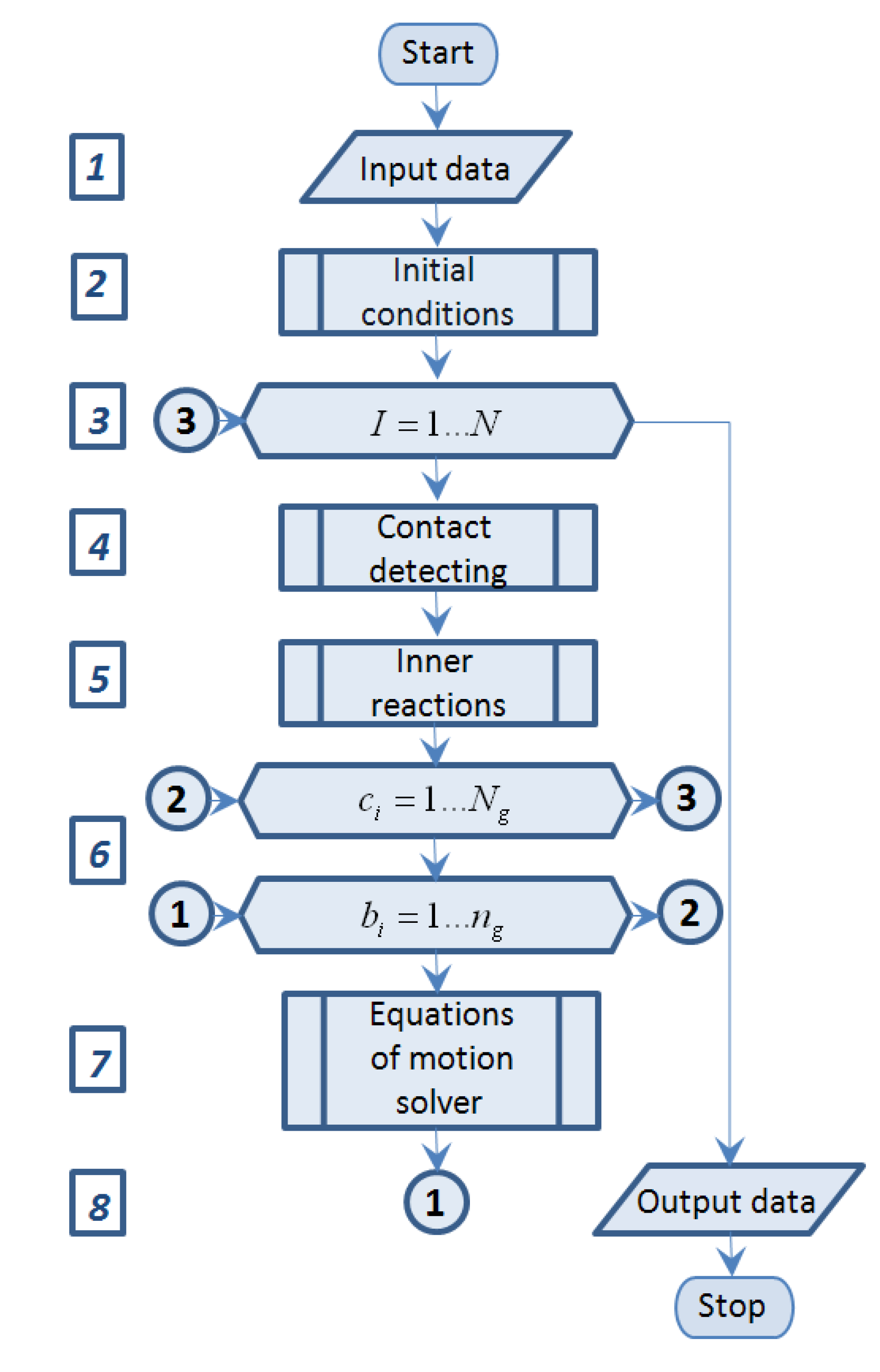
NA J, and σ = 3.47 A. In the process of calculation we controlled the motion of a single molecule of grease that is in contact with the bush and trunnion of bearing. At a certain point of time the value of the modulus of the molecule velocity was fixed for different values of time step. The results of a series of numerical experiments are presented in
Figure 4. The vertical line in the figure indicates the value of the time step, calculated according to the Formula (4). The figure shows that the value of the step recommended by Equation (4) provides sufficient convergence of result (indicated by a vertical line on the chart). It should also be noted that an increase of recommended magnitude of step by one order leads to the “explosion” of molecules in motion, and a decrease by one to two orders of magnitude improves convergence of results.
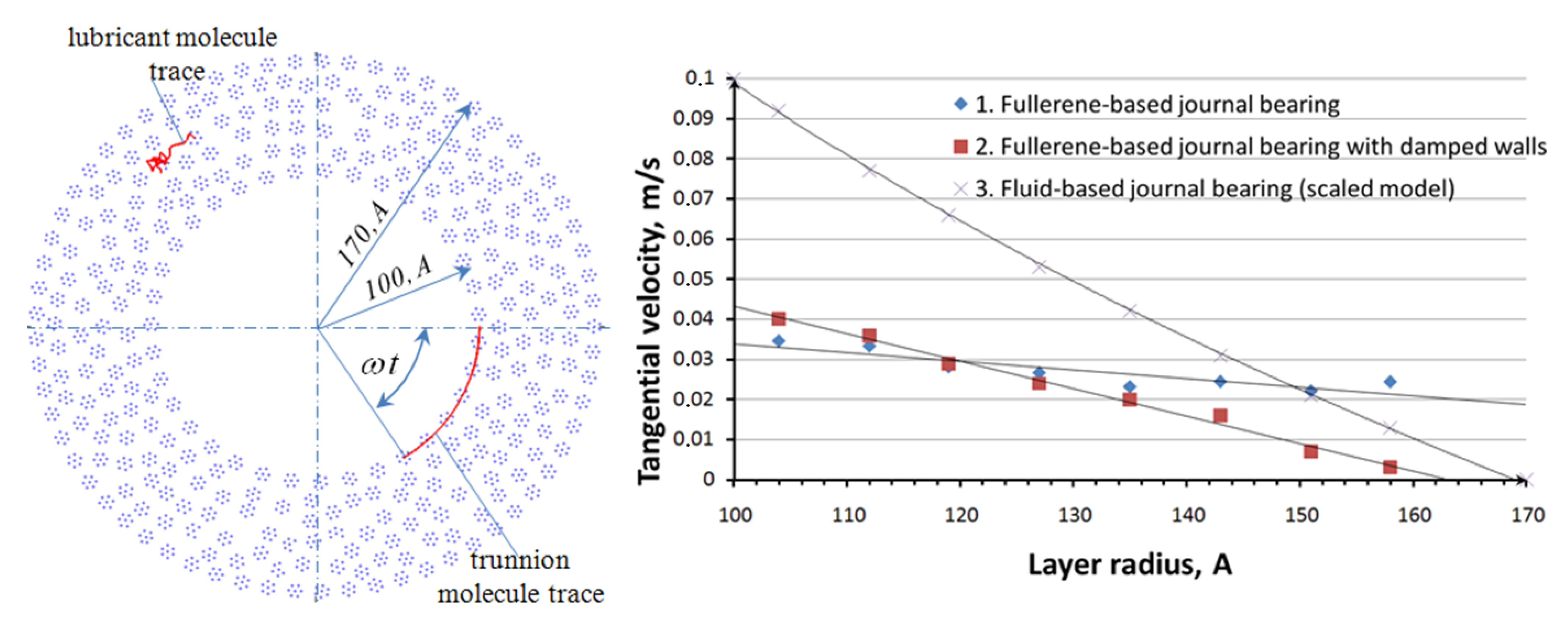
The second set of numerical experiments was carried out to study the shear viscosity effect appearance in fullerene-based journal bearing. The same bearing filled with fullerene lubricant was examined. The trunnion and the bush are coaxial.
Figure 4.
The convergence of the calculation results.
Figure 4.
The convergence of the calculation results.
According to the approaches of mechanics of continua [
10], the shear viscosity effect is inner friction, and the shear viscosity hypothesis is that the shear stress is proportional to the shear strain rate:
where
sρφ—shear stress in polar coordinates;
So, if the values of the shear stress and shear strain rate in a vicinity of the point (e.g., on the surface of the trunnion) are known, the shear viscosity can be found using Equation (5).
According to the Equation (1) dual atomic motion looks like undamped oscillation, and this means, firstly, that molecules cannot “stick” to each other, secondly, they cannot dissipate their energy. Both conclusions mean that the Lennard-Jones interaction (1) cannot simulate shear viscosity effect. It is commonly considere, that kinetic energy of the molecules is in correlation with shear viscosity, temperature and thermal conductivity [
11]. Moreover, the system isothermal condition simulation, for example, results in the molecules’ velocity regulation rule. Such rules are widely known [
6], but they are unacceptable for the research because the stochastic velocity regulation determines the probable appearance of the shear viscosity effect. That is why it was decided to skip the velocity regulation in lubricant film, but modify the Equation (2) for the molecules on the journal bearing surfaces:
where
b—dumping coefficient, Ns/m.
The value of b was obtained from experiments as the system isothermal condition factor.
The results of a series of numerical experiments are presented in
Figure 5 and
Table 1. Random sampling molecules: One in lubricant film and another on surface of the trunnion, with their traces are presented in
Figure 5 to the left. In the postprocess, the lubricant film was divided into eight parts, the tangential velocity component of each molecule was calculated in each part, the results of average tangential velocity calculation are presented in
Figure 5 to the right as the velocity profiles. There are three velocity profiles are presented of
Figure 5, profile 1 belongs to fullerene-based journal bearing simulation model according to the Equation (2), profile 2 belongs to fullerene-based journal bearing simulation model with damped walls according to the Equation (6), and profile 3 is similar to ordinary velocity profile of fluid flow between two cylinders [
10]. Profile 1 is closer to the ordinary velocity profile; it has a legible gradient and “stick” condition on the surface of bushing. In addition, the simulation process of fullerene-based journal bearing with dumped walls was close to isothermal, the system summary kinetic energy was stable as is seen from
Table 1. This is an improvement upon model 6. However, the values of the shear viscosity calculated according to Equation (5) are too small for real materials in real macroscopic journal bearings for all profiles (1–3) probably because of too large values of velocity gradient. This is a dissadvantage for the research.
Figure 5.
Fullerene-based journal bearing and the velocity profile.
Figure 5.
Fullerene-based journal bearing and the velocity profile.
Table 1.
Simulation results in terms of some integral characteristics.
Table 1.
Simulation results in terms of some integral characteristics.
| | Process time/(trunnion rotation angle), s/(radian) | Summary kinetic energy in fractions of its initial value, Ek0 ~ 10-20, J | Average friction force on the trunnion, N | Shear viscosity on the trunnion, Pa·s |
|---|
| Fullerene-based journal bearing | 10-7 /(1) | (1…1.25)Ek0 | 1.1×10-12 | 1.8×10-12 |
| Fullerene-based journal bearing with damped walls | 10-7 /(1) | (0.95…1.05)Ek0 | 1.3×10-12 | 4×10-12 |
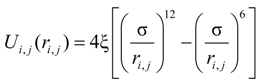
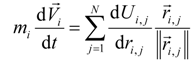
—speed of i-th atom, m/s;
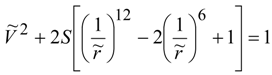
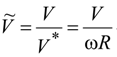 —dimensionless velocity of atoms;
—dimensionless velocity of atoms;—dimensionless criterion of the energy balance of atoms;
—dimensionless distance between atoms.