Water Isotopes as Environmental Tracers for Conceptual Understanding of Groundwater Flow: An Application for Fractured Aquifer Systems in the “Scansano-Magliano in Toscana” Area (Southern Tuscany, Italy)
Abstract
:1. Introduction
2. Study Area and Methods
2.1. Climate, Geology and Hydrogeology
- The first unit consists of alluvial deposits, travertine and Miocenic sand, and it is characterized by medium to high permeability;
- The second unit is composed by volcanic rocks, whose permeability is medium-high to high;
- The third unit, composed of Pliocene clays, is considered impermeable;
- The fourth unit consists of siltstones, shales and of a sequence of clays and marly-limestones (mainly Ligurian Units and Scaglia Toscana formation), and has medium-low to very low permeability;
- The fifth unit is represented by sandstones (mainly Macigno formation and to a lesser extent Pietraforte formation). This unit is considered to have medium to medium-low permeability.
- The sixth unit, made up by calcarenites, cherty-limestones, limestones and dolomitic-limestones of the Tuscan Nappe. Its permeability is medium to very high.
2.2. Methodology
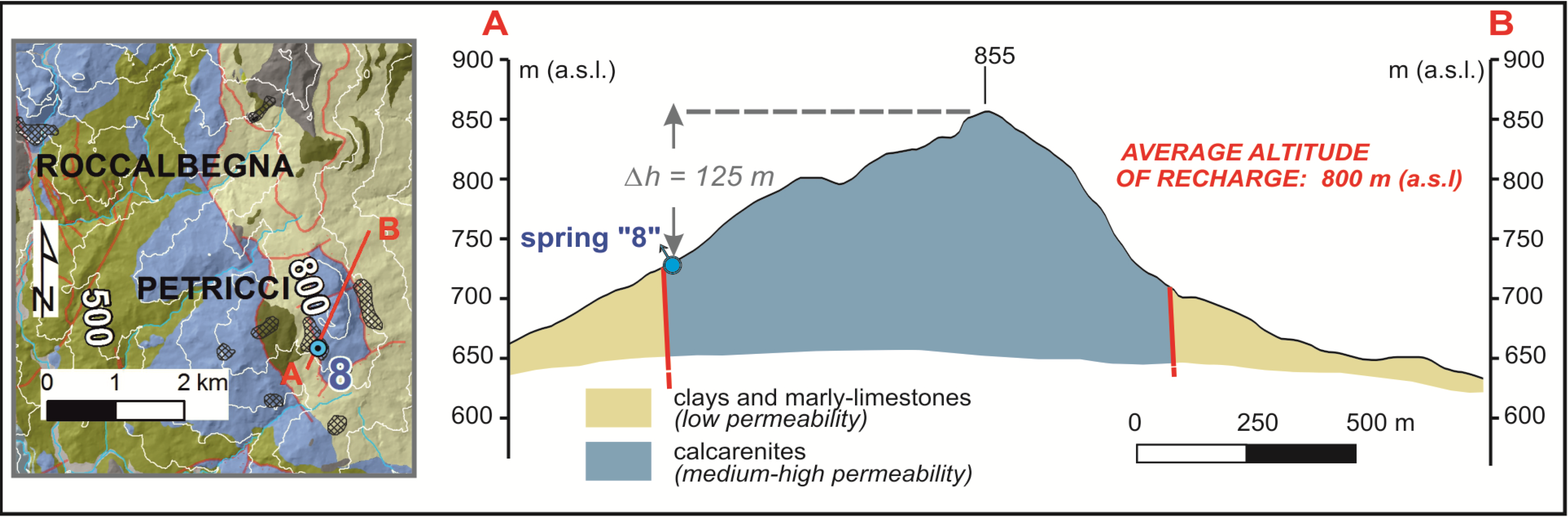
3. Results and Discussion
3.1. Isotopic Features of the Infiltration Water
| Sampled Springs | Spring Altitudes (m a.s.l.) | Infiltration Average Altitudes * (m a.s.l.) | δ18O‰ (VSMOW) (Precision 0.10‰) Mean Value or Single Datum | δ18O‰ Values (March 04/June–July 04/September 04/May–June 05/September 05/October 05) | δ2H‰ (VSMOW) (Precision 1.5‰) Mean Value or Single Datum | δ2H‰ Values (March 04/June–July 04/September 04/May–June 05/September 05/October 05) | 3H(TU) ± Err Mean Value or Single Datum | 3H(TU) Values (March 04/June–July 04/September 04/May–June 05/September 05/October 05) |
|---|---|---|---|---|---|---|---|---|
| 1 | 75 | 150 | −5.58 | (−5.53/−5.54/−5.63/ns/−5.62/ns) | −34.2 | (−33.6/−33.2/−35.8/ns/na/ns) | 2.9 ± 0.7 | (na/3.0/2.8/ns/na/ns) |
| 2 | 260 | 310 | −6.24 | (−6.28/−6.18/ns/−6.25/ns/ns) | −38.5 | (−38.1/−38.9/ns/na/ns/ns) | 4.7 ± 0.7 | (na/4.7/ns/na/ns/ns) |
| 3 | 490 | 530 | −6.68 | (−6.59/−6.71/−6.73/−6.67/ns/ns) | −39.4 | (−38.3/−40.4/−39.4/na/ns/ns) | na | (na/na/ns/na/ns/ns) |
| 4 | 380 | 500 | −6.64 | (−6.62/−6.65/ns/ns/ns/ns) | −40.3 | (−39.4/−41.2/ns/ns/ns/ns) | na | (na/na/ns/ns/ns/ns) |
| 4bis | 395 | 500 | −6.74 | (−6.79/−6.68/ns/ns/ns/ns) | −40.2 | (−38.6/−41.7/ns/ns/ns/ns) | na | (na/na/ns/ns/ns/ns) |
| 5 | 175 | 200 | −5.57 | (−5.54/−5.56/−5.55/−5.61/ns/ns) | −34.1 | (−34.4/−34.6/−32.3/na/ns/ns) | 4.2 ± 0.6 | (na/na/4.2/na/ns/ns) |
| 6 | 650 | 1300 | −7.89 | (−8.00/−7.83/−7.86/−7.86/ns/ns) | −48.3 | (−47.9/−47.4/−49.5/na/ns/ns) | 6.3 ± 0.7 | (na/na/6.3/na/ns/ns) |
| 7 | 995 | 1080 | −7.42 | (−7.52/−7.30/−7.33/−7.51/ns/ns) | −44.8 | (−44.8/−43.6/−45.9/na/ns/ns) | 5.5 ± 0.7 | (na/na/5.5/na/ns/ns) |
| 8 | 730 | 800 | −6.97 | (−7.03/−6.94/−6.96/−6.93/−6.99/ns) | −41.9 | (−40.4/−43.0/−42.3/na/na/ns) | 5.5 ± 0.8 | (na/na/5.5/na/na/ns) |
| 8bis | 845 | 950 | −7.17 | (−7.29/−7.17/−7.06/ns/ns/ns) | −44.2 | (−44.1/−44.5/−43.9/ns/ns/ns) | na | (na/na/na/ns/ns/ns) |
| 9 | 630 | 660 | −6.66 | (−6.67/−6.64/ns/ns/ns/ns) | −40.7 | (−39.6/−41.7/ns/ns/ns/ns) | 4.7 ± 0.7 | (na/4.7/ns/ns/ns/ns) |
| 10 | 690 | 730 | −6.81 | (−6.86/−6.79/−6.73/−6.85/ns/ns) | −41.4 | (−40.7/−41.5/−41.9/na/ns/ns) | 4.1 ± 0.6 | (na/4.2/4.0/na/ns/ns) |
| 21 | 460 | 510 | −6.69 | (ns/−6.69/ns/ns/ns/ns) | −39.7 | (ns/−39.7/ns/ns/ns/ns) | na | (ns/na/ns/ns/ns/ns) |
| 31 | 450 | 540 | −6.53 | (ns/ns/−6.50/−6.56/ns/ns) | −41.0 | (ns/ns/−41.0/na/ns/ns) | 4.8 ± 0.8 | (ns/ns/4.8/na/ns/ns) |
| 32 | 400 | 430 | −6.28 | (ns/ns/−6.27/−6.24/−6.32/ns) | −38.6 | (ns/ns/−38.6/na/na/ns) | na | (ns/ns/na/na/na/ns) |
| 33 | 180 | 250 | −6.03 | (ns/ns/−5.98/−6.08/ns/ns) | −36.6 | (ns/ns/−36.6/na/ns/ns) | na | (ns/ns/na/na/ns/ns) |
| 40 | 45 | 150 | −5.65 | (ns/ns/ns/−5.65/ns/ns) | −33.2 | (ns/ns/ns/−33.2/ns/ns) | na | (ns/ns/ns/na/ns/ns) |
| 43 | 545 | 630 | −6.74 | (ns/ns/ns/−6.74/ns/ns) | −40.5 | (ns/ns/ns/−40.5/ns/ns) | na | (ns/ns/ns/na/ns/ns) |
| 44 | 490 | 520 | −6.62 | (ns/ns/ns/−6.73/ns/−6.40) | −39.6 | (ns/ns/ns/−39.6/ns/na) | 3.4 ± 0.6 | (ns/ns/ns/3.4/ns/na) |
| 47 | 515 | 530 | −6.60 | (ns/ns/ns/ns/−6.60/−6.60) | −39.6 | (ns/ns/ns/ns/−39.6/na) | 5.9 ± 0.6 | (ns/ns/ns/ns/5.9/na) |
| 48 | 490 | 530 | −6.43 | (ns/ns/ns/ns/−6.46/−6.40) | −39.4 | (ns/ns/ns/ns/−39.4/na) | 5.8 ± 0.6 | (ns/ns/ns/ns/5.8/na) |
| 53 | 190 | 240 | −5.95 | (ns/ns/ns/ns/−5.95/ns) | −37.5 | (ns/ns/ns/ns/−37.5/ns) | na | (ns/ns/ns/ns/na/ns) |
| 57 | 40 | 50 | −5.55 | (ns/ns/ns/ns/ns/−5.55) | −34.3 | (ns/ns/ns/ns/ns/−34.3) | na | (ns/ns/ns/ns/ns/na) |
| 60 | 95 | 130 | −5.62 | (ns/ns/ns/ns/ns/−5.62) | −34.8 | (ns/ns/ns/ns/ns/−34.8) | 4.3 ± 0.5 | (ns/ns/ns/ns/ns/4.3) |
| 62 | 140 | 170 | −5.85 | (ns/ns/ns/ns/ns/−5.85) | −36.8 | (ns/ns/ns/ns/ns/−36.8) | na | (ns/ns/ns/ns/ns/na) |

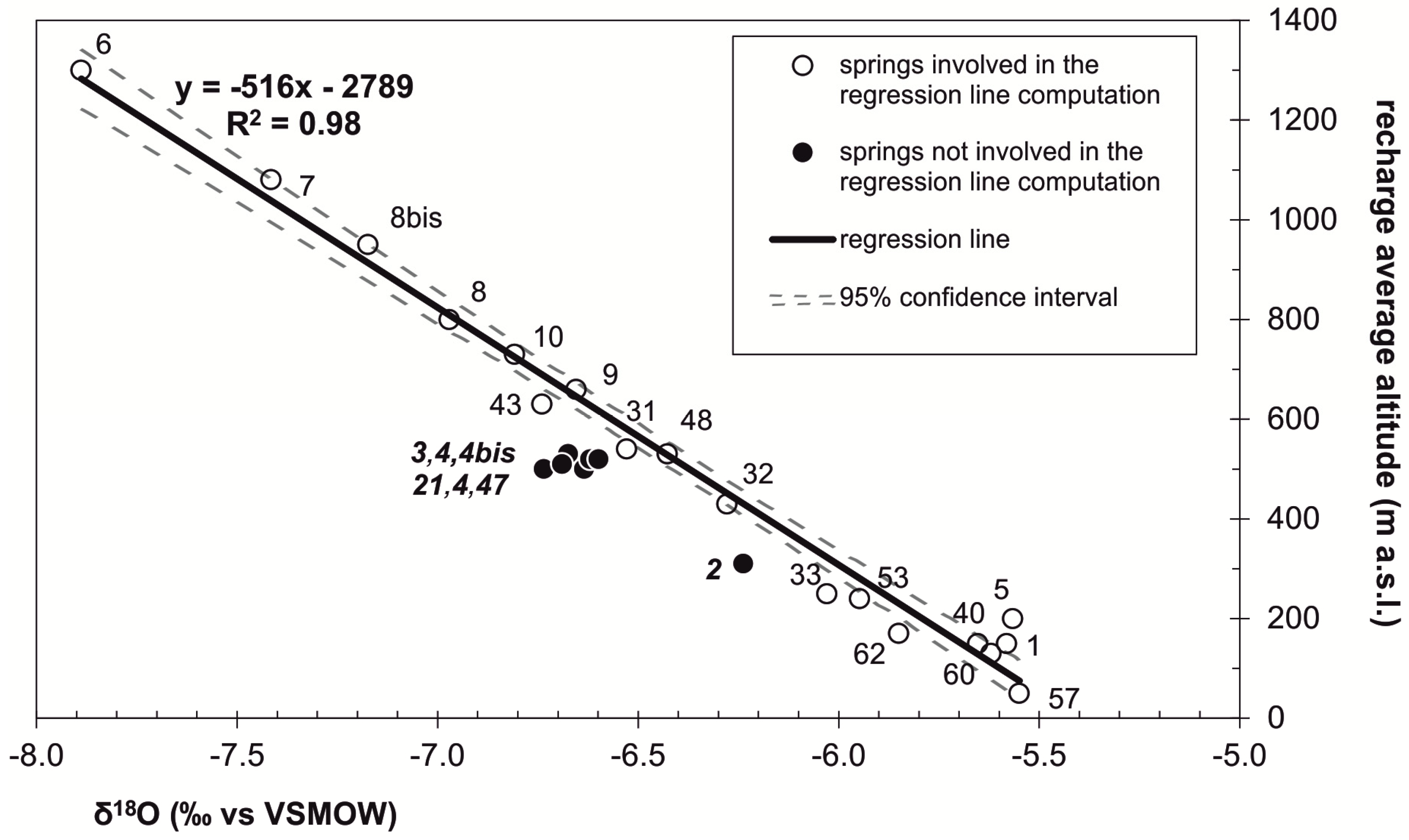
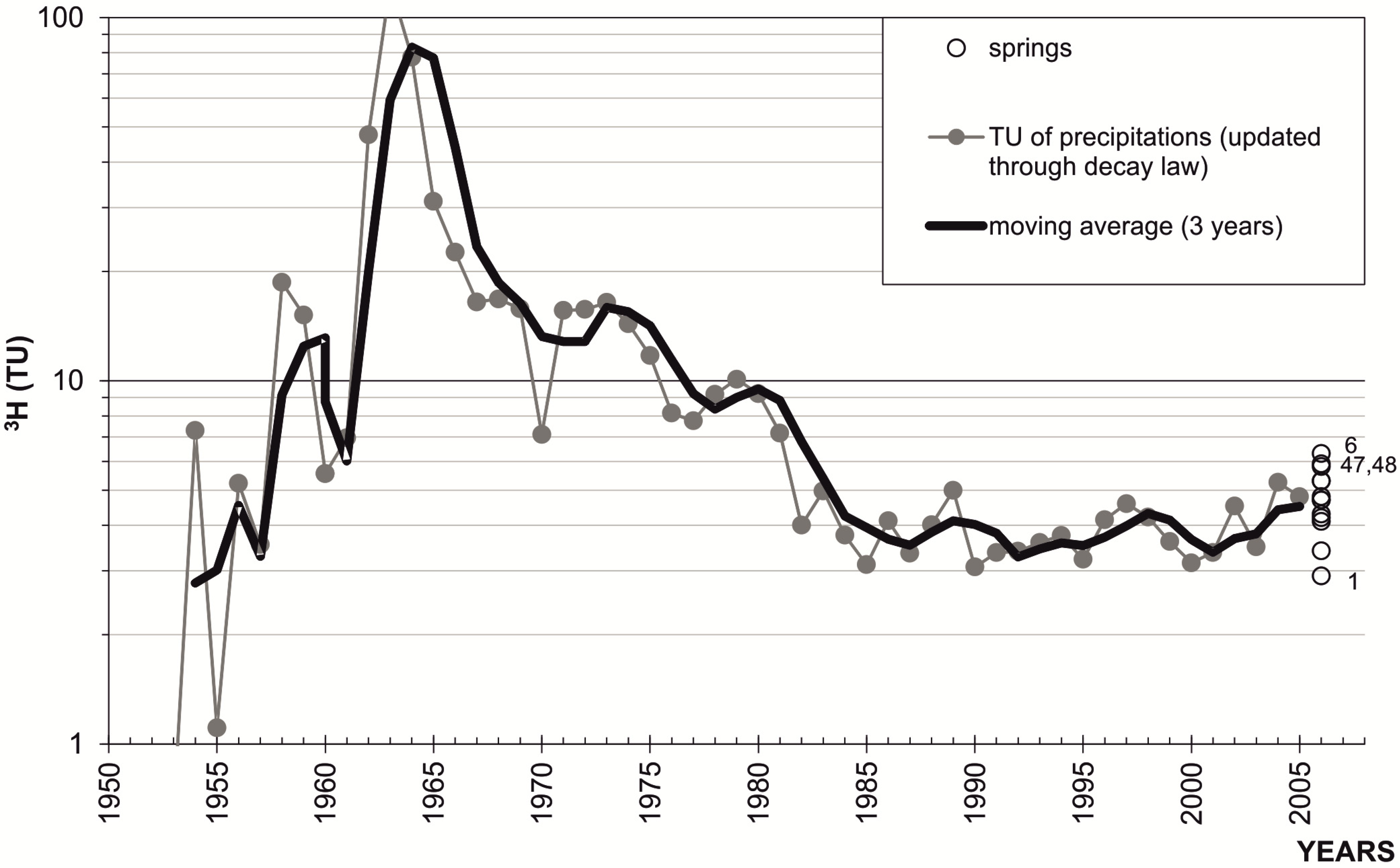
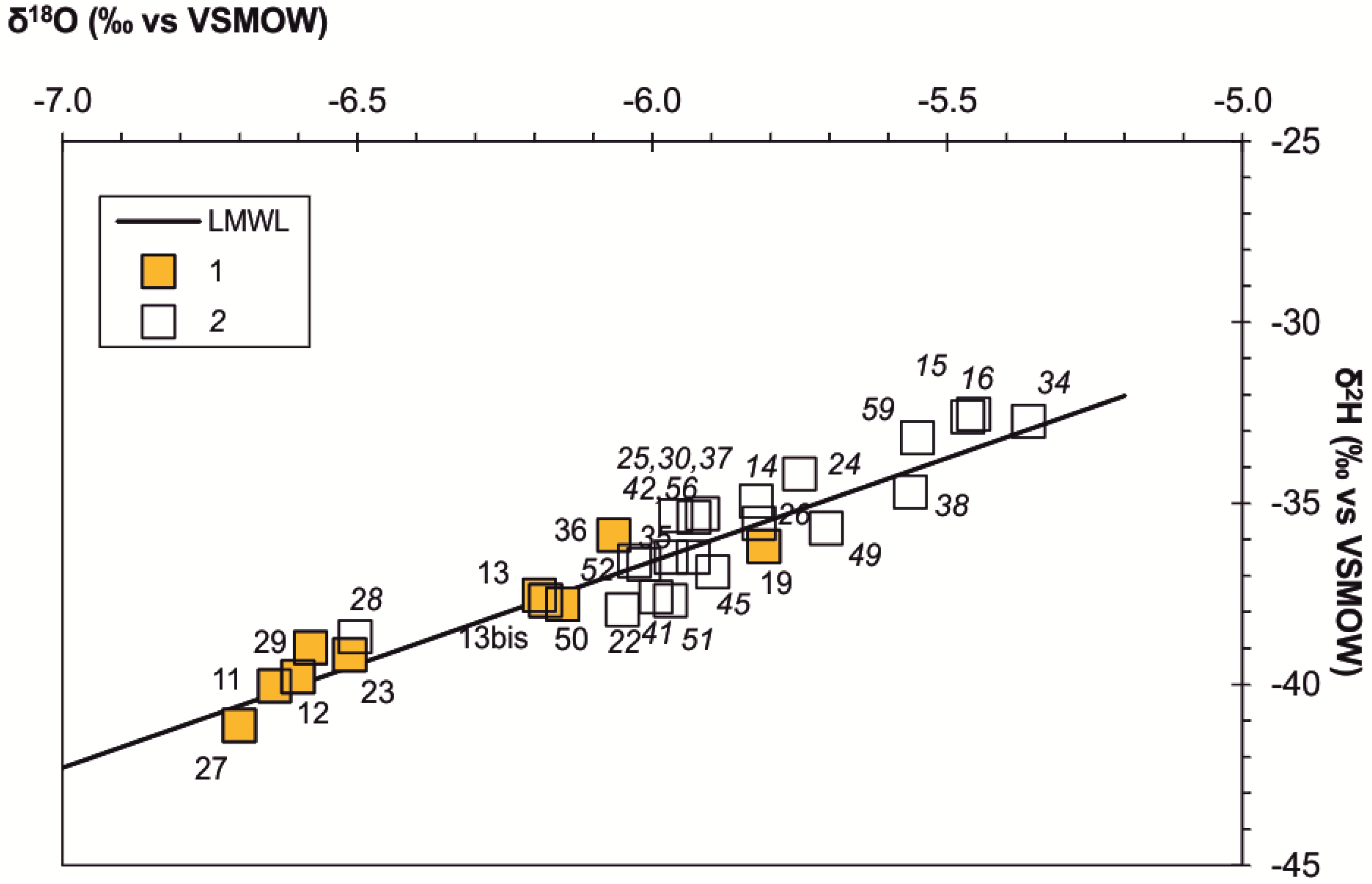
3.2. Groundwater Flow Framework
| Sampled Wells or Streamwaters | Altitudes of Ground Level (m a.s.l.) | Depth of Well (m) or Name of Streamwater | δ18O‰(VSMOW) (Precision 0.10‰) Mean Value or Single Datum | δ18O‰ Values (March 04/June–July 04/September 04/May–June 05/September 05/October 05) | δ2H‰(VSMOW) (Precision 1.5‰) Mean Value or Single Datum | δ2H‰ Values (March 04/June–July 04/September 04/May–June 05/September 05/October 05) | 3H(TU) ± Err Mean Value or Single Datum | 3H(TU) Values (March 04/June–July 04/September 04/May–June 05/September 05/October 05) | |
|---|---|---|---|---|---|---|---|---|---|
| 11 | 415 | 50 | −6.64 | (−6.67/−6.61/ns/ns/ns) | −40.1 | (−40.4/−39.7/ns/ns/ns) | 3.7 ± 0.6 | (na/3.7/ns/ns/ns) | |
| 12 | 545 | 80 | −6.60 | (−6.62/−6.58/ns/ns/ns) | −39.8 | (−39.2/−40.4/ns/ns/ns) | 4.2 ± 0.7 | (na/4.2/ns/ns/ns) | |
| 13 | 255 | 30 | −6.19 | (−6.23/−6.13/−6.21/ns/ns) | −37.6 | (−38.2/−36.9/na/ns/ns) | 3.7 ± 0.6 | (na/3.6/3.7/ns/ns) | |
| 13bis | 190 | 5 | −6.18 | (−6.18/ns/ns/ns/ns) | −37.7 | (−37.7/ns/ns/ns/ns) | na | (na/ns/ns/ns/ns) | |
| 14 | 185 | 11 | −5.82 | (−5.79/ns/ns/−5.86/ns) | −35.0 | (−35.0/ns/ns/na/ns) | 5.9 ± 0.7 | (5.9/ns/ns/na/ns) | |
| 15 | 60 | 40 | −5.46 | (−5.51/−5.40/ns/ns/ns) | −32.6 | (−33.1/−32.0/ns/ns/ns) | 6.6 ± 0.7 | (na/6.6/ns/ns/ns) | |
| 16 | 26 | 48 | −5.47 | (−5.42/−5.51/ns/ns/ns) | −32.6 | (−33.8/−31.5/ns/ns/ns) | 3.7 ± 0.7 | (na/3.7/ns/ns/ns) | |
| 19 | 58 | 85 | −5.81 | (−5.81/ns/ns/ns/ns) | −36.2 | (−36.2/ns/ns/ns/ns) | na | (na/ns/ns/ns/ns) | |
| 22 | 250 | 55 | −6.05 | (−6.00/−6.10/ns/ns/ns) | −38.0 | (−37.1/−38.8/ns/ns/ns) | 2.6 ± 0.6 | (2.5/2.7/ns/ns/ns) | |
| 23 | 400 | 66 | −6.51 | (−6.52/−6.46/−6.56/ns/ns) | −39.2 | (−38.5/−39.9/na/ns/ns) | na | (na/na/na/ns/ns) | |
| 24 | 365 | 54 | −5.75 | (−5.78/−5.72/ns/ns/ns) | −34.2 | (−35.2/−33.2/ns/ns/ns) | 4.3 ± 0.7 | (na/4.3/ns/ns/ns) | |
| 25 | 345 | 3 | −5.96 | (−5.93/ns/−5.99/ns/ns) | −35.4 | (−35.4/ns/na/ns/ns) | na | (na/ns/na/ns/ns) | |
| 26 | 120 | 60 | −5.82 | (−5.79/−5.78/−5.89/ns/ns) | −35.6 | (−35.3/−35.9/na/ns/ns) | 5.4 ± 0.8 | (na/5.4/na/ns/ns) | |
| 27 | 550 | 83 | −6.70 | (−6.67/−6.68/−6.75/ns/ns) | −41.2 | (−42.7/−39.6/na/ns/ns) | 3.7 ± 0.7 | (na/3.9/3.5/ns/ns) | |
| 28 | 495 | 8 | −6.50 | (ns/−6.42/−6.59/ns/ns) | −38.7 | (ns/−37.7/−39.7/ns/ns) | 5.0 ± 0.7 | (ns/5.0/na/ns/ns) | |
| 29 | 500 | 50 | −6.58 | (ns/−6.55/−6.61/ns/ns) | −39.0 | (ns/−39.0/na/ns/ns) | 2.4 ± 0.5 | (ns/2.5/2.3/ns/ns) | |
| 30 | 50 | 30 | −5.93 | (ns/−5.92/−5.94/ns/ns) | −35.4 | (ns/−35.4/na/ns/ns) | 4.6 ± 0.7 | (ns/4.1/5.0/ns/ns) | |
| 34 | 42 | 80 | −5.36 | (ns/−5.28/−5.44/ns/ns) | −32.8 | (ns/−31.7/−33.8/ns/ns) | 3.2 ± 0.6 | (ns/3.2/na/ns/ns) | |
| 35 | 223 | 70 | −6.01 | (ns/−6.09/ns/−5.94/ns) | −36.7 | (ns/−36.7/ns/na/ns) | 5.6 ± 0.7 | (ns/5.6/ns/na/ns) | |
| 36 | 185 | 32 | −6.06 | (ns/−6.08/−6.05/ns/ns) | −33.8 | (ns/−33.8/na/ns/ns) | 0.8 ± 0.4 | (ns/0.8/0.9/ns/ns) | |
| 37 | 285 | 80 | −5.91 | (ns/−5.81/−6.02/ns/ns) | −35.3 | (ns/−35.3/na/ns/ns) | 3.8 ± 0.7 | (ns/3.8/na/ns/ns) | |
| 38 | 80 | 5 | −5.56 | (ns/ns/−5.56/ns/ns) | −34.7 | (ns/ns/−34.7/ns/ns) | na | (ns/ns/na/ns/ns) | |
| 41 | 49 | 40 | −5.99 | (ns/ns/−6.02/−6.07/−5.89) | −37.6 | (ns/ns/−37.6/na/na) | na | (ns/ns/na/na/na) | |
| 42 | 49 | 35 | −5.97 | (ns/ns/−5.97/ns/ns) | −36.5 | (ns/ns/−36.5/ns/ns) | na | (ns/ns/na/ns/ns) | |
| 45 | 346 | 40 | −5.90 | (ns/ns/−5.90/ns/ns) | −36.9 | (ns/ns/−36.9/ns/ns) | 5.3 ± 0.7 | (ns/ns/5.3/ns/ns) | |
| 49 | 360 | 4 | −5.70 | (ns/ns/ns/−5.70/ns) | −35.7 | (ns/ns/ns/−35.7/ns) | 4.1 ± 0.6 | (ns/ns/ns/4.1/ns) | |
| 50 | 328 | 38 | −6.15 | (ns/ns/ns/−6.15/ns) | −37.8 | (ns/ns/ns/−37.8/ns) | na | (ns/ns/ns/na/ns) | |
| 51 | 38 | 50 | −5.97 | (ns/ns/ns/−5.97/ns) | −37.7 | (ns/ns/ns/−37.7/ns) | na | (ns/ns/ns/na/ns) | |
| 52 | 218 | 60 | −6.03 | (ns/ns/ns/−6.03/ns) | −36.6 | (ns/ns/ns/−36.6/ns) | na | (ns/ns/ns/na/ns) | |
| 56 | 355 | 50 | −5.93 | (ns/ns/ns/−5.93/ns) | −36.5 | (ns/ns/ns/−36.5/ns) | na | (ns/ns/ns/na/ns) | |
| 59 | 52 | 40 | −5.55 | (ns/ns/ns/ns/−5.55) | −33.2 | (ns/ns/ns/ns/−33.2) | na | (ns/ns/ns/ns/na) | |
| 39 | 53 | Patrignone | −5.53 | (ns/ns/−5.80/ns/−5.27) | −34.1 | (ns/ns/−34.1/ns/na) | 4.5 ± 0.6 | (ns/ns/4.5/ns/na) | |
| 63 | 72 | Castione | −5.84 | (ns/ns/ns/ns/−5.84) | −34.9 | (ns/ns/ns/ns/−34.9) | na | (ns/ns/ns/ns/na) |
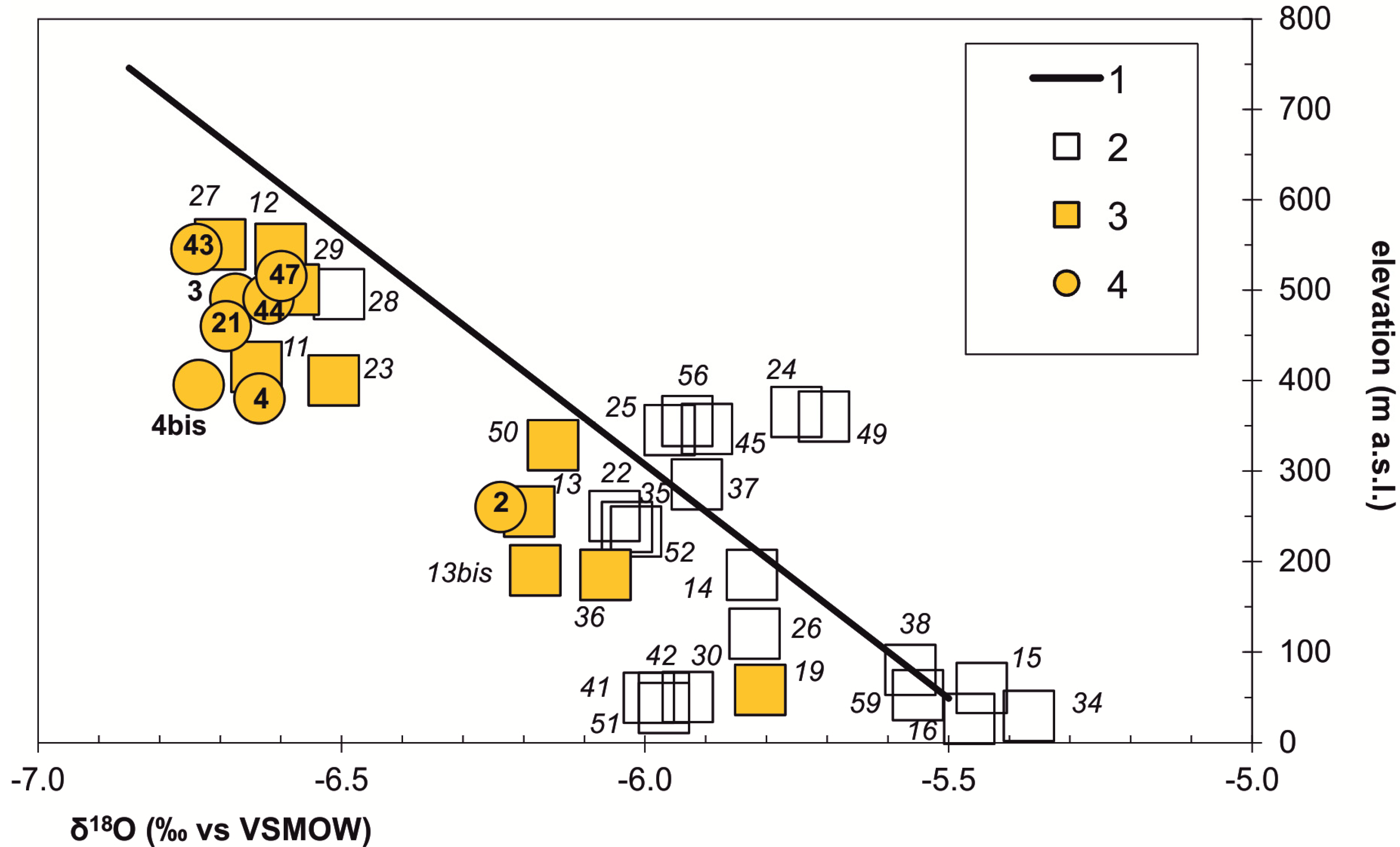
3.3. Preliminary Elaboration of the Conceptual Hydrogeological Model
- −6.4 (‰) is the value of δ18O for the local water. It corresponds to the approximation to first decimal place of the value (−6.37‰) achieved from the “infiltration average altitudes/δ18O values” relationship, considering the average altitude of the Scansano zone (500 m a.s.l.). At this value of altitude, the upper and lower limit of the 95% confidence interval of regression line in Figure 4 are −6.32‰ and −6.42‰, respectively;
- −6.6 (‰) is the value of δ18O for the result of the mixing. It is the approximation to first decimal place of the value (−6.64‰) achieved by the average of the data of the twelve water points (wells and springs) which are representative of such mixing. The standard deviation “σ” of the data set is 0.07;
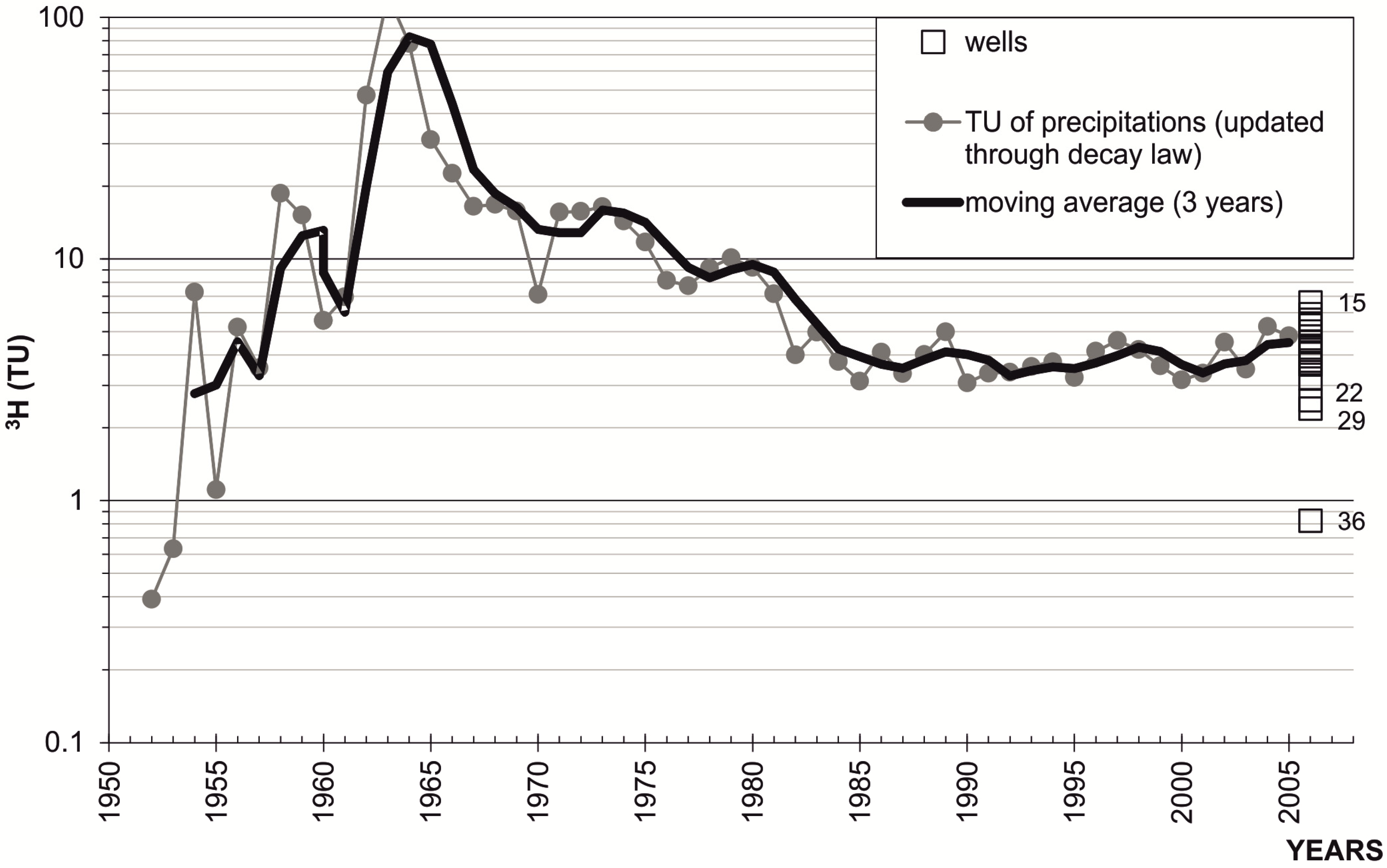
- 5 (TU) is the value of 3H for the local water. It corresponds to the approximation of the average value (5.1 TU; σ = 0.4) of the tritium annual data of rainfall for the years 2004 and 2005 (just before the study period);
- 4 (TU) is the value of 3H for the result of the mixing. It is the approximation of the value (3.8 TU) achieved by the average of the available data for the water points which are representative of the mixing (number of points = 4; σ = 0.3);
- (1 − R) and R are, respectively, the percentages of local and regional groundwater involved in the mixing;
- X and Y are, respectively, the δ18O and 3H values of the regional groundwater.
- based on the morphology, the average altitude achieved from the δ18O value of the mixing indicates as the regional groundwater flow is activated more than 13 km from Scansano. Especially in such hydrostructural context, a resident time of several tens of years is consequently probable, and in this case the range 0-3 TU is consistent with the tritium curve showed in Figure 9;
- as showed by the evolution of the δ18O values occurring in groundwater along the Scansano-Magliano in Toscana ridge, a significant rate of local infiltration in sandstone occurs, consequently to modify the value from 5 TU (local groundwater) up to 4 TU (mixing result) a tritium content abundantly lower than 4 TU is likely for regional groundwater.
- regional groundwater, mainly fed from the Mt. Labbro-Rocchette-Catabbio-Petricci zone, reaches the sandstones aquifer in the Scansano zone by means of an upflow in the fault systems, and mixes with the local infiltration water. An uprising of regional groundwater along such fault systems was also suggested by Francese et al. (2009) [24];
- groundwater resources resulting from such mixing are partially drained by springs and withdrawn by wells, and partially take part in a groundwater flow system that with continuity develops within sandstones at least up to Magliano in Toscana, where a groundwater transfer toward the alluvial system also occurs.
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Panichi, C.; Gonfiantini, R. Environmental isotopes in geothermal studies. Geothermics 1978, 6, 143–161. [Google Scholar] [CrossRef]
- Fontes, J.C. Environmental Isotopes in Groundwater Hydrology. In Handbook of Environmental Isotope Geochemistry, 1st ed.; Fritz, P., Fontes, J.C., Eds.; Elsevier Scientific Publishing: Amsterdam, The Netherlands, 1980; Volume 1, pp. 75–134. [Google Scholar]
- Yurtsever, Y.; Gat, J.R. Atmospheric waters. In Stable Isotope Hydrology (Deuterium and Oxygen-18 in the Water Cycle), 1st ed.; Technical Reports 210; Gat, J.R., Gonfiantini, R., Eds.; International Atomic Energy Agency (IAEA): Vienna, Austria, 1981; pp. 103–142. [Google Scholar]
- Clark, I.; Fritz, P. Precipitation. In Environmental Isotopes in Hydrogeology, 1st ed.; Stein, J., Starkweather, A.W., Eds.; Lewis Publishers CRC Press: Boca Raton, FL, USA, 1997; pp. 63–78. [Google Scholar]
- Wood, W.W.; Sanford, W.E. Chemical and isotopic methods for quantifying groundwater recharge in a regional, semiarid environment. Ground Water 1995, 33, 458–468. [Google Scholar] [CrossRef]
- Mohammad, Z.I. Application of environmental isotopes in storm-discharge analysis of two contrasting stream channel in a watershed. Water Res. 1998, 32, 2959–2968. [Google Scholar] [CrossRef]
- Marfia, A.M.; Krishnamurthy, R.V.; Atekwana, E.A.; Panton, W.F. Isotopic and geochemical evolution of ground and surface waters in a karst dominated geological setting: A case study from Belize, Central America. Appl. Geochem. 2004, 19, 937–946. [Google Scholar] [CrossRef]
- Doveri, M.; Menichini, M.; Cerrina Feroni, A. Stable water isotopes as fundamental tool in karst aquifer studies: Some results from isotopic applications in the Apuan Alps carbonatic complexes (NW Tuscany). Italian J. Eng. Geol. Environ. 2013, 1, 33–50. [Google Scholar]
- Consorzio Lamma. Territorio: Geologia, Carta Geologica Regionale 1:10,000. Available online: http://www.lamma.rete.toscana.it/territorio/geologia (accessed on 15 January 2013).
- Servizio Idrologico Regionale: Archivio dati. Available online: http://www.sir.toscana.it (accessed on 21 March 2013).
- Vittorini, S. Ricerche sul clima della Toscana in base all’evapotraspirazione potenziale e al bilancio idrico. Rivista Geografica Italiana 1972, 1, 1–30. [Google Scholar]
- Boccaletti, M.; Elter, P.; Guazzone, G. Plate tectonics models for the development of Western Alps and Northern Apennines. Nature 1971, 234, 108–111. [Google Scholar] [CrossRef] [PubMed]
- Boccaletti, M.; Coli, M.; Decandia, F.A.; Giannini, E.; Lazzarotto, A. Evoluzione dell’Appennino settentrionale secondo un nuovo modello strutturale. Memorie della Società Geologica Italiana 1981, 21, 359–373. [Google Scholar]
- Molli, G. Northern Apennine-Corsica orogenic system: An updated review. Geol. Soc. Lond. Spec. Publ. 2008, 298, 413–442. [Google Scholar] [CrossRef]
- Mongelli, F.; Zito, G. Flusso di calore nella regione Toscana. Studi Geologici Camerti 1991, 1, 91–98. [Google Scholar]
- Elter, P. L’ensemble ligure. Bulletin de la Société Géologique de France 1975, 17, 984–997. [Google Scholar]
- Marroni, M.; Treves, B. Hidden terranes in the northern Apennines, Italy: A record of Late Cretaceous-Oligocene transpressional tectonics. J. Geol. 1998, 106, 149–162. [Google Scholar] [CrossRef]
- Nirta, G.; Pandeli, E.; Principi, G.; Bertini, G.; Cipriani, N. The Ligurian Units of Southern Tuscany. Bollettino della Società Geologica Italiana 2005, 3, 29–54. [Google Scholar]
- Jolivet, L.; Daniel, J.M.; Truffert, C.; Goffé, B. Exhumation of deep crustal metamorphic rocks and crustal extension in back-arc regions. Lithos 1994, 33, 3–30. [Google Scholar] [CrossRef]
- Carmignani, L.; Decandia, F.A.; Disperati, L.; Fantozzi, P.L.; Lazzarotto, A.; Liotta, D.; Oggiano, G. Relationships between the Sardinia-Corsica-Provencal Domain and the Northern Apennines. Terra Nova 1995, 7, 128–137. [Google Scholar] [CrossRef]
- Brunet, C.; Monié, P.; Jolivet, L.; Cadet, J.P. Migration of compression and extension in the Tyrrhenian Sea: Insights from 40Ar/39Ar ages on micas along a transect from Corsica to Tuscany. Tectonophysics 2000, 321, 127–155. [Google Scholar] [CrossRef]
- Carmignani, L.; Kligfield, R. Crustal extension in the Northern Apennines: Transition from compression to extension in the Alpi Apuane core complex. Tectonics 1990, 9, 1275–1303. [Google Scholar] [CrossRef]
- Brogi, A.; Lazzarotto, A.; Liotta, D.; Ranalli, G. Extensional shear zones as imaged by reflection seismic lines: The Larderello geothermal field (Central Italy). Tectonophysics 2003, 363, 127–139. [Google Scholar] [CrossRef]
- Francese, R.; Mazzarini, F.; Bistacchi, A.; Morelli, G.; Pasquarè, G.; Praticelli, N.; Robain, H.; Wardell, N.; Zaja, A. A structural and geophysical approach to the study of fractured aquifers in the Scansano-Magliano in Toscana Ridge, southern Tuscany, Italy. Hydrogeol. J. 2009, 17, 1233–1246. [Google Scholar] [CrossRef]
- Fritz, P.; Fontes, J.C. Introduction. In Handbook of Environmental Isotope Geochemistry, 1st ed.; Fritz, P., Fontes, J.C., Eds.; Elsevier Scientific Publishing: Amsterdam, The Netherlands, 1980; Volume 1, pp. 1–19. [Google Scholar]
- Epstein, S.; Mayeda, T. Variation of O18 content of waters from natural sources. Geochim. Cosmochim. Acta 1953, 4, 213–224. [Google Scholar] [CrossRef]
- Coleman, M.L.; Shepherd, T.J.; Durham, J.J.; Rouse, J.E.; Moore, G.R. Reduction of water with zinc for hydrogen isotope analysis. Anal. Chem. 1982, 54, 993–995. [Google Scholar] [CrossRef]
- Longinelli, A.; Selmo, E. Isotopic composition of precipitation in Italy: A first overall map. J. Hydrogeol. 2003, 270, 75–88. [Google Scholar]
- Mussi, M.; Leone, G.; Nardi, I. Isotopic geochemistry of natural water from the Alpi Apuane-Garfagnana area, Northern Tuscany, Italy. Mineral. Petrogr. Acta 1998, 41, 163–178. [Google Scholar]
- Doveri, M.; Nisi, B.; Cerrina Feroni, A.; Ellero, A.; Menichini, M.; Lelli, M.; Masetti, G.; Da Prato, S.; Principe, C.; Raco, B. Geological, hydrodynamic and geochemical features of the volcanic aquifer of Mt. Amiata (Tuscany, central Italy): An overview. Acta Vulcanol. 2011–2012, 23–24, 51–72. [Google Scholar]
- International Atomic Energy Agency and World Meteorological Organization. Global Network of Isotopes in Precipitation: The GNIP Database. Available online: http://isohis.iaea.org (accessed on 24 November 2005).
- Doveri, M.; Leone, G.; Mussi, M.; Zanchetta, G. Composizione isotopica di acque ipogee nell’Antro del Corchia (Alpi Apuane, Toscana nord-occidentale). Memorie dell’Istituto Italiano di Speleologia Serie 2 2005, 18, 119–132. [Google Scholar]
- Barazzuoli, P.; Bosco, G.; Nante, N.; Rappuoli, D.; Salleolini, M. The aquifer of Mount Amiata: Evaluation of the perennial yield and its quality. Memorie della Società Geologica Italiana 1994, 48, 825–832. [Google Scholar]
- Craig, H. Isotopic Variation in meteoric waters. Science 1961, 133, 1702. [Google Scholar] [CrossRef] [PubMed]
- i>Gat, J.R.; Carmi, I. Evolution of the isotopic composition of atmosferic waters in the Mediterranean area. J. Geophys. Res. 1970, 75, 3039–3048. [Google Scholar] [CrossRef]
- Minissale, A.; Magro, G.; Vaselli, O.; Verrucchi, C.; Perticone, I. Geochemistry of water and gas discharges from the Mt. Amiata silic complex and surrounding areas (central Italy). J. Volcanol. Geotherm. Res. 1997, 79, 223–251. [Google Scholar] [CrossRef]
- Hauser, S.; Dongarrà, G.; Favara, R.; Longinelli, A. Composizione isotopica delle piogge in Sicilia. Riferimenti di base per studi idrogeologici e relazioni con altre aree mediterranee. Rendiconti della Società Italiana di Mineralogia e Petrologia 1980, 36, 671–680. [Google Scholar]
- Leone, G.; Mussi, M. Gli isotopi ambientali nelle acque di sorgenti e pozzi e nelle emergenze sulfuree sottomarine di Capo Palinuro, Salerno. Geologia tecnica e ambientale 2004, 3, 35–55. [Google Scholar]
- Celati, R.; Grassi, S.; D’Amore, F.; Marcolini, L. The low temperature hydrothermal system of Campiglia, Tuscany (Italy): A geochemical approach. Geothermics 1991, 20, 67–81. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Doveri, M.; Mussi, M. Water Isotopes as Environmental Tracers for Conceptual Understanding of Groundwater Flow: An Application for Fractured Aquifer Systems in the “Scansano-Magliano in Toscana” Area (Southern Tuscany, Italy). Water 2014, 6, 2255-2277. https://doi.org/10.3390/w6082255
Doveri M, Mussi M. Water Isotopes as Environmental Tracers for Conceptual Understanding of Groundwater Flow: An Application for Fractured Aquifer Systems in the “Scansano-Magliano in Toscana” Area (Southern Tuscany, Italy). Water. 2014; 6(8):2255-2277. https://doi.org/10.3390/w6082255
Chicago/Turabian StyleDoveri, Marco, and Mario Mussi. 2014. "Water Isotopes as Environmental Tracers for Conceptual Understanding of Groundwater Flow: An Application for Fractured Aquifer Systems in the “Scansano-Magliano in Toscana” Area (Southern Tuscany, Italy)" Water 6, no. 8: 2255-2277. https://doi.org/10.3390/w6082255
APA StyleDoveri, M., & Mussi, M. (2014). Water Isotopes as Environmental Tracers for Conceptual Understanding of Groundwater Flow: An Application for Fractured Aquifer Systems in the “Scansano-Magliano in Toscana” Area (Southern Tuscany, Italy). Water, 6(8), 2255-2277. https://doi.org/10.3390/w6082255




