Flow Forecasting using Deterministic Updating of Water Levels in Distributed Hydrodynamic Urban Drainage Models
Abstract
:1. Introduction
2. Update Procedure
2.1. Overall Structure of the MIKE URBAN Model
2.2. Theoretical Basis for the Update Procedure
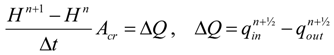
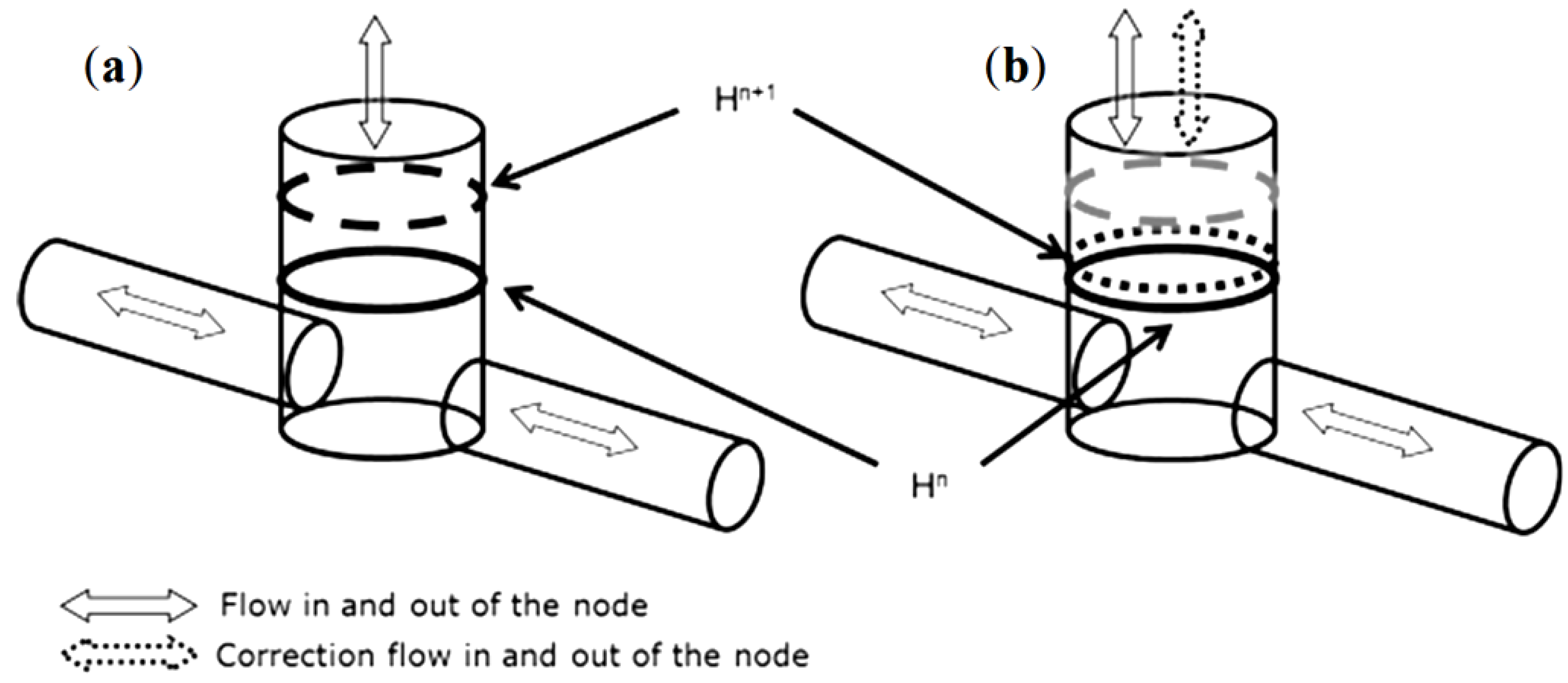
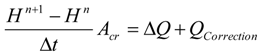
2.3. Water Balance
2.4. Controlling the Update Procedure
3. Evaluation Procedure
3.1. Downstream Flow Evaluation
3.2. Rainfall Input
3.3. Generating Forecast Time Series for Testing the Algorithm

4. Application Examples
4.1. A Simple Hypothetical Example



4.2. A Real Full-Scale Example



5. Discussion
6. Conclusions
- •
- Point-wise deterministic updating of water levels in a distributed hydraulic urban drainage model improves model simulations, even in locations where measurements are unavailable, and can thus be used to give a better evaluation of the state of the system than traditional simulations without updating;
- •
- Updating works best in systems with slow flow dynamics and where updating occurs in multiple upstream basins with slow water level variations, which represent a dominant part of the contributing area;
- •
- Updating improves forecasts compared to not updating, and there is hence some potential for using updated models in model-based warning and control systems;
- •
- An example, based on a real full-scale system, shows that a 3 hr forecast with updating provides flow predictions closer to the measured flow than a traditional simulation without updating;
- •
- Updating of water levels is a pragmatic tool that can help to compensate for the ever-present deviations between model simulations and measured data.
Nomenclature
| Acr | Wetted horizontal cross-sectional area of a model node (m3); |
| Qin | Sum of flows into a node (m3/s); |
| Qout | Sum of flows out of a node (m3/s); |
| Qcorrection | Correction flow in or out of a node (m3/s); |
| H | Water level in a node (m); |
| n | Time step index of hydrodynamic computations (-); |
| Δt | Time step size of the hydrodynamic computations (s); |
| tf | Forecast horizon (min); |
| ti | Time step size of the forecast time series (min). |
Acknowledgments
Conflicts of Interest
References
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters: A state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- Wagener, T.; Reed, P.; van Werkhoven, K.; Tang, Y.; Zhang, Z. Advances in the identification and evaluation of complex environmental systems models. J. Hydroinform. 2009, 11, 266–281. [Google Scholar] [CrossRef]
- Mark, O.; Lacoursiere, J.O.; Vought, L.B.; Amena, Z.; Babel, M.S. Application of hydroinformatics tools for water quality modeling and management: Case study of Vientiane, Lao PDR. J. Hydroinform. 2010, 12, 161–171. [Google Scholar] [CrossRef]
- Mynett, A.E.; Vojinovic, Z. Hydroinformatics in multi-colours-part red: Urban flood and disaster management. J. Hydroinform. 2009, 11, 166–180. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction theory. Trans. ASME J. Basic Eng. Ser. D. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Breinholt, A.; Thordarson, F.O.; Møller, J.K.; Grum, M.; Mikkelsen, P.S.; Madsen, H. Grey-Box modelling of flow in sewer systems with state-dependent diffusion. Environmetrics 2011, 22, 946–961. [Google Scholar] [CrossRef]
- Breinholt, A.; Møller, J.K.; Madsen, H.; Mikkelsen, P.S. A formal statistical approach to representing uncertainty in rainfall-runoff modelling with focus on residual analysis and probabilistic output evaluation—Distinguishing simulation and prediction. J. Hydrol. 2012, 472–473, 36–52. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. 1994, 99, 143–162. [Google Scholar] [CrossRef]
- Neal, J.C.; Atkinson, P.M.; Hutton, C.W. Flood inundation model updating using an ensemble Kalman filter and spatially distributed measurements. J. Hydrol. 2007, 336, 401–415. [Google Scholar] [CrossRef]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F.M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEEE Proc. F Radar Signal Proc. 1993, 140, 107–113. [Google Scholar] [CrossRef]
- Moradkhani, H.; Hsu, K.L.; Gupta, H.; Sorooshian, S. Uncertainty assessment of hydrologic model states and parameters: Sequential data assimilation using the particle filter. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- US Environmental Protection Agency: Storm Water Management Model (SWMM). Available online: http://www2.epa.gov/water-research/storm-water-management-model-swmm (accessed on 21 July 2014).
- MIKE by DHI: MIKE URBAN product page. Available online: http://mikebydhi.com/Products/Cities/MIKEURBAN.aspx (accessed on 21 July 2014).
- Innovyze: InfoWorks CS product page. Available online: http://www.innovyze.com/products/infoworks_cs (accessed on 21 July 2014).
- Rambøll; EnviDan; Odense Vandselskab. Intelligent wastewater handling, documentation of phase 2—Implemention, calibration and validation of simulation tools. Rambøll: Copenhagen, Denmark, 2010. (In Danish) [Google Scholar]
- Festersen, S.H.; Gøtterup, J.G. Monitoring and Modelling of Hydraulics and Water Quality in the Lynette Catchment. Master’s Thesis, Department of Environmental Engineering, Technical University of Denmark, Lyngby, Denmark, 1 August 2013. [Google Scholar]
- Madsen, H.; Skotner, C. Adaptive state updating in real-time river flow forecasting—A combined filtering and error forecasting procedure. J. Hydrol. 2005, 308, 302–312. [Google Scholar] [CrossRef]
- Borup, M. Real Time Updating in Distributed Urban Rainfall Runoff Modelling. Ph.D. Thesis, Department of Environmental Engineering, Technical University of Denmark, Lyngby, Denmark, June 2014. [Google Scholar]
- Hansen, L.S.; Borup, M.; Møller, A.; Breinholt, A.; Mikkelsen, P.S. Performance of MOUSE UPDATE for level and flow forecasting in Urban Drainage Systems. In Proceedings of International MIKE by DHI Conference—Modelling in a World of Change, Copenhagen, Denmark, 6–8 September 2010; p. 11, (CD-ROM).
- Hansen, L.S.; Borup, M.; Møller, A.; Mikkelsen, P.S. Flow forecasting in urban drainage systems using deterministic updating of water levels in distributed hydraulic models. In Proceedings of the 12th International Conference on Urban Drainage, Porto Alegre, Brazil, 11–16 September 2011; p. 8, (CD-ROM).
- Thorndahl, S.; Rasmussen, M. Short-term forecasting of urban storm water runoff in real-time using extrapolated radar rainfall data. J. Hydroinform. 2013, 15, 897–912. [Google Scholar] [CrossRef]
- Borup, M.; Grum, M.; Mikkelsen, P.S. Real time adjustment of slow changing flow components in distributed urban runoff models. In Proceedings of the 12th International Conference on Urban Drainage, Porto Alegre, Brazil, 11–16 September 2011; Full paper PAP005261. p. 8.
- Abbott, M.B.; Minns, A.W. Computational Hydraulics, 2nd ed.; Ashgate Publishing: Burlington, VT, USA, 1998; p. 557. [Google Scholar]
- DHI. MOUSE Pipe Flow Reference Manual; DHI: Hørsholm, Denmark, 2011. [Google Scholar]
- Einfalt, T.; Arnbjerg-Nielsen, K.; Golz, C.; Jensen, N.-E.; Quirmbach, M.; Vaes, G.; Vieux, B. Towards a roadmap for use of radar rainfall data in urban drainage. J. Hydrol. 2004, 299, 186–202. [Google Scholar] [CrossRef]
- Liguori, S.; Rico-Ramirez, M.A.; Schellart, A.N.A.; Saul, A.J. Using probabilistic radar rainfall nowcasts and NWP forecasts for flow prediction in urban catchments. Atmos. Res. 2012, 103, 80–95. [Google Scholar] [CrossRef]
- Nielsen, J.E.; Thorndahl, S.; Rasmussen, M.R. A numerical method to generate high temporal resolution precipitation time series by combining weather radar measurements with a nowcast model. Atmos. Res. 2014, 138, 1–12. [Google Scholar] [CrossRef]
- Rasmussen, M.R.; Thorndahl, S.; Grum, M.; Neve, S.; Borup, M. Weather Radar-Based Control of Wastewater Systems; (In Danish). Miljøministeriet, By- og Landskabsstyrelsen: Copenhagen, Denmark, 2009; ISBN 978-87-92548-28-3. [Google Scholar]
- Thorndahl, S.L.; Bøvith, T.; Rasmussen, M.R.; Gill, R.S. On combining NWP and radar QPF models for forecasting of urban runoff. IAHS Proc. Rep. 2012, 351, 620–625. [Google Scholar]
- Madsen, H.; Arnbjerg-Nielsen, K.; Mikkelsen, P.S. Update of regional intensity–duration–frequency curves in Denmark: Tendency towards increased storm intensities. Atmos. Res. 2009, 92, 343–349. [Google Scholar] [CrossRef]
- Alferes, J.; Tik, S.; Copp, J.; Vanrolleghem, P.A. Advanced monitoring of water systems using in situ measurement stations: Data validation and fault detection. Water Sci. Technol. 2013, 68, 1022–1030. [Google Scholar] [CrossRef]
- Borup, M.; Grum, M.; Mikkelsen, P.S. Comparing the impact of time displaced and biased precipitation estimates for on-line updated urban runoff models. Water Sci. Technol. 2012, 68, 109–116. [Google Scholar] [CrossRef]
- Storm- and Wastewater Informatics project homepage. Available online: Available online: www.swi.env.dtu.dk (accessed on 21 July 2014).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hansen, L.S.; Borup, M.; Møller, A.; Mikkelsen, P.S. Flow Forecasting using Deterministic Updating of Water Levels in Distributed Hydrodynamic Urban Drainage Models. Water 2014, 6, 2195-2211. https://doi.org/10.3390/w6082195
Hansen LS, Borup M, Møller A, Mikkelsen PS. Flow Forecasting using Deterministic Updating of Water Levels in Distributed Hydrodynamic Urban Drainage Models. Water. 2014; 6(8):2195-2211. https://doi.org/10.3390/w6082195
Chicago/Turabian StyleHansen, Lisbet Sneftrup, Morten Borup, Arne Møller, and Peter Steen Mikkelsen. 2014. "Flow Forecasting using Deterministic Updating of Water Levels in Distributed Hydrodynamic Urban Drainage Models" Water 6, no. 8: 2195-2211. https://doi.org/10.3390/w6082195




