Enhancing the Predicting Accuracy of the Water Stage Using a Physical-Based Model and an Artificial Neural Network-Genetic Algorithm in a River System
Abstract
:1. Introduction
2. Description of the Study Site
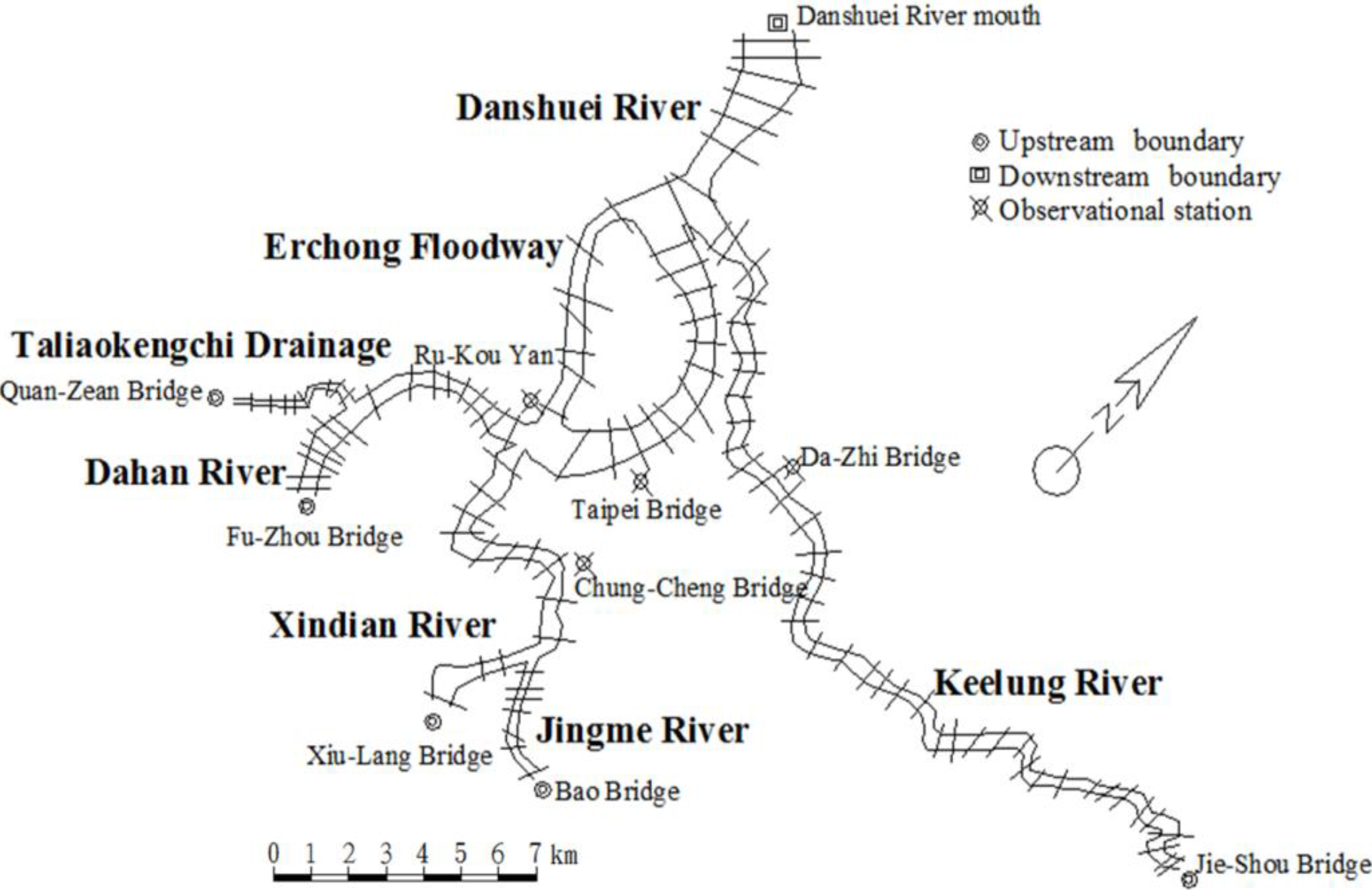
3. Materials and Methods
3.1. Flood Routing Hydrodynamic Model
3.1.1. Governing Equations
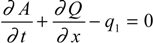
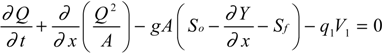
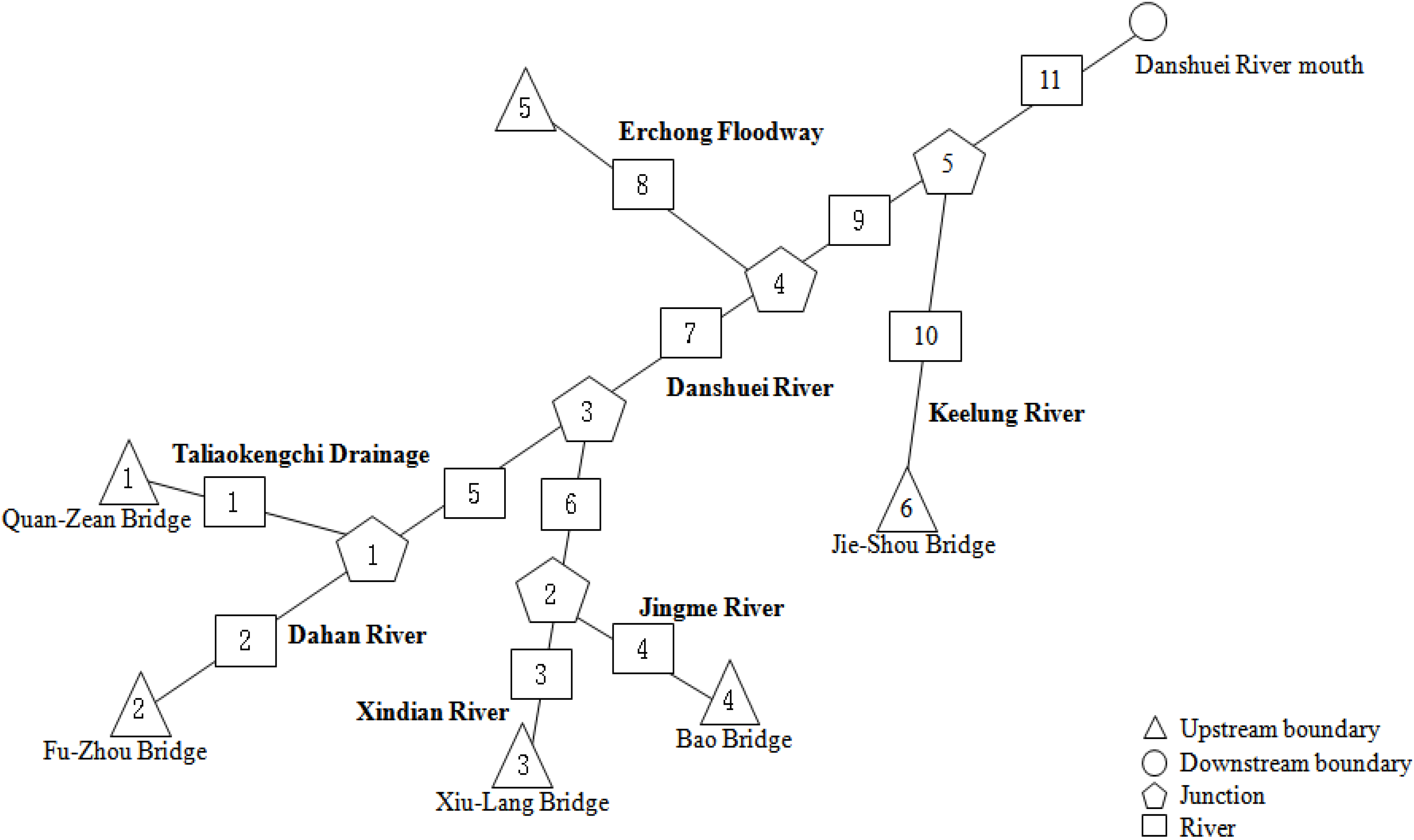
3.1.2. Model Setup
| River Reach Number | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Number of cross-section | 71 | 8 | 3 | 13 | 9 | 22 |
| Manning friction n | 0.025 | 0.033~0.039 | 0.033~0.040 | 0.035~0.045 | 0.033~0.039 | 0.030~0.035 |
| River Reach Number | 7 | 8 | 9 | 10 | 11 | |
| Number of cross-section | 22 | 10 | 2 | 137 | 13 | |
| Manning friction n | 0.022~0.027 | 0.022~0.030 | 0.025 | 0.019~0.090 | 0.023~0.028 |
3.2. Artificial Neural Network (ANN) Models
3.2.1. Back Propagation Neural Network (BPNN)
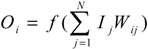
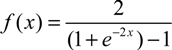
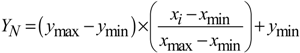
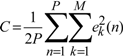
3.2.2. Hybrid Neural Networks and the Genetic Algorithm
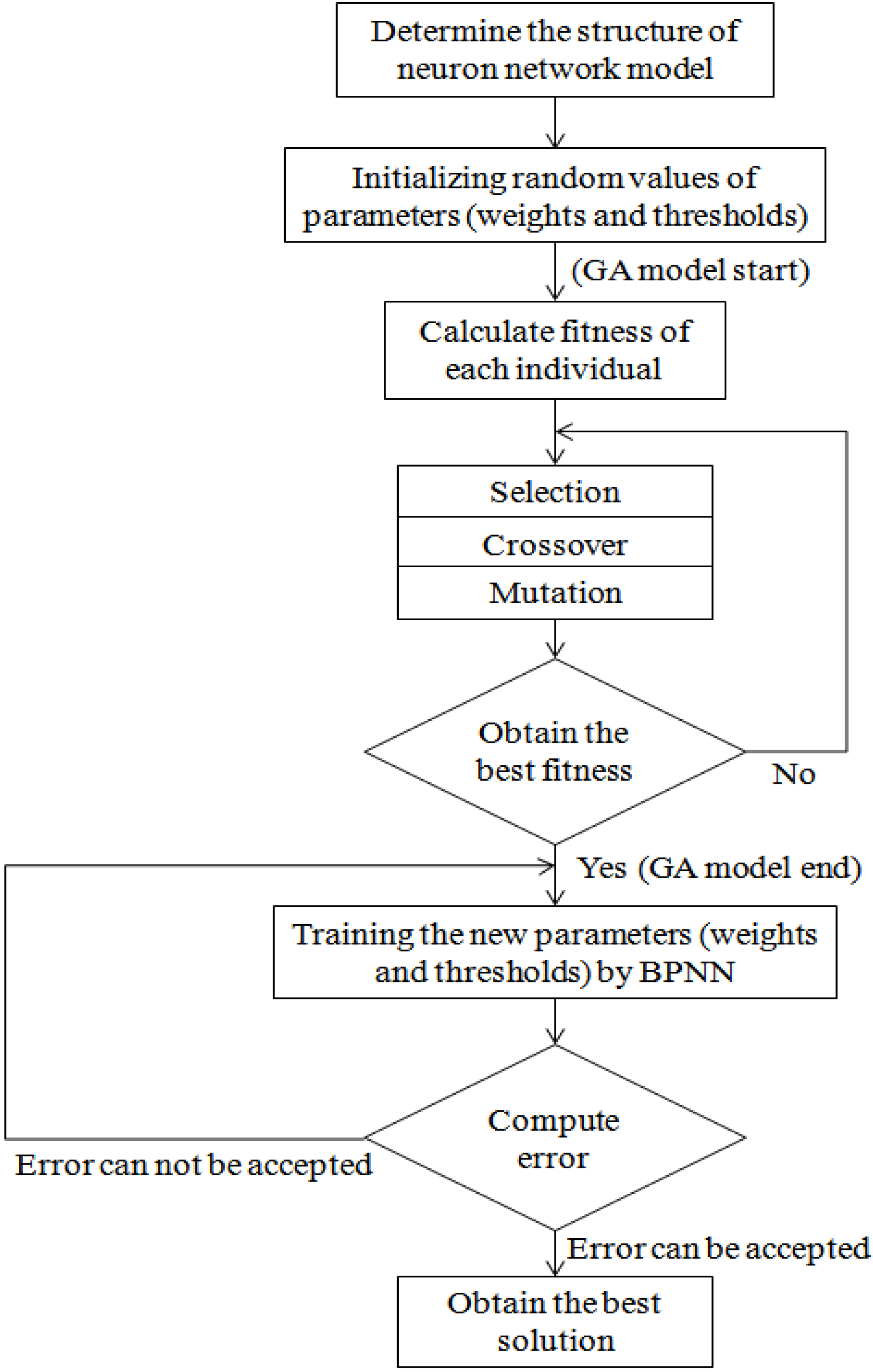
3.2.3. Indices of Simulation Performance
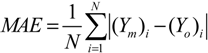
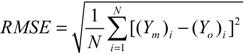
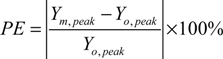
4. Results
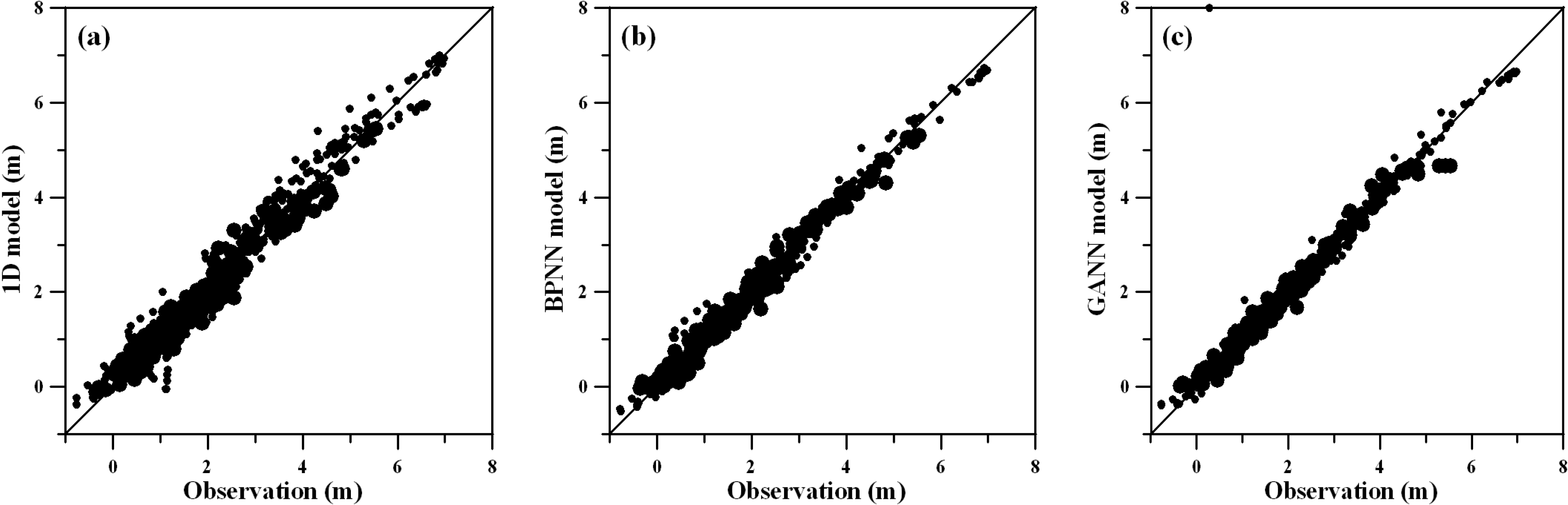
4.1. Flood Routing Hydrodynamic Model Calibration and ANN Model Training
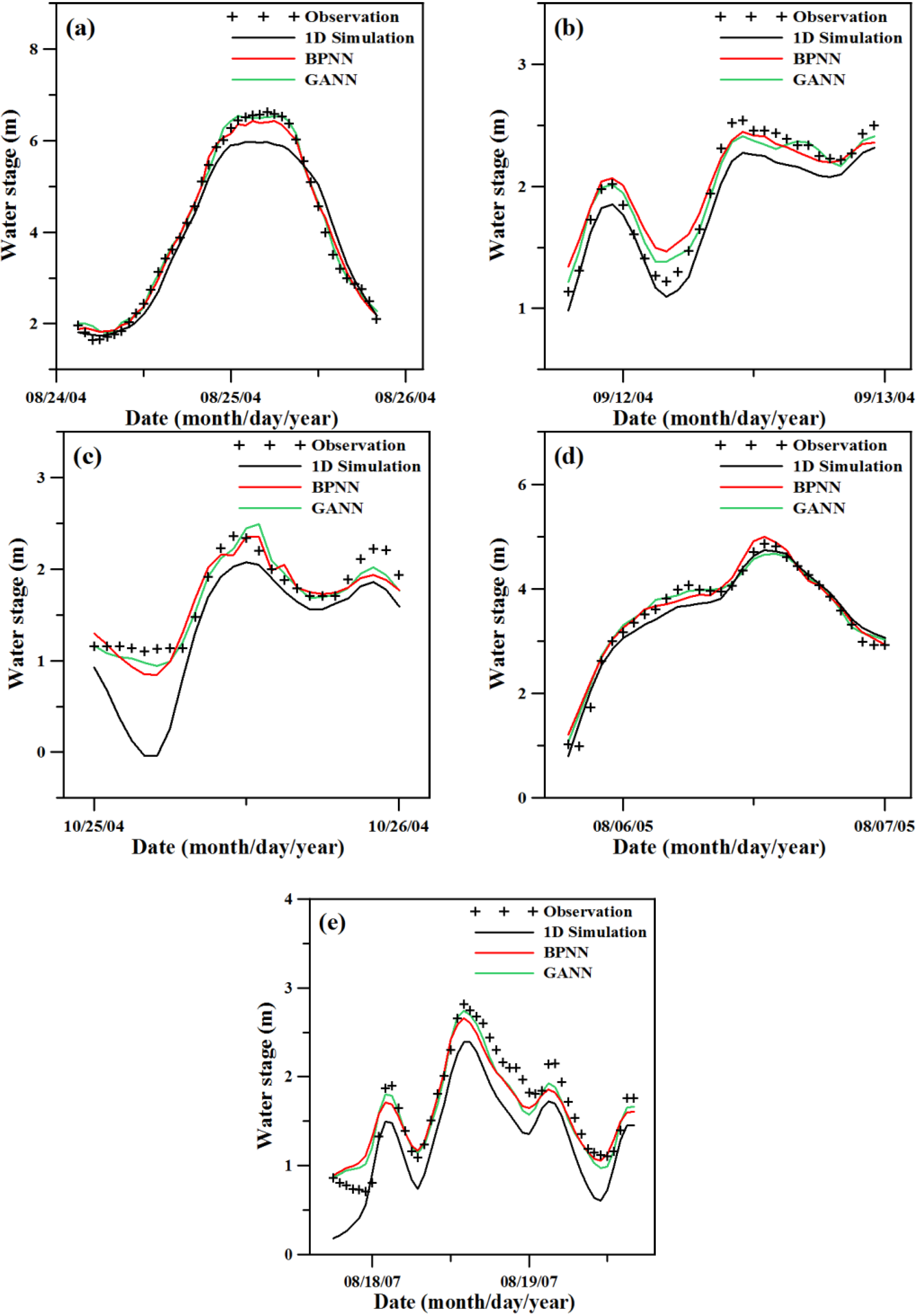
| Method | Taipei Bridge | Ru-Kou-Yan | Chung-Cheng Bridge | Da-Zhi Bridge | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE (m) | RMSE (m) | PE (%) | MAE (m) | RMSE (m) | PE (%) | MAE (m) | RMSE (m) | PE (%) | MAE (m) | RMSE (m) | PE (%) | |
| Calibration with one-dimensional hydrodynamic model | 0.26 | 0.32 | 7.61 | 0.29 | 0.36 | 10.87 | 0.26 | 0.35 | 5.46 | 0.21 | 0.26 | 8.96 |
| Training with BPNN model | 0.11 | 0.15 | 4.77 | 0.12 | 0.17 | 5.00 | 0.19 | 0.26 | 4.09 | 0.15 | 0.19 | 5.41 |
| Training with GANN model | 0.10 | 0.13 | 3.07 | 0.11 | 0.14 | 4.19 | 0.14 | 0.19 | 2.81 | 0.14 | 0.18 | 3.16 |


| Parameters | Taipei Bridge | Ru-Kou-Yan | Chung-Cheng Bridge | Da-Zhi Bridge |
|---|---|---|---|---|
| Input nodes | 7 | 7 | 7 | 7 |
| Hidden nodes | 7 | 14 | 11 | 7 |
| Output nodes | 1 | 1 | 1 | 1 |
| Learning rate | 0.01 | 0.01 | 0.01 | 0.01 |
| Momentum | 0.7 | 0.7 | 0.7 | 0.7 |
| Iterations | 2500 | 2500 | 2500 | 2500 |
| Parameters | Taipei Bridge | Ru-Kou-Yan | Chung-Cheng Bridge | Da-Zhi Bridge |
|---|---|---|---|---|
| Population size | 30 | 30 | 30 | 25 |
| Maximum generation | 2500 | 2500 | 2500 | 2500 |
| Crossover probability | 1.0 | 0.9 | 1.0 | 1.0 |
| Mutation probability | 0.01 | 0.01 | 0.01 | 0.01 |
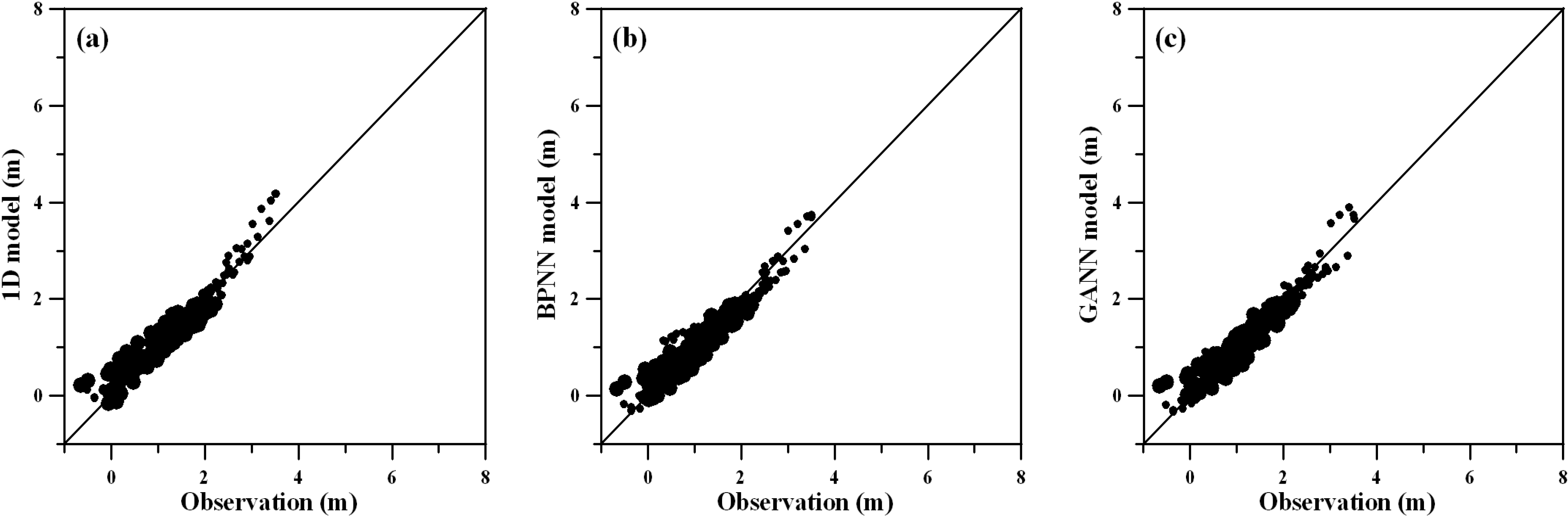
4.2. Flood Routing Hydrodynamic Model Verification and ANN Model Verification
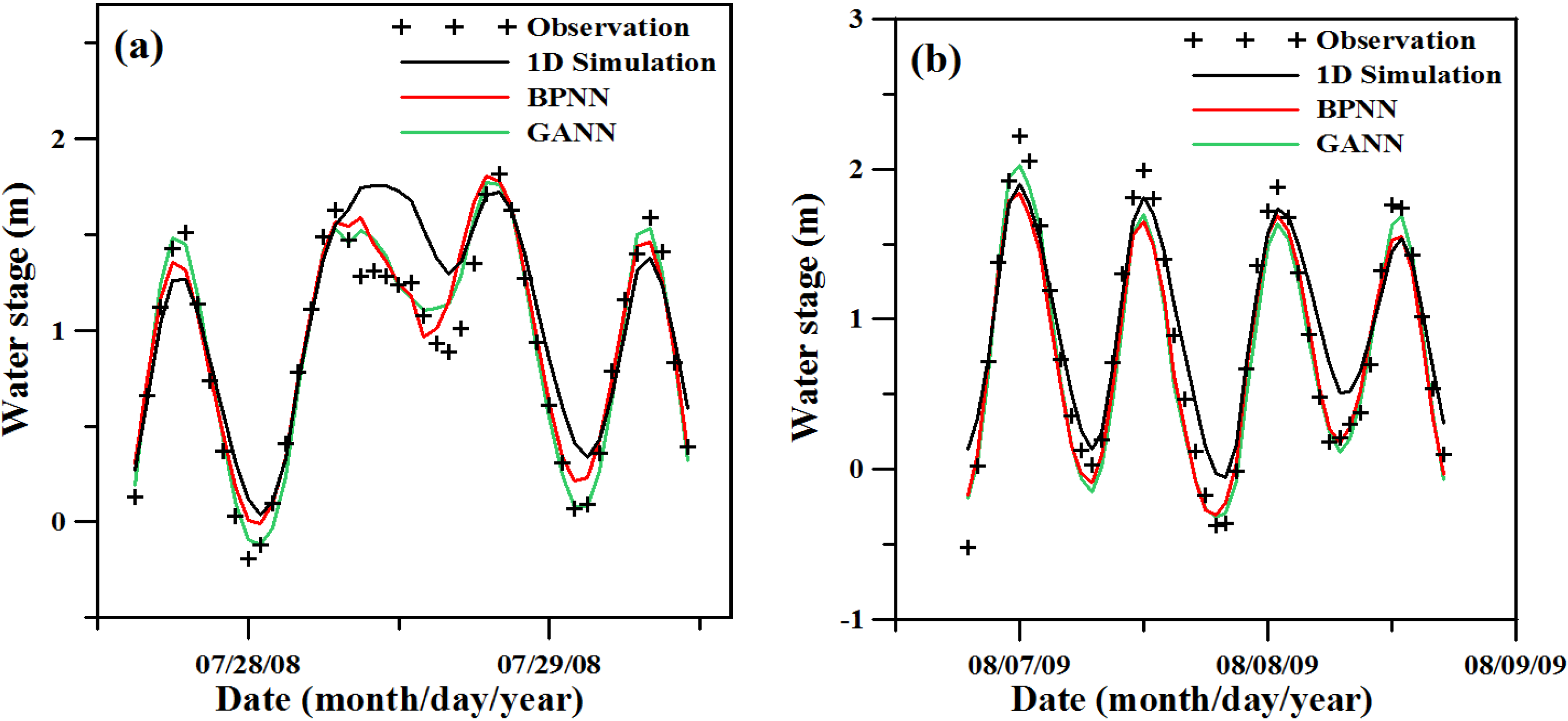
| Method | Taipei Bridge | Ru-Kou-Yan | Chung-Cheng Bridge | Da-Zhi Bridge | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE (m) | RMSE (m) | PE (%) | MAE (m) | RMSE (m) | PE (%) | MAE (m) | RMSE (m) | PE (%) | MAE (m) | RMSE (m) | PE (%) | |
| Verification with one-dimensional hydrodynamic model | 0.20 | 0.25 | 10.81 | 0.20 | 0.25 | 13.12 | 0.22 | 0.28 | 9.86 | 0.22 | 0.27 | 11.32 |
| Verification with BPNN model | 0.13 | 0.16 | 9.89 | 0.18 | 0.21 | 7.17 | 0.19 | 0.25 | 7.99 | 0.21 | 0.26 | 9.02 |
| Verification with GANN model | 0.09 | 0.15 | 6.77 | 0.l7 | 0.20 | 4.92 | 0.18 | 0.23 | 6.91 | 0.20 | 0.24 | 7.95 |
5. Discussions
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hsu, M.H.; Fu, J.C.; Liu, W.C. Flood routing with real-time stage correction method for flash flood forecasting in the Tanshui River, Taiwan. J. Hydrol. 2003, 283, 267–280. [Google Scholar] [CrossRef]
- Helmio, T. Unsteady 1D flow model of a river with partly vegetated floodplains—Application to the Rhine River. Environ. Model. Softw. 2005, 20, 361–375. [Google Scholar] [CrossRef]
- Tayefi, V.; Lane, S.N.; Hardy, R.J.; Yu, D. A comparison of one- and two-dimensional approaches to modeling flood inundation over complex upland floodplains. Hydrol. Process. 2007, 21, 3190–3202. [Google Scholar] [CrossRef]
- Patro, S.; Chatterjee, C.; Singh, R.; Raghuwanshi, N.S. Hydrodynamic modeling of a large flood-prone river system in India with limited data. Hydrol. Process. 2009, 23, 2774–2791. [Google Scholar] [CrossRef]
- Liu, W.C.; Chen, W.B.; Hsu, M.H.; Fu, J.C. Dynamic routing modeling for flash flood forecast in river system. Nat. Hazards 2010, 52, 519–537. [Google Scholar] [CrossRef]
- Malekmohammadi, B.; Zahraie, B.; Kerachian, R. A real-time operation optimization model for flood management in river-reservoir systems. Nat. Hazards 2010, 53, 459–482. [Google Scholar] [CrossRef]
- Costabile, P.; Macchione, F. Analysis of one-dimensional modeling for flood routing in compound channels. Water Resour. Manag. 2012, 26, 1065–1087. [Google Scholar] [CrossRef]
- Sanyal, J.; Carbonneua, P.; Densmore, A. Hydraulic routing of extreme floods in a large ungauged river and the estimation of associated uncertainties: A case study of the Damodar River, India. Nat. Hazards 2013, 66, 1153–1177. [Google Scholar] [CrossRef] [Green Version]
- Saleh, F.; Ducharne, A.; Flipo, N.; Oudin, L.; Ledoux, E. Impact of river bed morphology on discharge and water levels simulated by a 1D Saint-Venant hydraulic model at regional scale. J. Hydrol. 2013, 476, 169–177. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks—Fundamentals, computing, design, and application. J. Microbiol. Meth. 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Taromina, R.; Chau, K.W.; Sethi, R. Artificial neural network simulation of hourly groundwater levels in a coastal aquifer system of the Venice lagoon. Eng. Appl. Artif. Intel. 2012, 25, 1670–1676. [Google Scholar] [CrossRef]
- Cheng, C.T.; Chau, K.W.; Sun, Y.G.; Lin, J.Y. Long-term prediction of discharges in Manwan Reservoir using neural network models. Lect. Notes Comput. Sci. 2005, 3498, 1040–1045. [Google Scholar] [CrossRef]
- Chau, K.W.; Wu, C.L.; Li, Y.S. Comparison of several flood forecasting models in Yangtz River. J. Hydrol. Eng. ASCE 2005, 10, 485–491. [Google Scholar] [CrossRef]
- Chen, W.; Chau, K.W. Intelligent manipulation and calibration of parameters for hydrological models. Int. J. Environ. Pollut. 2006, 28, 432–447. [Google Scholar] [CrossRef]
- Kisi, O. Streamflow forecasting using different artificial neural network algorithm. J. Hydrol. Eng. ASCE 2007, 12, 532–539. [Google Scholar] [CrossRef]
- Kisi, O. River flow forecasting and estimation using different artificial neural network techniques. Hydrol. Res. 2008, 39, 27–40. [Google Scholar] [CrossRef]
- Pramanik, N.; Panda, R.K. Application of neural network and adaptive neuro-fuzzy inference systems for river flow prediction. Hydrol. Sci. J. 2009, 54, 247–260. [Google Scholar] [CrossRef]
- Mukerji, A.; Chatterjee, C.; Raghuwanshi, N.S. Flood forecasting using ANN, neuro-fuzzy, and neuro-GA models. J. Hydrol. Eng. ASCE 2009, 14, 647–652. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W. Predicting monthly streamflow using data-driven models coupled with data-preprocessing techniques. Water Resour. Res. 2009, 45, W08432. [Google Scholar]
- Talei, A.; Chua, L.H.C.; Wong, T.S.W. Evaluation of rainfall and discharges inputs used by Adaptive Network-based Fuzzy Inference Systems (ANFIS) in rainfall-runoff modeling. J. Hydrol. 2010, 391, 248–262. [Google Scholar] [CrossRef]
- Machado, F.; Mine, M.; Kaviski, E.; Fill, H. Monthly rainfall-runoff modelling using artificial neural networks. Hydrol. Sci. J. 2011, 56, 349–361. [Google Scholar] [CrossRef]
- Toukourou, M.; Johannet, A.; Dreyfus, G.; Ayral, P.A. Rainfall-runoff modeling of flash floods in the absence of rainfall forecasts: The case of “Cevenol flash floods”. Appl. Intell. 2011, 35, 178–189. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W. Rainfall-runoff modeling using artificial neural network coupled with singular spectrum analysis. J. Hydrol. 2011, 399, 394–409. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J.; Mustafa, T. Modeling rainfall-runoff process using soft computing techniques. Comput. Geosci. 2012, 51, 108–117. [Google Scholar] [CrossRef]
- Sattari, M.T.; Apaydin, H.; Ozturk, F. Flow estimations for the Sohu Stream using artificial neural networks. Environ. Earth Sci. 2012, 66, 2031–2045. [Google Scholar] [CrossRef]
- De Vos, N.J. Echo state networks as an alternative to traditional artificial neural networks in rainfall-runoff modelling. Hydrol. Earth Syst. Sci. 2013, 17, 253–267. [Google Scholar] [CrossRef] [Green Version]
- Rezaeianzadeh, M.; Tabari, H.; Yazdi, A.A.; Isik, S.; Kalin, L. Flood flow forecasting using ANN, ANFIS and regression models. Neural. Comput. Applic. 2013. [Google Scholar] [CrossRef]
- Alvisi, S.; Mascellani, G.; Franchini, M.; Bardossy, A. Water level forecasting through fuzzy logic and artificial neural network approach. Hydrol. Earth Syst. Sci. 2006, 10, 1–17. [Google Scholar] [CrossRef]
- Chau, K.W. Particle swarm optimization training algorithm for ANNs in stage prediction of Shing Mun River. J. Hydrol. 2006, 329, 363–367. [Google Scholar] [CrossRef]
- Bustami, R.; Bessaih, N.; Bong, C.; Suhaili, S. Artificial neural network for precipitation and water level predictions of Bedup River. IAENG Int. J. Comput. Sci. 2007, 34, 228–233. [Google Scholar]
- Sulaiman, M.; El-Shafie, A.; Karim, O.; Basri, H. Improved water level forecasting performance by using optimal steepness coefficients in an artificial neural network. Water Resour. Manag. 2011, 25, 2525–2541. [Google Scholar] [CrossRef]
- Nguyen, P.K.T.; Chua, L.H.C.; Son, L.H. Flood forecasting in large rivers with data-driven models. Nat. Hazards 2014, 71, 767–784. [Google Scholar] [CrossRef]
- Moeini, M.H.; Etemad-Shahidi, A.; Chegini, V.; Rahmani, I. Wave data assimilation using a hybrid approach in the Persian Gulf. Ocean. Dynam. 2012, 62, 785–797. [Google Scholar] [CrossRef]
- Demirel, M.C.; Venancio, A.; Kahya, E. Flow forecast by SWAT model and ANN in Pracana basin, Portugal. Adv. Eng. Softw. 2009, 40, 467–473. [Google Scholar] [CrossRef]
- Panda, R.K.; Pramanik, N.; Bala, B. Simulation of river stage using artificial network and MIKE 11 hydrodynamic model. Comput. Geosci. 2010, 36, 735–745. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C.; Hsu, M.H. Comparison of ANN approach with 2D and 3D hydrodynamic models for simulating estuary water stage. Adv. Eng. Softw. 2012, 45, 69–79. [Google Scholar] [CrossRef]
- Liu, W.C.; Chen, W.B.; Hsu, M.H. The influence of discharge reductions on salt water intrusion and residual circulation in Danshuei River. J. Mar. Sci. Technol. 2011, 19, 596–606. [Google Scholar]
- Hsu, M.H.; Kuo, A.Y.; Kuo, J.T.; Liu, W.C. Procedure to calibrate and verify numerical models of estuarine hydrodynamics. J. Hydraul. Eng. ASCE 1999, 125, 166–182. [Google Scholar] [CrossRef]
- Preissman, A. Propagation of Translatory Waves in Channels and Rivers. In Proceedings of the First Congress of French Association for Computation, Grenoble, France, 1961; pp. 433–442.
- Amein, M.; Fang, C.S. Implicit flood routing in natural channel. J. Hydraul. Div. ASCE 1970, 96, 2481–2500. [Google Scholar]
- Hsu, M.H.; Fu, J.C.; Liu, W.C. Dynamic routing model with real-time roughness updating for flood forecasting. J. Hydraul. Eng. ASCE 2006, 132, 605–619. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Zadeh, R.M.; Amin, S.; Khalili, D.; Singh, V.P. Daily outflow prediction by multi layer perceptron with logistic sigmoid and tangent sigmoid activation functions. Water Resour. Manag. 2010, 24, 2673–2688. [Google Scholar] [CrossRef]
- Yonaba, H.; Anctil, F.; Fortin, V. Comparing sigmoid transfer functions for neural network multistep ahead streamflow forecasting. J. Hydrol. Eng. ASCE 2010, 15, 275–283. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Zhu, H.; Jiao, L.; Pan, J. Multi-population genetic algorithm for feature selection. Lect. Notes Comput. Sci. 2006, 422, 480–487. [Google Scholar]
- Kisi, O.; Cengiz, T.M. Fuzzy genetic approach for estimating reference evapotranspiration of Turkey: Mediterranean region. Water Resour. Manag. 2013, 27, 3541–3553. [Google Scholar] [CrossRef]
- Wang, W.C.; Chau, K.W.; Cheng, C.T.; Qiu, L. A comparison of performance of several artificial intelligence methods for predicting monthly discharge time series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C.; Hsu, M.H. Predicting typhoon-induced storm surge tide with a two-dimensional hydrodynamic model and artificial neural network model. Nat. Hazards Earth Syst. Sci. 2012, 12, 3799–3809. [Google Scholar] [CrossRef]
- Ghose, D.K.; Panda, S.S.; Swain, P.C. Prediction of water table depth in western region, Oissa using BPNN and RBFN neural networks. J. Hydrol. 2010, 394, 296–304. [Google Scholar] [CrossRef]
- Goldberg, D. Genetic Algorithm in Search, Optimization and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Mulia, I.E.; Tay, H.; Roopsekhar, K.; Tkalich, P. Hybrid ANN-GA for predicting turbidity and chlorophyll-a concentrations. J. HydroEnviron. Res. 2013, 7, 279–299. [Google Scholar]
- Chatterjee, S.; Bandopadhyay, S. Reliability estimation using a genetic algorithm-based artificial neural network: An application to a load-haul-dump machine. Expert. Syst. Appl. 2012, 39, 10943–10951. [Google Scholar] [CrossRef]
- Karimi, H.; Yousefi, F. Application of artificial neural network-genetic algorithm (ANN-GA) to correlation of density in nanofluids. Fluid Phase Equilibr. 2012, 336, 79–83. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, A.; Malik, A.; Jain, G. Artificial neural network modeling of the river water quality-A case study. Ecol. Model. 2009, 220, 888–895. [Google Scholar] [CrossRef]
- Nourani, V.; Komasi, M.; Alami, M.T. Hybrid wavelet-genetic programming approach to optimize ANN modeling of rainfall-runoff process. J. Hydrol. Eng. ASCE 2012, 17, 724–741. [Google Scholar] [CrossRef]
- Cheng, C.T.; Ou, C.P.; Chau, K.W. Combining a fuzzy optimal with a genetic algorithm to solve multiobjective rainfall-runoff model calibration. J. Hydrol. 2002, 268, 72–86. [Google Scholar]
- Muttil, N.; Chau, K.W. Neural network and genetic programming for modelling coastal algal blooms. Int. J. Environ. Pollut. 2006, 28, 223–238. [Google Scholar] [CrossRef]
- Lin, J.Y.; Cheng, C.T.; Chau, K.W. Using support vector machines for long-term discharge prediction. Hydrol. Sci. J. 2006, 51, 599–612. [Google Scholar] [CrossRef]
- Tabari, H.; Kisi, O.; Ezani, A.; Hosseinzadeh, T.P. SVM, ANFIS, regression and climate based models for reference evapotranspiration modeling using limited climate data in a semi-arid highland environment. J. Hydrol. 2012, 444, 78–89. [Google Scholar]
- Muttil, N.; Chau, K.W. Machine-learning paradigms for selecting ecologically significant input variables. Eng. Appl. Artif. Intel. 2007, 20, 735–744. [Google Scholar] [CrossRef] [Green Version]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, W.-C.; Chung, C.-E. Enhancing the Predicting Accuracy of the Water Stage Using a Physical-Based Model and an Artificial Neural Network-Genetic Algorithm in a River System. Water 2014, 6, 1642-1661. https://doi.org/10.3390/w6061642
Liu W-C, Chung C-E. Enhancing the Predicting Accuracy of the Water Stage Using a Physical-Based Model and an Artificial Neural Network-Genetic Algorithm in a River System. Water. 2014; 6(6):1642-1661. https://doi.org/10.3390/w6061642
Chicago/Turabian StyleLiu, Wen-Cheng, and Chuan-En Chung. 2014. "Enhancing the Predicting Accuracy of the Water Stage Using a Physical-Based Model and an Artificial Neural Network-Genetic Algorithm in a River System" Water 6, no. 6: 1642-1661. https://doi.org/10.3390/w6061642






