Regional Calibration of SCS-CN L-THIA Model: Application for Ungauged Basins
Abstract
:1. Introduction
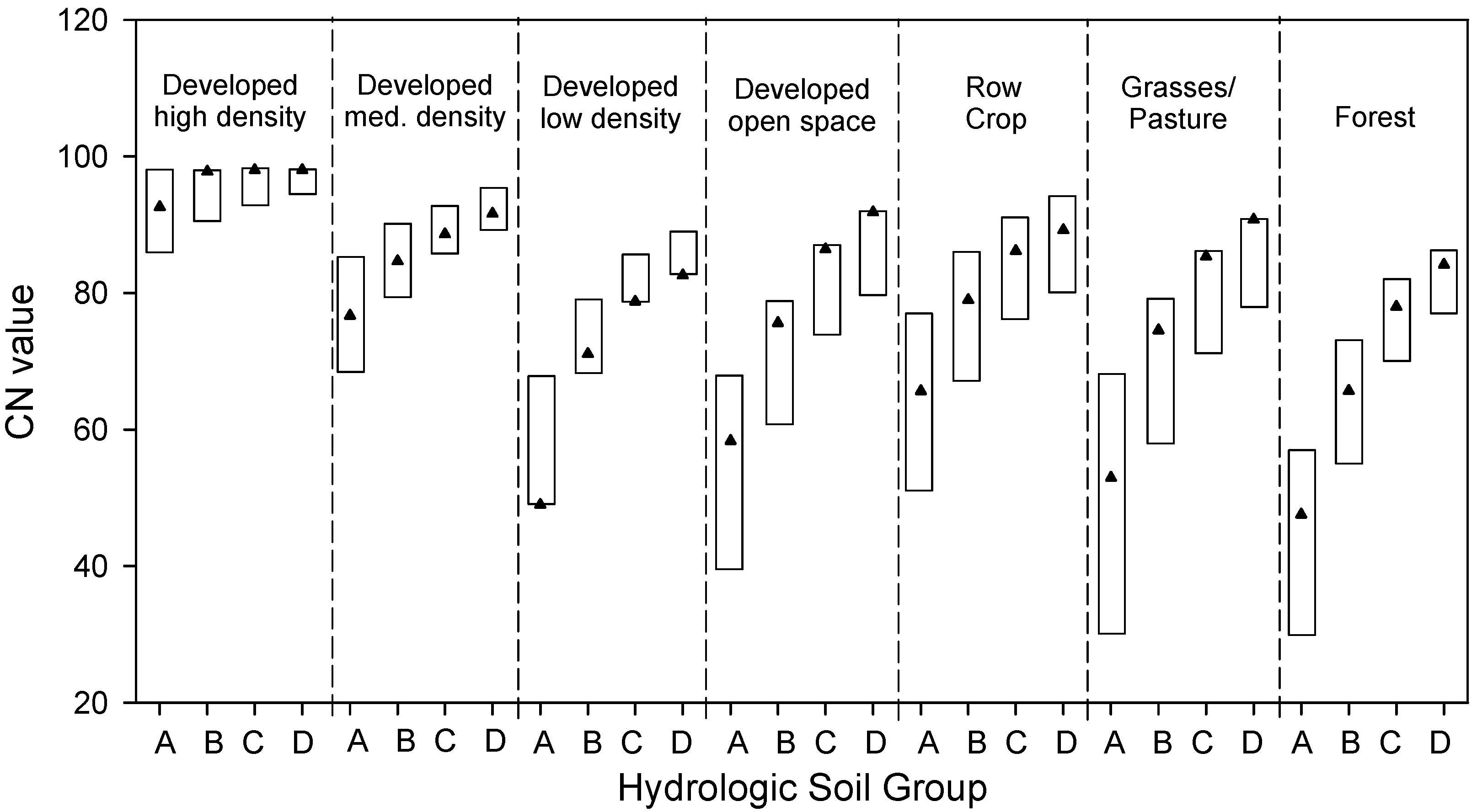
2. Background
2.1. Shuffled Complex Evolution Algorithm (SCE-UA)
2.2. Overview of L-THIA
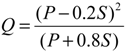
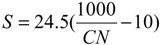
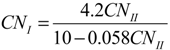
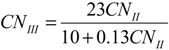
| Combination of land use and hydrologic soil group | Documented | This study | |||||
|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Average | Minimum | Maximum | Multiplication factor | ||
| Developed high density (Impervious area: 80%–100%) | A | 86 | 98 | 89 | 85 | 93 | 0.97–1.03 |
| B | 91 | 98 | 94 | 91 | 98 | ||
| C | 93 | 98 | 96 | 92 | 98 | ||
| D | 94 | 98 | 97 | 93 | 98 | ||
| Developed medium density (Impervious area: 50%–79%) | A | 68 | 85 | 77 | 74 | 80 | 0.97–1.03 |
| B | 79 | 90 | 85 | 81 | 88 | ||
| C | 86 | 93 | 89 | 86 | 93 | ||
| D | 89 | 94 | 92 | 88 | 95 | ||
| Developed low density (Impervious area: 20%–49%) | A | 51 | 68 | 51 | 49 | 53 | 0.96–1.04 |
| B | 68 | 79 | 74 | 71 | 76 | ||
| C | 79 | 86 | 82 | 79 | 85 | ||
| D | 84 | 89 | 86 | 83 | 90 | ||
| Developed open spaces | A | 39 | 68 | 54 | 49 | 58 | 0.92–1.08 |
| B | 61 | 79 | 70 | 64 | 76 | ||
| C | 74 | 86 | 80 | 74 | 86 | ||
| D | 80 | 89 | 85 | 78 | 91 | ||
| Cultivated crops | A | 51 | 77 | 64 | 59 | 69 | 0.92–1.08 |
| B | 67 | 86 | 77 | 70 | 83 | ||
| C | 76 | 91 | 84 | 77 | 90 | ||
| D | 80 | 94 | 87 | 80 | 94 | ||
| Pasture and Grasses | A | 30 | 68 | 49 | 45 | 53 | 0.92–1.08 |
| B | 58 | 79 | 69 | 63 | 74 | ||
| C | 71 | 86 | 79 | 72 | 85 | ||
| D | 78 | 89 | 84 | 77 | 90 | ||
| Forest | A | 30 | 57 | 44 | 40 | 47 | 0.92–1.08 |
| B | 55 | 73 | 64 | 59 | 69 | ||
| C | 70 | 82 | 76 | 70 | 82 | ||
| D | 77 | 86 | 82 | 75 | 88 | ||
3. Materials and Methods
CNB = 0.374 × Pimp + 60.666 (R2 = 1.0, n = 9)
CNC = 0.238 × Pimp + 74.070 (R2 = 1.0, n = 9)
CND = 0.175 × Pimp + 80.402 (R2 = 1.0, n = 9)
| AMC | Total 5-day antecedent rainfall (mm) | |
|---|---|---|
| Dormant Season | Growing Season | |
| I | Less than 12.70 | Less than 35.56 |
| II | 12.70–27.94 | 35.56–53.34 |
| III | Over 27.94 | Over 53.34 |
3.1. Study Watersheds and Data
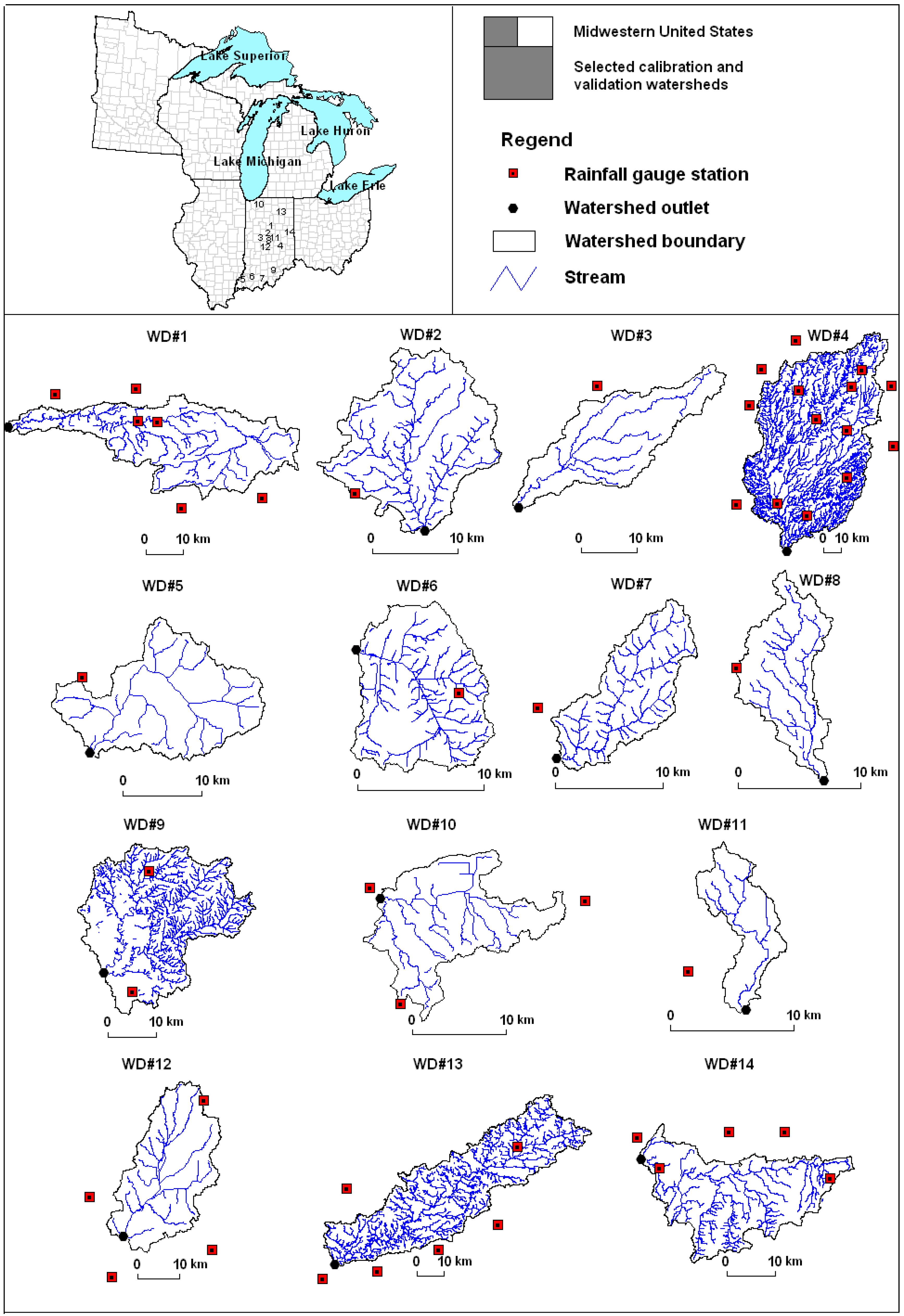
| Watershed (WD)# | Watershed name | Area (km2) | Calibration period | Validation period | USGS station | Rainfall station (COOPID) | Land use (%) * | Hyd. soil group (%) ** |
|---|---|---|---|---|---|---|---|---|
| 1 | Wildcat Creek | 1024.3 | 1996–2005 | 03334000 | 122638, 122931, 124662, 124667, 128784, 129905 | H: 1, M: 1, L: 4, O: 7, | A: 1, B: 52, | |
| 2 | Eagle Creek | 268.8 | 1996–2005 | 03353200 | 129557 | H: 0, M: 0, L: 2, O: 8, | A: 0, B: 50, | |
| 3 | Big Raccoon Creek | 364.7 | 1996–2005 | 03340800 | 121873 | H: 0, M: 0, L: 1, O: 5, | A: 0, B: 49, | |
| 4 | East Fork White River | 5844.1 | 1996–2005 | 03365500 | 121326, 121747, 123527, 123547, 124272, 124642, 124832, 125613, 125923, 126056, 126164, 126437, 127646, 127999 | H: 0, M: 1, L: 2, O: 6, | A: 0, B: 51, | |
| 5 | Big Creek | 269.2 | 1996–2005 | 03378550 | 127083 | H: 0, M: 0, L: 1, O: 7, | A: 0, B: 54, | |
| 6 | South Fork Patoka River | 110.7 | 1999–2004 | 03376350 | 128442 | H: 0, M: 0, L: 0, O: 3, | A: 0, B: 38, | |
| 7 | Middle Fork Anderson | 102.8 | 1996–2005 | 03303300 | 127724 | H: 0, M: 0, L: 0, O: 4, | A: 0, B: 61, | |
| 8 | Little Eagle Creek | 70.1 | 1996–2005 | 03353600 | 124249 | H: 10, M: 20, L: 38, O: 27, | A: 0, B: 33, | |
| 9 | Blue River | 730.9 | 1996–2005 | 03302800 | 126697, 127755 | H: 0, M: 0, L: 0, O: 5, | A: 0, B: 66, | |
| 10 | Little Calument River | 165.9 | 1996–2005 | 04094000 | 124244, 124837, 128999 | H: 0, M: 2, L: 6, O: 5, | A: 3, B: 57, | |
| 11 | Crooked Creek | 46.6 | 1996–2005 | 03351310 | 124249 | H: 5, M: 12, L: 32, O: 39, | A: 0, B: 54, | |
| 12 | Deer Creek | 623.7 | 1996–2005 | 03358000 | 121647, 122041, 125407, 128290 | H: 0, M: 0, L: 1, O: 5, | A: 0, B: 47, | |
| 13 | Ell River | 2042.5 | 1994–2004 | 03328500 | 121739, 124181, 125117, 126864, 127482, 129138, 129243 | H: 0, M: 0, L: 1, O: 6, | A: 4, B: 37, | |
| 14 | White River | 568.0 | 1996–2005 | 03347000 | 121229, 122825, 126023, 126164, 127398, 129678 | H: 0, M: 1, L: 3, O: 7, | A: 0, B: 35, |
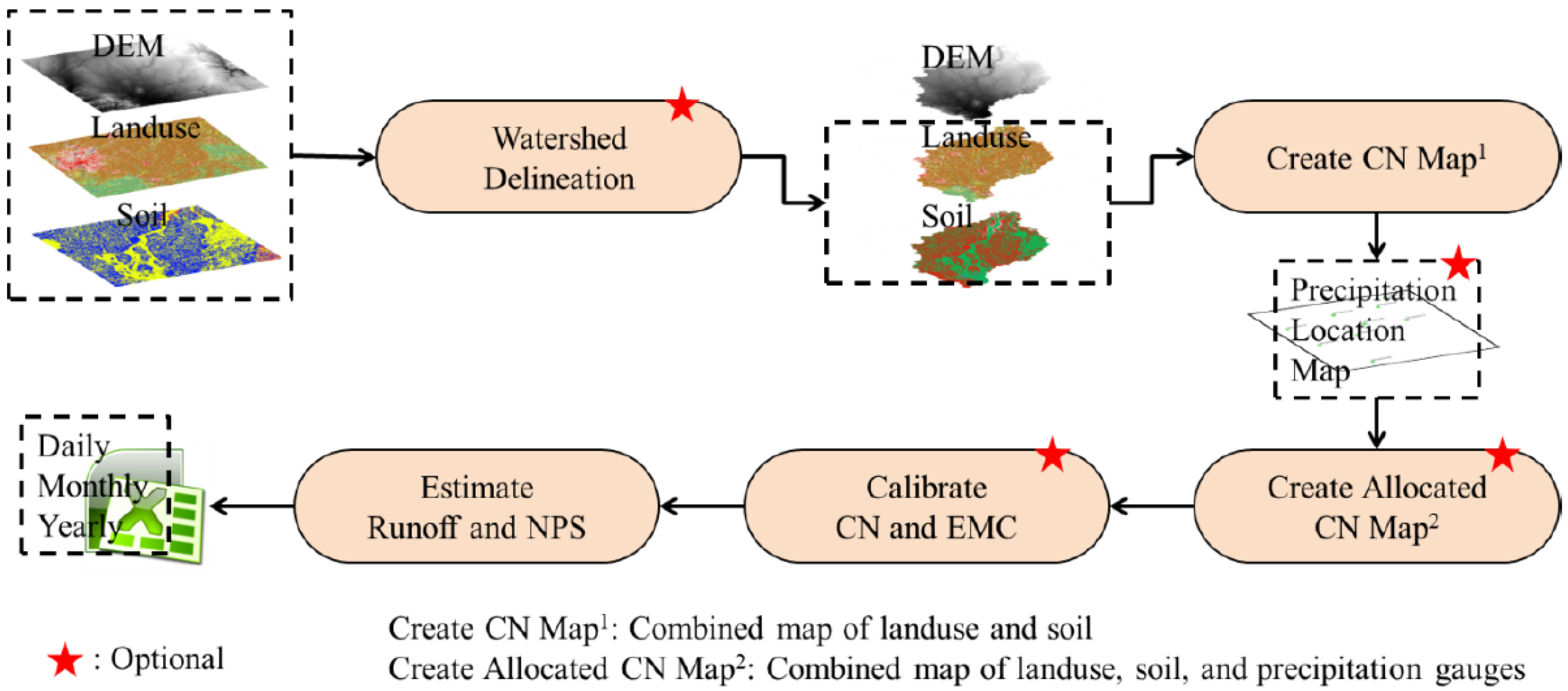
3.2. L-THIA Application
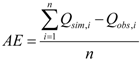
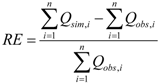
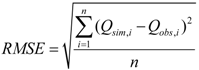
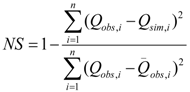
3.3. Baseline Simulations with SWAT Default Values
| NLCD 2001 land use type | Hydrologic soil group | Land use type | |||
|---|---|---|---|---|---|
| A | B | C | D | ||
| Developed-high density (80%–100%) | 87 | 92 | 94 | 95 | Industrial (84%) |
| Developed-medium density (50%–79%) | 71 | 82 | 88 | 90 | Residential-high density (60%) |
| Developed-low density (20%–49%) | 56 | 74 | 82 | 86 | Residential-medium density (38%) |
| Developed-open space | 35 | 62 | 74 | 80 | Residential-low density (12%) |
| Crop | 67 | 78 | 85 | 89 | Agricultural Land-Low Crop |
| Pasture & grass | 49 | 69 | 79 | 84 | Pasture |
| Forest | 35 | 62 | 74 | 80 | Forest-Mixed |
3.4. SCS-CN Parameters Regionalization Methods
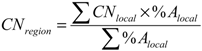
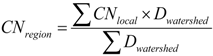

4. Results and Discussion
4.1. Baseline Simulation Results for SWAT Default SCS-CN Values
| WD ID | NS | AE | RE | RMSE |
|---|---|---|---|---|
| WD#1 | 0.53 | −6.27 | −49.12 | 13.03 |
| WD#2 | 0.49 | −8.15 | −54.57 | 15.10 |
| WD#3 | 0.44 | −6.82 | −54.32 | 14.28 |
| WD#4 | 0.36 | −8.74 | −54.94 | 16.48 |
| WD#5 | 0.46 | −11.22 | −50.11 | 20.61 |
| WD#6 | 0.40 | −5.53 | −33.63 | 11.17 |
| WD#7 | 0.10 | −12.76 | −73.63 | 24.55 |
| WD#8 | 0.27 | −12.55 | −60.33 | 17.48 |
4.2. Calibration Results
| WD ID | Individual | Global | WD ID | Individual | Global |
|---|---|---|---|---|---|
| WD#1 | 0.81 | 0.60 | WD#5 | 0.74 | 0.64 |
| WD#2 | 0.76 | 0.75 | WD#6 | 0.65 | 0.51 |
| WD#3 | 0.71 | 0.68 | WD#7 | 0.49 | 0.38 |
| WD#4 | 0.70 | 0.67 | WD#8 | 0.79 | 0.76 |
4.3. Comparison of Regionalization Methods
| Methods | Validation watershed # | |||||||
|---|---|---|---|---|---|---|---|---|
| #9 | #10 | #11 | #12 | #13 | #14 | Mean | STD | |
| Method 1 | 0.43 | 0.41 | 0.55 | 0.46 | 0.44 | 0.57 | 0.48 | 0.09 |
| Method 2 | 0.43 | 0.44 | 0.55 | 0.48 | 0.40 | 0.61 | 0.48 | 0.07 |
| Method 3 | 0.49 | 0.41 | 0.60 | 0.47 | 0.42 | 0.59 | 0.50 | 0.08 |
| Method 4 | 0.49 | 0.43 | 0.60 | 0.48 | 0.40 | 0.61 | 0.50 | 0.08 |
| Method 5 | 0.49 | 0.40 | 0.60 | 0.44 | 0.47 | 0.57 | 0.48 | 0.09 |
| Method 6 | 0.75 | 0.43 | 0.66 | 0.49 | 0.52 | 0.66 | 0.58 | 0.13 |
| Method 7 | 0.60 | 0.53 | 0.71 | 0.56 | 0.49 | 0.62 | 0.57 | 0.08 |
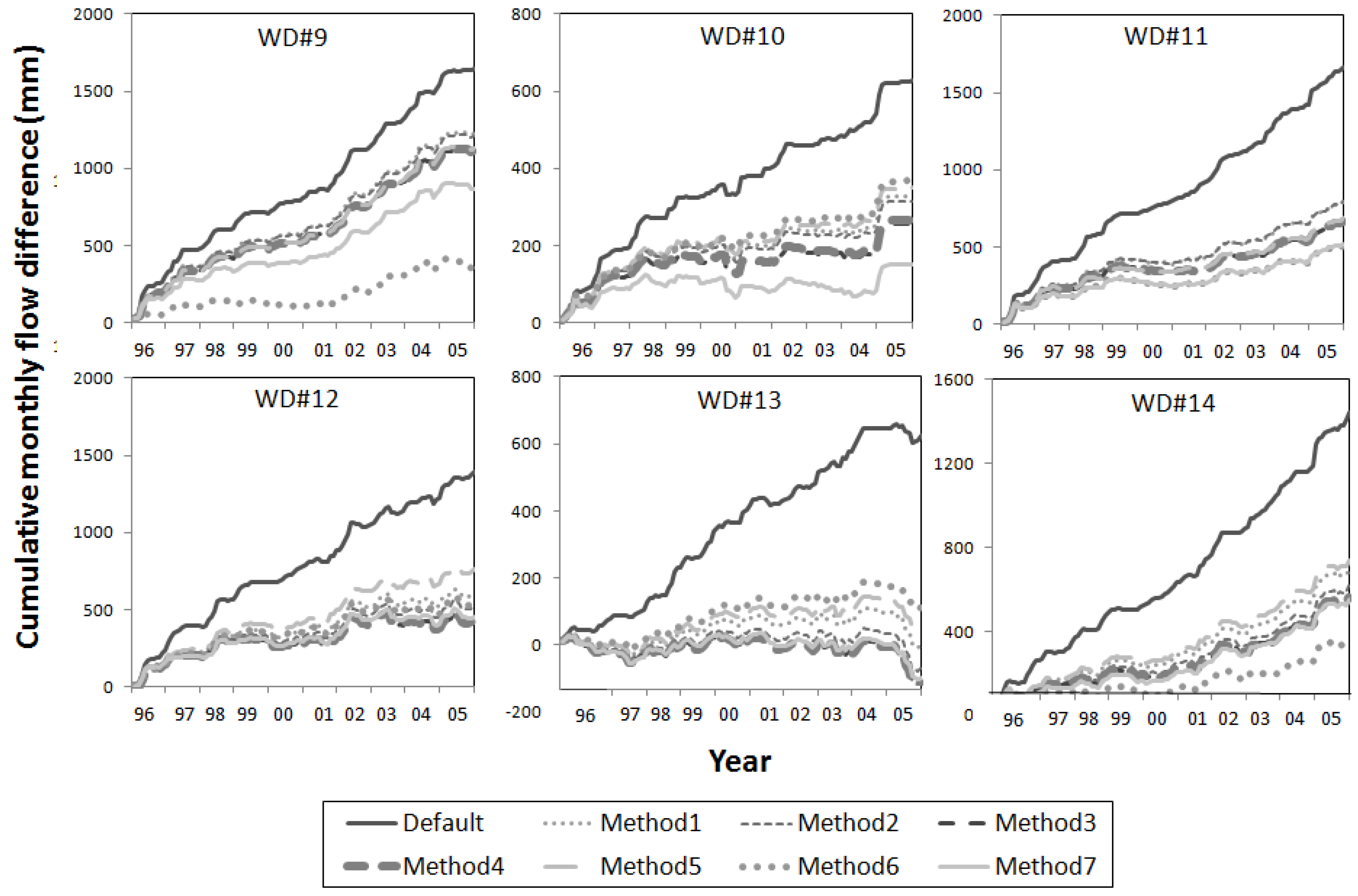
| Methods | Arithmetic mean | Area weighted | Distance weighted | Nearest | Global calibration | ||
|---|---|---|---|---|---|---|---|
| Land use | Soil | Both | |||||
| Default | 0.001 * | 0.001 * | 0.001 * | 0.001 * | 0.001 * | 0.001 * | 0.001 * |
| Method 1 | 0.507 | 0.167 | 0.146 | 0.303 | 0.093 | 0.008 * | |
| Method 2 | 0.482 | 0.233 | 0.735 | 0.141 | 0.022 ** | ||
| Method 3 | 0.456 | 0.797 | 0.105 | 0.003 * | |||
| Method 4 | 0.659 | 0.143 | 0.009 * | ||||
| Method 5 | 0.074 | 0.045 * | |||||
| Method 6 | 0.935 | ||||||
| Method 7 | |||||||

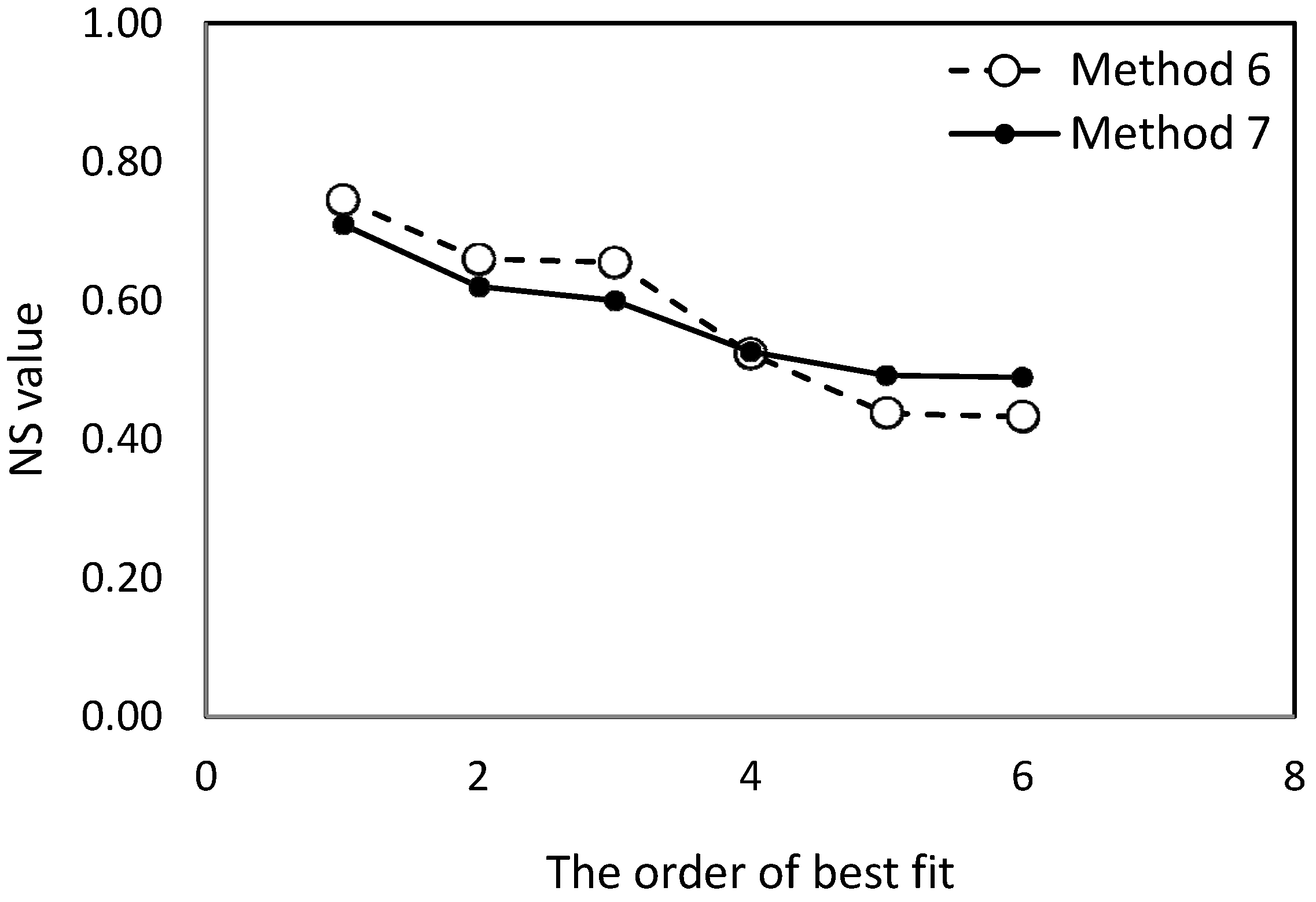
4.4. Regionalized SCS-CN Parameters for Indiana
| Cover description and AMC condition | Calibrated parameters | Hydrologic characteristics | |
|---|---|---|---|
| SCS-CN Value | Developed high density | A:93 B:98 C:98 D:98 | Impervious area: paved parking lots, roofs, and driveways |
| Developed medium density | A:80 B:88 C:93 D:96 | Industrial—75% of impervious area | |
| Developed low density | A:51 B:73 C:81 D:85 | Residential—average lot size: 1/3 acre | |
| Developed open space | A:50 B:64 C:74 D:78 | Grass cover—good condition (> 75%) | |
| Crop | A:66 B:79 C:86 D:89 | Row crops with straight row and crop residue cover, and poor hydrologic condition | |
| Pasture/Grass | A:53 B:75 C:85 D:91 | Continuous forage for grazing—poor * | |
| Wood | A:48 B:66 C:78 D:84 | Wood—poor ** | |
| Total 5-day rainfall (mm) | AMCI | Less than 0.08 | Dormant season |
| AMC II | 0.08–0.69 | ||
| AMC III | Over 0.69 | ||
| AMCI | Less than 17.12 | Growing season | |
| AMC II | 17.12–53.16 | ||
| AMC III | Over 53.16 | ||
5. Conclusions
Author Contributions
Conflicts of Interests
References
- Chapra, S.C. Surface Water-Quality Modeling; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Eckhardt, K.; Arnold, J.G. Automatic calibration of distributed catchment model. J. Hydrol. 2001, 251, 103–109. [Google Scholar] [CrossRef]
- Shoemaker, L.; Lahlou, M.; Bryer, M.; Kumar, D.; Kratt, K. Compendium of Tools for Watershed Assessment and TMDL Development; EPA-841-B-97-006; USEPA Office of Water: Washington, DC, USA, 1997.
- Kim, U.; Kaluarachchi, J.J. Application of parameter estimation and regionalization methodologies to ungauged basins of the Upper Blue Nile River Basin, Ethiopia. J. Hydol. 2008, 362, 39–56. [Google Scholar] [CrossRef]
- Mosley, M.P. Delimitation of New Zealand hydrologic regions. J. Hydrol. 1981, 49, 173–192. [Google Scholar] [CrossRef]
- Vandewiele, G.L.; Elias, A. Monthly water balance of ungauged catchments obtained by geographical regionalization. J. Hydrol. 1995, 170, 277–291. [Google Scholar] [CrossRef]
- Post, D.A.; Jones, J.A.; Grant, G.E. An improved methodology for predicting the daily hydrologic response of ungauged catchments. Environ. Model. Softw. 1998, 13, 395–403. [Google Scholar] [CrossRef]
- Beven, K.J.; Freer, J.; Schulz, K. The use of generalized likelihood measures for uncertainty estimation in higher-order models of environmental systems. In Nonlinear and Nonstaionary Signal Processing; Fizgerald, W.J., Smith, R.C., Walden, A.T., Young, P.C., Eds.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Wagener, T.; Wheater, H.S. Parameter estimation and regionalization for continuous rainfall-runoff models including uncertainty. J. Hydrol. 2006, 320, 132–154. [Google Scholar] [CrossRef]
- United States Department of Agriculture, Soil Conservation Service (USDA-SCS). National Engineering Handbook Hydrology Chapters: Chapter 10 Estimation of Direct Runoff from Storm Rainfall; USDA-SCS: Washington, DC, USA, 2004.
- United States Department of Agriculture, Soil Conservation Service (USDA-SCS). A Method for Estimating Volume and Rate of Runoff in Small Watersheds; Tech. Paper 149; USDA-SCS: Washington, DC, USA, 1973.
- Young, D.F.; Carleton, J.N. Implementation of a probabilistic curve number method in the PRZM runoff model. Environ. Model. Softw. 2006, 21, 1172–1179. [Google Scholar] [CrossRef]
- United States Department of Agriculture, Natural Resources Conservation Service (USDA-NRCS). Urban Hydrology for Small Watersheds; Technical Release 55, USDA-NRCS, 210-VI-TR-55; USDA-NRCS: Washington, DC, USA, 1986.
- Mohammed, H.; Yohannes, F.; Zeleke, G. Validation of agricultural non-point source (AGNPS) pollution model in Kori watershed, South Wollo, Ethiopia. Int. J. Appl. Earth Obs. Geoinf. 2004, 6, 97–109. [Google Scholar] [CrossRef]
- Grunwald, S.; Norton, L.D. Calibration and validation of a non-point source pollution model. Agric. Water Manag. 2000, 45, 17–39. [Google Scholar] [CrossRef]
- Cooper, V.A.; Nguyen, V.T.V.; Nicell, J.A. Evaluation of global optimization methods for conceptual rainfall-runoff model calibration. Water Sci. Technol. 1997, 36, 53–60. [Google Scholar] [CrossRef]
- Kuczera, G. Efficient subspace probabilistic parameter optimization for catchment models. Water Resour. Res. 1997, 33, 177–185. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 1015–1031. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Effective and efficient global optimization for conceptual rainall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Duan, Q.; Gupta, V.K.; Sorooshian, S. A shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Grove, M.; Harbor, J.; Engel, B.A.; Muthukrishnan, S. Impact of urbanization on surface hydrology, Little Eagle Creek, Indiana, and analysis of L-THIA model sensitivity to data resolution. Phys. Geogr. 2001, 22, 135–153. [Google Scholar]
- Kim, Y.; Engel, B.A.; Lim, K.J.; Larson, V.; Duncan, B. Runoff impacts of land-use change in Inidana river lagoon watershed. J. Hydrol. Eng. 2002, 7, 245–251. [Google Scholar] [CrossRef]
- Park, Y.S.; Lim, K.J.; Theller, L.; Engel, B.A. L-THIA GIS Manual; Department of Agricultural and Biological Engineering, Purdue University: West Lafayette, IN, USA, 2013. [Google Scholar]
- Tang, Z.; Engel, B.A.; Pijanowski, B.C.; Lim, K.L. Forecasting land use change and its environmental impact at a watershed scale. J. Environ. Manag. 2005, 76, 35–45. [Google Scholar] [CrossRef]
- Lim, K.J.; Engel, B.A.; Muthukrishnan, S.; Harbor, J. Effect of initial abstraction and urbanization on estimated runoff using CN technology. J. Am. Water Resour. Assoc. 2006, 42, 629–644. [Google Scholar] [CrossRef]
- Long Term Hydrologic Impact Analysis (L-THIA). Available online: https://engineering.purdue.edu/~lthia/ (accessed on 11 March 2014).
- Mack, M.J. HER-Hydrologic evaluation of runoff; the soil conservation service curve number technique as an interactive computer model. Comput. Geosci. 1995, 21, 929–935. [Google Scholar] [CrossRef]
- National Geospatial Center of Excellence. Available online: http://www.nrcs.usda.gov/wps/portal/nrcs/main/national/ngce/ (accessed on 11 March 2014).
- Multi-Resolution Land Characteristics Consortium (MRLC). Available online: http://www.mrlc.gov/index.php (accessed on 11 March 2014).
- Lyne, V.D.; Hollick, M. Stochastic Time-Variable Rainfall-Runoff Modeling; Hydrology and Water Resources Symposium, Institution of Engineers Australia: Perth, Australia, 1979. [Google Scholar]
- Arnold, J.G.; Allen, P.M. Validation of automated methods for estimating baseflow and groundwater recharge from stream flow records. J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- Eckhardt, K. How to construct recursive digital filters for baseflow separation. Hydrol. Process. 2005, 19, 507–515. [Google Scholar] [CrossRef]
- Lim, K.J.; Engel, B.A.; Tang, Z.; Choi, J.; Kim, K.S.; Muthukrishnan, S.; Tripathy, D. Automated web GIS based hydrograph analysis tool, WHAT. J. Am. Water Resour. Assoc. 2005, 41, 1407–1416. [Google Scholar] [CrossRef]
- WHAT: Web-based Hydrograph Analysis Tool. Available online: https://engineering.purdue.edu/~what/ (accessed on 11 March 2014).
- Environmental Systems Research Institute (ESRI). What’s New in ArcView 3.1, 3.2, and 3.3; ESRI: Redlands, CA, USA, 2002. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual model. Part 1: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Loague, K.; Green, R.E. Statistical and graphical methods for evaluating solute transport models: Overview and application. J. Contam. Hydrol. 1991, 7, 51–73. [Google Scholar] [CrossRef]
- Parajka, J.; Merz, R.; Blöschl, G. A comparison of regionalization methods for catchment model parameters. Hydrol. Earth Syst. Sci. 2005, 9, 157–171. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modeling—A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Zhang, M. A comparison of the curve number and Green-Ampt models in a agricultural watershed. Trans. ASABE 2013, 56, 61–69. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Romano, N. Green-Ampt curve-number mixed procedure as an empirical tool for rainfall-runoff modeling in small and ungauged basins. Hydrol. Process. 2013, 27, 1253–1264. [Google Scholar] [CrossRef]
- Garen, D.C.; Moore, D.S. Curve number hydrology in water quality modeling: Uses, abuses, and future directions. J. Am. Water Resour. Assoc. 2005, 41, 377–388. [Google Scholar]
- Woodward, D.E.; Hoeft, C.C.; Mullem, J.V.; Ward, T.J. Discussion of “Modifications to SCS-CN method for long-term hydrologic simulation” by K. Geetha, S.K. Mishra, T.I. Eldho, A.K. Rastogi, and R.P. Pandey. J. Irrig. Drain Eng. 2010, 136, 444–446. [Google Scholar]
- Eli, R.N.; Lamont, S.J. Curve numbers and urban runoff modeling—Application limitations. In Low Impact Development 2010: Redefining Water in the City, Proceedings of the 2010 International Low Impact Development Conference, San Francisco, CA, USA, 11–14 April 2010; pp. 405–418.
- Grimaldi, G.; Petroselli, A.; Romano, N. Curve-number/Green-Ampt mixed procedure for streamflow predictions in ungauged basins: Parameter sensitivity analysis. Hydrol. Process. 2013, 27, 1265–1275. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jeon, J.-H.; Lim, K.J.; Engel, B.A. Regional Calibration of SCS-CN L-THIA Model: Application for Ungauged Basins. Water 2014, 6, 1339-1359. https://doi.org/10.3390/w6051339
Jeon J-H, Lim KJ, Engel BA. Regional Calibration of SCS-CN L-THIA Model: Application for Ungauged Basins. Water. 2014; 6(5):1339-1359. https://doi.org/10.3390/w6051339
Chicago/Turabian StyleJeon, Ji-Hong, Kyoung Jae Lim, and Bernard A. Engel. 2014. "Regional Calibration of SCS-CN L-THIA Model: Application for Ungauged Basins" Water 6, no. 5: 1339-1359. https://doi.org/10.3390/w6051339
APA StyleJeon, J.-H., Lim, K. J., & Engel, B. A. (2014). Regional Calibration of SCS-CN L-THIA Model: Application for Ungauged Basins. Water, 6(5), 1339-1359. https://doi.org/10.3390/w6051339





