A New Method for Urban Storm Flood Inundation Simulation with Fine CD-TIN Surface
Abstract
:1. Introduction
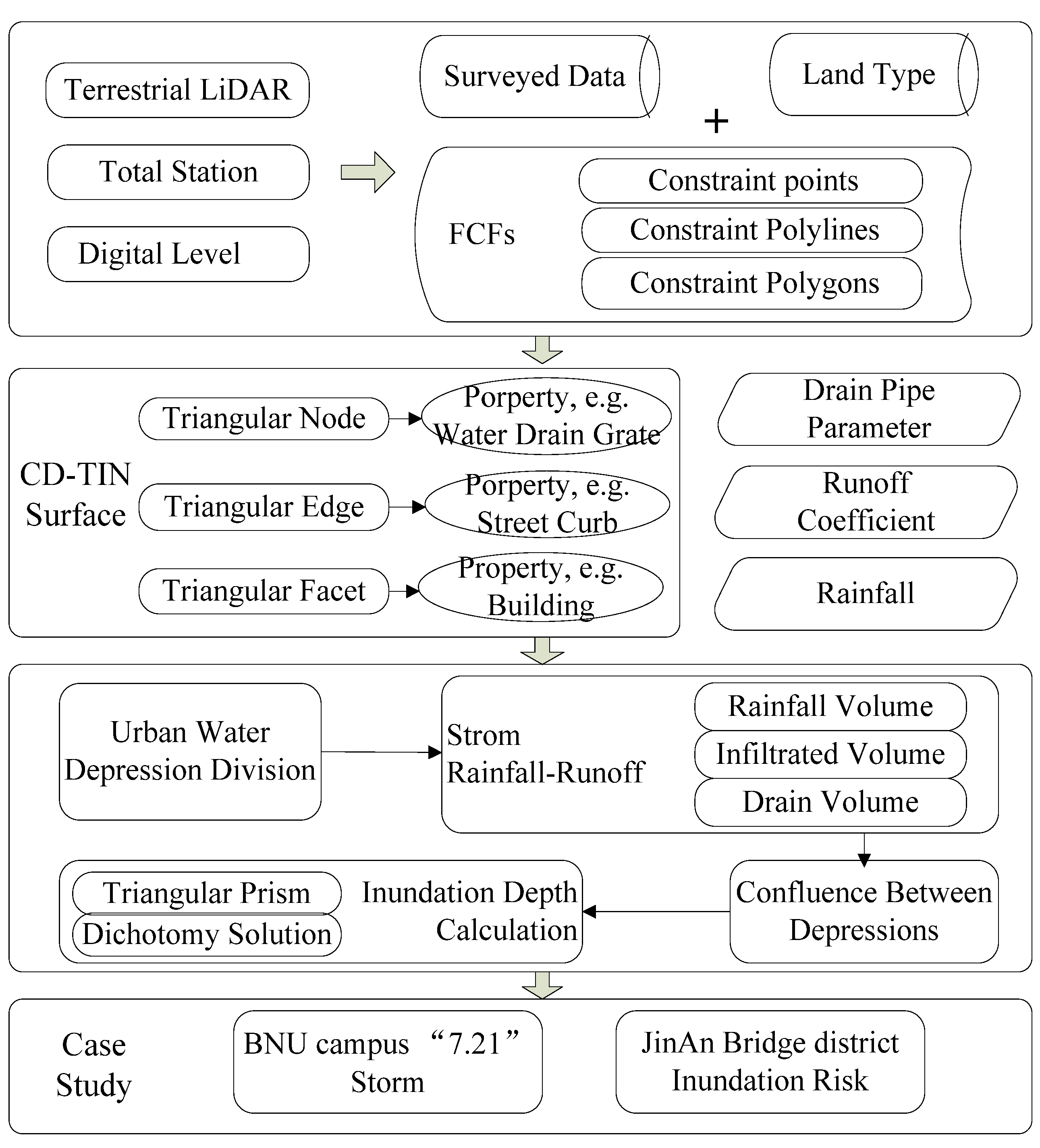
2. Data Acquisition and Urban Surface Modeling
2.1. Data Acquisition and Preprocess
| Constrain Features | Data Type | Data Organization |
|---|---|---|
| Water drain grates, Down comers, Outlet of a region, etc. | Constrained point | Shapefile PointZM |
| Road cambers, Street curbs, Road isolation strip, Walls, etc. | Constrained polyline | Shapefile PolylineZM |
| Buildings (or other man-made structures), Grass lands, Playgrounds, Lakes (or other water bodies), etc. | Constrained polygon | Shapefile PolygonZM |
2.2. Modeling Urban Surface with CD-TIN
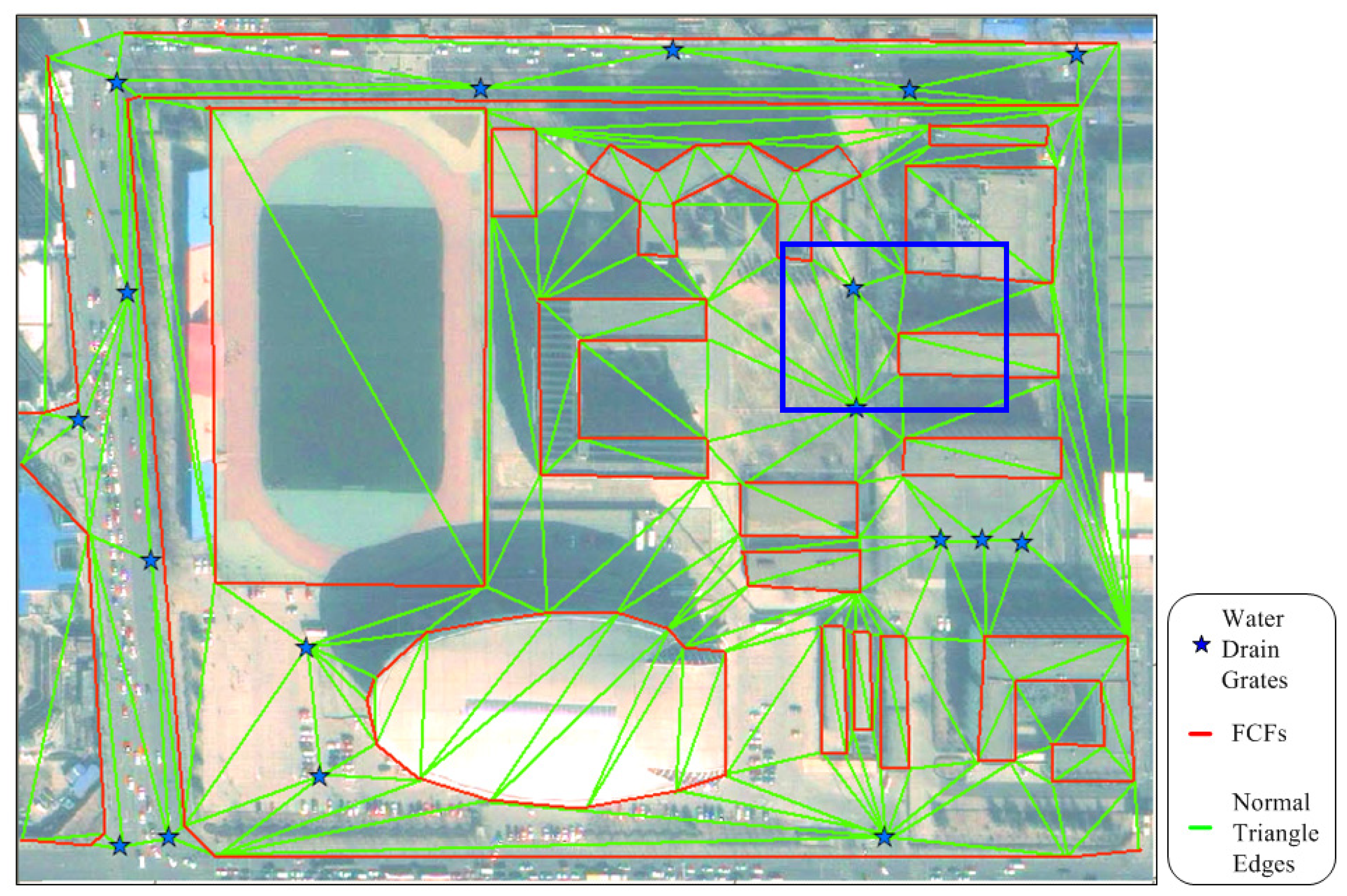
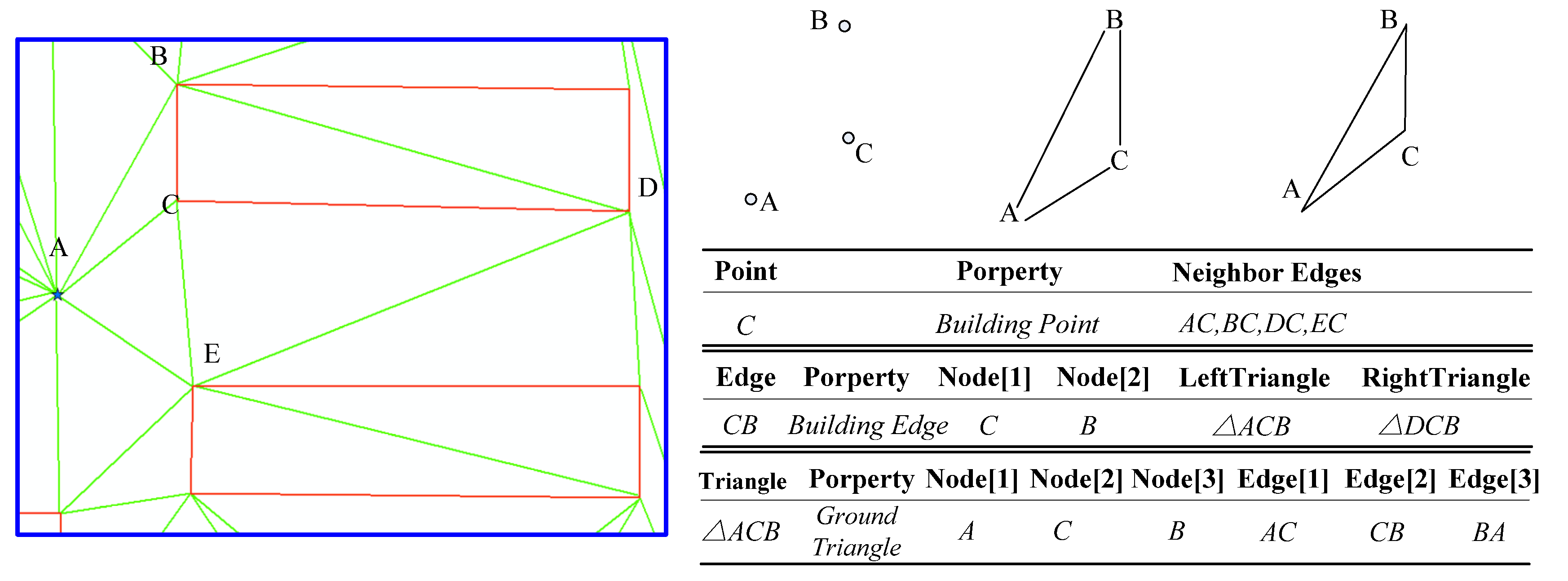
3. Runoff and Confluence
3.1. Computational Urban Water Depression Division


3.2. Storm Rainfall Runoff
3.2.1. Rainfall Volume Qf

3.3.2. Infiltrated Volume Qu
| Land type | Runoff coefficient | Value #1 | Value #2 | Value #3 |
|---|---|---|---|---|
| Building surface, concrete, or asphalt pavement road | 0.85~0.95 | 0.85 | 0.90 | 0.95 |
| Large rubble paved road, or gravel road with asphalt surface | 0.55~0.65 | 0.55 | 0.60 | 0.65 |
| Gradation macadam road | 0.40~0.50 | 0.40 | 0.45 | 0.50 |
| Masonry brick or gravel road | 0.35~0.40 | 0.35 | 0.375 | 0.40 |
| Unpaved soil road | 0.25~0.35 | 0.25 | 0.275 | 0.35 |
| Garden or green land | 0.10~0.20 | 0.10 | 0.15 | 0.20 |
| Water area | 0 | 0 | 0 | 0 |
3.3.3. Drain Volume Qd
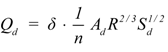
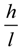 , where h is the elevation difference of original node and end node; l is the length of conduit.
, where h is the elevation difference of original node and end node; l is the length of conduit.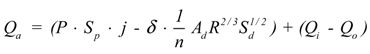
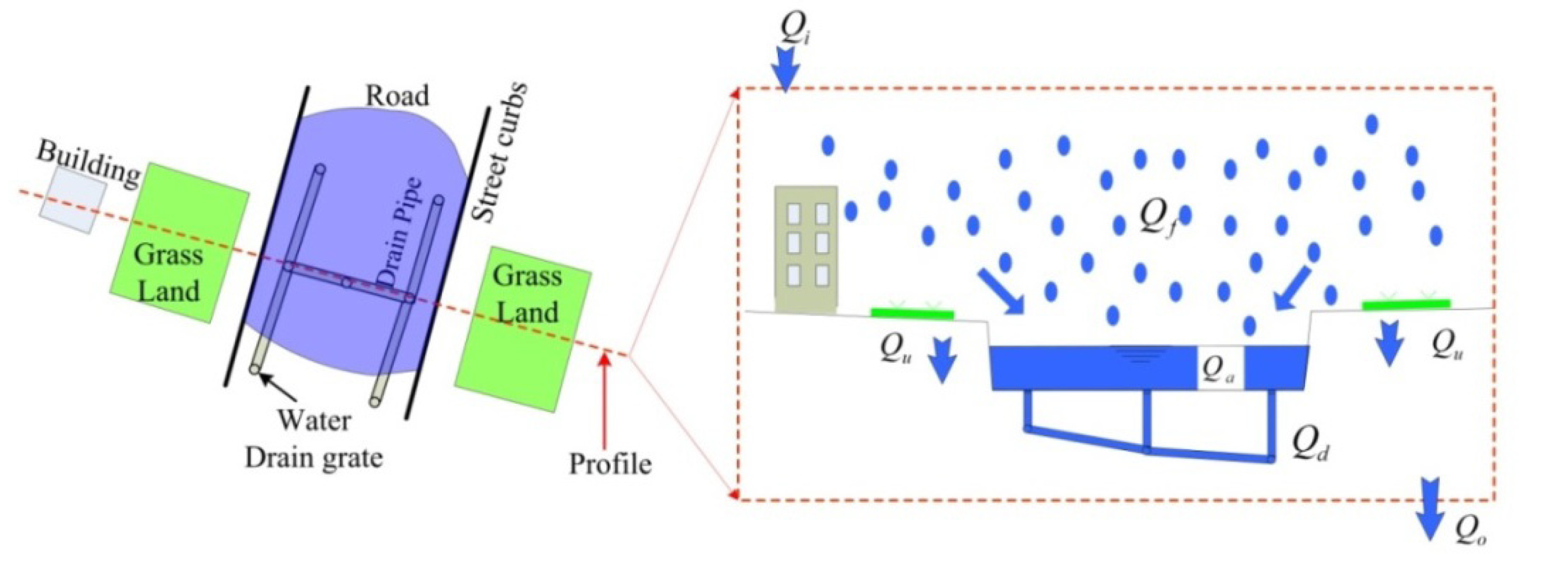
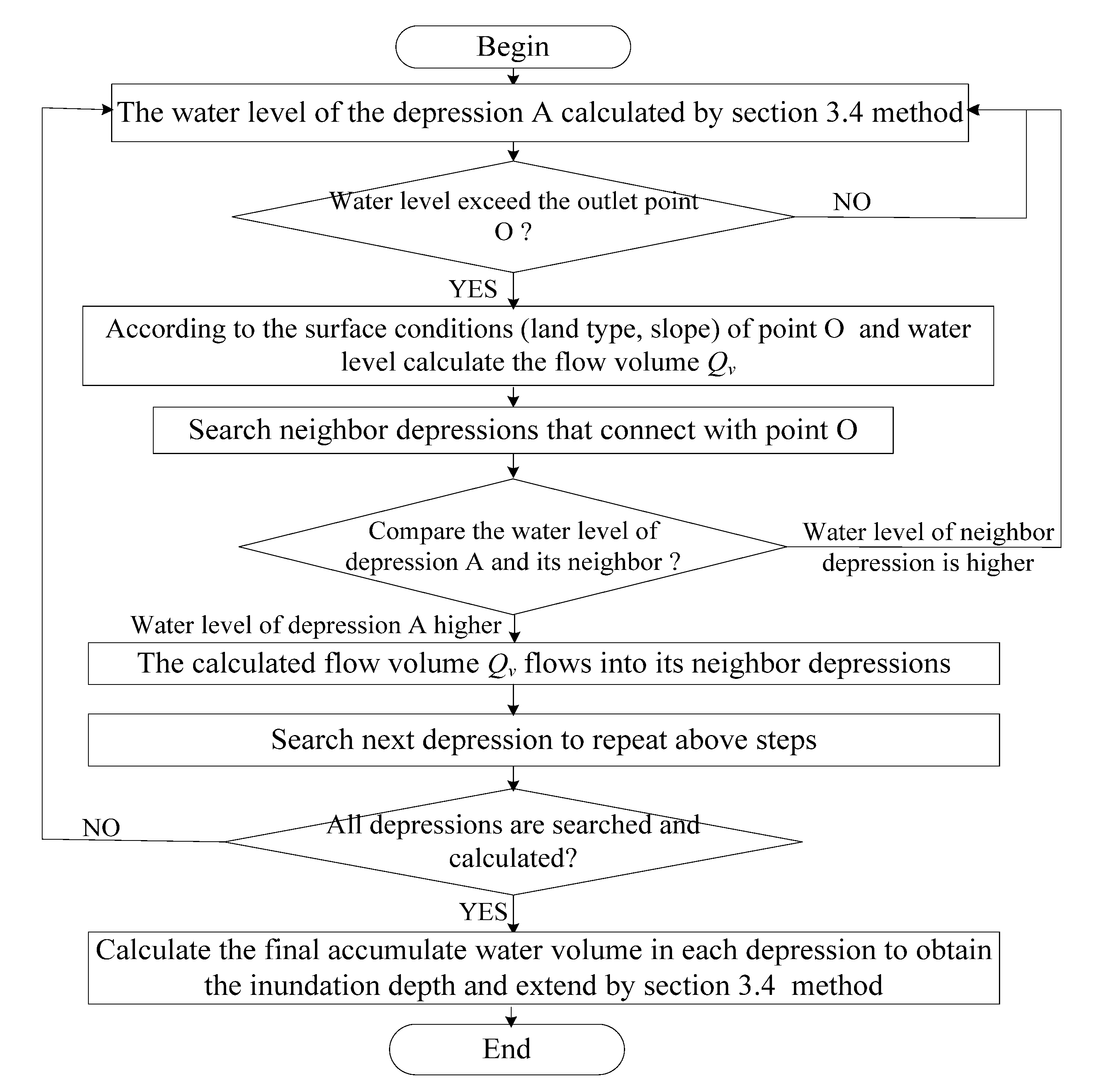
3.3. Confluence between Depressions (Qi, Qo)
- (1)
- Judge whether the water level of depression A (Ha) arrive at the outlet point O; If not, Ha continues to rise, else go to step (2);
- (2)
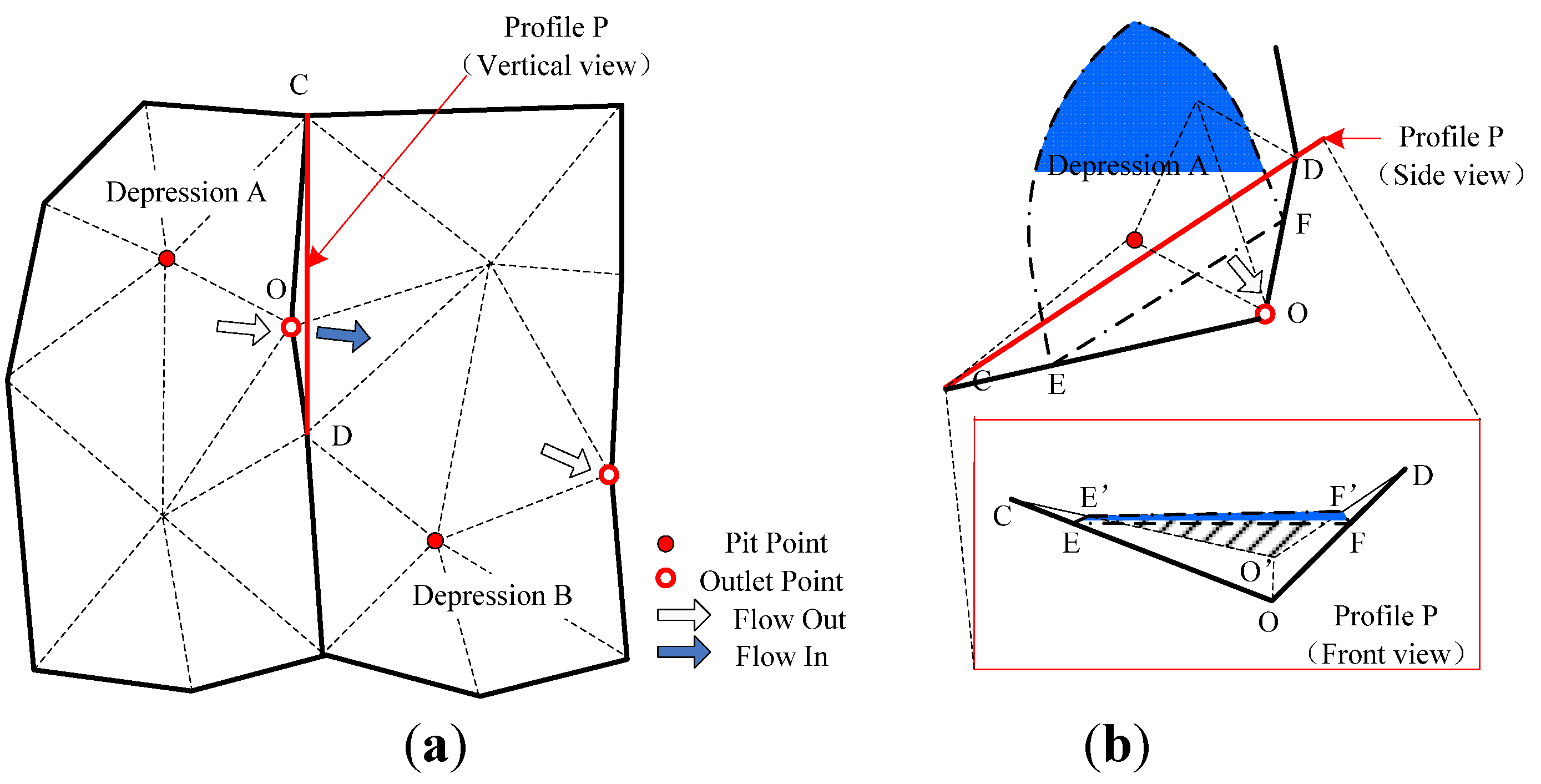
- Refer to the conditions of urban surface (land type, slope) and water level; employ empirical Equation (7) [50] to calculate the overland flow water volume Qv:Where, As is the cross section of accumulated water on the outlet point O (m2); k is the constant parameter of overland flow (m/s), which can be obtained from Hao’s research [49]; S is the average slope of the ground. To calculate As, as shown in Figure 8b, we draw the vertical profile P along CD. Then the water surface (blue polygon) insects CO, DO at E and F. Point E, O, F project on P as E’, O’, F’. Thus, As is calculated as the area of △E’O’F’;
- (3)
- Search the water depressions that connect with O; Judge Ha>Hb, then the accumulated water in depression A flows to depression B at the volume of Qv. Hence, the Qo of depression A is Qv, Qi of depression B is Qv, and vice versa;
- (4)
- All urban water depressions repeat Steps (1)–(3) to calculate the water confluence which are quantified as the Qi and Qo;
- (5)
- Calculate the final accumulated water volume in each depression referring to Equation (6).
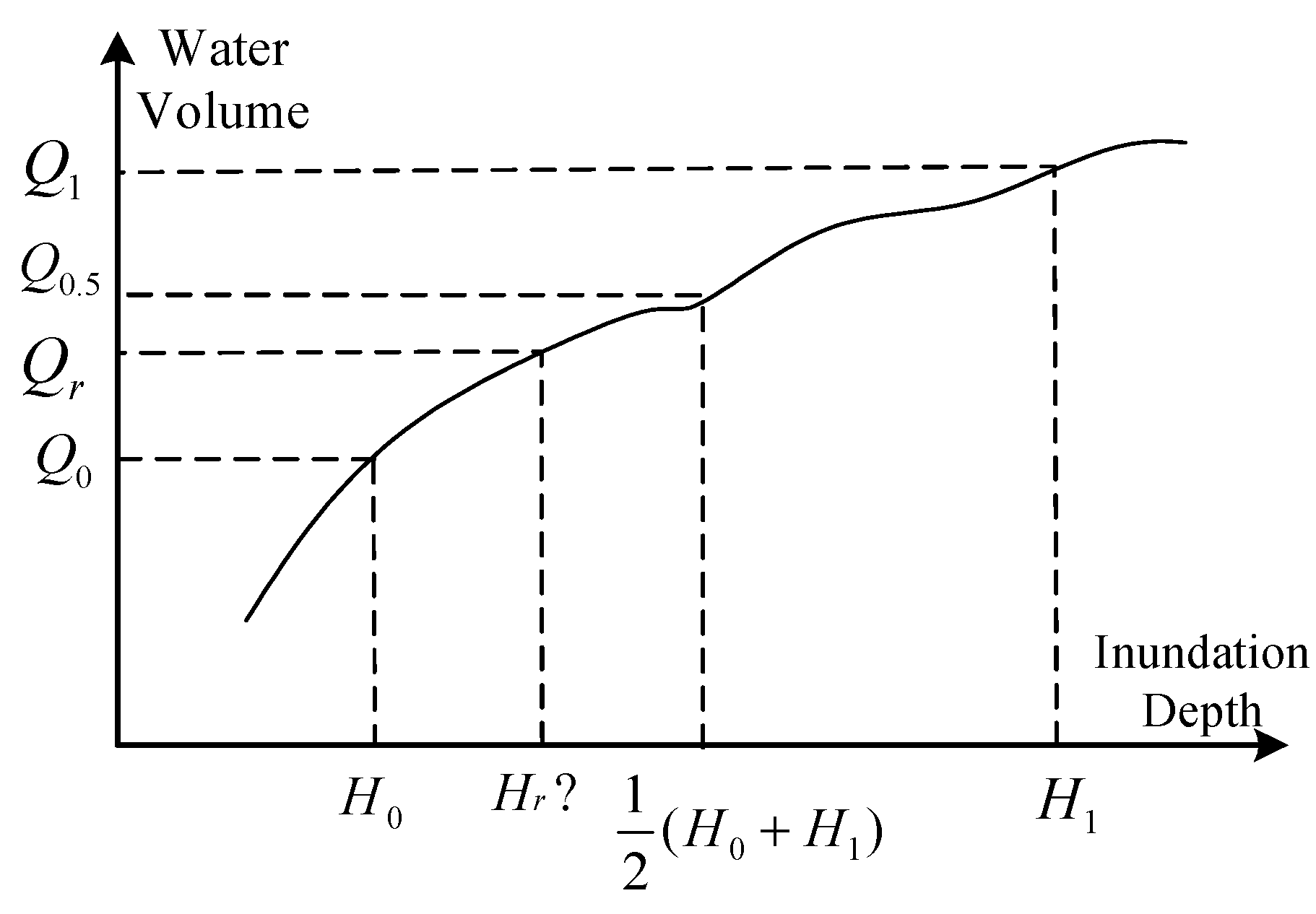
3.4. Inundation Depth Calculation
- (1)
- Initialize the maximum (H1) and minimum (H0) inundation depth;
- (2)
- Within each basin which consist of triangular-prism sets, calculate the water volume Q0, Q1 under the inundation depth of H0 and H1;
- (3)
- If Q0 = Qr then Hr = H0; else if Q1 = Qr then Hr = H1; otherwise calculate the water volume Q0.5 under the water surface of H0.5, which equals
;
- (4)
- If Q0.5 = Qr, then Hr = H0.5; else if Q0.5 > Qr, then Q1 = Q0.5 and H1 = H0.5; otherwise if Q0.5 < Qr, then Q0 = Q0.5 and H0 = H0.5;
- (5)
- Go to Step (2) until obtaining the Hr.

4. BNU Main Campus Case Study
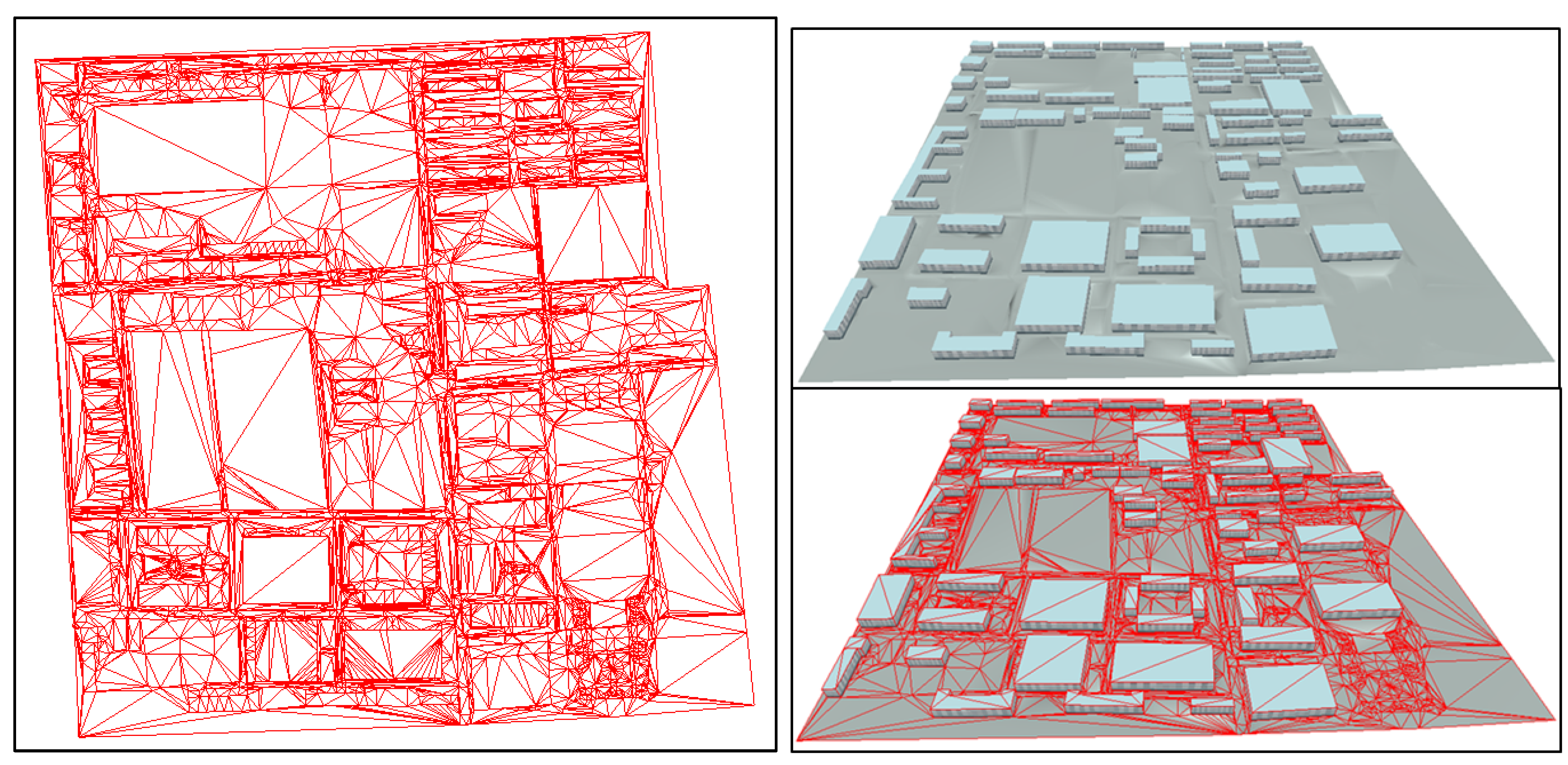
4.1. Urban Surface Modeling


4.2. Inundation Simulation
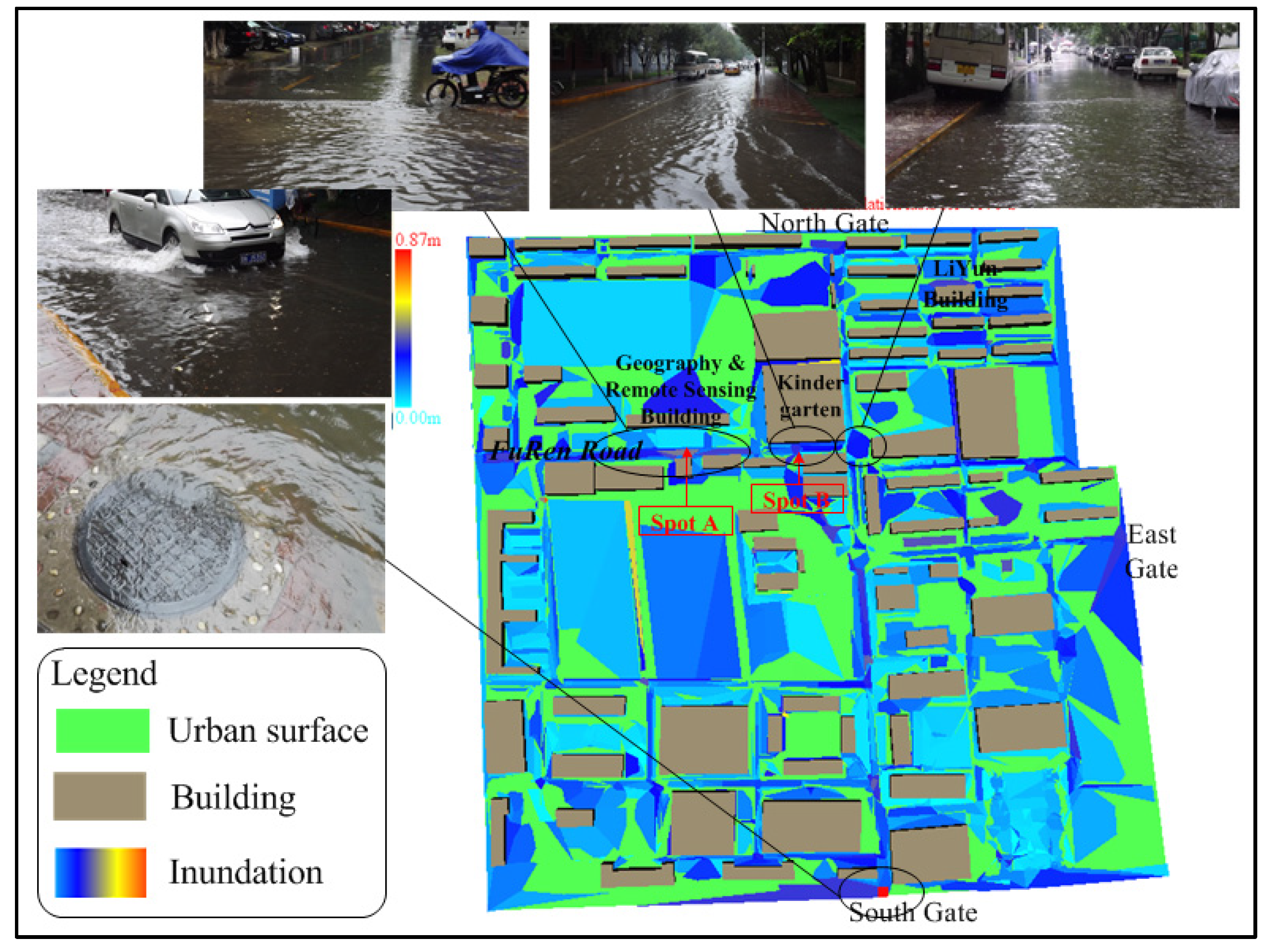
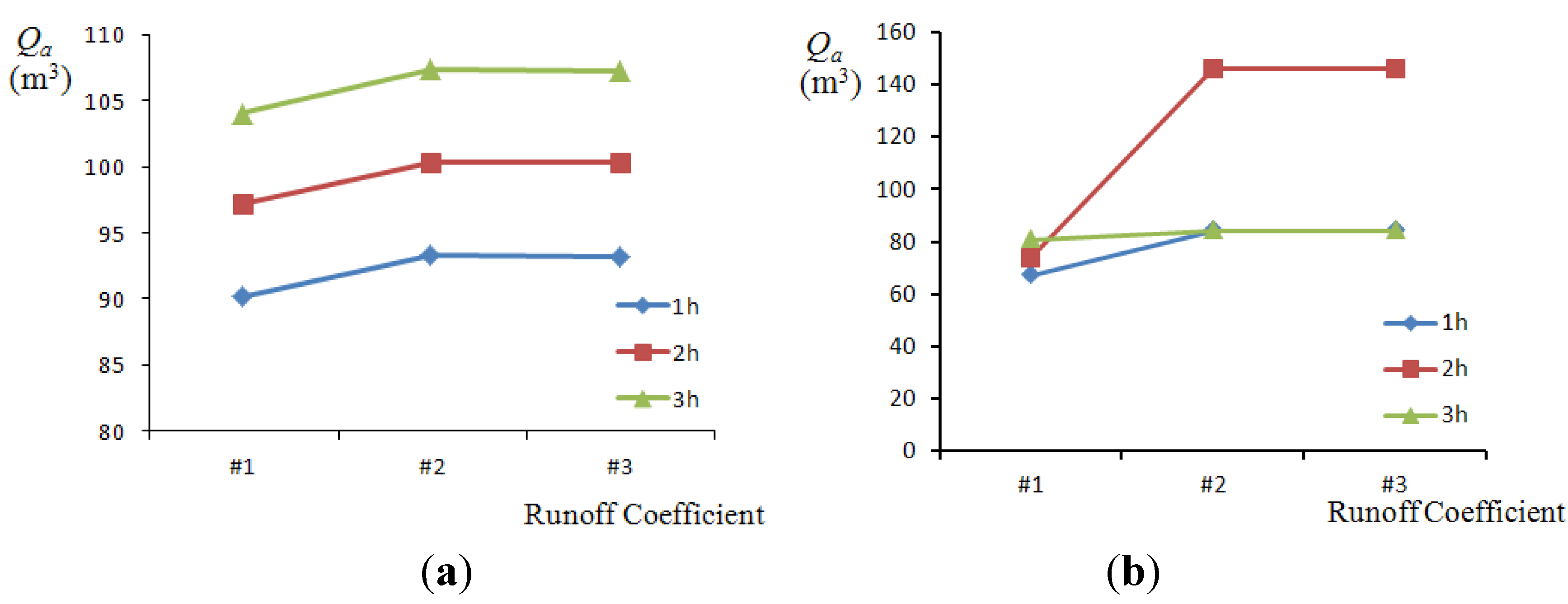
| Used Runoff Coefficient | Record Depth A | Simulation Result | Relative Error | Record Depth B | Simulation Result | Relative Error |
|---|---|---|---|---|---|---|
| Value #1 | 42 | 35 | 16.7% | 36 | 34 | 5.6% |
| Value #2 | 42 | 37 | 9.6% | 36 | 33 | 8.3% |
| Value #3 | 42 | 38 | 9.5% | 36 | 33 | 8.3% |

5. Conclusions and Discussion
- (a)
- The model focuses on the detailed surveyed urban surfaces with fine CD-TIN representation instead of raster. It couples the fine constrained urban features, such as street curbs, road cambers, ans water drain grates, which greatly influence urban water flow;
- (b)
- The model can handle the storm flood with a lack of detailed drainage data, especially the discharge of the subsurface drainage system, or urban environments with a built-in sewer system;
- (c)
- The model employs the GIS-based dichotomy numerical simulation method, which avoids the time-consuming problem of 1D or 2D equation numerical calculation. It can provide a practical rapid inundation solution for urban storm flood simulation.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fewtrell, T.J.; Duncan, A.; Sampson, C.C.; Neal, J.C.; Bates, P.D. Benchmarking urban flood models of varying complexity and scale using high resolution terrestrial LiDAR data. Phys. Chem. Earth Parts A B C 2011, 36, 281–291. [Google Scholar] [CrossRef]
- Smith, M.B. Comment on ‘Analysis and modeling of flooding in urban drainage systems’. J. Hydrol. 2006, 317, 355–363. [Google Scholar] [CrossRef]
- Schmitt, T.G.; Thomas, M.; Ettrich, N. Analysis and modeling of flooding in urban drainage systems. J. Hydrol. 2004, 299, 300–311. [Google Scholar] [CrossRef]
- Maksimović, Č.; Prodanović, D.; Boonya-Aroonnet, R.S.; Leitão, J.P.; Djordjević, S.; Allitt, D.R. Overland flow and pathway analysis for modelling of urban pluvial flooding. J. hydraul. Res. 2009, 47, 512–523. [Google Scholar] [CrossRef]
- Djordjević, S.; Prodanović, D.; Maksimović, C.; Ivetić, M.; Savić, D. SIPSON—Simulation of interaction between pipe flow and surface overland flow in networks. Water Sci. Technol. 2005, 52, 275–289. [Google Scholar]
- Djordjević, S.; Prodanović, D.; Maksimović, Č. An approach to simulation of dual drainage. Water Sci. Technol. 1999, 39, 95–103. [Google Scholar] [CrossRef]
- Carr, R.S.; Smith, G.P. Linking of 2D and Pipe Hydraulic Models at Fine Spatial Scales. In Proceedings of the 4th International Conference on Water Sensitive Urban Design, Melbourne, Australia, 3–7 April 2006; pp. 888–895.
- Chen, A.; Hsu, M.; Chen, T.; Chang, T.J. An integrated inundation model for highly developed urban areas. Water Sci. Technol. 2005, 51, 221–230. [Google Scholar]
- Chen, A.S.; Djordjevic, S.; Leandro, J.; Savic, D. The Urban Inundation Model with Bidirectional Flow Interaction between 2D Overland Surface and 1D Sewer Networks. In Proceedings of the 6th International Conference on Sustainable Techniques and Strategies in Urban Water Management (NOVATECH), Lyon, France, 25–28 June 2007; pp. 465–472.
- Dey, A.K.; Kamioka, S. An integrated modeling approach to predict flooding on urban basin. Water Sci. Technol. 2007, 55, 19–29. [Google Scholar]
- Seyoum, S.; Vojinovic, Z.; Price, R.; Weesakul, S. Coupled 1D and noninertia 2D flood inundation model for simulation of urban flooding. J. Hydraul. Eng. 2012, 138, 23–34. [Google Scholar] [CrossRef]
- Li, W.; Chen, Q.; Mao, J. Development of 1D and 2D coupled model to simulate urban inundation: An application to Beijing Olympic Village. Chin. Sci. Bull. 2009, 54, 1613–1621. [Google Scholar] [CrossRef]
- Bates, P.D.; De Roo, A.P.J. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Hunter, N.M.; Horritt, M.S.; Bates, P.D.; Wilson, M.D.; Werner, M.G.F. An adaptive time step solution for raster-based storage cell modelling of floodplain inundation. Adv. Water Resour. 2005, 28, 975–991. [Google Scholar] [CrossRef]
- Leandro, J.; Chen, A.; Djordjević, S.; Savić, D.D.A. Comparison of 1D/1D and 1D/2D coupled (Sewer/Surface) hydraulic models for urban flood simulation. J. Hydraul. Eng. 2009, 135, 495–504. [Google Scholar] [CrossRef]
- Leandro, J.; Djordjević, S.; Chen, A.S.; Savić, D.A.; Stanić, M. Calibration of a 1D/1D urban flood model using 1D/2D model results in the absence of field data. Water Sci. Technol. 2011, 64, 1016–1024. [Google Scholar] [CrossRef]
- Chen, A.S.; Evans, B.; Djordjević, S.; Savić, D.A. Multi-layered coarse grid modelling in 2D urban flood simulations. J. Hydrol. 2012, 470–471, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Hunter, N.; Bates, P.; Neelz, S.; Pender, G.; Villanueva, I.; Wright, N.; Liang, D.; Falconer, R.; Lin, B.; Waller, S. Benchmarking 2D hydraulic models for urban flooding. Proc. ICE Water Manag. 2008, 161, 13–30. [Google Scholar] [CrossRef] [Green Version]
- Neal, J.; Fewtrell, T.; Trigg, M. Parallelisation of storage cell flood models using OpenMP. Environ. Model. Softw. 2009, 24, 872–877. [Google Scholar] [CrossRef]
- Kalyanapu, A.J.; Shankar, S.; Pardyjak, E.R.; Judi, D.R.; Burian, S.J. Assessment of GPU computational enhancement to a 2D flood model. Environ. Model. Softw. 2011, 26, 1009–1016. [Google Scholar] [CrossRef]
- Néelz, S.; Pender, G. Benchmarking of 2D Hydraulic Modeling Packages; Environment Agency: Bristol, UK, 2010. [Google Scholar]
- Chen, J.; Hill, A.; Urbano, L.D. A GIS-based model for urban flood inundation. J. Hydrol. 2009, 373, 184–192. [Google Scholar] [CrossRef]
- Zerger, A.; Smith, D.I.; Hunter, G.J.; Jones, S.D. Riding the storm: A comparison of uncertainty modelling techniques for storm surge risk management. Appl. Geogr. 2002, 22, 307–330. [Google Scholar] [CrossRef]
- Zerger, A. Examining GIS decision utility for natural hazard risk modelling. Environ. Model. Softw. 2002, 17, 287–294. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2000, 387, 33–35. [Google Scholar]
- Liu, Y.; Snoeyink, J. Flooding Triangulated Terrain. In Developments in Spatial Data Handling; Springer Berlin: Heidelberg, Germany, 2005; pp. 137–148. [Google Scholar]
- Zhou, Q.; Liu, X. Error assessment of grid-based flow routing algorithms used in hydrological models. Int. J. Geogr. Inf. Sci. 2002, 16, 819–842. [Google Scholar] [CrossRef]
- Liu, X.J.; Wang, Y.J.; Ren, Z. Algorithm for extracting drainage network based on triangulated irregular network. J. Hydraul. Eng. 2008, 39, 27–35. (In Chinese) [Google Scholar]
- Leitão, J.P.; Boonya-aroonnet, S.; Prodanovic, D.; Maksimovic, C. The influence of digital elevation model resolution on overland flow networks for modelling urban pluvial flooding. Water Sci. Technol. 2009, 60, 3137–3149. [Google Scholar] [CrossRef]
- Chou, T.-Y.; Lin, W.-T.; Lin, C.-Y.; Chou, W.-C.; Huang, P.-H. Application of the PROMETHEE technique to determine depression outlet location and flow direction in DEM. J. Hydrol. 2004, 287, 49–61. [Google Scholar] [CrossRef]
- Martz, L.W.; Garbrecht, J. The treatment of flat areas and depressions in automated drainage analysis of raster digital elevation models. Hydrol. Processes 1998, 12, 843–855. [Google Scholar] [CrossRef]
- Marks, D.; Dozier, J.; Frew, J. Automated basin delineation from digital elevation data. Geo Process. 1984, 2, 299–311. [Google Scholar]
- Vogt, J.V.; Colombo, R.; Bertolo, F. Deriving drainage networks and catchment boundaries: A new methodology combining digital elevation data and environmental characteristics. Geomorphology 2003, 53, 281–298. [Google Scholar] [CrossRef]
- Lin, W.T.; Chou, W.C.; Lin, C.Y.; Huang, P.H.; Tsai, J. WinBasin: Using improved algorithms and the GIS technique for automated watershed modelling analysis from digital elevation models. Int. J. Geogr. Inf. Sci. 2008, 22, 47–69. [Google Scholar] [CrossRef]
- Theobald, D.M.; Goodchild, M.F. Artifacts of TIN-based surface flow modeling. Proc. GIS LIS 90 1990, 2, 955–967. [Google Scholar]
- Bänninger, D. Technical note: Water flow routing on irregular meshes. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 3675–3689. [Google Scholar] [CrossRef]
- Tucker, G.E.; Lancaster, S.T.; Gasparini, N.M.; Bras, R.L.; Rybarczyk, S.M. An object-oriented framework for distributed hydrologic and geomorphic modeling using triangulated irregular networks. Comput. Geosci. 2001, 27, 959–973. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Vivoni, E.R.; Bras, R.L.; Entekhabi, D. Catchment hydrologic response with a fully distributed triangulated irregular network model. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Sampson, C.C.; Fewtrell, T.J.; Duncan, A.; Shaad, K.; Horritt, M.S.; Bates, P.D. Use of terrestrial laser scanning data to drive decimetric resolution urban inundation models. Adv. Water Resour. 2012, 41, 1–17. [Google Scholar] [CrossRef]
- Mason, D.C.; Horritt, M.S.; Hunter, N.M.; Bates, P.D. Use of fused airborne scanning laser altimetry and digital map data for urban flood modelling. Hydrol. Processes 2007, 21, 1436–1447. [Google Scholar] [CrossRef]
- Fewtrell, T.J.; Bates, P.D.; Horritt, M.; Hunter, N.M. Evaluating the effect of scale in flood inundation modelling in urban environments. Hydrol. Processes 2008, 22, 5107–5118. [Google Scholar] [CrossRef]
- Wu, L.; Shi, W. Principle and Algorithem of GIS; Science Press: Beijing, China, 2003; pp. 156–160. [Google Scholar]
- Frank, A.U.; Palmer, B.; Robinson, V. Formal Methods for the Accurate Definition of Some Fundamental Terms in Physical Geography. In Proceedings of 2nd International Symposium on Spatial Data Handling, Seattle, WA, USA, 5–10 July 1986; pp. 583–599.
- Apirumanekul, C. Modeling of Urban Flooding in Dhaka City; No. WM-00-13; Asian Institute of Technology: Bangkok, Thailand, 2001. [Google Scholar]
- Beijing General Municipal Engineering Design and Research Institute. Water Supply and Drainage Design Manual: Volume 5th Urban Drainage; China Building Industry Press: Beijing, China, 2004. [Google Scholar]
- Holtan, H.N. Time condensation in hydrograph analysis. Trans. Am. Geophys. Union 1945, 26, 407–413. [Google Scholar] [CrossRef]
- Sharp, A.L.; Holtan, H.N. Extension of graphic methods of analysis of sprinkled-plot hydrographs to the analysis of hydrographs of control plots and small homogeneous watersheds. Trans. Am. Geophys. Union 1942, 23, 578–593. [Google Scholar] [CrossRef]
- Mays, L.W. Water Resources Engineering; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Hsu, M.H.; Chen, S.H.; Chang, T.J. Inundation simulation for urban drainage basin with storm sewer system. J. Hydrol. 2000, 234, 21–37. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.; Li, L.; Wang, J.; Luo, J. Distributed Hydrological Model Theory and Method; Science Press: Beijing, China, 2010; pp. 256–260. [Google Scholar]
- Li, Z.F.; Wu, L.X.; Zhang, Z.X.; Xu, Z.H. Triangular-Prism-Based Algorithm on Urban Flood Inundation Simulation by Employing Dichotomy Numerical Solution. In Proceedings of International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Austrilia, 21–26 July 2013; 2013; pp. 790–793. [Google Scholar]
- Wu, L.X.; Wang, Y.B.; Shi, W.Z. Integral ear elimination and virtual point-based updating algorithms for constrained Delaunay TIN. Sci. China Ser. E Technol. Sci. 2008, 51, 135–144. [Google Scholar] [CrossRef]
- Beijing “7.21” Storm Event. Available online: http://www.weather.com.cn/zt/kpzt/696656.shtml (accessed on 20 August 2013). (In Chinese)
- Beijing encountered the strongest storm with 61 year return period and the average precipitation as high as 215 mm. Available online: http://news.sohu.com/20120722/n348744539.shtml (accessed on 20 August 2013). (In Chinese)
- Ministry of Development of the People’s Republic of China. Outdoor Drainage Design Standard (GB 50014–2006); China Planning Press: Beijing, China, 2011.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, Z.; Wu, L.; Zhu, W.; Hou, M.; Yang, Y.; Zheng, J. A New Method for Urban Storm Flood Inundation Simulation with Fine CD-TIN Surface. Water 2014, 6, 1151-1171. https://doi.org/10.3390/w6051151
Li Z, Wu L, Zhu W, Hou M, Yang Y, Zheng J. A New Method for Urban Storm Flood Inundation Simulation with Fine CD-TIN Surface. Water. 2014; 6(5):1151-1171. https://doi.org/10.3390/w6051151
Chicago/Turabian StyleLi, Zhifeng, Lixin Wu, Wei Zhu, Miaole Hou, Yizhou Yang, and Jianchun Zheng. 2014. "A New Method for Urban Storm Flood Inundation Simulation with Fine CD-TIN Surface" Water 6, no. 5: 1151-1171. https://doi.org/10.3390/w6051151






