1. Motivation
Many authors have called for improvements in water use efficiency or increases in water productivity in rainfed and irrigated settings, with the goal of increasing agricultural output to meet future food demands [
1,
2,
3,
4,
5]. Some of the phrases that appear often in the agricultural and water management literature include the need to produce “more food with less water” and to generate “more crop per drop” [
6,
7,
8,
9]. The motivating rationale for such phrases is clear and legitimate. We must produce more food in future to support a larger global population. The competition for water is increasing in many sectors and water is a critical input in agriculture. Thus we must use the resource wisely to ensure that future generations will have access to reliable and affordable food supplies [
10,
11,
12,
13,
14,
15].
The notion of increasing crop water productivity is compelling at first glance, precisely because it suggests we need to generate more agricultural output per unit of the water input. Yet, focusing on water alone might not be sufficient to fully understand current crop production activities or to gain insight regarding the best measures for increasing crop yields or agricultural incomes in future.
Water is just one of many inputs in agriculture. Plant and crop responses to water generally depend on the availability of other inputs, such as nutrients, sunshine, and management effort [
2,
16,
17,
18]. Farmers seeking to increase crop yields or to achieve some other objective must optimize over an array of agricultural inputs, while considering also their market opportunities. In addition, farmers in both rainfed and irrigated settings must manage the risk and uncertainty inherent in their production activities, to determine optimal choices.
My goal in this paper is to consider whether estimates of crop water productivity are helpful in gaining a better understanding of water management in agriculture, and whether they are useful in evaluating crop production opportunities at the farm level. My primary concern is that estimates of crop water productivity lack the depth and breadth of information needed to understand a crop’s response to water and a farmer’s response to the natural, policy, and market environments in which he or she operates. By considering only one of many inputs, measures of crop water productivity omit much of the information that farmers consider and many of the issues that influence crop response to rainfall, irrigation, and cultural practices.
I hope also to motivate greater consideration of the risk and uncertainty many smallholder farmers face when making decisions regarding water and other inputs. In many developing countries, small-scale farmers struggle to gain access to irrigation water, to increase crop and livestock output, and enhance their livelihoods [
19,
20,
21,
22,
23]. They operate in an environment of considerable risk and uncertainty. It is not clear that they could or should endeavor to maximize water productivity. Both farmers and policy makers must incorporate risk and uncertainty in their analyses of production opportunities and in decisions regarding natural resources.
I begin by describing measures of water productivity in the context of crop water production functions, with the goal of distinguishing between average and marginal measures of crop responses to farm inputs. Using published crop water production functions, I show that farmers seeking to maximize water productivity would generate less yield and smaller net income than if they sought to maximize net revenue. Thus, it is not clear that farmers would pursue the goal of maximizing water productivity, as proposed or implied by many authors. In cases in which water is limiting, relative to land, the profit-maximizing solution will be the same as that which maximizes the average productivity of water, but that is a special case result of the more general objective of maximizing net revenue.
I discuss also the random nature of measures of water productivity. Both the numerator and denominator of the estimated ratios contain deterministic and stochastic components. Crop yields and evapotranspiration are influenced by farmer decisions and input use, and also by random effects due to weather, pests, and disease. Thus, estimates of crop water productivity are random variables that represent point estimates from underlying probability distributions.
I also depict the challenge of comparing any two estimates of water productivity, whether they pertain to different settings or different times. The information contained in point estimates of water productivity is not sufficient for declaring that observations reflecting higher measures of water productivity should be preferred over those with lower measures. It is not clear that we gain helpful information or insight by comparing water productivities across locations or over time.
2. Average vs. Marginal Productivity
Crop water productivity, as defined by most authors, is the ratio of crop yield or crop value, to a selected measure of water consumed, applied, or evaporated in the process of growing a crop [
2,
24]. As such, the ratio represents the average productivity of the input, rather than the incremental productivity. For example, when the ratio of interest is the water productivity of applied water, the ratio often is defined as:
If the crop yield is 4 tons per ha and the applied water is 8000 m3 per ha, then the crop water productivity is 0.0005 tons per m3. In addition to neglecting consideration of other inputs, this measure of average productivity is not sufficient for determining whether the application rate of 8000 m3 per ha is optimal from the farm-level or societal perspective. The question of optimality can be addressed only by considering the marginal (or incremental) productivity of water, in comparison with its marginal cost. If the marginal productivity of water is 0.004 tons per m3, and the price of the crop is $1,000 per ton, then the decision to apply the last m3 of water is sensible, provided the marginal cost of water is less than or equal to $4.00 per m3.
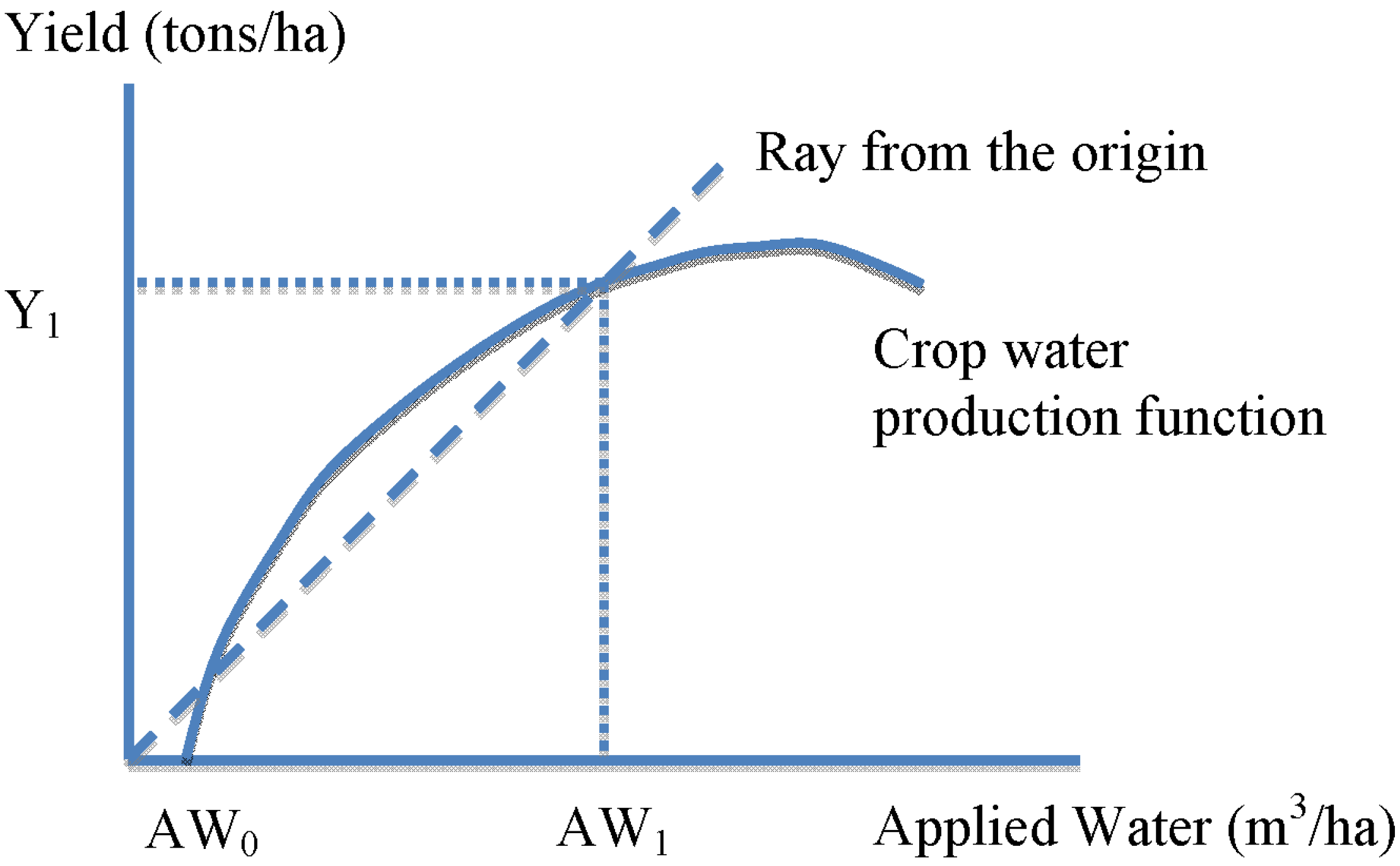
The average and marginal productivities of water can be depicted readily in the context of a crop water production function. This context is helpful also for describing why average productivities are not sufficient for determining optimal levels of water use. A typical crop water production function resembles the following diagram, which describes crop yield as a function of applied water.
The slope of a ray from the origin, through any point on the production function, depicts the average productivity of that amount of applied water. For example, as depicted in
Figure 1, the average productivity of AW
1 (m
3 per ha) is calculated by dividing Y
1 by AW
1. That calculation is precisely the slope of the ray from the origin through the production function. Thus, the slope of the ray also represents the value of WP
AW in this example, or the crop water productivity when applying AW
1 units of water.
Beginning from AW
0, the value of WP
AW will increase with larger volumes of applied water, to a point, before beginning to decline. The point at which the value of WP
AW reaches its maximum is precisely the point at which a ray from the origin is just tangent to the production function. This occurs where the amount of applied water is AW
MAX (
Figure 2). Beyond this level of applied water, the estimated water productivity will decline throughout the remaining range of applied water values. One can infer from the diagram that the point of maximum water productivity might be very different from the point of maximum crop yield. It might also be quite different from the point of maximum net revenue.
Figure 1.
Depicting the water productivity of applied water in a typical crop water production function.
Figure 1.
Depicting the water productivity of applied water in a typical crop water production function.
Figure 2.
Depicting the maximum value of the water productivity of applied water.
Figure 2.
Depicting the maximum value of the water productivity of applied water.
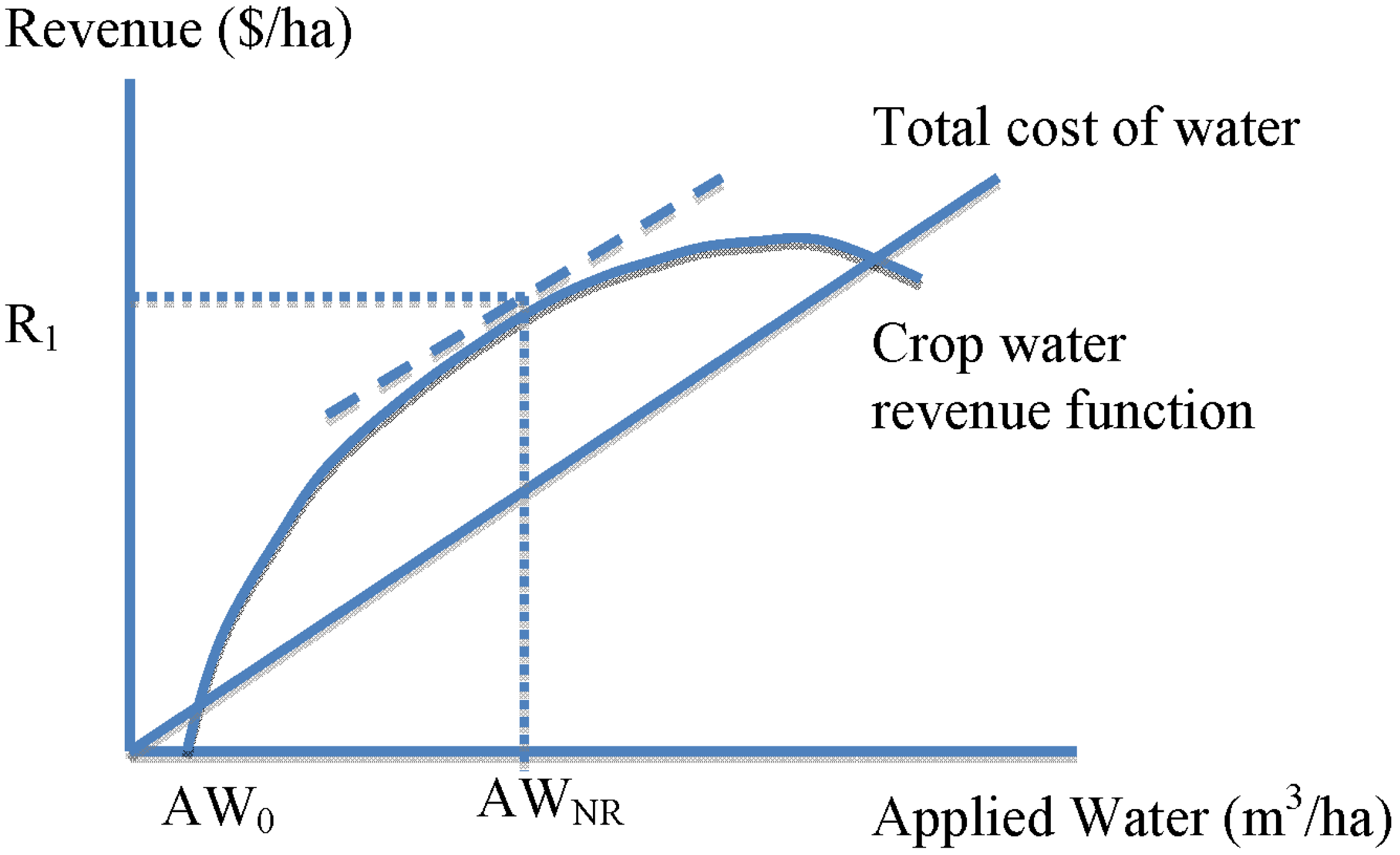
The profit-maximizing amount of applied water, AW
NR, is found where marginal revenue is equal to marginal cost. To determine this amount, we first transform the crop water production function into a crop revenue function by multiplying by crop price. The shape of the crop revenue function will be the same as the crop water production function. We can depict the total cost of water as a straight line from the origin, provided that the unit price of water is constant. As shown in
Figure 3, the profit-maximizing amount of applied water is larger than the volume that would maximize water productivity, and yet smaller than the volume that would maximize crop yield. This will be the case for many crops in a range of settings. Indeed, there is no particular importance attached to the water volume that maximizes water productivity, or equivalently, the average productivity of water.
It is also worth noting that for a crop water production function that arises from the origin or has a positive intercept on the vertical axis, water productivity will decline throughout the entire range of volumes of applied water. In that case, it is easy to determine that maximizing water productivity would not be the appropriate optimizing criterion, as it would generate the recommendation of using zero applied water. Such a production function would pertain in cases in which rainfall is sufficient to generate some yield, but farmers apply supplemental irrigation water to enhance crop production. The water productivity of the applied irrigation water would decline throughout the range of applied water volumes.
Figure 3.
Depicting the profit-maximizing amount of applied water.
Figure 3.
Depicting the profit-maximizing amount of applied water.
3. Empirical Examples
Several authors provide empirical examples of production functions that are useful in demonstrating the difference in outcomes when maximizing water productivity or maximizing crop yield or net revenue. Igbadun
et al. [
25] examined onion production in Nigeria. They presented the following estimated crop water production function in which the yield of onion bulbs is expressed as a function of seasonal applied water:
The applied water variable, AW, is expressed in mm.
Given this empirical production function, farmers could maximize water productivity by applying 390 mm of irrigation water. The yield of onion bulbs would be 21 tons per ha and the water productivity would be 54 kg of onion bulbs per mm of applied water (
Table 1). As noted above, this is equivalent to the average productivity of applied water.
Farmers could achieve the maximum yield of 28 tons per ha by applying 660 mm of irrigation water. The crop water productivity would decline to 42 kg per mm at maximum yield, but the farmers would be producing an additional 7 tons of onion bulbs per ha. Lacking a cost function, it is not possible to determine the profit-maximizing volume of applied water. However, we can expect that if onion production is profitable, the optimal volume of applied water will be between 390 mm, where crop water productivity is maximum, and 660 mm, where yield is maximum and the marginal productivity of water is zero.
Zhang and Oweis [
26] examine durum wheat production in Syria, where farmers rely partly on rainfall and partly on supplemental irrigation. Their estimated production is the following:
Both the supplemental irrigation (AW) and precipitation (P) are expressed in mm.
We determine the volumes of water that will maximize crop water productivity, yield, and net revenue, after choosing a seasonal precipitation level of 250 mm. In such a season, farmers can maximize crop water productivity by applying an additional 270 mm of irrigation water (
Table 1). The yield would be 5.4 tons of wheat per ha, and the crop water productivity would be 2.00 kg of wheat per m
3 of applied water. The maximum wheat yield of 6.65 tons per ha can be achieved with supplemental irrigation of 510 mm. Crop water productivity would decline to 1.30 kg per m
3, but farmers would be producing an additional 1.25 tons of wheat per ha.
Table 1.
Examples of water levels that maximize water productivity, net revenue, and yields, from empirical crop water production functions.
Table 1.
Examples of water levels that maximize water productivity, net revenue, and yields, from empirical crop water production functions.
| Citation | Crop and Location | Applied Water (mm) | Yield (t/ha) | CWP (kg/m3) | Net Rev. ($/ha) |
|---|
| Igbadun et al., 2012 [25] | Onions, Nigeria | Y = −14.88 + 0.131 AW − 0.0001 AW2 |
| | Max. CWP | 390 | 21.0 | 5.38 | 1709 |
| Max. Net Rev | n/a | n/a | n/a | n/a |
| Max. Yield | 660 | 28.0 | 4.24 | 2141 |
| Zhang and Oweis, 1999 [26] | Wheat, Syria | Y = −5.8556 + 0.0329 (AW + P) − 0.00002164 (AW + P)2 |
| | Max. CWP | 270 | 5.40 | 2.00 | 866 |
| Max. Net Rev | 454 | 6.58 | 1.45 | 1048 |
| Max. Yield | 510 | 6.65 | 1.30 | 1032 |
| Zhang et al., 1999 [27] | Wheat, Syria | Y = 307 + 1.839 AW − 0.00402 AW2 |
| | Max. CWP | 0 | 3.07 | n/a | 491 |
| Max. Net Rev | 195 | 5.13 | 2.63 | 737 |
| Max. Yield | 230 | 5.17 | 2.25 | 729 |
Zhang and Oweis [
26] provide cost information that enables us to determine the profit-maximizing amount of supplemental irrigation. In a season with 250 mm of rainfall and a wheat price of $0.25 per kg, farmers would maximize profit by applying 454 mm or supplemental irrigation, generating a wheat yield of 6.58 tons per ha. Crop water productivity would be 1.45 kg per m
3. As expected, this profit-maximizing result lies between the volumes of water that maximize water productivity and crop yield. The difference in profit between the water applications that maximize crop water productivity and net revenue is $182 per ha.
Zhang
et al. [
27] provide an empirical production function for winter wheat in China, which has a positive intercept on the yield axis. Given this characteristic, as noted above, crop water productivity will decline throughout all values of applied water. The estimated production is the following:
Farmers wishing to maximize crop water productivity would abstain from irrigating, thus obtaining a yield of 307 g per m
2, or 3.07 tons per ha. Crop water productivity is not defined at the value of zero mm of irrigation water. Yet the pertinent point is that water productivity declines for any positive value of applied water. Farmers could achieve the maximum yield of 5.2 tons per ha by applying 230 mm of irrigation water (
Table 1). Farmers wishing to maximize net revenue would apply 195 mm of irrigation water, thus generating a yield of 5.1 tons per ha and obtaining a profit of $737 per ha. Here again, the profit-maximizing volume of applied water lies between the volumes that maximize water productivity and crop yield.
A Special Case
The above examples demonstrate empirically that farmers applying irrigation water would not have an interest in maximizing water productivity, as that strategy would not maximize yields or net revenue. Yet there is a special case in which the goal of maximizing net revenue generates a strategy that involves maximizing the average productivity of water. In particular, when water is limiting, relative to land, the profit maximizing solution will be the same as that which maximizes water productivity.
We can demonstrate this result using the empirical production function for maize, presented by Zand-Parsa and Sepaskhah [
28], in which maize yield is a function of nitrogen and irrigation water:
In this equation, W represents the depth of irrigation water applied (m), N is nitrogen applied (kg per ha), and N
r is residual nitrogen in the soil before planting (kg per ha). The empirical values of the coefficients a
0 through a
8 are −1.862, 6.0386, −3.580, −0.178, 0.0005, 0.5733, −0.00148, −0.3021, and 0.000806. The assumed value of N
r is 54.6 kg per ha. The prices in the original analysis of Zand-Parsa and Sepaskhah [
28] for output, water, and nitrogen are $200 per ton, $31 per m ($0.003 per m
3), and $0.13 per kg, respectively.
In the standard case, in which water is plentiful, but the farmer’s land is limited, the profit maximizing levels of water and nitrogen are 990 mm and 212 kg per ha (
Table 2). As expected, the net revenue of $2,556 per ha is larger than the net revenue that would be achieved if the farmer chose to maximize water productivity. Given that goal, the farmer would apply 723 mm of irrigation water and 207 kg per ha of nitrogen, while earning net revenue of $2,152 per ha.
Table 2.
Optimizing water and nitrogen applications for maize, when either land or water is the limiting input.
Table 2.
Optimizing water and nitrogen applications for maize, when either land or water is the limiting input.
| Citation | Crop and Location | Applied Water (mm) | Applied N (kg/ha) | Yield (t/ha) | CWP (tons/m) | Net Rev. ($/ha) |
|---|
| [28] | Maize, Iran | Yield (t/ha) = a0 + a1 × W + a2 × W2 + a3 × (N + Nr) + a4 × (N + Nr)2 + a5 × (W)(N + Nr) + a6 × (W)(N + Nr)2 + a7 × (W2)(N + Nr) + a8 × (W2)(N + Nr)2 |
| Land is limiting | Max. CWP: | 723 | 207 | 11.0 | 15.2 | 2,152 |
| Max. Net Rev: | 990 | 212 | 13.1 | 13.2 | 2,556 |
| Max. Yield: | 1,000 | 212 | 13.1 | 13.1 | 2,555 |
| Water is limiting | Max. CWP: | 723 | 207 | 11.0 | 15.2 | 2,152 |
| Max. Net Rev: | 723 | 207 | 11.0 | 15.2 | 2,152 |
| Uniform water: | 567 | 254 | 8.2 | 14.5 | 1,588 |
When water is limiting, relative to land, the amount of irrigation water that maximizes profit is the same as that which maximizes water productivity. Thus, the farmer would choose to apply 723 mm of irrigation water, while leaving some land idle. For example, suppose a farmer has 3.0 ha of land available, but only the equivalent of 1.7 m of irrigation water available. The farmer could plant all 3 ha in maize and apply 567 mm of irrigation water on those planted hectares. If the farmer also applies 254 kg/ha of nitrogen, he or she will achieve a yield of 8.2 tons/ha, while generating a net revenue of $1,588 per ha, or $4,764 per season for the farm (
Table 2). By contrast, if the farmer plants only 2.35 ha in maize and applies 723 mm of water and 207 kg/ha of nitrogen on those hectares, he or she will generate a net revenue of $2,152 per cultivated ha, or $5,057 for the farm.
This empirical example applies to situations in which water is limiting, relative to land. In such cases, the profit maximizing amount of land in cultivation can be determined by dividing the amount of water available by the amount of water per hectare that maximizes average productivity. In this example, the area of 2.35 ha can be determined by dividing the 1.7 m available by the 0.723 m at which water productivity is maximized. Thus, the strategy of maximizing water productivity in this instance is a special case result of the broader economic objective of maximizing profit.
4. The Productivity of Water Evapotranspired
The production functions examined above depict the empirical relationship between crop yield and applied water. The curvature of each function reflects the diminishing and eventually negative incremental returns to applied water, as some of the water is not used productively by the plants. Functions describing crop yield or biomass as an outcome of evapotranspiration (ET) are essentially linear, for a given production setting [
24,
29,
30]. Thus, additional evapotranspiration generates additional yield at a rate that is essentially constant. Despite this constant rate of transformation, estimated values of water productivity can increase, decline, or remain the same, as the volume of water evapotranspired increases.
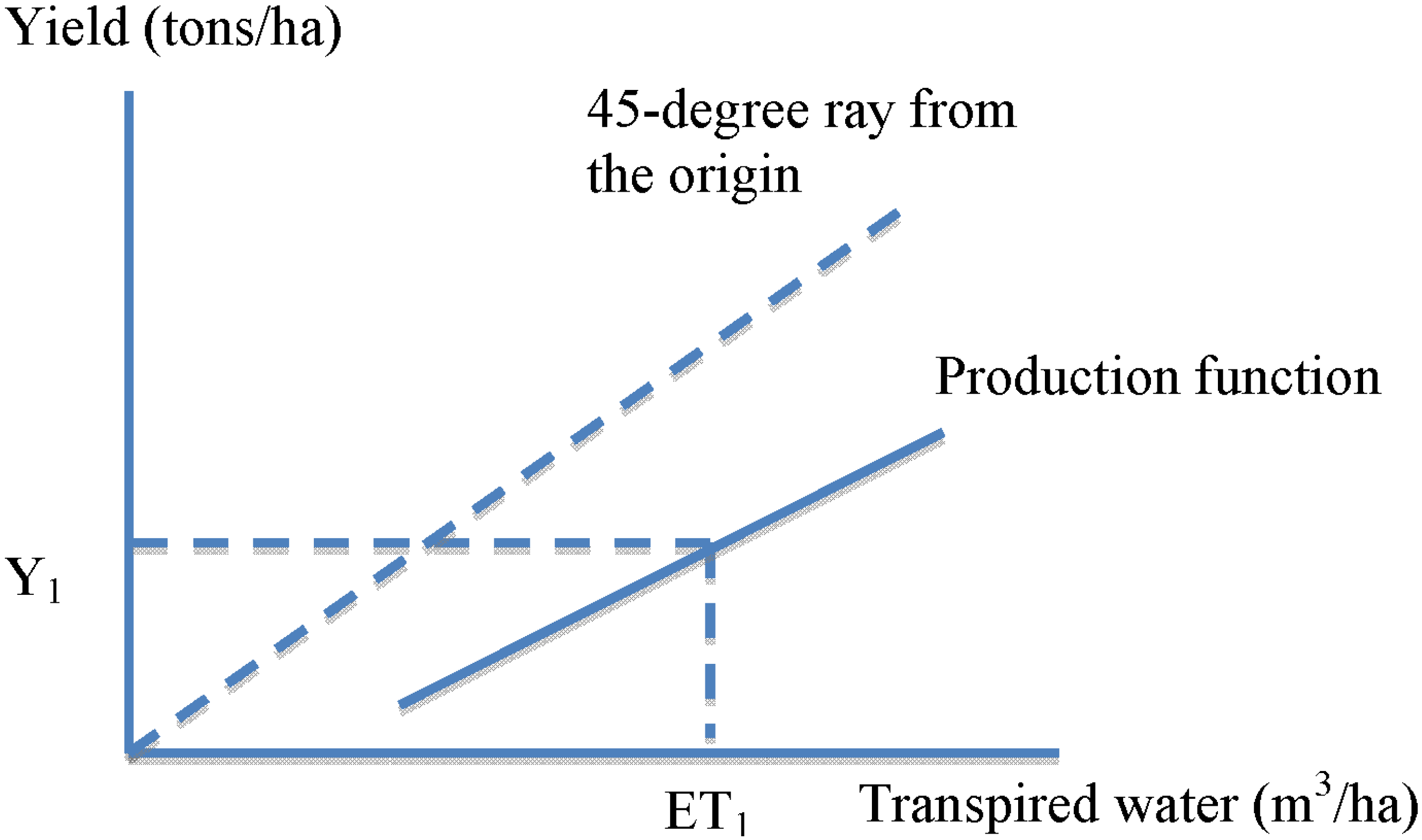
Linear segments depicting crop yield as a function of evapotranspiration cannot intercept the vertical axis, as it is not possible to achieve a positive yield with no ET. Yet one can project where the vertical axis intercept would occur, if the linear segment were extended to the axis. Such an exercise is helpful in determining whether water productivity will increase or decrease at higher levels of ET for a given crop-ET relationship.
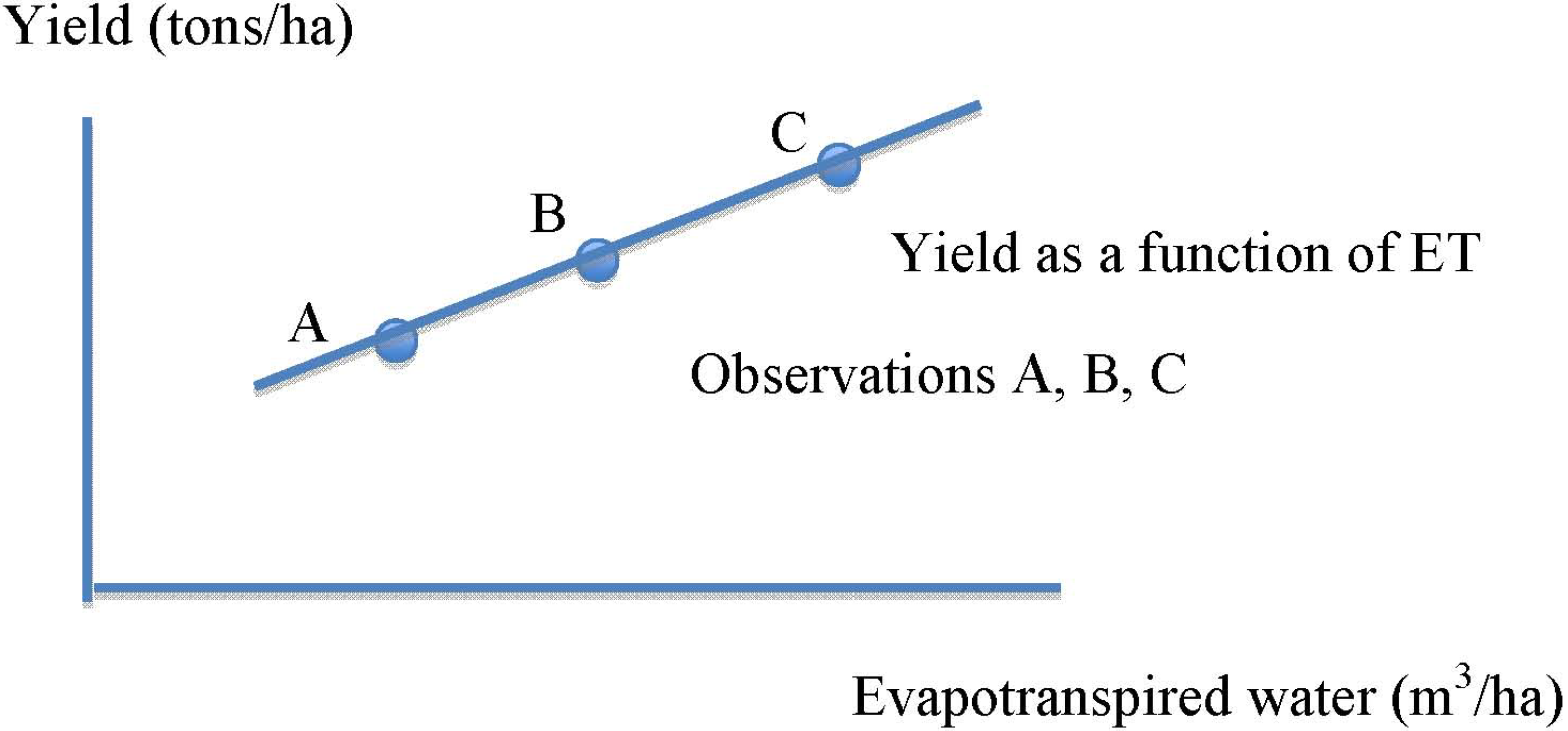
For example, if the linear segment depicting crop yield as a function of ET projects a positive vertical axis intercept, the empirical value of crop water productivity will decline as ET increases. This can be verified by noting that the slope of a ray from the origin through a point on the production function diminishes at higher levels of ET (
Figure 4). By analogy, if the linear segment depicting crop yield as a function of ET projects a negative vertical axis intercept, the empirical value of crop water productivity will increase as ET increases (
Figure 5). If the linear segment happens to be coincident with a 45-degree ray from the origin, the value of crop water productivity will be the same for all amounts of evapotranspiration.
Given that water productivity can increase or decrease monotonically along the linear segment depicting crop yield as a function of ET, it is not clear that the objective of increasing or maximizing water productivity, with respect to ET, is pertinent. If the empirical relationship between yield and ET resembles the one in
Figure 4, water productivity will be maximized at the smallest amount of ET. Yet that level would also generate the smallest yield. By contrast, if the empirical relationship resembles
Figure 5, there is no apparent upper bound to the value of water productivity. Higher measures of water productivity can be achieved at ever higher levels of ET. Such a relationship is not helpful in determining the optimal amount of evapotranspiration at the farm level.
Figure 4.
Depicting crop water productivity of evapotranspired (ET) water, when the linear segment projects a positive vertical axis intercept.
Figure 4.
Depicting crop water productivity of evapotranspired (ET) water, when the linear segment projects a positive vertical axis intercept.
Figure 5.
Depicting crop water productivity of evapotranspired water, when the linear segment projects a negative vertical axis intercept.
Figure 5.
Depicting crop water productivity of evapotranspired water, when the linear segment projects a negative vertical axis intercept.
Empirical examples of linear relationships involving crop yield and ET are presented in
Table 3. Three of these examples project a negative vertical intercept, while one projects a positive intercept. The R
2 values for these estimated relationships are higher than some others that appear in the literature, in part because the equations are estimated using relatively small numbers of observations. In larger scale studies, the scatter of observations is substantial, such that the measures of R
2 are much smaller. Depictions of linear yield-ET relationships for wheat, rice, cotton, and maize in Zwart and Bastiaanssen [
24] carry R
2 values ranging from 0.09 to 0.39. Those authors acknowledge that the empirical description of crop yield and ET in any setting is determined by “many factors that influence the soil-plant-water relationship.”
Table 3.
Examples of linear crop production functions expressing yield as a function of evapotranspiration (ET).
Table 3.
Examples of linear crop production functions expressing yield as a function of evapotranspiration (ET).
| Citation | Crop and Location | Estimated Production Function and R2 |
|---|
| Zhang and Oweis, 1999 [26] | Bread wheat, Syria | Y = −2.4969 + 0.016 ET R2 = 0.68 |
| Yield is in tons per ha, ET is in mm. |
| Zhang and Oweis, 1999 [26] | Durum wheat, Syria | Y = −0.1093 + 0.116 ET R2 = 0.68 |
| Yield is in tons per ha, ET is in mm. |
| Karam et al., 2009 [31] | Wheat, Lebanon | Y = 1364.6 + 5.0601 ET R2 = 0.60 |
| Yield is in kg per ha, ET is in mm. |
| Igbadun et al., 2012 [25] | Onions, Nigeria | Y = −0.4956 + 0.052 ET R2 = 0.87 |
| Yield is in tons per ha, ET is in mm. |
5. Estimates of Water Productivity are Random Variables
Crop yield is a random variable in both rainfed and irrigated settings. So too is soil moisture, at any point in time, or as measured cumulatively throughout a season. Thus, the ratio representing water productivity, whether defined as biomass, crop yield, or revenue per unit of water applied or consumed, is essentially a ratio involving two random variables. Farmers certainly can influence the yields they achieve each season through their choices and timing of crop inputs, such as water, nutrients, pesticides, and labor, but the yields they obtain are random draws from a probability distribution. The same is true for soil moisture.
Farmers with access to irrigation can modify soil moisture to some degree, but they cannot determine with certainty the amount of moisture available to a plant or the amount of moisture the plant takes up. Nonetheless, farmers with irrigation can notably influence plant growth and crop yield. Farmers lacking irrigation can manage soil moisture through their choices of crops and varieties, soil preparation, planting dates, plant densities, and cultural practices [
32,
33,
34,
35], but they generally cannot supplement soil moisture autonomously. For both groups of farmers, the amount of soil moisture available at any point in time, and the uptake of soil moisture by plants, are random draws from probability distributions.
Given that measures of water productivity are ratios of two random variables, it is not clear how much influence farmers can exert on the empirical values observed on farms or computed across agricultural areas. Thus, the seemingly compelling goal of increasing water productivity might have limited relevance in most agricultural settings. Rather than attempting to increase water productivity, farmers might endeavor instead to reduce the variance in crop yields and soil moisture, while also increasing the mean values of crop yields, over time, in part by gaining greater influence over the seasonal pattern of soil moisture. Many farmers, particularly those in rainfed settings, likely already adopt such a management objective, either explicitly or implicitly. It is not possible to farm successfully in rainfed settings without paying close attention to soil moisture conditions, and managing accordingly.
Farmers in rainfed and partially irrigated settings can reduce the variance and increase the mean of their crop yields by investing in measures that modify soil moisture availability [
36,
37]. Farmers who capture rainwater in a small pond for irrigation, or pump groundwater from a shallow aquifer, can manage the amount of soil moisture available during crop growth and reproductive stages. They have the options of stimulating rapid growth of the plant canopy early in the season to reduce evaporation, and applying supplemental water during particularly dry stretches of a crop production cycle [
38].
The actions taken by farmers to modify soil moisture might cause the observed value of water productivity to increase or decrease, depending on the final measured values of crop yields and water applied or consumed. Given the random nature of both outcomes, and interactions with other inputs, it is not possible to know in advance the eventual measure of water productivity. Yet the farmers will have made better use of the water within their control, by modifying the pattern of soil moisture to match crop water demands, and by striving to maximize transpiration while minimizing non-beneficial evaporation.
6. Comparing Estimates of Water Productivity
Many authors compare estimates of water productivity, over time or in selected locations. Examples include the comprehensive review by Zwart and Bastiaanssen [
24] and smaller, regional reviews by Hussain
et al. [
39] and Yan and Wu [
40]. One goal of such studies is to highlight differences in crop water productivities that might provide insight regarding policy measures or technological interventions that might improve water management and thus lead to greater output per unit of water used in agriculture. This goal is compelling, yet it is not clear if the comparisons provide sufficient information to enhance understanding of the underlying issues that generate the observed values of water productivity.
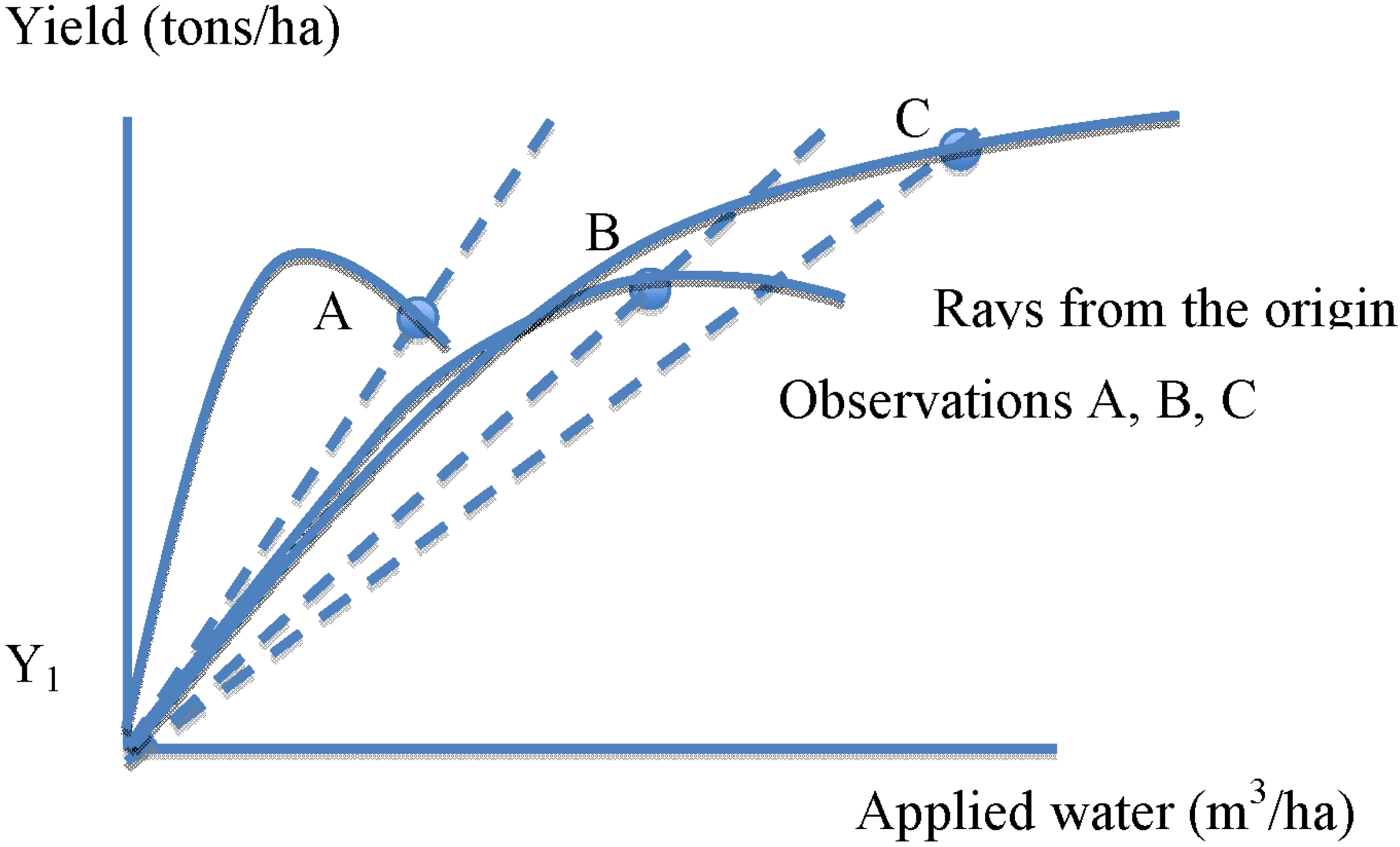
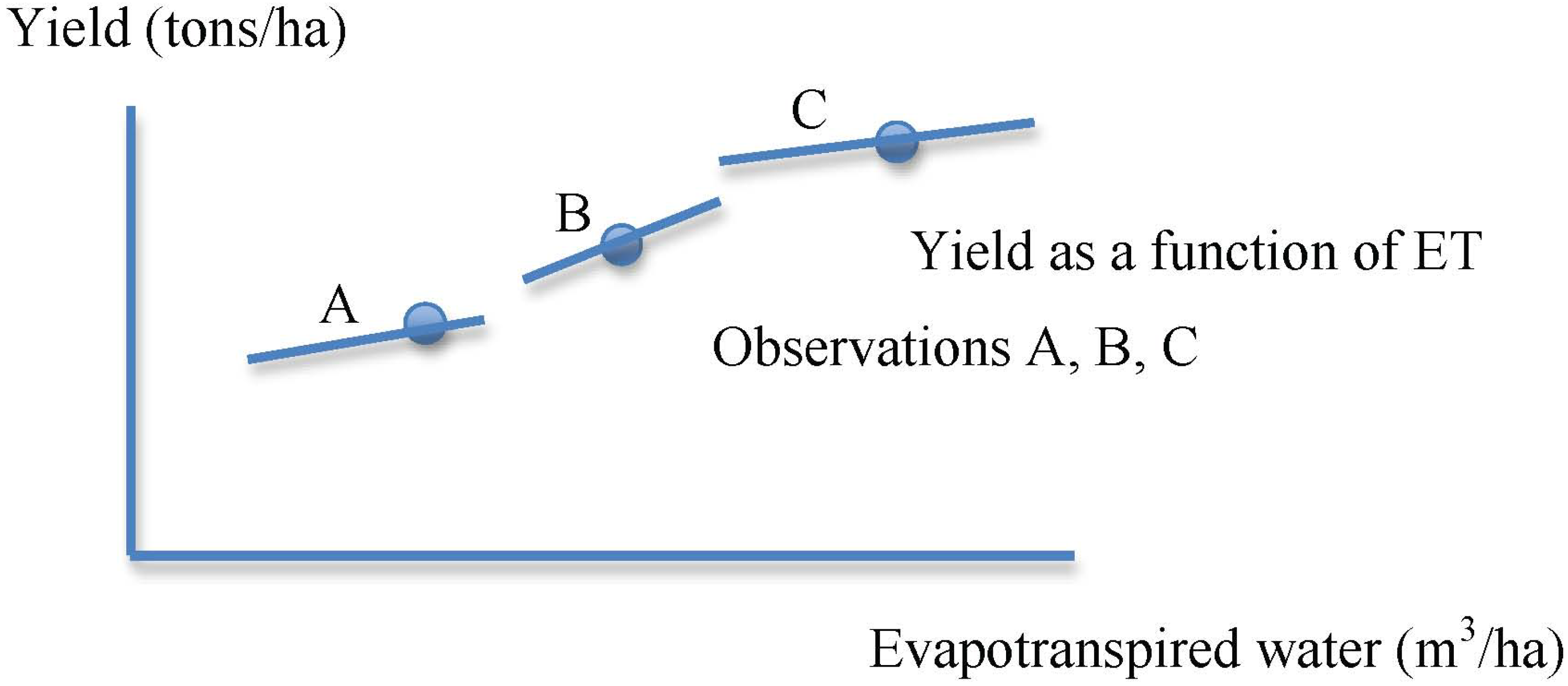
Recalling the framework presented above, we can depict observations of water productivity in coordinate space defined either by crop yields and applied water, or by crop yields and ET, or water consumed. Choosing the first of these, suppose we observe three estimates of water productivity, perhaps in three locations or on three farms. We can represent these observations as points A, B, and C in
Figure 6. Recalling that the slope of a ray from the origin, through each point, depicts the water productivity for each, we can readily observe that the water productivity for observation A is greater than that for observation B, which is greater than that for observation C. A strict preference for points reflecting higher water productivity would result in the choice of Point A as most desirable. Yet that choice might be inappropriate. Observing the points, alone, does not provide information regarding the underlying production functions. It is possible that any of the points represents an inefficient use of water, or that all points represent efficient use. We need to know more about the production setting to determine which point or points might be desirable.
Suppose the underlying production functions are those depicted in
Figure 7. It would appear that the production situation at Point A is least desirable, as Point A lies to the right of the point of maximum yield. Thus, the same amount of yield could be generated with less applied water. Point B might also be inefficient, as it appears production is very close to the point of maximum yield. If there is a positive opportunity cost of the applied water, it is likely that the incremental cost exceeds the incremental again at Point B. It is therefore possible that Point C is the most desirable point of those depicted in
Figure 7, even though the estimated water productivity at that point is the smallest.
Figure 6.
Comparing observations of water productivity, with respect to applied water.
Figure 6.
Comparing observations of water productivity, with respect to applied water.
Figure 7.
Considering the underlying production functions.
Figure 7.
Considering the underlying production functions.
This is just one of many possible depictions of the underlying production functions that might generate the observations represented by Points A, B, and C. Differences in climate, soils, irrigation systems, and human capital can generate an array of empirical production functions within a given region. Observed values of crop yields might lie on the same function, or they might all lie on different functions, as depicted in
Figure 7. In any event, it is not possible to evaluate the desirability of Points A, B, and C using only the measure of water productivity. This perspective can be demonstrated also in yield-ET space.
Suppose we observe three production situations, depicted as Points A, B, and C in
Figure 8. We can see by inspection that Point A has the highest measure of water productivity, followed by Point B, and then Point C. Yet we could not conclude that Point A is preferable, without knowing the incremental costs and benefits of moving from Point A to Point B. If the incremental cost of providing the additional ET is less than the incremental gain, Point B would be preferred to Point A. The same analysis pertains to the potential move from Point B to Point C. The information provided by the estimated water productivity is not sufficient for determining which of these points is best from either the farm-level or societal perspective.
It is quite possible also that we observe situations in which farmers are operating on different production functions, due to differences in the amount or quality of the other, non-water inputs available to them. For example, farmers with better access to high-quality seeds, fertilizer, and pesticides will have the ability to generate higher yields per unit of transpired water. Their production functions will lie above those pertaining to farmers with limited access or with less financial ability to purchase and apply complementary inputs in a timely fashion. This information, while pertinent to discussions of agricultural policy and livelihoods, will not be reflected in estimates of water productivity.
Figure 8.
Comparing observations of water productivity, with respect to ET.
Figure 8.
Comparing observations of water productivity, with respect to ET.
We might observe points such as those depicted in
Figure 8, yet they might lie along different production functions, as depicted in
Figure 9. The policy challenges implied by these depictions are different. In the case of
Figure 8, the challenge is to determine whether or not additional transpiration is desirable, and then how to motivate greater use of water per hectare. The challenge implied by
Figure 9 is that of determining how to motivate farm-level shifts in the yield-ET function. Investments in efforts to provide farmers with more affordable access to complementary inputs might be among the pertinent policy actions.
Figure 9.
Comparing observations of water productivity, with respect to ET.
Figure 9.
Comparing observations of water productivity, with respect to ET.
The situation depicted in
Figure 9 suggests also that estimates of water productivity from different points in time must be interpreted with care. Over time, with improvements in agricultural technology and human capital, we expect to see crop water production functions shift upward. As this occurs, it is likely that transpiration rates per hectare also will increase, coincident with higher crop yields. Observations such as Point C in
Figure 9 likely will replace observations such as Points A and B. As depicted in
Figure 9, the higher output per hectare comes at the cost of greater evapotranspiration per hectare, such that the measure of water productivity is smaller. Yet the value of the additional output might exceed the opportunity cost of the additional water evapotranspired. In the future, we might aspire to observe yield-ET combinations that lie above and to the left of Point B, if advances in plant genetics enable the production of higher yields with less evapotranspiration.
An Empirical Example
Li and Barker [
41] describe the higher crop yields and improvements in water management made possible by the alternate wetting and drying method of rice irrigation (AWD), in which the soil is allowed to dry between irrigation events. The authors suggest that water deliveries and losses to percolation and seepage are reduced when using the alternate wetting and drying method. They provide estimates of crop water productivity for traditional and AWD irrigation in four provinces of China. Those data are helpful in depicting the difficulty in gaining insight when comparing estimates of crop water productivity over time, locations, and crop types.
The data in
Table 4 were compiled originally by authors other than Li and Barker [
41]. Thus, it is not possible to know the numbers of observations that generate each value in
Table 4 or to know the characteristics of the underlying distributions. Yet, taken on face value, the data reflect several interesting comparisons, within and across provinces, and over time. For example, in Hubei, the yield of traditional, middle-season rice in 1998 was higher than the yield of traditional, early-season rice in 1997, and yet the estimated water productivity is higher in 1997. Similarly, in Zhejiang, the yield of traditional, late-season rice is higher than the yield of traditional, early-season rice in 1998, yet the estimated water productivity is higher for the early-season rice. These are certainly plausible observations. The question is whether or not the estimates of water productivity are helpful in determining which production setting is better, or which should be preferred over the other.
Table 4.
Rice yields and estimates of farm-level water productivity for rice, irrigated with traditional methods and using alternate wetting and drying. Source: This table is reproduced from the paper by Li and Barker (2004) [
41].
Table 4.
Rice yields and estimates of farm-level water productivity for rice, irrigated with traditional methods and using alternate wetting and drying. Source: This table is reproduced from the paper by Li and Barker (2004) [41].
| Province | Year | Rice Type | Yield (kg/ha) | CWP (kg/m3) |
|---|
| (season) | Traditional | AWD | Traditional | AWD |
|---|
| Hubei | 1997 | Early | 5,438 | 6,393 | 0.889 | 1.183 |
| 1998 | Middle | 7,767 | 8,790 | 0.856 | 1.122 |
| Guangxi | 1980 | Early | 6,975 | 7,518 | 1.333 | 1.688 |
| 1980 | Early | 6,876 | 7,242 | 1.217 | 1.519 |
| Shandong | 1986 | Middle | 8,799 | 9,954 | 1.006 | 1.419 |
| 1989 | Middle | 8,242 | 10,359 | 0.853 | 1.858 |
| Zhejiang | 1998 | Early | 6,075 | 6,746 | 1.168 | 1.775 |
| 1998 | Late | 6,363 | 6,746 | 0.994 | 1.599 |
Looking across provinces, the yields of traditional rice are higher in Shandong than in Guangxi, yet the estimates of water productivity are higher for Guangxi. Lacking information regarding the opportunity cost of water in the two provinces and the costs of other, complementary inputs, it is not possible to determine if the higher values of water productivity in Guangxi are meaningful from a policy perspective. Similarly, the yields of AWD rice in Zhejiang are smaller than in Guangxi, yet the estimates of water productivity are higher for Zhejiang.
The yields and water productivities for AWD rice generally are higher than the yields and productivities for traditionally irrigated rice (
Table 4). Yet without information describing the incremental costs and benefits associated with the change in water management, it is not possible to know if the higher yields and water productivities are desirable. For example, if weeding costs are higher or more pesticides are needed when using alternate wetting and drying, the incremental cost of achieving higher yields might negate the value of the incremental gain. In any event, it is not possible to derive helpful conclusions from the limited information presented in
Table 4. Much more is needed, regarding the opportunity costs of key inputs and the stochastic nature of crop yields, rainfall, percolation, ET, and the resulting estimates of water productivity.
7. Summing Up
The motivation for increasing water productivity is well-stated and compelling. With increasing competition for freshwater resources, farmers, researchers, and public officials must continuously pursue opportunities to improve agricultural productivity, while promoting also the wise use of renewable and non-renewable resources. Estimates of water productivity seem pertinent, particularly in water scarce areas. It is indeed compelling to think about increasing the returns per unit of water consumed in agriculture. Yet estimates of water productivity, by themselves, do not provide the information needed to fully understand the production opportunities, constraints, and livelihood considerations that determine farm input choices and the resulting probabilistic distributions of crop and livestock output.
Many authors compare estimates of water productivity across locations and over time. Yet the estimates are point observations, calculated by dividing some measure of crop or livestock production by some measure of water applied or consumed. It is not possible to derive helpful insight from such comparisons, without knowing much more about the production settings, the availability of complementary inputs, the distribution of rainfall, and the risk and uncertainty farmers face when making decisions regarding crop choices, input levels, and markets. We need also to know more about the incremental costs and gains of water use in each setting, rather than simply comparing measures of average productivity.
In summary, estimates of water productivity do not enhance understanding of farm-level water management in rainfed and irrigated settings in a manner that would guide researchers or policy makers toward wise interventions and investments. Water interacts with many other inputs in crop and livestock production. Thus, to ensure sufficient food production in future we must analyze production settings in greater detail, measuring interactions involving water and other inputs, and evaluating strategies that acknowledge those interactions, just as farmers must do each season. We must also invest greater effort in understanding risk and uncertainty, particularly from the perspective of smallholder farmers, who have little freeboard for accommodating crop failures or recovering from mistakes in input allocation. We can develop more useful guidance for smallholders if we enhance our analysis in ways that look beyond point estimates of water productivity.