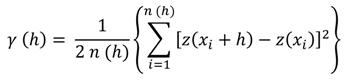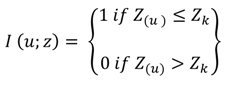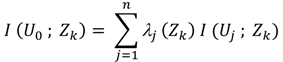1. Introduction
Groundwater is one of the most significant natural sources [
1,
2], and can be used as an alternative to surface water for drinking, irrigation and industry usage. Poor drinking water quality, high cost of water purification, human health problems, and loss of water supply are attributable to groundwater contamination. The monitoring of the chemical, physical and biological conditions of groundwater is considered to be critical for the planning strategy for the protection of groundwater quality [
1]. The data obtained from a groundwater monitoring network are valuable for understanding, identifying, and describing modifications in the condition of the groundwater [
3,
4]. A good monitoring network should be indicative of both adequate and appropriate information concerning the groundwater quality as well as be effective in terms of cost [
5]. Although the amount of information collected from a monitoring network could be increased by more sampling wells, it is costly and probably provides redundant information. Therefore, the optimal monitoring network should provide sufficient data concerning the groundwater quality using the minimum number of monitoring wells [
5]. Some of the monitoring network designs are inefficient due to the shortage or redundancy of information [
6]. A new technique can be developed from the probability estimation of the groundwater contaminant concentrations, hydrogeological approaches and evaluation of the pollution risk from anthropogenic activities to assess the groundwater quality monitoring network and evaluate the risky zones of the aquifers.
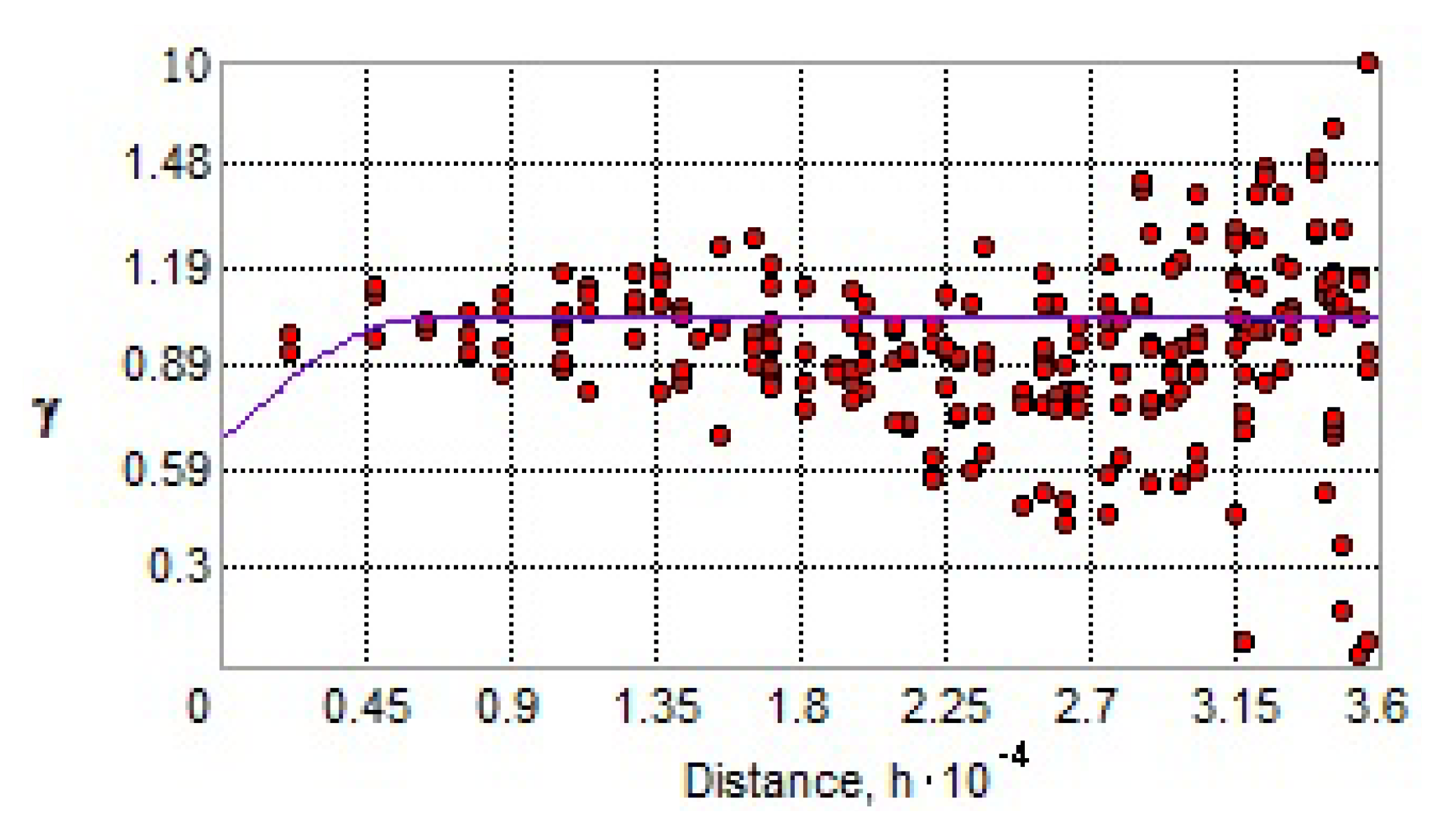
Geostatistics is a spatial statistical technique that can be used to assess and represent the distribution of concentration over space and time [
7]. This technique predicts the estimated values based on the relationship between the sample points and estimates the uncertainty of that prediction [
8,
9,
10]. Kriging is a linear interpolation procedure that is used to create probabilistic models of uncertainty relating to the values of the attributes. Indicator kriging (IK) is an efficient non-parametric geostatistical method with no assumption regarding the distribution of variables [
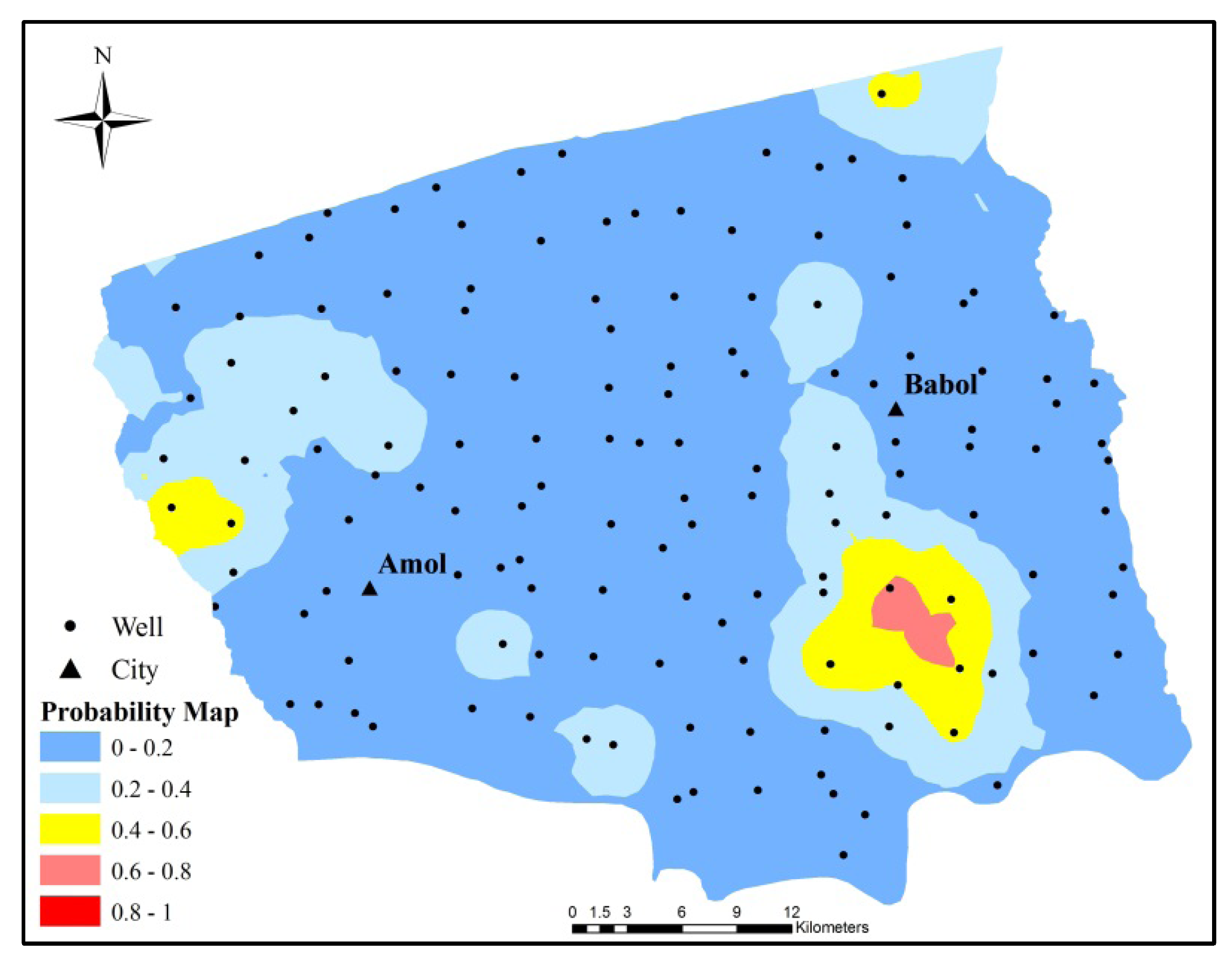
11], and has the ability to take the data uncertainty into account and predict the conditional probability of certain data for an unsampled location [
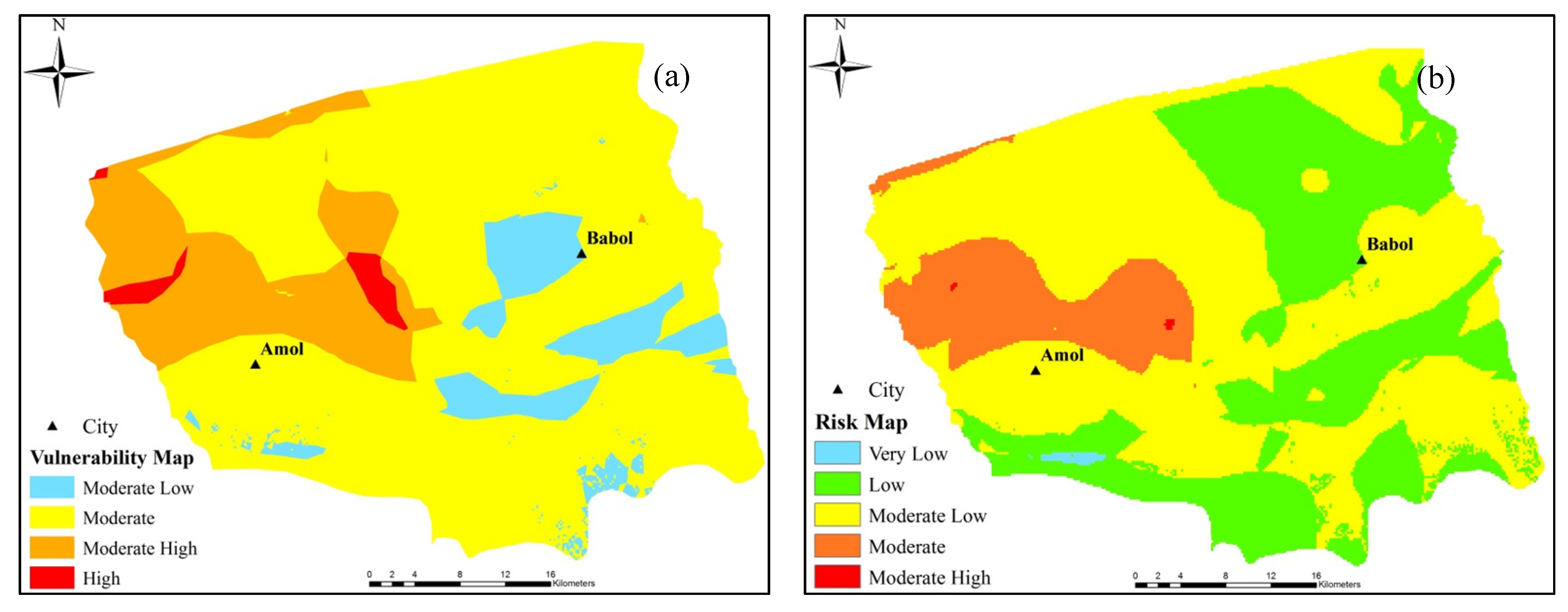
12]. Indicator kriging is also used to identify areas of high probability as potential sites for monitoring based on the current monitoring wells. However, this method alone is not sufficient for the optimal design of monitoring wells, without considering the potential risk from anthropogenic activities and the vulnerable hydrogeological characteristics. The vulnerability of groundwater is characterized by the hydrogeological and geological attributes of the aquifer [
13] to specific areas that are more prone to contamination. The DRASTIC model is the most commonly applied vulnerability model based on the physical environmental aquifer parameters to assess groundwater vulnerability [
14,
15,
16,
17,
18]. The existence of potential contamination activities should be considered as a risk for groundwater pollution since the vulnerability only represents the intrinsic characteristic of the aquifer. As the population of an area grows, intensive agricultural activities, inappropriate placement of commercial and industrial regions and high intensity residential areas can potentially cause pollution of the groundwater. Therefore, land use is an additional parameter that can be integrated into the DRASTIC method to evaluate the potential risk in different areas [
13,
15].
Few researchers have applied the integration of geostatistical techniques and vulnerability assessment as a new approach for redesigning the groundwater monitoring networks [
5,
19,
20,
21]. The density of monitoring wells was considered together with vulnerability assessments by Dawoud [
22]. Yeh
et al. [
21] applied a genetic algorithm and the factorial kriging method for nine variables—electrical conductivity (EC), total dissolved solids (TDS), Cl
−, Na
+, Ca
2+, Mg
2+, SO
42−, Mn, and Fe—for optimal selection of monitoring wells in Pingting Plain, Taiwan. To reach a similar objective, Baalousha [
5] developed a new methodology by combining vulnerability and ordinary kriging maps based on the nitrate concentration from groundwater in the Heretaunga Plain, New Zealand. Preziosi
et al. [
20] developed a GIS based procedure to select the most appropriate monitoring points by combining the actual contamination data, the attributes of water points, and the vulnerability conditions for a variable density network design.
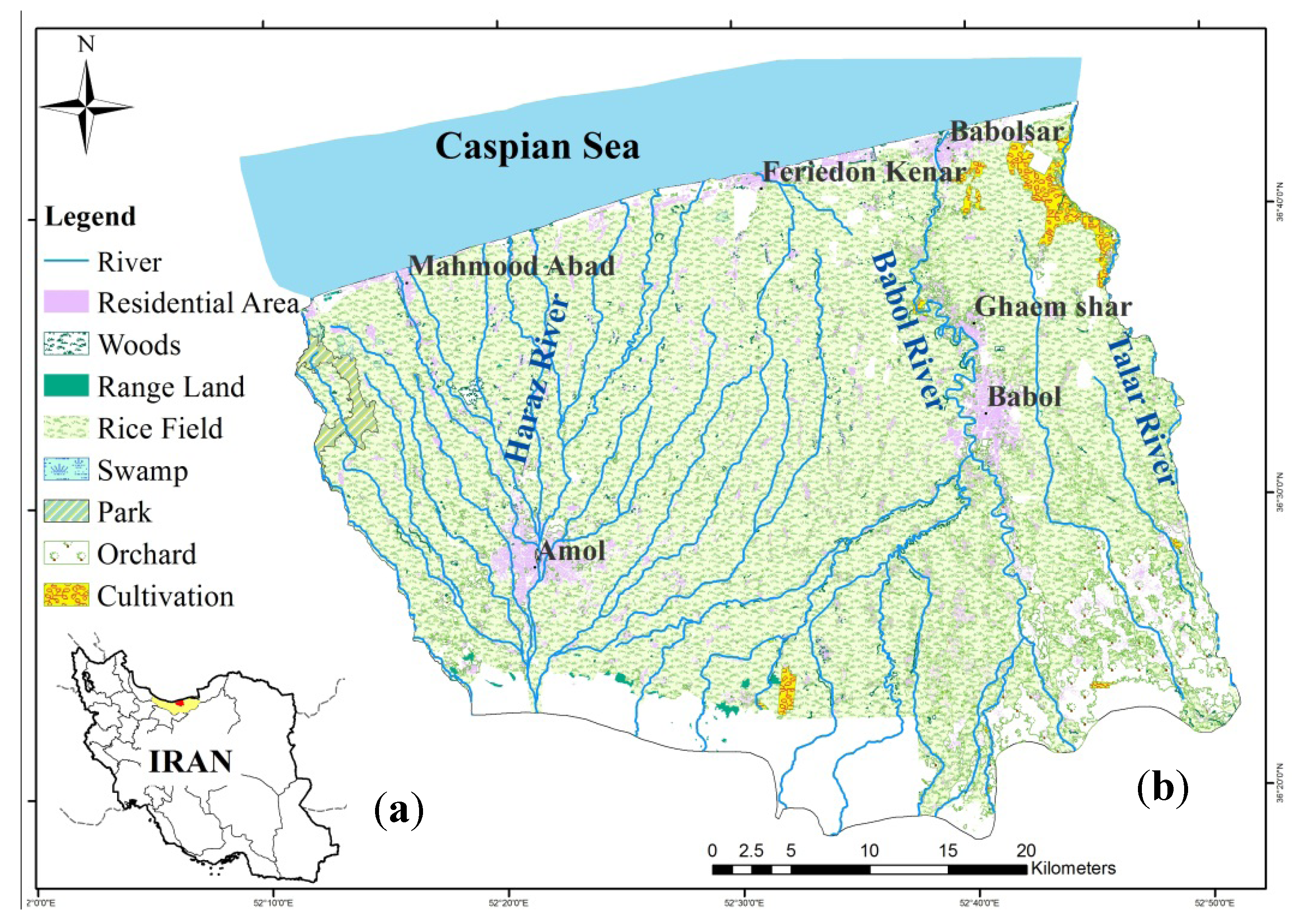
In this study, the data collected from 147 monitoring wells were applied to estimate the potential contamination risk of nitrate in drinking water using indicator kriging on the Amol-Babol Plain, in northern Iran. Moreover, the potential risk zones of groundwater to pollution are specified by integrating the vulnerability and risk mapping in the study area. The main purpose of this study was to develop a new approach to identify areas with high potential pollution and assess the efficiency of the current monitoring wells by probability risk assessment method.
4. Conclusions
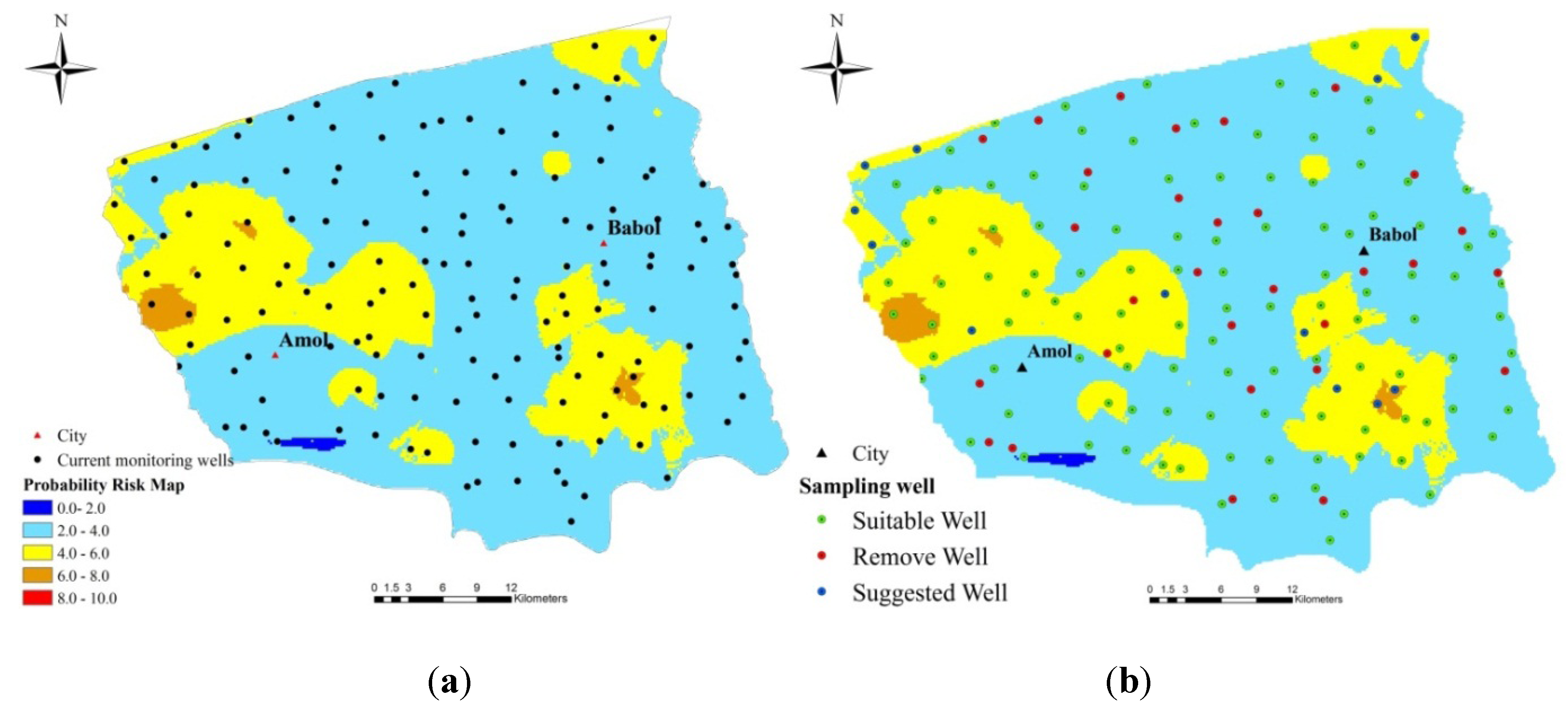
This paper developed an approach to assess and delineate areas that require groundwater quality monitoring. The proposed approach assesses the efficiency of the existing network of monitoring wells, considering not only the samples collected from the wells, but also the hydrogeological characteristics of the aquifer and the potential for anthropogenic pollution in the study area. The combination of indicator kriging to estimate the probability of nitrate concentration, together with the vulnerability and risk assessment by the DRASTIC method, represents a powerful and reliable method for identifying optimal sampling locations in the study area. The methodology was designed and successfully applied in the Amol-Babol Plain (Iran). The resultant map of the overlaid factors shows that some areas with strong nitrate probability and high risk of pollution on the south side of Babol City, the northeastern part of the plain and the northwestern part of Amol City are not covered by an adequate number of monitoring wells. However, the majority of the plain, which has a weak probability of nitrate concentration and low risk of contamination, is monitored by multiple sampling wells. Therefore, the existing monitoring wells should be reduced in the lower risk areas and increased in the areas with the highest risk of nitrate contamination. The proposed methodology is general and can be applied to any type of aquifer that is threatened by natural or anthropogenic pollution. In future studies, the proposed method could be applied to assess and redesign the monitoring wells based on various types of pollutants in the aquifer.