Inter-Event Time Definition Setting Procedure for Urban Drainage Systems
Abstract
:1. Introduction
2. IETD Determination in Urban Drainage Systems
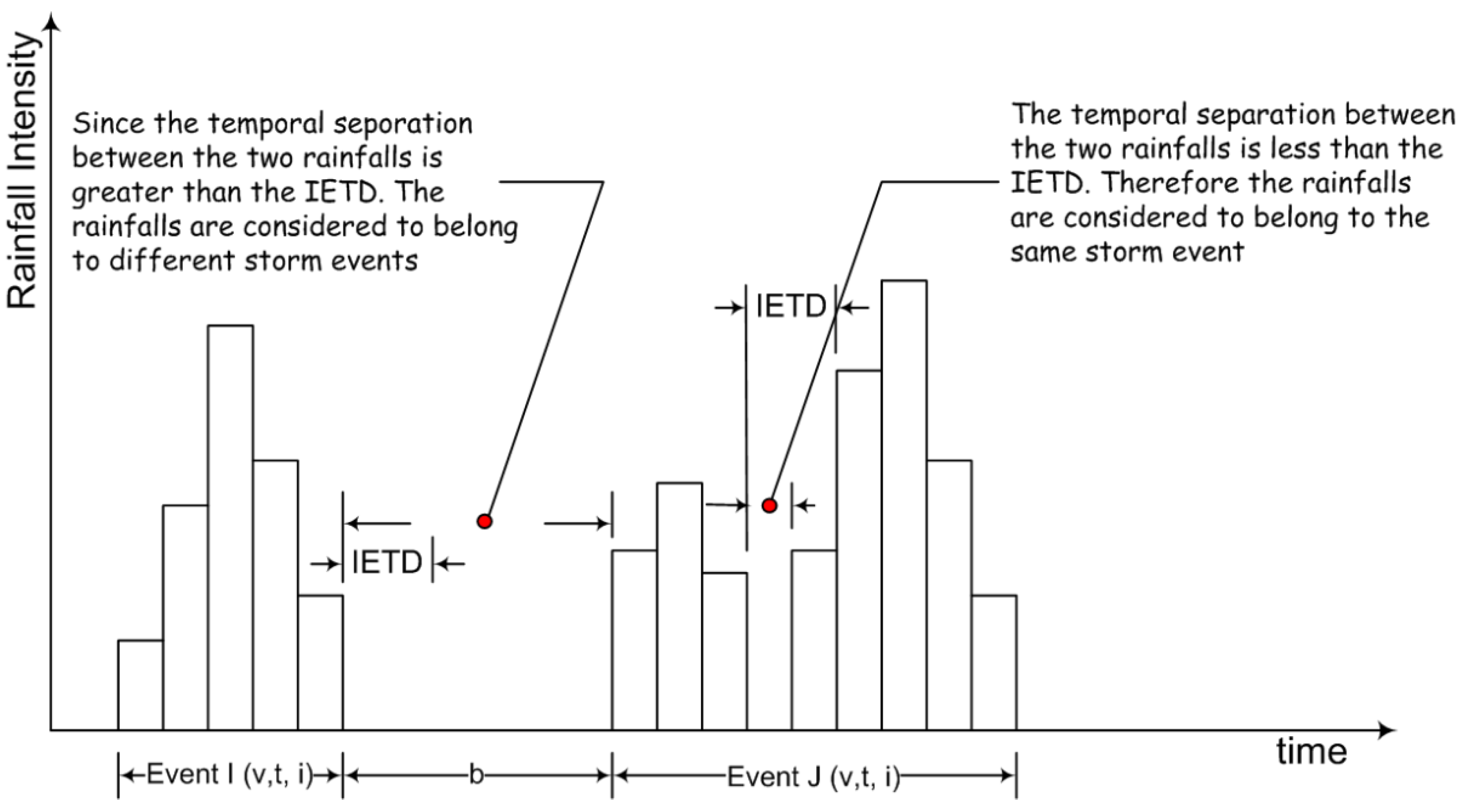
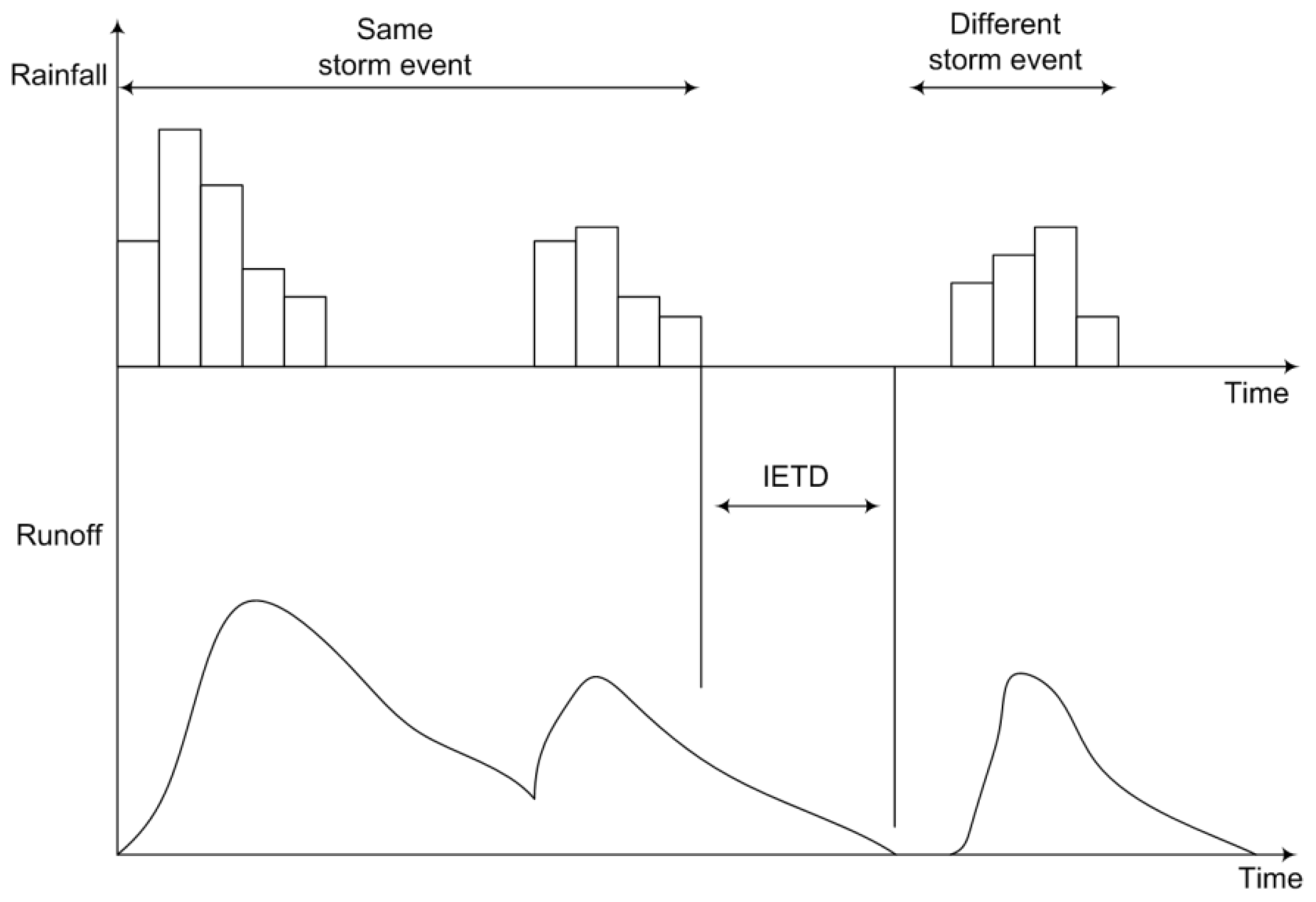
2.1. Traditional IETD Determination Methods


| Basin type | City | Observation period | Population density (person/km2) | IETD by coefficient of variation (h) |
|---|---|---|---|---|
| Urban catchment | Seoul | 1961–2002 | 16,221 | 10 |
| Busan | 1961–2000 | 4,609.4 | 15 | |
| Daegu | 1961–2000 | 2,786.5 | 12 | |
| Daejeon | 1969–2000 | 2,673.0 | 12 | |
| Rural basin | Sokcho | 1968–2000 | 803.8 | 13 |
| Jinju | 1969–2000 | 465.3 | 12 | |
| Jeongeup | 1973–2000 | 187.5 | 12 | |
| Buyeo | 1973–2000 | 134.0 | 11 | |
| Cheorwon | 1988–2000 | 53.7 | 14 | |
| Hongcheon | 1973–2000 | 35.5 | 11 |
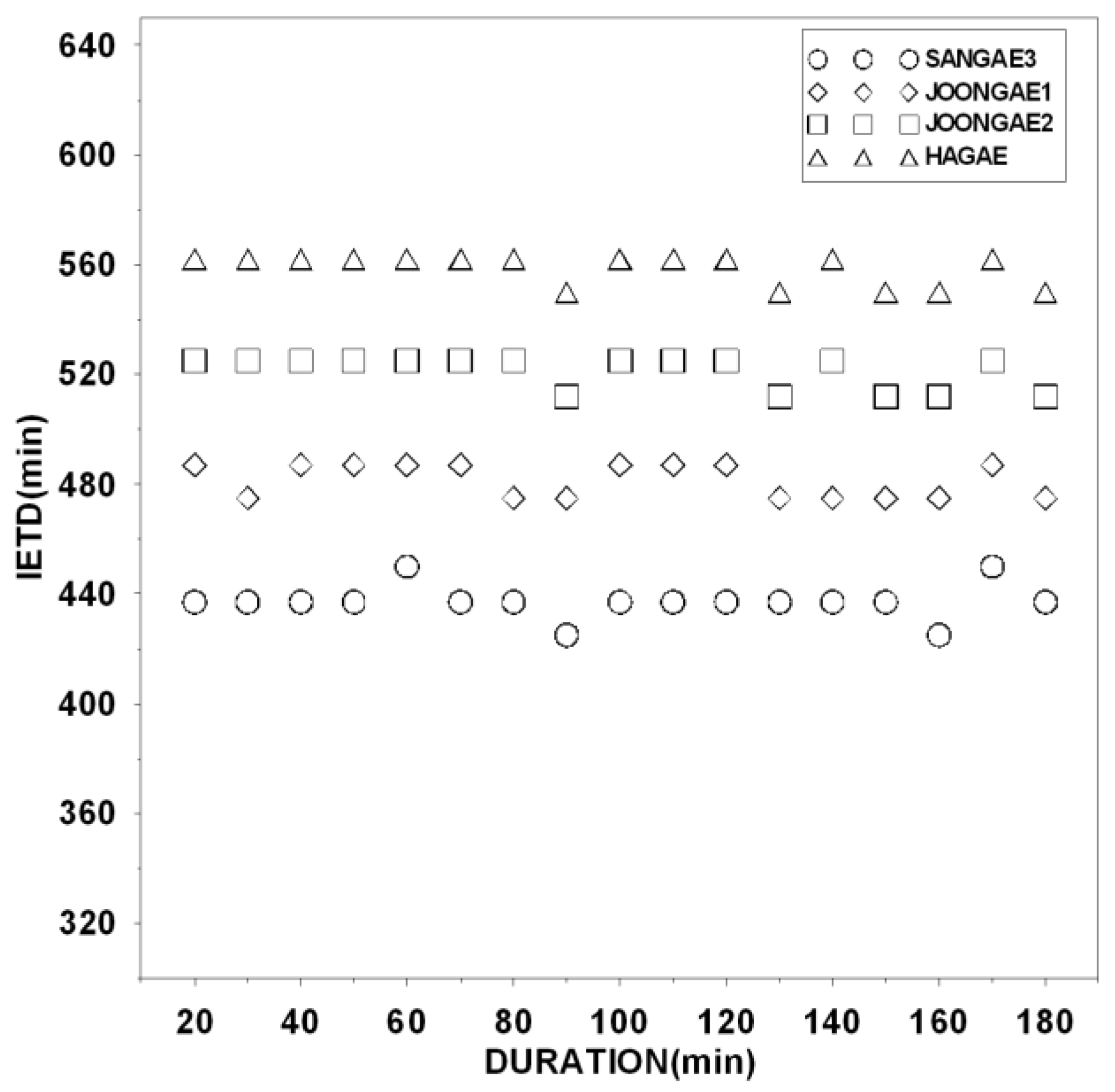
2.2. Development of an IETD Determination Method for Urban Watersheds
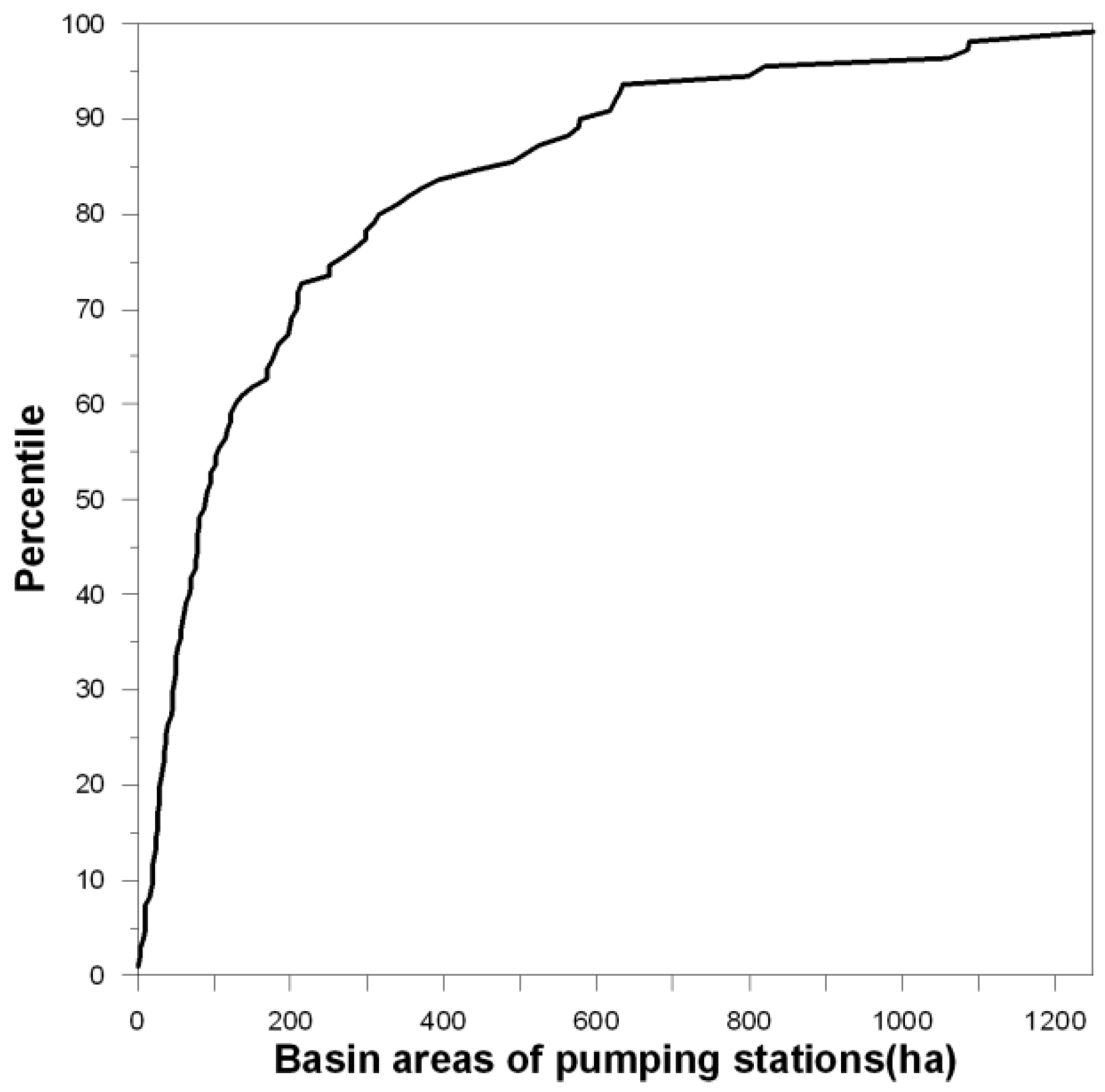
2.3. Application of the Suggested IETD Determination Method

| Duration (min) | Rainfall Events | Mean Depth (mm) | Mean Intensit (mm/h) | ||
|---|---|---|---|---|---|
| Number | Percent (%) | Cumulative Percent (%) | |||
| 11~20 | 79 | 8.87 | 8.87 | 10.77 | 32.32 |
| 21~30 | 90 | 10.10 | 18.97 | 12.13 | 24.27 |
| 31~40 | 82 | 9.20 | 28.17 | 16.75 | 25.13 |
| 41~50 | 89 | 9.99 | 38.16 | 23.60 | 28.32 |
| 51~60 | 69 | 7.74 | 45.90 | 36.38 | 36.38 |
| 61~70 | 63 | 7.07 | 52.97 | 29.57 | 25.35 |
| 71~80 | 59 | 6.62 | 59.60 | 35.78 | 26.09 |
| 81~90 | 46 | 5.16 | 64.76 | 21.71 | 14.47 |
| 91~100 | 45 | 5.05 | 69.81 | 56.58 | 33.95 |
| 101~110 | 33 | 3.70 | 73.51 | 36.54 | 19.93 |
| 111~120 | 48 | 5.39 | 78.90 | 39.02 | 19.51 |
| 121~130 | 41 | 4.60 | 83.50 | 17.95 | 8.29 |
| 131~140 | 32 | 3.59 | 87.09 | 24.66 | 10.57 |
| 141~150 | 24 | 2.69 | 89.79 | 18.69 | 7.48 |
| 151~160 | 33 | 3.70 | 93.49 | 27.63 | 10.36 |
| 161~170 | 28 | 3.14 | 96.63 | 37.61 | 13.27 |
| 171~180 | 30 | 3.37 | 100.00 | 23.49 | 7.83 |
| Total | 891 | – | – | – | – |


3. Temporal Distribution of Rainfall Using the Suggested IETD for Urban Drainage Systems

| Name of drainage zone | Sang-Gea | Joong-Gok | Jang-An | Su-Yoo |
|---|---|---|---|---|
| Area (ha) | 427.4 | 294.8 | 286.5 | 583.1 |
| Stream Name | Dang-Hyun | Joong-Rang | Joong-Rang | Woo-I |
| IETD (min) | 150 | 120 | 120 | 180 |
| Time (%) Method | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | sum | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| This study (mm) | Sang-Gea | 34.08 | 41.53 | 22.31 | 17.46 | 9.74 | 11.66 | 6.12 | 3.35 | 1.99 | 1.76 | 150 |
| (22.72) | (27.69) | (14.87) | (11.64) | (6.49) | (7.77) | (4.08) | (2.23) | (1.33) | (1.17) | (100%) | ||
| Joong-Gok | 34.08 | 40.08 | 22.30 | 17.40 | 9.75 | 8.68 | 9.54 | 3.94 | 2.07 | 2.16 | 150 | |
| (22.72) | (26.72) | (14.87) | (11.60) | (6.50) | (5.79) | (6.36) | (2.63) | (1.38) | (1.44) | (100%) | ||
| Jang-An | 34.08 | 40.08 | 22.30 | 17.40 | 9.75 | 8.68 | 9.54 | 3.94 | 2.07 | 2.16 | 150 | |
| (22.72) | (26.72) | (14.87) | (11.60) | (6.50) | (5.79) | (6.36) | (2.63) | (1.38) | (1.44) | (100%) | ||
| Su-Yoo | 33.13 | 41.03 | 23.76 | 17.18 | 10.12 | 10.61 | 7.07 | 3.57 | 1.80 | 1.72 | 150 | |
| (22.09) | (27.35) | (15.84) | (11.45) | (6.75) | (7.07) | (4.71) | (2.38) | (1.20) | (1.15) | (100%) | ||
| Huff (mm) | 31.50 | 36.30 | 25.95 | 14.85 | 8.10 | 8.70 | 6.60 | 7.35 | 6.00 | 4.65 | 150 | |
| (21.00) | (24.20) | (17.30) | (9.90) | (5.40) | (5.80) | (4.40) | (4.90) | (4.00) | (3.10) | (100%) | ||
| Subbasin | This study | Huff | Ratio of peak flow by suggested and Huff methods (A/B) (%) | ||||
|---|---|---|---|---|---|---|---|
| IETD (min) | Peak flow rate (cm) (A) | Peak time (min) | IETD (min) | Peak flow rate (cm) (B) | Peak time (min) | ||
| Sang-Gea | 150 | 79.1 | 57 | 360 | 68.8 | 57 | 115 |
| Joong-Gok | 120 | 52.6 | 60 | 360 | 47.5 | 65 | 111 |
| Jang-An | 120 | 50.6 | 72 | 360 | 45.5 | 72 | 111 |
| Su-Yoo | 180 | 108.4 | 67 | 360 | 95.7 | 70 | 113 |
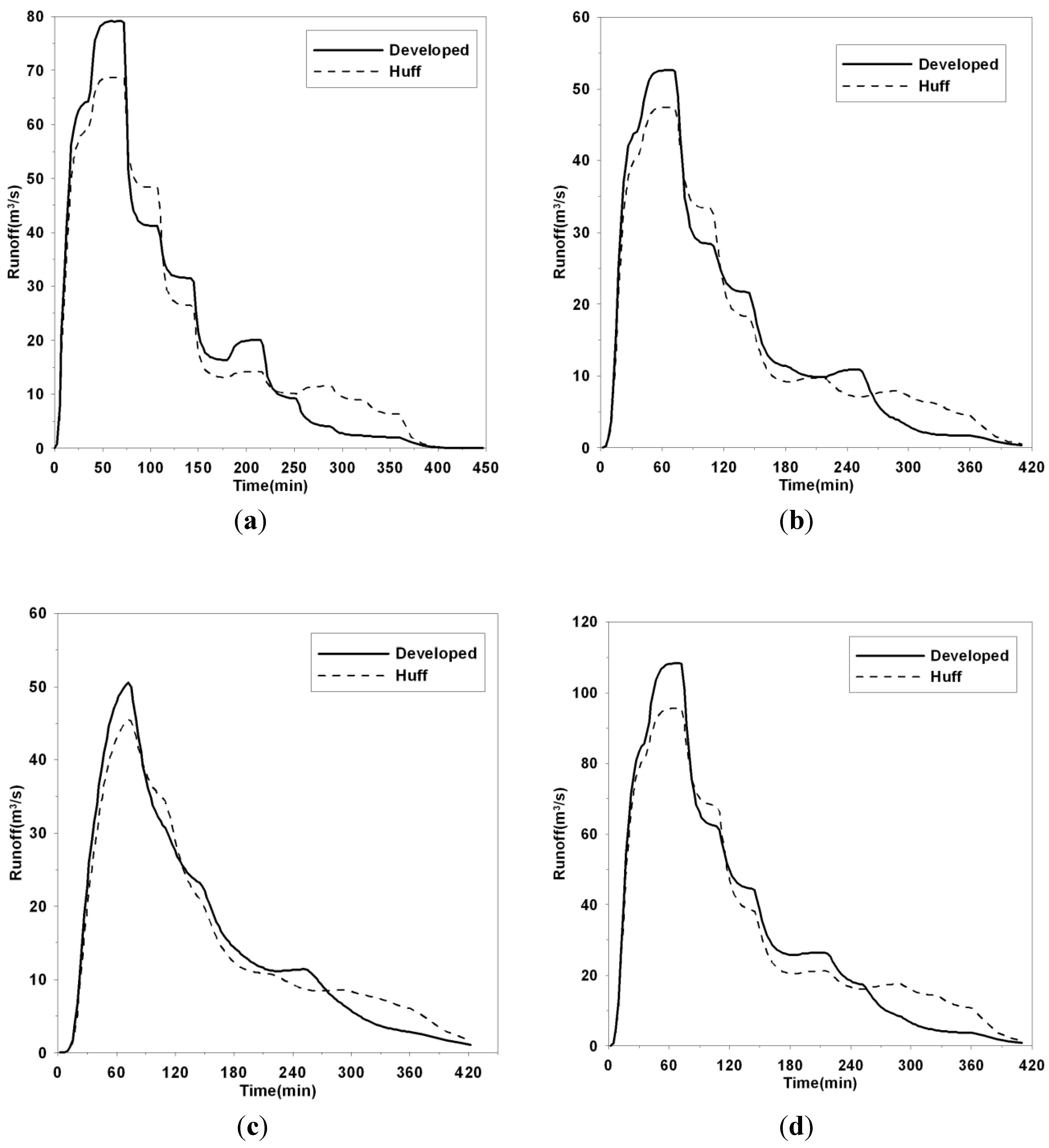
4. Summary and Conclusions
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Adams, B.J. Analysis of storage facilities for urban stormwater quantity control. Adv. Water Resour. 2005, 28, 377–392. [Google Scholar] [CrossRef]
- Behera, P.K.; Adams, B.J.; Li, J.Y. Runoff quality analysis of urban catchments with analytical probabilistic models. J. Water Resour. Plan. Manag. ASCE 2006, 132, 4–14. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Grossi, G.; Ranzi, R. Design Storm Selection for Mixed Urban and Agricultural Drainage Systems: A Case Study in the Northern Delta-Vietnam. In Proceedings of 11th International Conference on Urban Drainage, Edinburgh, UK, 31 August–5 September 2008.
- Guo, Y.; Liu, S.; Baetz, B.W. Probabilistic rainfall-runoff transformation considering both infiltration and saturation excess runoff generation processes. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Balistrocchi, M.; Bacchi, B. Modelling the statistical dependence of rainfall event variables by a trivariate copula function. Hydrol. Earth Syst. Sci. Discuss. 2011, 8, 429–481. [Google Scholar] [CrossRef] [Green Version]
- Adams, B.J.; Hugh, G.F.; Charles, D.D.; Sami, M.H. Meteorological data analysis for drainage system design. J. Environ. Eng. 1986, 112, 827–848. [Google Scholar] [CrossRef]
- Grace, R.A.; Eagleson, P.S. A Model for Generating Synthetic Sequences of Short-Time-Interval Rainfall Depths. In Proceedings of the International Association Hydrologic Science Symposium, Fort Collins, CO, USA, 6–8 September 1967; pp. 268–276.
- Sariahmed, A.; Kisiel, C.C. Synthesis of Sequences of Summer Thunderstorm Volumes for the Atterbury Watershed in the Tucson Area. In Proceedings of the International Association Hydrologic Science Symposium on Use of Analog and Digital Computers in Hydrology, Tucson, AZ, USA, 1968; pp. 439–447.
- Howard, C.D.D. Theory of storage and treatment-plant overflows. J. Environ. Eng. Div. 1976, 102, 709–722. [Google Scholar]
- Heaney, J.P.; Huber, W.C.; Medina, M.A.; Murphy, M.P.; Nix, S.J.; Hasan, S.M. Nationwide Assessment of Combined Sewer Overflows and Urban Stormwater Discharges: Volume II, Cost Assessment and Impacts; U.S. Environment Protection Agency: Cincinnati, OH, USA, 1977. [Google Scholar]
- Nix, S.J. Urban Stormwater Modeling and Simulation; Lewis Publishers: Boca Raton, FL, USA, 1994. [Google Scholar]
- Restrepo-Posada, P.J.; Eagelson, P.S. Identification of independent rainstorms. J. Hydrol. 1982, 55, 303–319. [Google Scholar] [CrossRef]
- Joo, J.G.; Lee, J.H.; Jun, H.D.; Kim, J.H.; Jo, D.J. A New Approach to Determine IETD Considering Runoff Characteristics of Urban Watersheds. In Proceedings of the Asia Oceania Geosciences Society 3rd Annual Meeting & Exhibition (AOGS2006), Singapore, 9–14 July 2006.
- Balistrocchi, M.; Grossi, G.; Bacchi, B. An analytical probabilistic model of the quality efficiency of a sewer tank. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Balistrocchi, M.; Grossi, G.; Bacchi, B. Deriving a practical analytical-probabilistic method to size flood routing reservoirs. Adv. Water Resour. 2013, 62, 37–46. [Google Scholar] [CrossRef]
- Adams, B.J.; Papa, F. Urban Stormwater Management Planning with Analytical Probabilistic Models; John Wiley Sons: New York, NY, USA, 2000. [Google Scholar]
- Huber, W.; Dickinson, R.E. Storm Water Management Model, Version 4: User’s Manual; United States Environmental Protection Agency: Athens, GA, USA, 1988. [Google Scholar]
- Keifer, C.J.; Chu, H.H. Synthetic storm pattern for drainage design. J. Hydraul. Div. 1957, 83, 1–25. [Google Scholar]
- Huff, F.A. Time distribution of rainfall in heavy storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
- Soil Conservation Service (SCS). Engineering Field Manual. Available online: http://directives.sc.egov.usda.gov/viewerFS.aspx?hid=21429 (accessed on 23 December 2013).
- Yen, B.C.; Chow, V.T. Feasibility Study on Research of Local Design Storms; U.S. Department of Transportation, Federal Highway Administration: Washington, DC, USA, 1977. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Joo, J.; Lee, J.; Kim, J.H.; Jun, H.; Jo, D. Inter-Event Time Definition Setting Procedure for Urban Drainage Systems. Water 2014, 6, 45-58. https://doi.org/10.3390/w6010045
Joo J, Lee J, Kim JH, Jun H, Jo D. Inter-Event Time Definition Setting Procedure for Urban Drainage Systems. Water. 2014; 6(1):45-58. https://doi.org/10.3390/w6010045
Chicago/Turabian StyleJoo, Jingul, Jungho Lee, Joong Hoon Kim, Hwandon Jun, and Deokjun Jo. 2014. "Inter-Event Time Definition Setting Procedure for Urban Drainage Systems" Water 6, no. 1: 45-58. https://doi.org/10.3390/w6010045




