Hydraulic Features of Flow through Emergent Bending Aquatic Vegetation in the Riparian Zone
Abstract
:1. Introduction
2. Laboratory Experiments
2.1. Materials
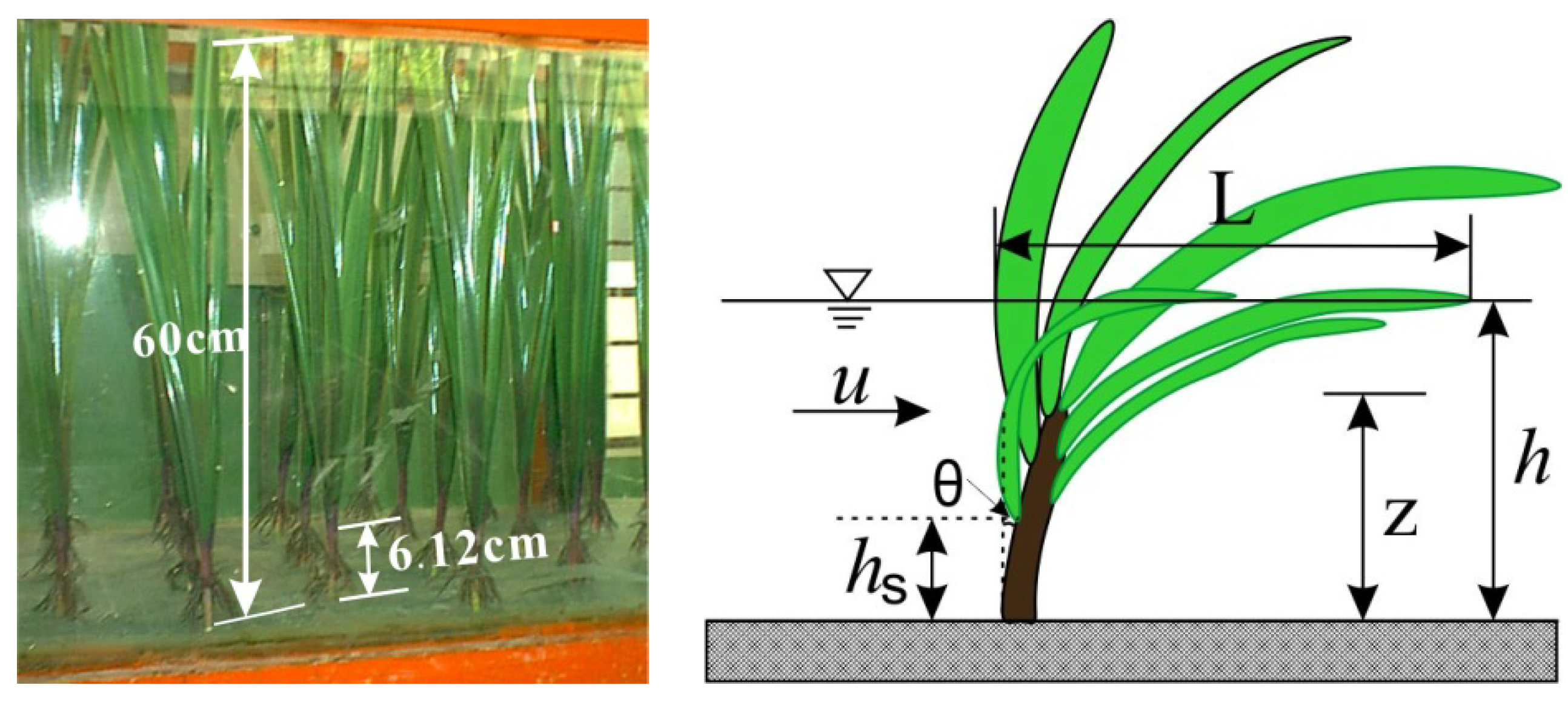
2.2. Experimental Setup and Measurement Technique
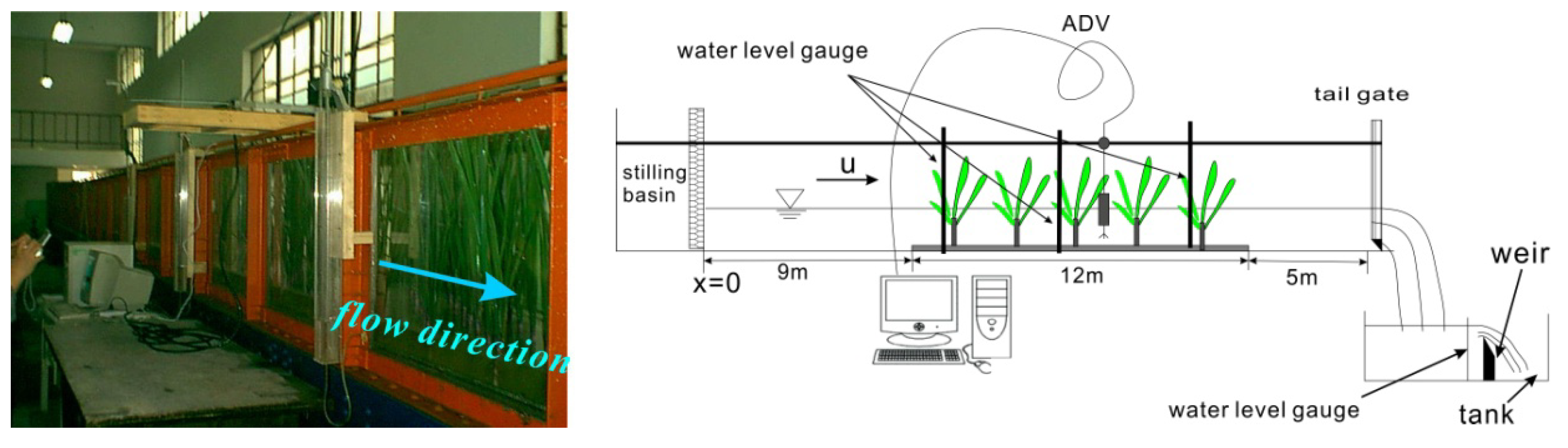
2.3. Test Series Description
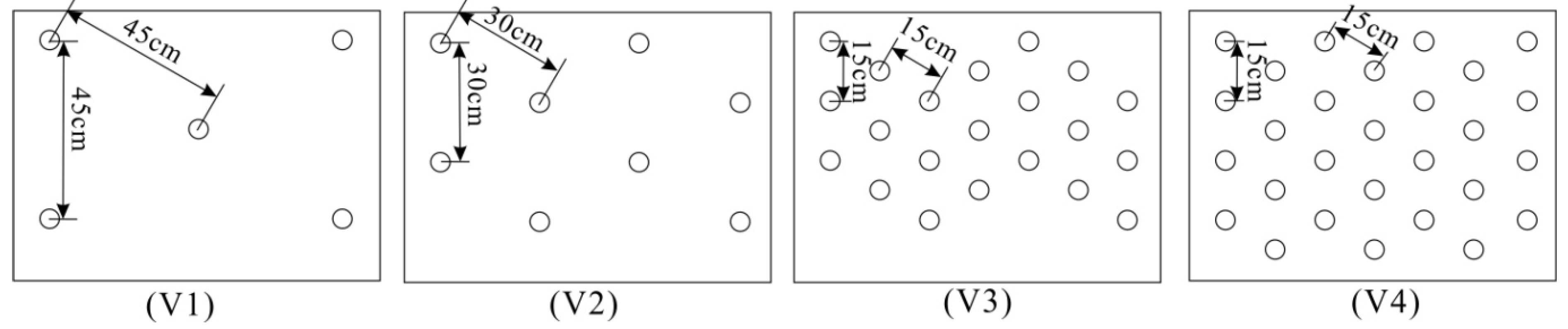
| Series | Description | Test runs | Q(m3/s) | Re | Fr | h(cm) | u(m/s) |
|---|---|---|---|---|---|---|---|
| V0 | No vegetation | V0-1 | 0.00650 | 12996 | 0.502 | 4.09 | 0.318 |
| V0-2 | 0.00796 | 15918 | 0.527 | 4.53 | 0.351 | ||
| V0-3 | 0.01090 | 21792 | 0.533 | 5.55 | 0.393 | ||
| V0-4 | 0.01347 | 26942 | 0.532 | 6.40 | 0.421 | ||
| V0-5 | 0.01900 | 38000 | 0.514 | 8.23 | 0.462 | ||
| V0-6 | 0.02140 | 42781 | 0.510 | 8.95 | 0.478 | ||
| V0-7 | 0.02520 | 50394 | 0.566 | 9.32 | 0.541 | ||
| V0-8 | 0.03095 | 61801 | 0.604 | 10.22 | 0.605 | ||
| V1 | 45 cm, 40 plants | V1-1 | 0.00616 | 12324 | 0.267 | 6.01 | 0.205 |
| V1-2 | 0.00804 | 16072 | 0.278 | 6.98 | 0.230 | ||
| V1-3 | 0.01040 | 20805 | 0.269 | 8.47 | 0.246 | ||
| V1-4 | 0.01208 | 24159 | 0.263 | 9.51 | 0.254 | ||
| V1-5 | 0.01514 | 30273 | 0.248 | 11.50 | 0.263 | ||
| V1-6 | 0.01612 | 32246 | 0.238 | 12.34 | 0.261 | ||
| V1-7 | 0.01879 | 37571 | 0.224 | 14.20 | 0.265 | ||
| V1-8 | 0.02204 | 44080 | 0.221 | 15.95 | 0.276 | ||
| V1-9 | 0.02391 | 47922 | 0.216 | 17.10 | 0.280 | ||
| V2 | 30 cm, 60 plants | V2-1 | 0.00498 | 9957 | 0.226 | 5.82 | 0.171 |
| V2-2 | 0.00606 | 12127 | 0.233 | 6.51 | 0.186 | ||
| V2-3 | 0.00843 | 16861 | 0.227 | 8.25 | 0.205 | ||
| V2-4 | 0.00902 | 18044 | 0.224 | 8.72 | 0.207 | ||
| V2-5 | 0.01154 | 23074 | 0.217 | 10.49 | 0.220 | ||
| V2-6 | 0.01381 | 27610 | 0.214 | 11.93 | 0.231 | ||
| V2-7 | 0.01405 | 28103 | 0.207 | 12.35 | 0.228 | ||
| V2-8 | 0.01854 | 37077 | 0.188 | 15.85 | 0.234 | ||
| V2-9 | 0.02056 | 41121 | 0.170 | 18.13 | 0.227 | ||
| V3 | 15 cm, 240 plants | V3-1 | 0.00288 | 9320 | 0.130 | 5.75 | 0.100 |
| V3-2 | 0.00369 | 7372 | 0.118 | 7.36 | 0.100 | ||
| V3-3 | 0.00466 | 5752 | 0.133 | 8.06 | 0.116 | ||
| V3-4 | 0.00530 | 10600 | 0.121 | 9.23 | 0.115 | ||
| V3-5 | 0.00610 | 12195 | 0.122 | 10.05 | 0.121 | ||
| V3-6 | 0.00750 | 14999 | 0.107 | 12.56 | 0.119 | ||
| V3-7 | 0.00980 | 19602 | 0.090 | 16.73 | 0.117 | ||
| V3-8 | 0.01158 | 23152 | 0.081 | 20.26 | 0.114 | ||
| V3-9 | 0.01290 | 25758 | 0.070 | 22.80 | 0.113 | ||
| V4 | 15 cm, 280 plants | V4-1 | 0.00298 | 5955 | 0.104 | 6.94 | 0.086 |
| V4-2 | 0.00305 | 6100 | 0.104 | 7.05 | 0.087 | ||
| V4-3 | 0.00350 | 6999 | 0.108 | 7.55 | 0.093 | ||
| V4-4 | 0.00420 | 8397 | 0.118 | 8.01 | 0.105 | ||
| V4-5 | 0.00550 | 10996 | 0.121 | 9.45 | 0.116 | ||
| V4-6 | 0.00618 | 12357 | 0.114 | 10.63 | 0.116 | ||
| V4-7 | 0.00640 | 12785 | 0.109 | 11.22 | 0.114 | ||
| V4-8 | 0.00736 | 14714 | 0.098 | 13.22 | 0.111 | ||
| V4-9 | 0.01090 | 21801 | 0.079 | 19.86 | 0.101 |
3. Analytical Method
3.1. Vegetation Density
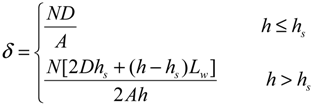
3.2. Resistance Coefficient
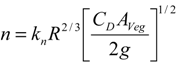
3.3. Turbulence Intensity
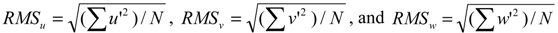
4. Results and Discussion
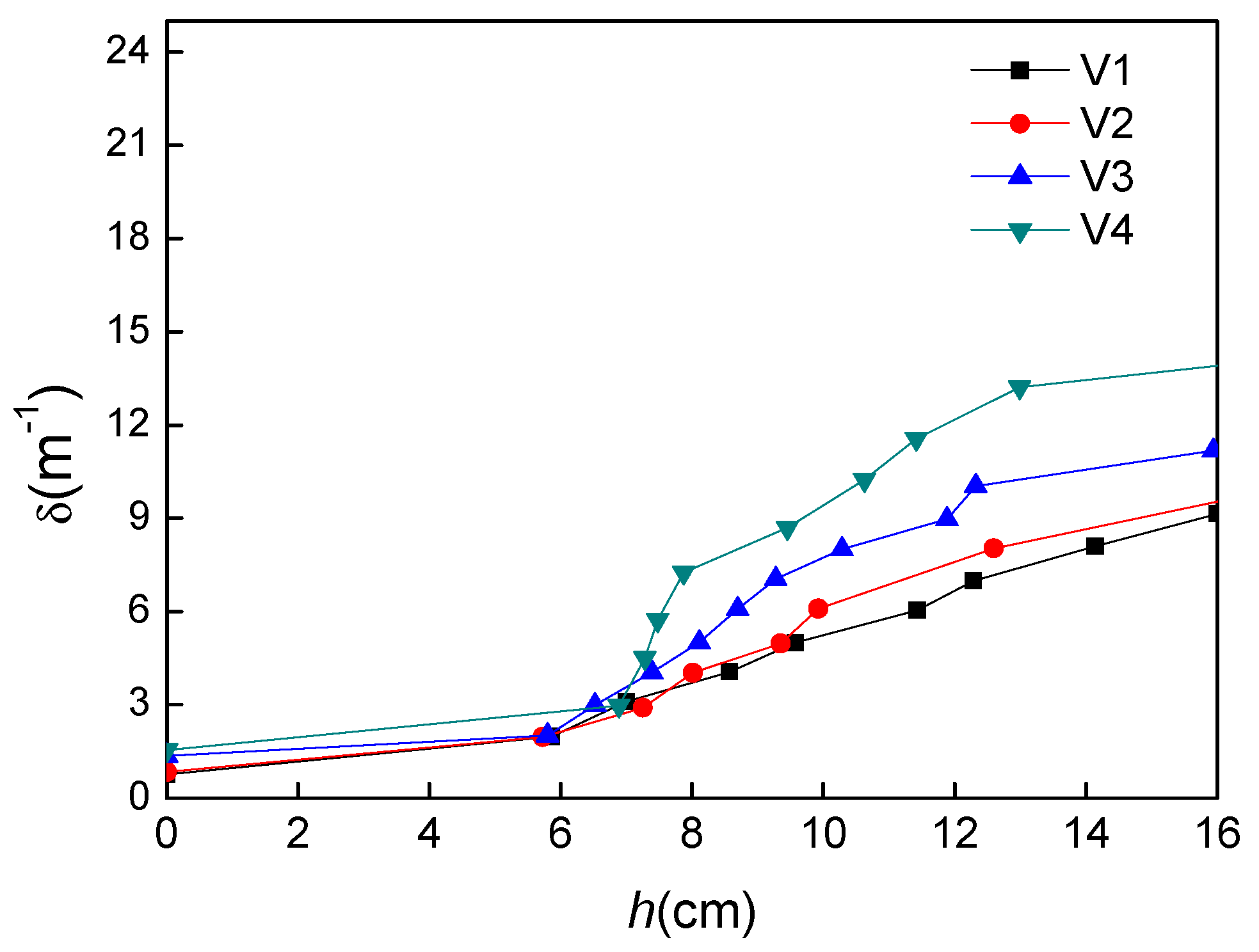
4.1. Vegetation Density
4.2. Manning Coefficient n
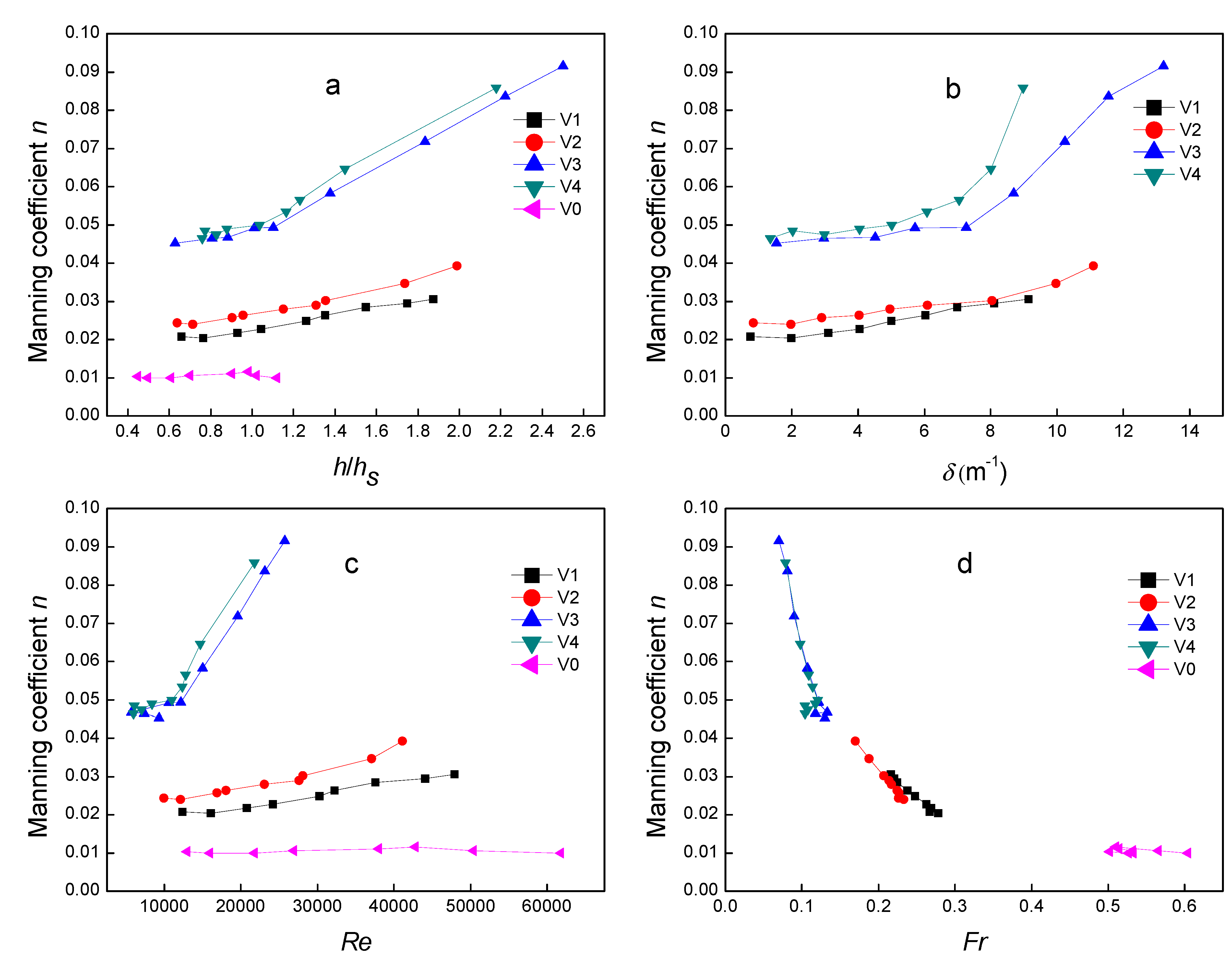
4.3. Velocity Distribution
 , where J is the flume slope [26].
, where J is the flume slope [26].
4.4. Turbulence
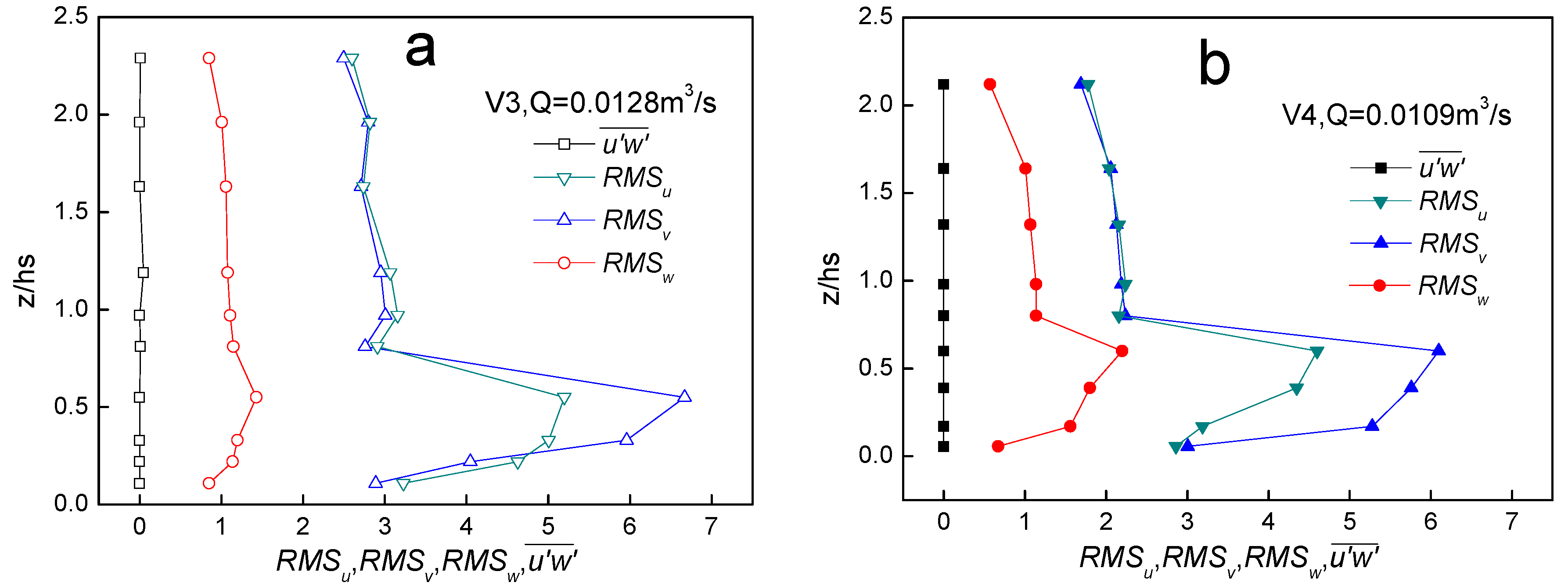
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Naiman, R.J.; Decamps, H.; McClain, M.E. Riparia: Ecology, Conservation, and Management of Streamside Communities; Elsevier Academic Press: New York, NY, USA, 2005; pp. 1–2. [Google Scholar]
- Wilson, C.A.M.E.; Stoesser, T.; Bates, P.D.; Pinzen, A.B. Open channel flow through different forms of submerged flexible vegetation. J. Hydraul. Eng. 2003, 129, 847–853. [Google Scholar] [CrossRef]
- Merritt, D.M.; Scott, M.L.; Poff, N.L.; Auble, G.T.; Lytle, D.A. Theory, methods and tools for determining environmental flows for riparian vegetation: Riparian vegetation-flow response guilds. Freshw. Biol. 2010, 55, 206–225. [Google Scholar] [CrossRef]
- Bernhardt, E.S.; Palmer, M.A. Restoring streams in an urban context. Freshw. Biol. 2007, 52, 738–751. [Google Scholar] [CrossRef]
- Stone, M.C.; Chen, L.; Mckay, S.K.; Goreham, J.; Acharya, K.; Fischenich, C.; Stone, A.B. Bending of submerged woody riparian vegetation as a function of hydraulic flow conditions. River Res. Appl. 2013, 29, 195–205. [Google Scholar] [CrossRef]
- López, F.; García, M. Mean flow and turbulence structure of open-channel flow through non-emergent vegetation. J. Hydraul. Eng. 2001, 127, 392–402. [Google Scholar] [CrossRef]
- Aberle, J.; Järvelä, J. Flow resistance of emergent rigid and flexible floodplain vegetation. J. Hydraul. Res. 2013, 51, 33–45. [Google Scholar] [CrossRef]
- Järvelä, J.; Aberle, J.; Dittrich, A.; Schnauder, I.; Rauch, H.P. Flow–Vegetation–Sediment Interaction: Research Challenges. In Proceedings of International Conference River Flow, London, UK, 6–8 September 2006; Ferreira, R.M.L., Alves, E.C.T.L., Leal, J.G.A.B., Cardoso, A.H., Eds.; Taylor & Francis: London, UK, 2006; Volume 2, pp. 2017–2026. [Google Scholar]
- Stephan, U.; Gutknecht, D. Hydraulic resistance of submerged flexible vegetation. J. Hydrol. 2002, 269, 27–43. [Google Scholar] [CrossRef]
- Chen, L.; Stone, M.C.; Acharya, K.; Steinhaus, K.A. Mechanical analysis for emergent vegetation in flowing fluids. J. Hydraul. Res. 2011, 49, 766–774. [Google Scholar] [CrossRef]
- Kouwen, N.; Li, R.M.; Simons, D.B. Flow resistance in vegetated waterways. Transp. ASAE 1981, 24, 684–698. [Google Scholar] [CrossRef]
- Kouwen, N. Modern approach to design of grassed channels. J. Irrig. Drain. Eng. 1992, 118, 773–743. [Google Scholar]
- Defina, A.; Bixio, A.C. Mean flow and turbulence in vegetated open channel flow. Water Resour. Res. 2005, 41, W07006. [Google Scholar]
- Järvelä, J. Flow resistance of flexible and stiff vegetation: A flume study with natural plants. J. Hydrol. 2002, 269, 44–54. [Google Scholar] [CrossRef]
- Stone, B.M.; Shen, H.T. Hydraulic resistance of flow in channels with cylindrical roughness. J. Hydraul. Eng. 2002, 128, 500–506. [Google Scholar] [CrossRef]
- Tsujimoto, T.; Shimizu, Y.; Kitamura, T.; Okada, T. Turbulent open-channel flow over bed covered by rigid vegetation. J. Hydrosci. Hydraul. Eng. 1992, 10, 13–25. [Google Scholar]
- Nepf, H.; Vivoni, E.R. Turbulence Structure in Depth-Limited Vegetated Flow: Transistion between Emergent and Submerged Regimes. In Proceedings of 28th International Association for Hydraulic Resources Congress, Graz, Austria, 22–27 August 1999.
- Yagci, O.; Tschiesche, U.; Kabdasli, M.S. The role of different forms of natural riparian vegetation on turbulence and kinetic energy characteristics. Adv. Water Resour. 2010, 33, 601–614. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Carollo, F.G.; Ferro, V.; Termini, D. Flow velocity measurements in vegetated channels. J. Hydraul. Eng. 2002, 128, 664–673. [Google Scholar] [CrossRef]
- Kothyari, U.; Hayashi, K.; Hashimoto, H. Drag coefficient of unsubmerged rigid vegetation stems in open channel flows. J. Hydraul. Res. 2009, 47, 691–699. [Google Scholar] [CrossRef]
- Chen, S.; Kuo, Y.; Li, Y. Flow characteristics within different configurations of submerged flexible vegetation. J. Hydrol. 2011, 398, 124–134. [Google Scholar] [CrossRef]
- Fischnich, J.C. Resistance Due to Vegetation; Engineer Research and Development Center: Vicksburg, MS, USA, 2000. [Google Scholar]
- Robert, A. River Process: An Introduction to Fluvial Dynamics; Arnold, Distributed in the United States of America by Oxford University Press Inc.: New York, NY, USA, 2003; pp. 35–50. [Google Scholar]
- Hall, B.R.; Freeman, G.E. Study of hydraulic roughness in wetland vegetation takes new look at Manning’s n. Wetl. Res. Program Bull. US Army Corps Eng. Waterways Exp. Stn. 1994, 4, 1–4. [Google Scholar]
- Kironoto, B.; Graf, W.H. Turbulence characteristics in rough uniform open-channel. Proc. Inst. Civ. Eng. Waters Marit. Energy 1995, 106, 233–241. [Google Scholar]
- Afzalimehr, H.; Najfabadi, E.F.; Singh, V.P. Effect of vegetation on banks on distributions of velocity and Reynolds stress under accelerating flow. J. Hydrol. Eng. 2010, 15, 708–713. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Xia, J.; Nehal, L. Hydraulic Features of Flow through Emergent Bending Aquatic Vegetation in the Riparian Zone. Water 2013, 5, 2080-2093. https://doi.org/10.3390/w5042080
Xia J, Nehal L. Hydraulic Features of Flow through Emergent Bending Aquatic Vegetation in the Riparian Zone. Water. 2013; 5(4):2080-2093. https://doi.org/10.3390/w5042080
Chicago/Turabian StyleXia, Jihong, and Launia Nehal. 2013. "Hydraulic Features of Flow through Emergent Bending Aquatic Vegetation in the Riparian Zone" Water 5, no. 4: 2080-2093. https://doi.org/10.3390/w5042080
APA StyleXia, J., & Nehal, L. (2013). Hydraulic Features of Flow through Emergent Bending Aquatic Vegetation in the Riparian Zone. Water, 5(4), 2080-2093. https://doi.org/10.3390/w5042080




