On the Vulnerability of Water Limited Ecosystems to Climate Change
Abstract
:1. Introduction
2. Description of the Case Study

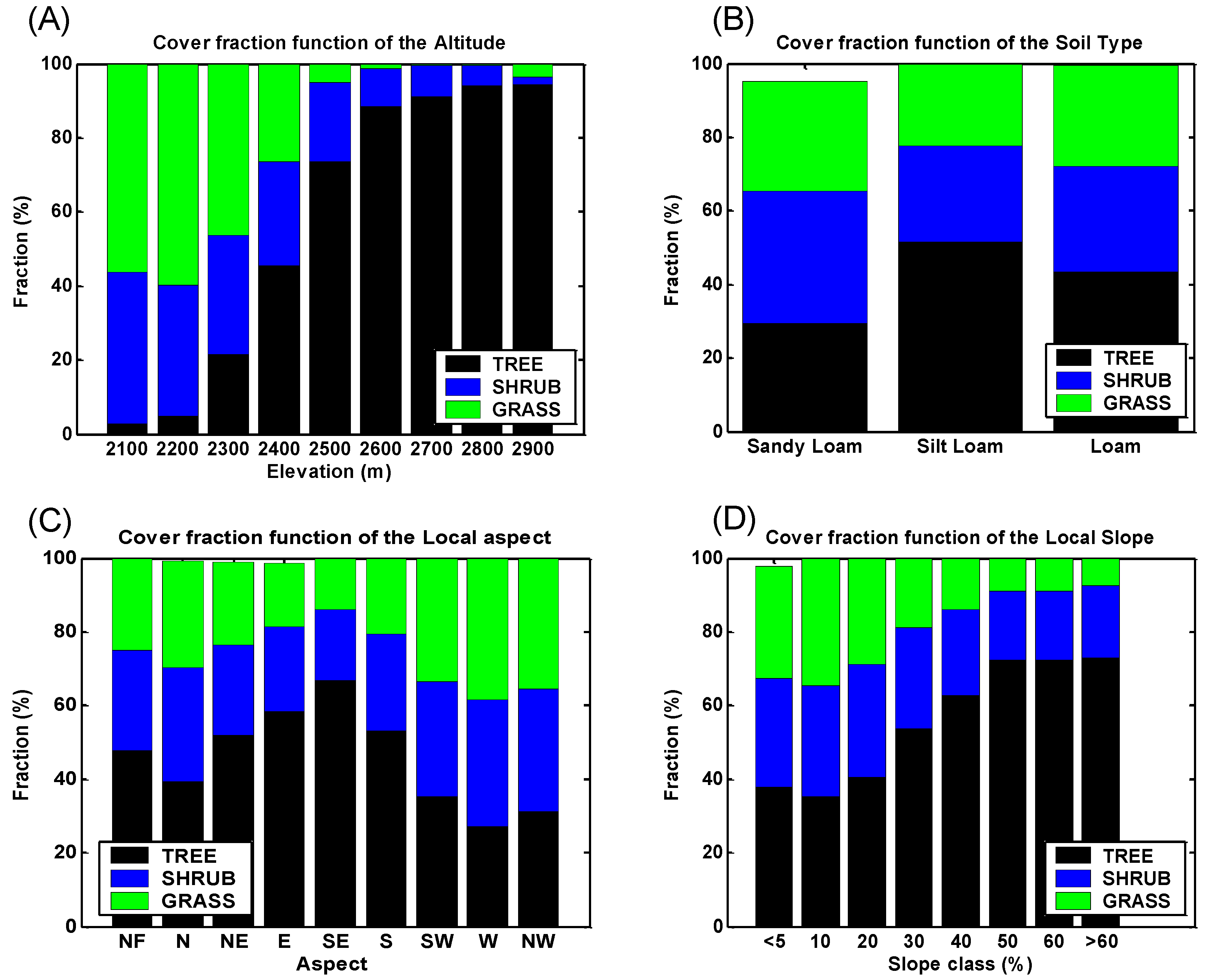
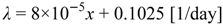
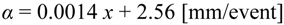

3. Methodological Approach
3.1. Soil Moisture and Vegetation Water Stress
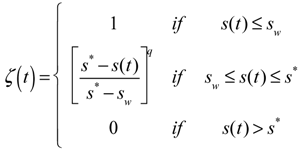
 , of such intervals during the growing season.
, of such intervals during the growing season.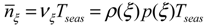
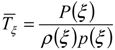
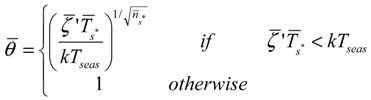
 is the average static water stress during the periods of stress conditions; k is an index of plant resistance to water stress; Tseas is the length of growing season;
is the average static water stress during the periods of stress conditions; k is an index of plant resistance to water stress; Tseas is the length of growing season;  is the average length of water stress evaluated in s*;
is the average length of water stress evaluated in s*; 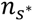 is the mean rate of water stress in s*. In this case considering the climatic characteristics of the area, we adopt a parameter k equal 0.75.
is the mean rate of water stress in s*. In this case considering the climatic characteristics of the area, we adopt a parameter k equal 0.75.3.2. Vegetation Model
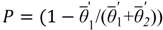
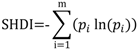
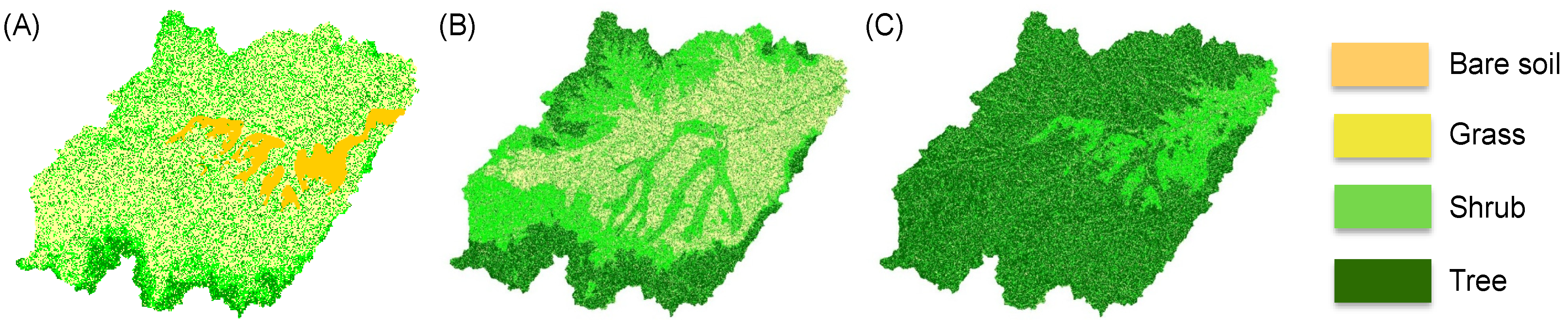
4. Discussion: Impact of Climate on Vegetation Patterns
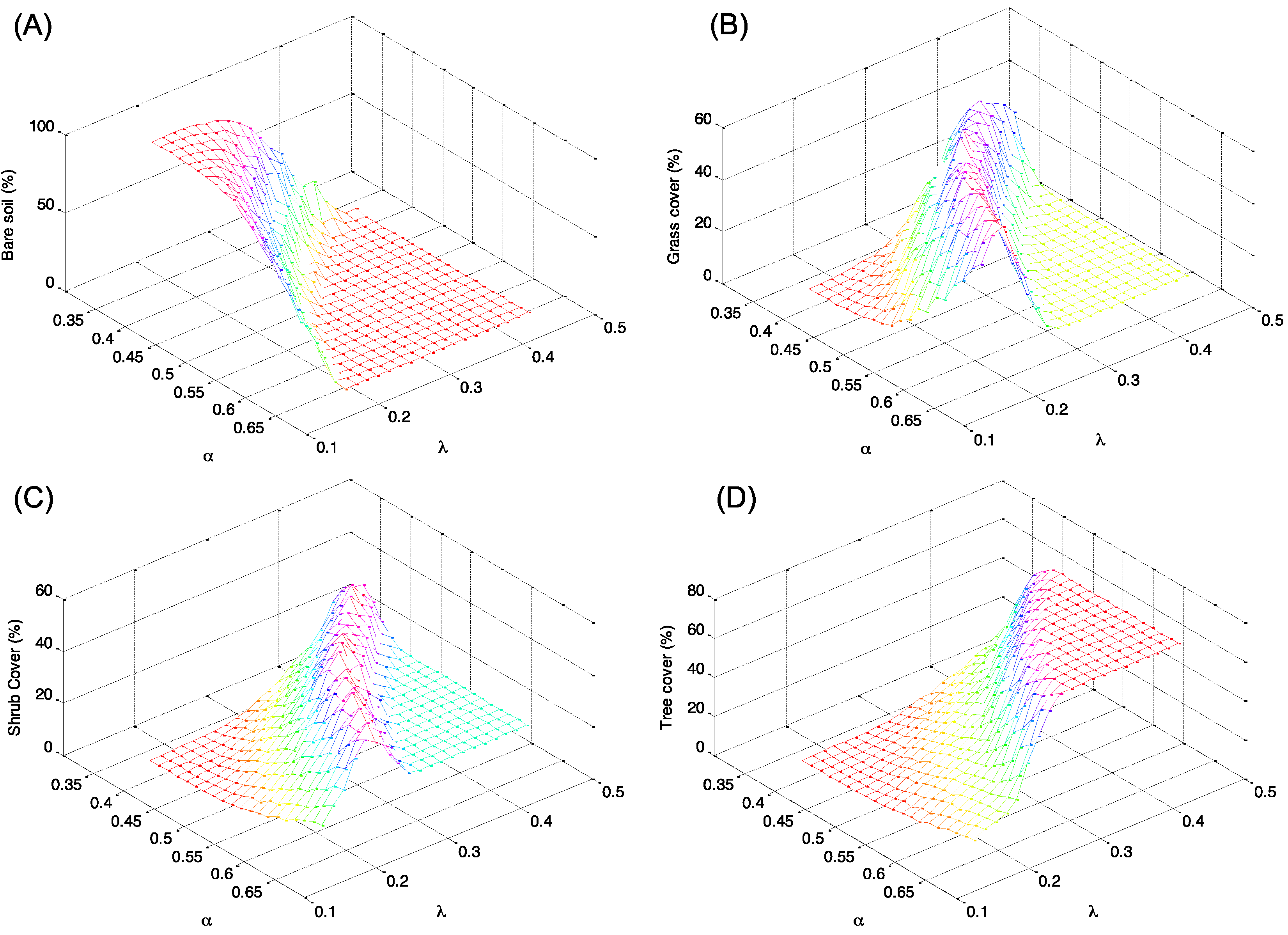
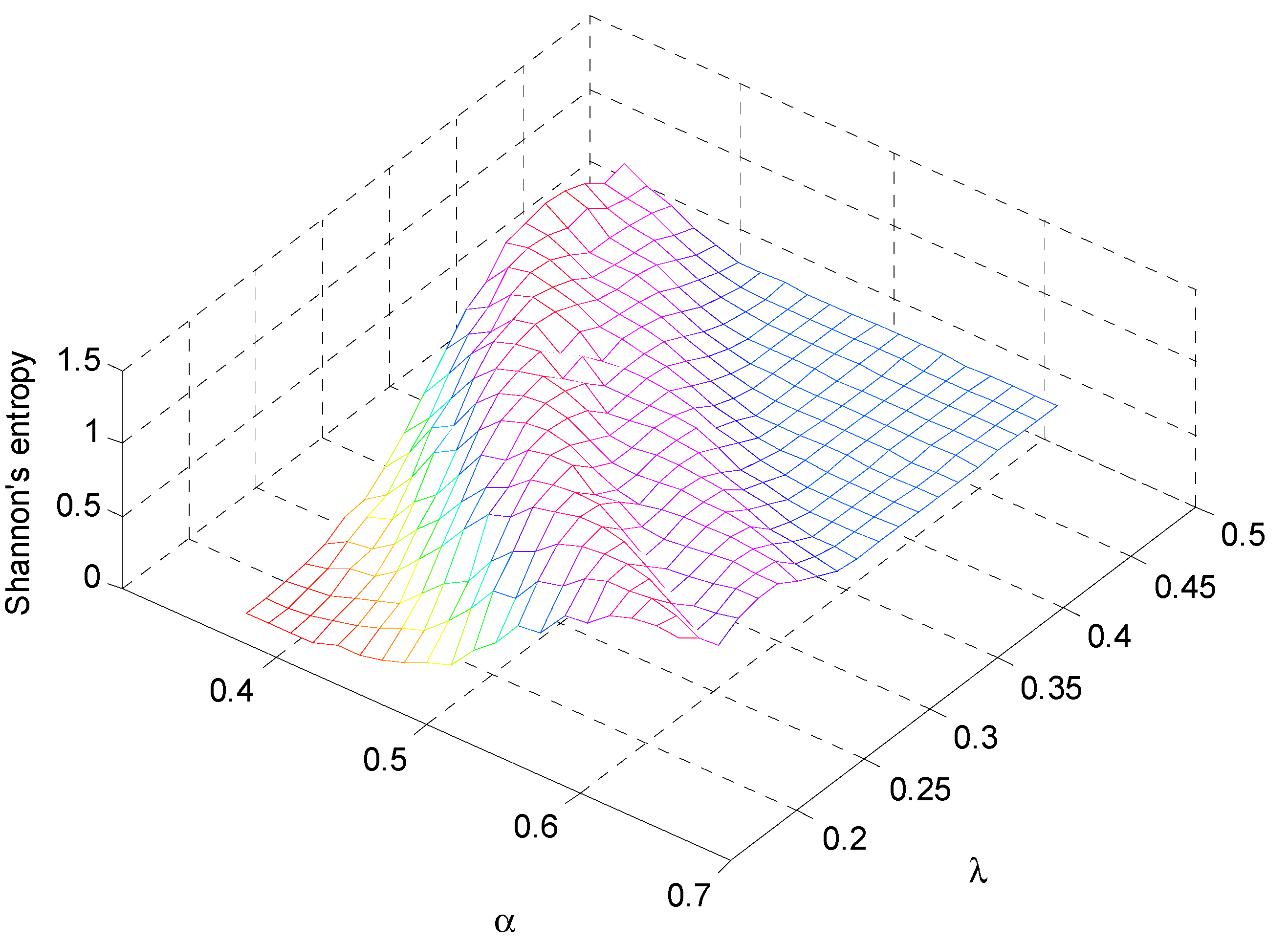
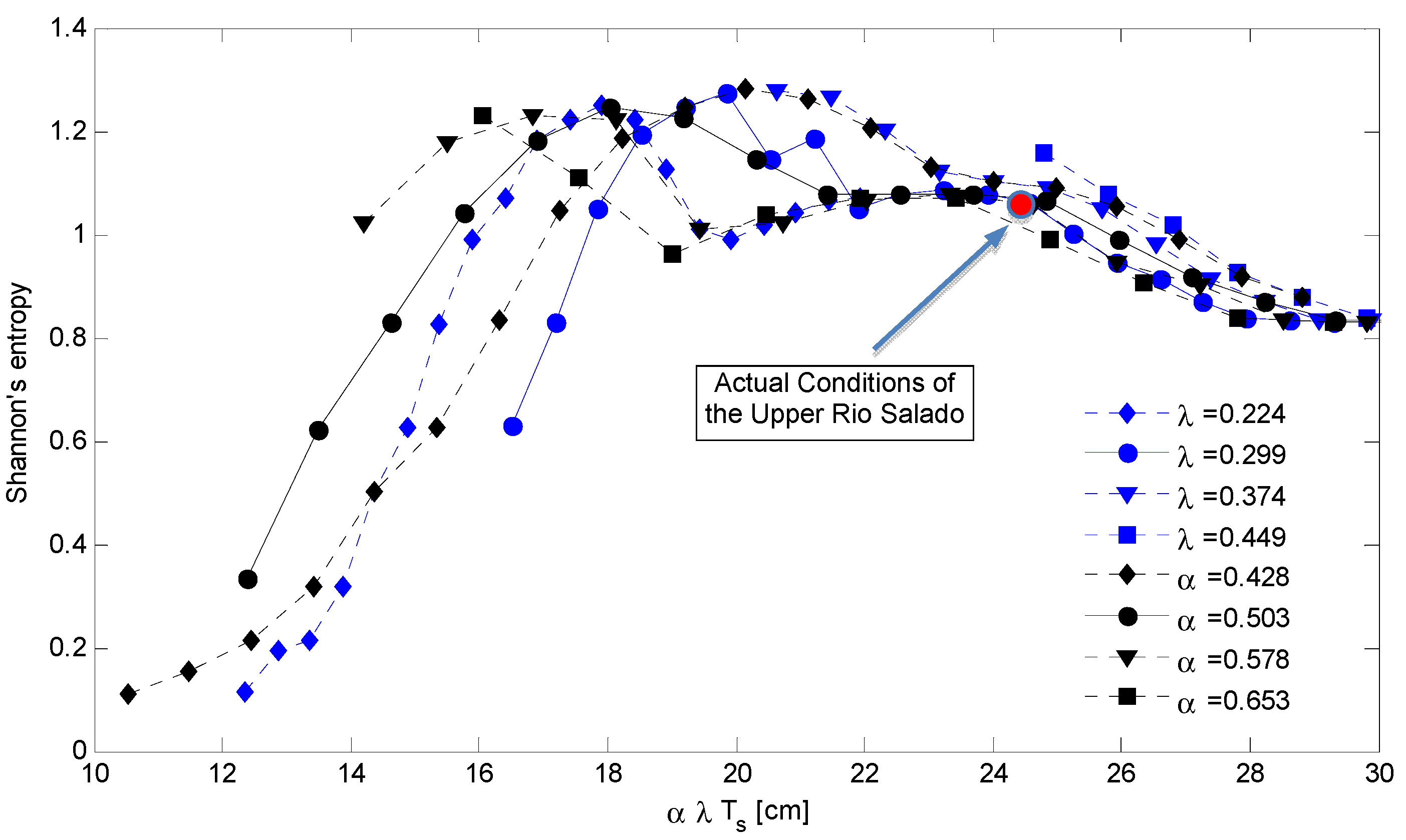
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Ricard, J.P.; Messier, C. Abundance, growth, and allometry of red raspberry (Rubus idaeus L.) along a natural light gradient in a northern hardwood forest. For. Ecol. Manag. 1996, 81, 153–160. [Google Scholar] [CrossRef]
- Martens, S.N.; Breshears, D.D.; Meyer, C.W. Spatial distributions of understory light along the grassland/forest continuum: Effects of cover, height, and spatial pattern of tree canopies. Ecol. Model. 2000, 126, 79–93. [Google Scholar] [CrossRef]
- Tilman, D. Secondary succession and the pattern of plant dominance along experimental nitrogen gradients. Ecol. Monogr. 1987, 57, 189–214. [Google Scholar] [CrossRef]
- Lejeune, O.; Tlidi, M.; Couteron, P. Localized vegetation patches: A self-organized response to resource scarcity. Phys. Rev. E 2002, 66, 010901(R). [Google Scholar]
- Rietkerk, M.; Dekker, S.C.; de Ruiter, P.C.; van de Koppel, J. Self-organized patchiness and catastrophic shifts in ecosystems. Science 2004, 305, 1926–1929. [Google Scholar] [CrossRef]
- Klausmeier, A. Regular and irregular patterns in semiarid vegetation. Science 1999, 284, 1826–1828. [Google Scholar] [CrossRef]
- Couteron, P.; Lejeune, O. Periodic spotted patterns in semiarid vegetation explained by a propagation-inhibition model. J. Ecol. 2001, 89, 616–628. [Google Scholar] [CrossRef]
- Myneni, R.B.; Nemani, R.R.; Running, S.W. Estimation of global leaf area index and absorbed par using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef]
- Dunne, J.A.; Harte, J.; Taylor, K.J. Subalpine meadow flowering phenology responses to climate change: Integrating experimental and gradient methods. Ecol. Monogr. 2003, 73, 69–86. [Google Scholar] [CrossRef]
- Scheiner, S.M.; Rey Benayas, J.M. Global patterns of plant diversity. Evol. Ecol. 1994, 8, 331–338. [Google Scholar] [CrossRef]
- Kramer, P.J.; Boyer, J.S. Water Relations of Plants and Soils; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Larcher, W. Physiological Plant Ecology; Springer-Verlag: New York, NY, USA, 1995. [Google Scholar]
- Levis, S.; Coe, M.T.; Foley, J.A. Hydrologic budget of a land surface model: A global application. J. Geophys. Res. 1996, 101, 16921–16930. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Xu, L.; Kiang, N. How plant functional-type, weather, seasonal drought, and soil physical properties alter water and energy fluxes of an oak-grass savanna and an annual grassland. Agric. For. Meteorol. 2004, 123, 13–39. [Google Scholar] [CrossRef]
- Heimann, M.; Reichstein, M. Terrestrial ecosystem carbon dynamics and climate feedbacks. Nature 2008, 451, 289–292. [Google Scholar] [CrossRef]
- D’Odorico, P.; Laio, F.; Ridolfi, L.; Lerdau, M.T. Biodiversity enhancement induced by environmental noise. J. Theor. Biol. 2008, 255, 332–337. [Google Scholar] [CrossRef]
- Pignatti, S. Ecologia del Paesaggio [in Italian]; UTET: Torino, Italy, 1994. [Google Scholar]
- Manfreda, S. Ecohydrology: A new interdisciplinary approach to investigate on climate-soil-vegetation interactions. Ann. Arid Zone 2009, 48, 219–228. [Google Scholar]
- Chahine, M.T. The hydrological cycle and its influence on climate. Nature 1992, 359, 373–380. [Google Scholar] [CrossRef]
- Dickinson, R.E.; Kennedy, P. Impacts on regional climate of Amazon deforestation. Geophys. Res. Lett. 1992, 19, 1947–1950. [Google Scholar] [CrossRef]
- Lean, J.; Rowntree, P.R. Understanding the sensitivity of a GCM simulation of amazonian deforestation to the specification of vegetation and soil characteristics. J. Climate 1997, 10, 1216–1235. [Google Scholar] [CrossRef]
- Turner, M.G. Landscape ecology: The effect of pattern on process. Ann. Rev. Ecol. 1989, 20, 171–197. [Google Scholar]
- Levin, S.A. The problem of pattern and scale in ecology. Ecology 1992, 73, 1943–1967. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Jones, P.A.; Bojariu, R.; Easterling, D.; Klein Tank, A.; Parker, D.; Rahimzadeh, F.; Renwick, J.A.; Rusticucci, M.; Soden, B.; et al. Observations: Surface and Atmospheric Climate Change. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Ghange; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Körner, C.H.; Walther, G.R. Fingerprints of Climate Change—Concluding Remarks. In Fingerprints of Climate Change; Walther, G.R., Burga, C.A., Edwards, P.J., Eds.; Kluwer: New York, NY, USA, 2001; pp. 305–316. [Google Scholar]
- Duffy, J.E.; Stachowicz, J.J. Why biodiversity is important to oceanography, potential roles of genetic, species, and trophic diversity in pelagic ecosystem processes. Mar. Ecol. Progr. Ser. 2006, 311, 179–189. [Google Scholar] [CrossRef]
- Hughes, L. Biological consequences of global warming: Is the signal already apparent? Trends Ecol. Evol. 2000, 15, 56–61. [Google Scholar] [CrossRef]
- Walther, G.-R.; Post, E.; Convey, P.; Menzel, A.; Parmesan, C.; Beebee, T.J.C.; Fromentin, J.-M.; Hoegh-Guldberg, O.; Bairlein, F. Ecological responses to recent climate change. Nature 2002, 416, 389–395. [Google Scholar] [CrossRef]
- Maselli, F.; Chiesi, M.; Rodolfi, A.; Maracchi, G. Uso Di Serie Temporali NDVI Per Stimare L'effetto Dei Cambiamenti Climatici Sugli Ecosistemi Forestali [in Italian]. In Clima e Cambiamenti Climatici–Le Attività Di Ricerca Del CNR; Carli, B., Cavarretta, G., Colacino, M., Fuzzi, S., Eds.; Consiglio Nazionale delle Ricerche: Roma, Italy, 2007; pp. 701–704. [Google Scholar]
- Menzel, A.; Estrella, N.; Fabian, P. Spatial and temporal variability of the phenological seasons in Germany from 1951 to 1996. Glob. Change Biol. 2001, 7, 657–666. [Google Scholar] [CrossRef]
- Studer, S.; Appenzeller, C.; Defila, C. Inter-annual variability and decadal trends in alpine spring phenology: A multivariate analysis approach. Clim. Change 2005, 73, 395–414. [Google Scholar] [CrossRef]
- Smith, T.M.; Goodman, P.S. Successional dynamics in an Acacia nilotica-Euclea divinorum savannah in southern Africa. J. Ecol. 1987, 75, 603–610. [Google Scholar] [CrossRef]
- Skarpe, C. Spatial patterns and dynamics of woody vegetation in an arid savanna. J. Veg. Sci. 1991, 2, 565–572. [Google Scholar] [CrossRef]
- Jeltsch, F.; Moloney, K.; Milton, S.J. Detecting process from snapshot pattern: Lessons from tree spacing in the southern Kalahari. Oikos 1999, 85, 451–466. [Google Scholar] [CrossRef]
- Rodrìguez-Iturbe, I.; D’Odorico, P.; Porporato, A.; Ridolfi, L. On the spatial and temporal links between vegetation, climate, and soil moisture. Water Resour. Res. 1999, 35, 3709–3722. [Google Scholar] [CrossRef]
- Smit, G.; Rethman, N. The inuence of tree thinning on the soil water in a semi-arid savanna of Southern Africa. J. Arid Environ. 2000, 44, 41–59. [Google Scholar] [CrossRef]
- Rodrìguez-Iturbe, I.; Porporato, A. Ecohydrology of Water-Controlled Ecosystems: Soil Moisture and Plant Dynamics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Eagleson, P.S. Ecological optimality in water-limited natural soil-vegetation systems. 1. Theory and hypothesis. Water Resour. Res. 1982, 18, 325–340. [Google Scholar] [CrossRef]
- Eagleson, P.S.; Segarra, R.I. Water-limited equilibrium of savanna vegetation systems. Water Resour. Res. 1985, 21, 1483–1493. [Google Scholar] [CrossRef]
- Huang, C.; Marsh, S.E.; McClaran, M.; Archer, S. Postfire stand structure in a semiarid savanna: Cross-scale challenges estimating biomass. Ecol. Appl. 2007, 17, 1899–1910. [Google Scholar] [CrossRef]
- Kerkhoff, A.J.; Martens, S.N.; Shore, G.A.; Milne, B.T. Contingent effects of water balance variation on tree cover density in semiarid woodlands. Glob. Ecol. Biogeogr. 2004, 13, 237–246. [Google Scholar] [CrossRef]
- Schymanski, S.J.; Sivapalan, M.; Roderick, M.L.; Beringer, J.; Hutley, L.B. An optimality-based model of the coupled soil moisture and root dynamics. Hydrol. Earth Syst. Sci. 2008, 12, 913–932. [Google Scholar] [CrossRef]
- Caylor, K.K.; Scanlon, T.M.; Rodrìguez-Iturbge, I. Ecohydrological optimization of pattern and processes in water-limited ecosystems: A tradeoff-based hypothesis. Water Resour. Res. 2009, 45, W08407. [Google Scholar]
- Van Wijk, M.T.; Rodriguez-Iturbe, I. Tree-grass competition in space and time: Insights from a simple cellular automata model based on ecohydrological dynamics. Water Resour. Res. 2002, 38, 18-1–18-15. [Google Scholar]
- Fernandez-Illescas, C.P.; Rodriguez-Iturbe, I. The impact of interannual rainfall variability on the spatial and temporal patterns of vegetation in a water-limited ecosystem. Adv. Water Resour. 2004, 27, 83–95. [Google Scholar] [CrossRef]
- Scanlon, T.M.; Caylor, K.K.; Manfreda, S.; Levin, S.A.; Rodrıguez-Iturbe, I. Dynamic response of grass cover to rainfall variability: Implications the function and persistence of savanna ecosystems. Adv. Water Resour. 2005, 28, 291–302. [Google Scholar] [CrossRef]
- Jeltsch, F.; Weber, G.E.; Grimm, V. Ecological buffering mechanisms in savannas: A unifying theory of long-term tree-grass coexistence. Plant. Ecol. 2000, 150, 161–171. [Google Scholar] [CrossRef]
- Wooten, J. Local interactions predict large-scale pattern in empirically derived cellular automata. Nature 2001, 413, 841–844. [Google Scholar] [CrossRef]
- Caylor, K.K.; Scanlon, T.M.; Rodríguez-Iturbe, I. Feasible optimality of vegetation patterns in river basin. Geophys. Res. Lett. 2004, 31, L13502. [Google Scholar]
- Caylor, K.K.; Manfreda, S.; Rodrìguez-Iturbe, I. On the coupled geomorphological and ecohydrological organization of river basins. Adv. Water Resour. 2005, 28, 69–86. [Google Scholar]
- Laio, F.; Porporato, A.; Ridolfi, L.; Rodrìguez-Iturbe, I. Plants in water controlled ecosystems: Active role in hydrological processes and response to water stress, II. Probabilistic soil moisture dynamics. Adv. Water Resour. 2001, 24, 707–723. [Google Scholar]
- Porporato, A.; Laio, F.; Ridolfi, L.; Rodrìguez-Iturbe, I. Plants in water-controlled ecosystems: Active role in hydrological processes and response to water stress—III. Vegetation water stress. Adv. Water Resour. 2001, 24, 725–744. [Google Scholar]
- Milly, P.C.D. An analytical solution of the stochastic storage problem applicable to soil water. Water Resour. Res. 1993, 29, 3755–3758. [Google Scholar]
- Neilson, R.P. A model for predicting continental scale vegetation distribution and water balance. Ecol. Appl. 1995, 5, 362–385. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I. Ecohydrology: A hydrologic perspective of climate-soil-vegetation dynamics. Water Resour. Res. 2000, 36, 3–9. [Google Scholar]
- Scholes, R.J.; Archer, S.R. Tree-grass interactions in Savannas. Ann. Rev. Ecol. Syst. 1997, 28, 517–544. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I.; Isham, V.; Cox, D.R.; Manfreda, S.; Porporato, A. Space-time modeling of soil moisture: Stochastic rainfall forcing with heterogeneous vegetation. Water Resour. Res. 2006, 42, W06D05. [Google Scholar]
- Manfreda, S.; McCabe, M.; Wood, E.F.; Fiorentino, M.; Rodríguez-Iturbe, I. Spatial patterns of soil moisture from distributed modeling. Adv. Water Resour. 2007, 30, 2145–2150. [Google Scholar]
- Rodríguez-Iturbe, I.; Porporato, A.; Ridolfi, L.; Isham, V.; Cox, D.R. Probabilistic modeling of water balance at a point: The role of climate, soil and vegetation. Proc. R. Soc. A Math. Phys. Eng. Sci. 1999, 455, 3789–3805. [Google Scholar]
- Porporato, A.; D’Odorico, P.; Laio, F.; Rodríguez-Iturbe, I. Hydrologic controls on soil carbon and nitrogen cycles. I. Modeling scheme. Adv. Water Resour. 2003, 26, 45–58. [Google Scholar]
- Wagner, H.H.; Fortin, M.J. Spatial analysis of landscapes: Concepts and statistics. Ecology 2005, 86, 1975–1987. [Google Scholar]
- Cao, Y.; Ou, Y.H.; Xiao, D.; Chen, G. Landscape patterns analysis based on APACK for Ejin natural oasis. J. Nat. Resour. 2004, 19, 776–785. [Google Scholar]
- Chen, L.; Liu, Y.; Lv, Y.; Feng, X.; Fu, B. Pattern analysis in landscape ecology: Progress, challenges and outlook. Acta Ecol. Sin. 2008, 28, 5521–5531. [Google Scholar]
- Shmida, A.; Burgess, T.L. Plant Growt-Form Strategies and Vegetation Types in Arid Environments. In Plant form and Vegetation Structure; Werger, M.J.A., van der Aart, P.J.M., During, H.J., Verhoeven, J.T.A., Eds.; SBP Academic Publishing: The Hague, The Netherlands, 1988. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Manfreda, S.; Caylor, K.K. On the Vulnerability of Water Limited Ecosystems to Climate Change. Water 2013, 5, 819-833. https://doi.org/10.3390/w5020819
Manfreda S, Caylor KK. On the Vulnerability of Water Limited Ecosystems to Climate Change. Water. 2013; 5(2):819-833. https://doi.org/10.3390/w5020819
Chicago/Turabian StyleManfreda, Salvatore, and Kelly K. Caylor. 2013. "On the Vulnerability of Water Limited Ecosystems to Climate Change" Water 5, no. 2: 819-833. https://doi.org/10.3390/w5020819





