A Simple Scheme for Modeling Irrigation Water Requirements at the Regional Scale Applied to an Alpine River Catchment
Abstract
:1. Introduction
2. Study Region
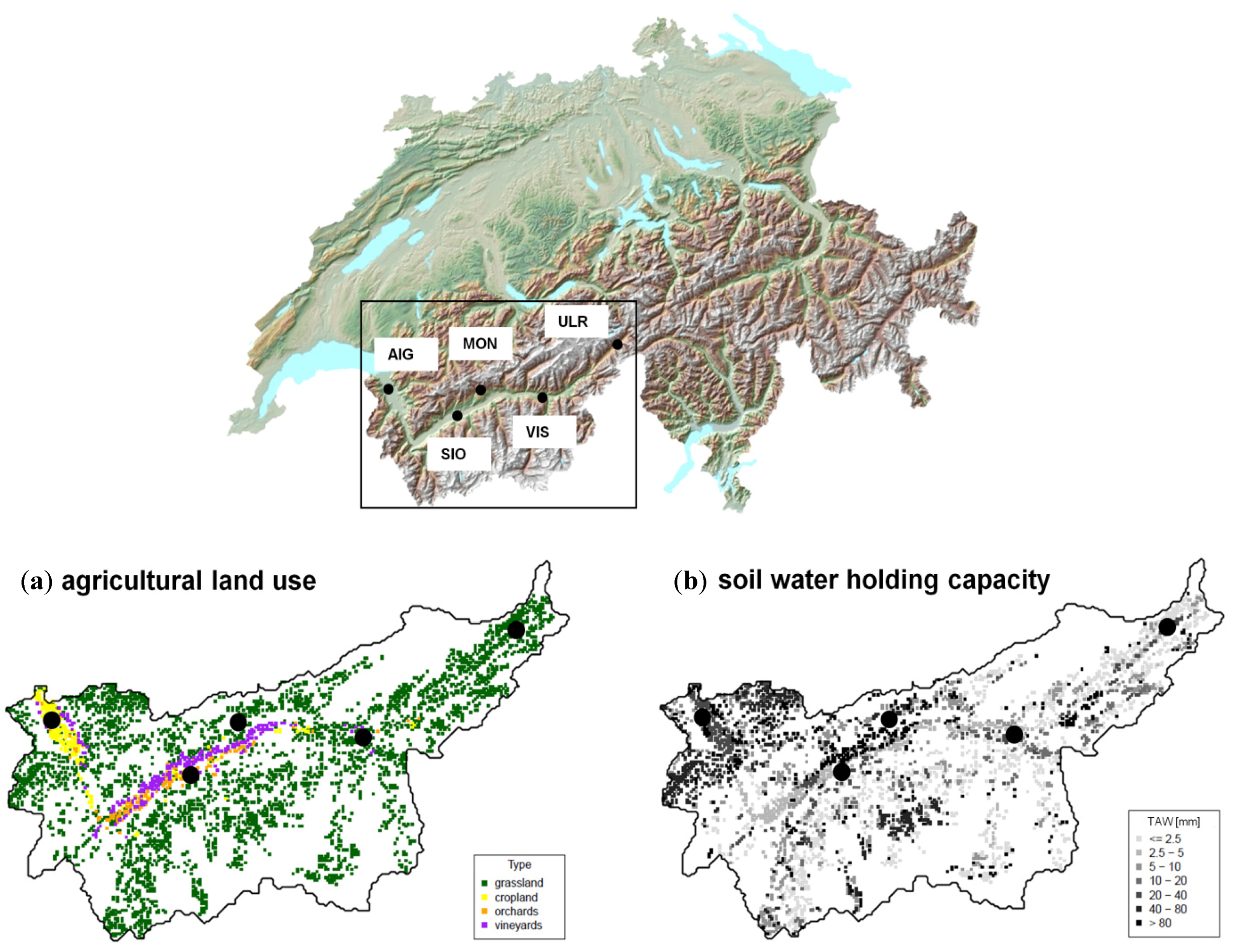
2.1. Characteristics
| Site | Long./Lat. | Elevation (m a.s.l.) | April-September air temperature (°C) | April-September precipitation (mm) |
|---|---|---|---|---|
| AIG | 6.9 E/46.3 N | 382 | 14.8 | 747 |
| SIO | 7.3 E/46.2 N | 481 | 16.1 | 489 |
| VIS | 7.8 E/46.3 N | 639 | 15.4 | 314 |
| MON | 7.5 E/46.3 N | 1431 | 10.8 | 589 |
| ULR | 8.3 E/46.5 N | 1395 | 10.4 | 624 |
2.2. Current Irrigation Estimates
3. Methods
3.1. Overall Approach
- Computing daily irrigation requirements (IWRday) at the point scale for a selection of representative sites (Section 3.3). This was done by solving the soil water balance equation for the root zone and assuming that irrigation is required to avoid water stress whenever the actual root zone water depletion exceeds a pre-defined threshold;
- Integrating IWRday over the growing season to obtain corresponding seasonal estimates (IWR). The growing season was defined according to the seasonal evolution of the crop coefficient, Kc, which was computed as function of the leaf-area index (Section 3.4);
- 3. Linking seasonal IWR to the atmospheric water budget through a statistical analysis of the results obtained in the previous step. It was found that the assumed linear relation could be generalized across soil and crop types provided that its parameters are expressed as a function of the soil water holding capacity and crop coefficient (Section 3.4).
3.2. Weather, Land Use and Soil Data
3.3. Point-Scale Estimation of Daily Irrigation Requirements
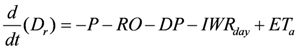

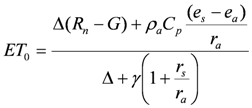
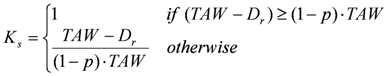
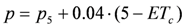
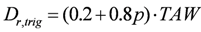
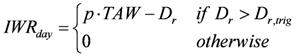
- 10 values of the total water holding capacity ranging from 5 to 240 mm;
- 6 crop categories, including cut grasslands and pastures, maize, apple, apricot and vineyards, each of which was defined through different setups of the crop coefficient.

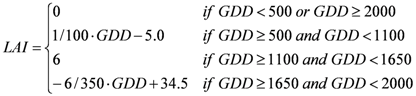
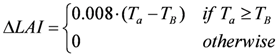
3.4. Seasonal Integration and Modeling of Seasonal Irrigation Requirements
| Crop type | Growing season mean Kc (−) | Growing season mean length (days) |
|---|---|---|
| Grassland (cut or grazed) | 0.95 or 0.88 | 190 or 208 |
| Cropland (maize) | 1.09 | 122 |
| Orchards (apple or apricot) | 0.82 or 0.51 | both 183 |
| Vineyards | 0.36 | 216 |
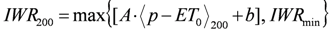
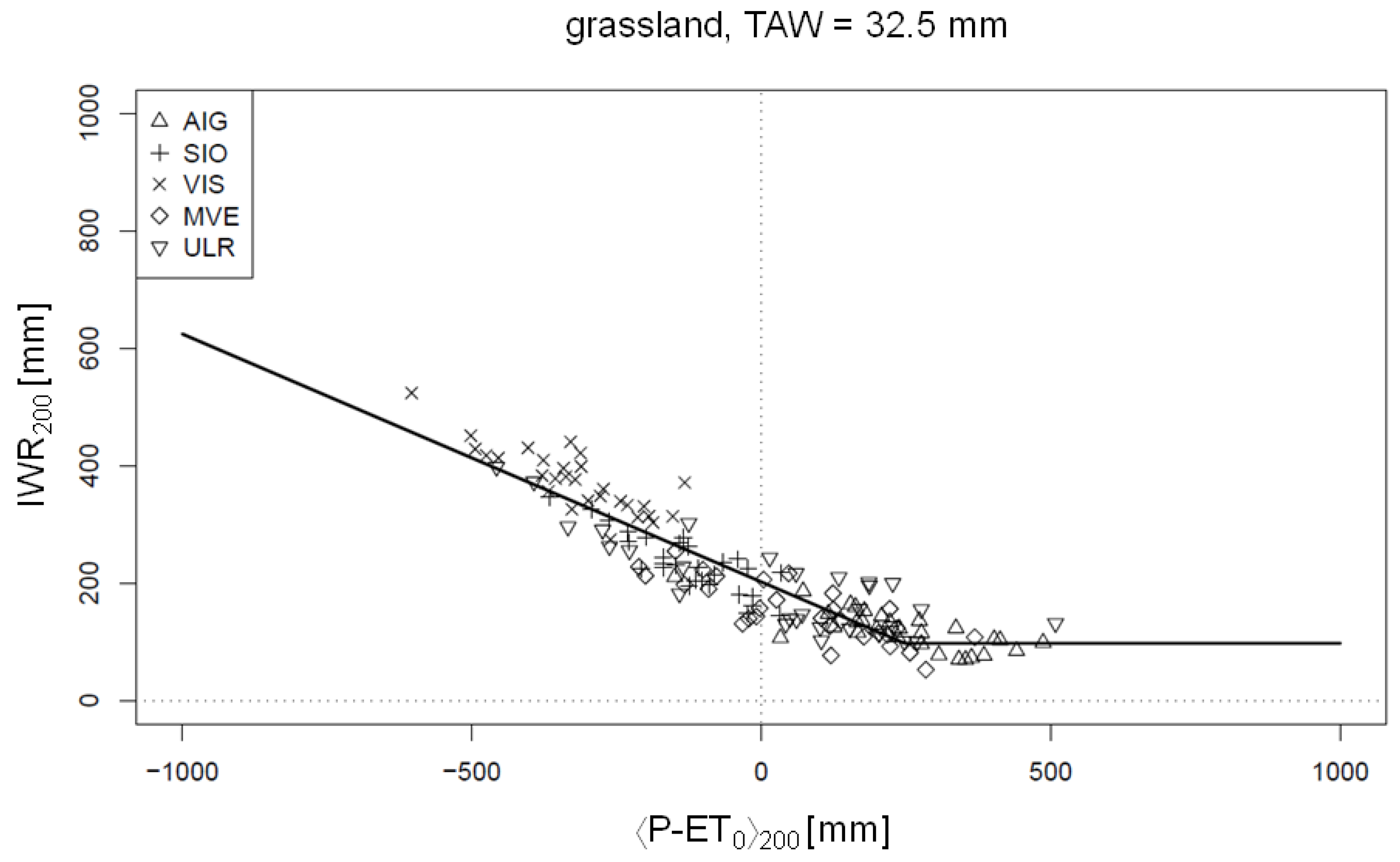
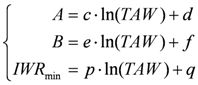
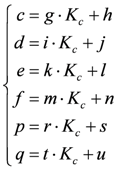
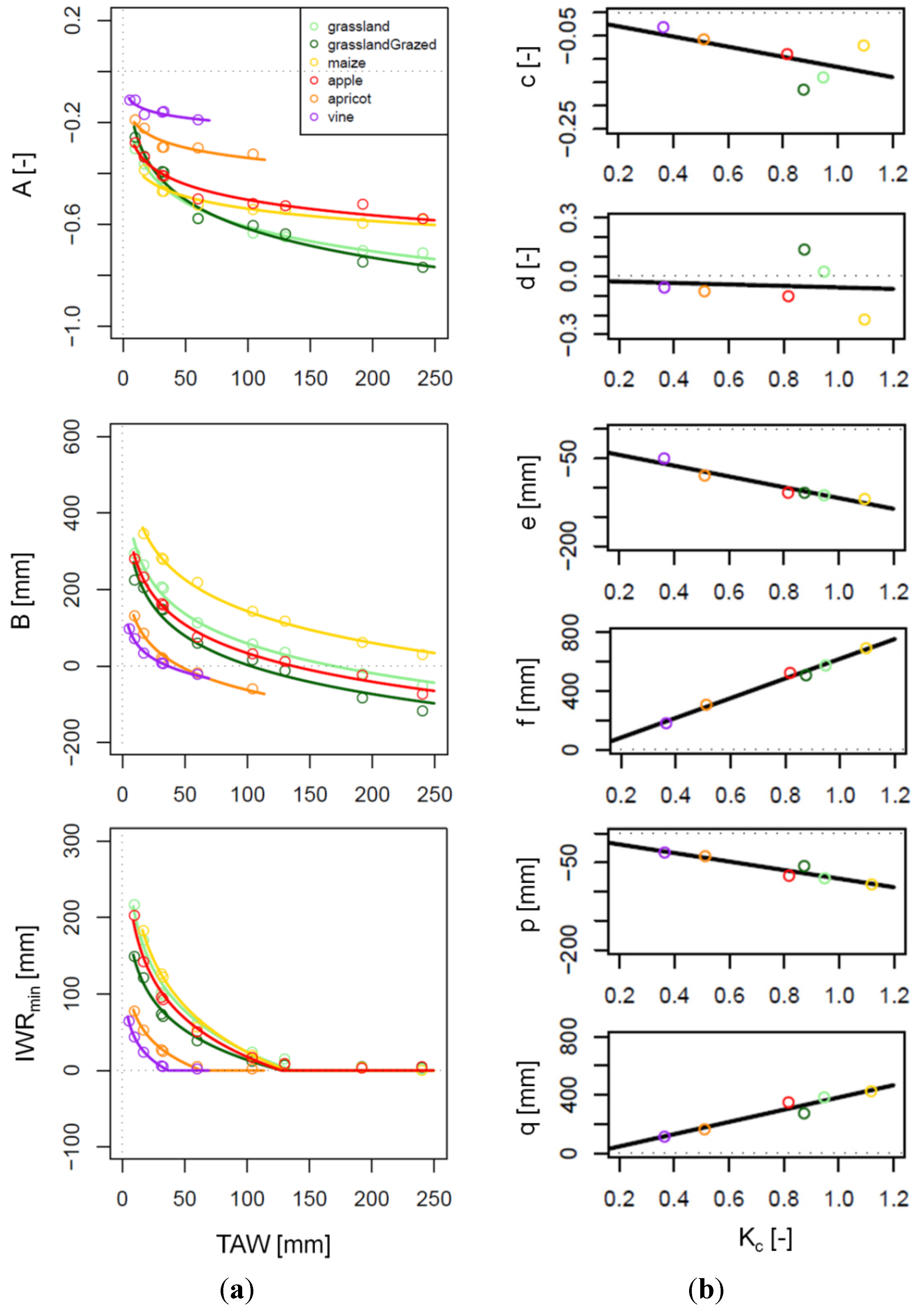
4. Results
4.1. Model Calibration and Assessment

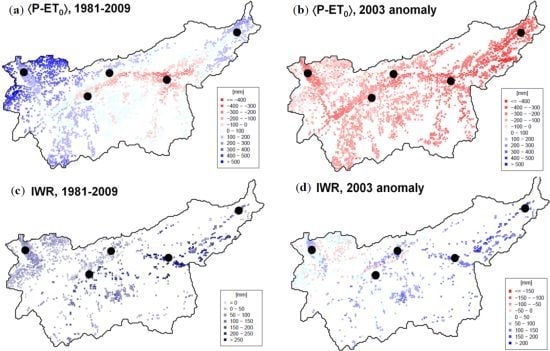
4.2. Spatial Patterns of Mean and Extreme IWR

4.3. Time Series of IWR Aggregated over the Catchment
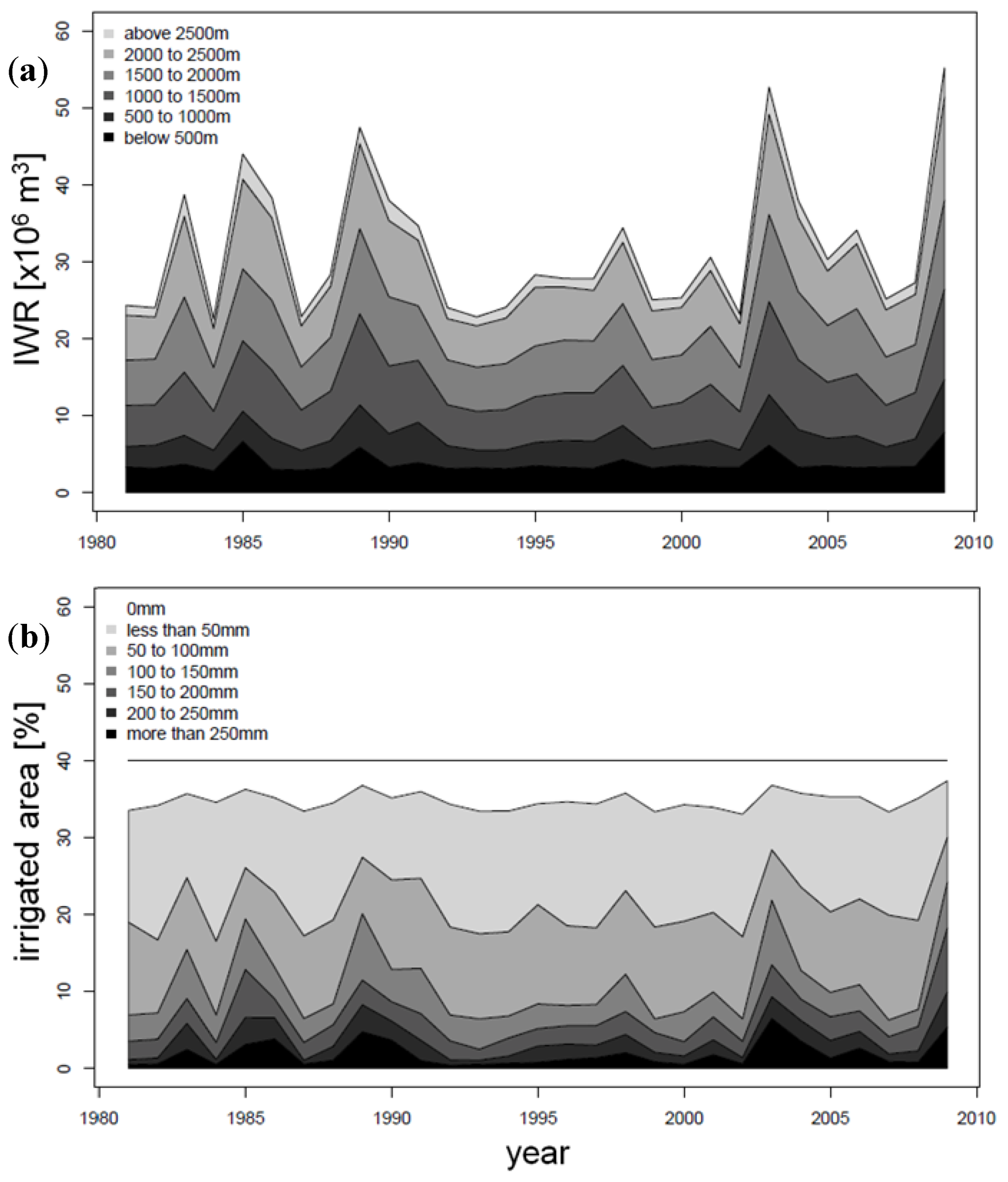
5. Discussion
6. Conclusions
Acknowledgments
References
- United Nations Environment Programme (UNEP), Global Environmental Outlook 2000; Earthscan: London, UK, 1999.
- Shiklomanov, I.A. Assessment of water resources and water availability in the world. In UN Report: Comprehensive Assessment of the Freshwater Resources of the World; Stockholm Environment Institute: Stockholm, Sweden, 1997. [Google Scholar]
- Wriedt, G.; van der Velde, M.; Aloe, A.; Bouraoui, F. A European irrigation map for spatially distributed agricultural modelling. Agric. Water Manag. 2009, 96, 771–789. [Google Scholar] [CrossRef]
- Van der Velde, M.; Wriedt, G.; Bouraoui, F. Estimating irrigation use and effects on maize yield during the 2003 heatwave in France. Agric. Ecosyst. Environ. 2010, 135, 90–97. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Biradar, C.M.; Turral, H.; Noojipady, P.; Li, Y.J.; Vithanage, J.; Dheeravath, V.; Velpuri, M.; Schull, M.; Cai, X.L.; Dutta, R. An Irrigated Area Map of the World (1999) Derived from Remote Sensing; Research Report No. 105; International Water Management Institute: Colombo, Sri Lanka, 2006. [Google Scholar]
- Siebert, S. Global Map of Irrigation Areas Version 4.0.1. Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2007. Available online: http://www.fao.org/nr/water/ aquastat/quickWMS/irrimap.htm (accessed on 21 July 2012).
- Döll, P.; Siebert, S. Global modelling of irrigation water requirements. Water Resour. Res. 2002, 38, 8:1–8:10. [Google Scholar]
- Wriedt, G.; van der Velde, M.; Aloe, A.; Bouraoui, F. Estimating Irrigation water requirements in Europe. J. Hydrol. 2009, 373, 527–544. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998. [Google Scholar]
- ACQWA EU-FP7 Project (Assessing Climate impacts on the Quantity and quality of Water, Seventh Research Framework Programme). Available online: http://www.acqwa.ch (accessed on 1 November 2012).
- Schreier, H.; Lavkulich, L.; Brown, L. Real and Virtual Water and Water Footprints: A Comparison between the Lower Fraser Valley and the Okanagan Basin; Technical Report For Walter and Duncan Gordon Foundation: Toronto, Canada, 2007. [Google Scholar]
- Fuhrer, J.; Jasper, K. Demand and supply of water for agriculture: Influence of topography and climate in pre-alpine, mesoscale catchments. Nat. Resour. 2012, 3, 145–155. [Google Scholar]
- Weber, M.; Schild, A. Stand der Bewässerung in der Schweiz (in German); Bericht zur Umfrage 2006-Report; Federal Office of Agriculture: Bern, Switzerland, 2007. [Google Scholar]
- Weingartner, R.; Viviroli, D.; Schädler, B. Water resources in mountain regions: a methodological approach to assess the water balance in a highland-lowland system. Hydrol. Process. 2007, 21, 578–585. [Google Scholar] [CrossRef]
- Huss, M. Present and future contribution of glacier storage change to runoff from macroscale drainage basins in Europe. Water Resour. Res. 2011, 47, W07511:1–W07511:14. [Google Scholar]
- MeteoSwiss Norm Values. Available online: http://www.meteoswiss.admin.ch/web/de/klima/klima_schweiz/tabellen.Par.0011.DownloadFile.ext.tmp/niederschlagssummen.pdf (accessed on 21 July 2012).
- Swiss Federal Statistical Office, Bodennutzung im Wandel: Arealstatistik der Schweiz (in German); Swiss Federal Statistical Office: Neuchâtel, Switzerland, 2001.
- Swiss Federal Statistical Office, Digital Map of the Soil Aptitudes; Swiss Federal Statistical Office: Neufchâtel, Switzerland, 2004.
- Schulla, J. Hydrologische Modellierung von Fluss-gebieten zur Abschätzung der Folgen von Klimaänderungen (in German), 1997; dx.doi.org/10.3929/ethz-a-001763261; ETH E-Collection. Available online: http://e-collection.library.ethz.ch/view/eth:40649 (accessed on 1 November 2012).
- Schulla, J.; Jasper, K. WASIM-ETH Model Documentation. Available online: http://www.wasim.ch/downloads/doku/wasim/interpolation_meteodata_2009_en.pdf (accessed on 21 July 2012).
- Davies, J.A. A note on the relationship between net radiation and solar radiation. Quart. J. R. Meteorol. Soc. 1967, 93, 109–115. [Google Scholar] [CrossRef]
- Office d’arboriculture du Valais, Gestion de l’irrigation en Arboriculture-Rapport Annuel 2008 (in French); Département de l’économie et du Territoire, Service Cantonal d’agriculture: Sion, France, 2008.
- Goodwin, I. Irrigation of Vineyards; Institute of Sustainable Agriculture: Victoria, Tatura, Australia, 1995. [Google Scholar]
- Lazzarotto, P.; Calanca, P.; Fuhrer, J. Dynamics of grass-clover mixtures-An analysis of the response to management with the PROductive GRASsland Simulator (PROGRASS). Ecol. Model. 2009, 220, 703–724. [Google Scholar] [CrossRef]
- Brisson, N.; Ruget, F.; Gate, P.; Lorgeou, J.; Nicoullaud, B.; Tayot, X.; Plenet, D.; Jeuffroy, M.H.; Bouthier, A.; Ripoche, D. STICS: A generic model for simulating crops and their water and nitrogen balances. II. Model validation for wheat and maize. Agronomie 2002, 22, 69–92. [Google Scholar] [CrossRef]
- Boland, A.-M.; Bewsell, D.; Kaine, G. Adoption of sustainable irrigation management practices by stone and pome fruit growers in the Goulburn/Murray Valleys, Australia. Irrig. Sci. 2006, 24, 137–145. [Google Scholar] [CrossRef]
- Bravin, E.; Hofmann, M.D.; Monney, P. Klimaveränderung: Welche Zunahme der Bewässerungskosten in der Apfelproduktion ist tragbar (in German). Schweiz. Ges. Agrarwirtsch. Agrarsoziol. 2008, pp. 133–160. Available online: www.volkskunde.ch/dms/agrarwirtschaft/Internetseite/Yearbook/Ausgaben/Yearbook-2008/06_Bravin_neu-_4_/Esther-Bravin.pdf (accessed on 1 November 2012).
- Zurwerra, R. Die Wiesebbewässerung im Wallis-Zwischen tradition und moderne (in German). Géomat. Suisse 2010, 10, 454–457. [Google Scholar]
- Schär, C.; Vidale, P.L.; Lüthi, D.; Frei, C.; Häberli, C.; Liniger, M.A.; Appenzeller, C. The role of increasing temperature variability in European summer heatwaves. Nature 2004, 427, 332–336. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Smith, P.C.; Calanca, P.; Fuhrer, J. A Simple Scheme for Modeling Irrigation Water Requirements at the Regional Scale Applied to an Alpine River Catchment. Water 2012, 4, 869-886. https://doi.org/10.3390/w4040869
Smith PC, Calanca P, Fuhrer J. A Simple Scheme for Modeling Irrigation Water Requirements at the Regional Scale Applied to an Alpine River Catchment. Water. 2012; 4(4):869-886. https://doi.org/10.3390/w4040869
Chicago/Turabian StyleSmith, Pascalle C., Pierluigi Calanca, and Jürg Fuhrer. 2012. "A Simple Scheme for Modeling Irrigation Water Requirements at the Regional Scale Applied to an Alpine River Catchment" Water 4, no. 4: 869-886. https://doi.org/10.3390/w4040869
APA StyleSmith, P. C., Calanca, P., & Fuhrer, J. (2012). A Simple Scheme for Modeling Irrigation Water Requirements at the Regional Scale Applied to an Alpine River Catchment. Water, 4(4), 869-886. https://doi.org/10.3390/w4040869