Sea Level Rise Effects on the Sedimentary Dynamics of the Douro Estuary Sandspit (Portugal)
Abstract
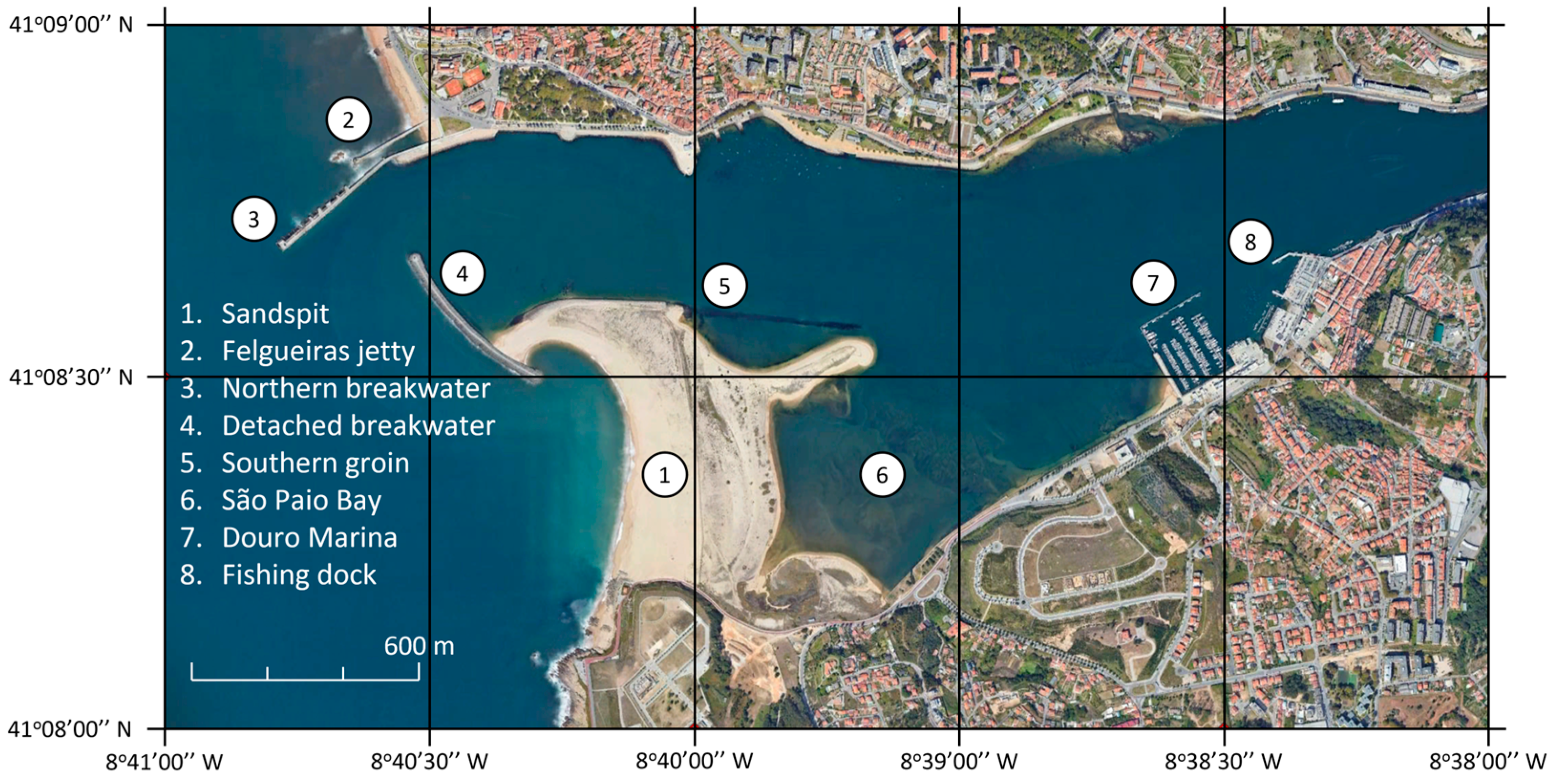
:1. Introduction
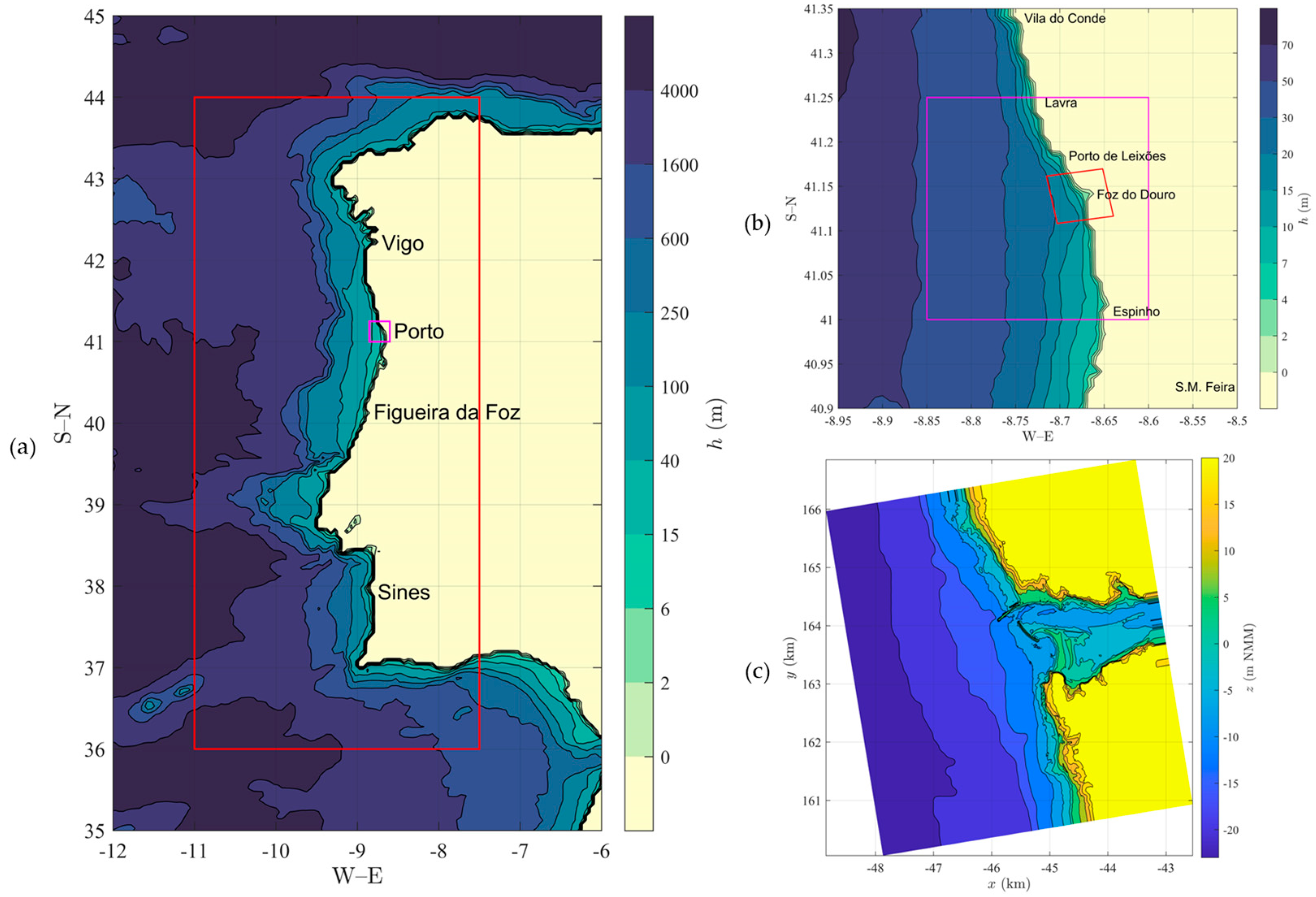
2. Materials and Methods
2.1. Numerical Models
2.2. Calibration of SWAN
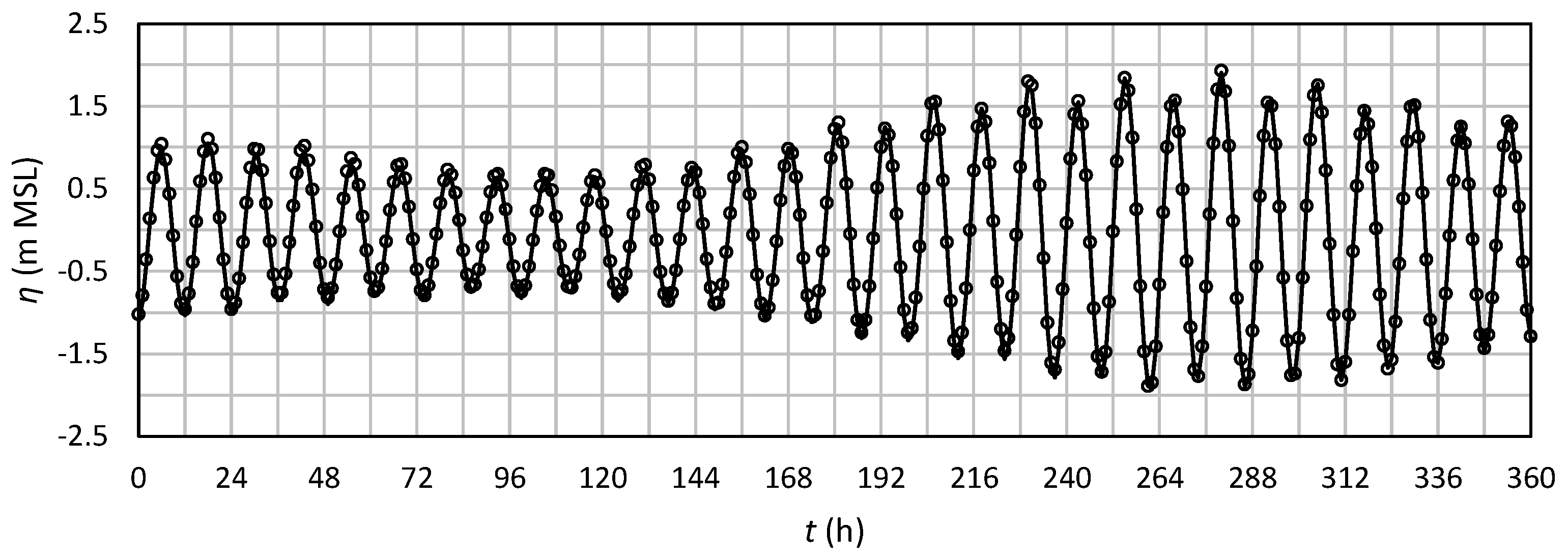
2.3. Model Set-Up and Validation
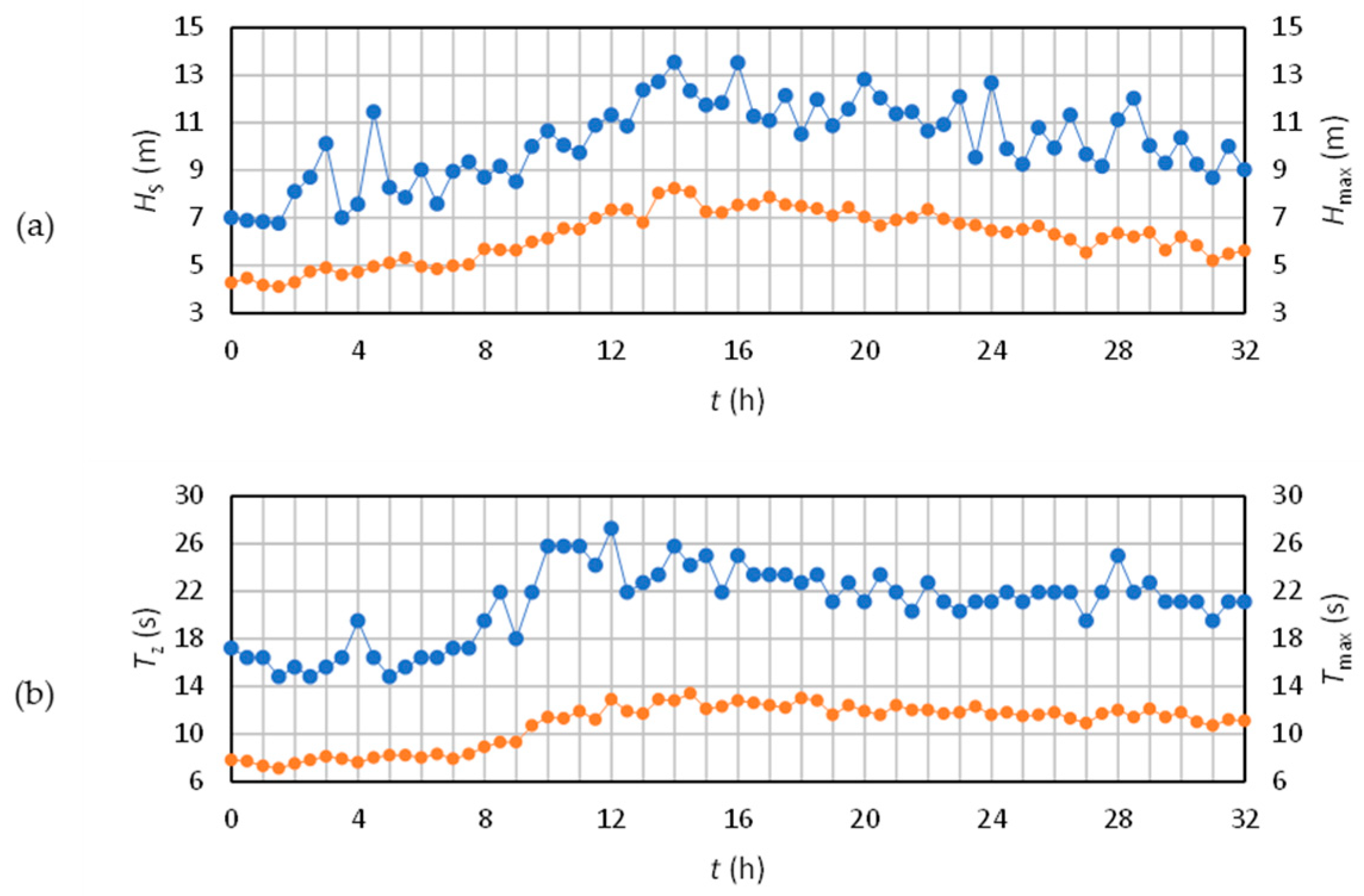
2.4. Storm Christina Coastal Model Validation
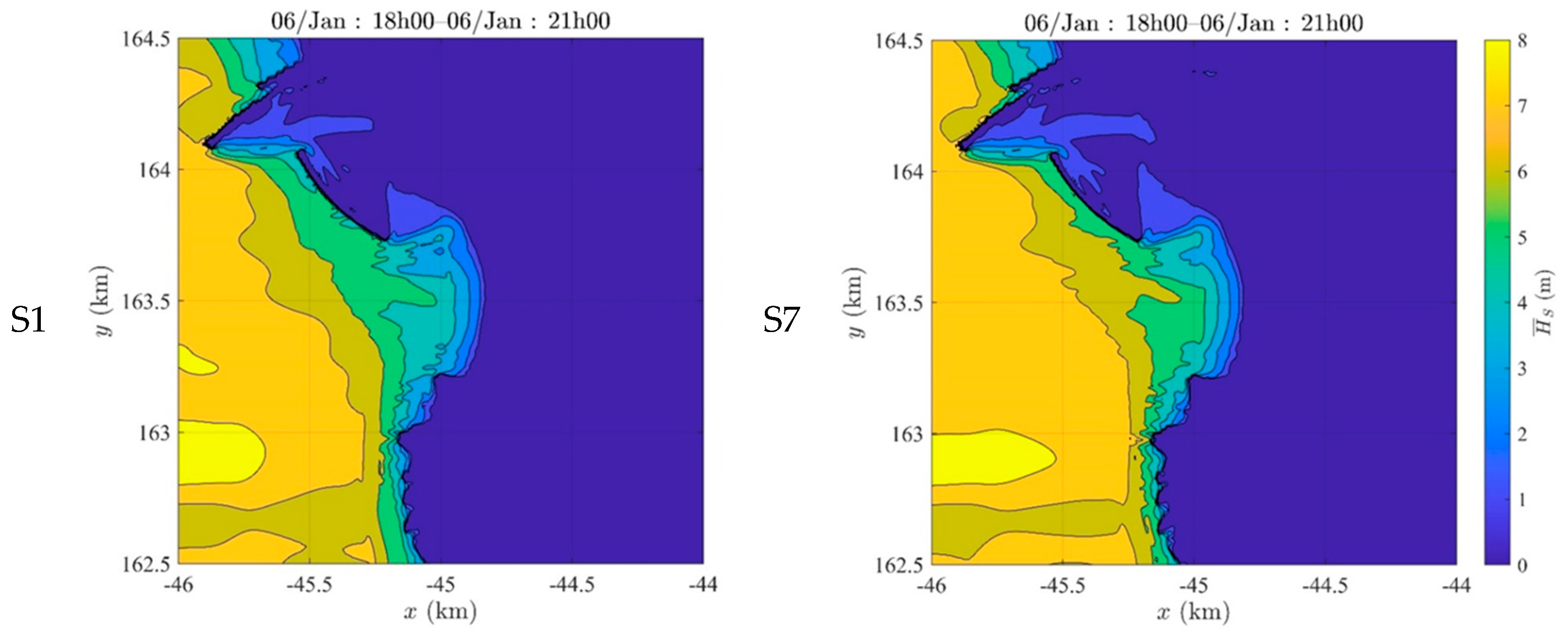
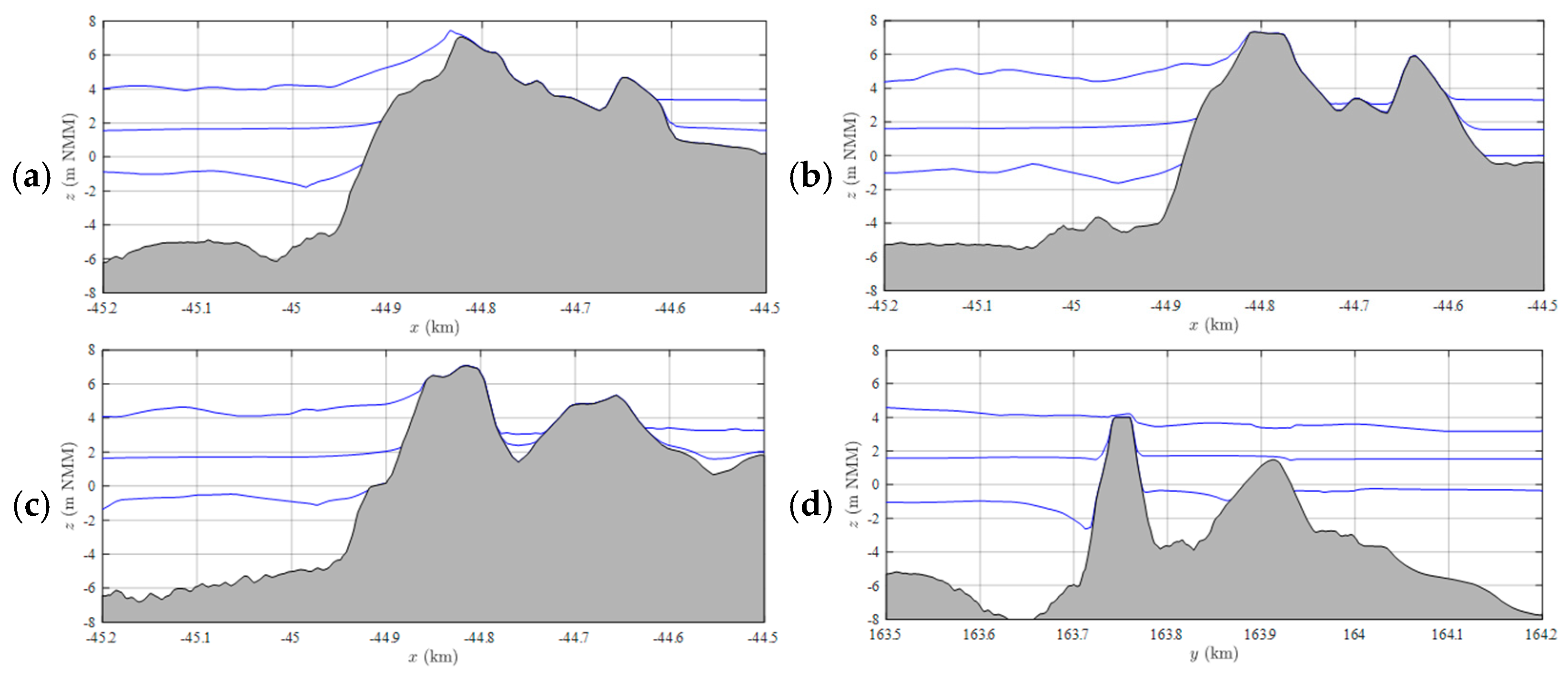
3. Results and Discussion
Storm Christina Simulation Scenarios
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bastos, L.; Bio, A.; Pinho, J.L.S.; Granja, H.; Jorge da Silva, A. Dynamics of the Douro Estuary Sand Spit before and after Breakwater Construction. Estuar. Coast. Shelf Sci. 2012, 109, 53–69. [Google Scholar] [CrossRef]
- Schwartz, M. The Encyclopedia of Beaches and Coastal Environments; Encyclopedia of Earth Sciences Series; Springer: New York, NY, USA, 1984. [Google Scholar]
- Robin, N.; Levoy, F.; Anthony, E.J.; Monfort, O. Sand Spit Dynamics in a Large Tidal-Range Environment: Insight from Multiple LiDAR, UAV and Hydrodynamic Measurements on Multiple Spit Hook Development, Breaching, Reconstruction, and Shoreline Changes. Earth Surf. Process. Landf. 2020, 45, 2706–2726. [Google Scholar] [CrossRef]
- Sakho, I.; Mesnage, V.; Deloffre, J.; Lafite, R.; Niang, I.; Faye, G. The Influence of Natural and Anthropogenic Factors on Mangrove Dynamics over 60 Years: The Somone Estuary, Senegal. Estuar. Coast. Shelf Sci. 2011, 94, 93–101. [Google Scholar] [CrossRef]
- Suursaar, Ü.; Jaagus, J.; Kont, A.; Rivis, R.; Tõnisson, H. Field Observations on Hydrodynamic and Coastal Geomorphic Processes off Harilaid Peninsula (Baltic Sea) in Winter and Spring 2006–2007. Estuar. Coast. Shelf Sci. 2008, 80, 31–41. [Google Scholar] [CrossRef]
- Liu, H.; Tajima, Y.; Sato, S. Long-Term Monitoring on the Sand Spit Morphodynamics at the Tenryu River Mouth. Int. Conf. Coastal. Eng. 2011, 1, sediment.87. [Google Scholar] [CrossRef] [Green Version]
- Santos, I.; Teodoro, A.C.; Taveira-Pinto, F. Análise da evolução morfológica da restinga do rio Douro. In Proceedings of the 5as Jornadas de Hidráulica, Recursos Hídricos e Ambiente, FEUP, Porto, Portugal, 25 October 2010; p. 13. [Google Scholar]
- Teixeira, R. Quebramares Portugueses. Inventário e Análise Comparativa de Soluções. Master’s Thesis, Faculdade de Engenharia, Universidade do Porto, Porto, Portugal, 2012. [Google Scholar]
- Viitak, M.; Avilez-Valente, P.; Bio, A.; Bastos, L.; Iglesias, I. Evaluating Wind Datasets for Wave Hindcasting in the NW Iberian Peninsula Coast. J. Oper. Oceanogr. 2021, 14, 152–165. [Google Scholar] [CrossRef]
- Veloso-Gomes, F.; Taveira-Pinto, F.; Paredes, G.M. Estudo da evolução da fisiografia da restinga do Douro desde 2002. In Proceedings of the 4as Jornadas de Hidráulica, Recursos Hídricos e Ambiente, FEUP, Porto, Portugal, 26 October 2009; p. 10. [Google Scholar]
- Iglesias, I.; Venâncio, S.; Pinho, J.L.; Avilez-Valente, P.; Vieira, J.M.P. Two Models Solutions for the Douro Estuary: Flood Risk Assessment and Breakwater Effects. Estuaries Coasts 2019, 42, 348–364. [Google Scholar] [CrossRef]
- Holzapfel, J. Tiefdruckgebiet CHRISTINA. Available online: https://page.met.fu-berlin.de/wetterpate/static/lebensgeschichten/Tief_CHRISTINA_03_01_14.htm (accessed on 9 June 2022).
- Santos, Â.; Mendes, S.; Corte-Real, J. Impacts of the storm Hercules in Portugal. Finisterra 2014, 49, 197–220. [Google Scholar] [CrossRef] [Green Version]
- IPMA Informação Mais Detalhada Sobre o Temporal no Atlântico Norte, Entre 3 e 6 Janeiro 2014. Available online: https://www.ipma.pt/pt/media/noticias/news.detail.jsp?f=/pt/media/noticias/arquivo/2014/temporal-atlantico-norte-3-6-jan-2014.html (accessed on 12 March 2022).
- Aleixo Pinto, C. Registo das Ocorrências No Litoral—Temporal de 3 a 7 de Janeiro de 2014; Agência Portuguesa do Ambiente: Amadora, Portugal, 2014; p. 123. [Google Scholar]
- Andrade, C.; Pires, H.O.; Taborda, R.; Freitas, M.C. Projecting Future Changes in Wave Climate and Coastal Response in Portugal by the End of the 21st Century. J. Coast. Res. 2007, 50, 253–257. [Google Scholar]
- Gulev, S.K.; Zolina, O.; Grigoriev, S. Extratropical Cyclone Variability in the Northern Hemisphere Winter from the NCEP/NCAR Reanalysis Data. Clim. Dyn. 2001, 17, 795–809. [Google Scholar] [CrossRef]
- Geng, Q.; Sugi, M. Variability of the North Atlantic Cyclone Activity in Winter Analyzed from NCEP–NCAR Reanalysis Data. J. Clim. 2001, 14, 3863–3873. [Google Scholar] [CrossRef]
- Wang, X.L.; Zwiers, F.W.; Swail, V.R. North Atlantic Ocean Wave Climate Change Scenarios for the Twenty-First Century. J. Clim. 2004, 17, 2368–2383. [Google Scholar] [CrossRef]
- Coelho, C.; Silva, R.; Veloso-Gomes, F.; Taveira-Pinto, F. Potential Effects of Climate Change on Northwest Portuguese Coastal Zones. ICES J. Mar. Sci. 2009, 66, 1497–1507. [Google Scholar] [CrossRef] [Green Version]
- Duc Anh, N.Q.; Tanaka, H.; Tam, H.S.; Tinh, N.X.; Tung, T.T.; Viet, N.T. Comprehensive Study of the Sand Spit Evolution at Tidal Inlets in the Central Coast of Vietnam. J. Mar. Sci. Eng. 2020, 8, 722. [Google Scholar] [CrossRef]
- Lisboa, P.V.; Fernandes, E.H. Anthropogenic Influence on the Sedimentary Dynamics of a Sand Spit Bar, Patos Lagoon Estuary, RS, Brazil. RGCI 2015, 15, 35–46. [Google Scholar] [CrossRef]
- Bugajny, N.; Furmańczyk, K.; Dudzińska-Nowak, J.; Paplińska-Swerpel, B. Modelling Morphological Changes of Beach and Dune Induced by Storm on the Southern Baltic Coast Using XBeach (Case Study: Dziwnow Spit). Coas 2013, 65, 672–677. [Google Scholar] [CrossRef]
- Allard, J.; Bertin, X.; Chaumillon, E.; Pouget, F. Sand Spit Rhythmic Development: A Potential Record of Wave Climate Variations? Arçay Spit, Western Coast of France. Mar. Geol. 2008, 253, 107–131. [Google Scholar] [CrossRef]
- Gruwez, V.; Verheyen, B.; Wauters, P.; Bolle, A. Hindcasting Sand Spit Morphodynamics after Groyne Construction in Ghana. J. Appl. Water Eng. Res. 2017, 5, 167–176. [Google Scholar] [CrossRef]
- Boudet, L.; Sabatier, F.; Radakovitch, O. Modelling of Sediment Transport Pattern in the Mouth of the Rhone Delta: Role of Storm and Flood Events. Estuar. Coast. Shelf Sci. 2017, 198, 568–582. [Google Scholar] [CrossRef]
- Fox-Kemper, B.; Hewitt, H.T.; Xiao, C.; Aðalgeirsdóttir, G.; Drijfhout, S.S.; Edwards, T.L.; Golledge, N.R.; Hemer, M.; Kopp, R.E.; Krinner, G.; et al. Ocean, Cryosphere and Sea Level Change. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 1211–1362. [Google Scholar]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A Third-Generation Wave Model for Coastal Regions: 1. Model Description and Validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef] [Green Version]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A Third-Generation Wave Model for Coastal Regions: 2. Verification. J. Geophys. Res. Ocean. 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- GEBCO Compilation Group. GEBCO 2021 Grid. 2021. [CrossRef]
- Roelvink, D.; Reniers, A.; van Dongeren, A.; van Thiel de Vries, J.; McCall, R.; Lescinski, J. Modelling Storm Impacts on Beaches, Dunes and Barrier Islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; van Dongeren, A.; van Thiel de Vries, J.; Lescinski, J.; McCall, R. XBeach Model Description and Manual; Unesco-IHE Institute for Water Education, Deltares and Delft University of Technology: Delft, The Netherlands, 2010; p. 108. [Google Scholar]
- EMODnet Bathymetry Consortium. EMODnet Digital Bathymetry (DTM). 2020. Available online: https://sextant.ifremer.fr/record/bb6a87dd-e579-4036-abe1-e649cea9881a/ (accessed on 28 July 2023). [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Dullaart, J.C.M.; Muis, S.; Bloemendaal, N.; Aerts, J.C.J.H. Advancing Global Storm Surge Modelling Using the New ERA5 Climate Reanalysis. Clim. Dyn. 2020, 54, 1007–1021. [Google Scholar] [CrossRef] [Green Version]
- Baordo, F.; Clementi, E.; Iovino, D.; Masina, S. Intercomparison and Assessement of Wave Models at Global Scale; Centro Euro-Mediterraneo sui Cambiamenti Climatici: Lecce, Italy, 2020; p. 49. [Google Scholar]
- Sharmar, V.; Markina, M. Validation of Global Wind Wave Hindcasts Using ERA5, MERRA2, ERA-Interim and CFSRv2 Reanalyzes. IOP Conf. Ser. Earth Environ. Sci. 2020, 606, 012056. [Google Scholar] [CrossRef]
- Monteiro, N.M.R.; Oliveira, T.C.A.; Silva, P.A.; Abdolali, A. Wind–Wave Characterization and Modeling in the Azores Archipelago. Ocean Eng. 2022, 263, 112395. [Google Scholar] [CrossRef]
- Beyramzadeh, M.; Siadatmousavi, S.M.; Derkani, M.H. Calibration and Skill Assessment of Two Input and Dissipation Parameterizations in WAVEWATCH-III Model Forced with ERA5 Winds with Application to Persian Gulf and Gulf of Oman. Ocean Eng. 2021, 219, 108445. [Google Scholar] [CrossRef]
- Çalışır, E.; Soran, M.B.; Akpınar, A. Quality of the ERA5 and CFSR Winds and Their Contribution to Wave Modelling Performance in a Semi-Closed Sea. J. Oper. Oceanogr. 2023, 16, 106–130. [Google Scholar] [CrossRef]
- Akinsanola, A.A.; Ogunjobi, K.O.; Abolude, A.T.; Salack, S. Projected Changes in Wind Speed and Wind Energy Potential over West Africa in CMIP6 Models. Environ. Res. Lett. 2021, 16, 044033. [Google Scholar] [CrossRef]
- García San Martín, L.; Barrera, E.; Toledo, C.; Sotillo, M. Atlantic-Iberian Biscay Irish-Ocean Wave Reanalysis; E.U. Copernicus Marine Service Information (CMEMS); Marine Data Store (MDS). 2012. Available online: https://cmems-catalog-ro.cls.fr/geonetwork/srv/api/records/25d28fb7-231c-4fc4-b97c-59495d87ec22 (accessed on 27 June 2023).
- Egbert, G.D.; Bennett, A.F.; Foreman, M.G.G. TOPEX/POSEIDON Tides Estimated Using a Global Inverse Model. J. Geophys. Res. Ocean. 1994, 99, 24821–24852. [Google Scholar] [CrossRef] [Green Version]
- Parker, B.B. Tidal Analysis and Prediction; NOAA Special Publication NOS CO-OPS 3; NOAA, NOS Center for Operational Oceanographic Products and Services: Washington, DC, USA, 2007; p. 378. [Google Scholar]
- MarRISK-Plataforma Interoperável Para Observações e Indicadores. Available online: https://marrisk.inesctec.pt/public/#!/timeseries (accessed on 2 April 2022).
- Bryant, M.A.; Hesser, T.J.; Jensen, R.E. Evaluation Statistics Computed for the Wave Information Studies (WIS); US Army Corps of Engineers: Washington, DC, USA, 2016. [Google Scholar]
- Perez, V. Monitorização e Evolução Da Restinga; Centro Interdisciplinar de Investigação Marinha e Ambiental, Universidade do Porto: Porto, Portugal, 2013. [Google Scholar]
- Van Rijn, L.C. Unified View of Sediment Transport by Currents and Waves. I: Initiation of Motion, Bed Roughness, and Bed-Load Transport. J. Hydraul. Eng. 2007, 133, 649–667. [Google Scholar] [CrossRef] [Green Version]
- Van Rijn, L.C. Unified View of Sediment Transport by Currents and Waves. II: Suspended Transport. J. Hydraul. Eng. 2007, 133, 668–689. [Google Scholar] [CrossRef]
- Van Thiel de Vries, J.S.M. Dune Erosion during Storm Surges; Deltares Select Series; IOS Press: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific: Singapore, 1991. [Google Scholar]





| Boundary Conditions | Physical Processes | ||||||
|---|---|---|---|---|---|---|---|
| ECMWF | CMEMS-IBI | Friction | Linear Growth | Exponential Growth | Whitecapping | Wind Drag | |
| T01 | ✓ | JONSWAP | Activated | Komen | Komen | Fit | |
| T02 | ✓ | JONSWAP | Activated | Komen | Janssen | Fit | |
| T03 | ✓ | JONSWAP | Activated | Komen | Komen | Wu | |
| T04 | ✓ | JONSWAP | Activated | Rogers/Babanin | Rogers/Babanin | Hwang | |
| T05 | ✓ | JONSWAP | Activated | Komen | Komen | Fit | |
| T06 | ✓ | JONSWAP | Activated | Westhhuysen/Yan | Alves-Banner | Fit | |
| T01 | T02 | T03 | T04 | T05 | T06 | |||
|---|---|---|---|---|---|---|---|---|
| (m) | 0.580 | 0.625 | 0.567 | 0.492 | 0.456 | 0.440 | ||
| (—) | 0.147 | 0.159 | 0.144 | 0.125 | 0.116 | 0.112 | ||
| (m) | −0.336 | −0.392 | −0.315 | −0.182 | 0.031 | −0.020 | ||
| (—) | 0.894 | 0.880 | 0.899 | 0.937 | 0.990 | 0.989 | ||
| (—) | 0.960 | 0.957 | 0.959 | 0.956 | 0.955 | 0.957 | ||
| (s) | 0.999 | 0.958 | 0.931 | 0.593 | 1.950 | 1.594 | ||
| (—) | 0.113 | 0.108 | 0.105 | 0.067 | 0.221 | 0.180 | ||
| (s) | 0.692 | 0.609 | 0.600 | −0.038 | 1.769 | 1.451 | ||
| (—) | 1.084 | 1.075 | 1.073 | 0.996 | 1.207 | 1.165 | ||
| (—) | 0.933 | 0.933 | 0.936 | 0.936 | 0.936 | 0.930 | ||
| (s) | 0.765 | 0.789 | 0.779 | 1.348 | 1.281 | 0.711 | ||
| (—) | 0.087 | 0.089 | 0.088 | 0.153 | 0.145 | 0.080 | ||
| (s) | 0.009 | −0.114 | −0.129 | −1.203 | 0.626 | −0.291 | ||
| (—) | 1.009 | 0.995 | 0.993 | 0.861 | 1.085 | 0.967 | ||
| (—) | 0.926 | 0.922 | 0.924 | 0.932 | 0.891 | 0.920 | ||
| (1) | (°N) | 21.31 | 21.53 | 20.52 | 20.60 | 21.75 | 22.00 | |
| (°N) | 7.64 | 6.93 | 7.44 | 7.47 | 9.05 | 8.99 | ||
| (—) | 0.661 | 0.672 | 0.698 | 0.693 | 0.603 | 0.586 |
| Scenario | Year | ||||
|---|---|---|---|---|---|
| (%) | (m MSL) | (m NMM) | |||
| S1 | Historical | 2021 | 0.000 | 0.221 | |
| S2 | SSP2-4.5 | 2100 | 5 | 0.253 | 0.480 |
| S3 | SSP2-4.5 | 2100 | 50 | 0.473 | 0.753 |
| S4 | SSP2-4.5 | 2100 | 95 | 0.867 | 1.206 |
| S5 | SSP5-8.5 | 2100 | 5 | 0.424 | 0.651 |
| S6 | SSP5-8.5 | 2100 | 50 | 0.784 | 0.949 |
| S7 | SSP5-8.5 | 2100 | 95 | 1.391 | 1.502 |
| (m, s, °) | (—) | (m, s, °) | (—) | (—) | |
|---|---|---|---|---|---|
| 0.447 | 0.093 | −0.171 | 0.958 | 0.957 | |
| 1.319 | 0.094 | 0.593 | 1.006 | 0.764 | |
| 0.667 | 0.074 | 0.149 | 0.997 | 0.911 | |
| 8.744 | −0.182 | 0.937 | 0.613 |
| Scenario | Volume | Area | ||||||
|---|---|---|---|---|---|---|---|---|
| Accretion | Erosion | Budget | Accretion | Erosion | ||||
| (%) | (m NMM) | (m3) | (m3) | (m3) | (%) | (%) | ||
| S1 | Historical | 0.221 | 187,862 | 193,761 | −5899 | 44 | 35 | |
| S2 | SSP2-4.5 | 5 | 0.480 | 196,804 | 201,908 | −5104 | 45 | 35 |
| S3 | SSP2-4.5 | 50 | 0.753 | 198,131 | 196,242 | +1889 | 48 | 34 |
| S4 | SSP2-4.5 | 95 | 1.206 | 217,982 | 211,624 | +6358 | 51 | 33 |
| S5 | SSP5-8.5 | 5 | 0.651 | 208,310 | 214,428 | −6117 | 45 | 36 |
| S6 | SSP5-8.5 | 50 | 0.949 | 216,886 | 209,653 | +7233 | 48 | 33 |
| S7 | SSP5-8.5 | 95 | 1.502 | 239,407 | 239,354 | +53 | 54 | 34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caeiro-Gonçalves, F.; Bio, A.; Iglesias, I.; Avilez-Valente, P. Sea Level Rise Effects on the Sedimentary Dynamics of the Douro Estuary Sandspit (Portugal). Water 2023, 15, 2841. https://doi.org/10.3390/w15152841
Caeiro-Gonçalves F, Bio A, Iglesias I, Avilez-Valente P. Sea Level Rise Effects on the Sedimentary Dynamics of the Douro Estuary Sandspit (Portugal). Water. 2023; 15(15):2841. https://doi.org/10.3390/w15152841
Chicago/Turabian StyleCaeiro-Gonçalves, Francisca, Ana Bio, Isabel Iglesias, and Paulo Avilez-Valente. 2023. "Sea Level Rise Effects on the Sedimentary Dynamics of the Douro Estuary Sandspit (Portugal)" Water 15, no. 15: 2841. https://doi.org/10.3390/w15152841





