Abstract
Since the prime days of stochastic hydrology back in 1960s, autoregressive (AR) and moving average (MA) models (as well as their extensions) have been widely used to simulate hydrometeorological processes. Initially, AR(1) or Markovian models with Gaussian noise prevailed due to their conceptual and mathematical simplicity. However, the ubiquitous skewed behavior of most hydrometeorological processes, particularly at fine time scales, necessitated the generation of synthetic time series to also reproduce higher-order moments. In this respect, the former schemes were enhanced to preserve skewness through the use of non-Gaussian white noise— a modification attributed to Thomas and Fiering (TF). Although preserving higher-order moments to approximate a distribution is a limited and potentially risky solution, the TF approach has become a common choice in operational practice. In this study, almost half a century after its introduction, we reveal an important flaw that spans over all popular linear stochastic models that employ non-Gaussian white noise. Focusing on the Markovian case, we prove mathematically that this generating scheme provides bounded dependence patterns, which are both unrealistic and inconsistent with the observed data. This so-called “envelope behavior” is amplified as the skewness and correlation increases, as demonstrated on the basis of real-world and hypothetical simulation examples.
1. Introduction: A Glimpse of History
“Remember that all models are wrong; the practical question is how wrong do they have to be to not be useful.”—George Box and Norman Draper [1]
The celebrated Harvard water program and the development of the so-called Thomas-Fiering (TF) model in the early 60s [2,3,4,5] played a historically crucial role in definition and advancement of the scientific discipline of stochastic hydrology—more specifically, of synthetic hydrology. The emergence of this field was mainly motivated by the need to generate synthetic streamflow data, to be used in water resources planning and management models [6,7,8]. The use of synthetic streamflow generators (or more generally weather generators) allowed for representing the operation of complex hydrosystems and deriving risk-related quantities that could not be obtained through classical statistics. Among the many different alternative models (see references below), the TF model prevailed for many years and still remains a popular choice. To date, the original Thomas-Fiering paper [4] and the related works of the Harvard water program [2,3,4,5] have been cited in the literature almost 2000 times, a fact highlighting its vast popularity and reasonably justifying its denomination as the “Ford’s Model T” of stochastic hydrology [9]. Additionally, more than half a century since its conception, the TF model, its variants, and the associated approach to handle skewness (see below) are standard educational material in most stochastic-hydrology courses and are disclosed in prominent positions in many classic and contemporary textbooks [10,11,12,13,14,15]. The wide acceptance of the model is also acknowledged by Salas and Pielke [16], who asserted that “the PAR(1) model (also known as the Thomas-Fiering model) is likely one of the most widely used models in hydrology”.
The original TF model is essentially a cyclostationary version of the classic stationary linear autoregressive model of order 1 (AR(1)), also formulated as a periodic autoregressive of order 1 (PAR(1)), in order to account for systematic changes and non-stationarities of statistical characteristics across seasons. The fact that the marginal distributions of many hydrometeorological processes are not Gaussian, motivated Thomas and Fiering [17] to propose the replacement of the Gaussian white noise with Gamma ( or Pearson type-III (III) distributed white noise [3] (pp. 53–57) in order to account for the skewness coefficient (to our knowledge, this modification first appears in the book of Thomas and Burden [18]). Note that the III distribution is a simple generalization of the distribution, which introduces an additional location parameter.
This approach was subsequently adopted by many other researchers (e.g., [3,7,19,20,21,22,23,24,25,26,27,28,29,30,31,32]) and can be classified as an implicit one, since it aims to approximate the distribution of the target process via the introduction of non-Gaussian white noise [33]. Hereafter, we refer to the use of non-Gaussian white noise in linear stochastic models (e.g., AR(1)) as the TF approach.
Nevertheless, herein, we mainly focus on AR models with non-Gaussian white noise, which have been widely adopted in hydrology, and briefly discuss three alternative schemes, two of which are based on moving average (MA) models and one based on an autoregressive moving average model (ARMA). Specifically, we investigate the effect on the established dependence patterns that arise from the use of III white noise within stationary univariate and multivariate linear stochastic models for generating synthetic hydrological data via stochastic simulation. Based on theoretical reasoning and empirical evidence, it is shown that the use of the implicit TF approach results in bounded and thus unrealistic dependence patterns, highlighting this approach’s limitations in simulating skewed hydrometeorological processes.
Our motivation stems from an observation of Tsoukalas et al. [33], who noticed this dependence pattern flaw while simulating 2000 years of monthly streamflow data at Aswan dam through the TF approach (i.e., PAR(1) with skewed white noise), hereafter called “envelope behavior”. A characteristic sample of this work is shown Figure 1, where we depict the scatter plots of historical and synthetic data for three pairs of consecutive months (January–February, March–April, and September–October). It is observed that the synthetically-derived scatter is bounded by a linear threshold, while the historical data clearly extend below this limiting line. It is remarkable that the model reproduces almost perfectly the (often regarded as essential) statistical characteristics of historical data, i.e., the mean, variance, and skewness, as well as the month-to-month linear correlations (Pearson’s), which is the typical measure of statistical dependence that is encountered in all linear stochastic schemes. However, it seems that the preservation of the latter does not ensure the generation of fully consistent dependence patterns.
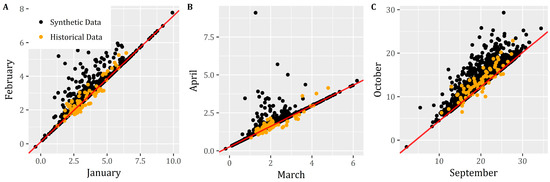
Figure 1.
Comparison of the (A) January–February, (B) March–April, and (C) September–October dependence patterns between historical and synthetic monthly runoff data (109 m3) of the Nile, at Aswan dam. Synthetic time series were generated by the cyclostationary Thomas-Fiering (TF) approach (adapted by Tsoukalas et al. [33]; the simulated negative values were not truncated to zero in order to avoid distortion of the dependence pattern). The red line (—) depicts the envelope equation of the TF model (when combined with III white noise. See also Appendix A).
2. The Envelope Behavior of Linear Stochastic Models with Non-Gaussian White Noise
2.1. The Thomas-Fiering Approach
The basic idea of the TF approach lies in using non-Gaussian, skewed, white noise within linear stochastic models in order to resemble the target marginal statistics, i.e., sample mean, variance, and skewness. Note that the derivation of a theoretical formula for the white noise skewness in AR() models of a higher order () aiming to reproduce skewness is theoretically possible but practically of no use, as it involves high-order joint statistics (that are difficult to estimate and are also subject to significant sample uncertainties [34]). Thus, application is possible only based on sample estimates of these joint statistics [35]. This is the major reason why the TF modification was originally restricted in AR(1) models, and thus similarly we also concentrate our main analysis in stationary univariate and multivariate AR(1) models with skewed white noise, while we briefly explore the cases of some other linear stochastic models (i.e., an ARMA and two variants of MA models).
Apparently, the selection of the underlying model determines the stochastic characteristics of the resulting simulation scheme. For example, when an AR(1) model is employed, the overall scheme will reproduce only Markovian autocorrelation structures, while if a more flexible MA-based scheme is used, the simulation scheme will be able to resemble a wider range of correlation structures.
However, regardless of the choice of the underlying model, such schemes exhibit a number of shortcomings and limitations, which are briefly summarized here [33]: (1) They provide just an approximation of the marginal distribution, as reproducing statistics generally is not equivalent to reproducing the distribution. Furthermore, the resulting distribution is not known a priori (e.g., in general the sum of Gamma distributed variables is not Gamma; see also, Moschopoulos [36]). We remark that this was acknowledged by the authors [3] (pp. 53–57) as well as later remarked by other researchers ([26,37,38], (p. 66)); (2) In order to reproduce the skewness of the underlying process it is required (due to central limit theorem) to use white noise with higher skewness [11,23,38,39], which can cause, in some cases, failure of the random number generator itself; (3) This simulation scheme generates time series that can have negative values, which is not consistent with many physical processes (e.g., rainfall, wind, streamflow, etc.). This is attributed to the fact that the lower bound of the white noise distribution may be negative in order to match the target statistics (as estimated from observed time series); (4) Finally, we prove and demonstrate in the next sections that this scheme leads to bounded and thus unrealistic dependence patterns that are not observed in natural processes (such as those depicted in Figure 1).
2.2. The Envelope Behavior in the Classical Univariate AR(1) Model
Let us assume we wish to simulate a continuous-state (not necessarily Gaussian), discrete-time, stationary AR(1) process (also referred to as the Markov process) , where is the time index. The main equation of the model reads:
where is a model parameter and denotes an i.i.d. random variable (RV) known as white noise or the innovation term. The theoretical autocorrelation function (ACF) of the AR(1) model is , where τ stands for the time lag. The mean and variance of are related with those of via the following equations (hereafter, due to stationarity, the index t will be omitted when possible):
Apparently, if the process of interest is Gaussian (or well-approximated by it), Equations (2) and (3) in combination with Gaussian white noise would be sufficient and “exact”, since a linear combination of Gaussian RVs is also Gaussian. However, this is not the case for most hydrometeorological processes. In this context, the TF approach attempts to approximate the non-Gaussian behavior of by employing non-Gaussian white noise for , where the skewness coefficient of is related with that of by [3,10,11,12,13]:
Hence, in order to capture the first three marginal moments of , one has to generate non-Gaussian white noise with certain statistical characteristics, which are all functions of the lag-1 autocorrelation coefficient of the process , given that . In Figure 2 we provide two alternative views of Equation (4), both depicting the variability of the required skewness of the white noise against the skewness and the lag-1 autocorrelation of the target process . Particularly, in Figure 2A we fix to specific values, ranging from 0 to 0.9, and with varying from 0 to 5, while in Figure 2B we set and vary from 0 to 0.9. Considering a high and aiming to reproduce a moderate skewness, e.g., , results in a white noise skewness , while for a highly skewed variable the deviation becomes much larger (related of course to ). For example, for a process with and , the required white noise skewness is , i.e., more than three times higher than the target value.

Figure 2.
Relationship between (A) the target skewness coefficient of process and the required skewness for white noise term for a given lag-1 autocorrelation coefficient ; and (B) the lag-1 autocorrelation coefficient and the required skewness coefficient of white noise term to attain the target skewness coefficient of process .
Within non-Gaussian simulations, the selection of the underlying statistical model of the white noise and the associated random number generation procedure is a pivotal step. Thomas and Fiering proposed the use of Pearson type-III (III) distribution, which is also one of the most commonly used distributions in hydrology. The probability density function (PDF) of III is given by:
where are shape, scale, and location parameters, respectively (if , then III reduces to the Gamma distribution). The mean , variance and skewness of the random variable are given by:
Of course, as Matalas and Wallis [37] noted, choosing the white noise distribution is a matter of convenience (see also discussion in Tsoukalas et al. [33]) and simplicity in generating random numbers, given obviously that the selected distribution can reproduce the desired statistics of white noise, i.e., .
The non-Gaussian formulation of the AR(1) model through the TF approach results in the so-called envelope behavior issue, which is associated with the distribution of the white noise. Let us write Equation (1) in the equivalent form:
where denotes the inverse cumulative density function (ICDF) of the white noise and expresses a uniform RV in [0, 1] (probability), i.e., . In the above formulation, we see that in the Gaussian case, where ), the random variable takes any value in ). However, when the distribution of has a finite left support, as in III or Gamma ( cases, then where stands for the lower bound of Hence, for given (e.g., specified from the data) and , we can estimate at any step of the generation procedure the lower bound of by:
and thus calculate the theoretical lower bound of the synthetic data. Similarly, when the distribution of is bounded from above (as in the III case adjusted for negative skewness), then where is the upper bound of the distribution of In this case the generation mechanism is bounded from above, i.e.:
This limitation is especially important since hydrometeorological variables, such as river discharge, cannot be considered unbounded from above, even when the sample statistics erroneously indicate negative skewness. To the best of our knowledge, despite the popularity of the TF model and the associated approach of coupling it with skewed white noise, this shortcoming has never been reported in literature, regardless of its straightforward and intuitive theoretical derivation. This limitation also holds for the univariate cyclostationary TF model (i.e., PAR(1) with III white noise), for which we provide the corresponding relationships in Appendix A.
Apart from the latter relationships, based on the previous formulation it can be shown that a simple recursive procedure facilitates the estimation of the theoretical minimum (or maximum) value of the TF approach. Without the loss of generality, assuming and by sequentially applying Equation (7) for q steps with we can obtain the model’s theoretical minimum, which can differ from (they are identical when ). The recursive procedure can be written as follows:
Alternatively, and more vigorously (depending on the support of ), the theoretical minimum and maximum are given, respectively, by and .
In order to better demonstrate the envelope behavior, we apply the AR(1) model coupled with III white noise (termed AR(1)-III) to 12 hypothetical scenarios by simulating 5000 time steps for each. For all scenarios we fix and combined with and (see Table 1 for a summary). Since the III is used for generating white noise and , in all cases a lower bound is anticipated.

Table 1.
Summary of target statistics for all scenarios (in all cases, and ).
As theoretically expected, the model reproduces the target ACF and target statistics for all scenarios with high accuracy (see Figure A1 and Table A1 of Appendix B). However, the envelope behavior of the dependence pattern is apparent and indicates its limitation, a fact clearly demonstrated by the scatter plots (Figure 3) corresponding to the 12 simulation scenarios. The theoretically-derived Equation (8), defining the lower bound of the feasible space of the () points, is depicted by a red line (Figure 3). Note that labels in each subplot follow the scenarios’ naming convention in Table 1 (e.g., panel C corresponds to scenario C of Figure 3). Apparently, in every case, regardless of the and values, the model generates bounded dependence patterns enveloped by Equation (8). This behavior appears even for low combinations of and (e.g., scenario A).
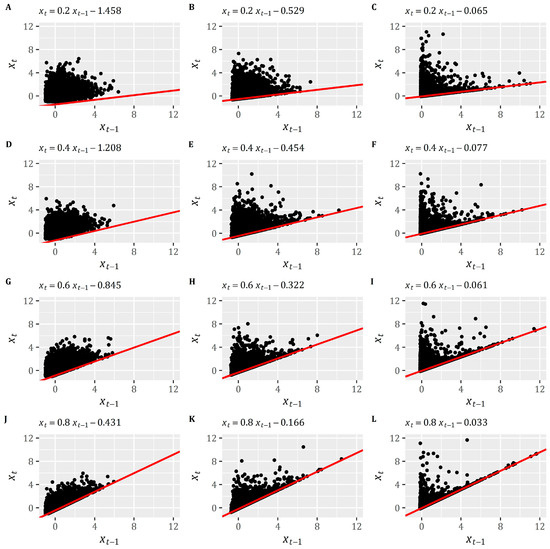
Figure 3.
Scatter plots depicting the simulated (using the TF model, i.e., the autoregressive model of order 1 (AR(1))-III) lag-1 dependence pattern among consecutive time steps (i.e., pair values (•) of the previous and current time steps). The labels of each plot resemble the corresponding scenarios of Table 1. The red line (—) depicts the envelope equation shown in the title of each plot.
2.3. From the Univariate to the Multivariate AR(1) Model
It is reasonable to expect that the envelope behavior will also be observed in the multivariate case, i.e., when the multivariate autoregressive process of order 1 is used (MAR(1)) in combination with non-Gaussian white noise. Let us assume that we wish to generate an m-dimensional vector of m cross-correlated AR(1) processes, indexed by i. The generation mechanism of the model is:
where is an matrix and is an m-dimensional column vector of cross-correlated yet serially independent RVs with covariance The model is often called the “multivariate lag-1 model” when a full matrix is employed, while there exists a variation that assumes a diagonal matrix, often called “multivariate Markov model” or “contemporaneous multivariate autoregressive model of order 1” (i.e., CMAR(1)). Both formulations explicitly account for the lag-0 cross-correlations of the variables while their major difference is that the former is able to explicitly account for the lag-1 cross-correlations [11,37,40]. On the other hand, the use of diagonal A1 ensures that each individual process is a Markov process and significantly simplifies the parameter estimation procedure, since the lag-1 cross-correlations are not explicitly modeled. Its use is often advocated by the literature, since several authors suggest that lag-1 cross-correlations can be neglected [14,22,26,33,40,41]. Yet it is noted that while this simplification could be valid for processes considered at a coarse time scale (e.g., monthly or annual), it should be used with caution in cases of fine time scale processes (e.g., hourly) or for modeling phenomena characterized by cause-effect relationships (e.g., rainfall-runoff). Nevertheless, here we focus on the so-called multivariate Markov model (i.e., CMAR(1)). Regarding its parameter estimation and assuming that is a diagonal matrix of the form:
where , the following holds true:
where is the lag-0 cross-covariance matrix. For instance, its ith, jth element is . The theoretical cross-covariance matrices can be obtained for any time lag τ by recursively applying the equation:
Meanwhile, the theoretical and cross-correlation matrices are obtained by . Furthermore, the covariance matrix can be expressed as:
where B is an , typically lower triangular, matrix (also known as the square root of ) obtained by standard decomposition techniques (e.g., the Cholesky technique) or optimization approaches [23,42]. The latter methods are usually employed when B is non-positive definite. Typically, such problems arise when the sample estimates of the required statistics are extracted from historical time series of different and/or limited lengths [11]. Nonetheless, given that is diagonal and assuming that , where is an m-dimensional column-vector of i.i.d. RVs, the decomposition of Equation (11) can be given as follows:
Additionally, the moments of and are interrelated through (index t is omitted due to stationarity):
where and denote column-vectors that contain the third central moments of and , respectively; we remark that coincides with the skewness coefficient, since the model assumes unit variance for . Similar to the univariate case, the white noise term is typically generated using the III distribution (Equation (5)). To illustrate the envelope behavior of the latter model, we rewrite the Equation (11) similarly to Equation (7), i.e.:
where denotes the quantile function of for a given probability . If the distribution of is bounded below or above by or , respectively, then , and . Therefore, we obtain:
for lower (left)- and above (right)-bounded cases, respectively.
However, in the multivariate case, and since depends on multiple values of , the limiting behavior (assuming that all RVs are left-bounded) is identified by setting . Of course, the envelope behavior diminishes if the white noise term is normally distributed (or more generally if )), yet in this case skewness cannot be preserved.
Without the loss of generality, we examine the bivariate case of where both processes exhibit zero autocorrelation but their lag-0 cross-correlation is equal to 0.8. For , , and we find:
(where is obtained by the Cholesky decomposition), while the generating equation (Equation (11)) becomes:
Given the target moments of , the statistics of the white noise term are calculated as , , and . Using the III for white noise generation we obtain the lower bound vector . Thus, from Equation (22) the limiting envelope equations are and . In this case, it is also possible to estimate the envelope relationship a priori between and as is a zero matrix. Particularly, since and , and substituting the former into the latter, we get , and by setting the envelope line is obtained.
In order to demonstrate the envelope behavior in the multivariate case, we employ the above model and synthesized a time series of 5000 time steps. Figure 4A–C depicts the established dependence patterns of each individual process for lag-1 (panels A and B), while panel C shows the pattern among the two processes for lag-0. Also, at each panel we display the corresponding envelope equation. We remark that the model was able to accurately reproduce the theoretical stochastic structure, expressed by the autocorrelation (ACF) and cross-correlation functions (CCF) shown in Figure 4D–F, as well as, to approximate very well the target moments (Table A2).

Figure 4.
Scatter plots depicting the simulated (using the contemporaneous multivariate autoregressive model of order 1 (CMAR(1) model) with III white noise) for (A) and (B) lag-1 dependence patterns of the zero-autocorrelated processes and , respectively, for consecutive time steps (i.e., pair values (•) of the previous and current time steps). Panel (C) depicts the contemporaneous dependence (lag-0) of and . The red line (—) depicts the envelope equation shown in the title of each plot. Panel (D) compares the simulated and theoretical autocorrelation function (ACF) of while panel (E) compares that of . Finally, panel (F) compares the simulated and theoretical cross-correlation function (CCF) of and .
In order to extend our working examples, we simulate another vector of bivariate time series (5000 time steps) using the same marginal moments as before, but this time with a different autocorrelation structure. Specifically, we assumed and . Thus, we get:
and the generating formula:
Similar to the previous analysis, Figure 5A–C depicts the established lag-1 and lag-0 dependence patterns, while the envelope equation of each process is displayed in the title of each panel. It is apparent that at each simulated step, the model poses significant constraints in the range of subsequent plausible values, which is far from reality. We remark that in this case the contemporaneous lag-0 relationship cannot be displayed in a two-dimensional (2D) plot since it involves the lag-1 values of and . Nevertheless, the model successfully reproduced the target stochastic structure (Figure 5D–F) and the marginal moments (see Table A3), at the cost, however, of unrealistically bounded dependence patterns.
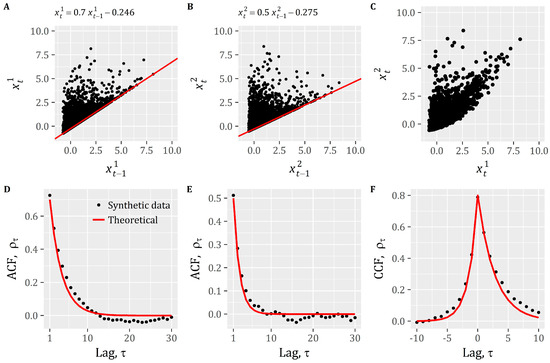
Figure 5.
Scatter plots depicting the simulated (using the CMAR(1) model with III white noise) for (A) and (B) lag-1 dependence pattern of the autocorrelated processes and , respectively, for consecutive time steps (i.e., pair values (•) of the previous and current time steps), while panel (C) depicts the contemporaneous dependence (lag-0) of and . The red line (—) depicts the envelope equation shown in the title of each plot. Panel (D) compares the simulated and theoretical ACF of while panel (E) compares that of . Lastly, panel (F) compares the simulated and theoretical CCF of and .
2.4. The Envelope Behavior beyond AR Models
To demonstrate the impact of employing non-Gaussian white noise in combination with other linear stochastic models, we employed (1) a low-order autoregressive moving average model ARMA(p,q); (2) a simple moving average model MA(q); and (3) its symmetric variant, termed SMA(q). The parameters p and q determine the order of the models. As shown by O’Connell [31] and later discussed by Lettenmaier [38], it is possible for the case of ARMA(1,1) to derive an analytical relationship that links the skewness of the white noise with the skewness of the target process. Furthermore, it has been shown [30] that similar relationships can be established for the two moving average schemes regardless of the order q (i.e., MA(q) and SMA(q)).
In this demonstration we utilized the aforementioned relationships for the simulation of a univariate stationary process with the characteristics of the hypothetical Scenario I of Table 1, which refers to the Markovian process with and . Regarding the ARMA(1,1) process, it is noted that its autocorrelation structure is somewhat different from the Markovian one, hence we carefully choose its parameters in order to have . On the other hand, both MA(q) and SMA(q) are able to resemble the Markovian autocorrelation structure with satisfactory accuracy by setting q = 32. Nonetheless, in all cases we used III distribution for the white noise, hence the models are termed ARMA(1,1)-III, MA(32)-III, and SMA(32)-III. However, due to a lack of analytical solution for the envelope function, and in order to derive a clear picture of the established dependence patterns, we generated very long realizations, each one consisting of 500,000 time steps. Figure 6 shows the lag-1 dependence pattern obtained by the three schemes as well as a comparison of the simulated and theoretical ACF, which is very well reproduced by all models. Despite the accurate reproduction of the target marginal statistics (mean, variance, and skewness) by all models, they establish peculiarly-shaped and always bounded dependence forms. However, it should be noted that the MA(q) and SMA(q) schemes are typically employed for the simulation of annual processes, which are typically well approximated by the Gaussian distribution, and thus it is reasonable to expect a minimization of this issue.

Figure 6.
Scatter plots depicting the simulated lag-1 dependence pattern among consecutive time steps (i.e., pair values (•) of the previous and current time steps) obtained by: (A) ARMA(1,1)-III; (B) MA(32)-III; and (C) SMA(32)-III models. Comparison of synthetic and theoretical autocorrelation function (ACF) obtained by: (D) ARMA(1,1)-III; (E) MA(32)-III; and (F) SMA(32)-III models.
3. Real-World Case Study
In this section we demonstrate the envelope behavior of the TF approach using a real-world and long dataset (1 January 1970 to 31 December 2008) of daily streamflow data (m3/s) of river Achelous at Kremasta dam in Western Greece. It is assumed that the autocorrelation structure of the daily streamflow of each month can be described by a stationary AR(1) model. The historical monthly and daily time series are clearly characterized by non-Gaussian distributions and skewness coefficients ranging from 1.6 (June) up to 6.7 (October). Specifically, we generate daily synthetic time series with a length of 1000 years, using for each month a different AR(1) model with III white noise (i.e., AR(1)-III). The model very satisfactorily reproduced the target historical marginal statistics of each month (Table A4), as well as the theoretical Markovian autocorrelation structure (see Figure A2 for a comparison among the empirical, synthetic, and theoretical ACFs), which however deviates from the empirical ACF for some months, showing a more persistent behavior. Yet a comparison of the lag-1 dependence patterns between the synthetic and the historical data, using scatter plots for each month (Figure 7), reveals the omnipresence of the envelope behavior. Evidently the model generates unrealistic dependence patterns that are far from the historical ones. The synthetic pairs of values are bounded by the theoretical envelope function (red line; embedded in each plot), while the historical pairs clearly extend beyond that line. In an effort to provide a quantitative metric, we calculate the empirical probability of a historical pair to lie below the envelope function. The overall mean value of this metric estimated from all months is 27%, while it ranges from 14% (in November) to 42% (in April).

Figure 7.
Scatter plots showing the lag-1 dependence pattern of the daily streamflow of the Achelous river at the Kremasta dam, Greece (orange dots; •) and of a synthetic time series generated using an AR(1)-III model (black dots; •). The red line (—) depicts the envelope equation embedded each plot.
4. Discussion
Historically, most of the questions raised regarding the TF approach have concerned the case of the AR(1) model and the range of attainable skewness coefficients [20,38,43]. This was mainly due to the use of Wilson-Hilferty transformation which was used for generating Gamma or Pearson type-III RVs [44]. Nowadays, this technical issue is out of interest, since such RVs can be easily generated with high accuracy by modern random number generators which are available in almost every programming language (e.g., R, MATLAB, etc.). Additionally, we note that McMahon and Miller [20] reported that Thomas and Burden [18] and Fiering [5] tested their approach for skewness values ranging in (−0.5, 1.0).
This work focused on the effect of using Pearson type-III white noise in AR(1) models and we show that this approach leads to unrealistic dependence patterns. Furthermore, preliminary investigations have also shown that this issue extends over other popular linear stochastic models when coupled with non-Gaussian white noise. Particularly, we demonstrated three such cases using III white noise in combination with (1) a classical ARMA(1,1); (2) a simple MA(q); and (3) its symmetrical variant SMA(q) [30]. In all cases the resulting dependence patterns exhibited a peculiar and unrealistic bounded shape which can be bounded from both directions.
Nevertheless, it is noteworthy that Song et al. [45] and Jeong and Lee [46] also observed this issue independently while studying AR(1) with exponential white noise [47,48,49] and periodic Gamma autoregressive (PGAR) processes [50], respectively. However, to the best of our knowledge, these works, or any other, have not revealed the envelope limitation, neither provided a theoretical proof and a justification for this behavior, which probably arises from the lack of explicit assumption regarding the joint dependence structure of the process. Particularly, the joint moment of order of two continuous RVs, and , is given by:
where denotes the joint probability distribution function (PDF) of and . The first cross product joint moment is embedded in the definition of covariance, as well as in the Pearson’s correlation, i.e.:
Hence, this points to the requirement for an assumption regarding . When both and are Gaussian, and simulated through a typical decomposition scheme (e.g., the Cholesky technique) which applies linear operations on them, the joint PDF of and is also Gaussian (due to the affine transformation property of Gaussian RVs). When and are not Gaussian, the latter convenient property does not hold. By analogy, the joint moment of order of a continuous-state, discrete-time stochastic process can be expressed as:
If is Gaussian and modeled using a linear stochastic process (e.g., AR or MA-type) with Gaussian white noise, then it is well known that the joint PDF is also Gaussian. This implies linear operations on Gaussian RVs. On the other hand, this does not hold for the TF approach, which uses non-Gaussian white noise and thus the form of is unclear.
We remind that summary statistics such as mean, variance, skewness, and correlation are nothing more than some useful measures of location, dispersion, asymmetry, and dependence, and do not involve in their estimation the actual joint distribution. A classic example is provided by the so-called Anscombe’s Quartet [51] and recently by Matejka and Fitzmaurice [52]. Both works stress the importance of data science’s first principle: “Visualize your data”. They demonstrate this issue by devising several examples of datasets that have the same summary statistics but completely different dependence patterns. Apparently, as shown in this work, the aforementioned simple principle also applies in synthetic hydrology.
Nowadays, multivariate random variables are typically modeled by copula functions [53,54], which despite the early-days skepticism [54] have found wide acceptance and practical use. In hydrology, copulas have been popularized by the studies of De Michele and Salvadori [55] and Favre et al. [56], and since then have been widely applied for the description of correlated yet time-independent variables [55,56,57,58,59,60,61,62,63], while only lately they have been adapted and modified accordingly to account for time-dependence, which led to the development of copula-based schemes for the simulation of hydrometeorological processes [64,65,66,67,68,69,70].
A conceptually related, yet until recently unknown to the hydrological community, approach relies on the so-called Nataf joint distribution model [71], which is associated to the well-known Gaussian copula [54,72]. Since their inception, Nataf-based models have been developed and applied for the simulation of univariate or multivariate autoregressive processes with arbitrary marginal distribution mainly within operations research, e.g., [73,74], while recently they have been aligned with hydrological stochastics [33,75,76,77,78] in order to account for non-Gaussian processes, both univariate and multivariate, exhibiting intermittency, periodicity, and any-range dependence.
Apparently, both Nataf- and copula-based approaches can provide a remedy to the limitations of the TF approach, as well as explicitly account for non-Gaussianity, which is omnipresent within hydrometeorological processes (e.g., [79,80,81,82,83,84,85]). We deem that Nataf-based models provide a convenient and more precise alternative given that they utilize (in an auxiliary or parent role) existing and well-known stochastic models which provide the basis for a straightforward and operational efficient generation scheme. It is also noted that the celebrated Log-Normal model of Matalas [7], which incidentally can be classified as a Nataf-based approach [33,76], does not exhibit the TF approach limitation and thus can provide a rather easy and consistent option for practitioners.
5. Conclusions
To conclude, we bring back the aphorism and the question set by Box and Draper. Paraphrasing, we could say that indeed since all models are wrong and TF is not an exception, the question is how wrong the TF approach has to be to not be useful. A way to answer this question is through impact assessments of the envelope behavior in real-world applications, e.g., in important engineering studies (reservoir design and sizing, hydropower assessment, reliability-based studies, etc.), and of its effect on decision-making related to water resources management. Another question arising here is why should one use a model with known limitations and flaws (irrespective of whether these flaws have minor or major impacts on real-world applications) which reproduces unrealistic rainfall or streamflow patterns? We recognize that the TF model and the associated approach was a major contribution of paramount importance that shaped stochastic hydrology, yet in practice linear stochastic models should be used cautiously when combined with non-Gaussian white noise, given the limitations shown herein. This approach preserves important summary statistics (i.e., mean, variance, and skewness) and correlations, yet for processes showing medium to high skewness values and/or correlations it will inevitably reproduce bounded and unrealistic dependence patterns that are next used in simulations. In this context, after half a century of blind use of this model and approach, we deem that it is time to move to alternative methods which are consistent in generating realistic dependence structures as well as the marginal distribution itself.
Author Contributions
I.T. conceived and designed the present study and developed the R code for the simulation examples. I.T., S.M.P., and A.E., organized and prepared the manuscript. C.M. supervised the work during all stages.
Acknowledgments
The Nile streamflow data at Aswan dam are available at: http://www.stats.uwo.ca/faculty/mcleod/epubs/mhsets/, while the streamflow data at Kremasta, Greece, are available upon request to the authors. We thank the three reviewers for their constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Herein we present the mathematical background of the univariate cyclostationary Thomas-Fiering (TF) model, also known as the univariate periodic autoregressive model of order 1 (i.e., PAR(1)), with Pearson type-III (III) white noise. Let be a cyclostationary (i.e., periodic) process with seasons , where denotes the total number of seasons (e.g., for a monthly model, ). The generating mechanism of the model is:
where are seasonally-varying parameters and denotes an i.i.d. variate. The parameter and .
The statistical characteristics of the white noise term, which is generated through III distribution, are related to those of the target process via the following relationships:
where denotes the third central moment of an arbitrary random variable , which in the case of coincides with its skewness coefficient since the model assumes unit variance. Furthermore, following the rationale of Section 2, the envelope function of the generation mechanism can be expressed as:
for positive skewness (i.e., III with ), hence forming a lower boundary, and:
for negative skewness (i.e., III with ), hence forming an upper boundary. In the above, and respectively denote the lower and upper supports of the distribution of the white noise at season s. We remark that similar derivations, yet much more complex, can be derived for other models that employ skewed white noise.
Appendix B

Table A1.
Scenario-based summary of theoretical (see Table 1 of the main manuscript; Section 2.2—“The envelope behavior in the classical univariate AR(1) model”) and simulated (synthetically generated; using an AR(1) with III white noise) statistics.
Table A1.
Scenario-based summary of theoretical (see Table 1 of the main manuscript; Section 2.2—“The envelope behavior in the classical univariate AR(1) model”) and simulated (synthetically generated; using an AR(1) with III white noise) statistics.
| Scenario | Type | Mean (μ) | Variance (σ2) | Skewness (Cs) | Autocorrelation (ρ1) |
|---|---|---|---|---|---|
| Scenario A | Theoretical | 0.50 | 1.00 | 1.00 | 0.20 |
| Simulated | 0.46 | 0.93 | 1.05 | 0.20 | |
| Scenario B | Theoretical | 0.50 | 1.00 | 2.00 | 0.20 |
| Simulated | 0.54 | 1.06 | 2.07 | 0.18 | |
| Scenario C | Theoretical | 0.50 | 1.00 | 4.00 | 0.20 |
| Simulated | 0.50 | 0.91 | 3.48 | 0.21 | |
| Scenario D | Theoretical | 0.50 | 1.00 | 1.00 | 0.40 |
| Simulated | 0.46 | 0.97 | 0.91 | 0.34 | |
| Scenario E | Theoretical | 0.50 | 1.00 | 2.00 | 0.40 |
| Simulated | 0.49 | 1.11 | 2.09 | 0.45 | |
| Scenario F | Theoretical | 0.50 | 1.00 | 4.00 | 0.40 |
| Simulated | 0.46 | 1.01 | 4.89 | 0.45 | |
| Scenario G | Theoretical | 0.50 | 1.00 | 1.00 | 0.60 |
| Simulated | 0.42 | 0.97 | 0.88 | 0.64 | |
| Scenario H | Theoretical | 0.50 | 1.00 | 2.00 | 0.60 |
| Simulated | 0.48 | 1.04 | 2.20 | 0.62 | |
| Scenario I | Theoretical | 0.50 | 1.00 | 4.00 | 0.60 |
| Simulated | 0.48 | 0.93 | 4.22 | 0.57 | |
| Scenario J | Theoretical | 0.50 | 1.00 | 1.00 | 0.80 |
| Simulated | 0.50 | 1.09 | 0.75 | 0.82 | |
| Scenario K | Theoretical | 0.50 | 1.00 | 2.00 | 0.80 |
| Simulated | 0.45 | 0.97 | 2.11 | 0.81 | |
| Scenario L | Theoretical | 0.50 | 1.00 | 4.00 | 0.80 |
| Simulated | 0.55 | 1.08 | 4.24 | 0.81 |
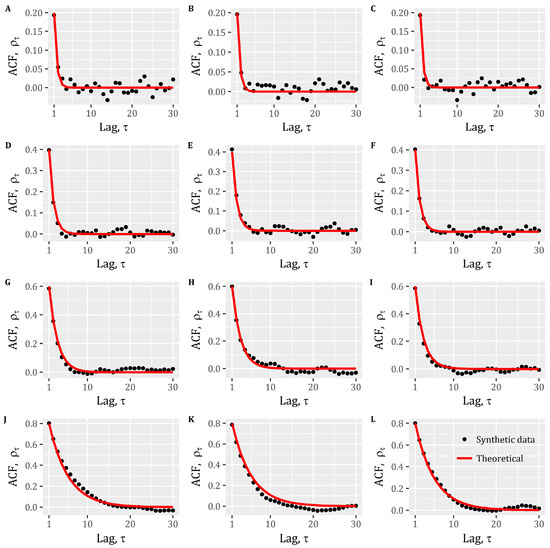
Figure A1.
Scenario-based (see Table 1 of the main manuscript; Section 2.2—“The envelope behavior in the classical univariate AR(1) model”) comparison of synthetic (using the an AR(1) with III white noise) and theoretical autocorrelation function (ACF). The labels of each plot resemble the corresponding scenarios of the aforementioned table (see also Table A1).

Table A2.
Summary of theoretical and simulated statistics for the first, zero-autocorrelated, bivariate AR(1) process with III white noise, employed in Section 2.3—“From the univariate to the multivariate AR(1) model” of the main manuscript.
Table A2.
Summary of theoretical and simulated statistics for the first, zero-autocorrelated, bivariate AR(1) process with III white noise, employed in Section 2.3—“From the univariate to the multivariate AR(1) model” of the main manuscript.
| Process | Type | Mean (μ) | Variance (σ2) | Skewness (Cs) | Autocorrelation (ρ1) |
|---|---|---|---|---|---|
| Theoretical | 0.50 | 1.00 | 2.00 | 0.00 | |
| Simulated | 0.50 | 1.06 | 2.39 | 0.00 | |
| Theoretical | 0.50 | 1.00 | 2.50 | 0.00 | |
| Simulated | 0.51 | 1.14 | 2.95 | 0.00 | |
| Theoretical cross-correlation (ρ0) = 0.80|Simulated cross-correlation (ρ0) = 0.79 | |||||

Table A3.
Summary of theoretical and simulated statistics for the second, autocorrelated, bivariate AR(1) process with III white noise, employed in Section 2.3—“From the univariate to the multivariate AR(1) model” of the main manuscript.
Table A3.
Summary of theoretical and simulated statistics for the second, autocorrelated, bivariate AR(1) process with III white noise, employed in Section 2.3—“From the univariate to the multivariate AR(1) model” of the main manuscript.
| Process | Type | Mean (μ) | Variance (σ2) | Skewness (Cs) | Autocorrelation (ρ1) |
|---|---|---|---|---|---|
| Theoretical | 0.50 | 1.00 | 2.00 | 0.70 | |
| Simulated | 0.52 | 1.08 | 2.00 | 0.70 | |
| Theoretical | 0.50 | 1.00 | 2.50 | 0.50 | |
| Simulated | 0.52 | 1.11 | 2.51 | 0.51 | |
| Theoretical cross-correlation (ρ0) = 0.80|Simulated cross-correlation (ρ0) = 0.80 | |||||

Table A4.
Monthly-based summary of historical and simulated (synthetically generated using an AR(1) with III white noise) statistics of the real-world case study employed in Section 3—“Real world case study” of the main manuscript.
Table A4.
Monthly-based summary of historical and simulated (synthetically generated using an AR(1) with III white noise) statistics of the real-world case study employed in Section 3—“Real world case study” of the main manuscript.
| Month | Type | Mean (μ) | Variance (σ2) | Skewness (Cs) | Autocorrelation (ρ1) |
|---|---|---|---|---|---|
| January | Historical | 167.89 | 33,973.86 | 3.89 | 0.69 |
| Simulated | 166.12 | 35,044.58 | 3.92 | 0.70 | |
| February | Historical | 179.50 | 32,317.25 | 3.95 | 0.66 |
| Simulated | 177.10 | 32,538.62 | 4.28 | 0.66 | |
| March | Historical | 172.07 | 13,773.37 | 2.69 | 0.75 |
| Simulated | 173.37 | 13,608.23 | 2.68 | 0.75 | |
| April | Historical | 172.47 | 10,253.59 | 4.04 | 0.74 |
| Simulated | 171.62 | 10,502.08 | 4.28 | 0.74 | |
| May | Historical | 107.83 | 4055.14 | 2.29 | 0.77 |
| Simulated | 110.20 | 4368.32 | 2.31 | 0.77 | |
| June | Historical | 50.86 | 591.95 | 1.59 | 0.64 |
| Simulated | 51.26 | 604.55 | 1.58 | 0.63 | |
| July | Historical | 31.13 | 177.42 | 2.19 | 0.45 |
| Simulated | 31.06 | 176.04 | 2.17 | 0.45 | |
| August | Historical | 24.00 | 96.04 | 2.41 | 0.47 |
| Simulated | 23.96 | 94.83 | 2.35 | 0.47 | |
| September | Historical | 24.86 | 492.39 | 5.99 | 0.63 |
| Simulated | 24.42 | 432.84 | 5.57 | 0.63 | |
| October | Historical | 51.77 | 8883.06 | 6.70 | 0.60 |
| Simulated | 50.71 | 7905.46 | 6.26 | 0.60 | |
| November | Historical | 114.63 | 24,332.88 | 3.49 | 0.61 |
| Simulated | 111.69 | 23,039.17 | 3.63 | 0.61 | |
| December | Historical | 197.14 | 68,785.55 | 4.87 | 0.62 |
| Simulated | 193.85 | 63,948.33 | 4.53 | 0.61 |
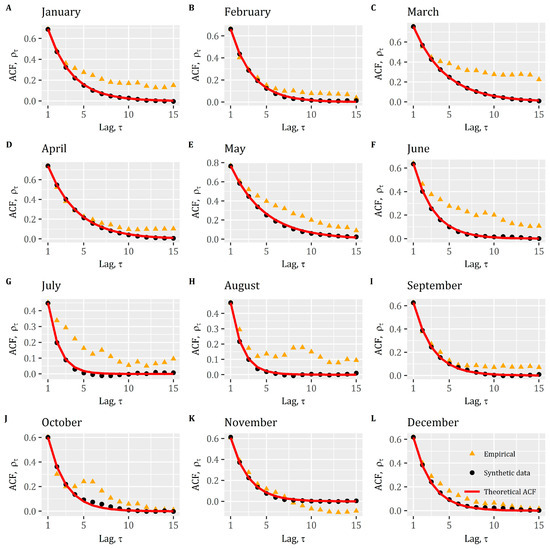
Figure A2.
Monthly-based comparison of empirical (historical), synthetic (using AR(1) with III white noise), and theoretical autocorrelation functions (ACFs) of the real-world case study employed in Section 3—“Real-world case study” of the main manuscript.
References
- Box, G.E.P.; Draper, N.R. Empirical Model-Building and Response Surfaces; Wiley: New York, NY, USA, 1987; Volume 424, p. 74. [Google Scholar]
- Maass, A.; Hufschmidt, M.M.; Dorfman, R.; Thomas, H.A.; Marglin, S.A.; Fair, G.M.; Bower, B.T.; Reedy, W.W.; Manzer, D.F.; Barnett, M.P. Design of Water-Resource Systems; Harvard University Press: Cambridge, UK, 1962. [Google Scholar]
- Fiering, B.; Jackson, B. Synthetic Streamflows (Water Resources Monograph); American Geophysical Union: Washington, DC, USA, 1971; Volume 1, ISBN 0-87590-300-2. [Google Scholar]
- Thomas, H.A.; Fiering, M.B. Mathematical synthesis of streamflow sequences for the analysis of river basins by simulation. In Design of Water Resources-Systems; Harvard University Press: Cambridge, UK, 1962; pp. 459–493. [Google Scholar]
- Fiering, M.B. Streamflow Synthesis; Harvard University Press: Cambridge, UK, 1967; p. 139. [Google Scholar]
- Jackson, B.B. The use of streamflow models in planning. Water Resour. Res. 1975, 11, 54–63. [Google Scholar] [CrossRef]
- Matalas, N.C. Mathematical assessment of synthetic hydrology. Water Resour. Res. 1967, 3, 937–945. [Google Scholar] [CrossRef]
- Hirsch, R.M. Synthetic hydrology and water supply reliability. Water Resour. Res. 1979, 15, 1603–1615. [Google Scholar] [CrossRef]
- Klemeš, V. Water storage: Source of inspiration and desperation. In Reflections on Hydrology: Science and Practice; American Geophysical Union: Washington, DC, USA, 1997; pp. 286–314. ISBN 9781118668085. [Google Scholar]
- Loucks, D.P.; van Beek, E. An Introduction to Probability, Statistics, and Uncertainty. In Water Resource Systems Planning and Management; Springer: Berlin, Germany, 2017; pp. 213–300. [Google Scholar]
- Kottegoda, N.T. Stochastic Water Resources Technology; Palgrave Macmillan: London, UK, 1980; ISBN 1349034673. [Google Scholar]
- Reddy, P.J.R. Stochastic Hydrology; Laxmi Publications, Ltd.: New Delhi, India, 1997; ISBN 817008086X. [Google Scholar]
- Bras, R.L.; Rodríguez-Iturbe, I. Random Functions and Hydrology; Addison-Wesley, Reading, Mass: Boston, MA, USA, 1985; ISBN 0486676269. [Google Scholar]
- Salas, J.D. Analysis and modeling of hydrologic time series. In Handbook of Hydrology; Maidment, D.R., Ed.; Mc-Graw-Hill, Inc.: New York, NY, USA, 1993; pp. 19.1–19.72. [Google Scholar]
- Hipel, K.W.; McLeod, A.I. Time Series Modelling of Water Resources and Environmental Systems; Elsevier: New York, NY, USA, 1994; Volume 45, ISBN 0080870368. [Google Scholar]
- Salas, J.D.; Pielke, R. A Stochastic characteristics modeling of hydroclima tic processes. In Handbook of Weather, Climate, and Water: Atmospheric Chemistry, Hydrology, and Societal Impact; Potter, T., Colman, B., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 2, pp. 587–605. ISBN 0471214892. [Google Scholar]
- Thomas, H.A.; Fiering, M.B. The nature of the storage yield function. In Operations Research in Water Quality Management; Harvard University Water Program: Cambridge, MA, USA, 1963. [Google Scholar]
- Thomas, H.A.; Burden, R.P. Operations Research in Water Quality Management; Division of Engineering and Applied Physics, Harvard University: Cambridge, MA, USA, 1963. [Google Scholar]
- Adeloye, A.J.; Soundharajan, B.-S.; Musto, J.N.; Chiamsathit, C. Stochastic assessment of Phien generalized reservoir storage–yield–probability models using global runoff data records. J. Hydrol. 2015, 529, 1433–1441. [Google Scholar] [CrossRef]
- McMahon, T.A.; Miller, A.J. Application of the Thomas and Fiering Model to Skewed Hydrologic Data. Water Resour. Res. 1971, 7, 1338–1340. [Google Scholar] [CrossRef]
- Montaseri, M.; Amirataee, B.; Nawaz, R. A Monte Carlo Simulation-Based Approach to Evaluate the Performance of three Meteorological Drought Indices in Northwest of Iran. Water Resour. Manag. 2017, 31, 1323–1342. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Dialynas, Y.G.; Kozanis, S.; Koutsoyiannis, D. A multivariate stochastic model for the generation of synthetic time series at multiple time scales reproducing long-term persistence. Environ. Model. Softw. 2014, 62, 139–152. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Optimal decomposition of covariance matrices for multivariate stochastic models in hydrology. Water Resour. Res. 1999, 35, 1219–1229. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Onof, C.; Wheater, H.S. Multivariate rainfall disaggregation at a fine timescale. Water Resour. Res. 2003, 39, 1–62. [Google Scholar] [CrossRef]
- Vogel, R.M.; Stedinger, J.R. The value of stochastic streamflow models in overyear reservoir design applications. Water Resour. Res. 1988, 24, 1483–1490. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Manetas, A. Simple disaggregation by accurate adjusting procedures. Water Resour. Res. 1996, 32, 2105–2117. [Google Scholar] [CrossRef]
- Unal, N.E.; Aksoy, H.; Akar, T. Annual and monthly rainfall data generation schemes. Stoch. Environ. Res. Risk Assess. 2004, 18. [Google Scholar] [CrossRef]
- Kim, U.; Kaluarachchi, J.J.; Smakhtin, V.U. Generation of Monthly Precipitation Under Climate Change for the Upper Blue Nile River Basin, Ethiopia. J. Am. Water Resour. Assoc. 2008, 44, 1231–1247. [Google Scholar] [CrossRef]
- Jothiprakash, V.; Shanthi, G. Comparison of Policies Derived from Stochastic Dynamic Programming and Genetic Algorithm Models. Water Resour. Manag. 2009, 23, 1563–1580. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. A generalized mathematical framework for stochastic simulation and forecast of hydrologic time series. Water Resour. Res. 2000, 36, 1519–1533. [Google Scholar] [CrossRef]
- O’Connell, P.E. Stochastic Modelling of Long-Term Persistence in Streamflow Sequences. Ph.D. Thesis, University of London, London, UK, 1974. [Google Scholar]
- Lawrance, A.J.; Kottegoda, N.T. Stochastic Modelling of Riverflow Time Series. J. R. Stat. Soc. Ser. A 1977, 140, 1. [Google Scholar] [CrossRef]
- Tsoukalas, I.; Efstratiadis, A.; Makropoulos, C. Stochastic Periodic Autoregressive to Anything (SPARTA): Modeling and Simulation of Cyclostationary Processes with Arbitrary Marginal Distributions. Water Resour. Res. 2018, 54, 161–185. [Google Scholar] [CrossRef]
- Lombardo, F.; Volpi, E.; Koutsoyiannis, D.; Papalexiou, S.M. Just two moments! A cautionary note against use of high-order moments in multifractal models in hydrology. Hydrol. Earth Syst. Sci. 2014, 18, 243–255. [Google Scholar] [CrossRef]
- Papalexiou, S.M. Stochastic modelling of skewed data exhibiting long-range dependence. In XXIV General Assembly of the International Union of Geodesy and Geophysics; Umbria Scientific Meeting Association: Perugia, Italy, 2007. [Google Scholar]
- Moschopoulos, P.G. The distribution of the sum of independent gamma random variables. Ann. Inst. Stat. Math. 1985, 37, 541–544. [Google Scholar] [CrossRef]
- Matalas, N.C.; Wallis, J.R. Generation of Synthetic Flow Sequences, Systems Approach to Water Management; Biswas, A.K., Ed.; McGraw-Hill: New York, NY, USA, 1976; p. 66. [Google Scholar]
- Lettenmaier, D.P.; Burges, S.J. An operational approach to preserving skew in hydrologic models of long-term persistence. Water Resour. Res. 1977, 13, 281–290. [Google Scholar] [CrossRef]
- Todini, E. The preservation of skewness in linear disaggregation schemes. J. Hydrol. 1980, 47, 199–214. [Google Scholar] [CrossRef]
- Pegram, G.G.S.; James, W. Multilag multivariate autoregressive model for the generation of operational hydrology. Water Resour. Res. 1972, 8, 1074–1076. [Google Scholar] [CrossRef]
- Camacho, F.; McLeod, A.I.; Hipel, K.W. Contemporaneous autoregressive-moving average (CARMA) modeling in water resources. J. Am. Water Resour. Assoc. 1985, 21, 709–720. [Google Scholar] [CrossRef]
- Higham, N.J. Computing the nearest correlation matrix--a problem from finance. IMA J. Numer. Anal. 2002, 22, 329–343. [Google Scholar] [CrossRef]
- Obeysekera, J.T.B.; Yevjevich, V. A Note on Simulation of Samples of Gamma-Autoregressive Variables. Water Resour. Res. 1985, 21, 1569–1572. [Google Scholar] [CrossRef]
- Kirby, W. Computer-oriented Wilson-Hilferty transformation that preserves the first three moments and the lower bound of the Pearson type 3 distribution. Water Resour. Res. 1972, 8, 1251–1254. [Google Scholar] [CrossRef]
- Song, W.T.; Hsiao, L.C.; Chen, Y.J. Generating pseudo-random time series with specified marginal distributions. Eur. J. Oper. Res. 1996, 94, 194–202. [Google Scholar] [CrossRef]
- Jeong, C.; Lee, T. Copula-based modeling and stochastic simulation of seasonal intermittent streamflows for arid regions. J. Hydro-Environ. Res. 2015, 9, 604–613. [Google Scholar] [CrossRef]
- Gaver, D.P.; Lewis, P.A.W. First-order autoregressive gamma sequences and point processes. Adv. Appl. Probab. 1980, 12, 727–745. [Google Scholar] [CrossRef]
- Lawrance, A.J.; Lewis, P.A.W. Generation of Some First-Order Autoregressive Markovian Sequences of Positive Random Variables with Given Marginal Distributions; Naval Postgraduate School: Monterey, CA, USA, 1981. [Google Scholar]
- Lawrance, A.J.; Lewis, P.A.W. A new autoregressive time series model in exponential variables (NEAR (1)). Adv. Appl. Probab. 1981, 13, 826–845. [Google Scholar] [CrossRef]
- Fernandez, B.; Salas, J.D. Periodic Gamma Autoregressive Processes for Operational Hydrology. Water Resour. Res. 1986, 22, 1385–1396. [Google Scholar] [CrossRef]
- Anscombe, F.J. Graphs in Statistical Analysis. Am. Stat. 1973, 27, 17–21. [Google Scholar] [CrossRef]
- Matejka, J.; Fitzmaurice, G. Same stats, different graphs: Generating datasets with varied appearance and identical statistics through simulated annealing. In Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems, Denver, CO, USA, 6–11 May 2017; ACM: New York, NY, USA, 2017; pp. 1290–1294. [Google Scholar]
- Sklar, M. Fonctions de repartition an dimensions et leurs marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Sklar, A. Random variables, joint distribution functions, and copulas. Kybernetika 1973, 9, 449–460. [Google Scholar]
- De Michele, C.; Salvadori, G. A Generalized Pareto intensity-duration model of storm rainfall exploiting 2-Copulas. J. Geophys. Res. 2003, 108, 4067. [Google Scholar] [CrossRef]
- Favre, A.; El Adlouni, S.; Perreault, L.; Thiémonge, N.; Bobée, B. Multivariate hydrological frequency analysis using copulas. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. On the Use of Copulas in Hydrology: Theory and Practice. J. Hydrol. Eng. 2007, 12, 369–380. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.-C. Everything you always wanted to know about copula modeling but were afraid to ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P.; Asce, F. Using the Copula Method. Water 2006, 11, 150–164. [Google Scholar]
- Wang, Y.; Li, C.; Liu, J.; Yu, F.; Qiu, Q.; Tian, J.; Zhang, M. Multivariate Analysis of Joint Probability of Different Rainfall Frequencies Based on Copulas. Water 2017, 9, 198. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Gumbel–Hougaard Copula for Trivariate Rainfall Frequency Analysis. J. Hydrol. Eng. 2007, 12, 409–419. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Frequency analysis via copulas: Theoretical aspects and applications to hydrological events. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Review of dependence modeling in hydrology and water resources. Prog. Phys. Geogr. 2016, 40, 549–578. [Google Scholar] [CrossRef]
- Serinaldi, F. A multisite daily rainfall generator driven by bivariate copula-based mixed distributions. J. Geophys. Res. 2009, 114, D10103. [Google Scholar] [CrossRef]
- Gyasi-Agyei, Y. Copula-based daily rainfall disaggregation model. Water Resour. Res. 2011, 47, 1–17. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Modeling multisite streamflow dependence with maximum entropy copula. Water Resour. Res. 2013, 49, 7139–7143. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G. Copula based multisite model for daily precipitation simulation. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 4485–4534. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S.; Zhou, J.; Zhang, J. Copula-based method for multisite monthly and daily streamflow simulation. J. Hydrol. 2015, 528, 369–384. [Google Scholar] [CrossRef]
- Lee, T.; Salas, J.D. Copula-based stochastic simulation of hydrological data applied to Nile River flows. Hydrol. Res. 2011, 42, 318–330. [Google Scholar] [CrossRef]
- Lee, T. Multisite stochastic simulation of daily precipitation from copula modeling with a gamma marginal distribution. Theor. Appl. Climatol. 2017. [Google Scholar] [CrossRef]
- Nataf, A. Statistique mathematique-determination des distributions de probabilites dont les marges sont donnees. C. R. Acad. Sci. Paris 1962, 255, 42–43. [Google Scholar]
- Lebrun, R.; Dutfoy, A. An innovating analysis of the Nataf transformation from the copula viewpoint. Probabilistic Eng. Mech. 2009, 24, 312–320. [Google Scholar] [CrossRef]
- Cario, M.C.; Nelson, B.L. Autoregressive to anything: Time-series input processes for simulation. Oper. Res. Lett. 1996, 19, 51–58. [Google Scholar] [CrossRef]
- Biller, B.; Nelson, B.L. Modeling and generating multivariate time-series input processes using a vector autoregressive technique. ACM Trans. Model. Comput. Simul. 2003, 13, 211–237. [Google Scholar] [CrossRef]
- Tsoukalas, I.; Efstratiadis, A.; Makropoulos, C. Stochastic simulation of periodic processes with arbitrary marginal distributions. In Proceedings of the 15th International Conference on Environmental Science and Technology, CEST 2017, Rhodes, Greece, 31 August–2 September 2017. [Google Scholar]
- Tsoukalas, I.; Makropoulos, C.; Koutsoyiannis, D. Simulation of stochastic processes exhibiting any-range dependence and arbitrary marginal distributions. 2018; submitted. [Google Scholar]
- Papalexiou, S.M. Unified theory for stochastic modelling of hydroclimatic processes: Preserving marginal distributions, correlation structures, and intermittency. Adv. Water Resour. 2018. [Google Scholar] [CrossRef]
- Serinaldi, F.; Lombardo, F. BetaBit: A fast generator of autocorrelated binary processes for geophysical research. Europhys. Lett. 2017, 118, 30007. [Google Scholar] [CrossRef]
- Blum, A.G.; Archfield, S.A.; Vogel, R.M. On the probability distribution of daily streamflow in the United States. Hydrol. Earth Syst. Sci. 2017, 21, 3093–3103. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. A global survey on the seasonal variation of the marginal distribution of daily precipitation. Adv. Water Resour. 2016, 94, 131–145. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Uncertainty, entropy, scaling and hydrological stochastics. 1. Marginal distributional properties of hydrological processes and state scaling/Incertitude, entropie, effet d’échelle et propriétés stochastiques hydrologiques. 1. Propriétés distributionnel. Hydrol. Sci. J. 2005, 50, 381–404. [Google Scholar] [CrossRef]
- McMahon, T.A.; Vogel, R.M.; Peel, M.C.; Pegram, G.G.S. Global streamflows—Part 1: Characteristics of annual streamflows. J. Hydrol. 2007, 347, 243–259. [Google Scholar] [CrossRef]
- Kroll, C.N.; Vogel, R.M. Probability Distribution of Low Streamflow Series in the United States. J. Hydrol. Eng. 2002, 7, 137–146. [Google Scholar] [CrossRef]
- Bowers, M.C.; Tung, W.W.; Gao, J.B. On the distributions of seasonal river flows: Lognormal or power law? Water Resour. Res. 2012, 48, 1–12. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. Entropy based derivation of probability distributions: A case study to daily rainfall. Adv. Water Resour. 2012, 45, 51–57. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).