The Evolution of Protein Structures and Structural Ensembles Under Functional Constraint
Abstract
: Protein sequence, structure, and function are inherently linked through evolution and population genetics. Our knowledge of protein structure comes from solved structures in the Protein Data Bank (PDB), our knowledge of sequence through sequences found in the NCBI sequence databases ( http://www.ncbi.nlm.nih.gov/), and our knowledge of function through a limited set of in-vitro biochemical studies. How these intersect through evolution is described in the first part of the review. In the second part, our understanding of a series of questions is addressed. This includes how sequences evolve within structures, how evolutionary processes enable structural transitions, how the folding process can change through evolution and what the fitness impacts of this might be. Moving beyond static structures, the evolution of protein kinetics (including normal modes) is discussed, as is the evolution of conformational ensembles and structurally disordered proteins. This ties back to a question of the role of neostructuralization and how it relates to selection on sequences for functions. The relationship between metastability, the fitness landscape, sequence divergence, and organismal effective population size is explored. Lastly, a brief discussion of modeling the evolution of sequences of ordered and disordered proteins is entertained.1. Introduction
The links between gene sequence, protein structure, and biological function are central to the development of a mechanistic understanding of molecular and cellular biological processes. Further, from an evolutionary perspective, changes in gene sequences, as filtered by protein structure and function, can drive phenotypic change through neutral and adaptive mechanisms. Selection can ultimately occur at the level of the fitness of the individual organism, filtered through the lens of cell biology down to the level of protein function, structure, and sequence. Not all proteins contribute equally to organismal fitness. The generation of high throughput genomic, proteomic, and structural datasets has enabled molecular evolutionary analysis of functional data. Ultimately, an understanding of the interplay of protein structure with both sequence evolution and functional/phenotypic evolution is necessary. This review will depict this understanding from several key perspectives.
2. Protein Structure Space
The nature of protein structure space is an important starting point for characterizing the link between sequence, structure, and function. Knowing how well protein structure space has been characterized (the degree to which the sampling is complete) is a necessary prerequisite for, understanding how it has evolved, the constraints on its evolution, and the constraints that it (and evolutionarily accessible alternatives) place on sequences and functions.
That protein structure is more conserved than sequence is a common perception among molecular life scientists. This is based upon an observation of the experimentally determined protein structures in the Protein Data Bank (PDB). However, if we remove the 100% identical proteins from PDB, we are left with about 40,000 PDB structures. If we compare that to the number of protein sequences in the RefSeq database (currently >10 million protein sequences), it is clear that our current knowledge of protein structure space is derived from a very small subset of proteins. This is especially true if it is the case that structure can vary among homologous proteins from different species with correspondingly more variation in structure than is sometimes appreciated. It is known that the protein composition of PDB is biased [1]. Membrane proteins and structurally disordered proteins are underrepresented in PDB and many proteins are modified (truncated and/or mutated) in order to facilitate crystal formation. Some proteins in fact show the hallmarks of crystal packing forces in their structures that cannot reasonably be expected to reflect that stable structure in solution [2]. There are also biases in the function, subcellular localization and protein coverage in PDB [1].
Despite these caveats, there are a lot of important data and trends to be found in the PDB. Protein structure classification, for instance CATH [3], further characterizes most multidomain structures in PDB at the domain level, as the domain is commonly regarded to be the smallest functional unit that can fold by itself. CATH currently has almost 1,300 different topologies or folds, some of which are used much more frequently than other folds. However, while this data is focused on the domain level, it misses structural organization at the multidomain level. Many multidomain proteins contain linker sequences between domains and the structural flexibility of these linkers has informational value for our understanding of the extended protein structure space. If we can estimate the extent of structural flexibility between domains, it would certainly add to the current understanding of how protein structures evolve on the tertiary and quaternary structural levels. Not only could intra-chain domain-domain packing be affected in the tertiary structure, but also inter-chain domain-domain packing can be affected in (for instance) the case of domain swaps. These studies are likely to increase our understanding of how domain-domain crosstalk and allostery evolve, which can improve current methods for homology modeling of multidomain complexes and correspondingly, our understanding of the evolution of protein function, interaction, and regulation.
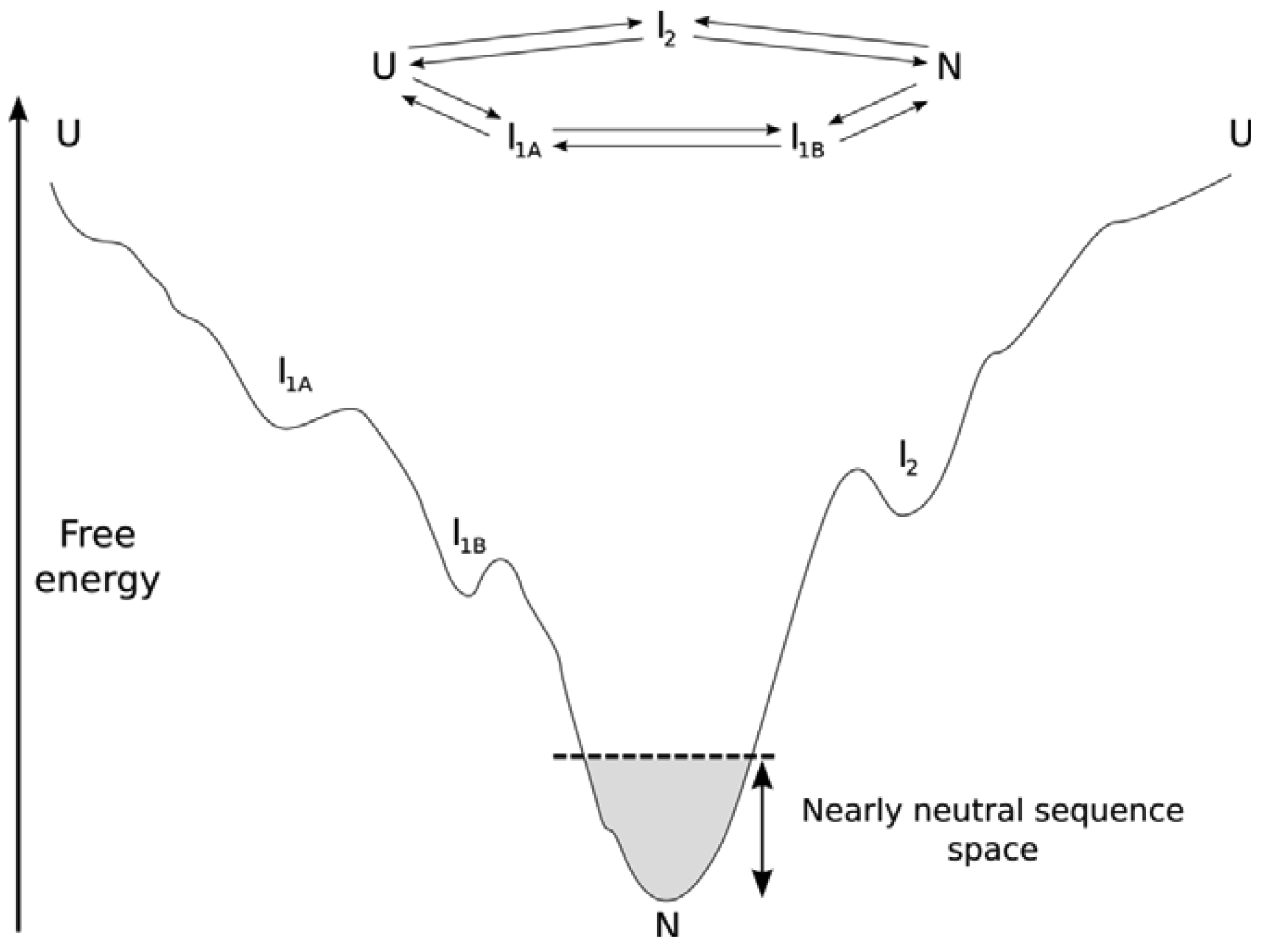
Focusing on the PDB as our source for protein structure information may lead us to a skewed view of protein structure space. From a structural rather than a functional perspective, proteins that rarely make it into the PDB simply because they are too dynamic are systematically missed. Due to the nature of the energy landscape (the relative energies of different conformations and ultimately different sequences in different conformations, see Figure 1), these are the proteins that exist in rapidly exchanging conformations and that may only progress down the folding funnel towards a stable conformation after being either post-translationally modified or when interacting with a binding partner. These proteins are commonly referred to as structurally disordered. Structurally disordered proteins can be fully or partially disordered, and what is intriguing about these proteins is their presence as a conformational ensemble that kinetically interconverts on cellular timescales. Here we cannot simply say that protein structure is more conserved than sequence because a mutation in the conformational ensemble is likely to shift the equilibrium of the conformational ensembles. Hence, the evolution of structurally disordered proteins may lead to non-conserved protein structures among homologs through this shift in the conformational ensemble. We call this phenomenon neostructuralization [4]. Starting with the structurally ordered proteins, we will attempt to systematically describe our understanding of how proteins evolve. As our understanding of protein sequence-structure links and the intertwining roles of physical chemistry and evolution improves, key aspects of our knowledge based on protein structural evolution may need revision.
3. Evolution of Structurally Ordered Proteins
Structured domains are characterized by a large proportion of secondary structure, as well as a single hydrophobic core and mostly hydrophilic surface. Distinct regions of non-enzymatic proteins with different evolutionary properties include the hydrophilic surface, the hydrophobic core, and more hydrophobic surface binding interfaces involved in protein-protein interaction. These regions show different rates of amino acid substitution, with the hydrophobic core evolving more slowly than the hydrophilic surface [5]. Quantitatively, core residues evolve up to 10x slower than surface residues [6], and include residues that are the most informative for determining the topology of the native fold [7]. In fact, rates of evolution correlate strongly with fractional residue burial [8]. Within protein families, backbone change in the core increases very slowly [9], mostly preserving the characteristic topology of the fold over relatively long evolutionary distances. Single substitutions are generally accommodated by side chain packing [10]. The structure dictates the inter-residue interactions that occur and the thermodynamic intramolecular coupling of substitutions is detectable from evolutionary data [11], leading to the use of contact maps and viewing proteins in a network context [12]. For proteins with a binding function, the binding interface is under functional constraint and may evolve the slowest, with differences in rate between affinity-determining and specificity-determining residues [13]. Different secondary structural elements also show different rates of evolution, with beta-sheet regions evolving more slowly than helical regions, and with random coil regions evolving fastest [5,14]. Beyond secondary structure, this may be influenced by differences in relative burial between different elements. In addition to point substitutions, insertion and deletion events (indels) also occur at varying rates [15].
While it sometimes supposed that Hidden Markov Model (HMM) emission probabilities from Pfam [16] reflect the allowed nature of sequence divergence within a structure and describe aspects of allowable sequences within structures, these have been generated without consideration of the phylogenetic scale on which sequences have been diverging. Kondrashov [17] has suggested that explored sequence space within folds of real proteins is still expanding. Consistent with this, evolutionary simulation imply that there are many sequences that have not been observed that can fold into a given known structure [18,19]. This is also consistent with observations from protein design [20–22]. These views may necessitate revision of our understanding of the uniqueness of superfolds and related concepts of designability, leading to alternative hypotheses for fold distributions rooted in evolutionary and population genetic processes [23–25].
For the subset of proteins that form a stable unique tertiary structure, the thermodynamic stability (ΔG) of the protein in the context of a folding funnel is important [26] (see Figure 1). It is therefore maintained throughout evolution despite the average destabilizing effect of non-synonymous mutations [27–29]. Proteins are only marginally stable, with a free-energy change of a few kcal/mol upon folding [30]. This has been attributed to population-level neutral processes, where there is more power to select for a larger energy gap in larger population species (organisms) or when there is a strong selective advantage to do so (as in hyperthermophiles) [31,32], or alternatively to functional requirements for protein flexibility [33]. To overcome the Levinthal Paradox, distal parts of the energy landscape must be gently sloping towards the native structure(s). However, the metastability of the folded structure relative to alternative folded structures combined with dN/dS data suggesting strong negative selection on the average protein against the average mutation [5] suggests that the local funnel near the native state is more rugged from a mutational perspective through evolution than other parts of the landscape, with allowable mutations forming a neutral network. Ultimately, structure is important as a scaffold for properly orienting functional residues (for example, a binding interface, catalytic residues, or a pore). Consequently, there is little selective pressure for particular sequences within a given structure over longer evolutuionary periods, generating a neutral network of sequences connected by those accessible through the mutational process. Folds with excess ΔG are thought to possess more potential for neofunctionalization (and gene family expansion [30,34–36]. But as expected from nearly-neutral theory [37], the majority of mutations are either deleterious or neutral rather than adaptive, both in terms of ΔG and fitness [27,29,38–40]. Compensatory mutation can play a selective role within nearly neutral sequence networks, whereby a deleterious mutation makes a subsequent otherwise neutral change selectively advantageous [9].
The processes described above can lead to structural transitions through two different processes. Within a neutral network that is functional, there may be multiple structural states that can exist. It is unclear that there is always a selective pressure for an energy gap near the native structure(s), especially in the case that closely related structures are functionally equivalent. Changes in secondary structure content after residue substitutions can occur due to varying helix/sheet propensity, with sheets being more plastic [5,14]. Some of these changes in secondary structural composition are likely to be evolutionarily neutral. A second mode of structural transition involves positive selection. In this case, a new fold that is mutationally accessible may enable the development of a new function that was not possible within the previous fold.
This raises an interesting question: is protein structure space continuous or discrete in enabling evolutionary transitions between distinct folds? A variety of measures of structural similarity have been applied to construct maps of protein structure space [41–43]. These maps consistently show highly populated regions roughly corresponding to the Class level of SCOP [43–45], and smaller clusters corresponding to the presumably homologous Superfamily level [43]. Depending on the algorithms and graph-theoretical measures employed, different groups have argued that this space is fully connected [42] or highly fragmented [43]. However, mechanistically protein evolution does not proceed via jumps in structural space/geometry as it is sometimes modeled, but via small changes in sequence space and the mapping between structural hierarchies and mutation-based hierarchies is unclear. While circular permutation and other larger scale mutational re-arrangements have been observed [46], the important consideration is that fold transitions occur through the mutational process at the sequence level rather than geometrically at the structural level as it is sometimes modeled. To rigorously evaluate the possibility of a fold transition one would have to determine the viability of a series of mutations that connect the two folds. Both thermodynamics and kinetics of folding must be taken into account, as well as fitness effects due to function, all within in a context of population genetics.
4. Evolution of Protein Folding Pathways
In addition to a unique and stable native state, structured proteins also have pathways through which they rapidly fold. In some cases, the folding pathway has been shown to affect the final structure that the sequence folds into, meaning that the folding pathway can be important to the ultimate fold and therefore the ultimate biological function (for example, [47]). It is only to the extent that folding pathway effects structure and ultimately function that it is evolutionarily important. Folding pathways do also have an important role in preventing aggregation, with proper folding driven at least partly by hydrophobic collapse. With these views in mind, the conservation of folding pathways is described.
The intermediates in the folding pathway are known to be conserved for some homologous proteins [48]. The correlation between native state contact order and folding kinetics [49] further suggests that the native state topology is the main evolutionary determinant of the folding pathway. A number of studies [50,51] subsequently showed that folding pathways are partially, but not fully, conserved in homologs of single-domain proteins. Folded subdomains (folding nuclei or foldons) can be strongly conserved, particularly if they define an intermediate or transition state late in the pathway [52,53]. However, even very small proteins appear to have multiple parallel pathways and intermediates [53,54], and the flux through each pathway can change appreciably after mutation [52,55,56]. Earlier stages of folding appear to be less conserved than later stages [57]. Variability in the ruggedness of the energy landscape containing a folding funnel [26] depending upon distance from the native state can explain these observations. In the early stages of folding, the funnel is very wide and multiple pathways may lead into it over a variety of transition states. As the bottom of the funnel is approached (for the classic funnel model with a single minimum), the width (i.e., number of available conformations) shrinks and fewer pathway options exist for proteins with a single native state. Additionally, as the number of native contacts increases, the choice of pathways becomes increasingly dominated by the topology of the native state, including specific residue contacts [50,58]. The early and intermediate conformations are stabilized by various non-native contacts, which do not contribute to the stability of the fully folded state and are therefore under less selective pressure to be maintained within a fold if they are not necessary for proper folding. Ultimately, the shape of the folding funnel near the folded conformation and towards the edges of the native sequence landscape in the context of marginal stability is an open question, as is the existence of divergent structures dependent upon folding pathway for some protein families.
5. Evolution of Conformational Ensembles and of Protein Dynamics
Given the potential continuity of fold space and of the underlying sequence space, it is clear that proteins can exist in conformational ensembles, both functionally and as evolutionary transitions. Beyond thermodynamic considerations of conformational ensembles is the role of kinetics in protein structure and function. This section will focus on the motion of individual proteins.
As a neutral baseline, Illergard et al. [6] established an approximately linear divergence between the rate of sequence evolution and of structural divergence measured by structural root mean square deviation (RMSD) evolution for static structures. There is a relationship between the lowest energy normal modes and the paths through which protein structure diverges through mutational opportunity [59]. Further, it has been established that the lowest normal modes also evolved with approximate rate of divergence proportionality to the structural divergence hierarchy [60,61]. Deviations from this clock-like rate may be expected to show a functional signal that may evolve particularly rapidly under processes like positive selective pressure. The hypothesis, then, is that rate accelerations in normal mode divergence may be useful in predicting functional divergence.
A confounding factor is the role of post-translational modification in modifying thermodynamic and kinetic conformational ensemble stabilities, especially as patterns of post-translational modification can evolve rapidly on evolutionary timescales. As will be discussed further below, post-translational modification can alter the equilibrium in a conformational ensemble and may therefore play a more major role than is commonly attributed in protein structure determination. From an evolutionary perspective, selection on folding stability and pathway may interplay with selection on sites for post-translational modification.
Given that ensembles of structures can play functional roles and can be found as either evolutionary intermediates or as evolutionarily stable functional proteins, the question emerges, how do these proteins that are disordered or in rapidly shifting equilibria between ordered structures evolve?
6. Evolution of Structurally Disordered Proteins
Study of the evolution of structurally disordered proteins is in its infancy. It has been predicted that the fraction of structurally disordered protein increases with organismal complexity [62], but why is unclear. This may be linked to the increase in the frequency of multidomain proteins with organismal complexity [63,64]. An increase in multidomain proteins also means more domain spacers or linkers, which often are structurally flexible. More fundamentally, more complex organisms (as defined by the number of distinct cell types) tend to have smaller population sizes and reduced strengths of selection. A null hypothesis for the rise of disorder in these lineages might simply be a reduction in the strength of selection along these lineages, including on proper protein folding [65]. To reject this hypothesis, we would need to detect selectable functions in disordered proteins that cannot be accomplished by ordered proteins. Fundamentally, we would also need to account for the ability to select for these features in evolutionary regimes where selection has less power, such as in small population size multicellular animals.
To understand how structural disorder evolves and if it is conserved or not, one needs to study the evolutionary dynamics of disordered regions in the phylogenetic context of homologous proteins. Studies of this kind are scarce, but it appears that structural order and disorder, as well as underlying secondary structural propensities, are conserved in some homologs, but not all [4]. For example, patterns of disorder, like other evolutionary features, appear more likely to shift among paralogs than among orthologs [4]. Further studies are needed to characterize these trends in greater detail. Like structured proteins, different structurally disordered proteins evolve at different rates, although there is a tendency for structurally disordered regions to evolve at higher amino acid substitution rates than structured proteins [66–68]. A recent effort to calculate a disordered protein specific substitution matrix also shows that specific matrices for these proteins can be generated [69] but unfortunately, the generality of such matrices is dependent upon the conservation of selective pressures within disordered regions and the conservation of disorder itself.
If we view proteins from the perspective of the folding energy landscape, the conformational dynamics vary from globular proteins with a well-defined global minimum to those that are present as highly dynamic ensembles of interconverting conformational states separated by low energy barriers, such as the structurally disordered proteins [70]. Structurally disordered proteins are prone to adopt different conformations (alter the conformational ensemble) in different environments and indeed structurally disordered regions show high conformational flexibility over different timescales and ranges of motion. Different conformational states are favored in interactions with different structural scaffolds and post-translational modifications are often involved in regulating conformational ensembles. As the structurally disordered proteins are characterized as conformational ensembles interconverting over a flattened energy landscape, mutations are likely to shift the conformational ensemble.
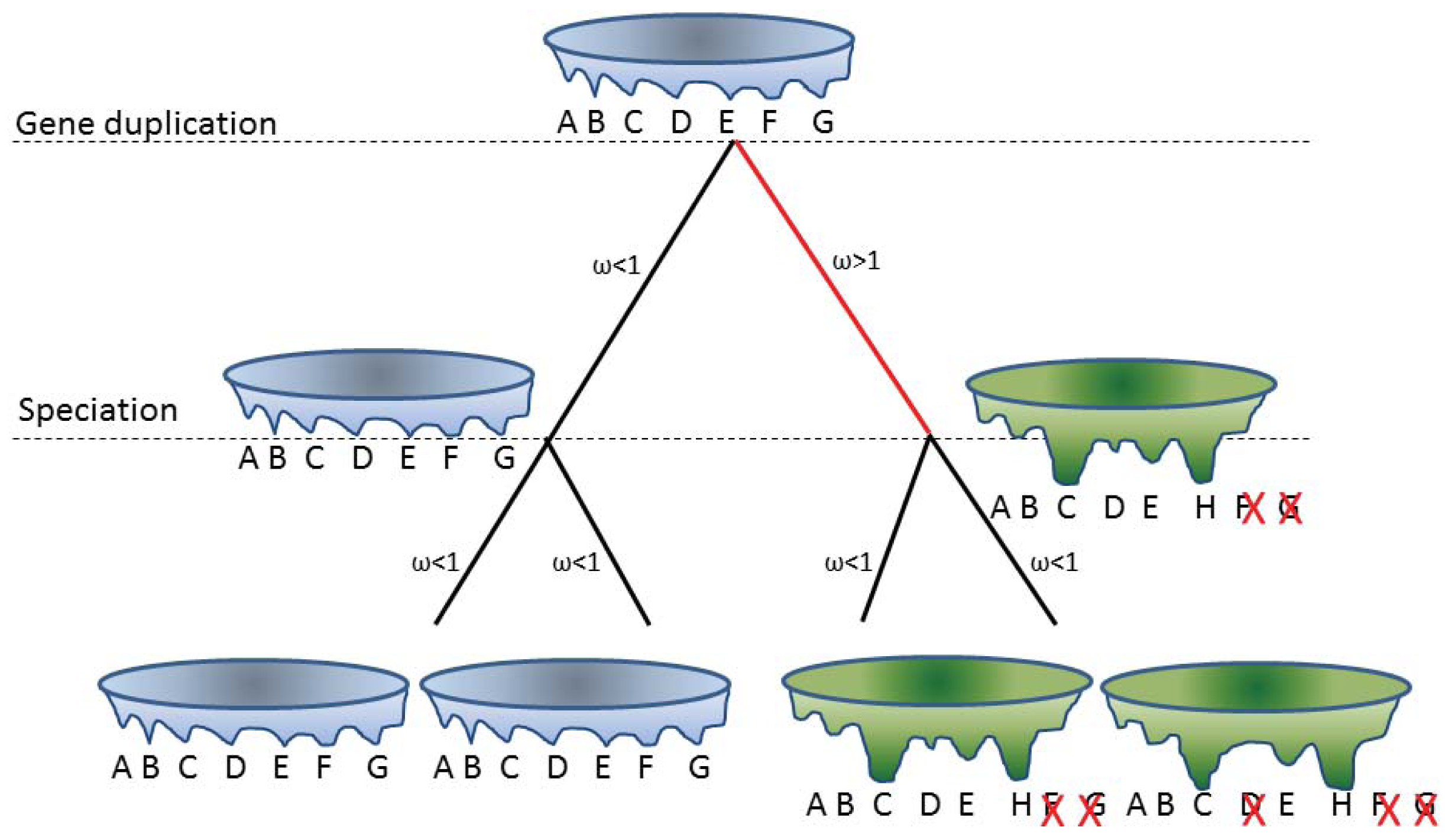
One of the mechanisms for generating novel or partitioned functions is through gene duplications/gene redundancy. It was recently shown that gene retention after gene duplication is higher for genes with many phosphorylation sites [71]. Structurally disordered proteins are enriched in phosphorylation sites and perhaps the thermodynamics of disorder in itself can provide an explanation. For globular structured proteins one main determinant for fixing a mutation is the effect of the mutation on the stability of the protein fold. Structurally disordered proteins are already less stable than the globular protein and exist as interconverting conformational ensembles. Therefore one might expect that these proteins will follow different rules. Here, a certain mutation may not abolish all conformations but simply a subset of the conformational ensemble. On shorter time scales, mutations that affect the equilibrium of the conformational ensemble can be regarded as influencing the function rather than the structure, while on longer time scales large changes in the conformational ensemble from a pair of gene duplicates may no longer overlap and can be regarded as changing the structure or fold. This would reflect a fold transition; a change from one fold or conformational ensemble into a distinctly different fold or conformational ensemble. Hence, structurally disordered proteins (proteins present as conformational ensembles) provide a mechanism for neostructuralization. An example of this concept is illustrated in Figure 2.
7. Designability of Structurally Disordered Proteins
Structurally disordered proteins are present as conformations of very low stability, distributed over a locally flat energy landscape. A mutation is likely to rearrange the conformational equilibrium and hence, mutations can be stabilizing, neutral, and destabilizing for different parts of the conformational ensemble at the same time. A mutation can alter the conformational ensemble, making a subset of conformations essentially unpopulated while functional conformations for which the mutation is stabilizing may gain population. This will result in a new energy landscape. If the new energy landscape is slightly less flat and has a few deeper wells, it could result in mutation driven conformational selection, which explains how structurally disordered proteins or regions can speed up the evolution of the protein structural landscape. Hence mutation driven conformation selection contributes to neostructuralization with different predominant conformations among homologs. Globular structured proteins that maintain their fold despite high sequence divergence have high designability (reviewed in [72]). Structurally disordered proteins evolve at elevated rates compared to many globular proteins [66–68], but does this mean that structural disorder has high designability with functional consequences or does it mean that most substitutions do not change the conformational ensemble significantly and are in fact functionally neutral? Can evolution of structurally disordered proteins provide a mechanism for neutral mutations to drive biological divergence [73]? Structurally disordered proteins are known to have a broad functional spectrum (reviewed in [74]), and this can lead to functional partitions after gene duplication. In a more subtle case, structurally disordered proteins can generate small changes in phenotype by a change in genotype that affects the conformational ensemble. If several conformational ensembles are altered in a small but cooperative manner, it could provide an underlying mechanism for structural divergence driving functional and phenotypic differences.
From an understanding of the evolutionary behavior of ordered and disordered proteins from a biophysical perspective comes the goal of modeling the evolution of proteins with more realistic models.
8. Modeling Evolution of Structurally Ordered Proteins
An overview of methods for modeling of the evolution of structurally ordered proteins has recently been described [24] and will only be summarized here. Two research trajectories have emerged that model the evolution of sequences in structurally ordered regions for evolutionary purposes. Retrospective analysis, particularly in the construction of phylogenetic trees [75–77] is one trajectory, where structural and biophysical considerations are viewed as an integral component of the evolution of proteins over long evolutionary distances and attempts have been made to replace purely statistical models that account for structure with the use of either a gamma distribution or a covarion process [78]. A second trajectory that has emerged is in the forward evolution of proteins, or sequence simulation constrained by a fold that does not vary [18,19].
For both of these trajectories, two classes of models are available, informational and physical models. In informational models, average interaction propensities extracted from PDB are summarized in matrices that reflect informational potentials [79,80]. These models can suffer from a lack of folding specificity [19,75–77]. An alternative is the use of models rooted in the physical principles of inter-atomic or inter-residue interaction. Because of the large number of calculations involved in both forward and retrospective evolutionary analysis, some degree of coarse-graining is necessary. The early physical coarse-grained models appear to be more specific than the informational potentials, but still have barriers to overcome, including a representation of side chains that leads to a properly packed hydrophobic core [19]. Research in these trajectories is ongoing.
9. Modeling Evolution of Structurally Disordered Proteins
One important trajectory will be to extend the models for structurally ordered regions to structurally disordered regions. Structurally disordered regions are functional in two key ways. Some structurally disordered regions become ordered upon binding and function as ordered regions [81]. In this case, the problem is simpler in that the proteins can be simulated as ordered while accounting in the model for the energy associated with the order to disorder transition. This will initially only approximate differences in the energy of this transition for different binding partners that is not reflected in differences in energy accounted for in the modeled ordered state. Nothing along these lines has yet been implemented.
A second class of disordered proteins are those that function as disordered regions [81]. To model such proteins, it will be important to uncover the sequence constraints on their disorder to be functional, as this will reflect a departure from neutrality in evolutionary rate. To the extent that this is a sequence rather than structural constraint, standard Markov Models will likely be appropriate [68]. One pitfall with Markov Models is that they generalize evolutionary properties that may be context dependent and better models are not conceivable without a better understanding of the evolutionary and biophysical properties of disordered regions.
In both cases, an important added constraint may be that the sequence in its unbound state is disordered rather than ordered. This constraint can be added to the model to select against mutations that would lead to a folded state. A random contacts model [82] could be implemented and a feature of this nature is implemented in IUPred, based upon an evaluation of the existence of favorable contacts for folding within the region [83].
10. Conclusions
As computational molecular biology and computational molecular evolution mature as fields, considerations of both the biophysical and the evolutionary attributes of proteins are increasingly being integrated. This coincides with an appreciation of the complexity of the biophysical chemistry of proteins in a cell, including the role of conformational ensembles, of post-translational modifications, of folding pathways, of protein kinetics, of protein complexes, and eventually of other cellular attributes, such as the role of chaperones. This is ultimately underpinned by an understanding of the energy landscape for a single sequence, and for homologous sequences linked through the mutational process. Simultaneously, protein structural and biophysical models will increasingly need to explicitly consider evolutionary processes as well in the field of structural bioinformatics. With these considerations, models will become more powerful (and slower) as the field moves forward.
Acknowledgments
We thank Jan Kubelka, Richard Goldstein, Vladimir Uversky, and three anonymous reviewers for helpful discussions. JSL, JAG, and DAL receive funding from NIH-INBRE P20 RR016474. DAL also receives funding from NSF DBI-0743374.
References
- Xie, L.; Bourne, P.E. Functional coverage of the human genome by existing structures, structural genomics targets, and homology models. PLoS Comput. Biol. 2005, 1. [Google Scholar] [CrossRef]
- Campbell, Z.T.; Baldwin, T.O.; Miyashita, O. Analysis of the bacterial luciferase mobile loop by replica-exchange molecular dynamics. Biophys. J. 2010, 99, 4012–4019. [Google Scholar]
- Pearl, F.M.; Bennett, C.F.; Bray, J.E.; Harrison, A.P.; Martin, N.; Shepherd, A.; Sillitoe, I.; Thornton, J.; Orengo, C.A. The CATH database: An extended protein family resource for structural and functional genomics. Nucleic Acids Res. 2003, 31, 452–455. [Google Scholar]
- Siltberg-Liberles, J. Evolution of structurally disordered proteins promotes neostructuralization. Mol. Biol. Evol. 2011, 28, 59–62. [Google Scholar]
- Roth, C.; Liberles, D.A. A systematic search for positive selection in higher plants (Embryophytes). BMC Plant Biol. 2006, 12. [Google Scholar] [CrossRef]
- Illergård, K.; Ardell, D.H.; Elofsson, A. Structure is three to ten times more conserved than sequence—A study of structural response in protein cores. Proteins 2009, 77, 499–508. [Google Scholar]
- Pereira de Araujo, A.F.; Onuchic, J.N. A sequence-compatible amount of native burial information is sufficient for determining the structure of small globular proteins. Proc. Natl. Acad. Sci. USA 2009, 106, 19001–19004. [Google Scholar]
- Ramsey, D.C.; Scherrer, M.P.; Zhou, T.; Wilke, C.O. The relationship between relative solvent accessibility and evolutionary rate in protein evolution. Genetics 2011, 188, 479–488. [Google Scholar]
- Williams, S.G.; Lovell, S.C. The effect of sequence evolution on protein structural divergence. Mol. Biol. Evol. 2009, 26, 1055–1065. [Google Scholar]
- Kellogg, E.H.; Leaver-Fay, A.; Baker, D. Role of conformational sampling in computing mutation-induced changes in protein structure and stability. Proteins 2011, 79, 830–838. [Google Scholar]
- Lockless, S.W.; Ranganathan, R. Evolutionarily conserved pathways of energetic connectivity in protein families. Science 1999, 286, 295–299. [Google Scholar]
- Böde, C.; Kovács, I.A.; Szalay, M.S.; Palotai, R.; Korcsmáros, T.; Csermely, P. Network analysis of protein dynamics. FEBS Lett. 2007, 581, 2776–2782. [Google Scholar]
- Pechmann, S.; Levy, E.D.; Tartaglia, G.G.; Vendruscolo, M. Physicochemical principles that regulate the competition between functional and dysfunctional association of proteins. Proc. Natl. Acad. Sci. USA 2009, 106, 10159–10164. [Google Scholar]
- Schaefer, C.; Schlessinger, A.; Rost, B. Protein secondary structure appears to be robust under in silico evolution while protein disorder appears not to be. Bioinformatics 2010, 26, 625–631. [Google Scholar]
- Kamneva, O.K.; Liberles, D.A.; Ward, N.L. Genome-wide influence of indel Substitutions on evolution of bacteria of the PVC superphylum, revealed using a novel computational method. Genome Biol. Evol. 2010, 870–886. [Google Scholar]
- Finn, R.D.; Mistry, J.; Tate, J.; Coggill, P.; Heger, A.; Pollington, J.E.; Gavin, O.L.; Gunasekaran, P.; Ceric, G.; Forslund, K.; et al. The Pfam protein families database. Nucleic Acids Res. 2010, 38, D211–D222. [Google Scholar]
- Povolotskaya, I.S.; Kondrashov, F.A. Sequence space and the ongoing expansion of the protein universe. Nature 2010, 465, 922–926. [Google Scholar]
- Rastogi, S.; Reuter, N.; Liberles, D.A. Evaluation of models for the evolution of protein sequences and functions under structural constraint. Biophys. Chem. 2006, 124, 134–144. [Google Scholar]
- Grahnen, J.A.; Nandakumar, P.; Kubelka, J.; Liberles, D.A. Biophysical and Structural Considerations for Protein Evolution. BMC Evol. Biol. 2011. submitted. [Google Scholar]
- Alvizo, O.; Mayo, S.L. Evaluating and optimizing computational protein design force fields using fixed composition-based negative design. Proc. Natl. Acad. Sci. USA 2008, 105, 12242–12247. [Google Scholar]
- Ding, F.; Dokholyan, N.V. Emergence of protein fold families through rational design. PLoS Comput. Biol. 2006, 2. [Google Scholar] [CrossRef]
- Dalal, S.; Balasubramanian, S.; Regan, L. Transmuting alpha helices and beta sheets. Fold. Des. 1997, 2, R71–79. [Google Scholar]
- Drummond, D.A.; Wilke, C.O. Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution. Cell 2008, 134, 341–352. [Google Scholar]
- Teufel, A.I.; Grahnen, J.A.; Liberles, D.A. Modeling Proteins at the Interface of Structure, Evolution, and Population Genetics. In Computational Modeling of Biological Systems: From Molecules to Pathways; Dokholyan, N., Ed.; Springer-Verlag: New York, NY, USA, 2011; in press. [Google Scholar]
- Fernández, A.; Lynch, M. Non-adaptive origins of interactome complexity. Nature 2011, 474, 502–505. [Google Scholar]
- Wolynes, P.G. Recent successes of the energy landscape theory of protein folding and function. Q. Rev. Biophys. 2005, 38, 405–410. [Google Scholar]
- Taverna, D.M.; Goldstein, R.A. Why are proteins so robust to site mutations? J. Mol. Biol. 2002, 315, 479–484. [Google Scholar]
- Kumar, M.D.; Bava, K.A.; Gromiha, M.M.; Prabakaran, P.; Kitajima, K.; Uedaira, H.; Sarai, A. ProTherm and ProNIT: Thermodynamic databases for proteins and protein-nucleic acid interactions. Nucleic Acids Res. 2006, 34, D204–206. [Google Scholar]
- Soskine, M.; Tawfik, D.S. Mutational effects and the evolution of new protein functions. Nat. Rev. Genet. 2010, 11, 572–582. [Google Scholar]
- Taverna, D.M.; Goldstein, R.A. Why are proteins marginally stable? Proteins 2002, 46, 105–109. [Google Scholar]
- Goldstein, R.A. The evolution and evolutionary consequences of marginal thermostability in proteins. Proteins 2011, 79, 1396–1407. [Google Scholar]
- Berezovsky, I.N.; Shakhnovich, E.I. Physics and evolution of thermophilic adaptation. Proc. Natl. Acad. Sci. USA 2005, 102, 12742–12747. [Google Scholar]
- DePristo, M.A.; Weinreich, D.M.; Hartl, D.L. Missense meanderings in sequence space: A biophysical view of protein evolution. Nat. Rev. Genet. 2005, 6, 678–687. [Google Scholar]
- Tokuriki, N.; Stricher, F.; Serrano, L.; Tawfik, D.S. How protein stability and new functions trade off. PLoS Comput. Biol. 2008, 4. [Google Scholar] [CrossRef]
- Shakhnovich, B.E.; Deeds, E.; Delisi, C.; Shakhnovich, E. Protein structure and evolutionary history determine sequence space topology. Genome Res. 2005, 15, 385–392. [Google Scholar]
- Bolon, D.N.; Grant, R.A.; Baker, T.A.; Sauer, R.T. Specificity versus stability in computational protein design. Proc. Natl. Acad. Sci. USA 2005, 102, 12724–12729. [Google Scholar]
- Ohta, T.; Gillespie, J.H. Development of neutral and nearly neutral theories. Theor. Popul. Biol. 1996, 49, 128–142. [Google Scholar]
- Hietpas, R.T.; Jensen, J.D.; Bolon, D.N. Experimental illumination of a fitness landscape. Proc. Natl. Acad. Sci. USA 2011, 108, 7896–7901. [Google Scholar]
- Lind, P.A.; Berg, O.G.; Andersson, D.I. Mutational robustness of ribosomal protein genes. Science 2010, 330, 825–827. [Google Scholar]
- Wylie, C.S.; Shakhnovich, E.I. A biophysical protein folding model accounts for most mutational fitness effects in viruses. Proc. Natl. Acad. Sci. USA 2011, 108, 9916–9921. [Google Scholar]
- Hou, J.; Jun, S.R.; Zhang, C.; Kim, S.H. Global mapping of the protein structure space and application in structure-based inference of protein function. Proc. Natl. Acad. Sci. USA 2005, 102, 3651–3656. [Google Scholar]
- Skolnick, J.; Arakaki, A.K.; Lee, S.Y.; Brylinski, M. The continuity of protein structure space is an intrinsic property of proteins. Proc. Natl. Acad. Sci. USA 2009, 106, 15690–15695. [Google Scholar]
- Pascual-García, A.; Abia, D.; Ortiz, A.R.; Bastolla, U. Cross-over between discrete and continuous protein structure space: Insights into automatic classification and networks of protein structures. PLoS Comput. Biol. 2009, 5. [Google Scholar] [CrossRef]
- Osadchy, M.; Kolodny, R. Maps of protein structure space reveal a fundamental relationship between protein structure and function. Proc. Natl. Acad. Sci. USA 2011, 108, 12301–12306. [Google Scholar]
- Andreeva, A.; Howorth, D.; Chandonia, J.M.; Brenner, S.E.; Hubbard, T.J.; Chothia, C.; Murzin, A.G. Data growth and its impact on the SCOP database: New developments. Nucleic Acids Res. 2008, 36, D419–425. [Google Scholar]
- Weiner, J., 3rd; Bornberg-Bauer, E. Evolution of circular permutations in multidomain proteins. Mol. Biol. Evol. 2006, 23, 734–743. [Google Scholar]
- Kimchi-Sarfaty, C.; Oh, J.M.; Kim, I.W.; Sauna, Z.E.; Calcagno, A.M.; Ambudkar, S.V.; Gottesman, M.M. A “silent” polymorphism in the MDR1 gene changes substrate specificity. Science 2007, 315, 525–528. [Google Scholar]
- Hollecker, M.; Creighton, T.E. Evolutionary conservation and variation of protein folding pathways. Two protease inhibitor homologues from black mamba venom. J. Mol. Biol. 1983, 168, 409–437. [Google Scholar]
- Plaxco, K.W.; Simons, K.T.; Baker, D. Contact order, transition state placement and the refolding rates of single domain proteins. J. Mol. Biol. 1998, 277, 985–994. [Google Scholar]
- Zarrine-Afsar, A.; Larson, S.M.; Davidson, A.R. The family feud: Do proteins with similar structures fold via the same pathway? Curr. Opin. Struct. Biol. 2005, 15, 42–49. [Google Scholar]
- Han, J.H.; Batey, S.; Nickson, A.A.; Teichmann, S.A.; Clarke, J. The folding and evolution of multidomain proteins. Nat. Rev. Mol. Cell Biol. 2007, 8, 319–330. [Google Scholar]
- Shakhnovich, E. Protein folding thermodynamics and dynamics: Where physics, chemistry, and biology meet. Chem. Rev. 2006, 106, 1559–1588. [Google Scholar]
- Lindberg, M.O.; Oliveberg, M. Malleability of protein folding pathways: A simple reason for complex behaviour. Curr. Opin. Struct. Biol. 2007, 17, 21–29. [Google Scholar]
- Amunson, K.E.; Ackels, L.; Kubelka, J. Site-specific unfolding thermodynamics of a helix-turn-helix protein. J. Am. Chem. Soc. 2008, 130, 8146–8147. [Google Scholar]
- Dill, K.A.; Ozkan, S.B.; Shell, M.S.; Weikl, T.R. The protein folding problem. Annu. Rev. Biophys. 2008, 37, 289–316. [Google Scholar]
- Nakamura, T.; Makabe, K.; Tomoyori, K.; Maki, K.; Mukaiyama, A.; Kuwajima, K. Different folding pathways taken by highly homologous proteins, goat alpha-lactalbumin and canine milk lysozyme. J. Mol. Biol. 2010, 396, 1361–1378. [Google Scholar]
- Forsyth, W.R.; Matthews, C.R. Folding mechanism of indole-3-glycerol phosphate synthase from Sulfolobus solfataricus: A test of the conservation of folding mechanisms hypothesis in (beta(alpha))(8) barrels. J. Mol. Biol. 2002, 320, 1119–1133. [Google Scholar]
- Nakamura, T.; Makabe, K.; Tomoyori, K.; Maki, K.; Mukaiyama, A.; Kuwajima, K. Different folding pathways taken by highly homologous proteins, goat alpha-lactalbumin and canine milk lysozyme. J. Mol. Biol. 2010, 396, 1361–1378. [Google Scholar]
- Echave, J.; Fernández, F.M. A perturbative view of protein structural variation. Proteins 2010, 78, 173–180. [Google Scholar]
- Maguid, S.; Fernandez-Alberti, S.; Echave, J. Evolutionary conservation of protein vibrational dynamics. Gene 2008, 422, 7–13. [Google Scholar]
- Hollup, S.M.; Fuglebakk, E.; Taylor, W.R.; Reuter, N. Exploring the factors determining the dynamics of different protein folds. Protein Sci. 2011, 20, 197–209. [Google Scholar]
- Dunker, A.K.; Obradovic, Z.; Romero, P.; Garner, E.C.; Brown, C.J. Intrinsic protein disorder in complete genomes. Genome Inform. Ser. Workshop Genome Inform. 2000, 11, 161–171. [Google Scholar]
- Apic, G.; Gough, J.; Teichmann, S.A. Domain combinations in archaeal, eubacterial and eukaryotic proteomes. J. Mol. Biol. 2001, 310, 311–325. [Google Scholar]
- Apic, G.; Gough, J.; Teichmann, S.A. An insight into domain combinations. Bioinformatics 2001, 17, S83–S89. [Google Scholar]
- Lynch, M. The frailty of adaptive hypotheses for the origins of organismal complexity. Proc. Natl. Acad. Sci. USA 2007, 104, 8597–8604. [Google Scholar]
- Brown, C.J.; Takayama, S.; Campen, A.M.; Vise, P.; Marshall, T.W.; Oldfield, C.J.; Williams, C.J.; Dunker, A.K. Evolutionary rate heterogeneity in proteins with long disordered regions. J. Mol. Evol. 2002, 55, 104–110. [Google Scholar]
- Szalkowski, A.M.; Anisimova, M. Markov models of amino acid substitution to study proteins with intrinsically disordered regions. PLoS One 2011, 6. [Google Scholar] [CrossRef]
- Ward, J.J.; Sodhi, J.S.; McGuffin, L.J.; Buxton, B.F.; Jones, D.T. Prediction and functional analysis of native disorder in proteins from the three kingdoms of life. J. Mol. Biol. 2004, 337, 635–645. [Google Scholar]
- Brown, C.J.; Johnson, A.K.; Daughdrill, G.W. Comparing models of evolution for ordered and disordered proteins. Mol. Biol. Evol. 2010, 27, 609–621. [Google Scholar]
- Turoverov, K.K.; Kuznetsova, I.M.; Uversky, V.N. The protein kingdom extended: Ordered and intrinsically disordered proteins, their folding, supramolecular complex formation, and aggregation. Prog. Biophys. Mol. Biol. 2010, 102, 73–84. [Google Scholar]
- Amoutzias, G.D.; He, Y.; Gordon, J.; Mossialos, D.; Oliver, S.G.; van de Peer, Y. Posttranslational regulation impacts the fate of duplicated genes. Proc. Natl. Acad. Sci. USA 2010, 107, 2967–2971. [Google Scholar]
- Goldstein, R.A. The structure of protein evolution and the evolution of protein structure. Curr. Opin. Struct. Biol. 2008, 18, 170–177. [Google Scholar]
- Stoltzfus, A. On the possibility of constructive neutral evolution. J. Mol. Evol. 1999, 49, 169–181. [Google Scholar]
- Tompa, P.; Szász, C.; Buday, L. Structural disorder throws new light on moonlighting. Trends Biochem. Sci. 2005, 30, 484–489. [Google Scholar]
- Kleinman, C.L.; Rodrigue, N.; Lartillot, N.; Philippe, H. Statistical potentials for improved structurally constrained evolutionary models. Mol. Biol. Evol. 2010, 27, 1546–1560. [Google Scholar]
- Lakner, C.; Holder, M.T.; Goldman, N.; Naylor, G.J. What's in a likelihood? Simple models of protein evolution and the contribution of structurally viable reconstructions to the likelihood. Syst. Biol. 2011, 60, 161–174. [Google Scholar]
- Nasrallah, C.A.; Mathews, D.H.; Huelsenbeck, J.P. Quantifying the impact of dependent evolution among sites in phylogenetic inference. Syst. Biol. 2011, 60, 60–73. [Google Scholar]
- Philippe, H.; Casane, D.; Gribaldo, S.; Lopez, P.; Meunier, J. Heterotachy and functional shift in protein evolution. IUBMB Life 2003, 55, 257–265. [Google Scholar]
- Miyazawa, S.; Jernigan, R.L. Estimation of effective inter-residue contact energies from protein crystal structures: Quasi-chemical approximation. Macromolecules 1985, 18, 534–552. [Google Scholar]
- Bastolla, U.; Farwer, J.; Knapp, E.W.; Vendruscolo, M. How to guarantee optimal stability for most representative structures in the Protein Data Bank. Proteins 2001, 44, 79–96. [Google Scholar]
- Dunker, A.K.; Oldfield, C.J.; Meng, J.; Romero, P.; Yang, J.Y.; Chen, J.W.; Vacic, V.; Obradovic, Z.; Uversky, V.N. The unfoldomics decade: An update on intrinsically disordered proteins. BMC Genomics 2008, 9. [Google Scholar] [CrossRef]
- Bryngelson, J.D.; Wolynes, P.G. Spin glasses and the statistical mechanics of protein folding. Proc. Natl. Acad. Sci. USA 1987, 84, 7524–7528. [Google Scholar]
- Dosztányi, Z.; Csizmók, V.; Tompa, P.; Simon, I. The pairwise energy content estimated from amino acid composition discriminates between folded and intrinsically unstructured proteins. J. Mol. Biol. 2005, 347, 827–839. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Siltberg-Liberles, J.; Grahnen, J.A.; Liberles, D.A. The Evolution of Protein Structures and Structural Ensembles Under Functional Constraint. Genes 2011, 2, 748-762. https://doi.org/10.3390/genes2040748
Siltberg-Liberles J, Grahnen JA, Liberles DA. The Evolution of Protein Structures and Structural Ensembles Under Functional Constraint. Genes. 2011; 2(4):748-762. https://doi.org/10.3390/genes2040748
Chicago/Turabian StyleSiltberg-Liberles, Jessica, Johan A. Grahnen, and David A. Liberles. 2011. "The Evolution of Protein Structures and Structural Ensembles Under Functional Constraint" Genes 2, no. 4: 748-762. https://doi.org/10.3390/genes2040748
APA StyleSiltberg-Liberles, J., Grahnen, J. A., & Liberles, D. A. (2011). The Evolution of Protein Structures and Structural Ensembles Under Functional Constraint. Genes, 2(4), 748-762. https://doi.org/10.3390/genes2040748



