The Rate and Tract Length of Gene Conversion between Duplicated Genes
Abstract
: Interlocus gene conversion occurs such that a certain length of DNA fragment is non-reciprocally transferred (copied and pasted) between paralogous regions. To understand the rate and tract length of gene conversion, there are two major approaches. One is based on mutation-accumulation experiments, and the other uses natural DNA sequence variation. In this review, we overview the two major approaches and discuss their advantages and disadvantages. In addition, to demonstrate the importance of statistical analysis of empirical and evolutionary data for estimating tract length, we apply a maximum likelihood method to several data sets.1. Introduction
Gene conversion is a recombinational process initiated by a double strand break (DSB), through which a DNA fragment is non-reciprocally transferred (copied and pasted) generally between allelic regions (i.e., allelic gene conversion [1]). In addition, gene conversion occurs between paralogs when they have sufficient sequence homology (non-allelic or interlocus gene conversion) [2,3]. Although the mechanism is not fully understood yet (see Hastings [4] and Ling et al. [5] in this special issue), interlocus gene conversion is a major mutational process that occurs in both meiosis [2] and mitosis [6]. Basic questions on gene conversion include (i) What is the rate of gene conversion under what condition? and (ii) What is the distribution of the tract length of gene conversion? Addressing these fundamental questions will provide great insights into how important role gene conversion plays as a mutational mechanism.
There are two potential approaches to estimate the rate and tract length of gene conversion. A straightforward empirical approach involves mutation (i.e., gene conversion) accumulation studies, in which the rate of gene conversion can be directly estimated. The other is an evolutionary approach, which utilizes DNA sequence data from multiple individuals, where the footprints of a number of gene conversion events are accumulated in the evolutionary history. The empirical approach provides more accurate estimates than the evolutionary approach, but the amounts of data are still limited because well-established experimental systems are available only for several model species including yeast and mouse. In contrast, the evolutionary approach can be readily applied to any species when sequence data for paralogs are available.
In this article, we first review researches that estimated the rate and tract length of interlocus gene conversion by the two approaches, and discuss their advantages and disadvantages. Furthermore, we reanalyze empirical data from yeast and rodent to estimate the mean tract length by using a simple maximum likelihood (ML) method. We also apply the ML method to large-scale human genotyping data of diseases genes, in which gene conversion is known to cause diseases. Based on these results, we point out the importance of statistical analysis of empirical and evolutionary data.
2. The Rate of Gene Conversion
2.1. Empirical Approach
Most transgenic systems for studying gene conversion use strains (or cell lines), in which a pair of genes are set up by transferring artificially edited DNA sequences (Figure 1), so that the nature of interlocus gene conversion can be investigated under an arbitrary condition [7]. The gene has a target marker site called “selected marker” (reversed triangles in Figure 1), and there is a trick that makes it possible to recognize if the selected marker is converted (e.g., in yeast, if a gene involved in nutrient requirement such as uracil or histidine is used, gene conversion induces prototroph formation). Therefore, it is easy to screen for strains that experienced gene conversions. Although Figure 1 illustrates a simple case, it is possible to set multiple selected markers.
In the baker's yeast Saccharomyces cerevisiae, one of the model species of gene conversion studies, there are a number of researches that estimated the interlocus gene conversion rate in various conditions [8–15]. Estimates have a wide range from ∼10−10 to ∼10−3 per cell division (we exclude classic works that reported estimates per culture). This great amount of variation between different researches largely depends on the fact that the gene conversion rate is affected by many factors.
First of all, the rate in meiosis is different from that in mitosis. Jinks-Robertson and Petes [12] showed that the former is 300 times higher than the latter, and slightly lower estimates for the meiosis-mitosis ratio were reported later (∼15 in [16] and ∼100 in [17]).
Second, genomic location matters. In general, the rate of intrachromosomal gene conversion may be higher than that of interchromosomal gene conversion. Lichten et al. [13,15] showed that the former is several times higher than the latter in both meiosis and mitosis (see also [14,18]). Lichten et al. [15] also investigated the positional effect on the gene conversion rate when two paralogs are located with variable distances between them. It was found that the gene conversion rate could be negatively correlated with the distance (see also [11]). It seems that the pattern may not be very different between in meiosis and in mitosis [13,15].

Third, the rate should be in a negative correlation with the sequence identity between paralogs. It is considered that gene conversion mainly occurs when the identity is more than 80% [19,20], but gene conversion can occur with identity <80% although the rate is low [21]. Recent works clearly identified a negative correlation between the sequence identity and gene conversion rate [22–25].
Fourth, it seems that the length of completely identical region has a significant effect on the rate of gene conversion. Ahn et al. [26] measured the rate with variable lengths of a recipient copy (from 26 bp to 702 bp), and found that although the rate was extremely low, gene conversion occurred even with the shortest paralog (i.e., 26 bp), suggesting gene conversion requires identical regions as small as ∼10 bp (see also Mezard et al. [21] for a similar result). A later work by Jinks-Robertson and Petes [14] found that the rates for paralogs that have identical regions with >250 bp were much higher than the background rate. This work brought the concept of the minimal efficient processing segment (MEPS), which was first introduced for homologous recombination in bacteria [27]. Jinks-Robertson and Petes [14] suggested that MEPS for yeast would be around 200 bp, which still serves as a good standard [7,28], but this does not necessarily rule out the possibility of gene conversion with paralogs that are shorter than MEPS [21,23,26,29,30].
The empirical approach has also been commonly applied to mouse (Mus musculus) and Chinese hamster (Cricetulus griseus). Extensive experiments exhibited quite similar results to those of yeast. It seems that the rate in meiosis may be 100∼1000 times higher than in mitosis [31]. A negative correlation between the gene conversion rate and paralogous distance was observed [32,33]. It was found that the rate is dramatically reduced for paralogs with identity ∼80% in comparison with the rate for 100% identical pairs [34–36]. MEPS was estimated to be roughly 200 bp [35], which was repeatedly confirmed by follow-up experiments [37,38].
Thus, we overviewed experimental studies of yeast and rodent which explored the factors that affect the rate of gene conversion. These findings should be robust because each of them was demonstrated under a certain experimental condition. However, we found that it is difficult to compare the absolute gene conversion rates between different experiments, and this is why we avoided arguments with absolute values. For example, some researches take advantage of specific sites where DSBs can be induced, (e.g., the HO site in the MAT locus [39] and target site of I-Sce I endonuclease [40]) and some did not. A technical problem is that, in a simple experimental design with a single selected marker, an estimated rate may include both gene conversion and unequal crossing-over because they have an identical outcome. Such a rate cannot be fairly compared with an estimate from a more sophisticated experiment, in which the two mechanisms can be distinguished, e.g., by using secondary markers. Furthermore, in vivo, the rate should largely depend on the genomic background, for example, the number of paralogs in the genome [11], special motives associated with recombination [41,42], activity of numerous enzymes involved in DNA repair and recombination (reviewed in [43]). Therefore, it is important to notice that the available estimates may not be representative values of the gene conversion rate.
2.2. Evolutionary Approach
The pattern of polymorphism e.g., SNP in duplicated regions is very informative because it should have many footprints of gene conversion. This approach heavily depends on theoretical understanding of population genetics on what kind of polymorphism pattern is likely expected under what rate of gene conversion. When the process of gene conversion is modeled in the framework of population genetics, it is usually assumed that a gene conversion event can be initiated at a random position at a certain rate, g, and the elongation of the gene conversion tract occurs either in the 5′ or 3′ direction. It is commonly assumed that the elongation can be terminated at any position with a constant probability, say q, such that the tract length follows a geometric distribution with parameter q, or an exponential distribution with continuous approximation [44]. As the average tract length is T = 1/q, the per-site rate of gene conversion is defined as c = Tg, which is the probability that a particular site is involved in a gene conversion event per generation. According to population genetic theory [45–47], c can be well estimated from SNP data. From genome-wide SNP data in yeast [48], estimates of the relative rate of gene conversion c to the point mutation rate typically ranges from 10 to 100, which is in agreement with estimates for several duplicates in Drosophila melaogaster [49,50]. There are many locus-specific estimates of c for a wide range of species including malaria parasite [51], plant [52], avian [53] and human [54–56].
A disadvantage of this approach is that estimates are model-dependent; therefore, they could be biased if the assumptions of the model do not hold. For example, as Innan's theory [45,46] assumes a constant-size population, an estimate may not be reliable if the population is growing or subdivided. This is a common problem shared by all estimates by population genetics-based methods, such as those of mutation rate and recombination rate. It is important to understand how population genetics-based estimates are quantitatively affected by violation of the assumptions. Coalescent simulations [46] would be one of the best ways to do this.
3. The Tract Length of Gene Conversion
3.1. Empirical Approach
It is relatively straightforward to develop an empirical system for estimating gene conversion tract length by modifying the transgenic system for estimating the gene conversion rate. Figure 1 illustrates such a strategy, which has a selected marker at position 432 bp. In addition to the selected marker, there are several silent markers inserted in the donor gene. Because silent markers could be coconverted with the selected marker, it is possible to identify the converted tract in the marker space. Figure 1 also illustrates an example of a gene conversion event, which includes four markers from positions 409 to 565. It can be inferred that the 5′ break point should be between positions 304 and 409 and the 3′ break point should locate between positions 565 and 667. Therefore, the maximum and minimum lengths of this conversion tract are 362 bp and 157 bp, respectively. Thus, the data of a number of detected gene conversion can be described by a simple matrix with the presence(+)/absence(−) of the markers in the recipient copy (Figure 1). Note that all data should have a positive sign (+) at the selected marker with the blue triangle.
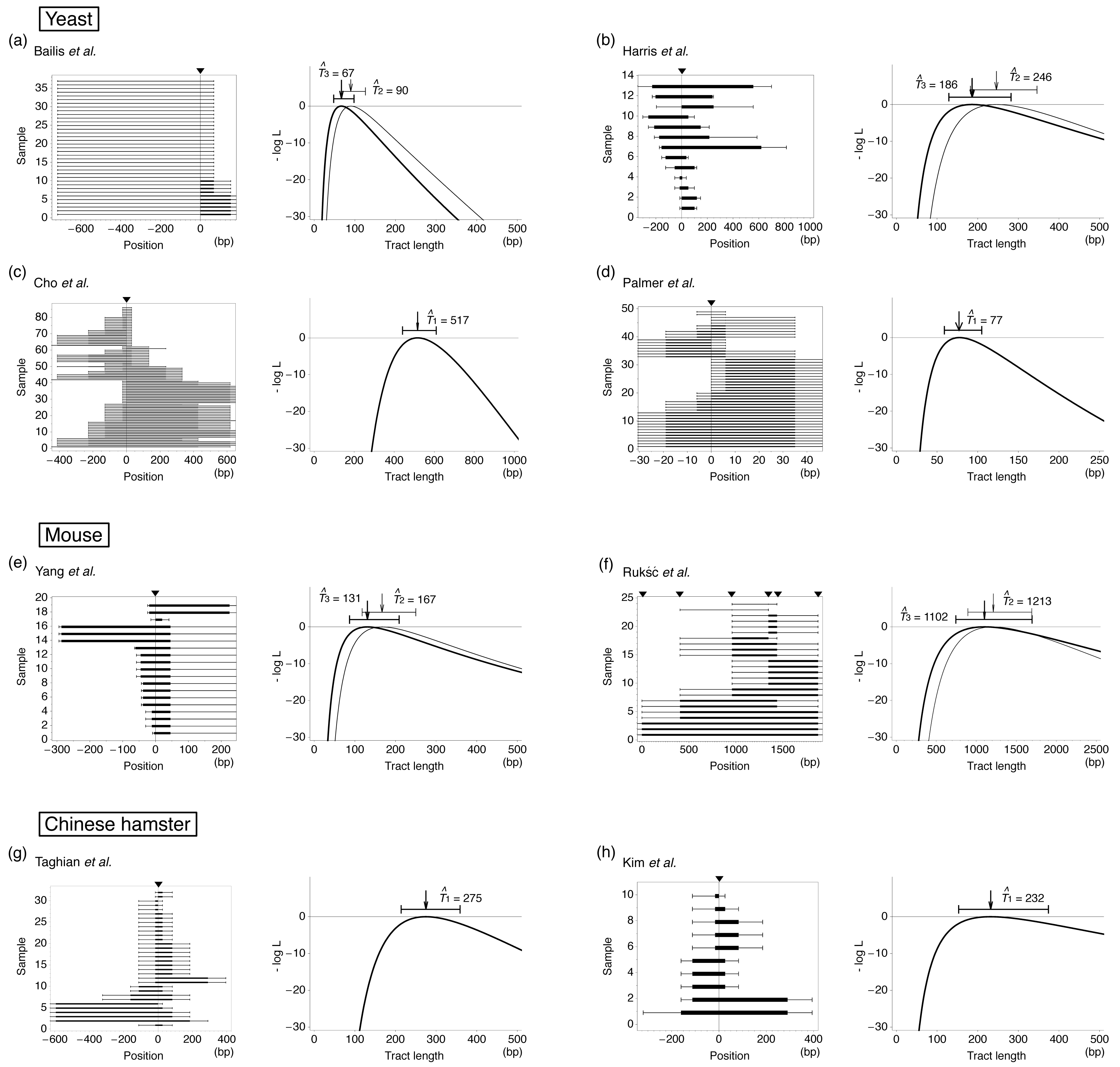
Motivated by classic works [57,58], Ahn et al. [59] extensively investigated the tract length of gene conversion in yeast, and found the average of the minimum lengths is about 500 bp. There are a number of follow-up studies, most of which reported an estimate of the average of 200–300 bp [60–64] (Note that most of them reported the mean of the maximum and minimum lengths). It seems that there is no big difference in the tract length of gene conversion between mitosis and meiosis [25]. Similar estimates (287–296 bp) have also been obtained for rodents (Chinese hamster) [63,64].
Thus, this experimental system has contributed to our understanding of the typical length of gene conversion. However, a problem is that the initiation and termination positions of the tract are usually identified between markers, and it is difficult to know the actual length. It is more serious when a tract covers all markers so that the tract is potentially very long. Therefore, to understand the distribution of actual tract length, it is needed to analyze the data statistically [65–69]. Here, we use a maximum likelihood (ML) method to estimate the mean tract length by assuming that the elongation of a gene conversion tract is terminated at a constant rate. This assumption should be reasonable because we found that the data of Taghian et al. [63] and others [59,61] exhibit a good fit to a geometric distribution, or an exponential distribution with continuous approximation (Figure 2).
Table 1 summarizes data which are suitable to infer the mean tract length of interlocus gene conversion with our ML method. We collected data sets with the number of markers M ≥ 4 and the sample size n ≥ 10. All data in Table 1 are for mitosis. For each detected gene conversion, the maximum and minimum lengths can be parsimoniously determined and summarized in Figure 3. We excluded data that need double conversion events to explain parsimoniously. Such data (called discontinuous tracts) arise at a low frequency [19,59–63]. Figure 3 shows that many tracts involve only the selected marker, indicting there are a large number of short gene conversion. On one hand, there are many tracts that could be potentially very long because they have positive signs at the left- and/or right-end markers.

| Data Set | Donor / Recipient Genesa | Length of Analyzed Region | Sequence Identity | M (# of Markers) | n (Sample Size) | Gene Conversion Rateb |
|---|---|---|---|---|---|---|
| Saccharomyces cerevisiae (yeast) | ||||||
| Bailis et al. [19] | SAM2 (IV) / SAM1 (XII) | 869 bp | 83% | 4 | 37 | 8.4 × 10−9 |
| Harris et al.[20] | PMA1 (VII) / PMA2 (XVI) | 1830 bp | 85% | 24 | 13 | 5.0 × 10−9 |
| Cho et al. [61] | ura3 / ura3 (4.9 kb) | 1130 bp | 99% | 11 | 86 | 1.6 × 10−5 (3.8 × 10−3) c |
| Palmer et al. [70] | ura3 / ura3 (4.9 kb) | 54 bp | 99% | 5 | 49 | 3.3 × 10−6 (1.1 × 10−3) c |
| Mus musculus (mouse) | ||||||
| Yang et al. [71] | HSV-1 tk / -2 tk (<6.5 kb) | 2500 bp | 81% | 14, 8d | 19 | 1.3 × 10−8 (2.3 × 10−7) |
| Rukść et al. [72] | Cμ5′ / Cμ3′ (<8 kb) | 1876 bp | 99% | 6 | 24 | n.d. |
| Cricetulus griseus (Chinese hamster) | ||||||
| Taghian et al. [63] | MMTVneo / neo12 (3.8 kb) | 989 bp | 99% | 13 | 32 | < 4.8 × 10−10 (2.7 × 10−5) e |
| Kim et al. [64] | MMTVneo / neo12 (3.8 kb) | 989 bp | 99% | 10 | 11 | < 5.6 × 10−10 (2.3 × 10−5) f |
aThe chromosome numbers of the donor and recipient genes are shown in the parentheses if they are located on different chromosomes. If they are on the same chromosome, the distance between them is shown.bEstimated rate from a strain with accelerated DSB is shown in parentheses.cComputed by assuming the doubling time is 3 h and the culturing time is 3 days.dWe pooled two data sets with different numbers of markers, 14 and 8.eComputed by assuming the doubling time is 15 h and the culturing time is14 days.fComputed by assuming the doubling time is 15 h and the culturing time is 12 days.
In order to estimate the average length of gene conversion, T, from these data, we use a simple ML method. Our method is a slightly modified version of Gloor et al. [65] (see also [66]) so that it is possible to apply to data with multiple selected markers. Let D be the data set obtained from a single pair of genes, which consists of n identified tracts. Each tract is characterized by (i, j) when the tract includes a region from the ith to jth markers (i ≤ j) but not i−1 or j+1th markers. Note that i ≤ k ≤ j when the kth marker is the selected marker that is used for detecting gene conversion. Then, D can be simply described as
To obtain the likelihood function of data D conditional on T, we consider three different models depending on the experimental design and the distribution of gene conversion tract. The first model (Model 1) can be applied to many experimental designs, in which DSBs are induced at a particular position (denoted by xk) and the selected marker is essentially identical to the induced position. In such a case, it is straightforward to assume that the elongation of converted tracts in the two directions independently follow an exponential distribution (see above and Figure 2). Let x1 and x2 be the 5′ and 3′ breakpoints of the tract. Then, the probability that a tract that includes the selected marker is from position x1 to x2 is given by a function of T:
Then, the likelihood of the data D is given by
In other cases, the location of DSBs should be treated to be unknown. If we assume the exponential elongation of a tract from a DSB in the two directions independently as defined in (1), then the total length follows a gamma distribution with shape parameter two. In this Model 2, we assume this gamma distribution for the length of an individual tract (t):
From (5), we can obtain the probability that a gene conversion event is captured in the experimental system. In other words, we are interested in the probability that the tract includes the selected marker (i.e., kth marker). Assume that B consists of all possible pairs of (i, j) that satisfy the condition, i ≤ k ≤ j. Then, this probability is given by
From (5) and (6), we have the probability that the detected tract is (i, j):
In addition, we consider Model 3, in which the entire length of a tract follows an exponential distribution:
This is a frequently used assumption in evolutionary models as introduced in the “Evolutionary approach” section. For this Model 3, the likelihood function of D is simply given by (5) by replacing p2(t) with p3(t).
Using these likelihood functions, we estimated T for each data set in Table 1 and the results are shown in Figure 3. If the data set has a selected marker at the position of induced DSB, Model 1 is applied, otherwise both Models 2 and 3 are used. ML estimates based on these three models are denoted by T̂1, T̂2 and T̂3. It was found that our method provides ML estimates of the mean tract length with relatively narrow confidence interval. The results of Models 2 and 3 are not very different to each other. For the four data sets of yeast, the estimates are within a quite small range from ∼50 to several hundred bp, which seems to be much smaller than allelic gene conversion [73]. The results for rodents are similar; our estimates are around 100 bp except for the data of Rukść et al. [72], which provide an estimate of >1 kb with a much wider confidence interval (roughly 1 kp) than the others. This may be partly because the marker density is very low (the average interval is 375 bp for this data set, while the average of the others is ∼160 bp).
Thus, the ML method makes it possible to estimate the mean tract length with relatively small amount of data. It is demonstrated that the empirical approach with statistical analyses is a powerful means to understand the tract length of gene conversion.
3.2. Evolutionary Approach
DNA sequence data potentially include information on the tract lengths of gene conversion events that occurred in their ancestral lineages. GENECONV is a software developed by Sawyer [74] to detect converted regions in aligned DNA sequences. GENECONV analyzes an alignment of multiple sequences in a pairwise manner, and identifies unusually long regions of high identity between the focal pair, which are candidates of gene conversion. The algorithm involves statistical treatment, which conditions on the pattern of variable sites in the other sequences in the alignment. The statistical significance is determined by random-shuffling of variable sites in the alignment.
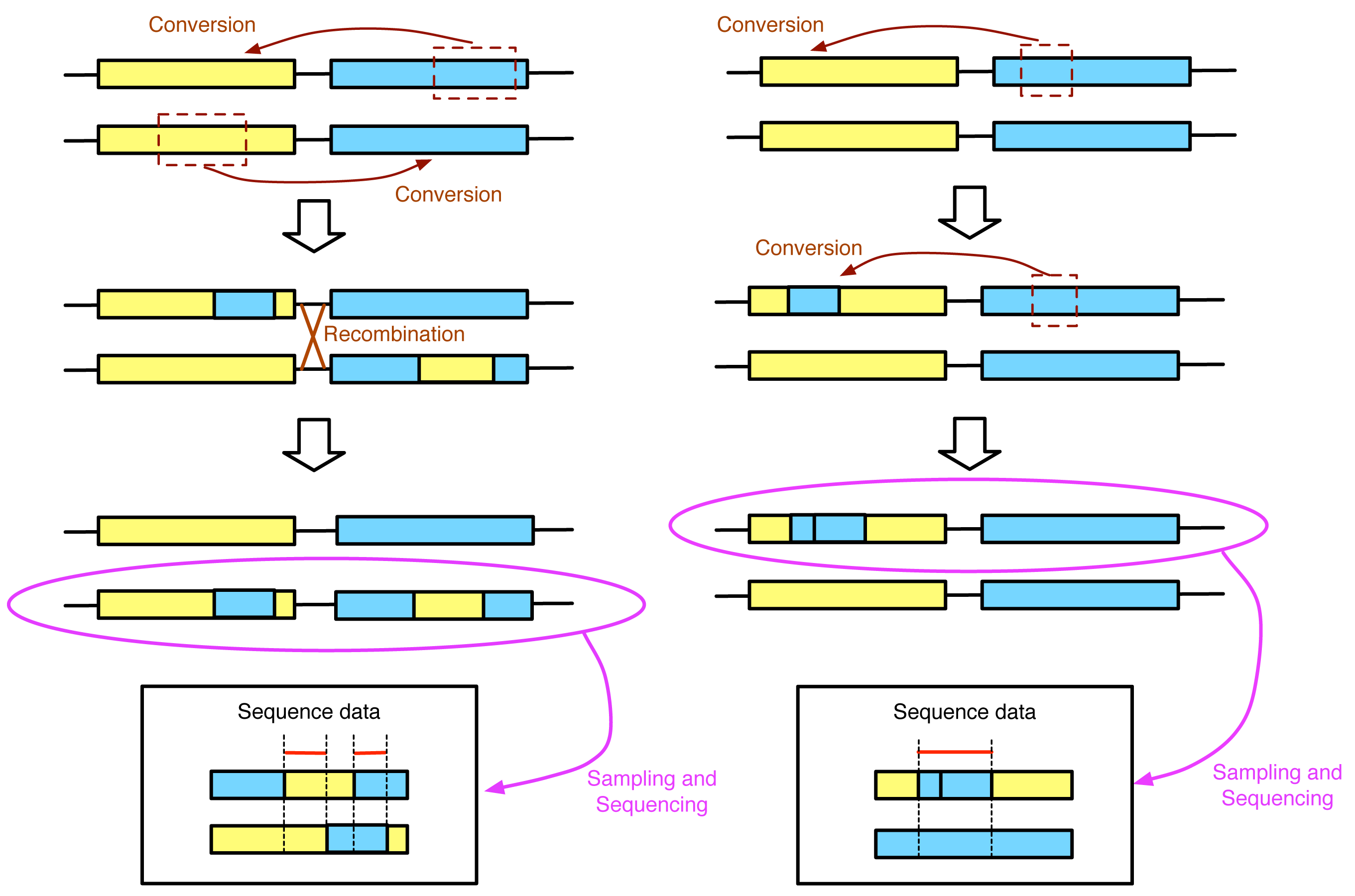
As was demonstrated by our recent simulation work [75], it is not appropriate to use GENECONV to infer the actual tract length. There is no doubt that the regions identified by GENECONV are strong candidate regions that have undergone recent gene conversion. However, the identified region is not necessarily to correspond to the region that was really transferred by a single gene conversion event. Accordingly, the result of GENECONV is sometimes misinterpreted as if the output (a list of candidate converted tracts) reflects the distribution of the tract length of gene conversion (i.e., Ref. [76]). This effect is easily demonstrated by simple illustrations in Figure 4. In the left panel, two conversions in the opposite directions share a part of the tract. If GENECONV is applied to the sequence data in the box, it will likely identify two regions (with red lines in Figure 4) with lengths much shorter than the real converted tract lengths. In contrast, the two overlapping conversion events in the same direction result in a large region identified by GENECONV. The real situation should be much more complicated with a number of overlapping recurrent gene conversion events, indicating that the empirical approach would be the only reliable means to investigate the tract length of gene conversion. It should be noted that there are several algorithms for detecting gene conversion tracts [77–81], and we here treated GENECONV as a representative of them because they share the basic idea. Thus, using natural variation in DNA sequences is not very suitable to investigate the tract length of gene conversion.
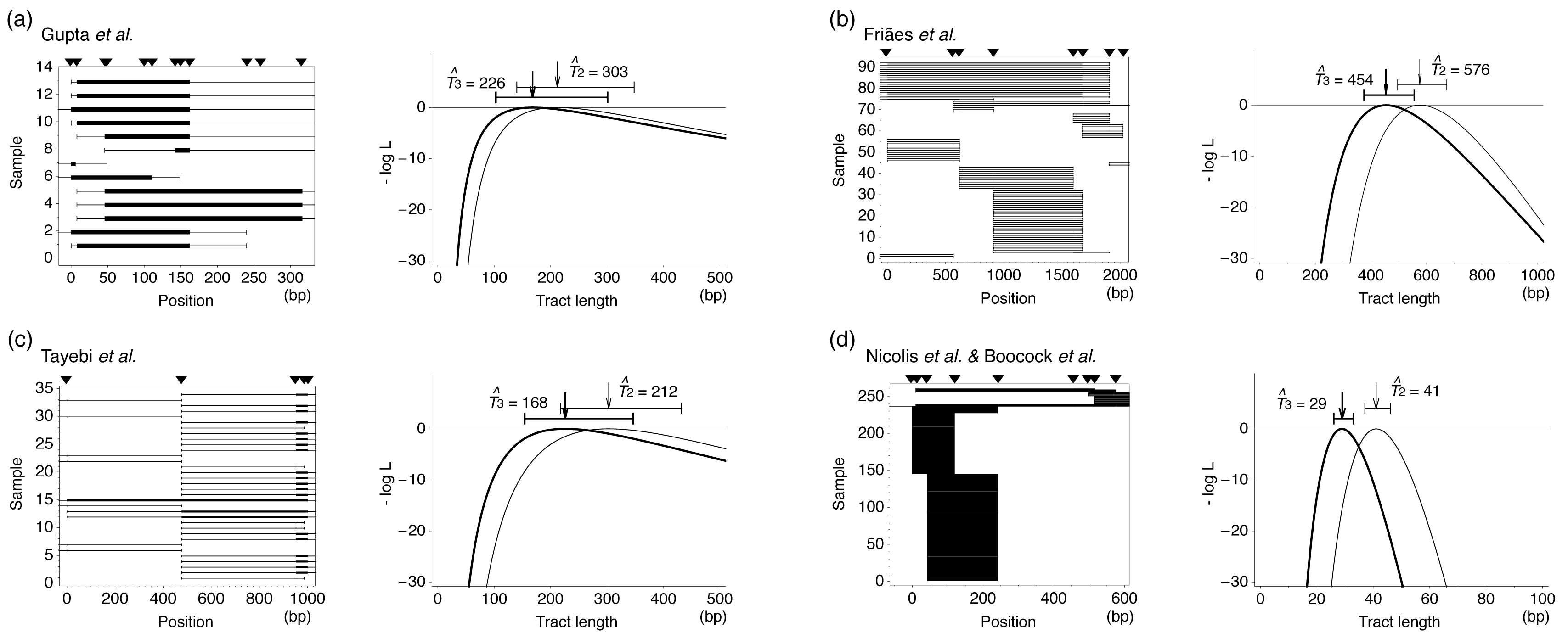
However, there are special cases where we can obtain high quality of data. One example is disease genes in humans. There are a number of human diseases caused by gene conversion, as reviewed by Chen et al. [41] in this issue (see also [3]). In many cases, diseases are caused by gene conversion that transfer a mutation from a pseudogenized duplicate to the functional copy, resulting in missense mutation [82–84], nonsense mutation [85], frameshift [86,87], change of splicing site [88]. These conversions occur between highly similar sequences (more than 90%, see [3]), which seems to be slightly higher than that for yeast and rodent. When the sequences of the functional and pseudogenized copies are known, the positions of causal mutations can be identified. In such a case, there are some interesting follow-up studies that a region encompassing the causal mutations is resequenced or genotyped for a number of patients. The ML method can be directly applied to such a data set to estimate the average tract length with one condition, that is, each of the detected gene conversions was created by a single gene conversion event. This assumption may be reasonable for serious diseases, for which the causal mutation can not increase in frequency in the human population. If so, almost all mutations should be eliminated from the population in a very short time, during which it is quite unlikely that another gene conversion occurs in the focal region. As a consequence, the identified gene conversion tracts in sequence data are most likely created by a single independent gene conversion. It should be noted that, gene conversions under our analyses here are those occurred in meiosis, while the data in Table 1 are for mitosis.
In Table 2, we summarize four genotyping data sets from human disease genes, for which our assumption of independent gene conversion should likely hold because the frequencies of patients are extremely low. The ML function (8) was applied to these four data sets and the results are summarized in Figure 5. The ML estimates of T are quite similar to those of the empirical approach for yeast and rodent.
| Data Set | Disease | Recipient Genea | Analyzed Region | Sequence Identity | n (Sample Size) | Frequency of Patientsb |
|---|---|---|---|---|---|---|
| Gupta et al. [89,90] | von Willebrand disease types 2M & 3 | vWF (12pl3.3/22qll.22—qll.23) | intron 27 and exon 28 | 97% | 13 | < 1/500 (type 2M) 1/500,000 (type 3) |
| Friães et al. [91] | congenital adrenal hyperplasia | CYP21A2 (6p21.3, 30 kb) | exons 1 — 10 and flanking regions | 96—98% | 92 | 1/15,500—1/280 |
| Tayebi etal. [92] | Gauchar disease | GBA (lq21, 16 kb) | exons 3—11 | 96% | 34 | 1/1,000,000 —1/850 |
| Nicolis et. al. [93] | Shwachman- Diamond syndrome | SBDS (7qll, 305 kb) | exons 1—5 and junction of exon/intron | 97% | 25 | 1/100,000 |
| Boocock et. al. [88] | 235 |
aThe chromosomal positions of the donor and recipient genes are shown in the parentheses if they are located on different chromosomes. If they are on the same chromosome, the position of the recipient gene and the distance between the two genes are shown. Note that all donor genes are pseudogenes of each functional gene.bThis frequency includes patients that are not caused by gene conversion.
4. Conclusions and Perspectives
As well as other mutational mechanisms, interlocus gene conversion could create changes in DNA sequences, which will potentially cause increase or decrease of the fitness of the host individual. When the fitness impact is strong, the conversion should be immediately selected for or against. To understand the role gene conversion plays in organism's life and evolution, it is crucial to know the rate and tract length of gene conversion.
In this review, we first overviewed the empirical and evolutionary approaches to estimate the rate of gene conversion between duplicated regions. The empirical approach generally involves mutation accumulation studies. Most studies use strains or cell lines, to which donor and/or recipient genes are transferred. This transgenic system, which is well established in yeast and rodent, is flexible enough to explore the rate under variable conditions. It has been demonstrated that the rate is determined by many factors including the genomic location and nucleotide identity between duplicates. Evolutionary approaches may be suitable to estimate the rate for non-model species, because they can be applied when DNA sequence data are available. Estimates based on polymorphism (SNP) data are roughly in agreement with those of the empirical approach.
Inferring tract lengths is more complicated in both of the two approaches. The empirical approach uses the transgenic system for estimating the rate with a modification; A number of markers are distributed in the donor (or recipient) sequences which make it possible to trap conversion tracts. As this system just allows one to identify the initiation and termination positions of the tract between markers, it is difficult to know the actual length. Therefore, we here used a simple ML method to estimate the mean tract length. The method well estimated the mean lengths with relatively narrow confidence intervals for many data sets, indicating the importance of statistical analysis of empirical data. Most estimates range from 50 to several hundred bp.
In contrast, evolutionary data are not very informative for the tract length mostly because evolutionary data accumulate a number of footprints of historical gene conversions that potentially overlap with one another. Exceptions include genotyping data of human disease genes, at which gene conversion causes serious disease when it transfers a deleterious mutation from a pseudogenized duplicate. With this condition, if we have a sample of patients that are not genetically related, most of the detected gene conversions in the gene should be very young and independent. Our ML method was successfully applied to such data.
The rate of gene conversion we considered in this review is a per-site rate, that is, the rate at which a particular site is involved in a gene conversion event. This rate is different from the rate that a gene conversion event occurs. Under the model we introduced above, the former is denoted by c and the latter is g. g can be estimated if we know the average tract length, T, because g is simply given by c/T. According our ML analysis, T would be on the order of 101∼2 bp, so that the initiation rate of gene conversion per site would be one or two orders of magnitude lower than c.
Thus, our knowledge on the rate and tract length of interlocus gene conversion is growing. However, data are still limited to several model systems. Because the rate should be highly variable across the genome, to understand the genomic landscape of gene conversion should be one of the future directions. It has been thought that many biological features are shared by gene conversion and recombination, and the recombination rate is also highly variable across the genome. There are a number of hotspots of recombination in genomes [73,94–97], and some of them would also be associated with interlocus gene conversion [98–100] although the amount of information is still limited. To fully understand the mechanisms behind the great variability of the gene conversion and recombination rates, we need much more data than currently available, part of which may be obtained by taking advantage of next-geneartion sequencing.
Acknowledgments
We thank K. Kurosawa and K. Ohta for technical help. This work was supported by grants from the Japan Society for the Promotion of Science (JSPS) and Japan Science and Technology Agency (JST) to HI.
References
- Mitchell, M.B. Aberrant recombination of pyridoxine mutants of Neurospora. Proc. Natl. Acad. Sci. USA 1955, 41, 215–220. [Google Scholar]
- Ernst, J.F.; Stewart, J.W.; Sherman, F. The cyc1-11 mutation in yeast reverts by recombination with a nonallelic gene: Composite genes determining the iso-cytochromes c. Proc. Natl. Acad. Sci. USA 1981, 78, 6334–6338. [Google Scholar]
- Chen, J.M.; Cooper, D.N.; Chuzhanova, N.; Férec, C.; Patrinos, G.P. Gene conversion: Mechanisms, evolution and human disease. Nat. Rev. Genet. 2007, 8, 762–775. [Google Scholar]
- Hastings, P.J. Mechanisms of ectopic gene conversion. Genes 2010, 1, 427–439. [Google Scholar]
- Ling, F.; Mikawa, T.; Shibata, T. Enlightenment of yeast mitochondrial homoplasmy: Diversified roles of gene conversion. Genes 2011, 2, 169–190. [Google Scholar]
- Esposito, M.S. Evidence that spontaneous mitotic recombination occurs at the two-strand stage. Proc. Natl. Acad. Sci. USA 1978, 75, 4436–4440. [Google Scholar]
- Mieczkowski, P.A.; Lemoine, F.J.; Petes, T.D. Recombination between retrotransposons as a source of chromosome rearrangements in the yeast Saccharomyces cerevisiae. DNA Repair 2006, 5, 1010–1020. [Google Scholar]
- Mikus, M.D.; Petes, T.D. Recombination between genes located on nonhomologous chromosomes in Saccharomyces cerevisiae. Genetics 1982, 101, 369–404. [Google Scholar]
- Sugawara, N.; Szostak, J.W. Recombination between sequences in nonhomologous positions. Proc. Natl. Acad. Sci. USA 1983, 80, 5675–5679. [Google Scholar]
- Jinks-Robertson, S.; Petes, T.D. High-frequency meiotic gene conversion between repeated genes on nonhomologous chromosomes in yeast. Proc. Natl. Acad. Sci. USA 1985, 82, 3350–3354. [Google Scholar]
- Haber, J.E.; Leung, W.Y.; Borts, R.H.; Lichten, M. The frequency of meiotic recombination in yeast is independent of the number and position of homologous donor sequences: Implications for chromosome pairing. Proc. Natl. Acad. Sci. USA 1991, 88, 1120–1124. [Google Scholar]
- Jinks-Robertson, S.; Petes, T.D. Chromosomal translocations generated by high-frequency meiotic recombination between repeated yeast genes. Genetics 1986, 114, 731–752. [Google Scholar]
- Lichten, M.; Borts, R.H.; Haber, J.E. Meiotic gene conversion and crossing over between dispersed homologous sequences occurs frequently in Saccharomyces cerevisiae. Genetics 1987, 115, 233–246. [Google Scholar]
- Jinks-Robertson, S.; Michelitch, M.; Ramcharan, S. Substrate length requirements for efficient mitotic recombination in Saccharomyces cerevisiae. Mol. Cell Biol. 1993, 13, 3937–3950. [Google Scholar]
- Lichten, M.; Haber, J.E. Position effects in ectopic and allelic mitotic recombination in Saccharomyces cerevisiae. Genetics 1989, 123, 261–268. [Google Scholar]
- Kupiec, M.; Petes, T.D. Allelic and ectopic recombination between Ty elements in yeast. Genetics 1988, 119, 549–559. [Google Scholar]
- Steele, D.F.; Morris, M.E.; Jinks-Robertson, S. Allelic and ectopic interactions in recombination-defective yeast strains. Genetics 1991, 127, 53–60. [Google Scholar]
- Jackson, J.A.; Fink, G.R. Meiotic recombination between duplicated genetic elements in Saccharomyces cerevisiae. Genetics 1985, 109, 303–332. [Google Scholar]
- Bailis, A.M.; Rothstein, R. A defect in mismatch repair in Saccharomyces cerevisiae stimulates ectopic recombination between homeologous genes by an excision repair dependent process. Genetics 1990, 126, 535–547. [Google Scholar]
- Harris, S.; Rudnicki, K.S.; Haber, J.E. Gene conversions and crossing over during homologous and homeologous ectopic recombination in Saccharomyces cerevisiae. Genetics 1993, 135, 5–16. [Google Scholar]
- Mézard, C.; Pompon, D.; Nicolas, A. Recombination between similar but not identical DNA sequences during yeast transformation occurs within short stretches of identity. Cell 1992, 70, 659–670. [Google Scholar]
- Datta, A.; Adjiri, A.; New, L.; Crouse, G.F.; Jinks-Robertson, S. Mitotic crossovers between diverged sequences are regulated by mismatch repair proteins in Saccharomyces cerevisiae. Mol. Cell Biol. 1996, 16, 1085–1093. [Google Scholar]
- Datta, A.; Hendrix, M.; Lipsitch, M.; Jinks-Robertson, S. Dual roles for DNA sequence identity and the mismatch repair system in the regulation of mitotic crossing-over in yeast. Proc. Natl. Acad. Sci. USA 1997, 94, 9757–9762. [Google Scholar]
- Chen, W.; Jinks-Robertson, S. Mismatch repair proteins regulate heteroduplex formation during mitotic recombination in yeast. Mol. Cell Biol. 1998, 18, 6525–6537. [Google Scholar]
- Chen, W.; Jinks-Robertson, S. The role of the mismatch repair machinery in regulating mitotic and meiotic recombination between diverged sequences in yeast. Genetics 1999, 151, 1299–1313. [Google Scholar]
- Ahn, B.Y.; Dornfeld, K.J.; Fagrelius, T.J.; Livingston, D.M. Effect of limited homology on gene conversion in a Saccharomyces cerevisiae plasmid recombination system. Mol. Cell Biol. 1988, 8, 2442–2448. [Google Scholar]
- Shen, P.; Huang, H.V. Homologous recombination in Escherichia coli: Dependence on substrate length and homology. Genetics 1986, 112, 441–457. [Google Scholar]
- Waldman, A.S. Ensuring the fidelity of recombination in mammalian chromosomes. Bioessays 2008, 30, 1163–1171. [Google Scholar]
- Sugawara, N.; Ira, G.; Haber, J.E. DNA length dependence of the single-strand annealing pathway and the role of Saccharomyces cerevisiae RAD59 in double-strand break repair. Mol. Cell Biol. 2000, 20, 5300–5309. [Google Scholar]
- Kijima, T.E.; Innan, H. On the estimation of the insertion time of LTR retrotransposable elements. Mol. Biol Evol. 2010, 27, 896–904. [Google Scholar]
- Murti, J.R.; Bumbulis, M.; Schimenti, J.C. High-frequency germ line gene conversion in transgenic mice. Mol. Cell Biol. 1992, 12, 2545–2552. [Google Scholar]
- Schildkraut, E.; Miller, C.A.; Nickoloff, J.A. Gene conversion and deletion frequencies during double-strand break repair in human cells are controlled by the distance between direct repeats. Nucleic Acids Res. 2005, 33, 1574–1580. [Google Scholar]
- Perez, C.; Guyot, V.; Cabaniols, J.P.; Gouble, A.; Micheaux, B.; Smith, J.; Leduc, S.; Pâques, F.; Duchateau, P. Factors affecting double-strand break-induced homologous recombination in mammalian cells. Biotechniques 2005, 39, 109–115. [Google Scholar]
- Waldman, A.S.; Liskay, R.M. Differential effects of base-pair mismatch on intrachromosomal versus extrachromosomal recombination in mouse cells. Proc. Natl. Acad. Sci. USA 1987, 84, 5340–5344. [Google Scholar]
- Waldman, A.S.; Liskay, R.M. Dependence of intrachromosomal recombination in mammalian cells on uninterrupted homology. Mol. Cell Biol. 1988, 8, 5350–5357. [Google Scholar]
- Elliott, B.; Richardson, C.; Winderbaum, J.; Nickoloff, J.A.; Jasin, M. Gene conversion tracts from double-strand break repair in mammalian cells. Mol. Cell Biol. 1998, 18, 93–101. [Google Scholar]
- Lukacsovich, T.; Waldman, A.S. Suppression of intrachromosomal gene conversion in mammalian cells by small degrees of sequence divergence. Genetics 1999, 151, 1559–1568. [Google Scholar]
- Yang, D.; Goldsmith, E.B.; Lin, Y.; Waldman, B.C.; Kaza, V.; Waldman, A.S. Genetic exchange between homeologous sequences in mammalian chromosomes is averted by local homology requirements for initiation and resolution of recombination. Genetics 2006, 174, 135–144. [Google Scholar]
- Nickoloff, J.A.; Chen, E.Y.; Heffron, F. A 24-base-pair DNA sequence from the MAT locus stimulates intergenic recombination in yeast. Proc. Natl. Acad. Sci. USA 1986, 83, 7831–7835. [Google Scholar]
- Plessis, A.; Perrin, A.; Haber, J.E.; Dujon, B. Site-specific recombination determined by I-SceI, a mitochondrial group I intron-encoded endonuclease expressed in the yeast nucleus. Genetics 1992, 130, 451–460. [Google Scholar]
- Chen, J.M.; Fe′rec, C.; Cooper, D.N. Gene conversion in human genetic disease. Genes 2010, 1, 550–563. [Google Scholar]
- Chuzhanova, N.; Chen, J.M.; Bacolla, A.; Patrinos, G.P.; Férec, C.; Wells, R.D.; Cooper, D.N. Gene conversion causing human inherited disease: Evidence for involvement of non-B-DNA-forming sequences and recombination-promoting motifs in DNA breakage and repair. Hum. Mutat. 2009, 30, 1189–1198. [Google Scholar]
- Harfe, B.D.; Jinks-Robertson, S. DNA mismatch repair and genetic instability. Annu. Rev. Genet. 2000, 34, 359–399. [Google Scholar]
- Wiuf, C.; Hein, J. The coalescent with gene conversion. Genetics 2000, 155, 451–462. [Google Scholar]
- Innan, H. A method for estimating the mutation, gene conversion and recombination parameters in small multigene families. Genetics 2002, 161, 865–872. [Google Scholar]
- Innan, H. The coalescent and infinite-site model of a small multigene family. Genetics 2003, 163, 803–810. [Google Scholar]
- Ohta, T. Allelic and nonallelic homology of a supergene family. Proc. Natl. Acad. Sci. USA 1982, 79, 3251–3254. [Google Scholar]
- Takuno, S.; Innan, H. Selection to maintain paralogous amino acid differences under the pressure of gene conversion in the heat-shock protein genes in yeast. Mol. Biol. Evol. 2009, 26, 2655–2659. [Google Scholar]
- Thornton, K.; Long, M. Excess of amino acid substitutions relative to polymorphism between X-linked duplications in Drosophila melanogaster. Mol. Biol. Evol. 2005, 22, 273–284. [Google Scholar]
- Arguello, J.R.; Chen, Y.; Yang, S.; Wang, W.; Long, M. Origination of an X-linked testes chimeric gene by illegitimate recombination in Drosophila. PLoS Genet. 2006, 2, e77. [Google Scholar]
- Nielsen, K.M.; Kasper, J.; Choi, M.; Bedford, T.; Kristiansen, K.; Wirth, D.F.; Volkman, S.K.; Lozovsky, E.R.; Hartl, D.L. Gene conversion as a source of nucleotide diversity in Plasmodium falciparum. Mol. Biol. Evol. 2003, 20, 726–734. [Google Scholar]
- Takuno, S.; Nishio, T.; Satta, Y.; Innan, H. Preservation of a pseudogene by gene conversion and diversifying selection. Genetics 2008, 180, 517–531. [Google Scholar]
- Eda, M.; Kuro-o, M.; Higuchi, H.; Hasegawa, H.; Koike, H. Mosaic gene conversion after a tandem duplication of mtDNA sequence in Diomedeidae (albatrosses). Genes Genet. Syst. 2010, 85, 129–139. [Google Scholar]
- Innan, H. A two-locus gene conversion model with selection and its application to the human RHCE and RHD genes. Proc. Natl. Acad. Sci. USA 2003, 100, 8793–8798. [Google Scholar]
- Rozen, S.; Skaletsky, H.; Marszalek, J.D.; Minx, P.J.; Cordum, H.S.; Waterston, R.H.; Wilson, R.K.; Page, D.C. Abundant gene conversion between arms of palindromes in human and ape Y chromosomes. Nature 2003, 423, 873–876. [Google Scholar]
- Ogorelkova, M.; Navarro, A.; Vivarelli, F.; Ramirez-Soriano, A.; Estivill, X. Positive selection and gene conversion drive the evolution of a brain-expressed snoRNAs cluster. Mol. Biol. Evol. 2009, 26, 2563–2571. [Google Scholar]
- Fogel, S.; Mortimer, R.; Lusnak, K. Mechanisms of Meiotic Gene Conversion, or Wanderings on a Foreign Strand; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 1981. [Google Scholar]
- Golin, J.E.; Esposito, M.S. Coincident gene conversion during mitosis in Saccharomyces. Genetics 1984, 107, 355–365. [Google Scholar]
- Ahn, B.Y.; Livingston, D.M. Mitotic gene conversion lengths, coconversion patterns, and the incidence of reciprocal recombination in a Saccharomyces cerevisiae plasmid system. Mol. Cell Biol. 1986, 6, 3685–3693. [Google Scholar]
- Sweetser, D.B.; Hough, H.; Whelden, J.F.; Arbuckle, M.; Nickoloff, J.A. Fine-resolution mapping of spontaneous and double-strand break-induced gene conversion tracts in Saccharomyces cerevisiae reveals reversible mitotic conversion polarity. Mol. Cell Biol. 1994, 14, 3863–3875. [Google Scholar]
- Cho, J.W.; Khalsa, G.J.; Nickoloff, J.A. Gene-conversion tract directionality is influenced by the chromosome environment. Curr. Genet. 1998, 34, 269–279. [Google Scholar]
- Weng, Y.; Barton, S.L.; Cho, J.W.; Nickoloff, J.A. Marker structure and recombination substrate environment influence conversion preference of broken and unbroken alleles in Saccharomyces cerevisiae. Mol. Genet. Genomics. 2001, 265, 461–468. [Google Scholar]
- Taghian, D.G.; Nickoloff, J.A. Chromosomal double-strand breaks induce gene conversion at high frequency in mammalian cells. Mol. Cell Biol. 1997, 17, 6386–6393. [Google Scholar]
- Kim, P.M.; Allen, C.; Wagener, B.M.; Shen, Z.; Nickoloff, J.A. Overexpression of human RAD51 and RAD52 reduces double-strand break-induced homologous recombination in mammalian cells. Nucleic Acids Res. 2001, 29, 4352–4360. [Google Scholar]
- Gloor, G.B.; Nassif, N.A.; Johnson-Schlitz, D.M.; Preston, C.R.; Engels, W.R. Targeted gene replacement in Drosophila via P element-induced gap repair. Science 1991, 253, 1110–1117. [Google Scholar]
- Hilliker, A.J.; Harauz, G.; Reaume, A.G.; Gray, M.; Clark, S.H.; Chovnick, A. Meiotic gene conversion tract length distribution within the rosy locus of Drosophila melanogaster. Genetics 1994, 137, 1019–1026. [Google Scholar]
- Johnson-Schlitz, D.M.; Engels, W.R. P-element-induced interallelic gene conversion of insertions and deletions in Drosophila melanogaster. Mol. Cell Biol. 1993, 13, 7006–7018. [Google Scholar]
- Preston, C.R.; Engels, W.R. P-element-induced male recombination and gene conversion in Drosophila. Genetics 1996, 144, 1611–1622. [Google Scholar]
- de Massy, B. Distribution of meiotic recombination sites. Trends Genet. 2003, 19, 514–522. [Google Scholar]
- Palmer, S.; Schildkraut, E.; Lazarin, R.; Nguyen, J.; Nickoloff, J.A. Gene conversion tracts in Saccharomyces cerevisiae can be extremely short and highly directional. Nucleic Acids Res. 2003, 31, 1164–1173. [Google Scholar]
- Yang, D.; Waldman, A.S. Fine-resolution analysis of products of intrachromosomal homeologous recombination in mammalian cells. Mol. Cell Biol. 1997, 17, 3614–3628. [Google Scholar]
- Rukść, A.; Bell-Rogers, P.; Smith, J.D.; Baker, M.D. Analysis of spontaneous gene conversion tracts within and between mammalian chromosomes. J. Mol. Biol. 2008, 377, 337–351. [Google Scholar]
- Mancera, E.; Bourgon, R.; Brozzi, A.; Huber, W.; Steinmetz, L.M. High-resolution mapping of meiotic crossovers and non-crossovers in yeast. Nature 2008, 454, 479–485. [Google Scholar]
- Sawyer, S. Statistical tests for detecting gene conversion. Mol. Biol. Evol. 1989, 6, 526–538. [Google Scholar]
- Mansai, S.P.; Innan, H. The power of the methods for detecting interlocus gene conversion. Genetics. 2010, 184, 517–527. [Google Scholar]
- Benovoy, D.; Drouin, G. Ectopic gene conversions in the human genome. Genomics 2009, 93, 27–32. [Google Scholar]
- Stephens, J.C. Statistical methods of DNA sequence analysis: Detection of intragenic recombination or gene conversion. Mol. Biol. Evol. 1985, 2, 539–556. [Google Scholar]
- Takahata, N. Comments on the detection of reciprocal recombination or gene conversion. Immunogenetics. 1994, 39, 146–149. [Google Scholar]
- Betrán, E.; Rozas, J.; Navarro, A.; Barbadilla, A. The estimation of the number and the length distribution of gene conversion tracts from population DNA sequence data. Genetics 1997, 146, 89–99. [Google Scholar]
- Jakobsen, I.B.; Wilson, S.R.; Easteal, S. The partition matrix: Exploring variable phylogenetic signals along nucleotide sequence alignments. Mol. Biol. Evol. 1997, 14, 474–484. [Google Scholar]
- Ezawa, K.; OOta, S.; Saitou, N.; Investigators, S.T.N.Y. Proceedings of the SMBE Tri-National Young Investigators' Workshop 2005. Genome-wide search of gene conversions in duplicated genes of mouse and rat. Mol. Biol. Evol. 2006, 23, 927–940. [Google Scholar]
- Adams, J.G., II; Morrison, W.T.; Steinberg, M.H. Hemoglobin Parchman: Double crossover within a single human gene. Science 1982, 218, 291–293. [Google Scholar]
- Eikenboom, J.C.; Vink, T.; Briët, E.; Sixma, J.J.; Reitsma, P.H. Multiple substitutions in the von Willebrand factor gene that mimic the pseudogene sequence. Proc. Natl. Acad. Sci. USA 1994, 91, 2221–2224. [Google Scholar]
- Watnick, T.J.; Gandolph, M.A.; Weber, H.; Neumann, H.P.; Germino, G.G. Gene conversion is a likely cause of mutation in PKD1. Hum. Mol. Genet. 1998, 7, 1239–1243. [Google Scholar]
- De Marco, P.; Moroni, A.; Merello, E.; de Franchis, R.; Andreussi, L.; Finnell, R.H.; Barber, R.C.; Cama, A.; Capra, V. Folate pathway gene alterations in patients with neural tube defects. Am J. Med. Genet. 2000, 95, 216–223. [Google Scholar]
- Hatton, C.; Cooper, A.; Whitehouse, C.; Wraith, J. Mutation analysis in 46 British and Irish patients with Gaucher's disease. Arch. Dis. Child. 1997, 77, 17–22. [Google Scholar]
- Vázquez, N.; Lehrnbecher, T.; Chen, R.; Christensen, B.L.; Gallin, J.I.; Malech, H.; Holland, S.; Zhu, S.; Chanock, S.J. Mutational analysis of patients with p47-phox-deficient chronic granulomatous disease: The significance of recombination events between the p47-phox gene (NCF1) and its highly homologous pseudogenes. Exp. Hematol. 2001, 29, 234–243. [Google Scholar]
- Boocock, G.R.; Morrison, J.A.; Popovic, M.; Richards, N.; Ellis, L.; Durie, P.R.; Rommens, J.M. Mutations in SBDS are associated with Shwachman-Diamond syndrome. Nat. Genet. 2003, 33, 97–101. [Google Scholar]
- Gupta, P.K.; Adamtziki, E.; Budde, U.; Jaiprakash, M.; Kumar, H.; Harbeck-Seu, A.; Kannan, M.; Oyen, F.; Obser, T.; Wedekind, I.; Saxena, R.; Schneppenheim, R. Gene conversions are a common cause of von Willebrand disease. Br. J. Haematol. 2005, 130, 752–758. [Google Scholar]
- Gupta, P.K.; Saxena, R.; Adamtziki, E.; Budde, U.; Oyen, F.; Obser, T.; Schneppenheim, R. Genetic defects in von Willebrand disease type 3 in Indian and Greek patients. Blood Cells Mol. Dis. 2008, 41, 219–222. [Google Scholar]
- Friães, A.; Rêgo, A.T.; Aragüés, J.M.; Moura, L.F.; Mirante, A.; Mascarenhas, M.R.; Kay, T.T.; Lopes, L.A.; Rodrigues, J.C.; Guerra, S.; Dias, T.; Teles, A.G.; Gonc¸alves, J. CYP21A2 mutations in Portuguese patients with congenital adrenal hyperplasia: Identification of two novel mutations and characterization of four different partial gene conversions. Mol. Genet. Metab. 2006, 88, 58–65. [Google Scholar]
- Tayebi, N.; Stubblefield, B.K.; Park, J.K.; Orvisky, E.; Walker, J.M.; LaMarca, M.E.; Sidransky, E. Reciprocal and nonreciprocal recombination at the glucocerebrosidase gene region: implications for complexity in Gaucher disease. Am J. Hum. Genet. 2003, 72, 519–534. [Google Scholar]
- Nicolis, E.; Bonizzato, A.; Assael, B.M.; Cipolli, M. Identification of novel mutations in patients with Shwachman-Diamond syndrome. Hum. Mutat. 2005, 25, 410. [Google Scholar]
- Petes, T.D. Meiotic recombination hot spots and cold spots. Nat. Rev. Genet. 2001, 2, 360–369. [Google Scholar]
- Myers, S.; Bottolo, L.; Freeman, C.; McVean, G.; Donnelly, P. A fine-scale map of recombination rates and hotspots across the human genome. Science 2005, 310, 321–324. [Google Scholar]
- Jeffreys, A.J.; Neumann, R.; Panayi, M.; Myers, S.; Donnelly, P. Human recombination hot spots hidden in regions of strong marker association. Nat. Genet. 2005, 37, 601–606. [Google Scholar]
- Paigen, K.; Petkov, P. Mammalian recombination hot spots: properties, control and evolution. Nat. Rev. Genet. 2010, 11, 221–233. [Google Scholar]
- Han, L.L.; Keller, M.P.; Navidi, W.; Chance, P.F.; Arnheim, N. Unequal exchange at the Charcot-Marie-Tooth disease type 1A recombination hot-spot is not elevated above the genome average rate. Hum. Mol. Genet. 2000, 9, 1881–1889. [Google Scholar]
- Bosch, E.; Hurles, M.E.; Navarro, A.; Jobling, M.A. Dynamics of a human interparalog gene conversion hotspot. Genome Res. 2004, 14, 835–844. [Google Scholar]
- Turner, D.J.; Miretti, M.; Rajan, D.; Fiegler, H.; Carter, N.P.; Blayney, M.L.; Beck, S.; Hurles, M.E. Germline rates of de novo meiotic deletions and duplications causing several genomic disorders. Nat. Genet. 2008, 40, 90–95. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Mansai, S.P.; Kado, T.; Innan, H. The Rate and Tract Length of Gene Conversion between Duplicated Genes. Genes 2011, 2, 313-331. https://doi.org/10.3390/genes2020313
Mansai SP, Kado T, Innan H. The Rate and Tract Length of Gene Conversion between Duplicated Genes. Genes. 2011; 2(2):313-331. https://doi.org/10.3390/genes2020313
Chicago/Turabian StyleMansai, Sayaka P., Tomoyuki Kado, and Hideki Innan. 2011. "The Rate and Tract Length of Gene Conversion between Duplicated Genes" Genes 2, no. 2: 313-331. https://doi.org/10.3390/genes2020313
APA StyleMansai, S. P., Kado, T., & Innan, H. (2011). The Rate and Tract Length of Gene Conversion between Duplicated Genes. Genes, 2(2), 313-331. https://doi.org/10.3390/genes2020313