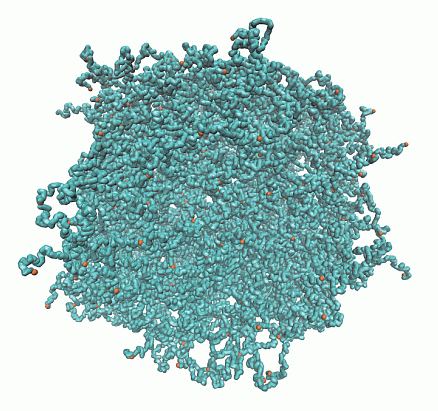
Structure of Microgels with Debye–Hückel Interactions
Abstract
:1. Introduction
2. Models
2.1. Microgel

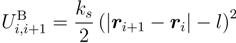
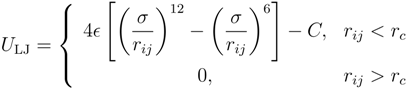
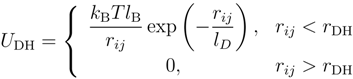
2.2. Brownian Multiparticle Collision Dynamics
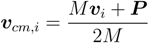
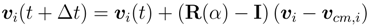
2.3. Parameters
 . The Lennard–Jones parameters are σ = 0.8l, ε/kBT = 0.5, 1.0 and 1.5 for a poor solvent and 1.0 for a good solvent. For the bonds, we set ks = 103kBT/l2. The collision time is Δt = 0.1τ, and we perform 20 molecular dynamics simulation steps between collisions. To achieve a reasonable statistical accuracy, we performed, at least, 5.0 × 104 collision steps, which corresponds to 106 molecular dynamics simulation steps, after reaching a stationary state in every simulation.
. The Lennard–Jones parameters are σ = 0.8l, ε/kBT = 0.5, 1.0 and 1.5 for a poor solvent and 1.0 for a good solvent. For the bonds, we set ks = 103kBT/l2. The collision time is Δt = 0.1τ, and we perform 20 molecular dynamics simulation steps between collisions. To achieve a reasonable statistical accuracy, we performed, at least, 5.0 × 104 collision steps, which corresponds to 106 molecular dynamics simulation steps, after reaching a stationary state in every simulation. 3. Results
3.1. Microgel in Good Solvent (lD = 0)
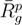 for Nc = 0, 147 and 729 . Here,
for Nc = 0, 147 and 729 . Here,  is the square root of the average over all polymers of the mean square radius of gyration, where the radius of gyration of a polymer (
is the square root of the average over all polymers of the mean square radius of gyration, where the radius of gyration of a polymer (  ) itself is defined by:
) itself is defined by:
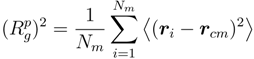
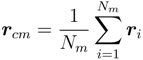
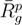 ~ (Nm − 1)v with the number of bonds. Thereby, the critical exponent, v, for the non-cross-linked polymers closely follows the theoretical prediction v ≈ 0.59 [39]. Similarly, the
~ (Nm − 1)v with the number of bonds. Thereby, the critical exponent, v, for the non-cross-linked polymers closely follows the theoretical prediction v ≈ 0.59 [39]. Similarly, the 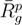 values for the systems with Nc = 147 and 729 follow a power law; however, with the somewhat larger exponent v ≈ 0.62. Hence, cross-linking leads to swelling of the polymer chains.
values for the systems with Nc = 147 and 729 follow a power law; however, with the somewhat larger exponent v ≈ 0.62. Hence, cross-linking leads to swelling of the polymer chains. 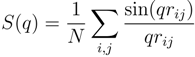
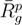 ~ (Nm − 1)0.62. Hence, the polymer conformations are determined by thermal fluctuations, intramolecular and intermolecular interactions and the cross-links.
~ (Nm − 1)0.62. Hence, the polymer conformations are determined by thermal fluctuations, intramolecular and intermolecular interactions and the cross-links.  of polymers on the bond number Nm − 1 for Nc = 0 (squares), 147 (open squares) and 729 (bullets) under good solvent conditions (lD = 0). The solid line is proportional to N0.59 and the dashed lineto N0.62.
of polymers on the bond number Nm − 1 for Nc = 0 (squares), 147 (open squares) and 729 (bullets) under good solvent conditions (lD = 0). The solid line is proportional to N0.59 and the dashed lineto N0.62.
 of polymers on the bond number Nm − 1 for Nc = 0 (squares), 147 (open squares) and 729 (bullets) under good solvent conditions (lD = 0). The solid line is proportional to N0.59 and the dashed lineto N0.62.
of polymers on the bond number Nm − 1 for Nc = 0 (squares), 147 (open squares) and 729 (bullets) under good solvent conditions (lD = 0). The solid line is proportional to N0.59 and the dashed lineto N0.62.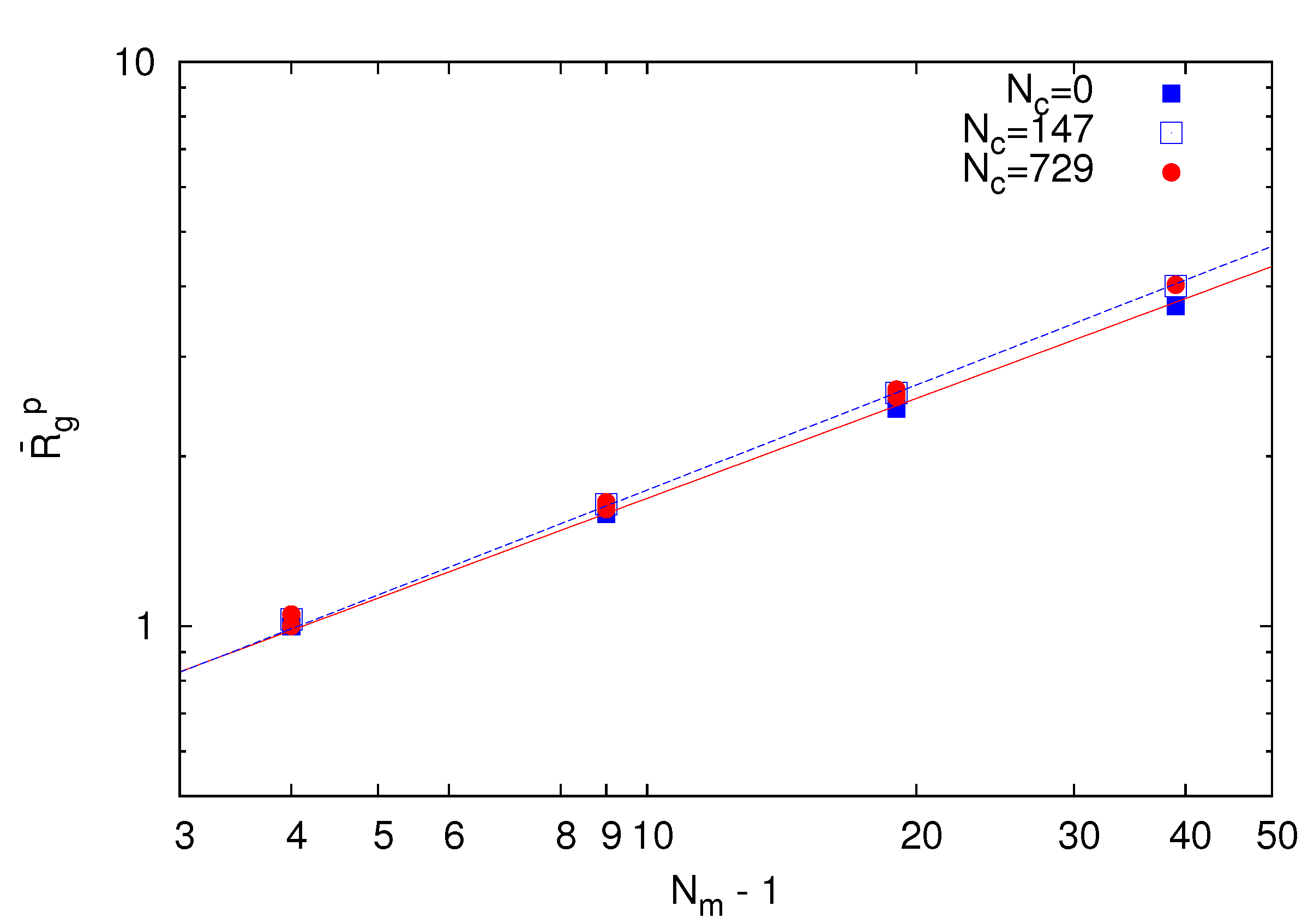
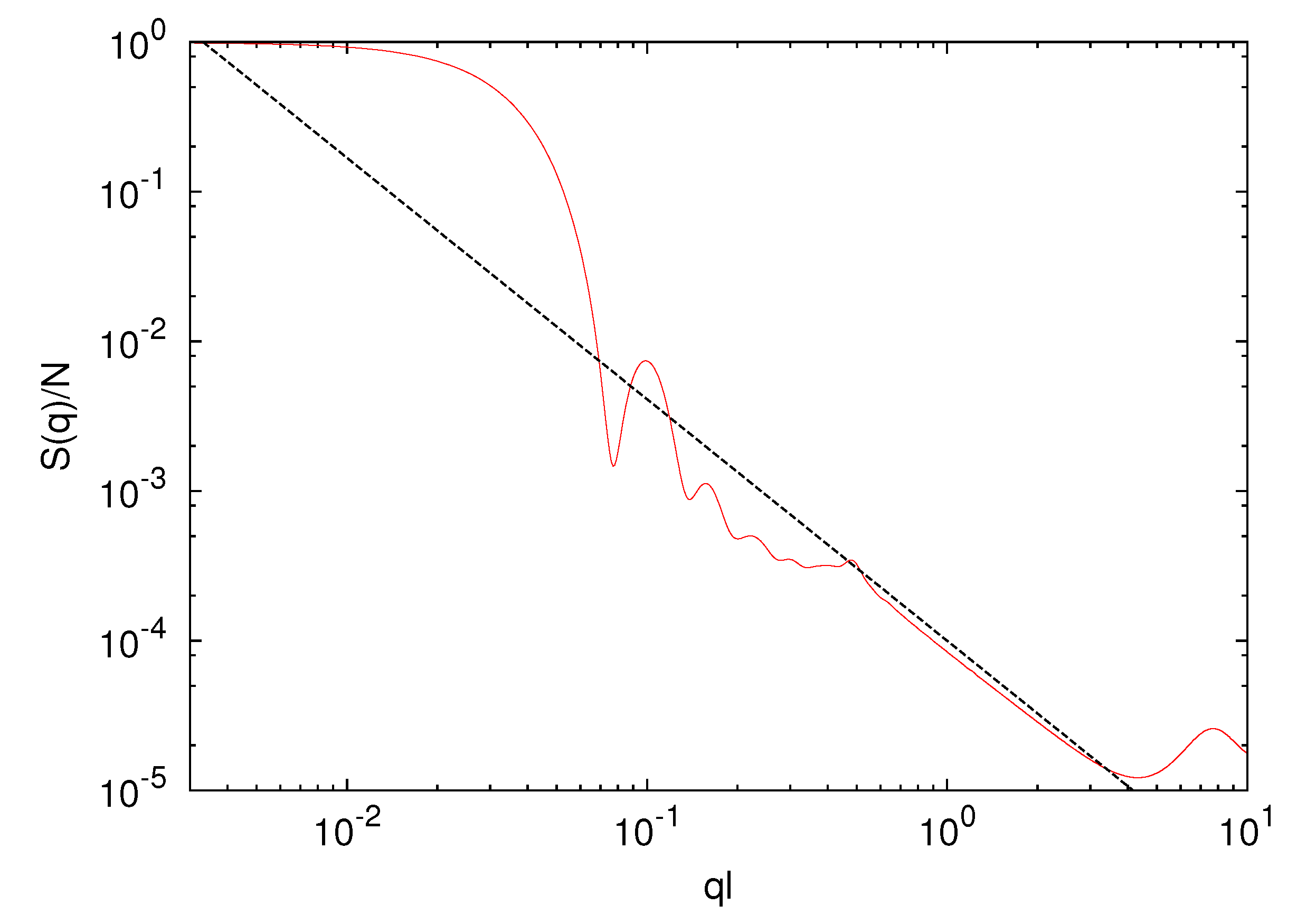
3.2. Microgel in Poor Solvent (lD = 0)
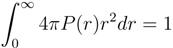
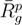 scales as
scales as 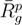 ∝ (Nm − 1)0.6 with polymer length, and the interface is less sharp. The scaling exponent, 0.6, is smaller than 0.62 obtained for microgels in a good solvent. Hence, the polymers are somewhat more compact for ε/kBT = 0.5 as compared to the bare good solvent system. The attractive interaction brings the polymers closer to the scaling behavior of free polymers.
∝ (Nm − 1)0.6 with polymer length, and the interface is less sharp. The scaling exponent, 0.6, is smaller than 0.62 obtained for microgels in a good solvent. Hence, the polymers are somewhat more compact for ε/kBT = 0.5 as compared to the bare good solvent system. The attractive interaction brings the polymers closer to the scaling behavior of free polymers.
3.3. Microgel with Debye–Hückel Interaction
3.3.1. Microgel Radius of Gyration
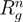 denotes the radius of gyration of a microgel under good solvent conditions.
denotes the radius of gyration of a microgel under good solvent conditions.
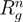 denotes the radius of gyration of a microgel under good solvent conditions.
denotes the radius of gyration of a microgel under good solvent conditions.
3.3.2. Microgel Structure Factor

3.3.3. Polymer Size Scaling
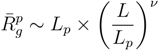
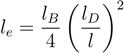
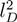 for freely jointed chains with fixed bond lengths [47,48,49]. Figure 8 shows the radii of gyration for the various considered systems. We obtain a rather good scaling behavior for all obtained values. For small L/Lp (≤ 2),
for freely jointed chains with fixed bond lengths [47,48,49]. Figure 8 shows the radii of gyration for the various considered systems. We obtain a rather good scaling behavior for all obtained values. For small L/Lp (≤ 2), 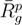 /Lp increases linearly with L/Lp, i.e., the polymers exhibit rod-like behavior, whereas for L/Lp ≳ 4, Rg/Lp ~ L0.6, i.e., it crosses over to self-avoiding walk behavior. Similar results have been reported in previous studies on a single polyelectrolyte chain [47,50]. The scaling results are in agreement with the observed dependencies of the structure factors of Figure 7.
/Lp increases linearly with L/Lp, i.e., the polymers exhibit rod-like behavior, whereas for L/Lp ≳ 4, Rg/Lp ~ L0.6, i.e., it crosses over to self-avoiding walk behavior. Similar results have been reported in previous studies on a single polyelectrolyte chain [47,50]. The scaling results are in agreement with the observed dependencies of the structure factors of Figure 7.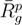 /Lp on the ratio L/Lp for Nc = 0, 147 and 729, Np = 20 and 40 and lB/l = 1,2,5 and 9. The black line is proportional to (L/Lp)0.6 and the red line to L/Lp.
/Lp on the ratio L/Lp for Nc = 0, 147 and 729, Np = 20 and 40 and lB/l = 1,2,5 and 9. The black line is proportional to (L/Lp)0.6 and the red line to L/Lp.
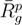 /Lp on the ratio L/Lp for Nc = 0, 147 and 729, Np = 20 and 40 and lB/l = 1,2,5 and 9. The black line is proportional to (L/Lp)0.6 and the red line to L/Lp.
/Lp on the ratio L/Lp for Nc = 0, 147 and 729, Np = 20 and 40 and lB/l = 1,2,5 and 9. The black line is proportional to (L/Lp)0.6 and the red line to L/Lp.
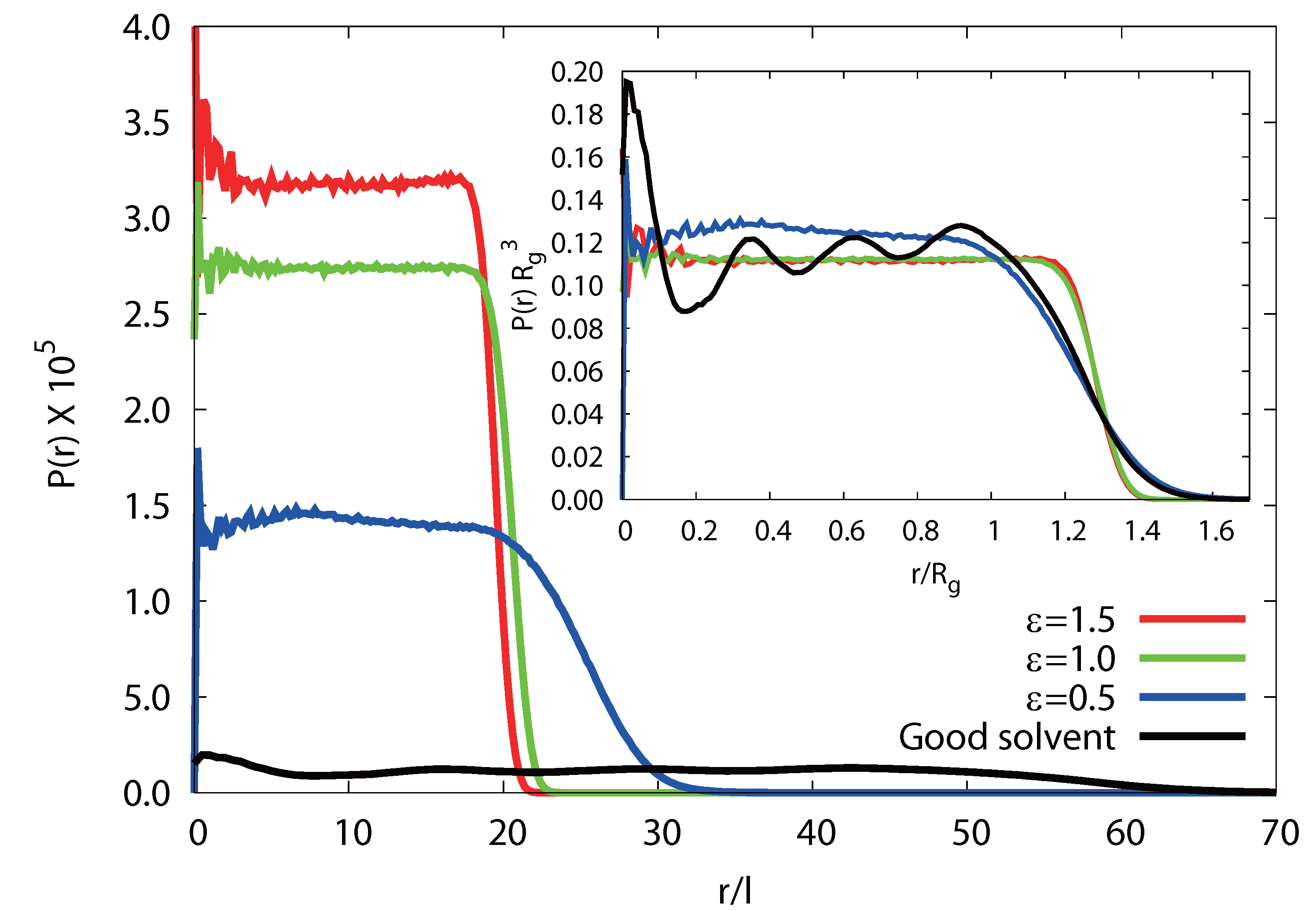
3.3.4. Radial Monomer Distribution
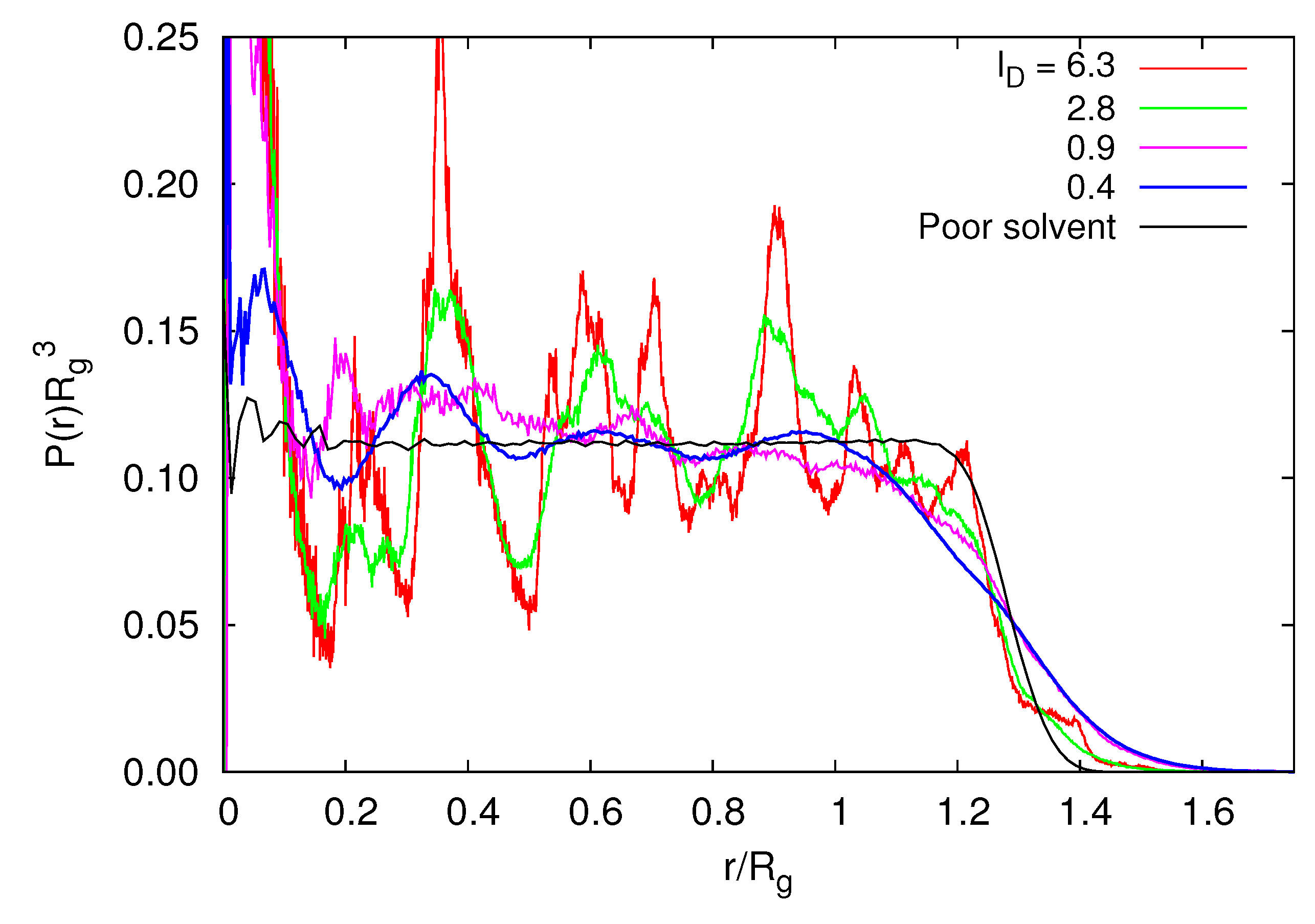
3.3.5. Radial Polymer Conformation
 (rcm), in a microgel. As shown in Figure 10, we find a qualitative difference for
(rcm), in a microgel. As shown in Figure 10, we find a qualitative difference for 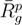 /Lp > 2.5 and
/Lp > 2.5 and 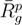 /Lp < 1. For
/Lp < 1. For 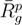 /Lp > 2.5, i.e., lD/l ≲ 0.45,
/Lp > 2.5, i.e., lD/l ≲ 0.45,  exceeds the mean value at large rcm/Rg. Hence, polymers near the surface are swollen as compared to internal polymers. We attribute the inhomogeneities to anisotropic intramolecular interactions by short-range repulsion. Internal polymers experience an almost isotropic interaction, whereas at the surface, the symmetry is broken and repulsion is stronger from inside to outside, which leads to a swelling. For
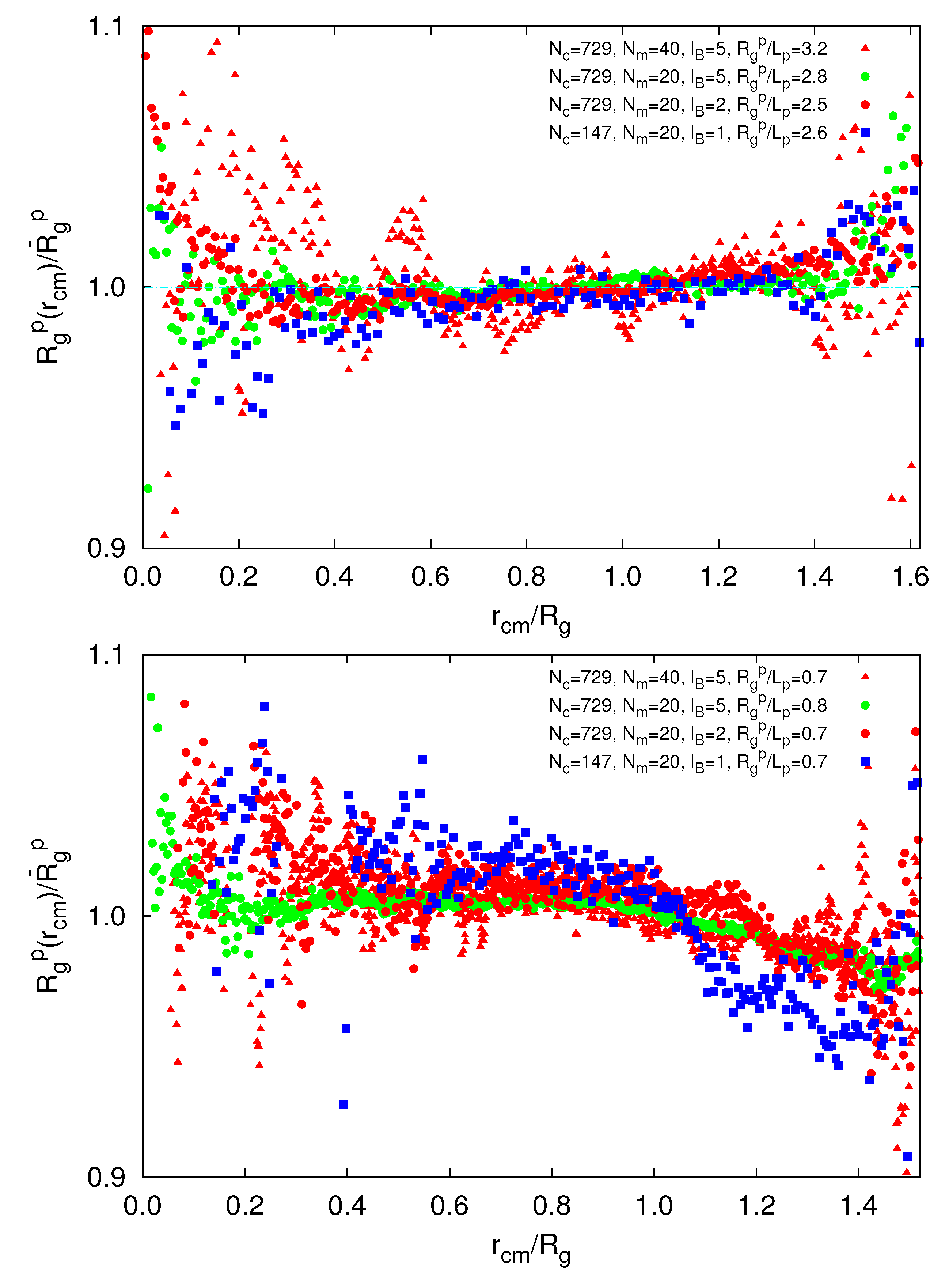
exceeds the mean value at large rcm/Rg. Hence, polymers near the surface are swollen as compared to internal polymers. We attribute the inhomogeneities to anisotropic intramolecular interactions by short-range repulsion. Internal polymers experience an almost isotropic interaction, whereas at the surface, the symmetry is broken and repulsion is stronger from inside to outside, which leads to a swelling. For 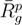 /Lp < 1, i.e., lD/l ≳ 2,
/Lp < 1, i.e., lD/l ≳ 2,  is smaller than the average value at large rcm/Rg. Thus, the outside polymers are somewhat more compact than the internal polymers. This is attributed to the inhomogeneous radial monomer distribution, as displayed in Figure 9. The larger interaction range of the Debye-Hückel potential for these parameters combined with a larger number of neighbors leads to the stronger swelling of internal polymers than those at the surface. Overall, the effect is small, but is a consequence of the finite size of a microgel and is thus not present in bulk systems.
is smaller than the average value at large rcm/Rg. Thus, the outside polymers are somewhat more compact than the internal polymers. This is attributed to the inhomogeneous radial monomer distribution, as displayed in Figure 9. The larger interaction range of the Debye-Hückel potential for these parameters combined with a larger number of neighbors leads to the stronger swelling of internal polymers than those at the surface. Overall, the effect is small, but is a consequence of the finite size of a microgel and is thus not present in bulk systems.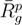 /Lp > 2.5 (top) and
/Lp > 2.5 (top) and 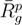 /Lp < 1 (bottom), Nc = 147 and 729 and Nm = 20 and 40. The upper bounds of rcm are defined by the condition
/Lp < 1 (bottom), Nc = 147 and 729 and Nm = 20 and 40. The upper bounds of rcm are defined by the condition 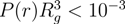 .
.
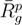 /Lp > 2.5 (top) and
/Lp > 2.5 (top) and 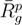 /Lp < 1 (bottom), Nc = 147 and 729 and Nm = 20 and 40. The upper bounds of rcm are defined by the condition
/Lp < 1 (bottom), Nc = 147 and 729 and Nm = 20 and 40. The upper bounds of rcm are defined by the condition 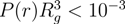 .
.
4. Summary and Conclusions
Acknowledgments
Conflicts of Interest
References
- Tanaka, T. Collapse of gels and the critical endpoint. Phys. Rev. Lett. 1978, 40, 820–823. [Google Scholar] [CrossRef]
- Ilmain, F.; Tanaka, T.; Kokufuta, E. Volume transition in a gel driven by hydrogen bonding. Nature 1991, 349, 400–401. [Google Scholar] [CrossRef]
- Tanaka, T.; Nishio, I.; Sun, S.T.; Ueno-Nishio, S. Collapse of gels in an electric field. Science 1982, 218, 467–469. [Google Scholar] [CrossRef]
- Polotsky, A.A.; Plamper, F.A.; Borisov, O.V. Collapse-to-swelling transitions in pH- and thermoresponsive microgels in aqueous dispersions: The thermodynamic theory. Macromolecules 2013, 46, 8702–8709. [Google Scholar]
- Das, M.; Zhang, H.; Kumacheva, E. MICROGELS: Old materials with new applications. Annu. Rev. Mater. Res. 2006, 36, 117–142. [Google Scholar]
- Richter, A.; Paschew, G.; Klatt, S.; Lienig, J.; Arndt, K.F.; Adler, H.J.P. Review on hydrogel-based pH sensors and microsensors. Sensors 2008, 8, 561–581. [Google Scholar] [CrossRef]
- Oh, J.K.; Drumright, R.; Siegwart, D.J.; Matyjaszewski, K. The development of microgels/nanogels for drug delivery applications. Prog. Polym. Sci. 2008, 33, 448–477. [Google Scholar] [CrossRef]
- Saunders, B.R.; Laajam, N.; Daly, E.; Teow, S.; Hu, X.; Stepto, R. Microgels: From responsive polymer colloids to biomaterials. Adv. Colloid Interface Sci. 2009, 147-148, 251–262. [Google Scholar] [CrossRef]
- Delcea, M.; Möhwald, H.; Skirtach, A.G. Stimuli-responsive LbL capsules and nanoshells for drug delivery. Adv. Drug Deliv. Rev. 2011, 63, 730–747. [Google Scholar] [CrossRef]
- Tan, B.H.; Tam, K.C. Review on the dynamics and micro-structure of pH-responsive nano-colloidal systems. Adv. Colloid Interface Sci. 2008, 136, 25–44. [Google Scholar] [CrossRef]
- Stuart, M.A.C.; Huck, W.T.S.; Genzer, J.; Müller, M.; Ober, C.; Stamm, M.; Sukhorukov, G.B.; Szleifer, I.; Tsukruk, V.V.; Urban, M.; et al. Emerging applications of stimuli-responsive polymer materials. Nat. Mater 2010, 9, 101–113. [Google Scholar] [CrossRef]
- Gokmen, M.T.; Prez, F.E.D. Porous polymer particles: A comprehensive guide to synthesis, characterization, functionalization and applications. Prog. Polym. Sci. 2012, 37. [Google Scholar] [CrossRef] [Green Version]
- Thorne, J.B.; Vine, G.J.; Snowden, M.J. Microgel applications and commercial considerations. Colloid Polym. Sci. 2011, 289, 625–646. [Google Scholar]
- Khokhlov, A.R.; Starodubtzev, S.G.; Vasilevskay, V.V. Conformational transitions in polymer gels: Theory and experiment. Adv. Polym. Sci. 1993, 109, 123–171. [Google Scholar] [CrossRef]
- Schneider, S.; Linse, P. Swelling of cross-linked polyelectrolyte gels. Eur. Phys. J. E Soft Matter 2002, 8, 457–460. [Google Scholar]
- Schneider, S.; Linse, P. Monte Carlo simulation of defect-free cross-linked polyelectrolyte gels. J. Phys. Chem. B 2003, 32, 8030–8040. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Hentschke, R. Computer simulation study on the swelling of a polyelectrolyte gel by a Stockmayer solvent. Phys. Rev. E 2003, 67. [Google Scholar] [CrossRef]
- Yan, Q.; de Pablo, J.J. Monte Carlo simulation of a coarse-grained model of polyelectrolyte networks. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef]
- Mann, B.A.; Everaers, R.; Holm, C.; Kremer, K. Scaling in polyelectrolyte networks. Europhys. Lett. 2004, 67, 786–792. [Google Scholar] [CrossRef]
- Schneider, S.; Linse, P. Discontinuous volume transitions in cross-linked polyelectrolyte gelsinduced by short-range attractions and strong electrostatic coupling. Macromolecules 2004, 37, 3850–3856. [Google Scholar] [CrossRef]
- Mann, B.A.; Holm, C.; Kremer, K. Swelling of polyelectrolyte networks. J. Chem. Phys. 2005, 122. [Google Scholar] [CrossRef]
- Edgecombe, S.; Linse, P. Monte Carlo simulations of cross-linked polyelectrolyte gels with oppositely charged macroions. Langmuir 2006, 22, 3836–3843. [Google Scholar]
- Mann, B.A.; Kremer, K.; Holm, C. The swelling behavior of charged hydrogels. Macromol. Symp. 2006, 237, 90–107. [Google Scholar] [CrossRef]
- Yin, D.W.; Horkay, F.; Douglas, J.F.; de Pablo, J.J. Molecular simulation of the swelling of polyelectrolyte gels by monovalent and divalent counterions. J. Chem. Phys. 2008, 129. [Google Scholar] [CrossRef]
- Yin, D.W.; de la Cruz, M.O.; de Pablo, J.J. Swelling and collapse of polyelectrolyte gels in equilibrium with monovalent and divalent electrolyte solutions. J. Chem. Phys. 2009, 131. [Google Scholar] [CrossRef]
- Quesada-Peres, M.; Ramos, J.; Forcada, J.; Martin-Molina, A. Computer simulations of thermo-sensitive microgels: Quantitative comparison with experimental swelling data. J. Chem. Phys. 2012, 136. [Google Scholar] [CrossRef]
- Quesada-Peres, M.; Maroto-Centeno, J.A.; Martin-Molina, A. Effect of the counterion valence on the behavior of thermo-sensitive gels and microgels: A monte carlo simulation study. Macromolecules 2012, 45, 8872–8879. [Google Scholar] [CrossRef]
- Claudio, G.C.; Kremer, K.; Holm, C.J. Comparison of a hydrogel model to the Poisson-Boltzmann cell model. J. Chem. Phys. 2009, 131. [Google Scholar] [CrossRef]
- Jha, P.K.; Zwanikken, J.W.; Detcheverry, F.A.; de Pablo, J.J.; de la Cruz, M.O. Study of volume phase transitions in polymeric nanogels by theoretically informed coarse-grained simulations. Soft Matter 2011, 7, 5965–5975. [Google Scholar] [CrossRef]
- Jha, P.K.; Zwanikken, J.W.; de Pablo, J.J.; de la Cruz, M.O. Electrostatic control of nanoscale phase behavior of polyelectrolyte networks. Curr. Opin. Solid State Mater. Sci. 2011, 15, 271–276. [Google Scholar] [CrossRef]
- Denton, A.R. Counterion penetration and effective electrostatic interactions in solutions of polyelectrolyte stars and microgels. Phys. Rev. E 2003, 67. [Google Scholar] [CrossRef]
- Ripoll, M.; Winkler, R.G.; Gompper, G. Hydrodynamic screening of star polymers in shear flow. Eur. Phys. J. E Soft Matter 2007, 23, 349–354. [Google Scholar] [CrossRef]
- Winkler, R.G.; Gold, M.; Reineker, P. Collapse of polyelectrolyte macromolecules by counterion condensation and ion pair formation: A molecular dynamics simulation study. Phys. Rev. Lett. 1998, 80. [Google Scholar] [CrossRef]
- Frank, S.; Winkler, R.G. Polyelectrolyte electrophoresis: Field effects and hydrodynamic interactions. EPL 2008, 83, 38004:1–38004:6. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Gompper, G.; Ihle, T.; Kroll, D.M.; Winkler, R.G. Multi-Particle Collision Dynamics: A particle-based mesoscale simulation approach to the hydrodynamics of complex Fluids. Adv. Polym. Sci. 2009, 221, 1–87. [Google Scholar]
- Winkler, R.G. Flow simulations with multiparticle collision dynamics. In Hierarchical Methods for Dynamics in Complex Molecular Systems: IAS Series; Grotendorst, J., Sutmann, G., Gompper, G., Marx, D., Eds.; Forschungszentrum Jülich GmbH: Jülich, Germany, 2012. [Google Scholar]
- Kapral, R. Multiparticle collision dynamics: Simulations of complex systems on mesoscale. Adv. Chem. Phys. 2008, 140. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Senff, H.; Richtering, W. Temperature sensitive microgel suspensions: Colloidal phase behavior and rheology of soft spheres. J. Chem. Phys. 1999, 111. [Google Scholar] [CrossRef]
- Stieger, M.; Richtering, W.; Pedersen, J.S.; Lindner, P. Small-angle neutron scattering study of structural changes in temperature sensitive microgel colloids. J. Chem. Phys. 2004, 120, 6197–6206. [Google Scholar]
- Scherzinger, C.; Holderer, O.; Richter, D.; Richtering, W. Polymer dynamics in responsive microgels: Influence of cononsolvency and microgel architecture. Phys. Chem. Chem. Phys. 2012, 14, 2762–2768. [Google Scholar] [CrossRef]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University: Ithaca, Greece, 1979. [Google Scholar]
- Odijk, T. Polyelectrolytes near the rod limit. J. Polym. Sci., Polym. Phys. Ed. 1977, 15, 477–483. [Google Scholar] [CrossRef]
- Skolnick, J.; Fixman, M. Electrostatic persistence length of a wormlike polyelectrolyte. Macromolecules 1977, 10, 944–948. [Google Scholar] [CrossRef]
- Fixman, M. Electrostatic persistence length. J. Chem. Phys. 2010, 114, 3185–3196. [Google Scholar]
- Ullner, M. Comments on the scaling behavior of flexible polyelectrolytes within the Debye-Hückel approximation. J. Phys. Chem. B 2003, 107, 8097–8110. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Shklovskii, B.I. Persistence length of a polyelectrolyte in salty water: Monte Carlo study. Phys. Rev. E 2002, 66. [Google Scholar] [CrossRef]
- Everaers, R.; Milchev, A.; Yamakov, V. The electrostatic persistence length of polymers beyond the OSF limit. Eur. Phys. J. E 2002, 8, 3–14. [Google Scholar] [CrossRef]
- Micka, U.; Kremer, K. Persistence length of the Debye-Hückel model of weakly charged flexible polyelectrolyte chains. Phys. Rev. E 1996, 54, 2653–2662. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kobayashi, H.; Winkler, R.G. Structure of Microgels with Debye–Hückel Interactions. Polymers 2014, 6, 1602-1617. https://doi.org/10.3390/polym6051602
Kobayashi H, Winkler RG. Structure of Microgels with Debye–Hückel Interactions. Polymers. 2014; 6(5):1602-1617. https://doi.org/10.3390/polym6051602
Chicago/Turabian StyleKobayashi, Hideki, and Roland G. Winkler. 2014. "Structure of Microgels with Debye–Hückel Interactions" Polymers 6, no. 5: 1602-1617. https://doi.org/10.3390/polym6051602