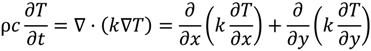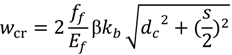1. Introduction
During the past decade, the civil engineering community has been very interested in applications of fibre reinforced polymer (FRP) reinforcement in concrete structures as an alternative to steel reinforcement [
1]. Outstanding characteristics of FRP materials such as high strength-to-weight ratios and resistance to corrosion make FRPs suitable for structures subjected to harsh environments. Progress in FRP manufacturing technology has reduced the material cost and increased the confidence in applications of FRP for civil engineering applications.
Among the many areas of application of FRP, strengthening of existing buildings has gained the most attention, given advantages for fast construction. Nevertheless, applications of FRPs as internal reinforcement in new construction of concrete structural members are growing rapidly. FRP reinforcing bars are now available in different forms for both flexural and shear reinforcement. Demand for FRP internal reinforcement in highly-corrosive environments such as bridges, barrier walls, parking lots, buildings in coastal areas and industrial structures has increased [
2]. Apart from notable advantages of FRPs, application of FRP in structures has a few drawbacks. One of the potential disadvantages of FRP materials is their performance in fire. Degradation of strength and stiffness of FRPs induced by high temperatures could cause substantial loss in load carrying capacity of concrete structures, specifically where they are the only form of reinforcement. On the contrary, conventional concrete structural members with internal steel reinforcement generally exhibit good performance in fire [
3].
Kodur and Bisby [
4] studied the behaviour of FRP reinforced concrete slabs in fire through numerical modelling. They discovered significant differences in the behaviour of FRP reinforced compared to steel reinforced concrete slabs. They have investigated the effects of the type of FRP bars, the overall thickness of the slab, and the cover of the slab on performance of slabs. Bisby and Kodur [
5] developed a simple numerical method to investigate the differences of FRP reinforced slabs with steel reinforced ones. Nigro
et al. [
6] conducted fire tests on 6 FRP reinforced slabs. They recommended to use continuous FRP bars from end to end of the concrete member, and to protect a portion of member at the ends from the effects of fire to avoid bond failure. In North America, design guidance for FRP reinforcement in building is given in ACI 440.1R [
7] and CAN/CSA S806-02 [
8]. Many other countries have similar documents. Although CSA S806 presents recommendations for estimating fire endurance of FRP reinforced concrete elements, the approach is based only on the temperature of the reinforcement and does not directly consider the strength of the FRP reinforced slab in fire. In view of this fact, this study focuses on numerical modelling of the structural behaviour of FRP reinforced slabs in fire. Specific attention has been given to details of reinforcement placement in order to increase the fire endurance.
2. Material Behaviour at High Temperatures
The behaviour of concrete at elevated temperatures is well understood [
9,
10,
11]. On the other hand, FRP behaviour at high temperature is more problematic. Firstly, the properties of commercially available materials can vary widely. Additionally, the time-dependent visco-elastic behaviour of matrix or adhesive makes experimental characterization difficult, and few tests have been conducted. In general, the mechanical properties of FRP degrade at high temperatures depending mainly on the properties of the matrix. Blontrock
et al. [
12] suggested the tensile strength of carbon fiber reinforced plastic (CFRP) and aramid fiber reinforced plastic (AFRP) remains unaffected up to 100 °C but that of GFRP bars decreased consistently with the increase of the temperature. In this paper, two models proposed by Saafi [
13] and Bisby [
14] for degradation of GFRP bars at elevated temperatures are considered.
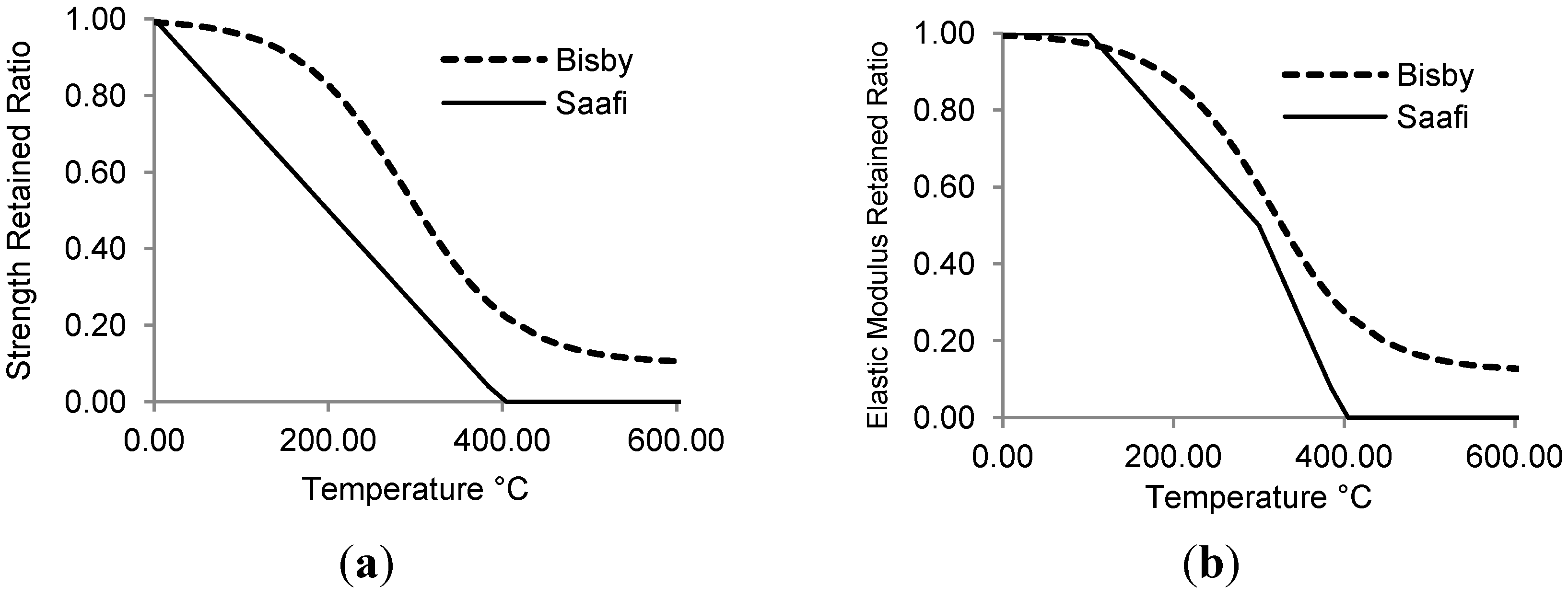
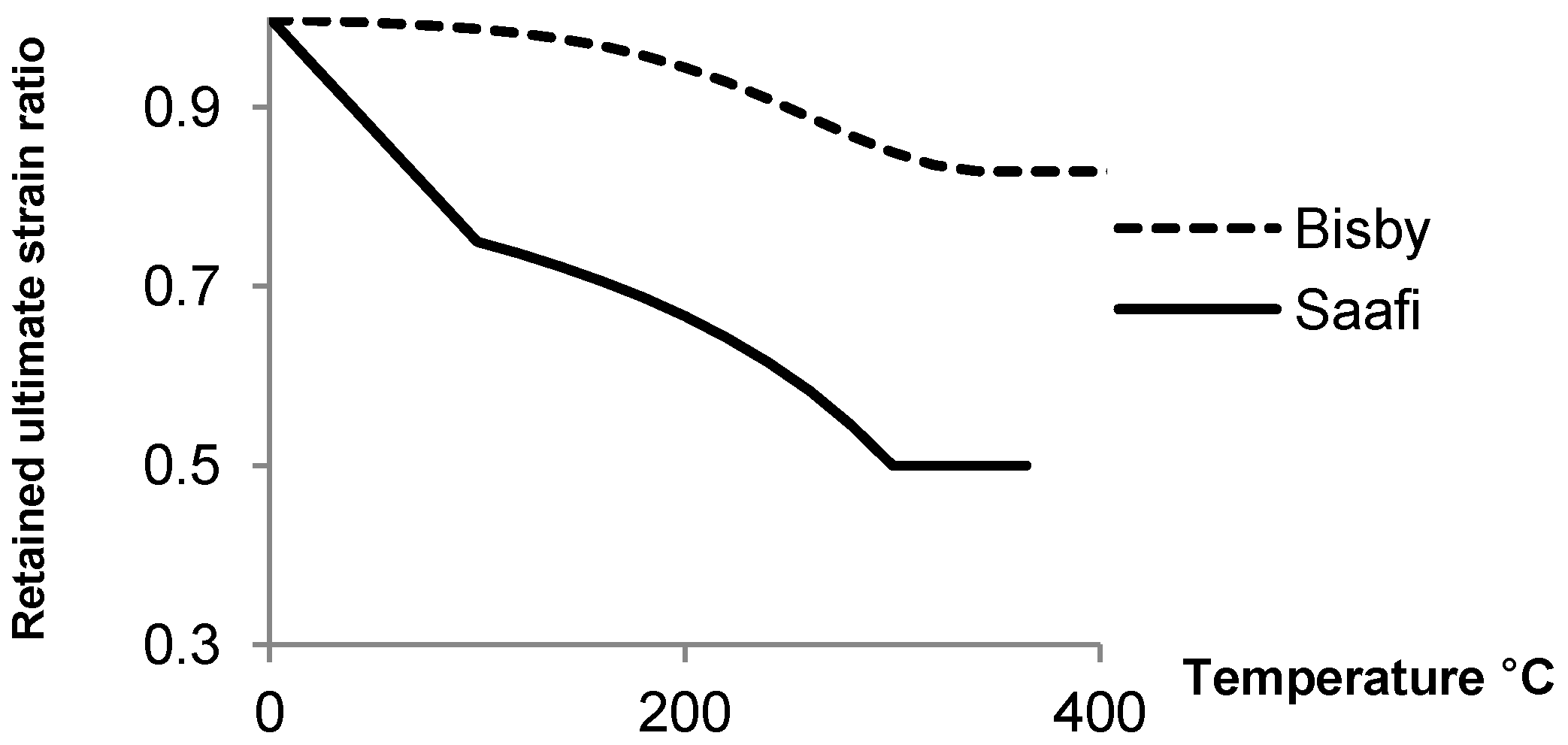
Figure 1 compares the strength and elastic modulus degradation for GFRP composites in Saafi and Bisby’s models. Saafi’s model produces conservative results compared to Bisby’s model, particularly for strength retention. Both models suffer from the dearth of experimental data on FRP bars that are currently employed for reinforced concrete. Nevertheless, Bisby’s model is more consistent with recent tests on commercially available FRP bars for reinforcing concrete [
15].
Figure 1.
Comparing Bisby’s and Saafi’s models; (a) Strength reduction; (b) Elastic modulus degradation for GFRP at elevated temperatures.
Figure 1.
Comparing Bisby’s and Saafi’s models; (a) Strength reduction; (b) Elastic modulus degradation for GFRP at elevated temperatures.
3. Heat Conduction Simulation in Reinforced Concrete Members
In this study, the ASTM E119 [
16] time temperature curve has been used to simulate the temperature rise due to compartment fire in heat transfer model. The heat transfer model formerly developed [
17] is a finite-volume code, which is capable of predicting temperature in an insulated concrete section. The partial differential equation of heat conduction can be expressed as:
where
T is temperature,
t is time,
k is thermal conductivity, ρ is density and
c is heat capacity. These field variables are functions of temperature and spatial variables. For the predictions in this paper, the thermal properties of the concrete are taken from the recommendations of Lie [
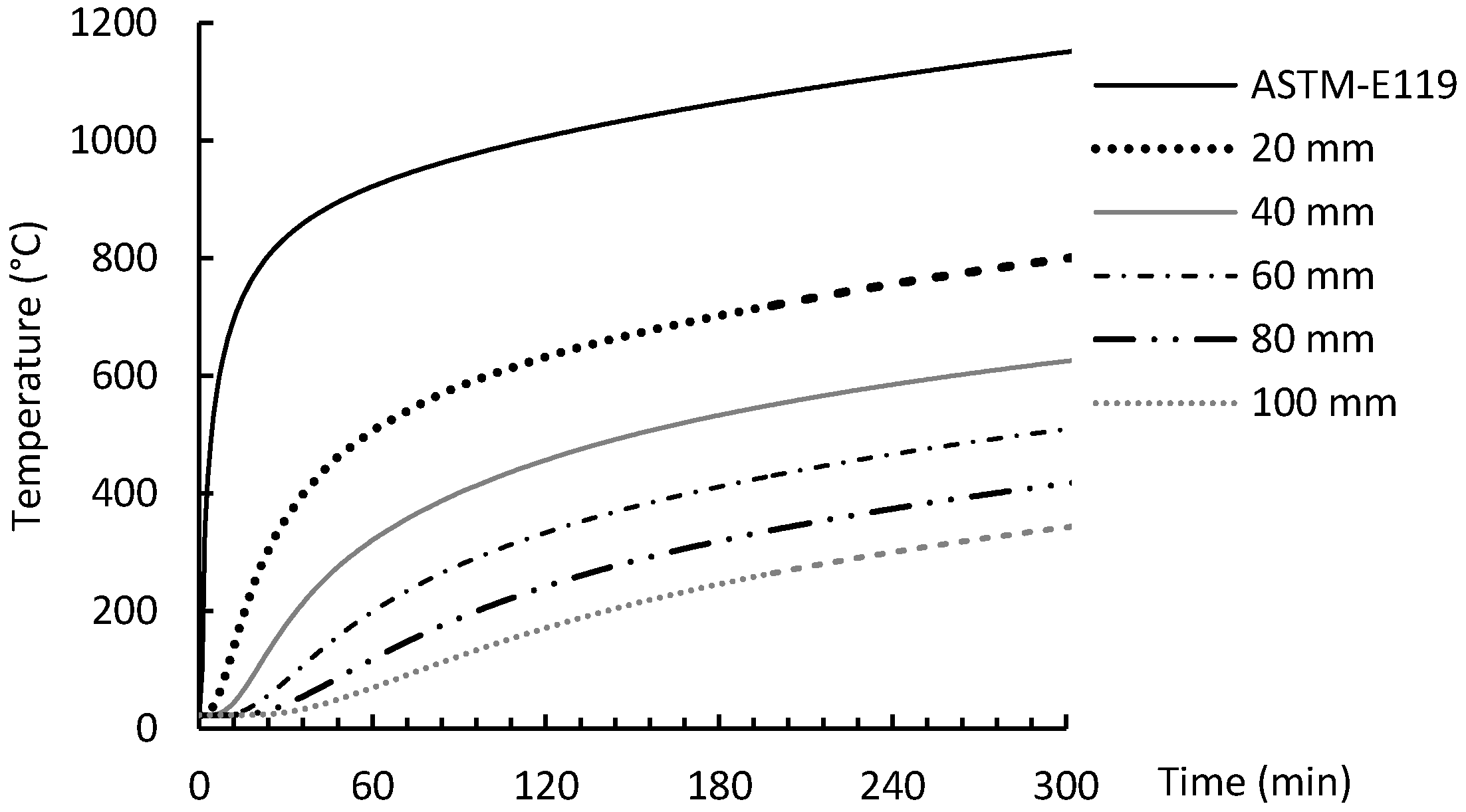
9] for concrete with carbonate aggregates. The thermal properties of the GFRP are assumed to be the same as that of concrete because of the relatively small amount of GFRP compared to the volume of concrete. The temperature-time curve of ASTM E119 temperature predictions at different concrete depths are presented [
18] in
Figure 2.
Figure 2.
Temperature predictions at different concrete depths vs. exposure time.
Figure 2.
Temperature predictions at different concrete depths vs. exposure time.
4. Load Capacity Model
Several studies carried out to determine temperature profile in cross section of concrete members [
19]. Once the distribution of temperatures throughout the slab is known at each time step during fire exposure, the flexural capacity of slab can be calculated using Euler-Bernoulli beam theory. The following assumptions are made in the model:
- (1)
Slabs are exposed to fire from the bottom of the slab only
- (2)
Slabs carry loads in bending in one direction only (one-way slab)
- (3)
Slabs are simply-supported and no axial restraint or axial forces are present
- (4)
The bond of FRP bars to concrete is unaffected by heat, and
- (5)
Plane sections remain plane throughout the analysis.
The fourth assumption regarding the bond of FRP is particularly important because recent tests have shown that bond often governs the failure of FRP reinforced slabs [
2,
20]. However, this work by Nigro
et al. [
2] also demonstrated that such bond failures can be prevented by special anchoring details such as bending the bars at the ends of the slabs. Thus, the information in this paper is applicable only to designs that have such suitable anchoring details.
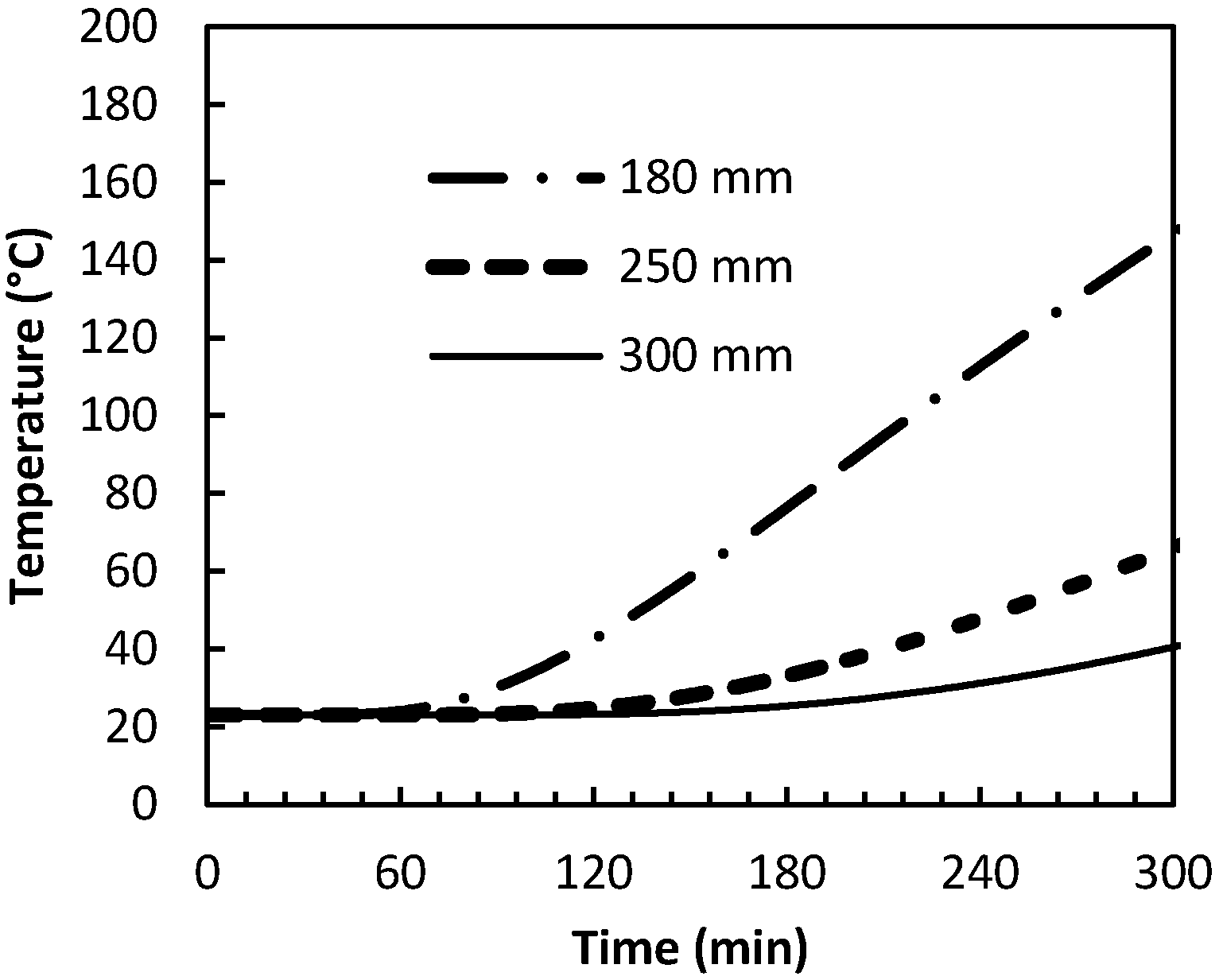
In order to calculate the flexural capacity of the section during fire, concrete and FRP characteristics have been adjusted at each step to account for the loss of strength due to fire exposure. However the loss of strength in concrete has been neglected during fire exposure. The reason for this simplification is that the temperature of the compressive portions of the slab is fairly low even after 6 h of standard fire exposure,
Figure 3. Therefore, the compressive strength of concrete is not affected by fire. The degradation of modulus of elasticity of concrete would not affect the flexural capacity of the section although it affects the deflection of the member. Therefore serviceability design criteria used for the initial design of the slabs will not be predicted during the fire.
Figure 3.
Temperatures at unexposed surface of slabs
Figure 3.
Temperatures at unexposed surface of slabs
The procedure for determining the ultimate capacity of FRP reinforced slab in fire is more complicated compared to the steel reinforced slab. In the case of steel reinforced slab, the nonlinear behaviour of steel after its yield point makes the calculation simpler. However, for FRP reinforced concrete slabs, the strain compatibility diagram changes continuously as the FRP loses strength at high temperature and the balanced FRP reinforcement ratio (ρFRP,b) increases continuously. Thus, at each time step, ρFRP,b is recalculated using temperature adjusted characteristics of FRP.
Properties of FRP bars at elevated temperature are obtained based on strength and stiffness degradation models given in
Figure 1. Once ρ
FRP,b is calculated, the existing FRP ratio (ρ
FRP) is compared to ρ
FRP,b to identify whether failure will be by crushing of concrete or by FRP rupture. In the case of slabs, with two or more layers of FRP the possibility of rupture in each FRP layer is considered at every time step, especially when the ultimate strain of FRP decreases as the temperature increases. For example in a slab with two layers of reinforcement, in some occasions the section reaches a higher flexural capacity because the bottom layer ruptures before the concrete crushes. The ultimate strain of concrete is set to be constant and equal to 0.0035. However the mechanical rupture strain of the FRP bars varies throughout the fire exposure as shown in
Figure 4. The curves in this figure were obtained by a combination of the strength and modulus curves presented in
Figure 1.
Figure 4.
Comparison of the models proposed by Bisby and Saafi for ultimate strain of GFRP bars at elevated temperatures.
Figure 4.
Comparison of the models proposed by Bisby and Saafi for ultimate strain of GFRP bars at elevated temperatures.
When ρFRP is greater than ρFRP,b, the governing failure mechanism is concrete crushing and the strain at top compression layer is 0.0035. The strain in FRP bars is determined using strain compatibility. As the strength of the FRP decreases due to temperature effects, the neutral axis depth decreases resulting in a smaller concrete stress block.
When ρ
FRP is less than ρ
FRP,b, the FRP will rupture before the concrete crushes. The strain in FRP bars is set to their ultimate strain at that temperature. Hence, the stress in the bar is known and the resultant tensile force can be calculated. A subroutine checks many different neutral axis depths to satisfy equilibrium of tensile and compressive forces in the slab cross-section. Once the equilibrium criterion is fulfilled and the neutral axis is determined, strains and stresses are calculated for any point in the section. The resultant forces and moment resistance are calculated once all the stresses are determined and this gives the moment resistance of concrete slab at any instant of fire exposure. The known parameters of the analysis are FRP reinforcement ratio, which is calculated beforehand by conforming to ACI 440.1R [
7] serviceability limitations, as well as dimensions of the slabs, and material properties of reinforced concrete at room temperature.
The reliability of the above mentioned analyses is highly dependent upon the model being used to predict the thermal and mechanical properties of the constituent materials. Although adequate tests and research on concrete and steel are available, a lack of information for FRP bars calls for more research in this area.
Figure 5 illustrates the significance of FRP material behaviour model in overall response of the slab. The solid line is the calculated moment capacity curve using the model proposed by Saafi’s and the dashed line is moment capacity calculated using Bisby’s model. The slab is 180 mm thick and the concrete cover is 50 mm over GFRP reinforcement. For this case, the Saafi model estimates the fire resistance as only 85 min compared to 140 min for Bisby’s model. Bisby’s model is employed in the remaining calculations in this paper because it appears more accurate based on recent test data. Nevertheless, the FRP material property models still need more tests and thus the results in this paper are intended to demonstrate the trends that changing different slab configurations will have on fire endurance rather than as accurate predictions of fire endurance.
Figure 5.
Moment curves using different FRP degradation model in high temperature.
Figure 5.
Moment curves using different FRP degradation model in high temperature.
To verify the results of the model, it was used to estimate the fire endurance of GFRP reinforced concrete beams tested by Abbasi
et al. [
21]. They tested two 4400 mm long beams with a cross section of 400 × 350 mm. The average cube compressive strength of concrete was reported as 42 MPa. Each beam was reinforced by 7 of 12.7 mm in diameter GFRP rebars in tension. For Beam “b1” the GFRP rebars’ ultimate strength and elastic modulus were 690 MPa and 40.8 GPa respectively, and for beam “b2” 1000 MPa and 41 GPa. During the fire test, the beams experienced spalling in the corners of the cross section and extensive cracking and failed under the sustained load after 124 min in the case of beam “b1” and 94 min in the case of beam “b2”. The fire endurance estimates from the model developed here (see
Figure 6) are 90 min for beam “b1” and 110 min for beam “b2”. Thus the model is conservative for beam “b1”. Considering that the model does not account for spalling, the fire endurance results from the model give a reasonable estimate of the fire endurance.
Figure 6.
Model prediction for tests of the beams tested by Abbasi
et al. [
21]
Figure 6.
Model prediction for tests of the beams tested by Abbasi
et al. [
21]
5. Slabs with One Layer of FRP
To study the effect of fire on slabs, several different slab configurations have been considered as shown in
Table 1. Since serviceability limitations are the governing criteria in FRP reinforced slabs, the slabs are designed for crack width and deflection serviceability criteria. The crack width of the slabs has been limited to 0.7 mm for interior exposure as suggested by ACI-440.1R [
7]. The permissible deflection is
L/360. For the two above defined limits, the required FRP reinforcement ratio is found for the all slabs. Slab thicknesses are 180, 250, and 300 mm and concrete cover ranges from 30 to 70 mm.
Table 1.
Characteristics of FRP reinforced slabs investigated in this study.
Table 1.
Characteristics of FRP reinforced slabs investigated in this study.
| Slab number | Thickness (mm) | Rebar type | f'c (MPa) | cover (mm) | L (mm) | Spacing (mm) | Af,req * | Mn ** (kN·m) | Mcr | Deflection (mm) Ma/Mcr = 1.5 |
|---|
| 1 | 180 | GFRP | 30 | 30 | 3600 | 150 | 1006 | 77.6 | 17.8 | 4.1 |
| 2 | 180 | GFRP | 30 | 40 | 3600 | 150 | 1243 | 74.1 | 17.8 | 4.1 |
| 3 | 180 | GFRP | 30 | 50 | 3600 | 150 | 1576 | 70.2 | 17.8 | 4.1 |
| 4 | 180 | GFRP | 30 | 60 | 3600 | 150 | 2051 | 65.6 | 17.8 | 4.0 |
| 5 | 180 | GFRP | 30 | 70 | 3600 | 150 | 2754 | 59.9 | 17.8 | 4.0 |
| 6 | 180 | GFRP | 30 | 80 | 3600 | 150 | 3845 | 53.1 | 17.8 | 3.9 |
| 7 | 250 | GFRP | 30 | 30 | 5000 | 150 | 1235 | 156.4 | 34.2 | 5.7 |
| 8 | 250 | GFRP | 30 | 40 | 5000 | 150 | 1446 | 153.5 | 34.2 | 5.7 |
| 9 | 250 | GFRP | 30 | 50 | 5000 | 150 | 1719 | 149.7 | 34.2 | 5.6 |
| 10 | 250 | GFRP | 30 | 60 | 5000 | 150 | 2072 | 145.4 | 34.2 | 5.6 |
| 11 | 250 | GFRP | 30 | 70 | 5000 | 150 | 2530 | 140.2 | 34.2 | 5.5 |
| 12 | 250 | GFRP | 30 | 80 | 5000 | 150 | 3136 | 134.0 | 34.2 | 5.4 |
| 13 | 300 | GFRP | 30 | 30 | 6000 | 150 | 1409 | 222.6 | 49.3 | 6.9 |
| 14 | 300 | GFRP | 30 | 40 | 6000 | 150 | 1617 | 227.2 | 49.3 | 6.8 |
| 15 | 300 | GFRP | 30 | 50 | 6000 | 150 | 1879 | 223.9 | 49.3 | 6.7 |
| 16 | 300 | GFRP | 30 | 60 | 6000 | 150 | 2206 | 220.2 | 49.3 | 6.7 |
| 17 | 300 | GFRP | 30 | 70 | 6000 | 150 | 2614 | 215.7 | 49.3 | 6.6 |
| 18 | 300 | GFRP | 30 | 80 | 6000 | 150 | 3122 | 210.0 | 49.3 | 6.5 |
For the purposes of illustration, consider a 250 mm thick concrete slab with a 28 day concrete compressive strength of 30 MPa with carbonate aggregate. If the concrete cover to the centre of the FRP bars is 50 mm, the required reinforcement area assuming
Ma/
Mcr = 1.50 is 1719 mm
2. Placing the required amount of reinforcement to satisfy serviceability criteria gives a nominal moment resistance 150 kN·m. The cracking moment (
Mcr) of the slab is 34 kN·m. Exposed to fire from below, the slab loses its moment capacity as a consequence of thermal degradation of the mechanical properties of the FRP. The initial flexural capacity of the slab drops to the applied moment (
Ma = 51 kN·m) at 140 min. It should be mentioned that the resistance model given by the model does not include member reduction factors as recommended by ACI 216 [
22]. The maximum likely crack width is calculated using the following equation:
in which
w = maximum crack width;
ff = reinforcement stress; β = ratio of distance between neutral axis and tension face to distance between neutral axis and centroid of reinforcement;
dc = thickness of cover from tension face to center of closest bar; and
s = bar spacing. Since crack width is a function of stress in the FRP bars, the design is affected by the service load level as expressed by the
Ma/
Mcr ratio. Three common ratios of 1, 1.25, and 1.5 are selected for the
Ma/
Mcr ratio.
As expected, by increasing the concrete cover, the initial moment capacity decreases. Because the defining design criteria relate to serviceability rather than strength, all slabs fulfill the strength requirements at room temperature. Fire performance of slabs considerably increases by increasing their concrete cover as shown in
Figure 7, but this performance improvement comes at the expense of higher reinforcement ratio due to crack width limitations. For example, a 180 mm slab with 30 mm of cover has approximately 1 h of fire endurance while the slab with 60 mm of concrete cover has in excess of 4 h of fire endurance. However, the required reinforcement ratio is 2 times higher in the slab with 60 mm of concrete cover to meet serviceability design criteria.
Figure 7.
Moment capacities of 180 mm thick slabs with various cover depths in fire, Ma/Mcr = 1.5, (a) 180 mm thick slab; (b) 250 mm; (c) 300 mm.
Figure 7.
Moment capacities of 180 mm thick slabs with various cover depths in fire, Ma/Mcr = 1.5, (a) 180 mm thick slab; (b) 250 mm; (c) 300 mm.
An interesting observation is that the fire endurance of slabs is independent of their level of applied service load. In other words, changing the
Ma/
Mcr ratio during the design process does not significantly affect the failure time of the slab within the range of
Ma/
Mcr between 1.0 and 1.5. This effect is illustrated in
Figure 8 where moment resistance (
Mr) curves are normalized
versus applied load or service load (
Ma). While slabs with different
Ma/
Mcr ratios behave differently in the beginning, they approach each other when the moment capacity reaches the service load level. For example, a slab with an initial
Ma/
Mcr = 1, has approximately the same fire endurance as a slab with
Ma/
Mcr =1.5. Obviously in a slab with
Ma/
Mcr = 1.5 the amount of reinforcement is higher due to crack width requirements but this extra reinforcement does not increase the fire endurance.
Figure 8.
Ratios of Mr/Ma in fire for various concrete covers for: (a) 180 mm and (b) 300 mm.
Figure 8.
Ratios of Mr/Ma in fire for various concrete covers for: (a) 180 mm and (b) 300 mm.
6. Strength-Domain and Temperature-Domain Failure
Another approach in determining fire endurance is temperature-domain approach. In the temperature-domain approach, the fire endurance of the slabs is specified based on the critical temperature of the reinforcement defined as the temperature at which the bar loses 50% of the its tensile strength at room temperature. For steel reinforcement, the critical temperature is 593 °C [
23]. Wang and Kodur [
24] have reported 325 °C as the critical temperature for GFRP bars. Robert and Benmokrane reported 46% of tensile strength loss at 300 °C [
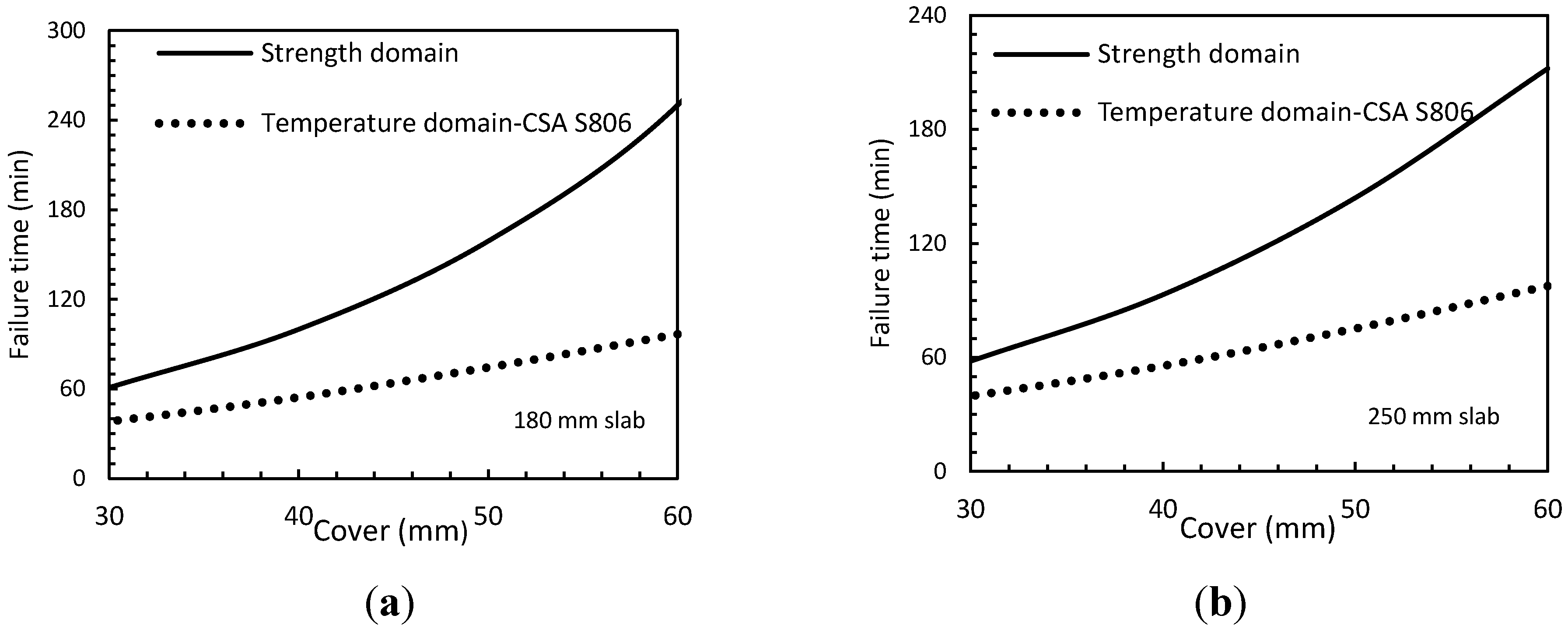
15]. The fire endurance prediction of the strength model described in previous sections is presented in
Figure 9 in comparison with results of temperature-domain method of CSA-S806. In the strength-domain method, the slab fails once its nominal flexural capacity drops below the applied moment (
Ma).
Figure 9 illustrates a considerable conservative prediction of temperature domain model. For instance, for a 180 mm slab, the fire endurance prediction of temperature domain failure for cover of 30 mm is 41% of the strength-domain failure. This is even lower for a slab with higher concrete cover. For the same slab with cover of 60 mm, the ratio is 24%. Bisby’s model for GFRP behaviour at fire is used here to predict the fire performance of the slabs. The results of strength-domain result would be closer to temperature-domain results if a more conservative FRP material model (e.g., Saafi’s model) is used in the calculation. For example, for a 180 mm thick slab with 50 mm of cover,
Figure 5 shows that Saafi’s model would estimate the fire endurance as 85 min compared to 75 min for the temperature-domain approach as shown in
Figure 9.
Figure 9.
Strength-domain fire rate versus temperature-domain of CSA-S806 for (a) slab 180; and (b) 250 mm.
Figure 9.
Strength-domain fire rate versus temperature-domain of CSA-S806 for (a) slab 180; and (b) 250 mm.
Given that the slabs in this study have been designed conforming to ACI-440-1R serviceability requirements, the nominal flexural capacities of the slabs are greater than that needed to resist the applied loads. This fact highlights the difference between FRP and steel reinforced slabs. The design of most steel reinforced slabs is governed by strength considerations. Since FRP reinforced slabs have reserve flexural strength because of serviceability considerations, a temperature-domain approach will always underestimate their fire endurance. This conclusion is also consistent with observations of Bisby and Kodur [
5].
7. Slabs with Two Layers of FRP
Simulation results for slabs with one layer of FRP show that to fulfill the requirements of serviceability in FRP reinforced slabs, the amount of FRP is considerably larger than the amount needed considering the strength requirements. Since the serviceability requirements during a fire event do not need to be fulfilled (especially crack width criteria), the FRP could be employed more effectively to increase the fire endurance by placing the FRP reinforcement in two or more layers. During fire, a slab with two layers of FRP will perform better because the inner layer has more protective cover. To further investigate the effectiveness of this approach (
i.e., placing FRP in two layers), simulations are performed on slabs with two FRP layers and their behaviour is compared to that of slabs with one layer of FRP with the same amount of FRP reinforcement. The two types of slabs were designed to meet the same criteria at room temperature. Slab thicknesses are 180, 250 and 300 mm. Half of the reinforcement is placed in one layer and the remaining half in the other layer. The covers chosen for the bottom FRP layers are 30, 40, 50, and 60 mm and the distances between FRP layers are 30, 40, and 50 mm. The cross-sectional area of FRP reinforcement is determined according to ACI-440.1R serviceability criteria, similar to the design procedure used for slabs with one layer of FRP. The relations for calculating crack width and deflection are modified for slabs with two layers of FRP. For strength design purposes, the FRP in each layer is considered separately rather than as a single bundled FRP layer. The crack width limit is set to be equal to 0.7 mm for both slabs.
Ma/
Mcr in all simulations is equal to 1.5 since fire endurance was found to be independent of the service load level. Sample moment capacity curves during fire are shown in
Figure 10. As expected, a slab with two layers of GFRP reinforcement outperforms a slab with same amount of reinforcement placed in one layer in terms of fire endurance. For example, a slab with GFRP placed at two layers with covers of 30 and 60 mm achieves approximately 2 h of fire endurance while the same slab with one layer of GFRP has a fire endurance of only 100 min. While the initial strength of the slab is higher for the one-layer slab, the decline in strength is faster during the fire exposure. Thus, the slab with two layers of reinforcement has more gradual fire degradation than the slab reinforced with one layer.
Figure 10.
Prediction of the flexural capacity in fire of a slab with two layers; (a) Slab thickness of 180 mm; (b) Slab thickness of 250 mm.
Figure 10.
Prediction of the flexural capacity in fire of a slab with two layers; (a) Slab thickness of 180 mm; (b) Slab thickness of 250 mm.
The obtained increase in fire endurance by placing reinforcements in two layers varies by slab thickness. For example, in a slab with 180 mm thickness, the fire endurance gain was approximately 15 min on average, which is not significant considering the amount of effort needed for placing FRP bars in two layers. On the other hand, for a slab with 250 mm thickness, the average gain is 35 min and for a 300 mm slab it is 45 min. Based on these observations, placing FRP in two layers is more effective in terms of fire endurance for thicker slabs.
Figure 11 shows fire endurance results for slabs with two layers of reinforcement and corresponding results for slabs with one layer of reinforcement. The slab thicknesses are 180, 250, and 300 mm and the results are plotted against the reinforcement ratio. Therefore two points on a vertical line have the same amount of GFRP reinforcement and their vertical separation is the amount of increased fire endurance in min. There is a strong linear relation between reinforcement ratio and fire endurance in one layer slabs. The same linear dependency is generally present for two layer slabs. The fluctuations in two layer data are because of a sudden change in the distance between two layers. For example the distance between two layers in the first three points from left in
Figure 11 is 30 mm and for the next three points it is 40 mm.
Figure 12 shows flexural behavior of slabs in fire. With the same amount of reinforcement in one layer slabs and two layers reinforced slabs, initial strength of one layer reinforced slabs are slightly higher. However, they have gained higher fire endurance rate.
Figure 11.
Fire endurance of one-layer compared to two-layer FRP reinforced concrete slab (a) 180 mm, (b) 250 mm, and (c) 300 mm.
Figure 11.
Fire endurance of one-layer compared to two-layer FRP reinforced concrete slab (a) 180 mm, (b) 250 mm, and (c) 300 mm.
Figure 12.
Comparison of flexural capacities of one-layer slab (180 mm) with two-layer with the same area of reinforcement for three cover thicknesses.
Figure 12.
Comparison of flexural capacities of one-layer slab (180 mm) with two-layer with the same area of reinforcement for three cover thicknesses.