A Comprehensive Review of Optical Stretcher for Cell Mechanical Characterization at Single-Cell Level
Abstract
:1. Introduction
2. Different Fabrication Techniques and Material
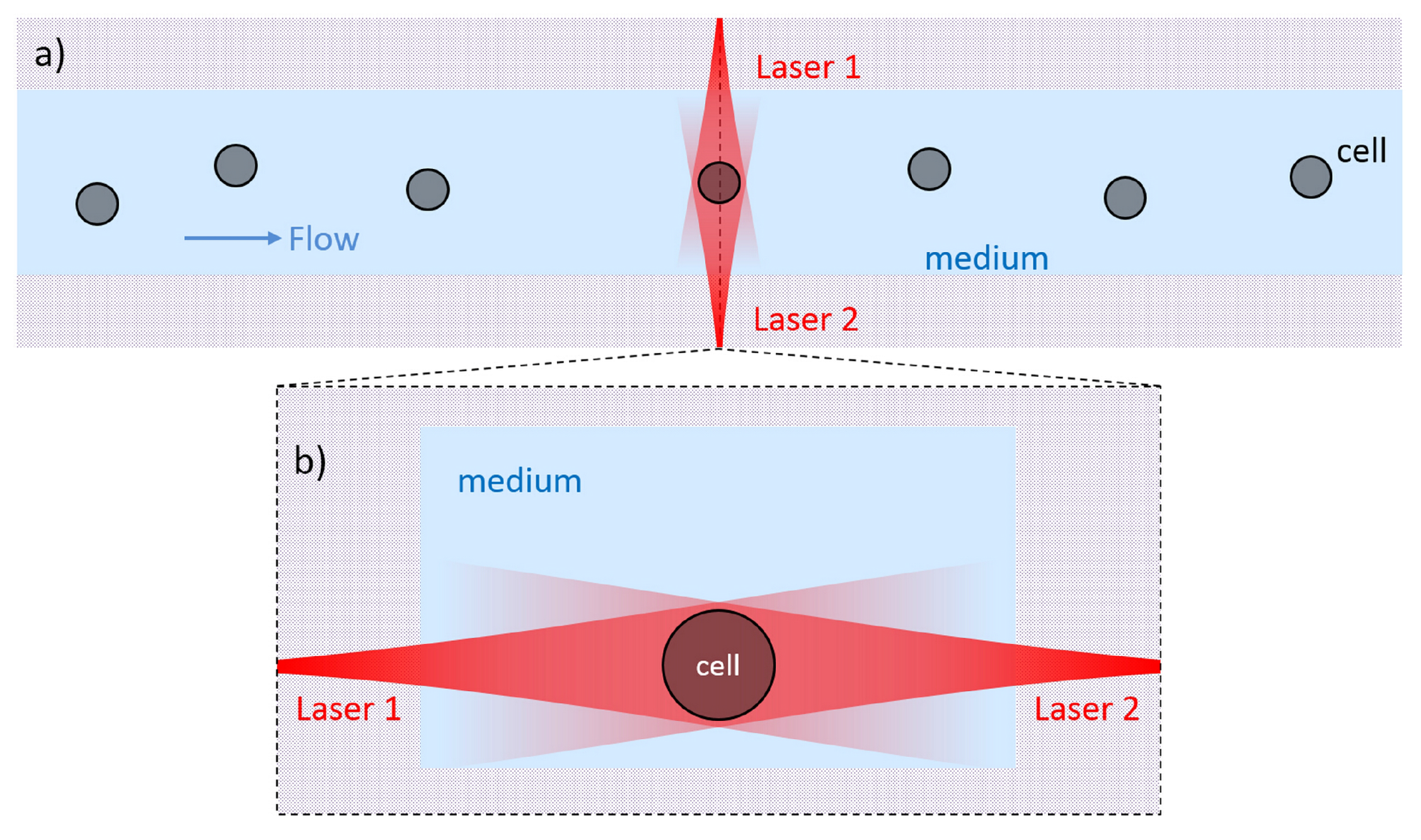
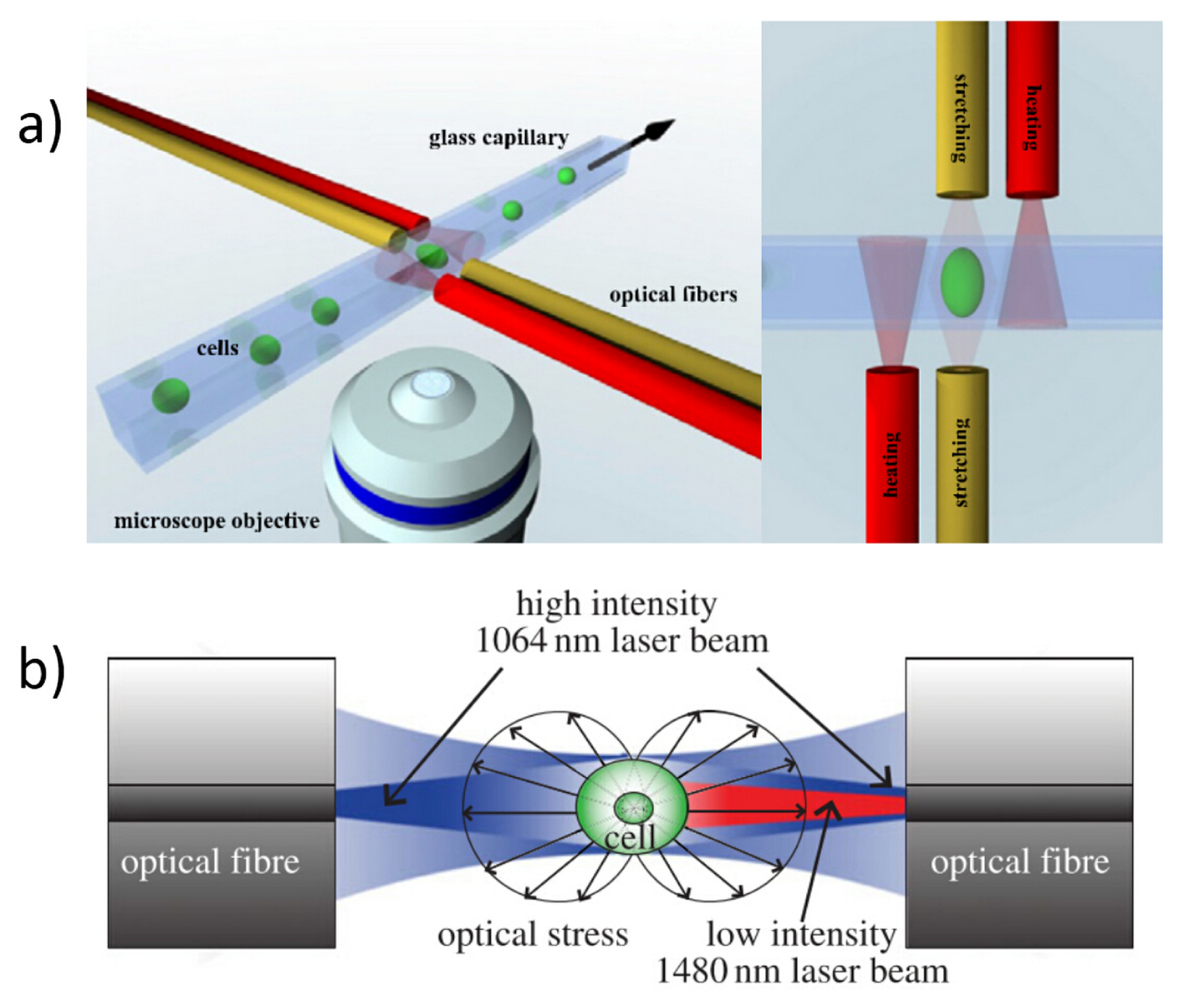
2.1. Basic Structure of an OS
2.2. Conventional Discrete-Elements OS
2.3. Second-Generation Assembled OS
2.4. Femtosecond Laser Fabricated Monolithic Optical Stretcher
3. Working Principle of the OS
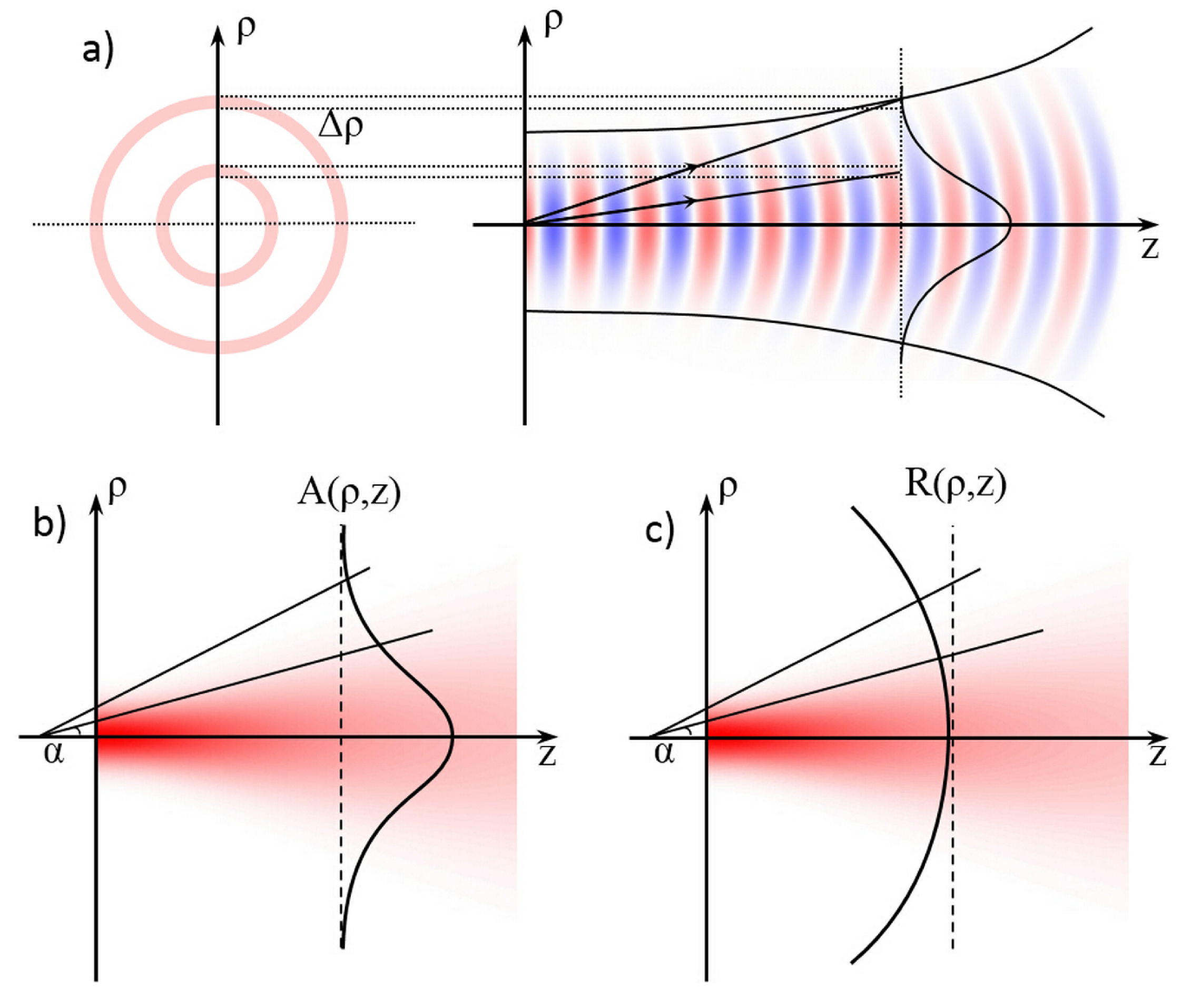
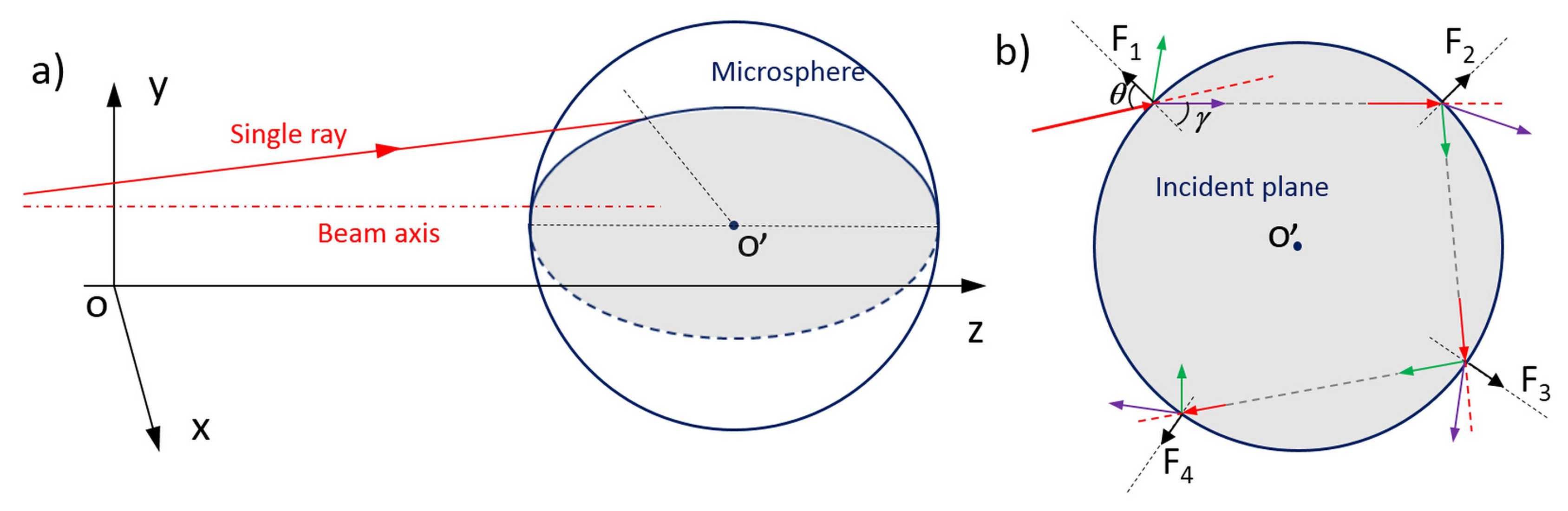
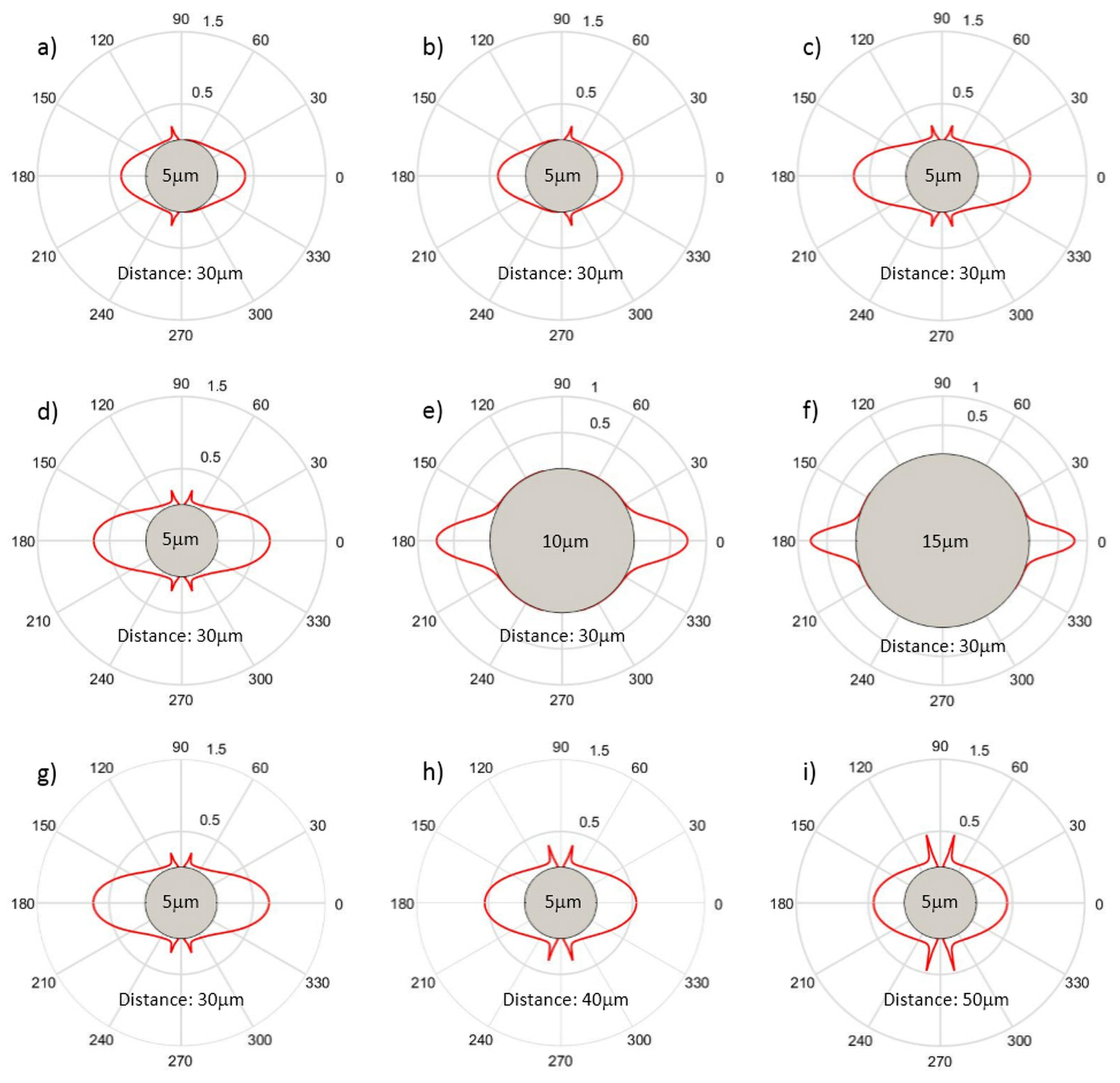
3.1. Optical Forces for Cell Stretching
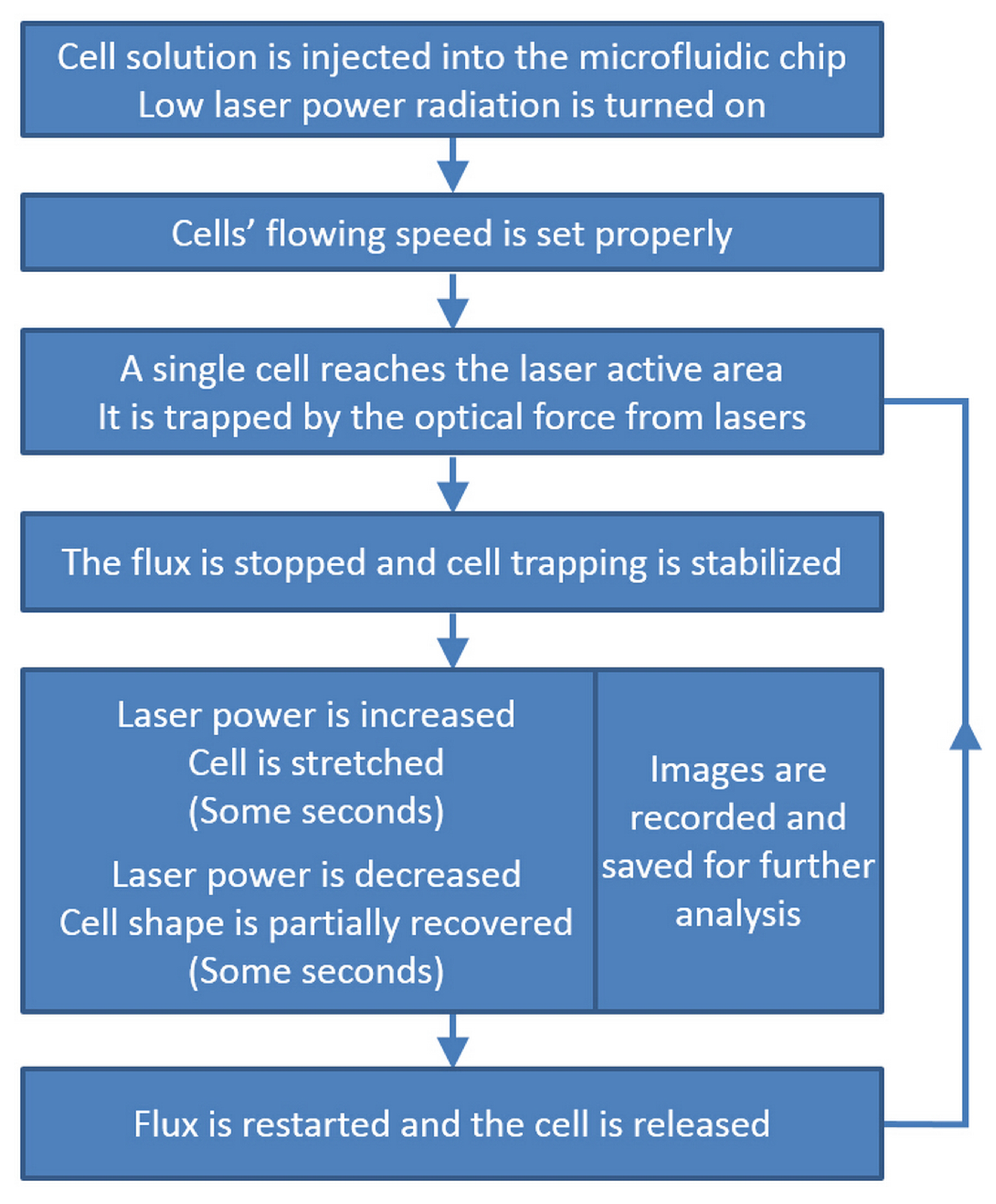
3.2. Cell Stretching Procedure
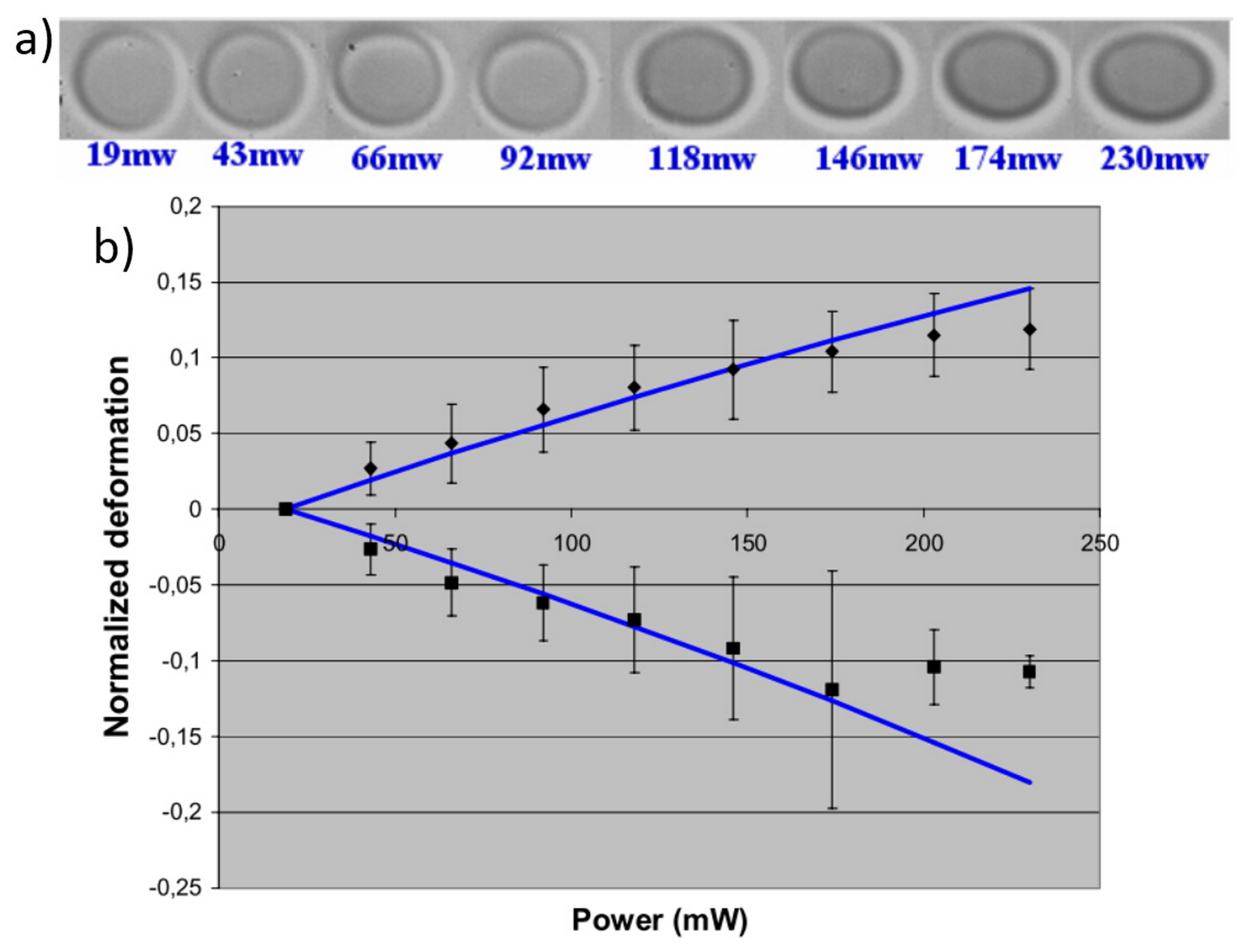
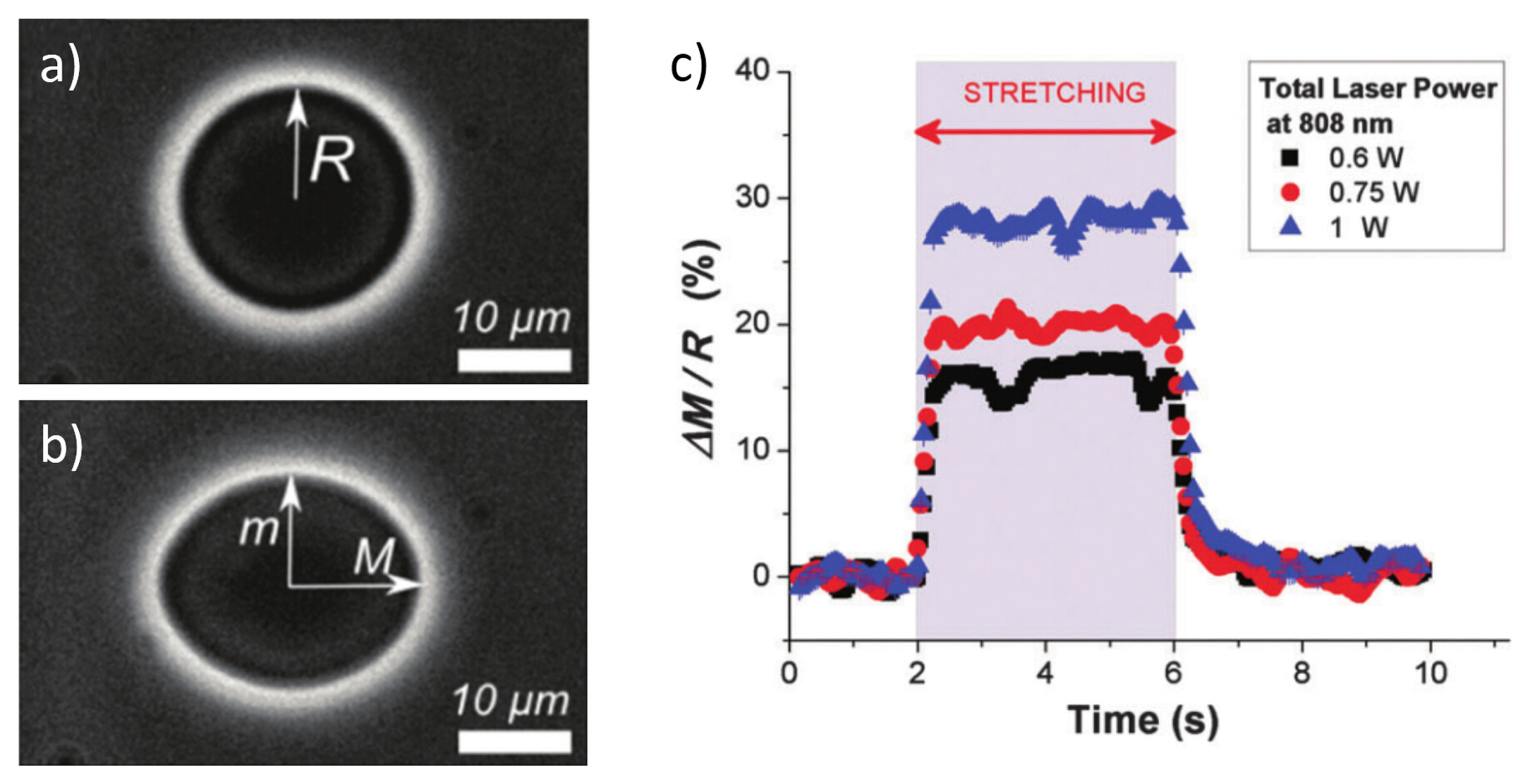
3.3. Characterization of Cell Optical Deformation
4. OS as a Tool to Analyze Cell Lines, Drug Treatments and Cellular Organelles
4.1. Optical Stretching of Red Blood Cells and Lipid Vesicles
4.2. Optical Stretching of Eukaryotic Cells and Drug Treatment Effect
5. Active Mechanical Sorting Based on Cellular Optical Deformability
5.1. Chip Layout for Cell Stretching and Sorting
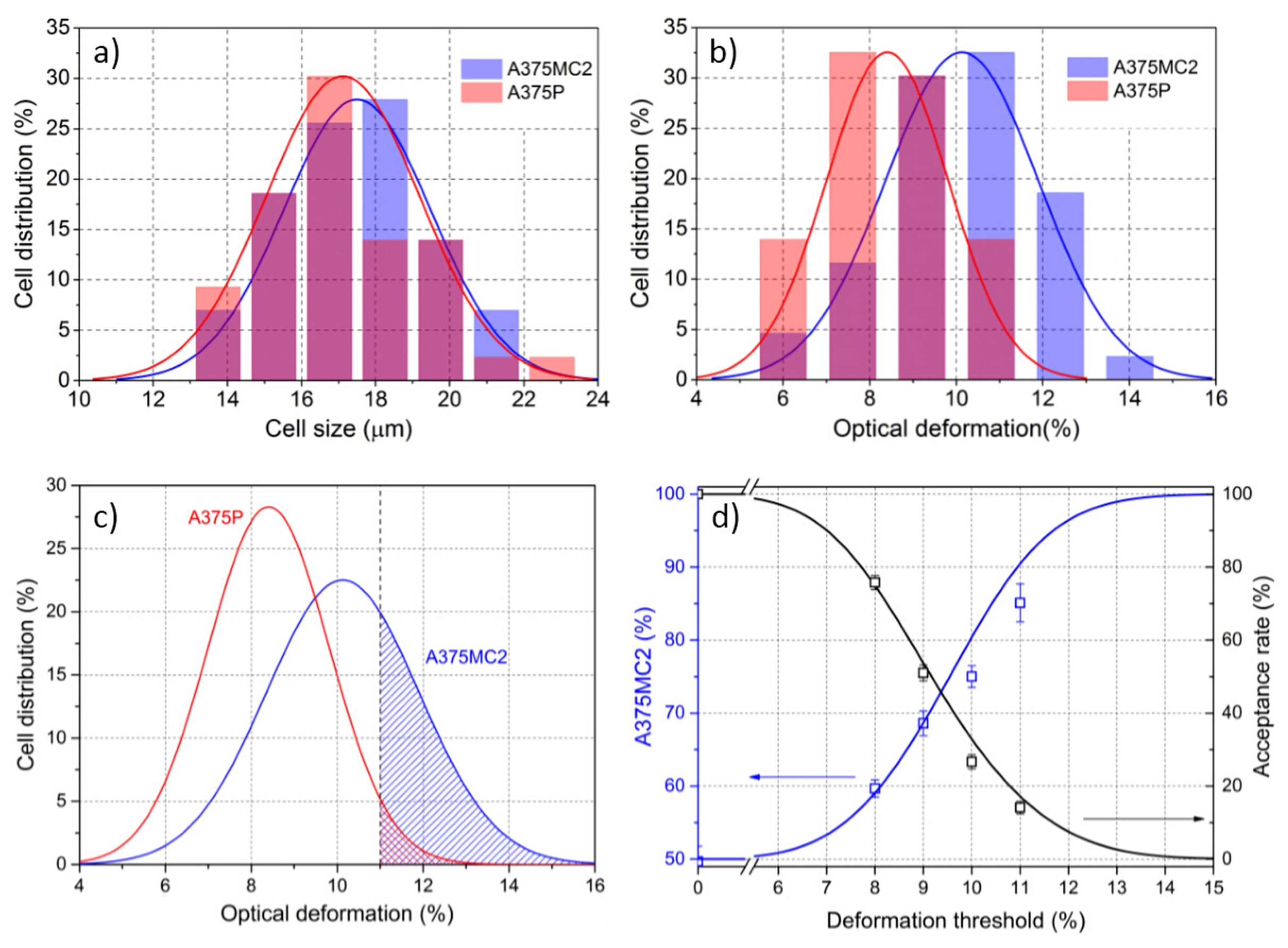
5.2. Cell Sorting Efficiency Discussion
6. Optical Heating and Temperature Effect
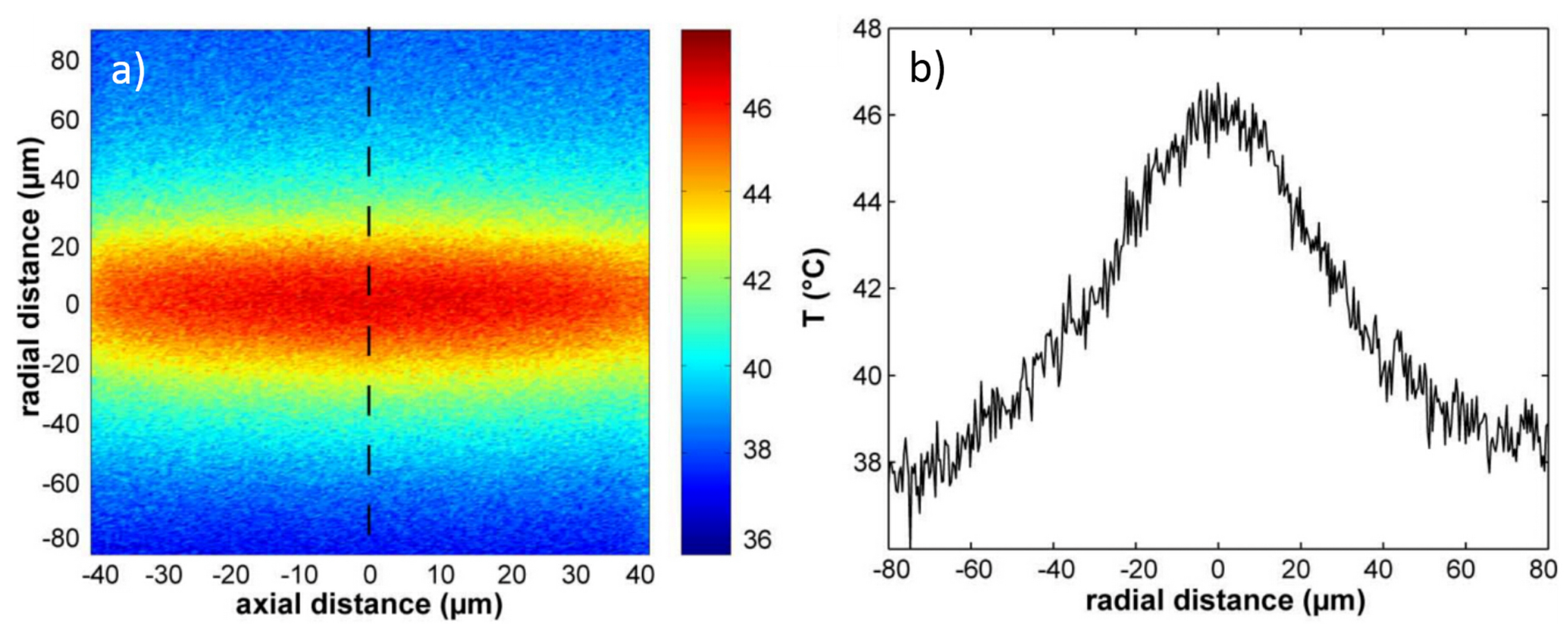
6.1. Optical Heating and Temperature Measurement
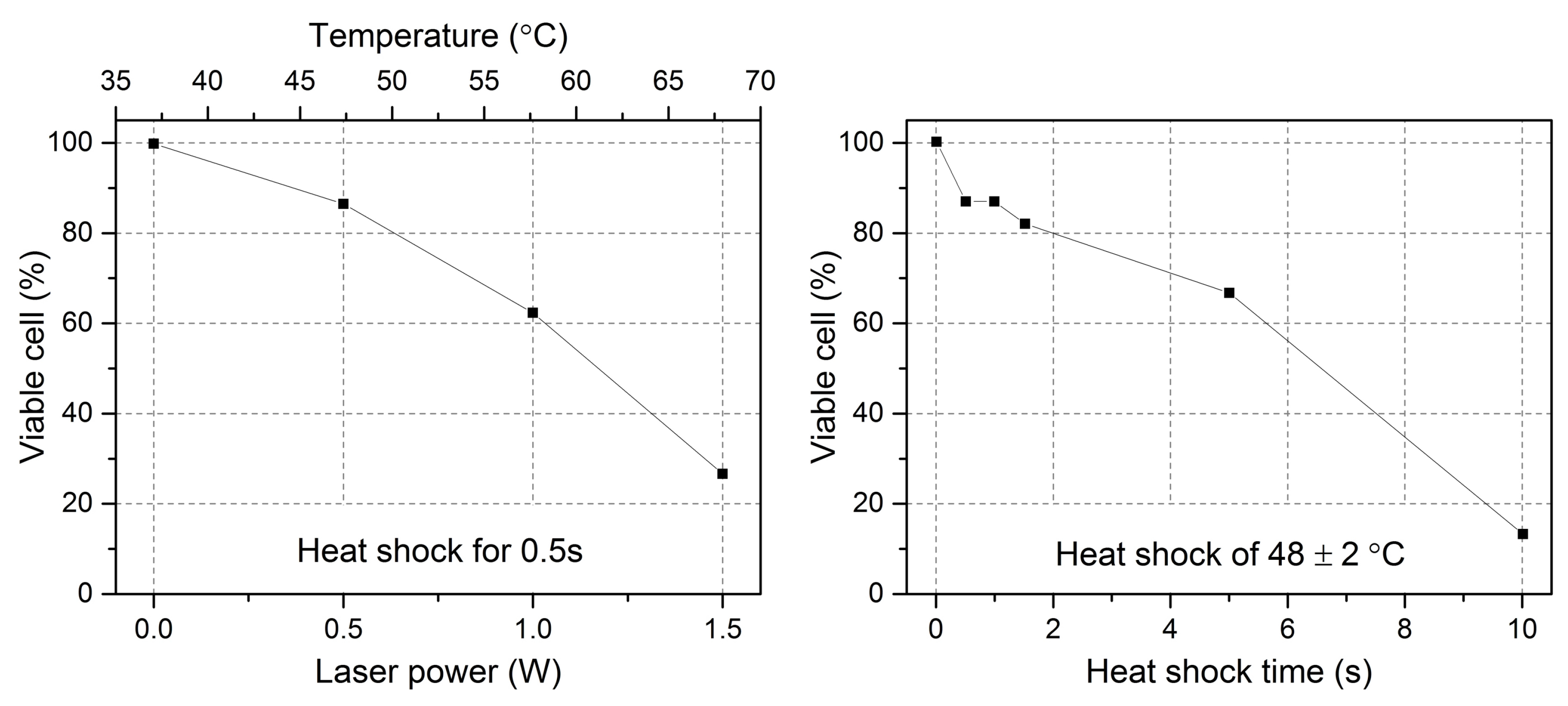
6.2. Optical Heating Impact on Cell’s Viability
6.3. Temperature Effect on Cell Mechanical Property
7. Other Related Studies
8. Final Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Suresh, S. Biomechanics and biophysics of cancer cells. Acta Mater. 2007, 55, 3989–4014. [Google Scholar] [CrossRef]
- Bao, G.; Suresh, S. Cell and molecular mechanics of biological materials. Nat. Mater. 2003, 2, 715–725. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, D.A.; Mullins, R.D. Cell mechanics and the cytoskeleton. Nature 2010, 463, 485–492. [Google Scholar] [CrossRef] [PubMed]
- Moeendarbary, E.; Harris, A.R. Cell mechanics: Principles, practices, and prospects. Wiley Interdiscip. Rev. Syst. Biol. Med. 2014, 6, 371–388. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Weaver, V. Mechanics, malignancy, and metastasis: The force journey of a tumor cell. Cancer Metastas. Rev. 2009, 28, 113–127. [Google Scholar] [CrossRef] [PubMed]
- Denis, W.; Konstantinos, K.; Peter, C.S. The physics of cancer: The role of physical interactions and mechanical forces in metastasis. Nat. Rev. Cancer 2011, 11, 512–522. [Google Scholar]
- Zhang, W.; Kai, K.; Choi, D.S.; Iwamoto, T.; Nguyen, Y.H.; Wong, H.; Landis, M.D.; Ueno, N.T.; Chang, J.; Qin, L. Microfluidics separation reveals the stem-cell-like deformability of tumor-initiating cells. Proc. Natl. Acad. Sci. USA 2012, 109, 18707–18712. [Google Scholar] [CrossRef] [PubMed]
- Guck, J.; Ananthakrishnan, R.; Mahmood, H.; Moon, T.J.; Cunningham, C.C.; Käs, J. The optical stretcher: A novel laser tool to micromanipulate cells. Biophys. J. 2001, 81, 767–784. [Google Scholar] [CrossRef]
- Ekpenyong, A.E.; Whyte, G.; Chalut, K.; Pagliara, S.; Lautenschläger, F.; Fiddler, C.; Paschke, S.; Keyser, U.F.; Chilvers, E.R.; Guck, J. Viscoelastic properties of differentiating blood cells are fate- and function-dependent. PLoS ONE 2012, 7, e45237. [Google Scholar] [CrossRef] [PubMed]
- Yap, B.; Kamm, R.D. Mechanical deformation of neutrophils into narrow channels induces pseudopod projection and changes in biomechanical properties. J. Appl. Physiol. 2005, 98, 1930–1939. [Google Scholar] [CrossRef] [PubMed]
- Vaziri, A.; Mofrad, M.R.K. Mechanics and deformation of the nucleus in micropipette aspiration experiment. J. Biomech. 2007, 40, 2053–2062. [Google Scholar] [CrossRef] [PubMed]
- Pachenari, M.; Seyedpour, S.M.; Janmaleki, M.; Babazadeh Shayan, S.; Taranejoo, S.; Hosseinkhani, H. Mechanical properties of cancer cytoskeleton depend on actin filaments to microtubules content: Investigating different grades of colon cancer cell lines. J. Biomech. 2014, 47, 373–379. [Google Scholar] [CrossRef] [PubMed]
- Mathur, A.B.; Collinsworth, A.M.; Reichert, W.M.; Kraus, W.E.; Truskey, G.A. Endothelial, cardiac muscle and skeletal muscle exhibit different viscous and elastic properties as determined by atomic force microscopy. J. Biomech. 2001, 34, 1545–1553. [Google Scholar] [CrossRef]
- Mackay, J.L.; Kumar, S. Measuring the elastic properties of living cells with atomic force microscopy indentation. Methods Mol. Biol. 2013, 931, 313–329. [Google Scholar] [PubMed]
- Rouven Brückner, B.; Pietuch, A.; Nehls, S.; Rother, J.; Janshoff, A. Ezrin is a major regulator of membrane tension in epithelial cells. Sci. Rep. 2015, 5, 14700. [Google Scholar] [CrossRef] [PubMed]
- Dao, M.; Lim, C.; Suresh, S. Mechanics of the human red blood cell deformed by optical tweezers. J. Mech. Phys. Solids 2003, 51, 2259–2280. [Google Scholar] [CrossRef]
- Chen, J.; Fabry, B.; Schiffrin, E.L.; Wang, N. Twisting integrin receptors increases endothelin-1 gene expression in endothelial cells. Am. J. Physiol. Cell Physiol. 2001, 280, C1475–C1484. [Google Scholar] [PubMed]
- Preira, P.; Valignat, M.P.; Bico, J.; Théodoly, O. Single cell rheometry with a microfluidic constriction: Quantitative control of friction and fluid leaks between cell and channel walls. Biomicrofluidics 2013, 7, 024111. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.N.; Chen, D.Y.; Zhao, Y.; Wei, C.; Zhao, X.T.; Yue, W.T.; Long, R.; Wang, J.B.; Chen, J. A Constriction channel based microfluidic system enabling continuous characterization of cellular instantaneous young’s modulus. Sens. Actuators B Chem. 2014, 202, 1183–1189. [Google Scholar] [CrossRef]
- Martinez Vazquez, R.; Nava, G.; Veglione, M.; Yang, T.; Bragheri, F.; Minzioni, P.; Bianchi, E.; Di Tano, M.; Chiodi, I.; Osellame, R.; et al. An optofluidic constriction chip for monitoring metastatic potential and drug response of cancer cells. Integr. Biol. 2015, 7, 477–484. [Google Scholar] [CrossRef] [PubMed]
- Otto, O.; Rosendahl, P.; Mietke, A.; Golfier, S.; Herold, C.; Klaue, D.; Girardo, S.; Pagliara, S.; Ekpenyong, A.; Jacobi, A.; et al. Real-time deformability cytometry: On-the-fly cell mechanical phenotyping. Nat. Methods 2015, 12, 199–202. [Google Scholar] [CrossRef] [PubMed]
- Mietke, A.; Otto, O.; Girardo, S.; Rosendahl, P.; Taubenberger, A.; Golfier, S.; Ulbricht, E.; Aland, S.; Guck, J.; Fischer-Friedrich, E. Extracting cell stiffness from real-time deformability cytometry: Theory and experiment. Biophys. J. 2015, 109, 2023–2036. [Google Scholar] [CrossRef] [PubMed]
- Guck, J.; Schinkinger, S.; Lincoln, B.; Wottawah, F.; Ebert, S.; Romeyke, M.; Lenz, D.; Erickson, H.M.; Ananthakrishnan, R.; Mitchell, D.; et al. Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Biophys. J. 2005, 88, 3689–3698. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Paiè, P.; Nava, G.; Bragheri, F.; Vazquez, R.M.; Minzioni, P.; Veglione, M.; Di Tano, M.; Mondello, C.; Osellame, R.; et al. An integrated optofluidic device for single-cell sorting driven by mechanical properties. Lab Chip 2015, 15, 1262–1266. [Google Scholar] [CrossRef] [PubMed]
- Faigle, C.; Lautenschläger, F.; Whyte, G.; Homewood, P.; Martín-Badosa, E.; Guck, J. A monolithic glass chip for active single-cell sorting based on mechanical phenotyping. Lab Chip 2015, 15, 1267–1275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lincoln, B.; Schinkinger, S.; Travis, K.; Wottawah, F.; Ebert, S.; Sauer, F.; Guck, J. Reconfigurable microfluidic integration of a dual-beam laser trap with biomedical applications. Biomed. Microdevices 2007, 9, 703–710. [Google Scholar] [CrossRef] [PubMed]
- Ren, K.; Zhou, J.; Wu, H. Materials for microfluidic chip fabrication. Acc. Chem. Res. 2013, 46, 2396–2406. [Google Scholar] [CrossRef] [PubMed]
- Guck, J.; Ananthakrishnan, R.; Moon, T.J.; Cunningham, C.C.; Käs, J. Optical deformability of soft biological dielectrics. Phys. Rev. Lett. 2000, 84, 5451–5454. [Google Scholar] [CrossRef] [PubMed]
- Bellini, N.; Bragheri, F.; Cristiani, I.; Guck, J.; Osellame, R.; Whyte, G. Validation and perspectives of a femtosecond laser fabricated monolithic optical stretcher. Biomed. Opt. Express 2012, 3, 2658–2668. [Google Scholar] [CrossRef] [PubMed]
- Matteucci, M.; Triches, M.; Nava, G.; Kristensen, A.; Pollard, M.; Berg-Sørensen, K.; Taboryski, R. Fiber-based, injection-molded optofluidic systems: Improvements in assembly and applications. Micromachines 2015, 6, 1971–1983. [Google Scholar] [CrossRef] [Green Version]
- Gattass, R.R.; Mazur, E. Femtosecond laser micromachining in transparent materials. Nat. Photonics 2008, 2, 219–225. [Google Scholar] [CrossRef]
- He, F.; Liao, Y.; Lin, J.; Song, J.; Qiao, L.; Cheng, Y.; Sugioka, K. Femtosecond laser fabrication of monolithically integrated microfluidic sensors in glass. Sensors 2014, 14, 19402–19440. [Google Scholar] [CrossRef] [PubMed]
- Osellame, R.; Maselli, V.; Vazquez, R.M.; Ramponi, R.; Cerullo, G. Integration of optical waveguides and microfluidic channels both fabricated by femtosecond laser irradiation. Appl. Phys. Lett. 2007, 90, 231118. [Google Scholar] [CrossRef]
- Osellame, R.; Hoekstra, H.; Cerullo, G.; Pollnau, M. Femtosecond laser microstructuring: An enabling tool for optofluidic lab-on-chips. Laser Photonics Rev. 2011, 5, 442–463. [Google Scholar] [CrossRef]
- Taylor, R.S.; Hnatovsky, C.; Simova, E.; Rayner, D.M.; Bhardwaj, V.R.; Corkum, P.B. Femtosecond laser fabrication of nanostructures in silica glass. Opt. Lett. 2003, 28, 1043–1045. [Google Scholar] [CrossRef] [PubMed]
- Bellini, N.; Vishnubhatla, K.C.; Bragheri, F.; Ferrara, L.; Minzioni, P.; Ramponi, R.; Cristiani, I.; Osellame, R. Femtosecond laser fabricated monolithic chip for optical trapping and stretching of single cells. Opt. Express 2010, 18, 4679–4688. [Google Scholar] [CrossRef] [PubMed]
- Nava, G.; Bragheri, F.; Yang, T.; Minzioni, P.; Osellame, R.; Cristiani, I.; Berg-Sørensen, K. All-silica microfluidic optical stretcher with acoustophoretic prefocusing. Microfluid. Nanofluid. 2015, 19, 837–844. [Google Scholar] [CrossRef]
- Bragheri, F.; Ferrara, L.; Bellini, N.; Vishnubhatla, K.C.; Minzioni, P.; Ramponi, R.; Osellame, R.; Cristiani, I. Optofluidic chip for single cell trapping and stretching fabricated by a femtosecond laser. J. Biophotonics 2010, 3, 234–243. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Nava, G.; Minzioni, P.; Veglione, M.; Bragheri, F.; Lelii, F.D.; Vazquez, R.M.; Osellame, R.; Cristiani, I. Investigation of temperature effect on cell mechanics by optofluidic microchips. Biomed. Opt. Express 2015, 6, 2991–2996. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A. Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime. Biophys. J. 1992, 61, 569–582. [Google Scholar] [CrossRef]
- Ashkin, A. Trapping of atoms by resonance radiation pressure. Phys. Rev. Lett. 1978, 40, 729–732. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Radiation pressure on a free liquid surface. Phys. Rev. Lett. 1973, 30, 139–142. [Google Scholar] [CrossRef]
- Ferrara, L.; Baldini, E.; Minzioni, P.; Bragheri, F.; Liberale, C.; Fabrizio, E.D.; Cristiani, I. Experimental study of the optical forces exerted by a Gaussian beam within the Rayleigh range. J. Opt. 2011, 13, 75712–75718. [Google Scholar] [CrossRef]
- Bareil, P.B.; Sheng, Y.; Chiou, A. Local scattering stress distribution on surface of a spherical cell in optical stretcher. Opt. Express 2006, 14, 12503–12509. [Google Scholar] [CrossRef]
- Bareil, P.B.; Sheng, Y.; Chen, Y.Q.; Chiou, A. Calculation of spherical red blood cell deformation in a dual-beam optical stretcher. Opt. Express 2007, 15, 16029–16034. [Google Scholar] [CrossRef] [PubMed]
- Ekpenyong, A.E.; Posey, C.L.; Chaput, J.L.; Burkart, A.K.; Marquardt, M.M.; Smith, T.J.; Nichols, M.G. Determination of cell elasticity through hybrid ray optics and continuum mechanics modeling of cell deformation in the optical stretcher. Appl. Opt. 2009, 48, 6344–6354. [Google Scholar] [CrossRef] [PubMed]
- Brevik, I. Experiments in phenomenological electrodynamics and the electromagnetic energy-momentum tensor. Phys. Rep. 1979, 52, 133–201. [Google Scholar] [CrossRef]
- Lincoln, B.; Wottawah, F.; Schinkinger, S.; Ebert, S.; Guck, J. High throughput rheological measurements with an optical stretcher. Methods Cell Biol. 2007, 83, 397–423. [Google Scholar] [PubMed]
- Wottawah, F.; Schinkinger, S.; Lincoln, B.; Ananthakrishnan, R.; Romeyke, M.; Guck, J.; Käs, J. Optical rheology of biological cells. Phys. Rev. Lett. 2005, 94, 98103. [Google Scholar] [CrossRef] [PubMed]
- Wottawah, F.; Schinkinger, S.; Lincoln, B.; Ebert, S.; Müller, K.; Sauer, F.; Travis, K.; Guck, J. Characterizing single suspended cells by optorheology. Acta Biomater. 2005, 1, 263–271. [Google Scholar] [CrossRef] [PubMed]
- Ananthakrishnan, R.; Guck, J.; Wottawah, F.; Schinkinger, S.; Lincoln, B.; Romeyke, M.; Kas, J. Modelling the structural response of an eukaryotic cell in the optical stretcher. Curr. Sci. 2005, 88, 1434–1440. [Google Scholar]
- Ananthakrishnan, R.; Guck, J.; Wottawah, F.; Schinkinger, S.; Lincoln, B.; Romeyke, M.; Moon, T.; Käs, J. Quantifying the contribution of actin networks to the elastic strength of fibroblasts. J. Theor. Biol. 2006, 242, 502–516. [Google Scholar] [CrossRef] [PubMed]
- Gladilin, E.; Gonzalez, P.; Eils, R. Dissecting the contribution of actin and vimentin intermediate filaments to mechanical phenotype of suspended cells using high-throughput deformability measurements and computational modeling. J. Biomech. 2014, 47, 2598–2605. [Google Scholar] [CrossRef] [PubMed]
- Ye, T.; Phan-Thien, N.; Khoo, B.C.; Lim, C.T. Stretching and relaxation of malaria-infected red blood cells. Biophys. J. 2013, 105, 1103–1109. [Google Scholar] [CrossRef] [PubMed]
- Mauritz, J.A.; Esposito, A.; Tiffert, T.; Skepper, J.; Warley, A.; Yoon, Y.Z.; Cicuta, P.; Lew, V.; Guck, J.; Kaminski, C. Biophotonic techniques for the study of malaria-infected red blood cells. Med. Biol. Eng. Comput. 2010, 48, 1055–1063. [Google Scholar] [CrossRef] [PubMed]
- Sawetzki, T.; Eggleton, C.D.; Desai, S.A.; Marr, D.W.M. Viscoelasticity as a biomarker for high-throughput flow cytometry. Biophys. J. 2013, 105, 2281–2288. [Google Scholar] [CrossRef] [PubMed]
- Sraj, I.; Eggleton, C.D.; Jimenez, R.; Hoover, E.; Squier, J.; Chichester, J.; Marr, D.W.M. Cell deformation cytometry using diode-bar optical stretchers. J. Biomed. Opt. 2010, 15, 47010. [Google Scholar] [CrossRef] [PubMed]
- Sraj, I.; Marr, D.W.M.; Eggleton, C.D. Linear diode laser bar optical stretchers for cell deformation. Biomed. Opt. Express 2010, 1, 482–488. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.P.; Liu, K.K.; Lai, A.C.K.; Li, C. The deformation of an erythrocyte under the radiation pressure by optical stretch. J. Biomech. Eng. 2006, 128, 830–836. [Google Scholar] [CrossRef] [PubMed]
- Tan, Y.; Sun, D.; Huang, W. Mechanical modeling of red blood cells during optical stretching. J. Biomech. Eng. 2010, 132, 044504. [Google Scholar] [CrossRef] [PubMed]
- Solmaz, M.E.; Biswas, R.; Sankhagowit, S.; Thompson, J.R.; Mejia, C.A.; Malmstadt, N.; Povinelli, M.L. Optical stretching of giant unilamellar vesicles with an integrated dual-beam optical trap. Biomed. Opt. Express 2012, 3, 2419–2427. [Google Scholar] [CrossRef] [PubMed]
- Delabre, U.; Feld, K.; Crespo, E.; Whyte, G.; Sykes, C.; Seifert, U.; Guck, J. Deformation of phospholipid vesicles in an optical stretcher. Soft Matter 2015, 11, 6075–6088. [Google Scholar] [CrossRef] [PubMed]
- Lautenschläger, F.; Paschke, S.; Schinkinger, S.; Bruel, A.; Beil, M.; Guck, J. The regulatory role of cell mechanics for migration of differentiating myeloid cells. Proc. Natl. Acad. Sci. USA 2009, 106, 15696–15701. [Google Scholar] [CrossRef] [PubMed]
- Schulze, C.; Wetzel, F.; Kueper, T.; Malsen, A.; Muhr, G.; Jaspers, S.; Blatt, T.; Wittern, K.P.; Wenck, H.; Käs, J.A. Stiffening of human skin fibroblasts with age. Clin. Plast. Surg. 2012, 39, 9–20. [Google Scholar] [CrossRef] [PubMed]
- Bragheri, F.; Minzioni, P.; Martinez Vazquez, R.; Bellini, N.; Paie, P.; Mondello, C.; Ramponi, R.; Cristiani, I.; Osellame, R. Optofluidic integrated cell sorter fabricated by femtosecond lasers. Lab Chip 2012, 12, 3779–3784. [Google Scholar] [CrossRef] [PubMed]
- Holmes, D.; Whyte, G.; Bailey, J.; Vergara-Irigaray, N.; Ekpenyong, A.; Guck, J.; Duke, T. Separation of blood cells with differing deformability using deterministic lateral displacement. Interface Focus 2014, 4. UNSP20140011. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Duffy, S.P.; Matthews, K.; Deng, X.; Santoso, A.T.; Islamzada, E.; Ma, H. Deformability based sorting of red blood cells improves diagnostic sensitivity for malaria caused by Plasmodium falciparum. Lab Chip 2016, 16, 645–654. [Google Scholar] [CrossRef] [PubMed]
- Beech, J.P.; Holm, S.H.; Adolfsson, K.; Tegenfeldt, J.O. Sorting cells by size, shape and deformability. Lab Chip 2012, 12, 1048–1051. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Mao, W.; Byler, R.; Patel, K.; Henegar, C.; Alexeev, A.; Sulchek, T. Stiffness dependent separation of cells in a microfluidic device. PLoS ONE 2013, 8, e75901. [Google Scholar] [CrossRef] [PubMed]
- Peterman, E.J.G.; Gittes, F.; Schmidt, C.F. Laser-induced heating in optical traps. Biophys. J. 2003, 84, 1308–1316. [Google Scholar] [CrossRef]
- Ebert, S.; Travis, K.; Lincoln, B.; Guck, J. Fluorescence ratio thermometry in a microfluidic dual-beam laser trap. Opt. Express 2007, 15, 15493–15499. [Google Scholar] [CrossRef] [PubMed]
- Wetzel, F.; Rönicke, S.; Müller, K.; Gyger, M.; Rose, D.; Zink, M.; Käs, J. Single cell viability and impact of heating by laser absorption. Eur. Biophys. J. EBJ 2011, 40, 1109–1114. [Google Scholar] [CrossRef] [PubMed]
- Gyger, M.; Rose, D.; Stange, R.; Kiessling, T.; Zink, M.; Fabry, B.; Käs, J.A. Calcium imaging in the optical stretcher. Opt. Express 2011, 19, 19212–19222. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.H.; Yang, K.J.; Wu, J.C.; Chang, K.J.; Wang, S.M. Effects of hyperthermia on the cytoskeleton and focal adhesion proteins in a human thyroid carcinoma cell line. J. Cell. Biochem. 1999, 75, 327–337. [Google Scholar] [CrossRef]
- Wang, X.M.; Terasaki, P.I.; Rankin, G.W.; Chia, D.; Zhong, H.P.; Hardy, S. A new microcellular cytotoxicity test based on calcein AM release. Hum. Immunol. 1993, 37, 264–270. [Google Scholar] [CrossRef]
- Kießling, T.R.; Stange, R.; Käs, J.A.; Fritsch, A.W. Thermorheology of living cells-impact of temperature variations on cell mechanics. New J. Phys. 2013, 15, 045026. [Google Scholar] [CrossRef]
- Warmt, E.; Kießling, T.R.; Stange, R.; Fritsch, A.W.; Zink, M.; Käs, J.A. Thermal instability of cell nuclei. New J. Phys. 2014, 16, 073009. [Google Scholar] [CrossRef]
- Schmidt, B.U.S.; Kießling, T.R.; Warmt, E.; Fritsch, A.W.; Stange, R.; Käs, J.A. Complex thermorheology of living cells. New J. Phys. 2015, 17, 073010. [Google Scholar] [CrossRef]
- Chan, C.J.; Whyte, G.; Boyde, L.; Salbreux, G.; Guck, J. Impact of heating on passive and active biomechanics of suspended cells. Interface Focus 2014, 4, 20130069. [Google Scholar] [CrossRef] [PubMed]
- Khoury, M.; Barnkob, R.; Laub Busk, L.; Tidemand-Lichtenberg, P.; Bruus, H.; Berg-Sørensen, K. Optical stretching on chip with acoustophoretic prefocusing. Proc. SPIE 2012, 8458, 84581E. [Google Scholar]
- Yang, T.; Bragheri, F.; Nava, G.; Chiodi, I.; Mondello, C.; Osellame, R.; Berg-Sørensen, K.; Cristiani, I.; Minzioni, P. A comprehensive strategy for the analysis of acoustic compressibility and optical deformability on single cells. Sci. Rep. 2016, 6, 23946. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kreysing, M.K.; Kießling, T.; Fritsch, A.; Dietrich, C.; Guck, J.R.; Käs, J.A. The optical cell rotator. Opt. Express 2008, 16, 16984–16992. [Google Scholar] [CrossRef] [PubMed]
- Kreysing, M.; Ott, D.; Schmidberger, M.J.; Otto, O.; Schürmann, M.; Martín-Badosa, E.; Whyte, G.; Guck, J. Dynamic operation of optical fibres beyond the single-mode regime facilitates the orientation of biological cells. Nat. Commun. 2014, 5, 5481. [Google Scholar] [CrossRef] [PubMed]
- Khoury, M.; Vannahme, C.; Sørensen, K.; Kristensen, A.; Berg-Sørensen, K. Monolithic integration of DUV-induced waveguides into plastic microfluidic chip for optical manipulation. Microelectron. Eng. 2014, 121, 5–9. [Google Scholar] [CrossRef]
- Tomlinson, W.J.; Kaminow, I.P.; Chandross, E.A.; Fork, R.L.; Silfvast, W.T. Photo induced refractive index increase in poly(Methylmethacrylate) and its application. Appl. Phys. Lett. 1970, 16, 486–489. [Google Scholar] [CrossRef]














© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Bragheri, F.; Minzioni, P. A Comprehensive Review of Optical Stretcher for Cell Mechanical Characterization at Single-Cell Level. Micromachines 2016, 7, 90. https://doi.org/10.3390/mi7050090
Yang T, Bragheri F, Minzioni P. A Comprehensive Review of Optical Stretcher for Cell Mechanical Characterization at Single-Cell Level. Micromachines. 2016; 7(5):90. https://doi.org/10.3390/mi7050090
Chicago/Turabian StyleYang, Tie, Francesca Bragheri, and Paolo Minzioni. 2016. "A Comprehensive Review of Optical Stretcher for Cell Mechanical Characterization at Single-Cell Level" Micromachines 7, no. 5: 90. https://doi.org/10.3390/mi7050090






