1. Introduction
Piezoelectric bending actuators are an important class of micro electro-mechanical systems (MEMS) that find wide use in applications involving relatively large displacements in millimeter scale applications. Example dynamic applications include flapping wing propulsion [
1,
2,
3,
4,
5,
6,
7], cooling fans [
8,
9,
10], vibration control [
11,
12], and energy harvesters [
13,
14]. Dynamic operation at resonance with light damping significantly increases the achievable displacement of the actuator compared to the achievable static displacement for the same magnitude of electrical input. Whilst piezoelectric bending actuators are geometrically simple, the solution of the dynamic design problem is non-trivial, and, in recent years, there has been significant interest in providing theoretical, numerical and experimental contributions to dynamic characterization of these devices [
13,
14,
15,
16,
17,
18,
19].
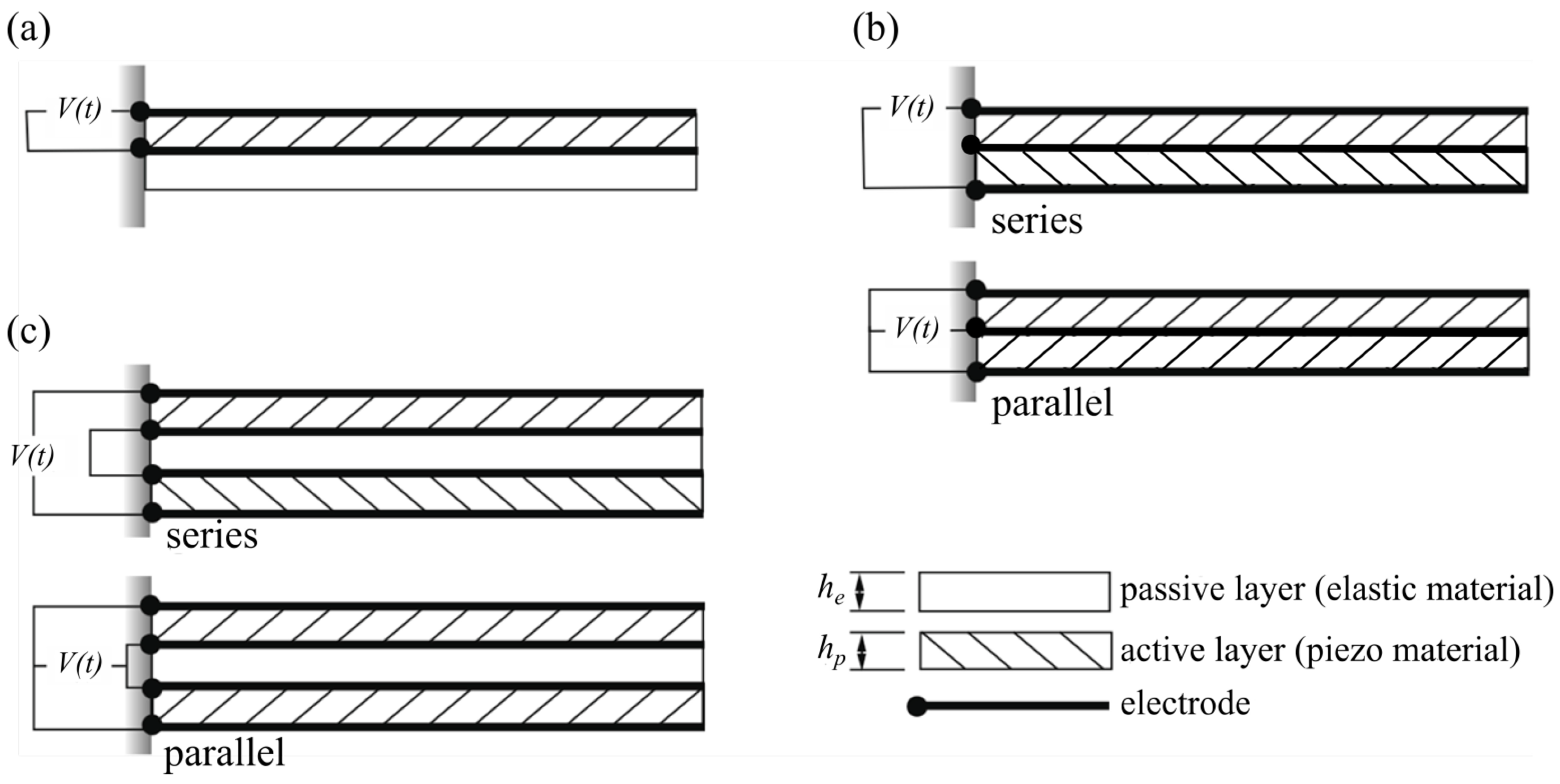
A summary of the commonly used configurations of piezoelectric bending actuators is shown in
Figure 1. It is assumed that actuators are made up of homogenous layers of active (piezoelectric) material or passive (elastic) material. The simplest viable configuration is comprised of one active layer and one passive layer and is referred to as a unimorph [
20],
Figure 1a. For configurations with two active layers, the general arrangement is one in which the two active layers are separated by an inner passive layer [
21],
Figure 1c. For the purposes of the present work, we will refer to this as a triple layer bimorph. In the limit when the thickness of the inner passive layer is reduced to zero, we reach the configuration shown in
Figure 1b, which we will refer to as a double layer bimorph. Note that for both types of bimorphs shown, the active layers may be connected in series or parallel depending on the poling direction of the piezoelectric material.
Figure 1.
Piezoelectric bending actuators; illustration of the main configurations of practical interest. (a) Unimorph; (b) Double layer bimorph; (c) Triple layer bimorph. Sign of hatching direction illustrates sign of poling for piezo material.
Figure 1.
Piezoelectric bending actuators; illustration of the main configurations of practical interest. (a) Unimorph; (b) Double layer bimorph; (c) Triple layer bimorph. Sign of hatching direction illustrates sign of poling for piezo material.
One of the goals of actuator electromechanical design is to identify materials and configurations that maximize mechanical output for a given input electrical input, that is, the actuator is electromechanically efficient. Actuator electromechanical efficiency is usually measured using the electromechanical coupling factor (EMCF) denoted by
k2, and the maximum energy transmission coefficient denoted by λ
max [
20,
22,
23]. The EMCF is defined as the ratio of stored mechanical energy to the input electrical energy to the actuator, whilst the energy transmission coefficient is defined as the ratio of the output mechanical energy to the input electric energy [
20,
22,
23]. The maximum energy transmission coefficient is a direct and single function of the EMCF [
20]; thus, best configurations with respect to EMCF are also best with respect to the maximum energy transmission coefficient, and it is therefore sufficient to consider optimum actuator configurations based only on optimization of EMCF.
The static electromechanical coupling factor and the maximum energy transmission coefficient of unimorphs and double layer bimorphs have been assessed by Wang
et al. [
20] using static actuation constituent equations. It was shown that for double layer bimorphs, these measures are only a function of the piezoelectric material transverse coupling coefficient,
k31, whereas for unimorphs, they are also a function of the Young’s modulus ratio and the thickness ratio of the actuator layers [
20]. In a later contribution, the static actuation constitutive equations were derived for the triple layer bimorph configuration [
21]; however its electromechanical coupling factor was not assessed. Maurini
et al. [
24] provided an extended Euler-Bernoulli beam model that considers the influence of 3D stresses and strains. The obtained coefficients of the static constituent equations for bimorph configurations were assessed against available standard models, and the achieved modeling improvement was demonstrated through comparisons with results from finite element simulations. The work [
24] considered simply supported beams without analyzing other boundary conditions (e.g., cantilevers), and the electromechanical coupling factor was not addressed. The dynamic electromechanical coupling of unimorphs has been assessed by Chung
et al. [
4] based on the product of resonant frequency and vibration amplitude. The electromechanical coupling factor of unimorph actuators in dynamic operations has also been comprehensively assessed by the present authors [
19]. It was found that the variation of dynamic EMCF with design variables is similar for both static and dynamic operation; however, for light damping, the dynamic EMCF will be an order of magnitude greater than for static operation.
The aim of the present work is to provide a comprehensive assessment of the electromechanical coupling characteristics of bimorph actuators in dynamic operation. Analytical expressions for double and triple layer bimorph actuators are derived in an explicit fashion allowing assessment of their dynamic actuation efficiency in a design context. The main contribution of this work is significantly improved understanding of the effect of configuration, material properties and operating conditions on the dynamic performance of bimorph actuators. The following section will provide a comprehensive theoretical model for the electromechanical coupling evaluation in dynamic operations. This will be followed by an analysis of the results from the theoretical model.
2. Dynamic Electromechanical Coupling Model
Following from references [
20,
22,
23], a general expression for the electromechanical coupling factor (EMCF) can be written down as:
where the
D elements of the above expression are the symmetric matrix elements representing the set of constitutive equations of the actuator:
where δ,
F,
Q and
V are the deflection, force, charge and voltage, respectively;
l is the actuator tip position,
t is time, and ω is the operation frequency. For details of the dynamic admittance matrix, see reference [
19]. For the present work, the expression for the terms in the dynamic admittance matrix are re-written in a generic form that is independent of the configuration of the actuator as follows:
where
n indicates the
nth vibration mode. Note that Equations (3)–(5) are derived based on the assumption of a uniform composite Euler–Bernoulli beam with very thin, perfectly conductive electrodes covering the entire top and bottom surfaces of the piezo layer [
13,
19]. Application of Euler–Bernoulli beam theory to composite beams is typically assumed to be valid for beams with length to thickness (aspect) ratios above 30 [
25]. This is typically the case for many practical actuator/harvester applications [
13,
14,
16,
17,
18,
19]. For geometrical configurations where 1D beam theory becomes inappropriate, a higher level model should be used, for example, see [
26].
Table 1 provides the configuration parameters for Equations (3)–(5) that will be used throughout the current derivation. These include: the neutral axis position,
, the rigidity,
YI, the mass per unit length, ρ
A, the voltage loading parameter, α
p, and the active layers’ thickness defining the electric field,
hE (
i.e.,
E =
V/
hE). In the above expressions,
d31 is the piezoelectric constant (piezoelectric material property),
k31 is the piezoelectric material transverse electromechanical coupling coefficient (piezoelectric material property),
b is the actuator width,
h is the thickness,
Y is the Young's modulus, ρ is the material density and the subscripts
e and
p denote the elastic and piezoelectric layers respectively. Note that the unimorph expressions are the most complex due to its non-symmetric configuration. In addition, note that there is some analytical redundancy in that the expressions for the double layer bimorph case can be obtained either by substituting
he =
hp,
Ye =
Yp and ρ
e = ρ
p in the unimorph expressions or by substituting
he = 0,
Ye = 0 and ρ
e = 0 in the triple layer bimorph expressions.
Table 1.
Configuration parameters for different actuators.
Table 1.
Configuration parameters for different actuators.
| Parameter | Unimorph [13,19] | Double Layer Bimorph | Triple Layer Bimorph [14] |
|---|
| | | |
| | | |
| | | |
| | | |
| | | |
The parameters that control the vibration response in Equations (3)–(5) are the damping ratio, ζ
n, and the frequency ratio,
rn = ω
/ω
n, where ω
n is the natural frequency given by [
27]:
where β
n denotes the wave number. Note that the natural frequency for light damping is approximately the damped resonant frequency.
Finally, the term
In is given by:
where
Xn is the mode shape function for fixed-free boundary conditions. For the current work, we define
Xn using [
27]:
where
We choose this definition of the mode shape function over other variants in the literature because of the characteristic:
and thus the so-called “generalized mass” [
28] becomes the actual actuator mass at the first resonant frequency:
This choice is of significance since it removes the need for numerical integration within the actuator design process and hence simple explicit analytical expressions can be obtained. Note also that the mode shape expression given by Equation (8) has the following useful characteristics:
where
We now return back to the dynamic matrix elements provided in Equations (3)–(5). For most piezoelectric MEMS applications, the fundamental vibration mode
rn =
r1 is of most interest as it delivers the maximum displacement gain for a given level of damping. We thus drop the summations in Equations (3)–(5). Making use of the mode shape properties given in Equations (12) and (13), Equations (3)–(5) reduce to:
Using the above expressions, a general expression for the dynamic EMCF at the first resonant frequency (
i.e.,
r1 = 1) can be obtained as:
where
Note that the configuration expressions for the double layer and triple layer bimorphs presented in
Table 1 are for the piezoelectric elements in series. For a parallel configuration,
D11(
l) will remain the same; however,
, and
[
14,
21]. Therefore, using the EMCF expression Equation (1), it can be seen that the parallel EMCF remains the same as the series as required by fundamental physical considerations.
Now, in order to provide explicit expressions for the dynamic EMCF for the different bimorph configurations, the configuration expressions in
Table 1 are substituted in Equations (17)–(19). Further to some mathematical manipulation, the following expression is obtained for the dynamic EMCF of the double layer bimorph:
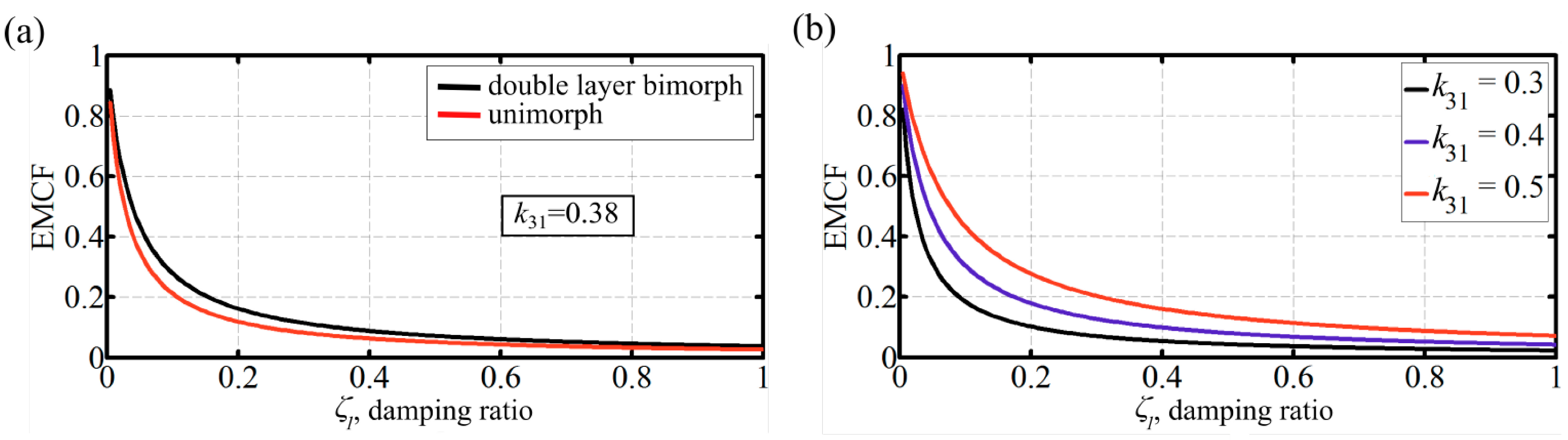
Thus, the dynamic EMCF of a double layer bimorph is function of the PZT material transverse electromechanical coupling coefficient, k31, and the operation damping ratio, ζ1, only. Note that if either or as required by fundamental physical considerations. In addition, it is directly inferred that there is no specific optimum values for k31 and ζ1 that would allow a maximum k2 value; that is, the higher the k31 value, the higher the dynamic EMCF, and the lower the ζ1 value, the higher the dynamic EMCF.
An explicit analytical expression for the dynamic EMCF is also obtained for the triple layer bimorph making use of its configuration properties in
Table 1 in conjunction with Equations (17)–(19). With some mathematical effort, it can be shown that the dynamic EMCF for this configuration is given by:
where
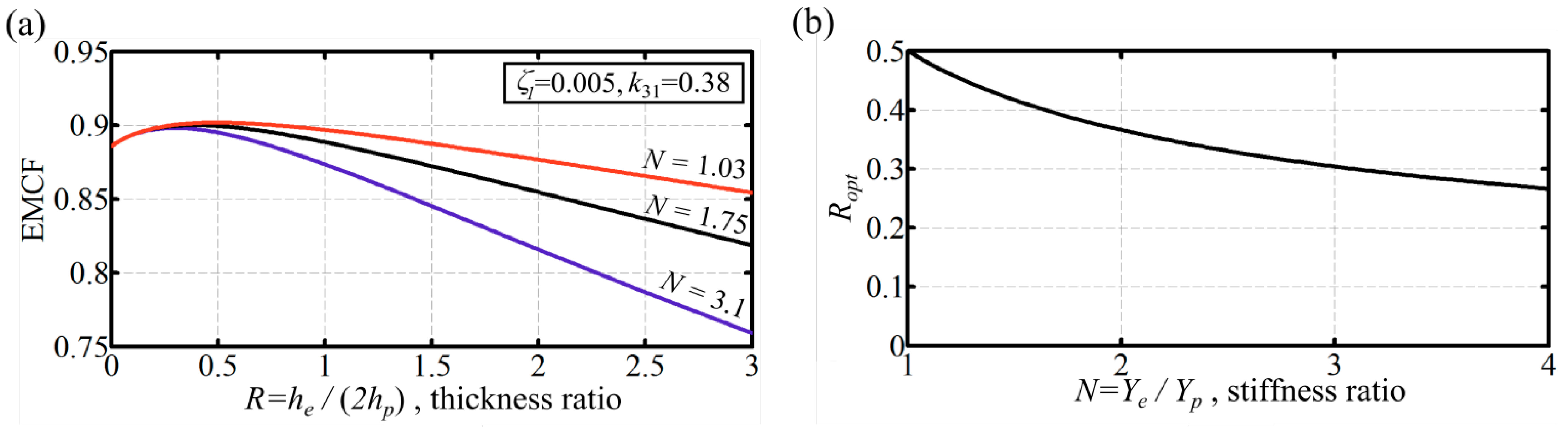
Note that for verification, Equation (21) returns to the double layer bimorph expression (Equation (20)) for the case R = 0, as required. Again, the higher the k31 value the higher the dynamic EMCF, and the lower the ζ1 value the higher the dynamic EMCF; however, the k2 value now depends on the layers’ thickness ratio, R, and the Young’s modulus ratio of the layers, N. Inspection of Equation (21) shows that the lower N values lead to higher k2 values; that is, an elastic material with lower Young’s modulus is favorable from a coupling point of view.
An expression for the optimum thickness ratio,
Ropt, can be derived using Equation (21). By differentiation with respect to
R and equating the resultant expression to zero, the following condition is obtained:
There are four roots for the above equation; however, the only valid solution for the above equation that would allow a meaningful explicit expression for
Ropt is:
where
Thus, the optimal thickness ratio of elastic to active layer thickness exists for triple layer bimorphs, and this optimum value depends only on the ratio of material stiffness for the layers.