Temperature Sensing in Modular Microfluidic Architectures
Abstract
:1. Introduction
2. Results
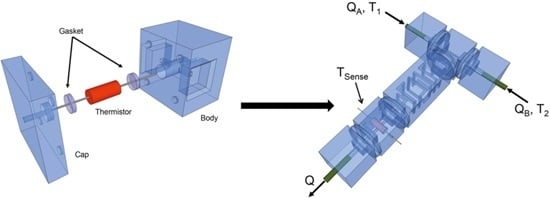
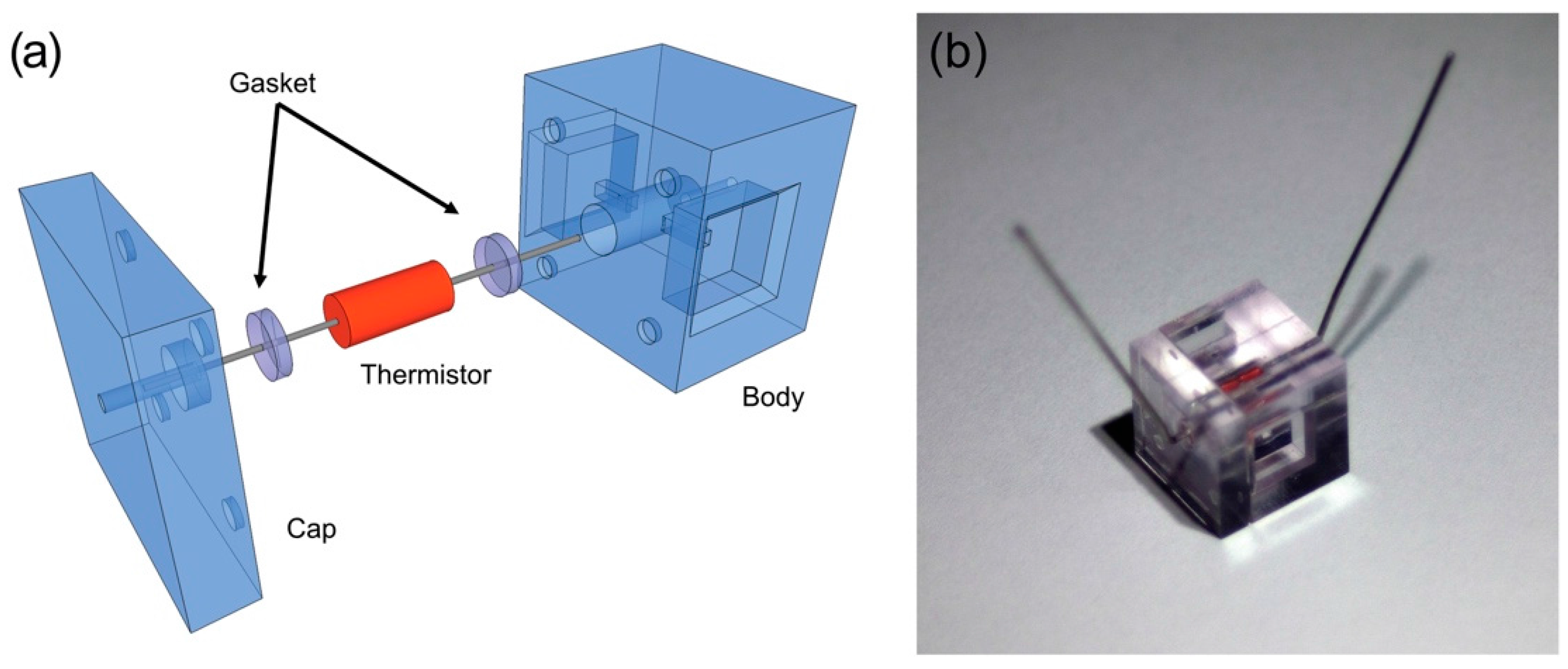
2.1. Design Principle
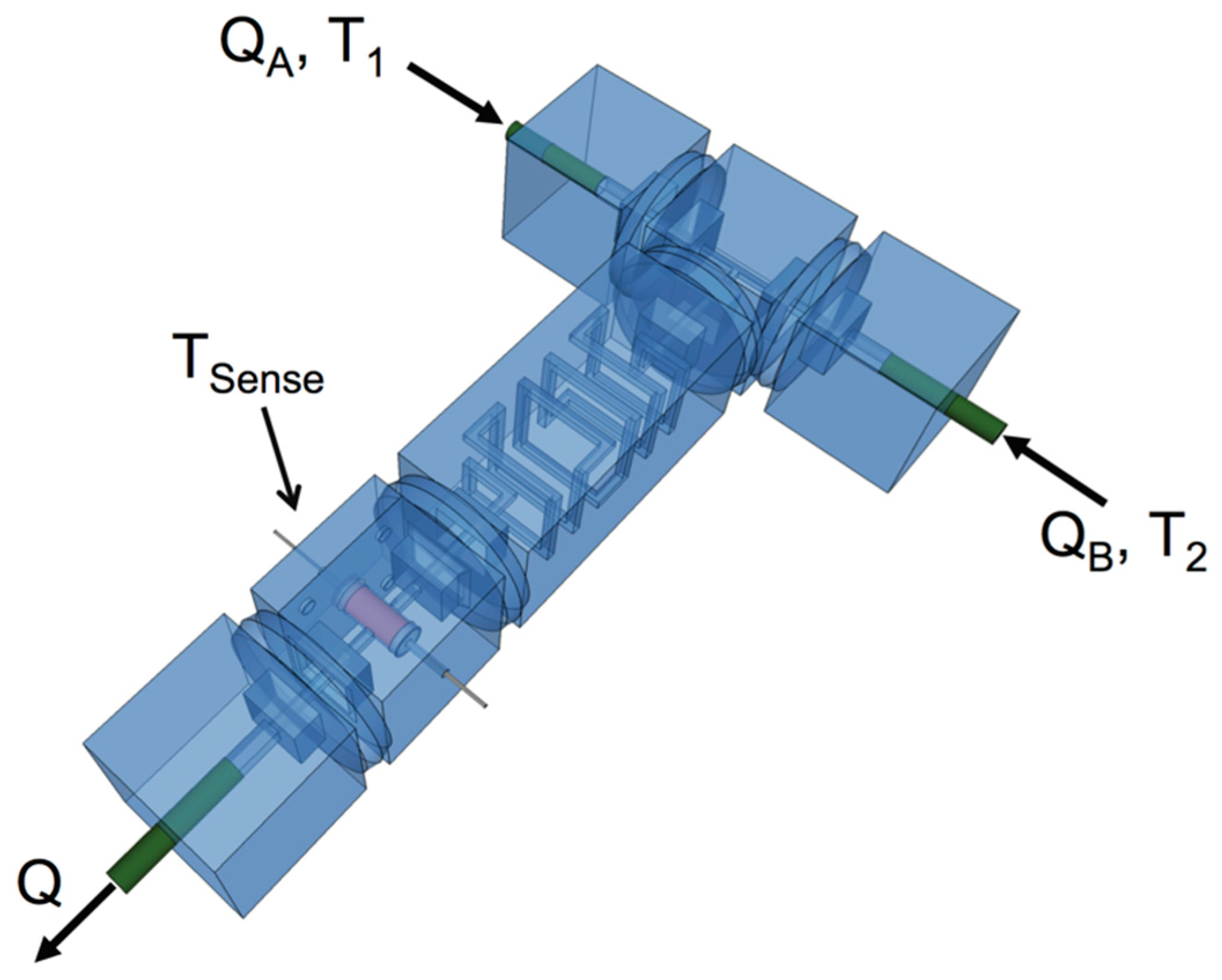
2.2. Flow Rate Dependent Response

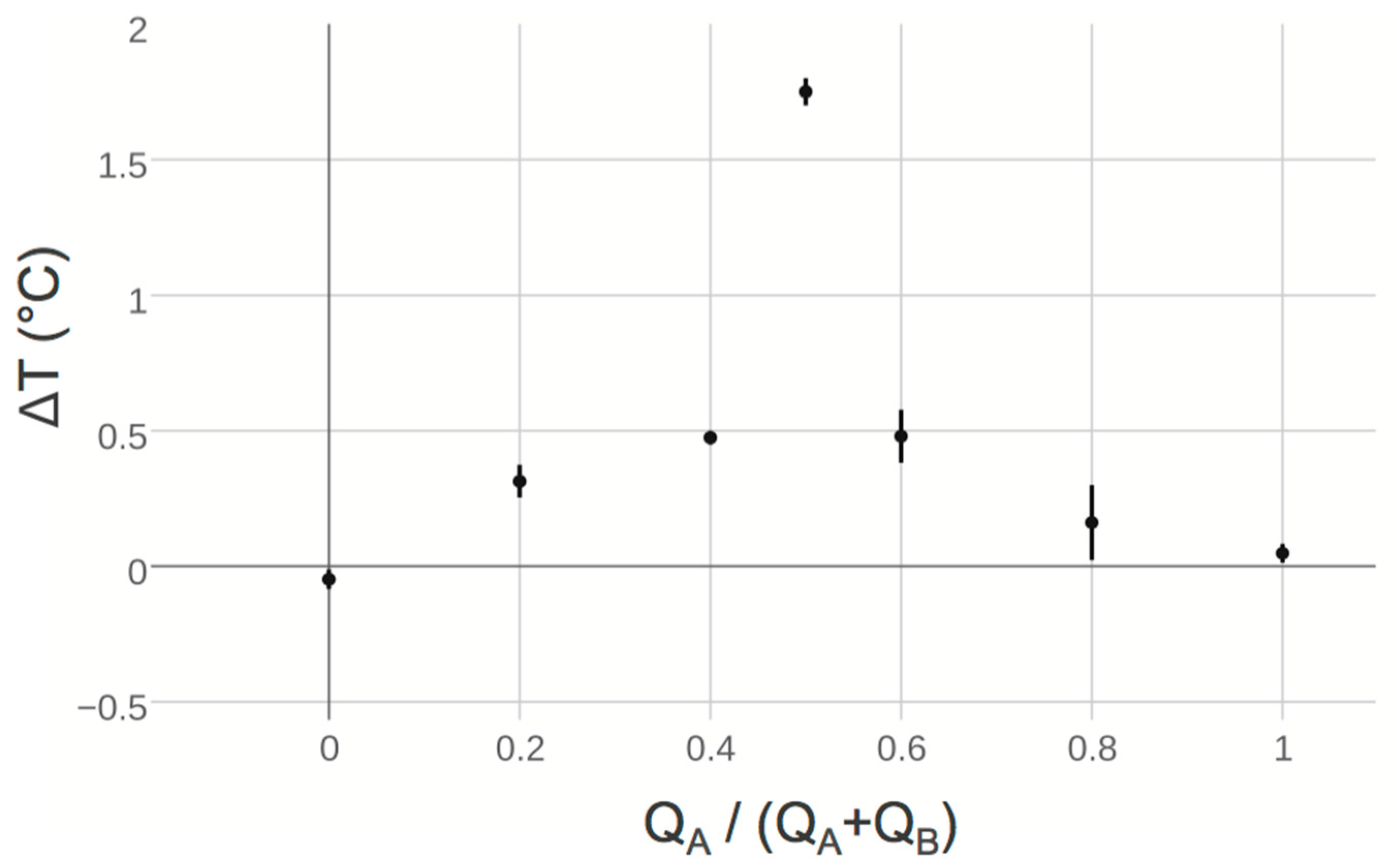
2.3. Continuous Flow Titration
3. Discussion
4. Materials and Methods
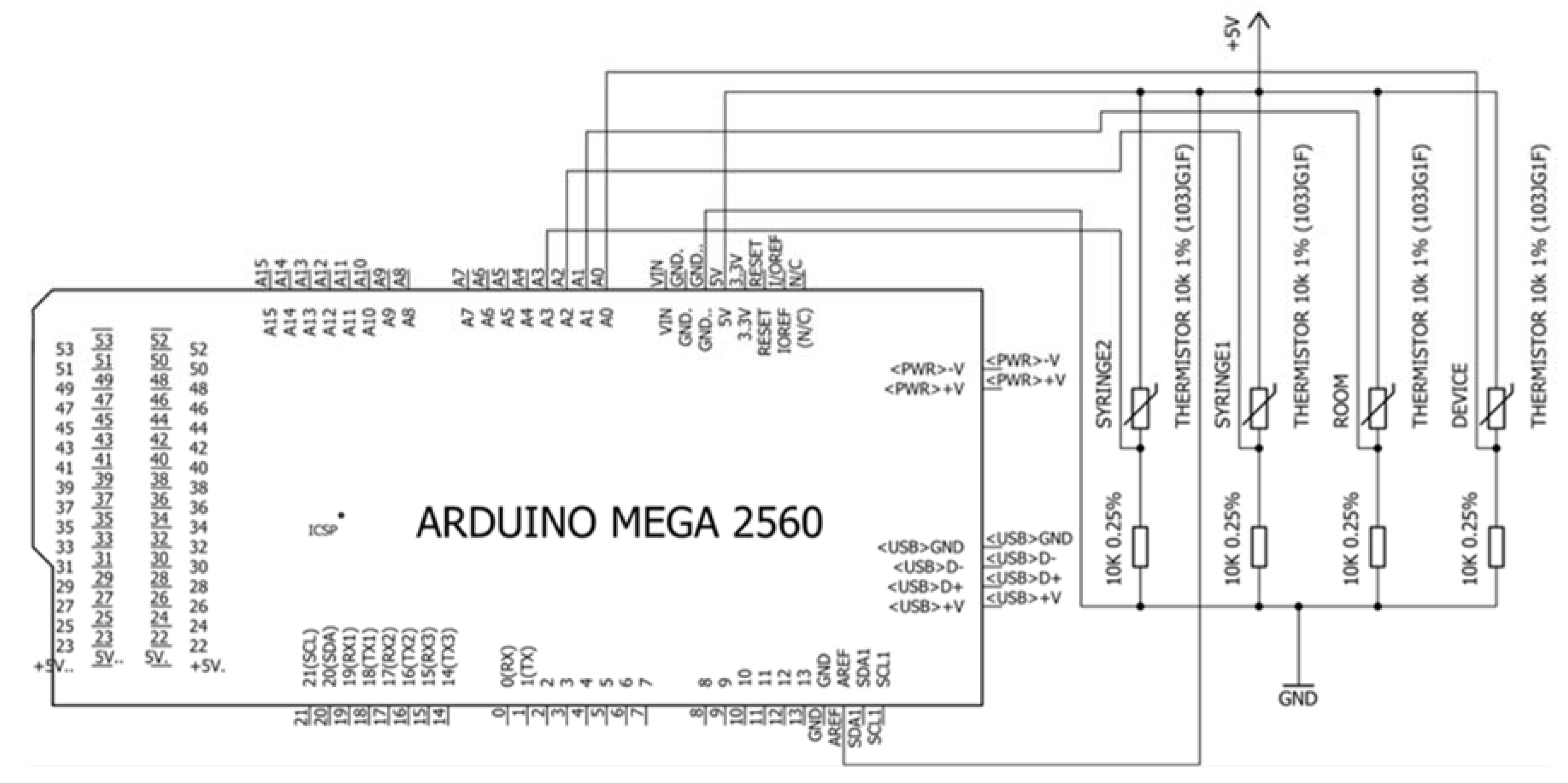
4.1. Electronic and Software Interfaces
4.2. Microfluidic Components and Experiments
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. System Components

Appendix B. Temperature Data
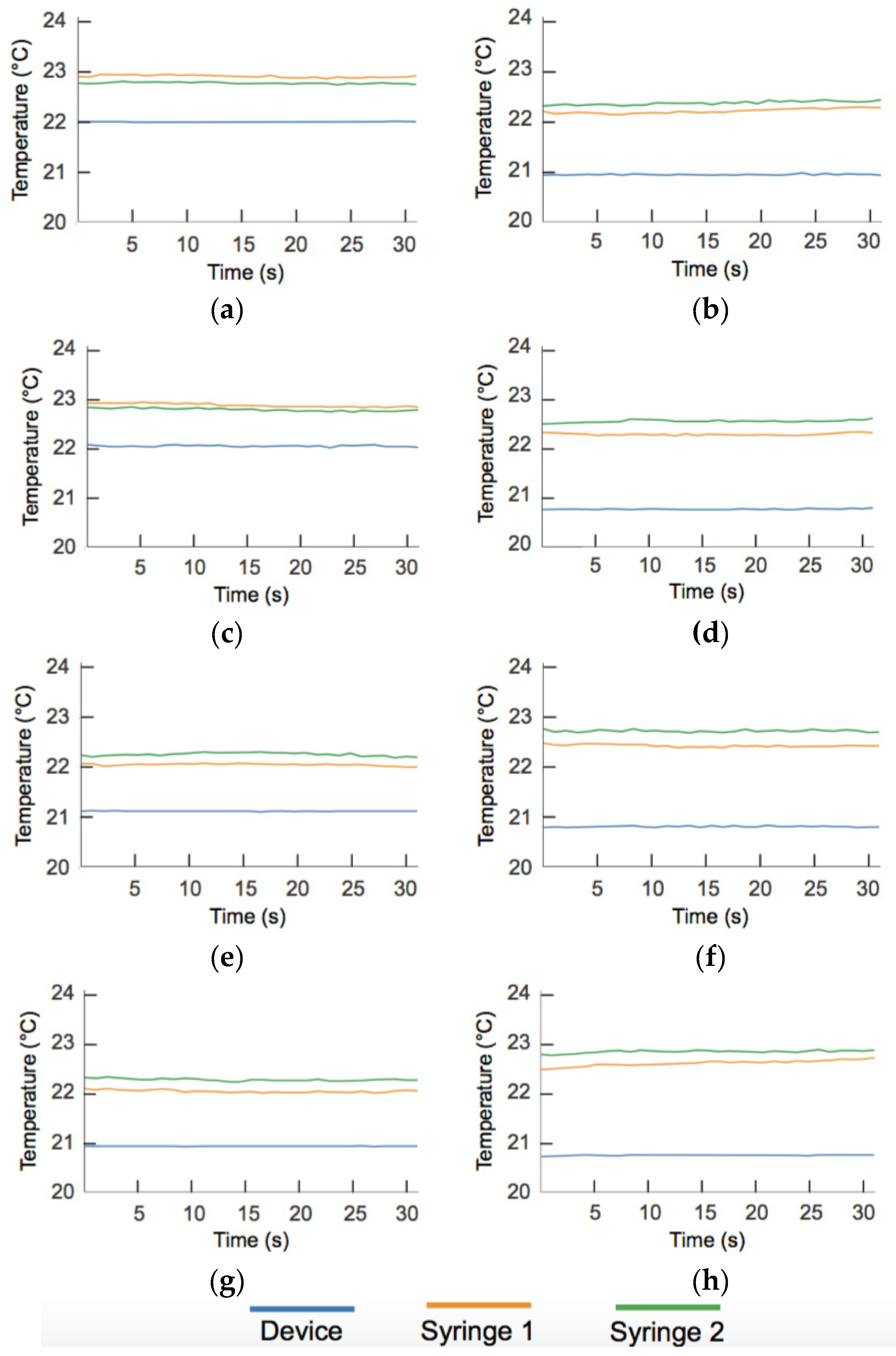
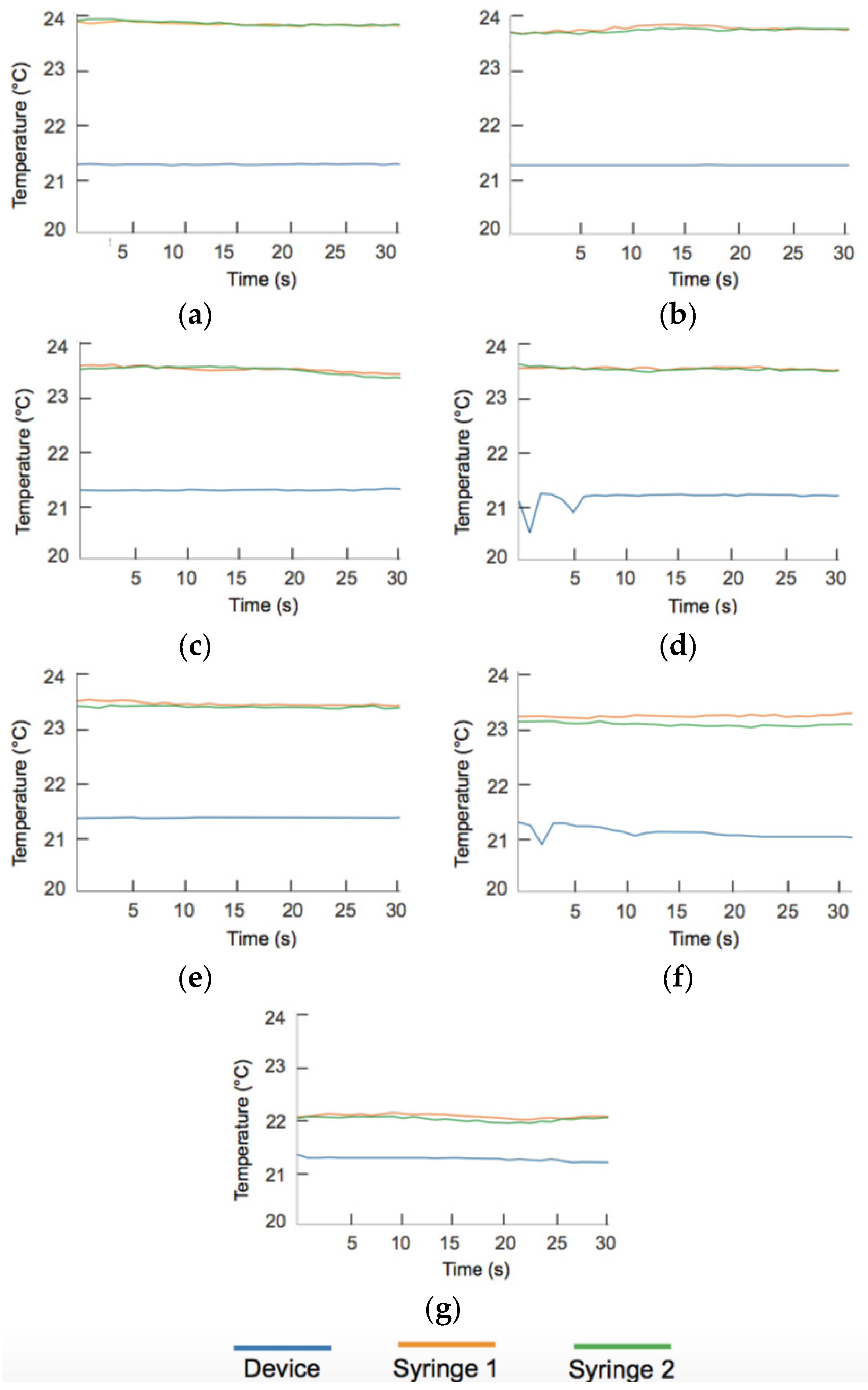
Appendix C. Circuit Schematic
References
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid Physics at the Nanoliter Scale. Rev. Mod. Phys. 2005, 77, 977–1024. [Google Scholar] [CrossRef]
- Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering Flows in Small Devices. Annu. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef]
- Whitesides, G.M. The Origins and the Future of Microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Beebe, D.J.; Mensing, G.A.; Walker, G.M. Physics and Applications of Microfluidics in Biology. Annu. Rev. Biomed. Eng. 2002, 4, 261–286. [Google Scholar] [CrossRef] [PubMed]
- Bennet, M.A.; Richardson, P.R.; Arlt, J.; McCarthy, A.; Buller, G.S.; Jones, A.C. Optically Trapped Microsensors for Microfluidic Temperature Measurement by Fluorescence Lifetime Imaging Microscopy. Lab Chip 2011, 11, 3821–3828. [Google Scholar] [CrossRef] [PubMed]
- Chaudhari, A.M.; Woudenberg, T.M.; Allin, M.; Goodson, K.E. Transient Liquid Crystal Thermometry of Microfabricated PCR Vessel Arrays. J. Microelectromechanical Syst. 1998, 7, 345–354. [Google Scholar] [CrossRef]
- Hoang, V.N.; Kaigala, G.V.; Backhouse, C.J. Dynamic Temperature Measurement in Microfluidic Devices Using Thermochromic Liquid Crystals. Lab Chip 2008, 8, 484–487. [Google Scholar] [CrossRef] [PubMed]
- Ross, D.; Gaitan, M.; Locascio, L.E. Temperature Measurement in Microfluidic Systems Using a Temperature-Dependent Fluorescent Dye. Anal. Chem. 2001, 73, 4117–4123. [Google Scholar] [CrossRef] [PubMed]
- Samy, R.; Glawdel, T.; Ren, C.L. Method for Microfluidic Whole-Chip Temperature Measurement Using Thin-Film Poly (dimethylsiloxane)/Rhodamine B. Measurement 2008, 80, 4117–4123. [Google Scholar] [CrossRef] [PubMed]
- Shah, J.J.; Gaitan, M.; Geist, J. Generalized Temperature Measurement Equations for Rhodamine B Dye Solution and Its Application to Microfluidics. Anal. Chem. 2009, 81, 8260–8263. [Google Scholar] [CrossRef] [PubMed]
- Hany, C.; Pradere, C.; Toutain, J.; Batsale, J.-C. A Millifluidic Calorimeter with Infrared Thermography for the Measurement of Chemical Reaction Enthalpy and Kinetics. Quant. Infrared Thermogr. J. 2008, 5, 211–229. [Google Scholar] [CrossRef] [Green Version]
- Pradere, C.; Joanicot, M.; Batsale, J.-C.; Toutain, J.; Gourdon, C. Processing of Temperature Field in Chemical Microreactors with Infrared Thermography. Quant. Infrared Thermogr. J. 2006, 3, 117–135. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Tadigadapa, S. Calorimetric Biosensors with Integrated Microfluidic Channels. Biosens. Bioelectron. 2004, 19, 1733–1743. [Google Scholar] [CrossRef] [PubMed]
- Lerchner, J.; Wolf, A.; Wolf, G.; Baier, V.; Kessler, E.; Nietzsch, M.; Krügel, M. A New Micro-fluid Chip Calorimeter for Biochemical Applications. Thermochim. Acta 2006, 445, 144–150. [Google Scholar] [CrossRef]
- Hany, C.; Lebrun, H.; Pradere, C.; Toutain, J.; Batsale, J.C. Thermal Analysis of Chemical Reaction with a Continuous Microfluidic Calorimeter. Chem. Eng. J. 2010, 160, 814–822. [Google Scholar] [CrossRef]
- Kwak, B.S.; Kim, B.S.; Cho, H.H.; Park, J.S.; Jung, H.I. Dual Thermopile Integrated Microfluidic Calorimeter for Biochemical Thermodynamics. Microfluid. Nanofluidics 2008, 5, 255–262. [Google Scholar] [CrossRef]
- Wang, L.; Wang, B.; Lin, Q. Demonstration of MEMS-based Differential Scanning Calorimetry for Determining Thermodynamic Properties of Biomolecules. Sens. Actuators B Chem. 2008, 134, 953–958. [Google Scholar] [CrossRef]
- Lee, W.; Fon, W.; Axelrod, W.B.; Roukes, M.L. High-sensitivity Microfluidic Calorimeters for Biological and Chemical Applications. Proc. Natl. Acad. Sci. USA 2009, 106, 15225–15230. [Google Scholar] [CrossRef] [PubMed]
- Burger, J.; Gross, A.; Mark, D.; Von Stetten, F.; Zengerle, R.; Roth, G. IR Thermocycler for Centrifugal Microfluidic Platform with Direct on-disk Wireless Temperature Measurement System. Proc. SPIE 2011, 8066. [Google Scholar] [CrossRef]
- McCormick, K.E.; Gaertner, B.E.; Sottile, M.; Phillips, P.C.; Lockery, S.R. Microfluidic Devices for Analysis of Spatial Orientation Behaviors in Semi-restrained Caenorhabditis Elegans. PLoS One 2011, 6, e25710. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Cisneros, C.S.; Ibáñez-García, N.; Valdés, F.; Alonso, J. LTCC Microflow Analyzers with Monolithic Integration of Thermal Control. Sens. Actuators A Phys. 2007, 138, 63–70. [Google Scholar] [CrossRef]
- Ernst, H.; Jachimowicz, A.; Urban, G. Dynamic Thermal Sensor—Principles in MEMS for Fluid Characterization. IEEE Sens. J. 2001, 1, 361–367. [Google Scholar] [CrossRef]
- Velve Casquillas, G.; Bertholle, F.; Le Berre, M.; Meance, S.; Malaquin, L.; Greffet, J.J.; Chen, Y. Thermo-resistance Based Micro-calorimeter for Continuous Chemical Enthalpy Measurements. Microelectron. Eng. 2008, 85, 1367–1369. [Google Scholar] [CrossRef]
- Stan, C.A.; Schneider, G.F.; Shevkoplyas, S.S.; Hashimoto, M.; Ibanescu, M.; Wiley, B.J.; Whitesides, G.M. A Microfluidic Apparatus for the Study of Ice Nucleation in Supercooled Water Drops. Lab Chip 2009, 9, 2293–2305. [Google Scholar] [CrossRef] [PubMed]
- Fürjes, P.; Légrádi, G.; Dücso, C.; Aszódi, A.; Bársony, I. Thermal Characterisation of a Direction Dependent Flow Sensor. Sens. Actuators, A Phys. 2004, 115, 417–423. [Google Scholar] [CrossRef]
- Burns, M.A.; Johnson, B.N.; Brahmasandra, S.N.; Handique, K.; Webster, J.R.; Krishnan, M.; Sammarco, T.S.; Man, P.M.; Jones, D.; Heldsinger, D.; et al. An Integrated Nanoliter DNA Analysis Device. Science 1998, 282, 484–487. [Google Scholar] [CrossRef] [PubMed]
- Bhargava, K.C.; Thompson, B.; Iqbal, D.; Malmstadt, N. Predicting the Behavior of Microfluidic Circuits Made from Discrete Elements. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Bhargava, K.C.; Thompson, B.; Malmstadt, N. Discrete Elements for 3D Microfluidics. Proc. Natl. Acad. Sci. USA 2014, 111, 15013–15018. [Google Scholar] [CrossRef] [PubMed]
- Bruus, H. Theoretical Microfluidics; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Steinhart, J.S.; Hart, S.R. Calibration Curves for Thermistors. Deep Sea Res. Oceanogr. Abstr. 1968, 15, 497–503. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhargava, K.C.; Thompson, B.; Tembhekar, A.; Malmstadt, N. Temperature Sensing in Modular Microfluidic Architectures. Micromachines 2016, 7, 11. https://doi.org/10.3390/mi7010011
Bhargava KC, Thompson B, Tembhekar A, Malmstadt N. Temperature Sensing in Modular Microfluidic Architectures. Micromachines. 2016; 7(1):11. https://doi.org/10.3390/mi7010011
Chicago/Turabian StyleBhargava, Krisna C., Bryant Thompson, Anoop Tembhekar, and Noah Malmstadt. 2016. "Temperature Sensing in Modular Microfluidic Architectures" Micromachines 7, no. 1: 11. https://doi.org/10.3390/mi7010011