This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Flexible structures are the main components in many precision measuring and research systems. They provide miniaturization, repeatability, minimal damping, low measuring forces, and very high resolution. This article focuses on the modeling, development, and comparison of three typical flexible micro- nano-structures: flexible helicoids, atomic force microscopy (AFM) cantilevers, and concave notch hinges. Our theory yields results which allow us to increase the accuracy and functionality of these structures in new fields of application such as the modeling of helicoidal DNA molecules’ mechanics, the definition of instantaneous center of rotation in concave flexure notch hinges, and the estimation of the increase of spring constants and resolution at higher mode vibration in AFM cantilevers with an additional concentrated and end extended mass. We developed the original kinetostatic, reverse conformal mapping of approximating contours, and non-linear thermomechanical fluctuation methods for calculation, comparison, and research of the micromechanical structures. These methods simplify complicated solutions in micro elasticity but provide them with necessary accuracy. All our calculation results in this article and in all corresponding referenced author’s publications are in a good agreement with experimental and finite element modeling data within 10% or less.
Flexible micro- and nano-helicoids are very sensitive to the stretching force and ambient temperature under which the helicoid proportionally untwists. These structures provide the basis for the design of extensometers, thermometers, precision measuring heads with visual readout at minimum resolution of order 50 nm, photoelectric automata for dimensional sorting with the measurement rate up to 10 measurement per second, and vibrating string transducers (multivibrators) with minimum resolution of order 5 nm [1]. This structure of twisted strips was first introduced in 1890 by J. Perry who attempted unsuccessfully to develop a theoretical model of the device [2]. A large role in the original mass production of the measurement instruments with pretwisted strips-“mikrokators” in 20 century was played by Swedish company Johansson Gage Co. Photoelectric transducers with pretwisted strips for sorting automata were produced at the Leningrad Instrumental Plant in Russia. Spring measuring heads with pretwisted strips and increased measuring range by the elastic compensator at decreased amplification rate and with multi-revolution pretwisted strip structure at the double end pointer were also developed in that Plant. A large set of the linear and non-linear, quasi-static and dynamic theoretical relations and experimental research of the structure with the pretwisted strips (flexible helicoids) was developed by the author of this paper in the 1960’s and 70’s [1,3]. Despite the decline in production of such systems in recent years due to the development of electronic systems with wide measurement range (inductive, capacitive) and atomic force microscopes (AFM) with micro-nano-cantilevers in quasi-static deformation, natural vibration and vibration at higher modes, flexible helicoidal strips continue to be of interest and use. For example, recently the present author designed a model of DNA molecules using the same helicoidal structure.
We consider in this paper the remaining problems with DNA nano-helicoidal model and vibrating helicoids the largest attainable frequencies, AFM cantilevers at the higher mode of vibration, and concave flexure hinges rotational compliance and instantaneous center of rotation in compliant micro mechanisms and MEMS. A combined presentation of these devices in one article allows us to compare their features in the case of possible application to the measurement and research.
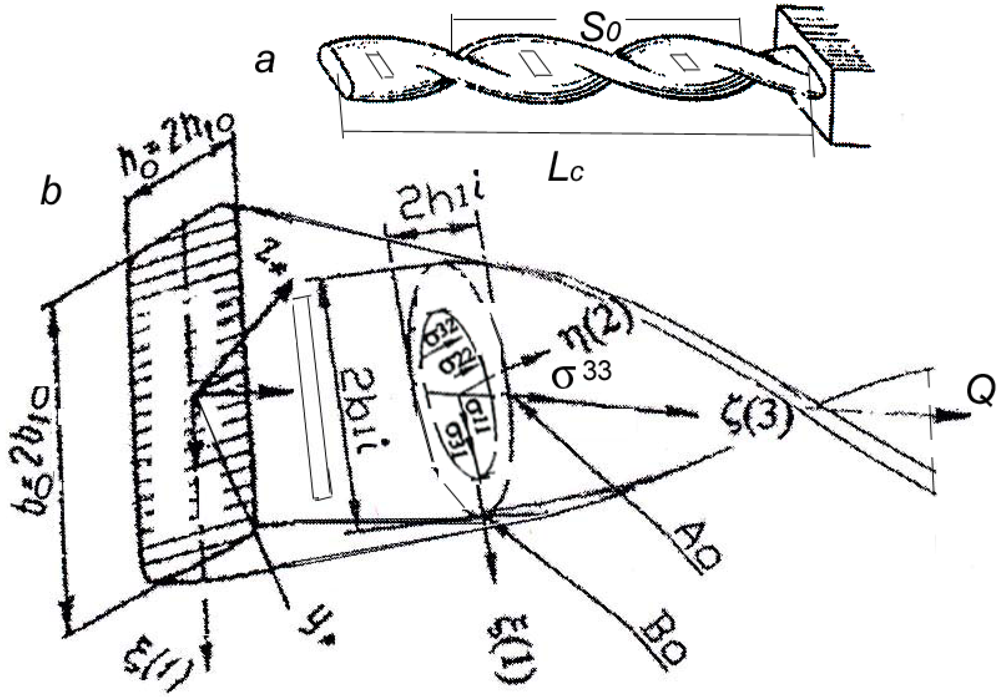
2. Flexure and Stiffness of DNA Nano-Helicoidal Model
In our previous study [4], we built an effective DNA helicoidal model, which reflects many mechanical features of DNA molecules including a possible overwinding and the nonlinear variance of thermomechanical molecular length fluctuations. Nonlinear unwinding and the thermomechanical length Lc fluctuation variance Var(Lc) of DNA molecules were found in the experimental studies at “remeasuring the double helix” [5,6,7]. Our model (Figure 1(a)) with the hollow pretwisted nanostrip sensor has those features. The length fluctuations correspond to the normal statistical distribution and are in agreement with the equipartition theorem. Hence,
where Ψ = 170 is units conversion factor between the left and right sides of the formula in our calculations, kB is Boltzmann’s constant, T is the absolute temperature in K, and js is the object stiffness.
We have previously derived an equation for the pretwisted nanostrip DNA model stretch nonlinear stiffness js as the product of the nonlinear average transformation ratio iθav and the torsional rigidity jθ at the pretwisted strip extension. The inverse value of nonlinear stiffness js−1 therefore [4] is given by:
where Lc is the molecular length, νif = 0.39–0.41 is the transformation form coefficient for punched pretwisted nanostrip, χkp = kp02(bo/2)2λ−1 = 190.9 is the dimensionless parameter of the strip’s relative pretwist, λ = (ho/bo)2 = 0.0197 with height ho = 0.295 nm and width bo = 2b1o = 2.1 nm dimensions of the outer rectangular contour (Figure 1(b)), kp0 = 2π/S0 = 1.847 nm−1 is the initial twist parameter with helical pitch S0 = 3.4 nm, Ee2 = 3,470 pN/nm2 is Young’s modulus of a DNA molecule in our model, and AcDNA = 0.317 nm2 is its cross-section area. Note that the product of Ee2 and AcDNA is equal to 1,100 pN as a so-called stretch modulus. The parameters νH = −θ/kp0Lc < 0 and θ are the stretched strip moving end’s rotation relative and absolute angles, respectively. The values of the parameter νH are inversely proportional to the molecular length Lc if the angle θ = constant. Therefore, νHi/νHj = Lcj/Lci.
Pretwisted hollow and punched nanostrip (a), its cross section (b) with helical coordinates ξ(1), η(2), ζ(3), following coordinates Z*, Y*, dimensions bo = 2b1o = 2.1 nm, bi = 2b1i = 1.75 nm are widths, ho = 2h1o = 0.295 nm, hi = 2h1i = 0.22 nm are heights, S0 = 3.4 nm is the helix pitch, Lc is the contour length, σij are components of stress tensor for calculation limits of motion and overwinds [4], and A0 and B0 are the points of a maximum stress.
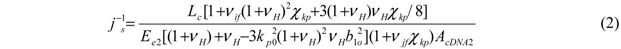
3. Scale Parameters of DNA Model Definition3.1. Stretch Stiffness Relations
The rigidity form coefficient
is given as the average of the corresponding coefficients [1] for rectangular (outer) and elliptical (inner) contours. We recall that Poisson’s ratio |νp| for different materials can be in the range 0.0–0.5. The latter value of 0.5 was assumed for our calculations in [4]. However, the real value of νjf and subsequently Poisson’s ratio νp can be verified through the experimental measurement of the DNA molecule’s stretch stiffness jsp = dF/ds, where F = Q (Figure 1(b)) is a stretching force and s is the strip’s corresponding stretch. In this case, we can use the simplified linear relations for the transformation ratio iθ and rotational stiffness jθo which are equal [1] to:
where G is the shear modulus of material.
As a result, the νjf value can be deduced (after multiplication and certain cancellations) as follows:
Here we assume vif = 0.41. If we assume from [8] that for nicked DNA with released torsion in the strand jsp = 27 pN/nm = 65/(0.7 × 3.4) and Lc = 6.93 nm as in the first line on the top in Table 1 for the version b*, then
and from Equation (3) |νp| = .
micromachines-03-00480-t001_Table 1
Thermomechanical variance of DNA molecule’s length Lc at T = 293 K, θ = 1/1.57 = 0.64 rad; νif = 0.39–0.41.
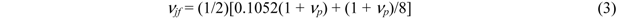
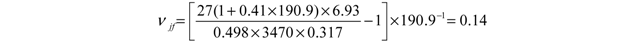
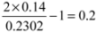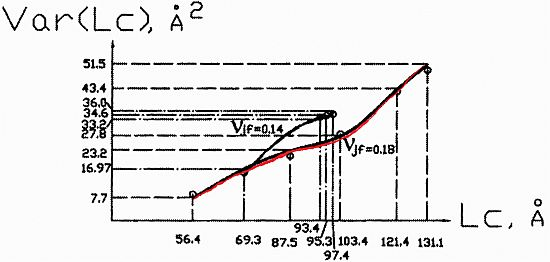
N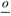
Calculation (1), (2), (3)
Experiment
|δ| (%)
νH
Lc (Å)
Var (Å2)
Lc (Å)
Var (Å2)
a
b*
a
b*
a
b*
ae
b*e
a e
b*e
a
b*
1
−0.35
−0.284
56.4
69.3
8.4
16.97
56.4
69.3
8.7
15.8
3.4
7.4
2
−0.228
−0.210
86.1
93.4
22.5
33.2
86.1
93.4
21.2
34.0
6.1
2.3
3
−0.194
−0.206
103.4
95.3
27.9
34.6
103.4
95.3
28.4
34.5
1.8
0.4
4
−0.167
−0.205
121.4
95.8
43.4
35.05
121.4
95.8
42.4
35.0
2.4
0.1
5
−0.15
−0.203
131.1
97.4
51.5
36.0
131.1
97.4
49.4
35.4
4.2
1.7
Version aνjf = 0.18, experimental ae after [5,6]; version b* νjf = 0.14, experimental b*e after [7].
3.2. Persistence Length Relations
The conditional Poisson’s ratio of DNA may be related to its persistence length Abp as well if we assume (similar to [8,9]) the following expression for the latter:
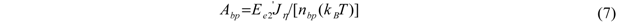
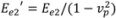where is an appropriately modified elastic modulus for the strip bending, 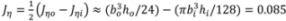nm4 is the moment of inertia for the hollow cross section (Figure 1(b)) of the model with pretwisted strip. We also assume that at different conditions (including temperature, type of solution) the value of nbp should be 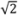or 2 for the helix body with two surfaces: outer (o) and inner (i). This follows from the possible combination of thermomechanical statistical influence on the two surfaces as 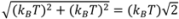or from a necessary thermomechanical energy 2(kBT) at larger material deformation with larger |νp|. Our experience with the published experimental data [5,6,7] shows that the first value nbp = 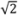is more appropriate for a molecule with νp ≤ 0.2, νjf= 0.14 and the second value nbp = 2 for a molecule with νp = 0.5, νjf = 0.18 in standard solution with 70 mM Tris-Hl, pH 8.0 and 10 mM ascorbic acid. Equation (7) yields persistence length values at T = 293 K within 49–53 nm for both cases. In any case, the experimental value of jsp and Abp should preferably be measured or evaluated at the corresponding conditions because the persistence length depends on them [7,10] as well as on the molecular length [11]. A mean experimental value of the DNA persistence length in different cases and different solutions is equal to Abp = (30 + 80)/2 = 55 nm. The value of νjf is indeed a scale factor in Equation (2) which can and should be verified on an experimental and theoretical basis for certain representative point of the function in evaluation.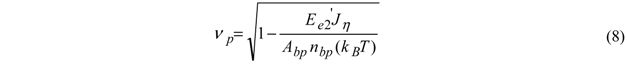
In accordance with Equation (7), the relevant Poisson’s ratio may be found from the following expression:
4. Calculation Results for DNA Model
Table 1 shows the results of our calculations using Equations (1), (2), and (3) and assuming νH (Lc = 131.1 Å) = −0.15, νjf(νp = 0.5) = 0.18 for version a. The difference, |δ| %, between the calculated and experimental values [5,6] is less than 10%. These data are also represented in Figure 2 where the solid red line (νjf = 0.18) denotes the calculated results and circles correspond to the experimental values [5,6]. Another set of experimental data [7] in Table 1 for version b* with νjf = 0.14 at νp = 0.2 also agrees well with the calculation using Equation (1) and is shown in Figure 2. For example, a DNA molecule in the standard buffer solution plus 200 mM NaCl has a persistence length 50 nm [7], while in the standard buffer solution with 0 mM Nacl the persistence length is Abp = 55.2 nm. Hence the average Abp = 52.6 nm. The experimental variance [7] is Var(Lc) = 35.0 Å2 at the length Lc = 95.8 Å. Calculations with Equation (1) at Lc = 95.8 Å, νH = −0.205, and νjf = 0.14 show a variance value of 35.05 Å2 which corresponds to the above experimental data with an uncertainty within 0.15%. Calculations with Equation (1) at Lc = 97.4 Å, νH = −0.203, and νjf = 0.14 show a variance value of 35.9997 Å2 which corresponds to the experimental result [7] of 34.9 Å2 with an uncertainty within 3.1% (see the solid line in Figure 2 with νjf = 0.14). Our calculations with Equation (1) for Lc = 69.3 Å at νH = −0.2838 and νjf = 0.14 show a variance of Var(Lc) = 16.97 Å2 which corresponds to the experimental data within 7.4%.
Results of this research show that our DNA helicoidal model works well for the evaluation of the nonlinear variance of the molecular length thermomechanical fluctuations in different solutions with an appropriate estimation of a conditional Poisson’s ratio, persistence length, and stretch spring constant of the DNA molecule. Here we have effective relations between the model scale parameters and the functioning conditions of DNA molecules. This research shows the close related features of nano-helicoidal structure in organic and inorganic field.
Thermomechanical variance of the molecular length with solid lines corresponding to our theory for cases with νjf = 0.14 and 0.18(red line), and experimental data denoted by circles.
5. Vibrating Transducers5.1. The Helicoidal Pretwisted String
Helicoidal pretwisted strings have been used by us in so-called helicoidal multivibrators (Figure 3(a–c)). In all cases, the pretwisted bronze strip-string passes through the poles NS of the permanent magnet which generates Lorentz force acting on the string in transverse direction when the electrical pulses from self-oscillator are applied to it. The change of string vibration frequency on the quasi-linear part of the transformation function in this case is proportional to the change of string’s tension. The latter, of course, is proportional to a measurand. The self-oscillators 3 are built as the operational amplifiers with positive feedback to the pretwisted strip and connection to the frequency (oscillation period) meters 4.
Double helicoidal multivibrators with (a) the pointer-arrow 1 on the string; (b) mirror-pointer 2 on the string; (c) differential type of helicoid-cable version [1], self oscillator3, and frequency meter 4 (reprint from [1], presented with the Springer permission).
The natural frequency of the pointer-arrow rotation on the pretwisted string is nearly 30 Hz, while the small (0.5 mg) mirror–pointer has natural frequency nearly 100 Hz. The working range of a string transducer we built with the pretwisted string is within 2,000–5,000 Hz at the string stretching within 24 μm for the version (Figure 3(b)) and corresponding rotation of the mirror within 90 (angular degree). Large difference in the pointer and the string frequencies guarantees a stable position of the pointer on the dial at the string vibration. As a result, we have a combination of a visual and electrical output on this system which is helpful for measurement purposes and calibration. The minimum spring constant in these structures of zinc bronze (G = 4.4 cN/mm2) in accordance with Equation (5) for strings with cross section 0.002 × 0.06 mm2, length L = 20 mm and pitch S0 = 2 mm is equal to 0.01 cN/(angular degree).
The pretwisted string has a lower longitudinal rigidity (stiffness) than the flat string with the same dimensions, shape of the cross section, and made of the same material. Therefore, the maximum attainable natural frequencies for the helicoidal strings are lower as well. This is easy to show, for example, on the basis of the helicoidal multivibrator. 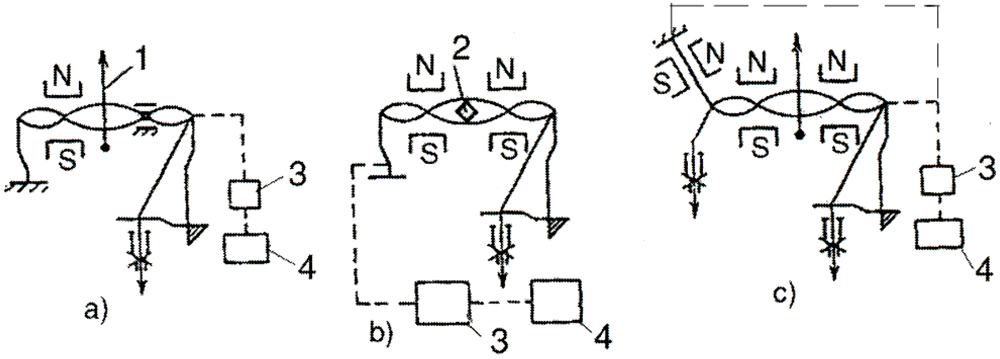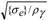If the maximum attainable natural frequency for the flat string equals fnmax = (nf/2L) , then for the helicoidal multivibrator we have the largest attainable natural frequency, which is equal to: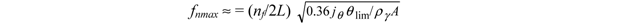
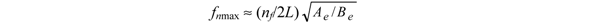
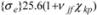where nf is the harmonic number.
Here θlim is the limit of untwist angle for the pretwisted strip used in the helicoidal multivibrator; jθ is the pretwisted strip stiffness at the longitudinal extension (in cN per angular degree), and A is the area of the strip’s cross section. Substituting the expressions for θlim and jθ yields the calculation formula for the attainable largest natural frequency in the helicoidal multivibrator such as
where Ae = and Be = 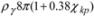, is a permissible yield stress for the string’s material, 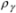is its specific gravity, 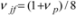is a coefficient of form rigidity as for an elliptical cross section.
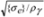Hence, for the used pretwisted strips in the helicoidal multivibrator [1] with χkp = 8 and νjf = 0.18, we have fnmax ≈ 0.78(nf/2L) which corresponds to the lowering of the string’s upper limit frequency by 22%. In deriving the relationship, we neglected the nonlinearity in the helicoidal multiplicator’s characteristics and a very small possible change of its density at the initial elastic-plastic twist. But the above shown lowering of the limit for attainable natural frequency in the helicoidal multivibrator is not important because with the increase of its pretension the sensitivity of the frequency transformation for the longitudinal displacement decreases. This shows that using the range of frequencies, which are close to the maximum attainable one for string, is pointless in the case of the helicoidal multivibrator.
5.2. AFM Cantilevers
AFM cantilevers are the main sensitive part of an atomic force microscope which works in a quasi-static mode and in a vibrating mode as well. Cantilevers in this application may have different shapes: rectangular, “dagger” with sharpen end, V-shaped, triangular, tuning fork tines, and special (T-form, doubled, etc.).
Cantilevers in the vibrating regime are more sensitive to out of plane deformations than in the quasi-static regime, because they have a larger spring constant especially in the higher modes (up to 1,000 times at the fourth mode). This has been found using a kinetostatic method developed by the author [12]. Higher mode oscillations are very sensitive (with resolution of femtogram, attonewton, picometer) to an addition of a small particle close to the end of a cantilever [13] and with atomic resolution in surface parameters measurements. The spring constant of a vibrating cantilever depends on the addition to it of a mass: concentrated, spread, or end expended. The latter is present in a V-shaped cantilever model and causes its specific behavior at vibration in comparison with a rectangular one [14]. The spring constant of AFM cantilevers depends also on the method of their application: permanent contact, non-contact, and tapping mode. Standard micro-cantilevers have small spring constants in a wide range beginning from 0.07 N/m in contact mode that is much lower than for the pretwisted micro-strips. They have larger range of working frequencies up to several megahertz (and nano-cantilevers have frequency up to 1 GHz in vacuum). Therefore AFM cantilevers are more suitable for a surface research with atomic resolution purposes than the pretwisted string transducers. However, we should be careful at the measuring of nano-steps between thin coating and substrate by cantilever at high mode vibration with increased spring constant which can cause increased contact bias [15]. The quasi-unified formula [1] for the fundamental frequency of rectangular, triangular, and V-shaped (Figure 4) cantilever may be presented in simple form as follows:
where h is the thickness of a cantilever. One can use this formula for a solid triangular cantilever, if to assume that L1 = 0, and for rectangular cantilever as well if to accept that L1 = L. The calculation results on this basis agree within few percent with the experimental data and more complicated theoretical methods presented in other publications. 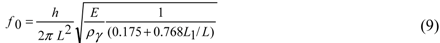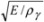If these cantilevers are manufactured by lithography from a tape (or sheet) with the constant thickness, we can estimate the block of parameters h at calibration the frequency fc0 of a rectangular cantilever with length Lr and then use the resulting value h 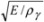= 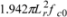for calculation of the fundamental frequency of cantilevers with the other shapes. In this case we don’t need to check the real values of thickness, Young’s modulus, and specific density of the cantilever separately, especially at a high Q-factor. Equation (9) can be used for cantilevers coated [1] by films of gold, platinum, and even immobilized DNA molecule short ligands as well. Our helicoidal DNA model parameters [4] are especially effective in the latter case.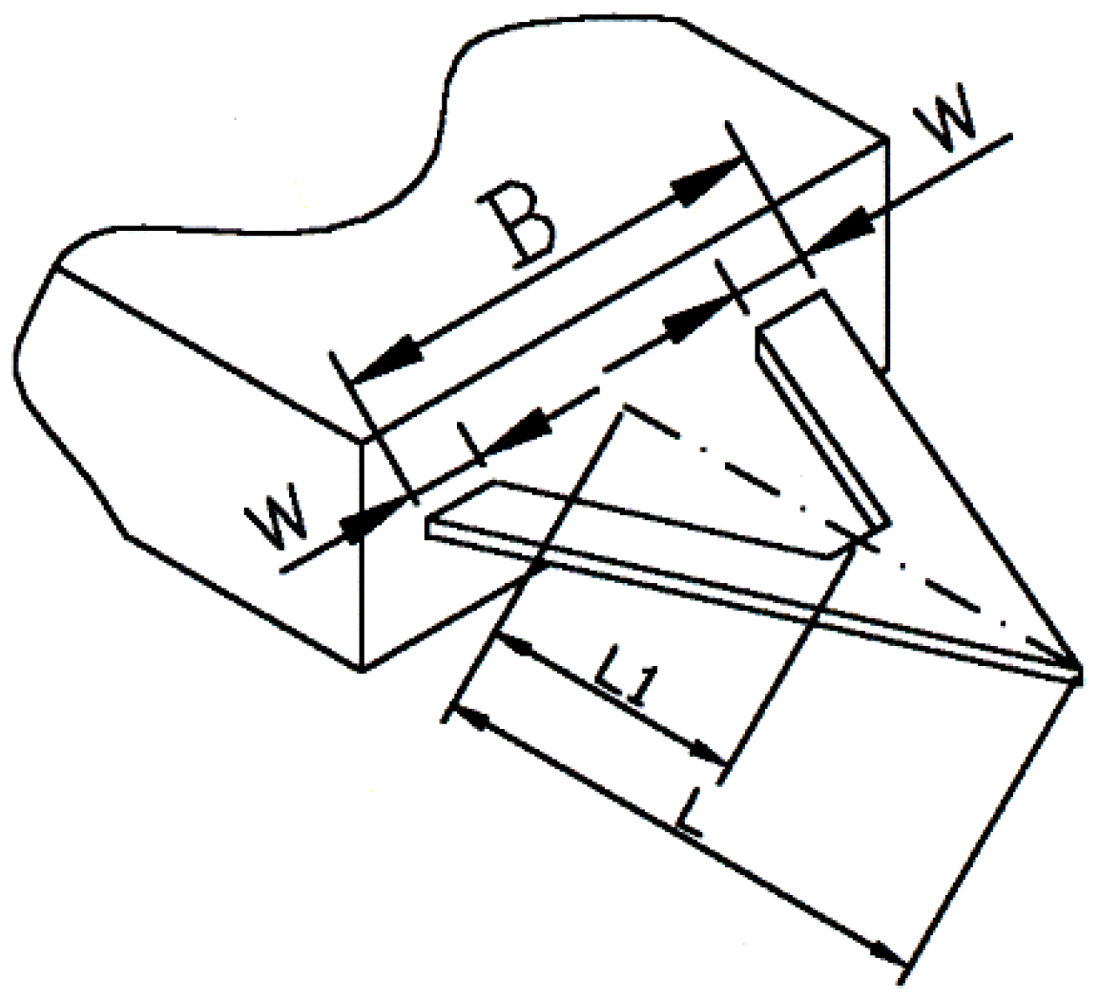
V-shaped cantilever parameters: L is the length, L1is the height of recess, B and w are the width features.
V-shaped cantilevers are widely used in AFM despite the fact that they have more complicated design and some uncertain features of their lateral stability in comparison with rectangular ones, which depends on the geometric parameters and the plane of lateral force application (the height of a tip). V-shaped cantilever can find even more use at higher vibration modes in the atomic force microscopy as a result of improved accuracy in the detection of their deflection by the optical lever because the sign of the slope does not vary along their triangular (trapezoid) part in the incident optical lever area unlike in rectangular cantilever at higher flexural mode [14], where the nodal points become closer and closer to each other and to the moving end of the rectangular cantilever with the increase of its higher flexural eigenmodes.
AFM cantilevers are very accurate and stable sensors but they require for high resolution much better stability of the environmental conditions (vibration, temperature, humidity, air pressure) than helicoidal micro-sensors.
In both cases, however, the calibration is necessary for the traceability to the primary standards of length and force units as in all precision measurements and research.
6. Concave Flexure Hinges and Their Instantaneous Center of Rotation
Coordinate measuring machines (CMM) and other precision measuring systems with compliant micromechanisms have flexible supports of different kind. Concave notch hinges with cylindrical, elliptic, parabolic, and hyperbolic contours, segmented and V-shaped ones are useful for the purposes of precision measuring and robotic systems miniaturization. Many publications in the scientific and engineering literature have been devoted to the problems of such hinges’ accuracy, calibration, and design. However, serious attention to these hinges as a kinematic elements has been developed only recently with the definition of their virtual instantaneous center of rotation (ICR) [16]. Let us recall that these elements do not have real guiding surfaces. Therefore, their design and rotational compliance accurate calculation are not effective without the evaluation of the ICR position as for rotational joint with the certain stable position of the axis. This evaluation has been found in the author’s research on the basis of inverse conformal mapping of approximating contours (Figure 5). An approximating contour in this case is presented by circles Rc shifted lx from the hinge geometrical center to contiguity with minimum possible deviation from a real concave hinge contour estimated by using Chebyshev’s polynomials for uniform or relative approximation. Relative approximation works better for segmented and V-shaped hinges, and their scale factor depends on the ratio between length of straight and curvilinear segments in the contour. The shift lx was estimated by us in analytical form for cylindrical and elliptic contours and by the three point circle method (circle 3P) in AutoCAD for the hinge contours such as parabolic, hyperbolic, segmented and V-shaped [16,17]. Rotational compliance of these hinges is estimated [1,16] with a following simple unified formula:
where αz is an angle of rotation at the action of the moment Mz, vp is Poisson’s ratio, G is a shear modulus of the hinge material, t = 2Δb is the thickness, and hw is the depth of the hinge body. Experimental verification and finite element modeling (FEM) prove the validity of these assumptions with uncertainty within less than 10%.
In general, the position of the ICR has some deviation dea from the geometric center O of a symmetrical notch hinge (Figure 6) that was not considered by many other researchers who supposed that these points always coincide. Our mathematical model for concave notch hinges allows us correct this problem. We showed that dea = lx/2π for the thin notch hinges with Δb/R ≤ 0.035, dea = lx/3 for the thick notch hinges with 0.1 < Δb/R ≤ 0.5, and dea = lx/5.1 for the intermediate hinges with 0.035 < Δb/R ≤ 0.1. Corresponding adjustment of a clamped to hinge 1 part 2 allows us to find the position of a virtual axis with ICR of the hinge rotation at minimum instability of the cylindrical part Oc axis position during part 2 on the hinge rotation. Eccentric shift Da in the axis of rotation position in part 2 can cause the change in the effective angle of rotation as αz1 = αz (1 ± Da/ρ) and the rotational compliance αz1/Mz estimation. The influence of different heuristic approaches to the problem of ICR position on the shift of the rotational axis in the flexure notch hinges is discussed in [18].
Concave contour R with center point O and center line CL approximation by circles Rc with contiguity in point O1 at shift lx and applied bending moment Mb = Mz (reprint from [1], presented with the Springer permission).
ICR of notch hinge1 position on the virtual axis z’ rotation in part 2 with cylindrical surface Oc of radius ρ (reprint from [17] with the AIP permission).
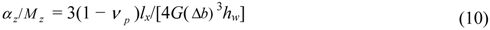
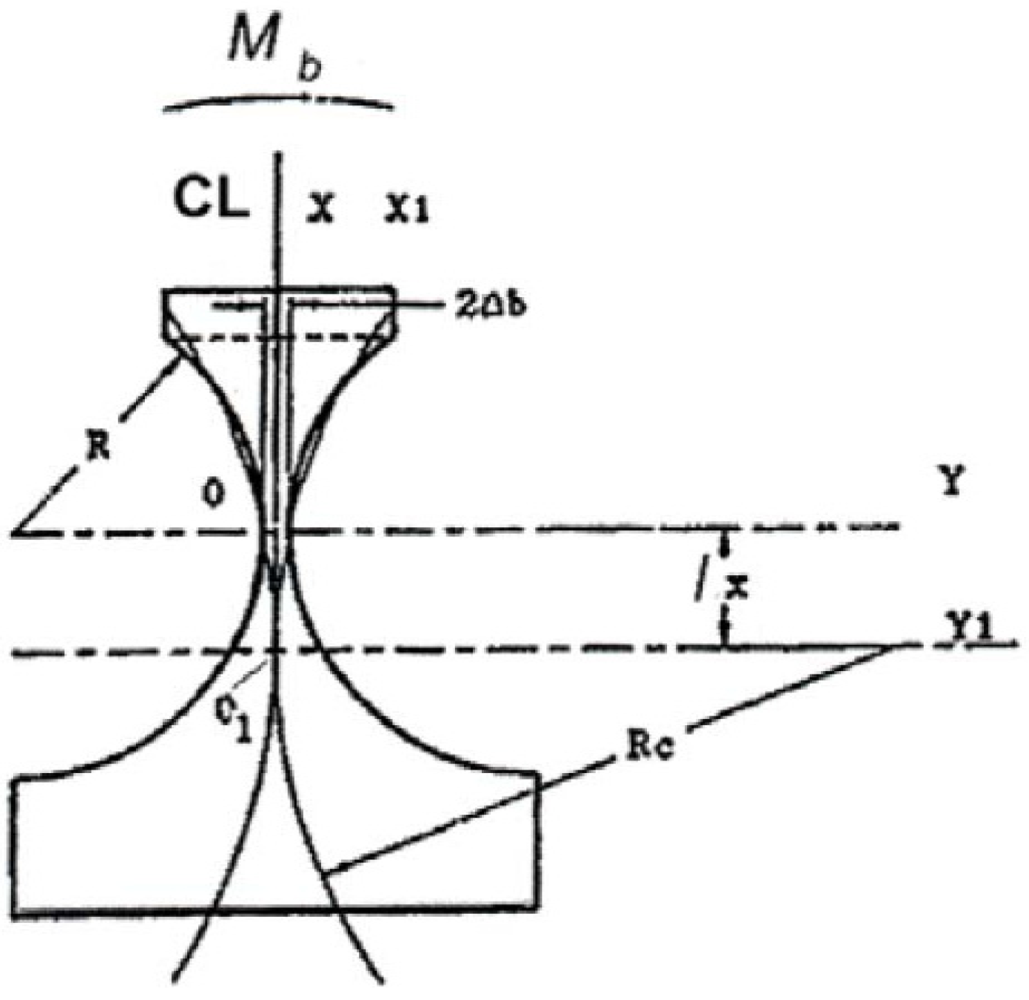
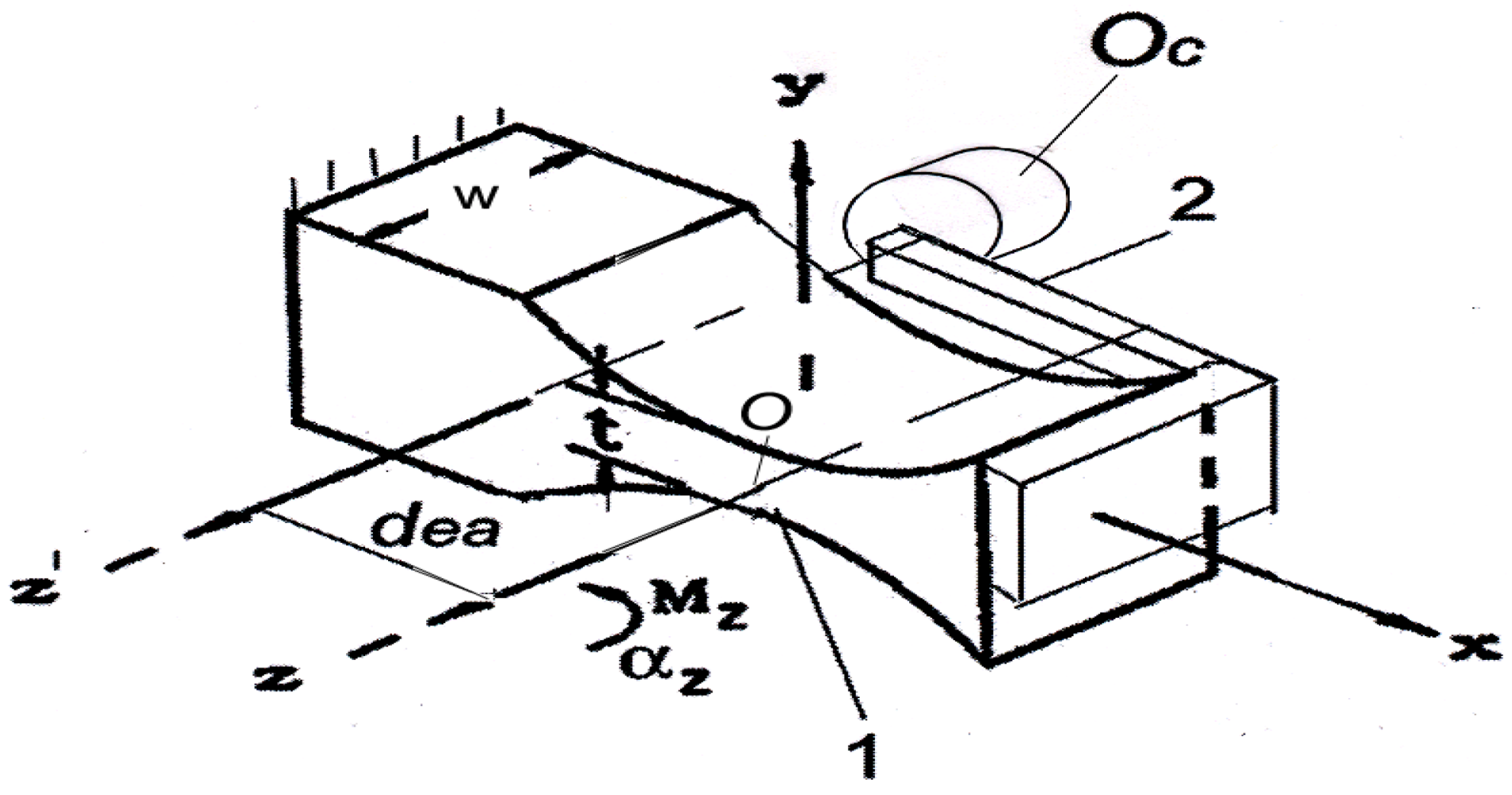
Let us recall that the small shift of ICR at a finite angle of rotation corresponds to cycloid which is close to semi-cubic parabola. At a finite angle of rotation within αz = 0.1 rad (5.7°), we have a small XICR = dea/6 = 0.00017dea and YICR = 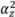dea/2 = 0.005dea shift of ICR coordinates from their initial (−dea, 0) position, which corresponds to the roll without sliding for circle of rolling on the pole tangent [1]. This may be considered in many cases as a practically negligible shift.
7. Conclusions
Flexible pretwisted helicoids, AFM cantilevers, and concave flex notch hinges are the important components of many precision measuring and research systems. Their effective applications have been known for a long time. However, research on their properties and development of their applications continues to this day. This article presents the author’s research results in this field of precision micro elasticity.
Pretwisted helicoids with micro-strings in vibrating mode (helicoidal multivibrators) can be used in the automatic measuring systems with resolution of order 5 nm. Pretwisted nano-strips version is good for the modeling of DNA helicoidal structure with rigidity scale factor and conditional Poisson’s ratio estimation on the basis of the molecule stretch stiffness and its persistence length in the corresponding conditions.
AFM cantilevers are very effective in higher vibrating mode with resolution on the order of femtograms, attonewtons, and picometers. Our kinetostatic method allows the evaluation of a cantilever’s spring constants increased ratio in the higher vibrating modes with dependence on the connected concentrated and end expended mass. The latter is especially important for modeling of V-shaped cantilevers by kinetostatic method.
The inverse conformal method of approximating contours is very effective for modeling the rotational compliance of concave flex notch hinges with different contours and the evaluation of the position of their instantaneous center of rotation (ICR). The latter was introduced for the first time in mathematical model by the author. It is clear that an accurate calculation of rotational compliance for a concave notch hinge is not effective without a proper its ICR definition. The results of all our calculations in this article and referenced publications agree to within less than 10% with experimental data and finite element method (FEM) estimations.
Acknowledgements
The author wishes to acknowledge the helpful editorial assistance of R. Pelcovits.
ReferencesTseytlinY.M.Structural Synthesis in Precision ElasticitySpringerNew York, NY, USA2006397PerryJ.Twisted stripsProc. Phys. Soc. Lond.1890XLIV343349TseytlinY.M.Computation of spring-loaded instrument mechanismMeas. Techniq.1965822322610.1007/BF00984266TseytlinY.M.An effective model of DNA like helicoid structure: With length fluctuation nonlinearityAIP Adv.20111012116:1012116:6Mathew-FennR.S.DasR.HarburyP.A.B.Remeasuring the double helixScience200832244644910.1126/science.115888118927394Mathew-FennR.S.DasR.SilvermanJ.A.WalkerP.A.HarburyP.A.B.A molecular ruler for measuring quantitive distance distributionPLoS One20083e322910.1371/journal.pone.000322918927606Mathew-FennR.S.DasR.FennT.D.SchneidersM.HarburyP.A.B.Response to comment on “Remeasuring the double helix”Science200910.1126/science.1168876BustamanteC.BryantZ.SmithS.B.Ten years of tension: Single-molecule DNA mechanicsNature200342142342710.1038/nature0140512540915BodalD.Mechanics of the CellCambridge University PressLondon, UK2002406DobryninA.V.Effect of counterion condensation on rigidity of semiflexible polyelectrolytesMacromolecules2006399519952710.1021/ma061030aEslami-MossallamB.EjtehadiM.R.Contribution of nonlocal interactions to DNA elasticityJ. Chem. Phys.2011134125106:1125106:9TseytlinY.M.Atomic force microscope cantilever spring constant evaluation for higher mode oscillations: A kinetostatic methodRev. Sci. Instrum.200879025102:1025102:7TseytlinY.M.High resonant mass sensor evaluation: An effective methodRev. Sci. Instrum.200576115101:1115101:6TseytlinY.M.Kinetostatic model of spring constant ratios for an AFM cantilever with end extended massUltramicroscopy201011012612910.1016/j.ultramic.2009.10.009TseytlinY.M.Nanostep and film-coating thickness traceabilityProceedings of the 53 IISTulsa, OK, USA30 April–3 May 2007470Papertp007iis006:1Papertp007iis006:6TseytlinY.M.Tractable model for concave flexure hingesRev. Sci. Instrum.201182015106:1015106:4TseytlinY.Note: Rotational compliance and instantaneous center of rotation in segmented and V-shaped notch hingesRev. Sci. Instrum.201283026102:1026102:3LinβS.ErbeT.TheskaR.ZentnerL.The influence of asymmetric flexure hinges on the axis of rotationProceedings of the 56th International Scientific ColloquiumIlmenau University of Technology, Ilmenau, Germany12–16 September 201110