Pure- and Pseudo-Lateral-Field-Excitation Characteristics of Relaxor Ferroelectric Single Crystal PMN-PT
Abstract
:1. Introduction
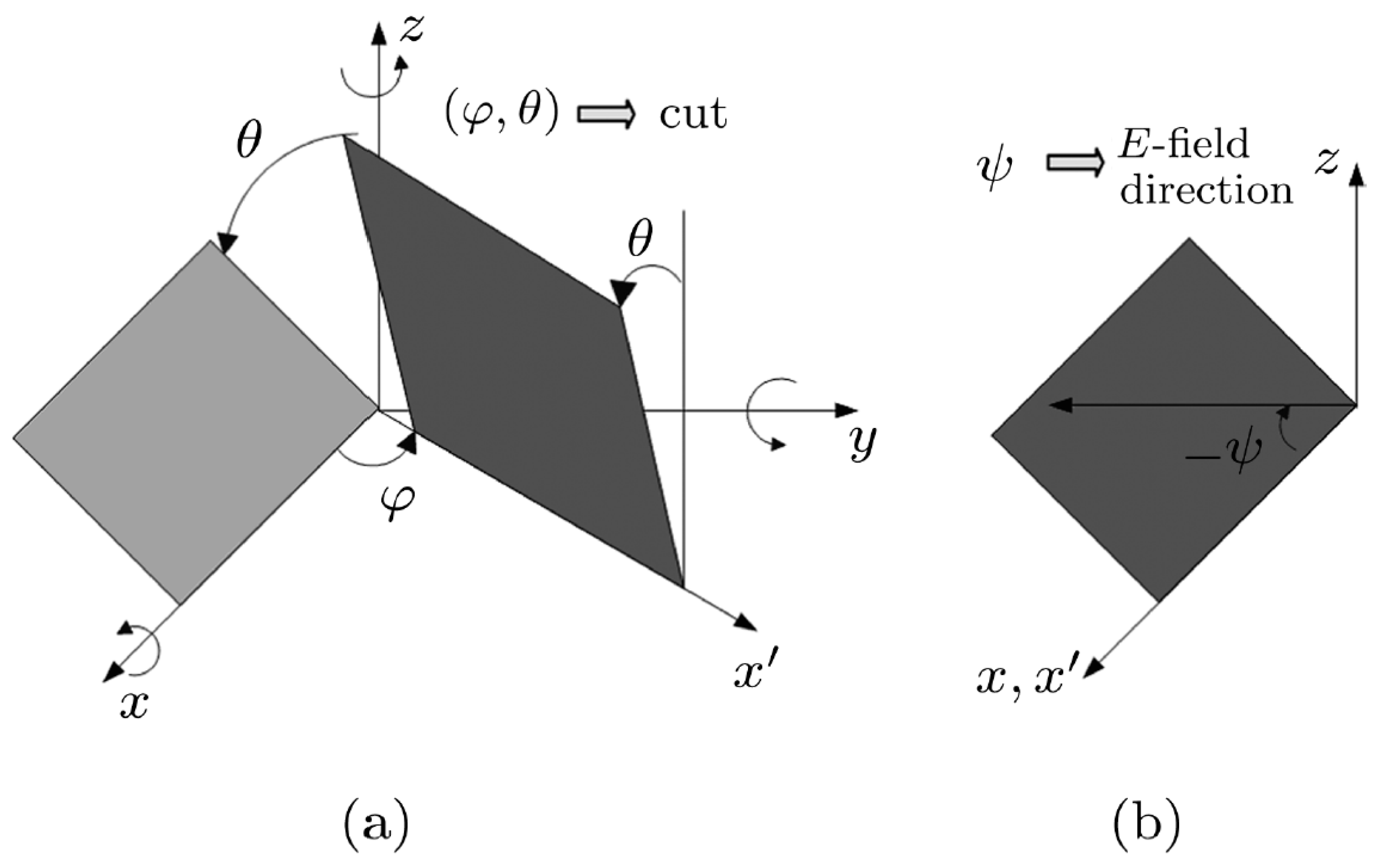
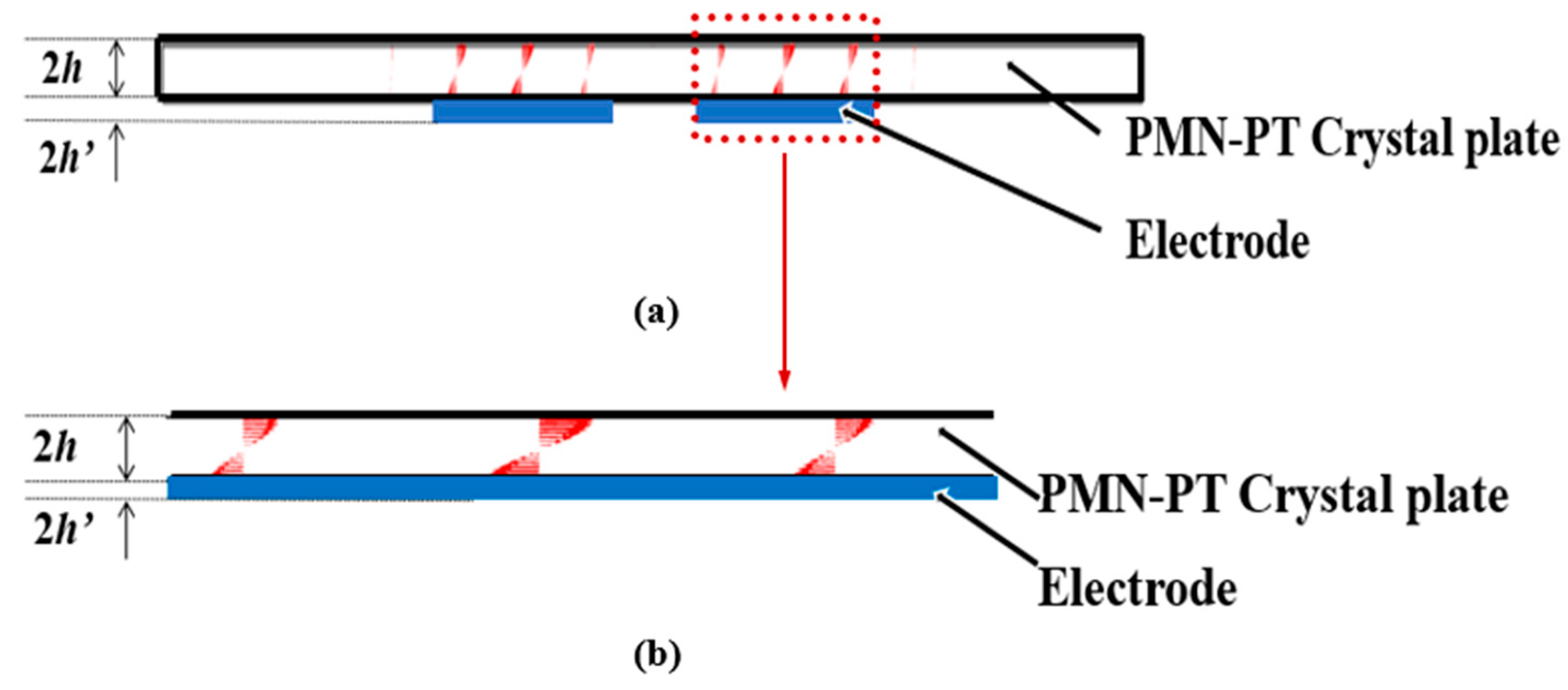
2. Lateral-Field-Excitation Characteristics of Relaxor Ferroelectric Single Crystal PMN-PT
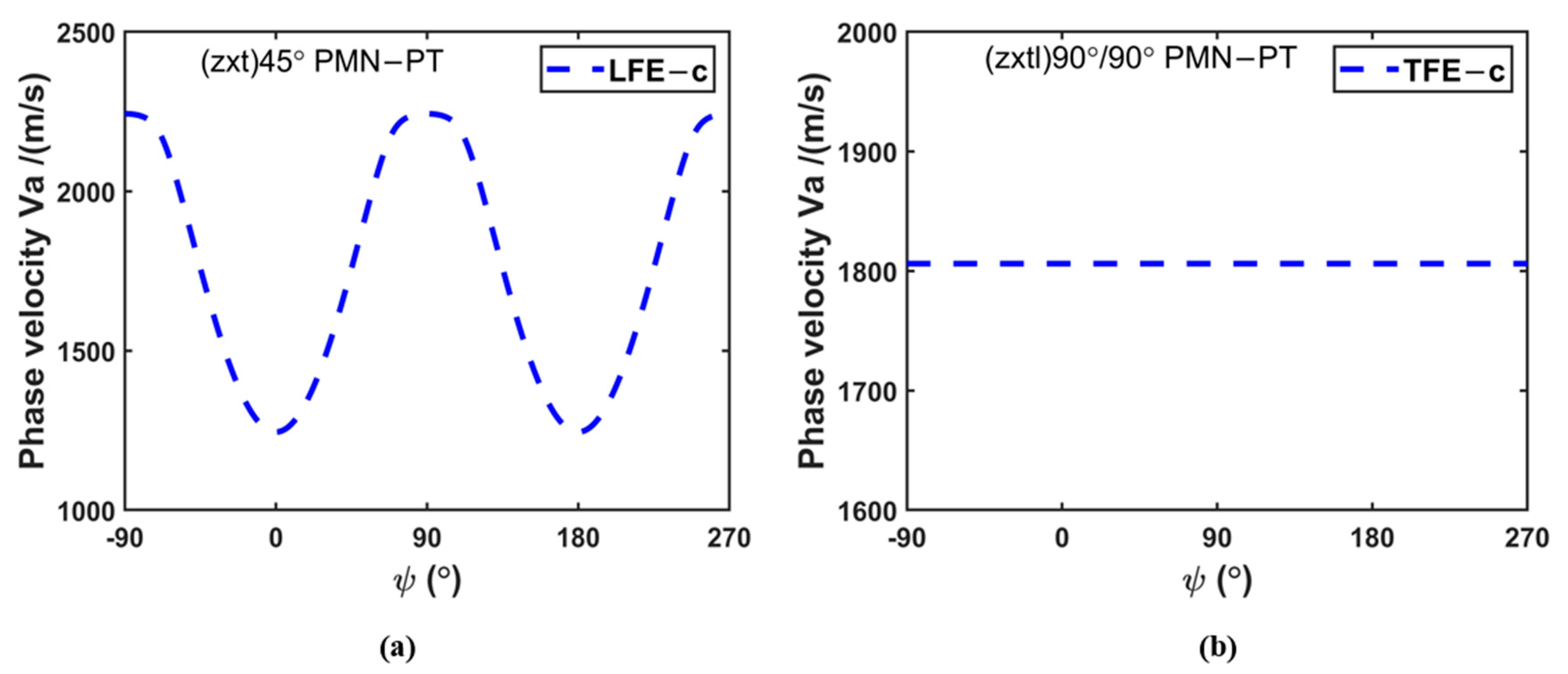
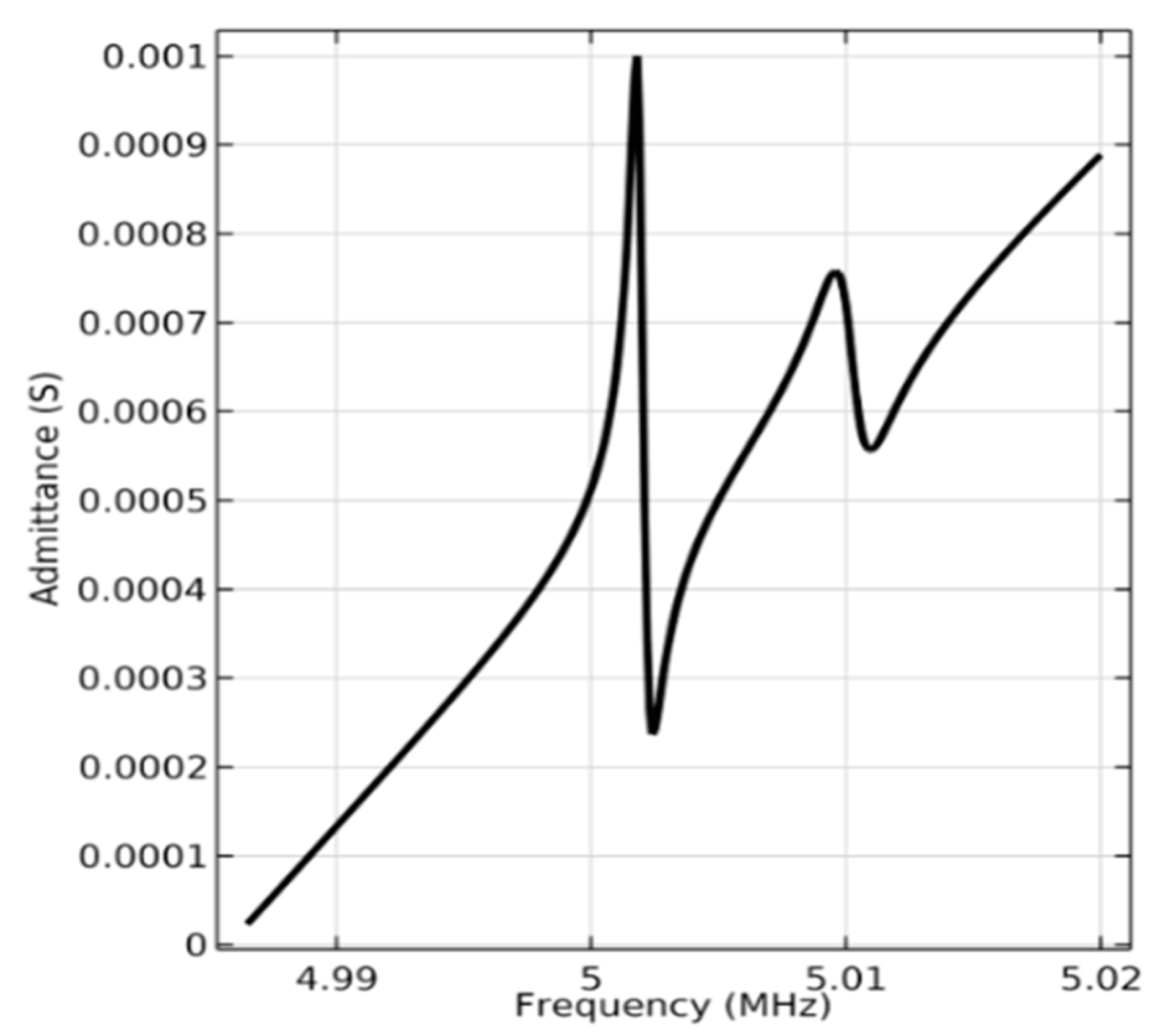
3. Calculation of Phase Velocity of Acoustic Waves of Pure-LFE and Pseudo-LFE Mode
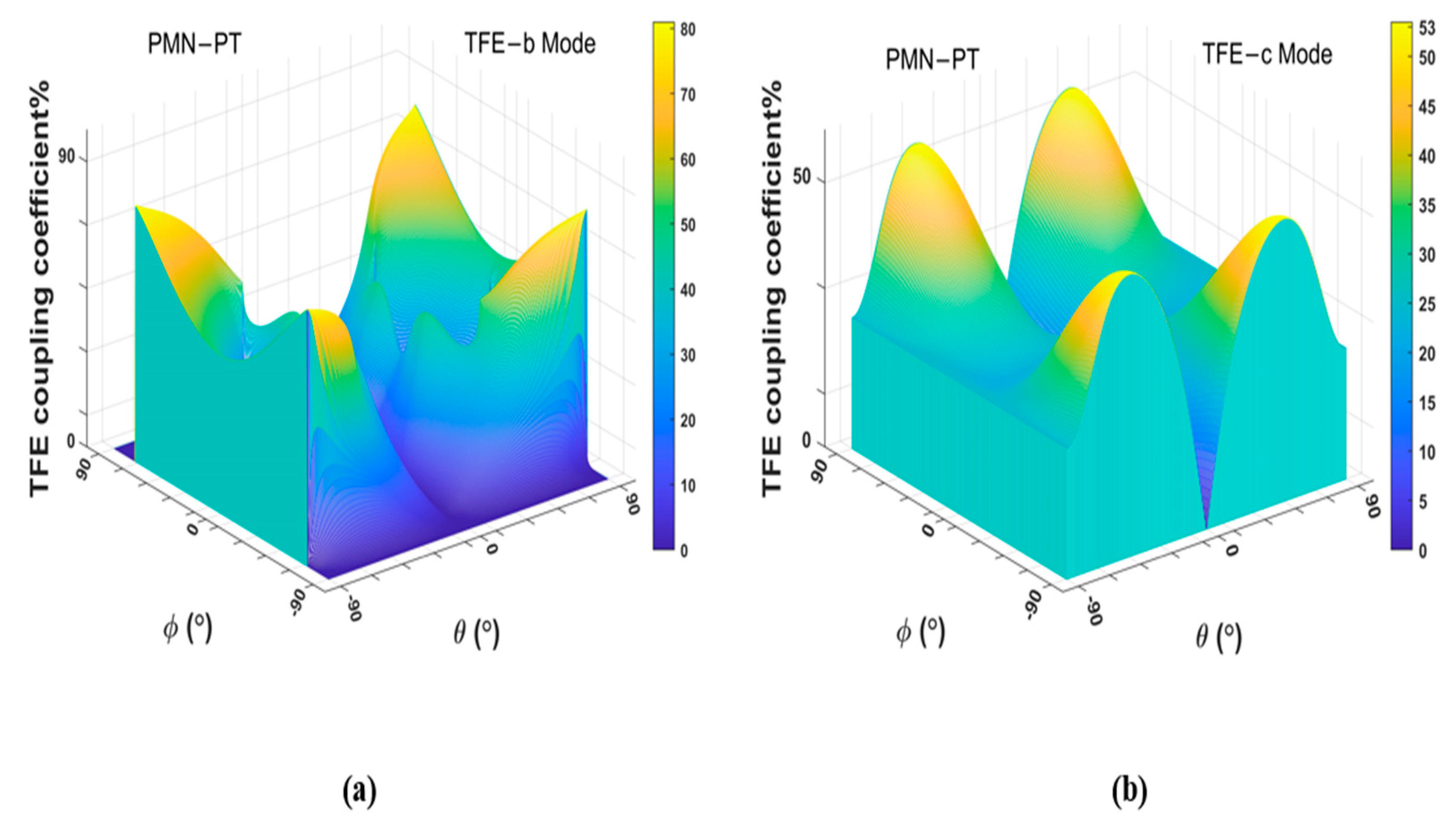
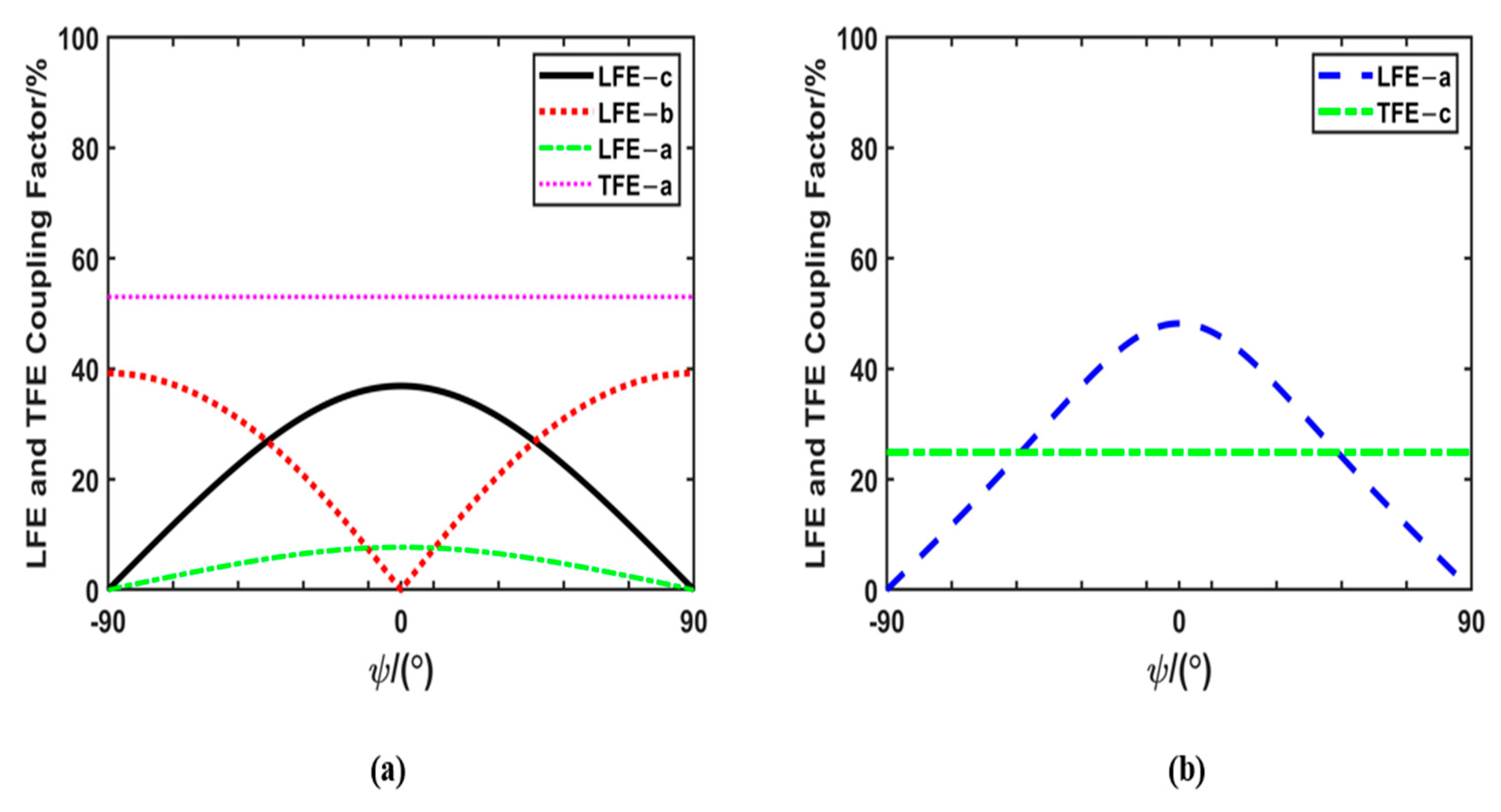
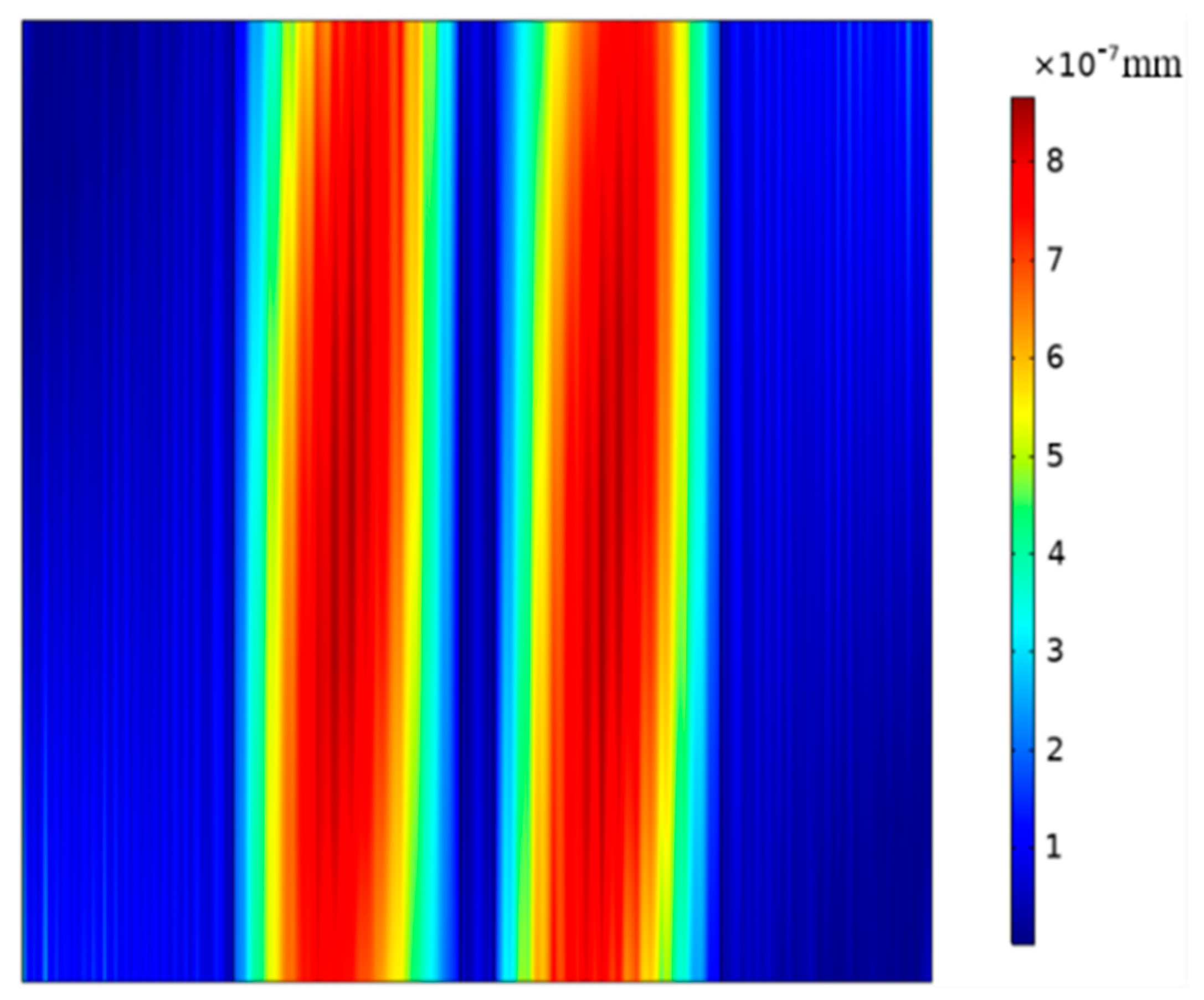
4. Energy-Trapping Effects of PMN-PT Acoustic Wave Devices on Pure- and Pseudo-LFE Modes
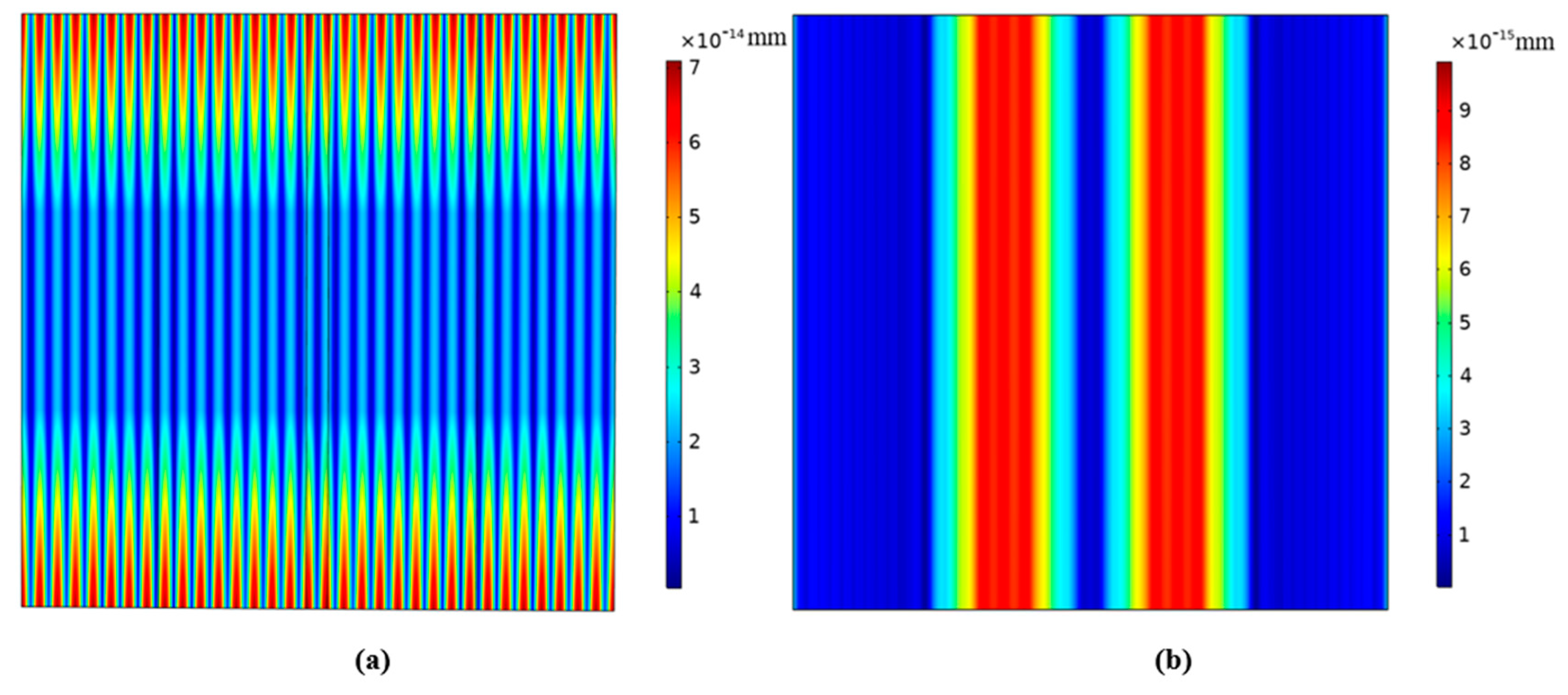
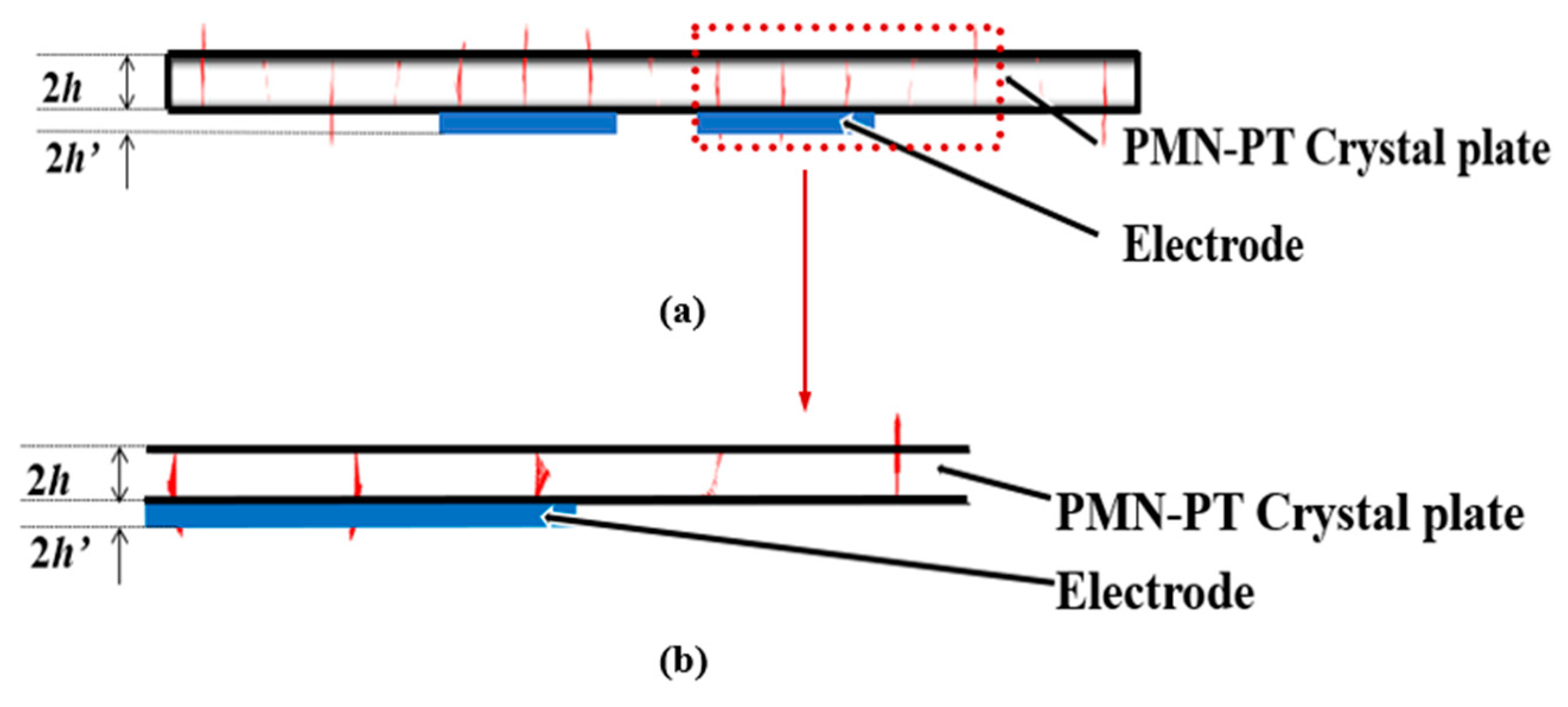
4.1. Pure-LFE Mode
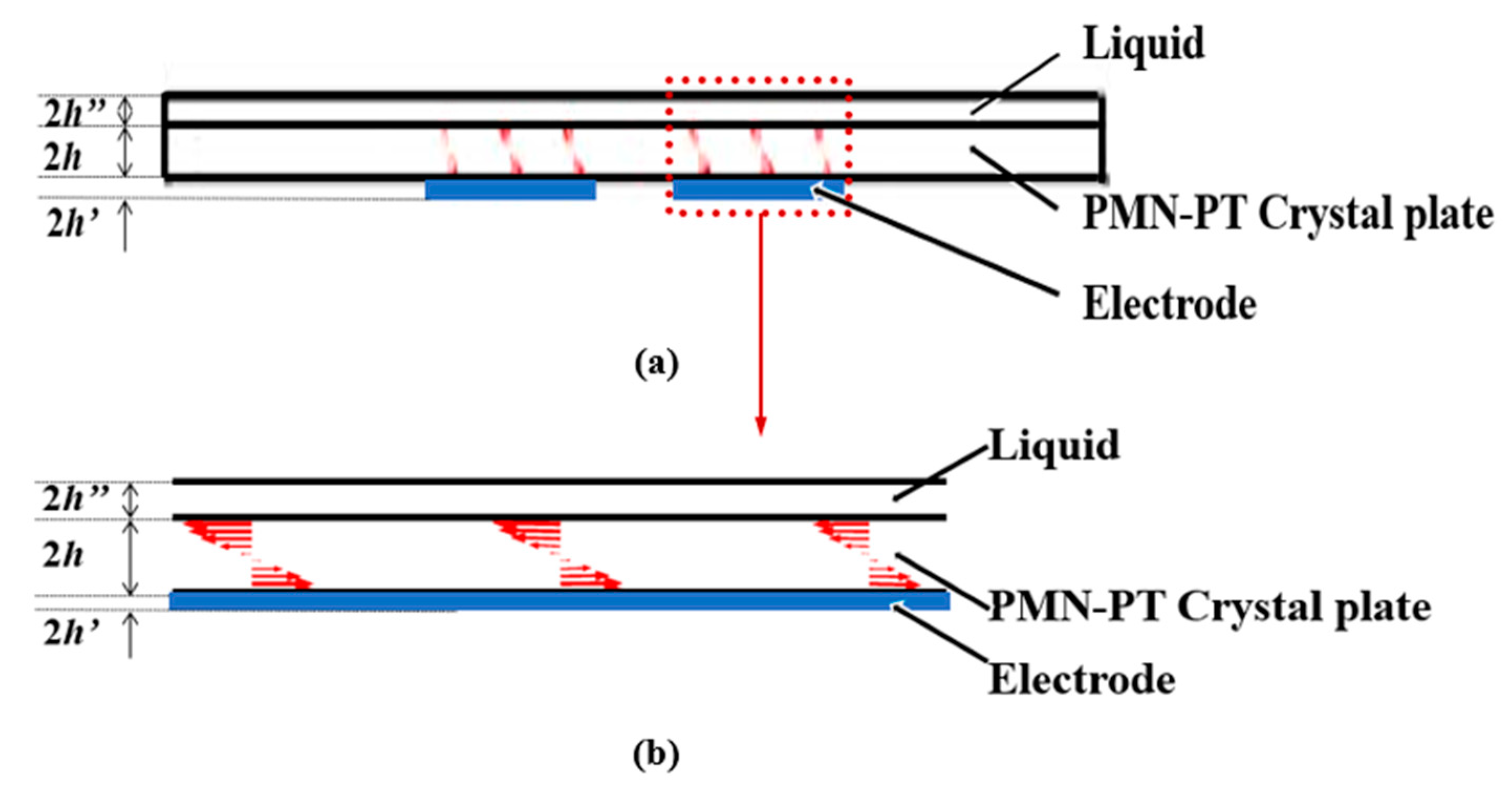
4.2. Pseudo-LFE Mode
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alev, O.; Sarıca, N.; Özdemir, O.; Arslan, L.C.; Büyükköse, S.; Öztürk, Z.Z. Cu-doped ZnO nanorods based QCM sensor for hazardous gases. J. Alloys Compd. 2020, 826, 154177. [Google Scholar] [CrossRef]
- Lin, A.; Kim, E.S. Selectivity and long-term reliability of resonant explosive-vapor-trace detection based on antigen-antibody binding. In Proceedings of the IEEE International Conference on Micro Electro Mechanical Systems, Sorrento, Italy, 25–29 January 2009; pp. 316–319. [Google Scholar]
- Benetti, M.; Cannatà, D.; Di, P.F.; Foglietti, V.; Verona, E. Microbalance chemical sensor based on thin-film bulk acoustic wave resonators. Appl. Phys. Lett. 2005, 87, 173504. [Google Scholar] [CrossRef]
- Zhang, D.; Song, X.; Wang, Z.; Chen, H. Ultra-highly sensitive humidity sensing by polydopamine/graphene oxide nanostructure on quartz crystal microbalance. Appl. Surf. Sci. 2021, 538, 147816. [Google Scholar] [CrossRef]
- Martin, S.; Frye, G.; Wessendorf, K. Sensing liquid properties with thickness-shear mode resonators. Sens. Actuators A Phys. 1994, 44, 209–218. [Google Scholar] [CrossRef]
- Li, P.; Jin, F.; Yang, J.S. Effects of semiconduction on electromechanical energy conversion in piezoelectrics. Smart Mater. Struct. 2012, 24, 025021. [Google Scholar] [CrossRef]
- Gueddida, A.; Pennec, Y.; Silveira Fiates, A.L.; Vellekoop, M.J.; Bonello, B.; Djafari-Rouhani, B. Acoustic Sensor Based on a Cylindrical Resonator for Monitoring a Liquid Flow. Crystals 2022, 12, 1398. [Google Scholar] [CrossRef]
- Zhou, Y.; Zou, Y.; Gao, C.; Xu, Q.; Tong, X.; Lin, B.; Liu, Y.; Soon, B.W.; Cai, Y.; Sun, C. Investigation of film bulk acoustic resonators for sensing applications in liquid environment. Appl. Phys. Lett. 2022, 121, 213501. [Google Scholar] [CrossRef]
- Hu, Y.; French, L.A.; Radecsky, K.; Da Cunha, M.P.; Millard, P.; Vetelino, J.F. A lateral field excited liquid acoustic wave sensor. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2004, 51, 1373–1380. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Pinkham, W.; French Jr, L.A.; Frankel, D.; Vetelino, J.F. Pesticide detection using a lateral field excited acoustic wave sensor. Sens. Actuators B Chem. 2005, 108, 910–916. [Google Scholar] [CrossRef]
- Meissner, M.; French, L.; Pinkham, W.; York, C.; Bernhardt, G.; da Cunha, M.P.; Vetelillo, J. Electrode optimization for a lateral field excited acoustic wave sensor. In Proceedings of the IEEE Ultrasonics Symposium, Montreal, QC, Canada, 23–27 August 2004; pp. 314–318. [Google Scholar]
- Liu, B.; Jiang, Q.; Xie, H.; Yang, J.S. Energy trapping in high-frequency vibrations of piezoelectric plates with partial mass layers under lateral electric field excitation. Ultrasonics 2011, 51, 376–381. [Google Scholar] [CrossRef]
- Ma, T.F.; Wu, R.X.; Wang, J.; Du, J.K.; Yuan, L.L.; Yu, F.P.; Xie, C. Coupled extension and thickness-twist vibrations of lateral field excited AT-cut quartz plates. Acta Mech. Sin. 2014, 30, 67–72. [Google Scholar] [CrossRef]
- Kim, K.; Zhang, S.; Jiang, X. Surface load induced electrical impedance shift in relaxor-PbTiO3 crystal piezoelectric resonators. Appl. Phys. Lett. 2012, 100, 253501. [Google Scholar] [CrossRef]
- Nie, G.; Zhang, K.; Liu, J.; Zhang, L. Effect of periodic corrugation on Lamb wave propagation in PMN-PT single crystal bilayer plates. Ultrasonics 2020, 108, 106176. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Lu, L.; Tian, Y.; Yi, Z.; Liu, J.; Yang, B. High Sensitivity Surface Acoustic Wave Strain Sensor Based on PMN-PT Thick Film. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators, Berlin, Germany, 23–27 June 2019; pp. 1866–1869. [Google Scholar]
- Kim, K.; Zhang, S.; Jiang, X. Surface acoustic load sensing using a face-shear PIN-PMN-PT single-crystal resonator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012, 59, 2548–2554. [Google Scholar] [CrossRef] [PubMed]
- Magalhães, A.; Oliveira, A.; Sales, A.; Aquino, F.; Gouveia, D.; Menezes, J.; Araújo, E.; Sombra, A. Fabrication and operational characteristics of step-down piezoelectric transformer based on PMN-PT ceramics. Ferroelectrics 2018, 535, 18–24. [Google Scholar] [CrossRef]
- Tian, F.; Liu, Y.; Ma, R.; Li, F.; Xu, Z.; Yang, Y. Properties of PMN-PT single crystal piezoelectric material and its application in underwater acoustic transducer. Appl. Acoust. 2021, 175, 107827. [Google Scholar] [CrossRef]
- Miao, H.C.; Li, F.X. Shear horizontal wave transducers for structural health monitoring and nondestructive testing: A review. Ultrasonics 2021, 114, 106335. [Google Scholar] [CrossRef]
- Peng, J. Novel Piezoelectric Single Crystals PMN-PT and Their Applications in Medical Ultrasonic Transducers; China University of Geosciences: Wuhan, China, 2005. [Google Scholar]
- Wang, W.Y.; Zhang, C.; Zhang, Z.; Liu, Y.; Feng, G. Three operation modes of lateral-field-excited piezoelectric devices. Appl. Phys. Lett. 2008, 93, 242906. [Google Scholar] [CrossRef]
- Wang, W.Y. Piezoelectric Bulk Acoustic Wave Sensors Based on Lateral Field Excitation; Tsinghua University: Beijing, China, 2009. [Google Scholar]
- Wang, W.Y.; Zhang, Z.; Zhang, C.; Liu, Y.; Feng, G.; Jing, G. Pseudo-LFE study in AT-cut quartz for sensing applications. In Proceedings of the IEEE Sensors, Lecce, Italy, 26–29 October 2008; pp. 1548–1551. [Google Scholar]
- Qin, Z.K.; Zhang, Z.Y.; Xiao, M.S.; Song, D.R.; Wang, Y.X. Piezoelectric Quartz Crystal; National Defense Industry Press: Beijing, China, 1980; pp. 163–169. [Google Scholar]
- Khan, A.; Ballato, A. Piezoelectric coupling factor calculations for plates of langatate driven in simple thickness modes by lateral-field-excitation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2002, 49, 922–928. [Google Scholar] [CrossRef]
- Wang, F.; Luo, L.; Zhou, D.; Zhao, X.; Luo, H. Complete set of elastic, dielectric, and piezoelectric constants of orthorhombic 0.71Pb(Mg1/3 Nb2/3)O3–0.29PbTiO3 single crystal. Appl. Phys. Lett. 2007, 90, 212903. [Google Scholar] [CrossRef]
- ANSI/IEEE 176-1987; IEEE Standard on Piezoelectricity. ANSI/IEEE Standard: New York, NY, USA, 1987.
- Brainerd, J.; Jensen, A.; Cumming, L.; Batcher, R.; Begun, S.; Black, H.; Grown, G.; Burrows, C.; Busignies, H.; Cady, W. Standards on piezoelectric crystals. Proc. IRE 1949, 37, 1378–1395. [Google Scholar]
- Rosenbaum, J.F. Bulk Acoustic Wave Theory and Devices; Artech House Acoustics Library: Boston, MA, USA, 1988. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, F.; Ma, T.; Kang, P.; Yao, Y.; Gan, N.; Yuan, L.; Hu, W.; Kuznetsova, I.; Nedospasov, I. Pure- and Pseudo-Lateral-Field-Excitation Characteristics of Relaxor Ferroelectric Single Crystal PMN-PT. Micromachines 2023, 14, 1136. https://doi.org/10.3390/mi14061136
Sun F, Ma T, Kang P, Yao Y, Gan N, Yuan L, Hu W, Kuznetsova I, Nedospasov I. Pure- and Pseudo-Lateral-Field-Excitation Characteristics of Relaxor Ferroelectric Single Crystal PMN-PT. Micromachines. 2023; 14(6):1136. https://doi.org/10.3390/mi14061136
Chicago/Turabian StyleSun, Fei, Tingfeng Ma, Pengfei Kang, Yuming Yao, Ning Gan, Lili Yuan, Wenhui Hu, Iren Kuznetsova, and Ilya Nedospasov. 2023. "Pure- and Pseudo-Lateral-Field-Excitation Characteristics of Relaxor Ferroelectric Single Crystal PMN-PT" Micromachines 14, no. 6: 1136. https://doi.org/10.3390/mi14061136





