Research on Stacked Piezoelectric Cymbal Vibrator
Abstract
:1. Introduction
2. Theoretical and Simulation Analysis of Piezoelectric Stack
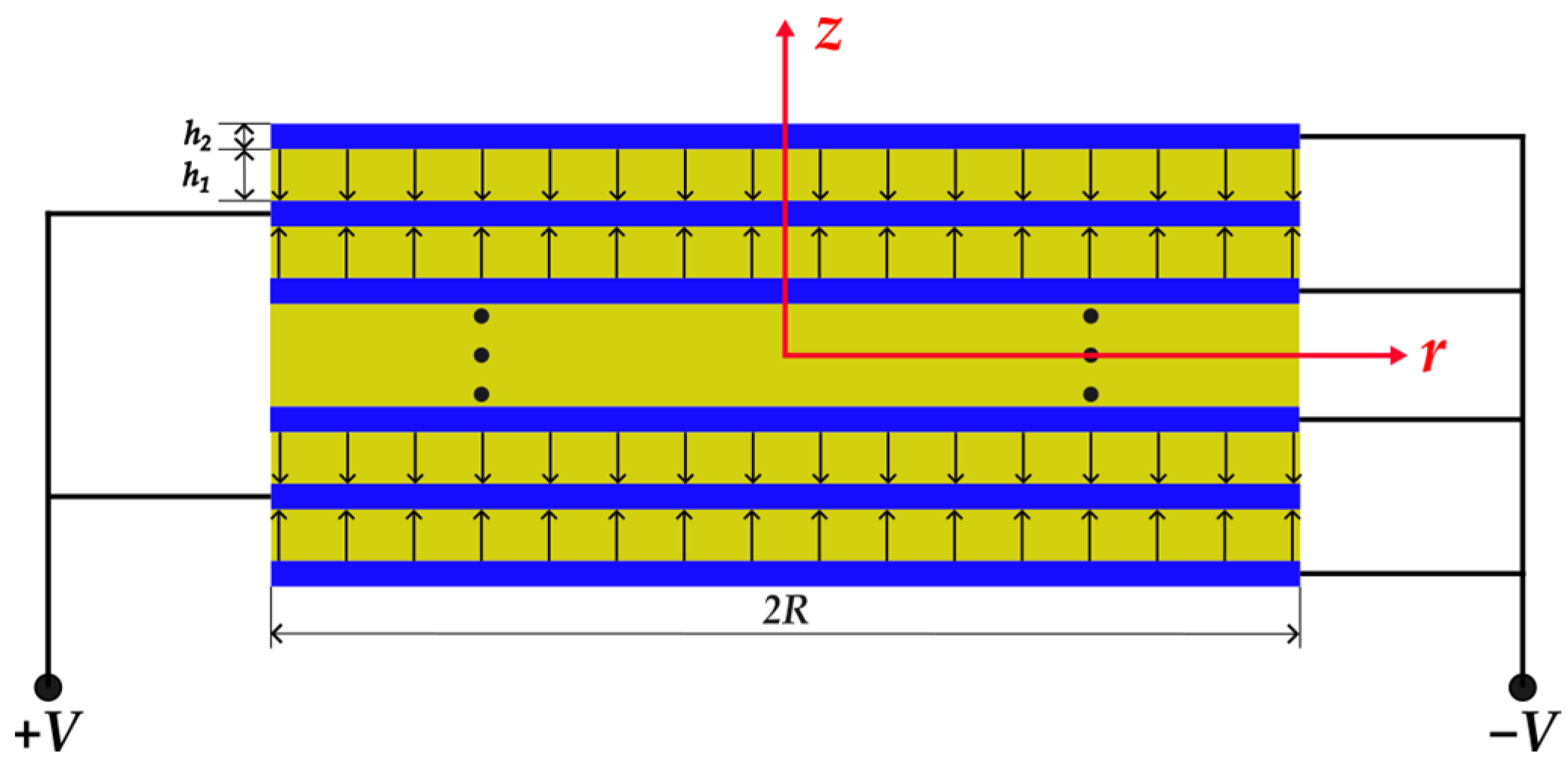
2.1. Theoretical Analysis of Piezoelectric Stack
2.2. Analyses of the Piezoelectric Stack
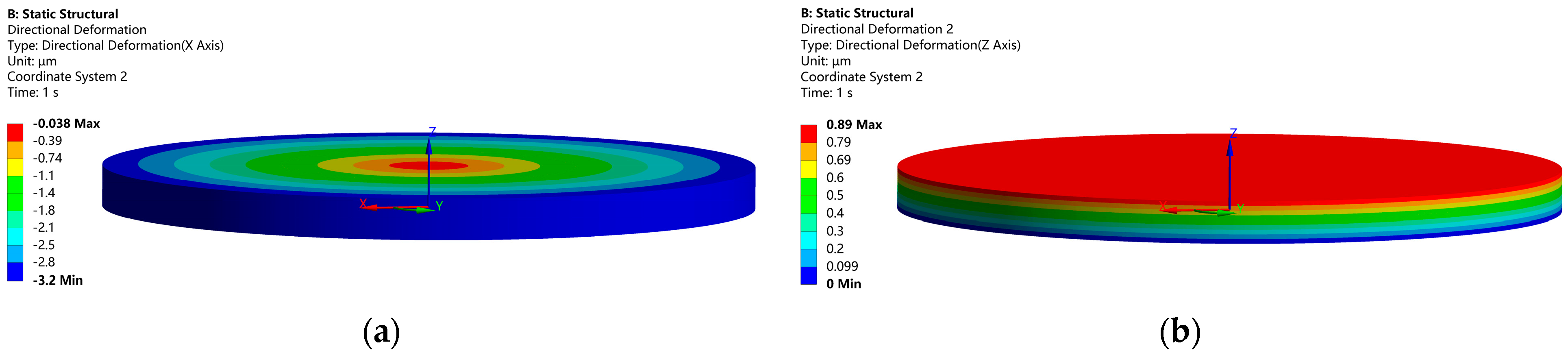
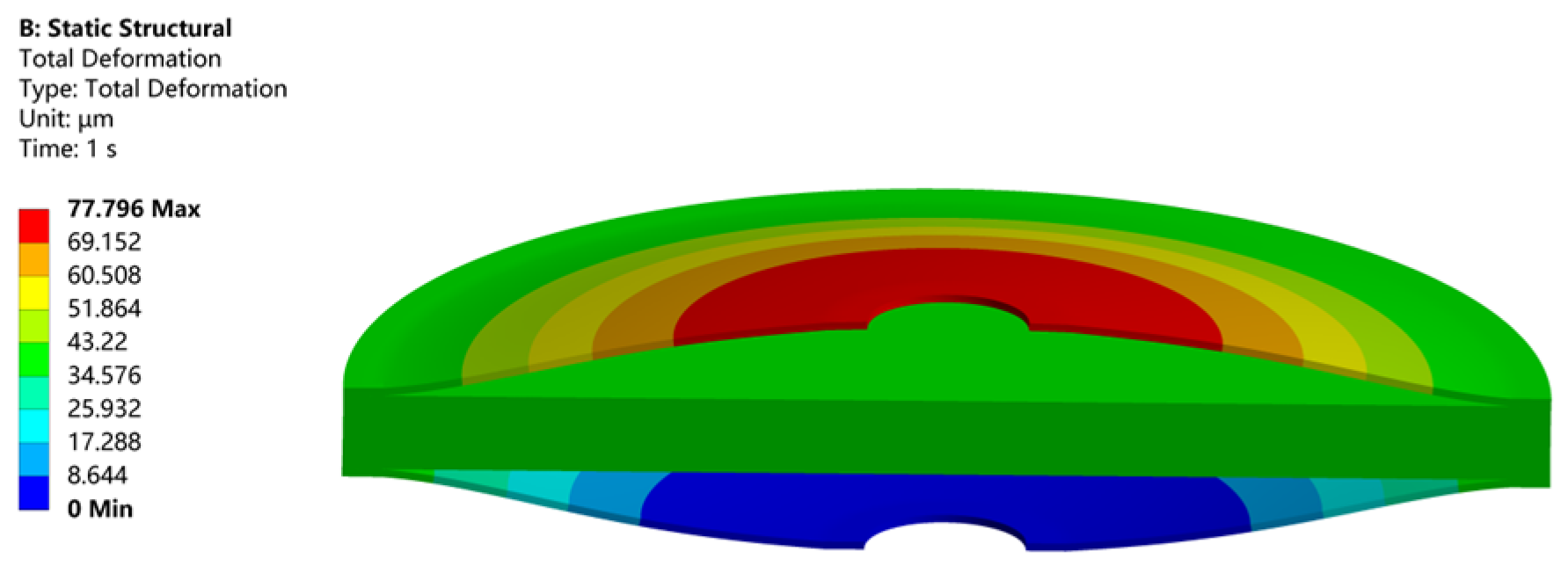
2.2.1. Static Analysis
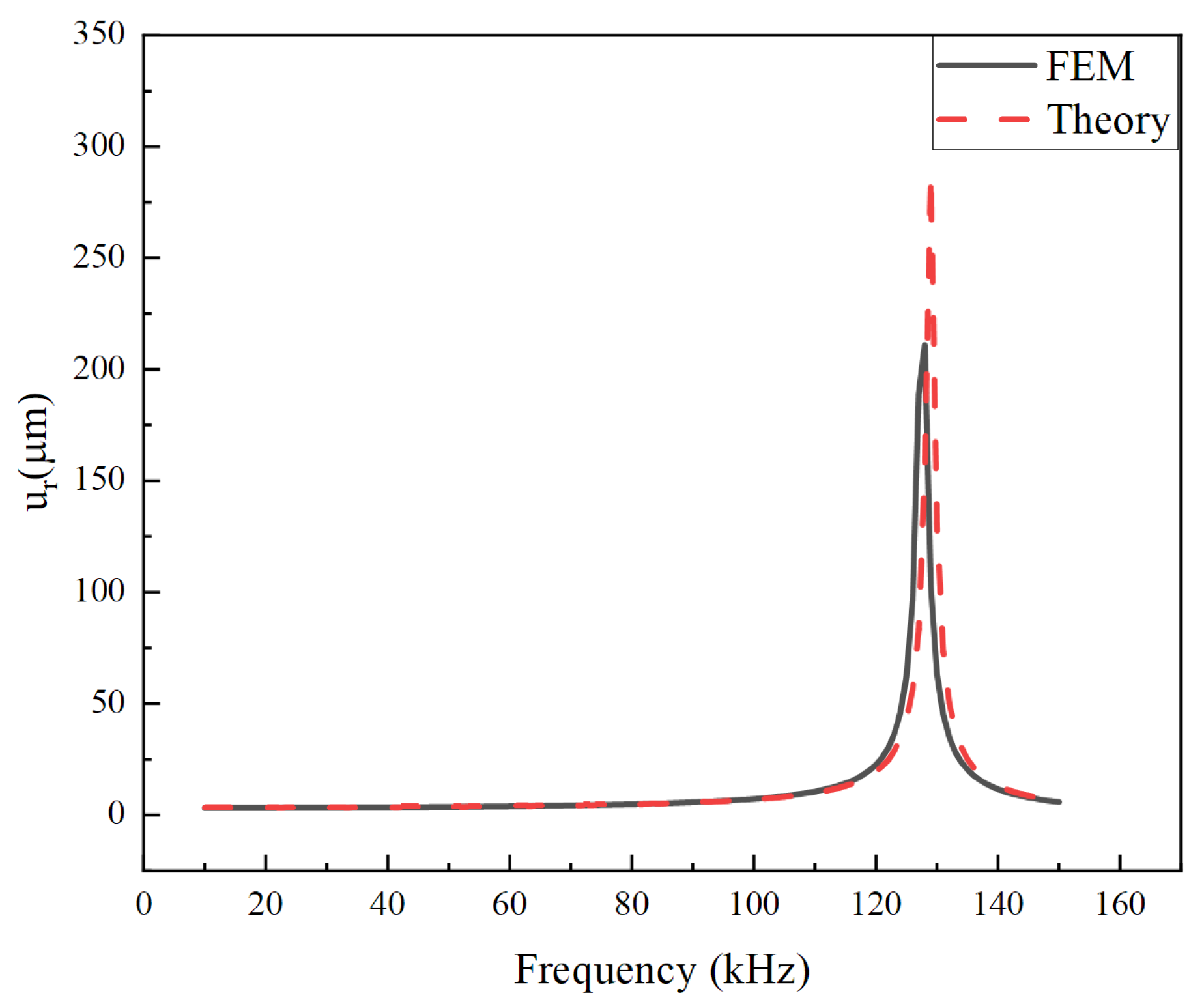
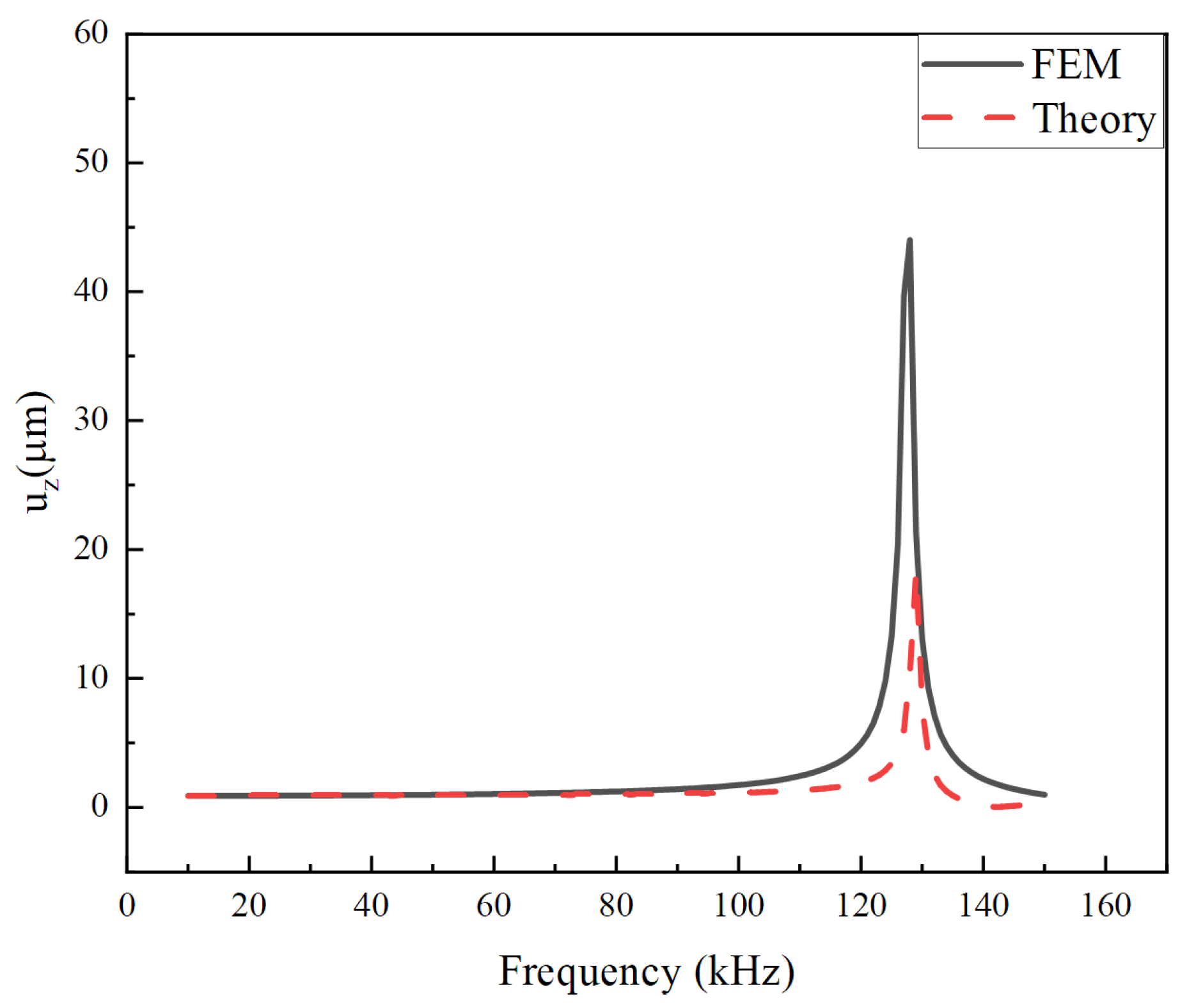
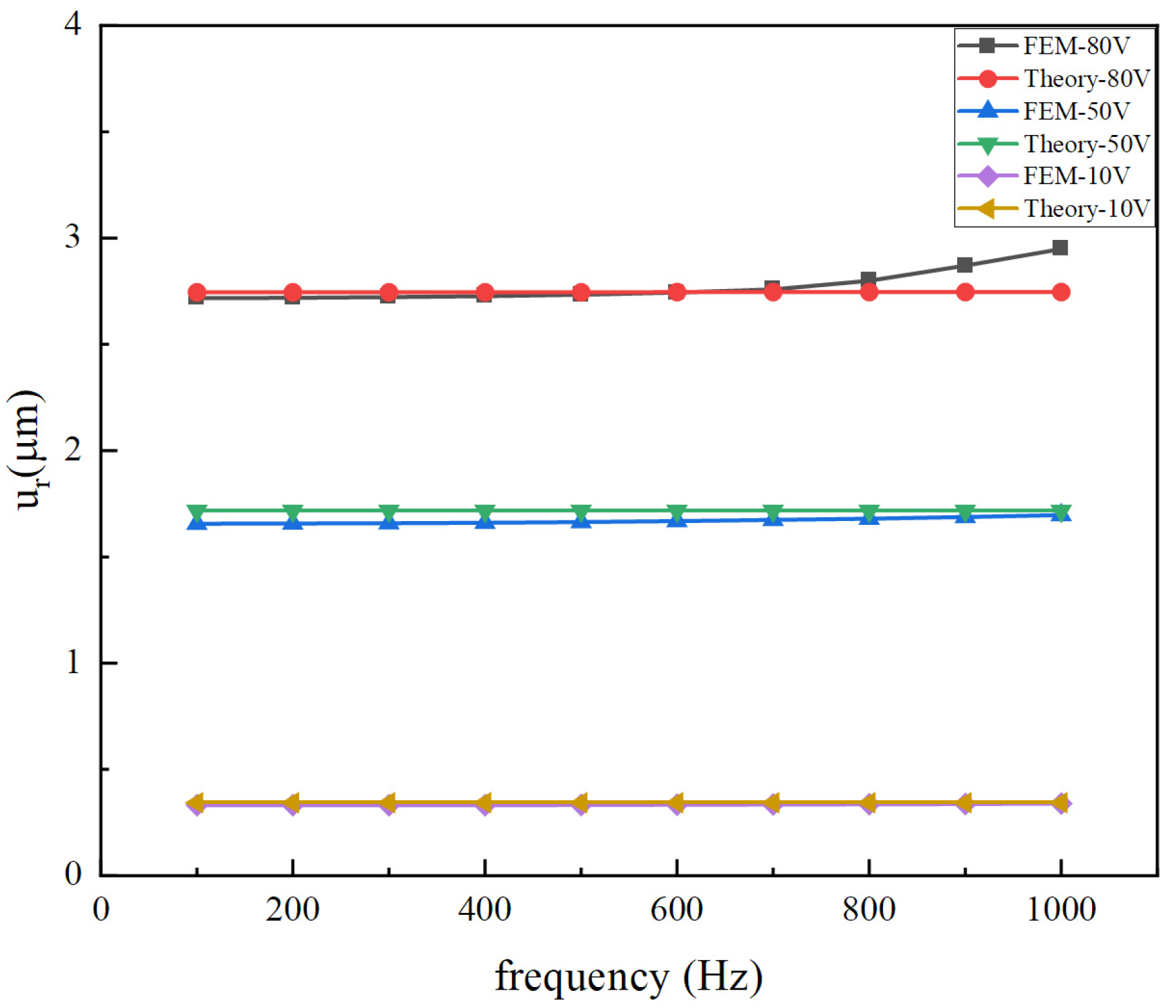
2.2.2. Harmonic Response Analysis
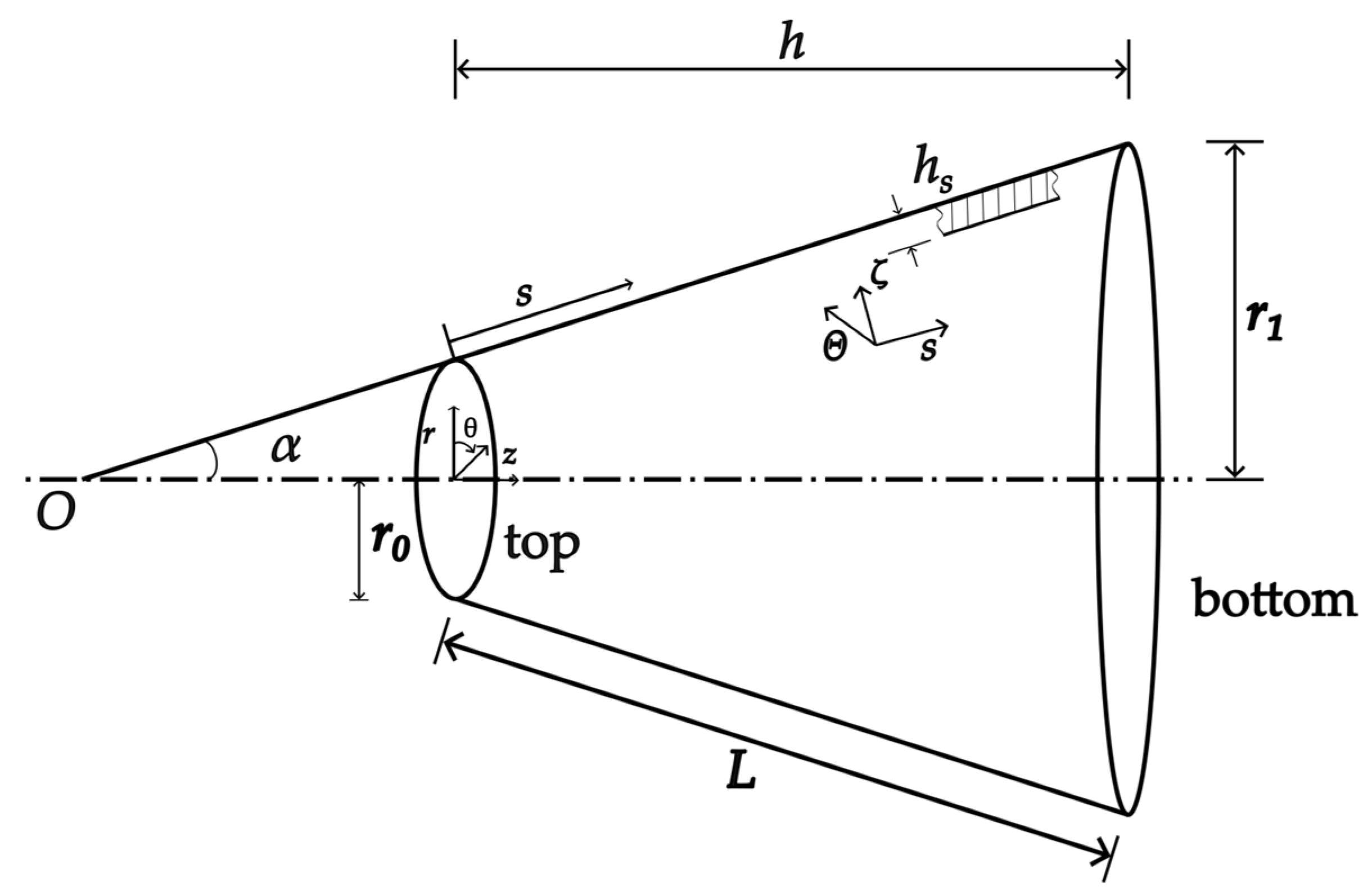
3. Theoretical Model and Simulation of the Cymbal Disk
3.1. Theoretical Model of the Cymbal Disk
3.2. Results and Discussion of Cymbal Disk
4. Overall Analysis of the Stacked Piezoelectric Cymbal Vibrator
4.1. Coupling between Piezoelectric Stack and Cymbal Disk
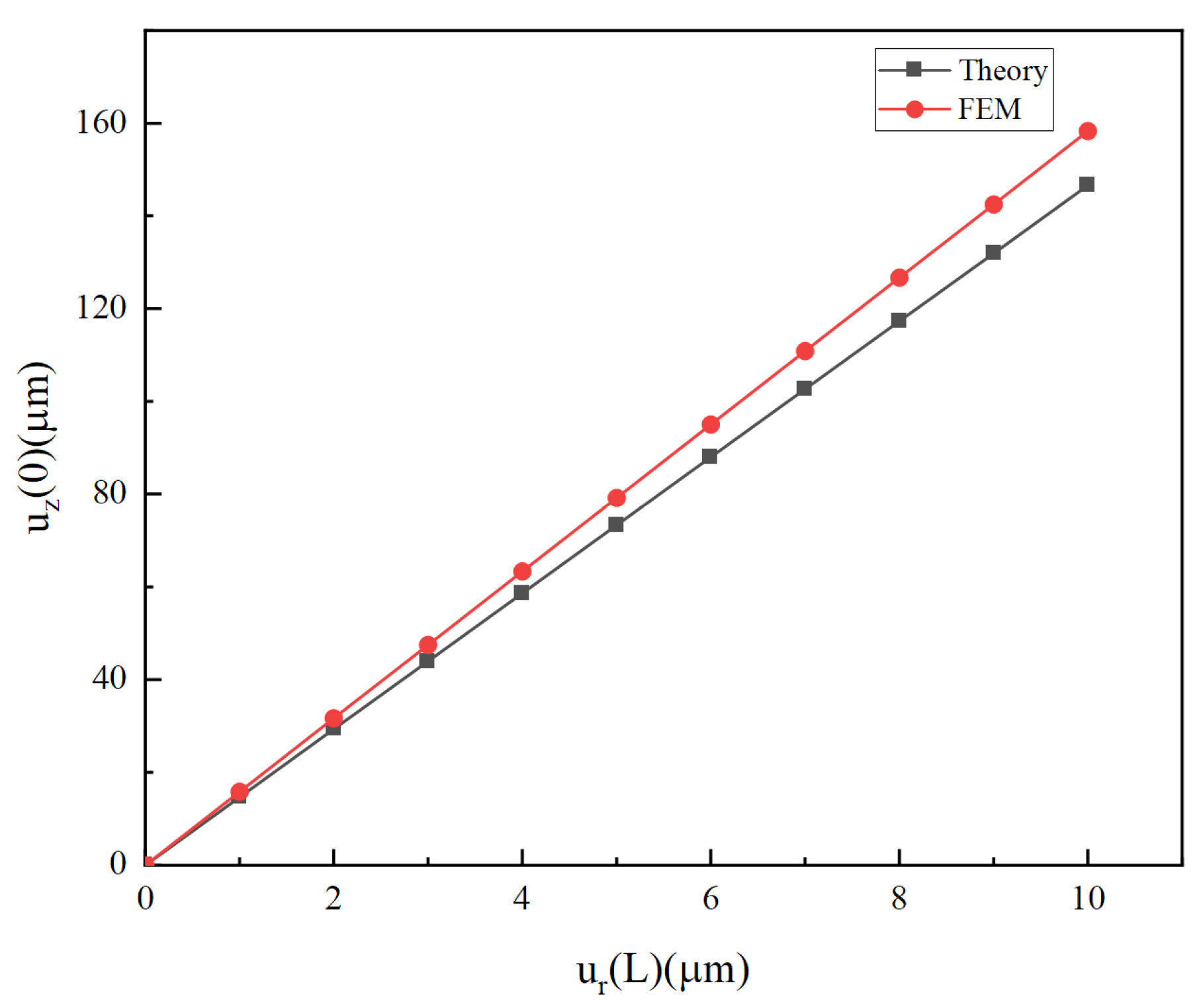
4.2. Overall Analysis and Comparison
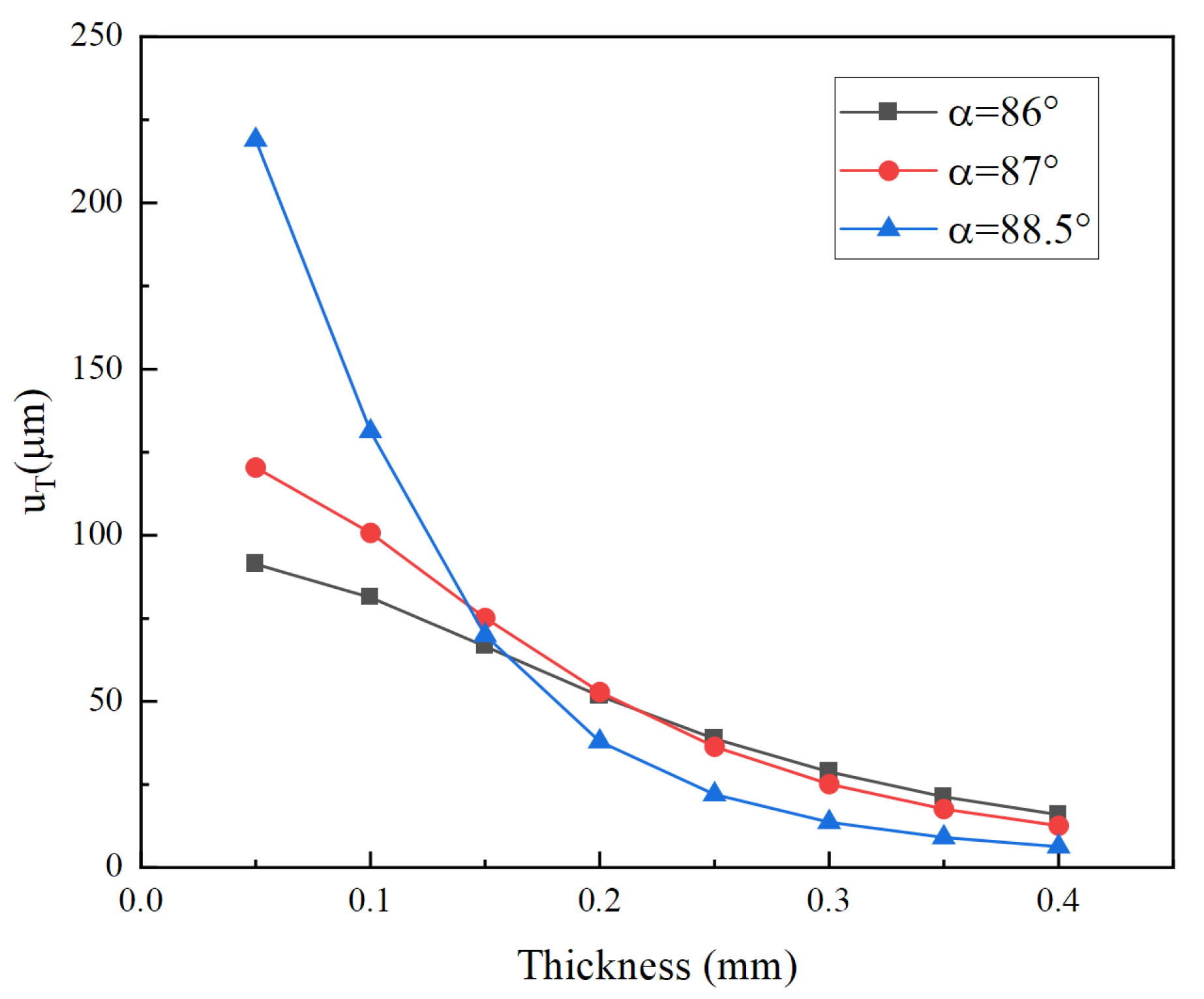
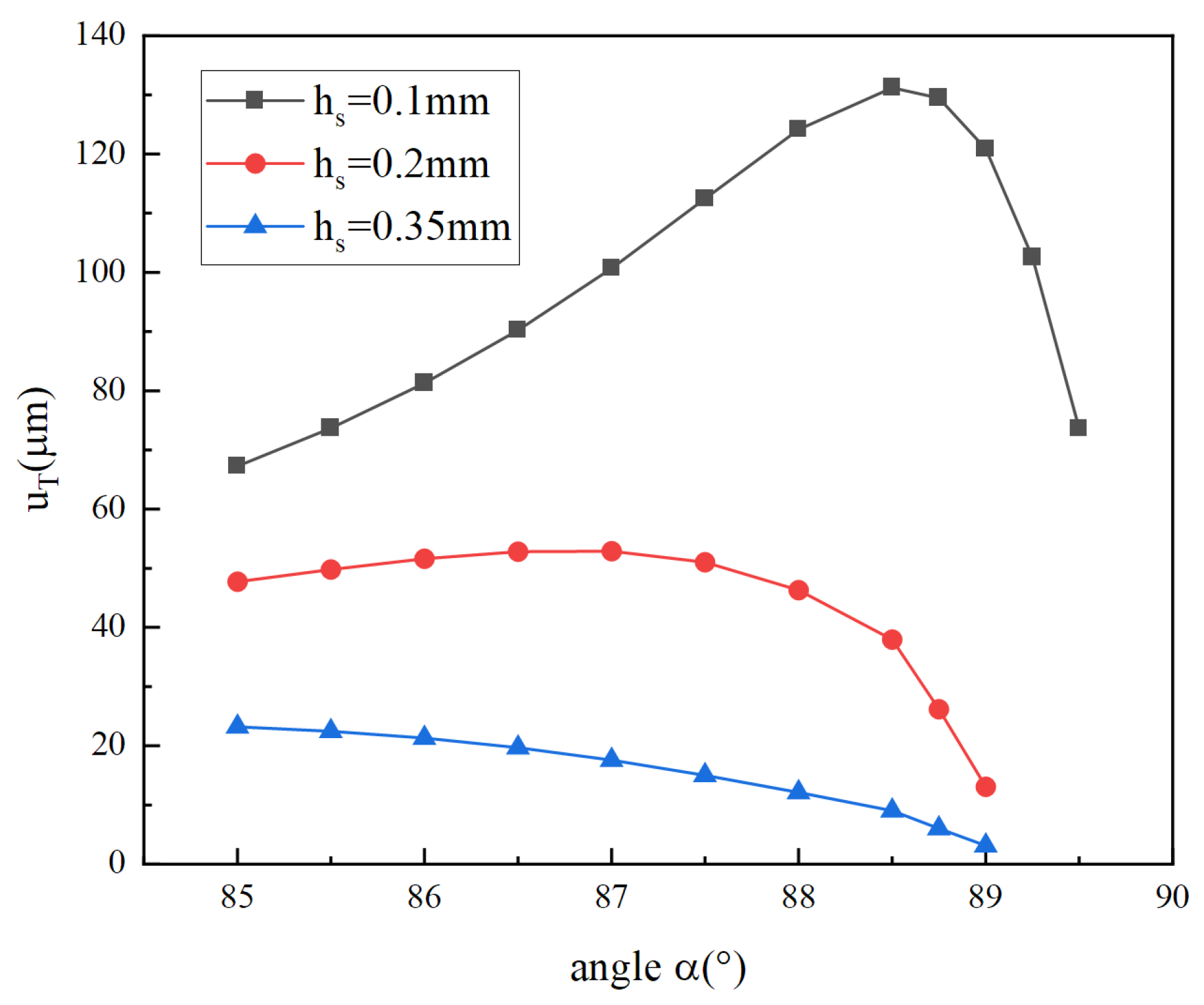
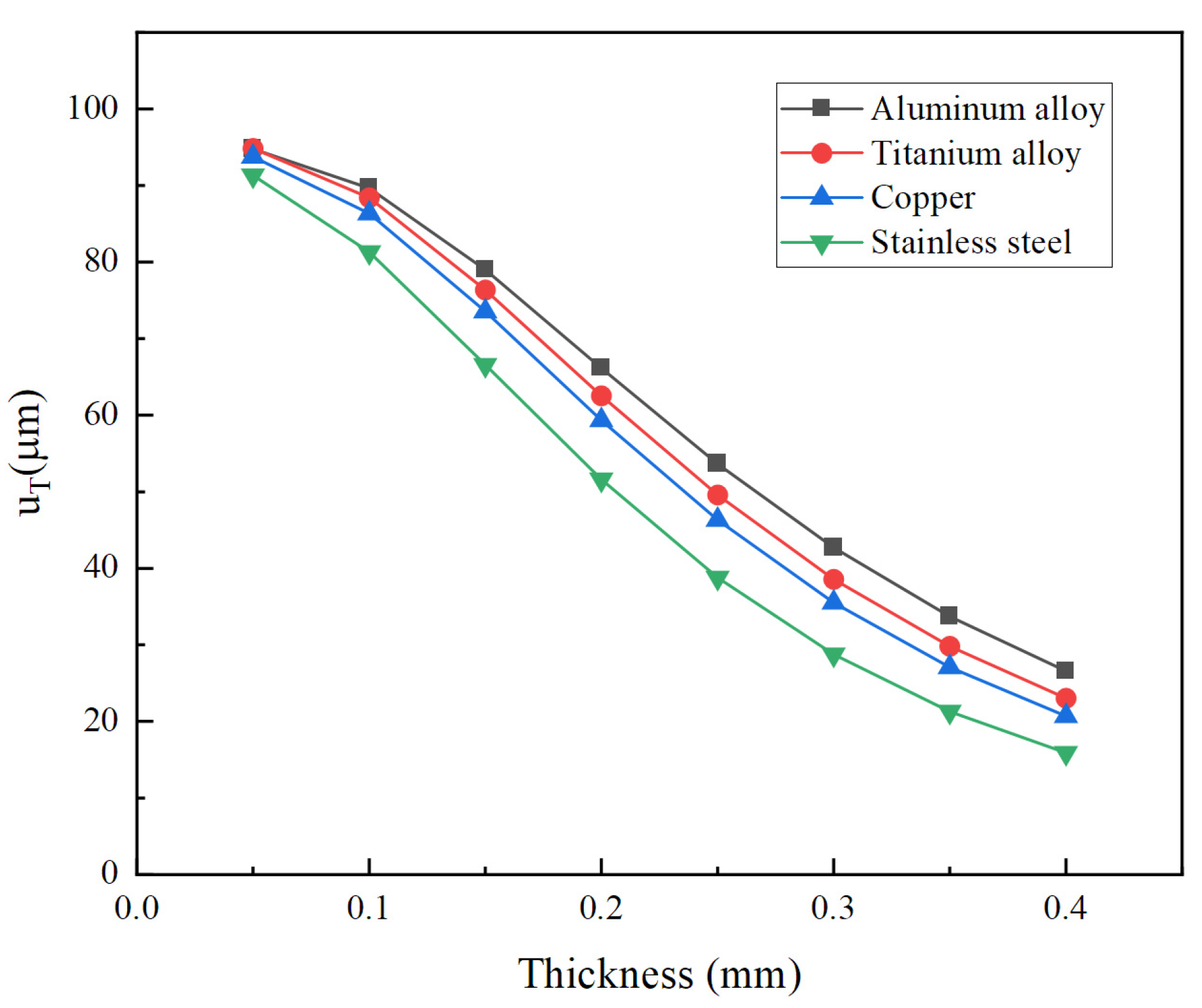
4.3. Influence of Cymbal Parameters on Total Longitudinal Displacements of the Overall Vibrator
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xing, J.; Liu, D. Free vibration analysis for a tactile feedback device of a piezoelectric ciliary body beam. Iran. J. Sci. Technol. Trans. Mech. Eng. 2019, 44, 949–959. [Google Scholar] [CrossRef]
- Pornthep, P.; Eric, R. Haplets: Finger-worn wireless and low-encumbrance vibrotactile haptic feedback for virtual and augmented reality. Front. Virtual Real. 2021, 2, 738613. [Google Scholar]
- Mullen, J.F., Jr.; Josh, M.; Sounak, C.; Anqi, C.; Tyler, W.; Losey, D.P. Communicating Inferred Goals With Passive Augmented Reality and Active Haptic Feedback. IEEE Robot. Autom. Lett. 2021, 6, 8522–8529. [Google Scholar] [CrossRef]
- Ge, C.; Cretu, E. Bionic MEMS for touching and hearing sensations: Recent progress, challenges, and solutions. J. Bionic Eng. 2022, 19, 590–615. [Google Scholar] [CrossRef]
- Itkowitz, B.; Handley, J.; Zhu, W.H. The OpenHaptics Toolkit: A Library for Adding 3D Touch Navigation and Haptics to Graphics Applications. In Proceedings of the 1st Joint Eurohaptics Conference/Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, Pisa, Italy, 18–20 March 2005; pp. 590–591. [Google Scholar]
- Lee, K.B.; Kim, J.H.; Kim, J.H. Design of horizontally vibrating linear motor for thin smart phone. Appl. Mech. Mater. 2014, 3147, 824–828. [Google Scholar]
- Pyo, D.; Yang, T.-H.; Ryu, S.; Kwon, D.-S. Novel linear impact-resonant actuator for mobile applications. Sens. Actuat A-Phys 2015, 233, 460–471. [Google Scholar] [CrossRef]
- Roy, N.; Choudhury, R.R.; Gowda, M.K. Communicating Through Physical Vibration. U.S. Patent US20160119168, 28 April 2016. [Google Scholar]
- Zhang, F.D.; Jia, Q.F.; Zhang, S.X. Study on Nonlinear Vibration of Motor Rotor System. In Proceedings of the International Conference on Vibration, Structural Engineering and Measurement (ICVSEM2012), Shanghai, China, 19–21 October 2012; pp. 221–226. [Google Scholar]
- Delibas, B.; Koc, B. A method to realize low velocity movability and eliminate friction induced noise in piezoelectric ultrasonic motors. IEEE/ASME Trans. Mechatron. 2020, 25, 2677–2687. [Google Scholar] [CrossRef]
- Gao, X.; Yang, J.; Wu, J.; Xin, X.; Li, Z.; Yuan, X.; Shen, X.; Dong, S. Piezoelectric actuators and motors: Materials, designs, and applications. Adv. Mater. Technol. 2020, 5, 1900716. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Behera, B.; Kumar, J. A brief review on the recent evolution in piezoelectric linear ultrasonic motors. Eng. Res. Express 2021, 3, 042003. [Google Scholar] [CrossRef]
- Nam, J.; Han, S.; Jang, G. A Resonant Piezoelectric S-Morph Actuator With a Large Vibration Force Operating at a Haptic Frequency in a Hexahedral Smart Watch With a Small Form Factor. IEEE/ASME Trans. Mechatron. 2018, 23, 2881–2887. [Google Scholar] [CrossRef]
- Nam, J.; Kim, Y.; Jang, G. Resonant Piezoelectric Vibrator With High Displacement at Haptic Frequency for Smart Devices. IEEE/ASME Trans. Mechatron. 2016, 21, 394–401. [Google Scholar] [CrossRef]
- Pokines, B.J.; Garcia, E. A smart material microamplification mechanism fabricated using LIGA. Smart Mater. Struct. 1998, 7, 105. [Google Scholar] [CrossRef]
- Uchino, K. Piezoelectric ultrasonic motors: Overview. Smart Mater. Struct. 1998, 7, 273. [Google Scholar] [CrossRef]
- Kim, H.; Priya, S.; Uchino, K. Modeling of piezoelectric energy harvesting using cymbal transducers. Jpn. J. Appl. Phys. 2006, 45, 5836–5840. [Google Scholar] [CrossRef]
- Wang, L.N.; Li, D.H.; Jia, M.J.; Ju, W.J. Research on voltage sensitivity of vibration accelerometer based on cymbal transducer. J. Electroceramics 2008, 21, 770–773. [Google Scholar] [CrossRef]
- Duan, Q.; Zheng, Y.; Jin, J.; Hu, N.; Zhang, Z.; Hu, H. Design and experimental study of a stepping piezoelectric actuator with large stroke and high speed. Micromachines 2023, 14, 267. [Google Scholar] [CrossRef] [PubMed]
- Lucinskis, R.; Mazeika, D.; Bansevicius, R. Investigation of oscillations of piezoelectric actuators with multi-directional polarization. Mech. Syst. Signal Process. 2018, 99, 450–458. [Google Scholar] [CrossRef]
- Saadabad, N.A.; Moradi, H.; Vossoughi, G. Dynamic modeling, optimized design, and fabrication of a 2DOF piezo-actuated stick-slip mobile microrobot. Mech. Mach. Theory 2019, 133, 514–530. [Google Scholar] [CrossRef]
- Wang, J.R.; Qin, F.; Zhang, Y.H.; Liang, T.W.; Wang, Z.X.; Xu, B.W.; Sun, Y.F.; Liu, X.Y.; Zhao, H.W. Design, analysis and experiments of a linear piezoelectric actuator adopting a flexible mechanism with wing skeletal structure. Smart Mater. Struct. 2019, 28, 085034. [Google Scholar] [CrossRef]
- Zou, W.; Hu, N.; Yang, X.; Hu, H. Low-frequency broadband multidirectional vibration isolation by piezoelectric smart platform with active control. J. Low Freq. Noise Vib. Act. Control 2023, 14613484231176127. [Google Scholar] [CrossRef]
- Bejarano, F.; Feeney, A.; Lucas, M. Optimisation of a Cymbal Transducer for its Use in a High-power Ultrasonic Cutting Device for Bone Surgery. In Proceedings of the 44th Annual Symposium of the Ultrasonic-Industry-Association, Washington, DC, USA, 20–22 April 2015; pp. 35–41. [Google Scholar]
- Xu, X.F. Cymbal Piezoelectric Composite Transducer for Soccer Robot Attitude Detection Application. In Proceedings of the International Conference on Advances in Materials Science and Information Technologies in Industry (AMSITI), Xi’an, China, 11–12 January 2014; pp. 2851–2854. [Google Scholar]
- Bao, B.; Chen, J.; Zhang, L.; Du, H. Study on acceleration sensor based on new type of piezoelectric transducer. Intstrument Tech. Sens. 2016, 09, 10–12. [Google Scholar]
- Lee, S.; Smith, N.B.; Markley, D.; Snyder, B.; Uzgur, A.E.; Pishko, M.; Newnham, R.E. Composite transducer arrays for the treatment of diabetes. Int. J. Appl. Ceram. Technol. 2005, 2, 308–316. [Google Scholar] [CrossRef]
- Zhang, J.D.; Hladky-Hennion, A.C.; Hughes, W.J.; Newnham, R.E. Modeling and Underwater Characterization of Cymbal Transducers and Arrays. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 560–568. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.D.; Yu, J.A.; Ling, J.M. Finite element analysis of Cymbal piezoelectric transducers for harvesting energy from asphalt pavement. J. Ceram. Soc. Jpn. 2010, 118, 909–915. [Google Scholar] [CrossRef]
- Gao, Q. Analysis of influencing factors of equivalent piezoelectric constant of cymbal piezoelectric transducer. Piezoelectrics Acoustooptics 2012, 34, 388–391. [Google Scholar]
- Lu, Y.; Yan, Z. Finite element analysis on energy harvesting with cymbal transducer. J. Vib. Shock 2013, 32, 157–162. [Google Scholar]
- Sun, C.; Shang, G.; Yu, J. FEM analysis of cymbal transducer for electricity generation. Mech. Sci. Technol. 2011, 30, 138–141. [Google Scholar]
- Wang, G.; Tian, W.; Lin, G.; Luan, G.; Zhang, F. Mechanical and electrical characteristics of cymbal transducer. Acta Acust. 2005, 30, 279–287. [Google Scholar]
- Wang, G.; Yu, L.; Li, G.; Luan, G.; Zhang, F. Research on structure parameters and electromechanical characteristics of cymbal transducer. Piezoelectrics Acoustooptics 2005, 27, 320–323. [Google Scholar]
- Wang, L.N.; Li, D.H.; Wu, M.; Jia, M.J.; Ju, W.J. The analysis of cymbal transducer’s effective piezoelectric coefficients based on ANSYS. Integr. Ferroelectr. 2006, 80, 297–302. [Google Scholar] [CrossRef]
- Li, D.H.; Gao, J.M.; Liang, S.; Li, G. Finite Element Analysis on Micro-Cymbal Piezoelectric Composite Transducer. In Proceedings of the International Conference on Informational Technology and Environmental System Science, Henan Polytechnic University, Jiaozuo, China, 15–17 May 2008; pp. 386–390. [Google Scholar]
- Yang, Q.F.; Wang, P.; Wang, Y.H.; Zhang, K. Simulation Analysis on Cymbal Transducer. In Proceedings of the International Conference on Mechatronics and Information Technology (ICMIT 2011), Shenyang, China, 16–19 August 2011; pp. 140–143. [Google Scholar]
- Uzgur, A.E.; Dogan, A.; Suvaci, E.; Newnham, R.E. Computational analysis on cymbal transducer. Chem. Eng. Commun. 2003, 190, 853–860. [Google Scholar] [CrossRef]
- Ganilova, O.A.; Lucas, M.; Cardoni, A. An analytical model of cymbal transducer dynamics. Radial vibration of a piezoelectric disc. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2011, 225, 1077–1086. [Google Scholar] [CrossRef]
- Gao, Q. Modeling and analyzing the voltage-displacement performance of cymbal piezoelectric transducers. Chin. J. Sens. Actuators 2012, 25, 492–495. [Google Scholar]
- Pan, Z.; Liu, B. Mathematical model of cymbal --type piezoelectric transducers. China Mech. Eng. 2006, 17, 283–286. [Google Scholar]
- Sun, C.L.; Guo, S.S.; Li, W.P.; Xing, Z.B.; Liu, G.C.; Zhao, X.Z. Displacement amplification and resonance characteristics of the cymbal transducers. Sens. Actuat A-Phys. 2005, 121, 213–220. [Google Scholar] [CrossRef]
- Rajapurkar, A.; Puchleitner, R.; Neuwirth, D.; Prall, M. Device that Conveys Haptic Feedback, and Component Comprising the Device. US 11640205 B2, 2 May 2023. [Google Scholar]
- Yang, J. An Introduction to the Theory of Piezoelectricity; Springer: Boston, MA, USA, 2005. [Google Scholar]
- Huang, C.-H.; Li, C.-C.; Wu, Y.-C.; Ma, C.-C. Theoretical analysis of transverse and planar vibrations for the piezoceramic disk based on Mindlin plate theory. Appl. Math. Model. 2021, 97, 568–587. [Google Scholar] [CrossRef]
- Piao, C.; Kim, J.O. Vibration characteristics of a piezoelectric disk laminated with an elastic disk. J. Mech. Sci. Technol. 2016, 30, 5351–5362. [Google Scholar] [CrossRef]
- Chen, F.X.; Zhang, Q.J.; Gao, Y.Z.; Dong, W. A Review on the Flexure-Based Displacement Amplification Mechanisms. IEEE Access 2020, 8, 205919–205937. [Google Scholar] [CrossRef]
- Timonshenko, S. Strength of Materials, Part 2, 1st ed.; D. Van Nostrand Co.: New York, NY, USA, 1930. [Google Scholar]
- Wu, C.; Pang, F. Free vibration characteristics of the conical shells based on precise integration transfer matrix method. Lat. Am. J. Solids Struct. 2018, 15, e03. [Google Scholar] [CrossRef]





| Materials | Density ρ (kg/m3) | Young’s Modulus E2 (GPa) | Poisson Ratio μ2 | Piezoelectric Constants (C/m2) | Thickness (μm) | ||
|---|---|---|---|---|---|---|---|
| e31 | e33 | e15 | |||||
| PZT-5H | 7500 | \ | \ | −6.5 | 23.3 | 17 | 45 |
| silver | 10,490 | 73 | 0.38 | \ | \ | \ | 5 |
| Material | Density ρ (kg/m3) | Young’s Modulus E (GPa) | Poisson Ratio μ | α (°) | r0 (mm) | r1 (mm) | h (mm) | hS (mm) |
|---|---|---|---|---|---|---|---|---|
| 304SS | 7750 | 193 | 0.31 | 86 | 1.5 | 7 | 0.48 | 0.1 |
| Materials | Aluminum Alloy | Titanium Alloy | Copper | Stainless Steel |
|---|---|---|---|---|
| Density (kg/m3) | 2770 | 4620 | 8960 | 7750 |
| Young’s modulus (GPa) | 71 | 96 | 120 | 193 |
| Poisson ratio | 0.33 | 0.36 | 0.34 | 0.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zheng, Y.; Guo, Y.; Hu, N.; Hu, H. Research on Stacked Piezoelectric Cymbal Vibrator. Micromachines 2023, 14, 2039. https://doi.org/10.3390/mi14112039
Liu X, Zheng Y, Guo Y, Hu N, Hu H. Research on Stacked Piezoelectric Cymbal Vibrator. Micromachines. 2023; 14(11):2039. https://doi.org/10.3390/mi14112039
Chicago/Turabian StyleLiu, Xinhu, Yajun Zheng, Yanming Guo, Ningdong Hu, and Hongping Hu. 2023. "Research on Stacked Piezoelectric Cymbal Vibrator" Micromachines 14, no. 11: 2039. https://doi.org/10.3390/mi14112039






