Topographic Correction of ZY-3 Satellite Images and Its Effects on Estimation of Shrub Leaf Biomass in Mountainous Areas
Abstract
:1. Introduction
2. Material and Methods
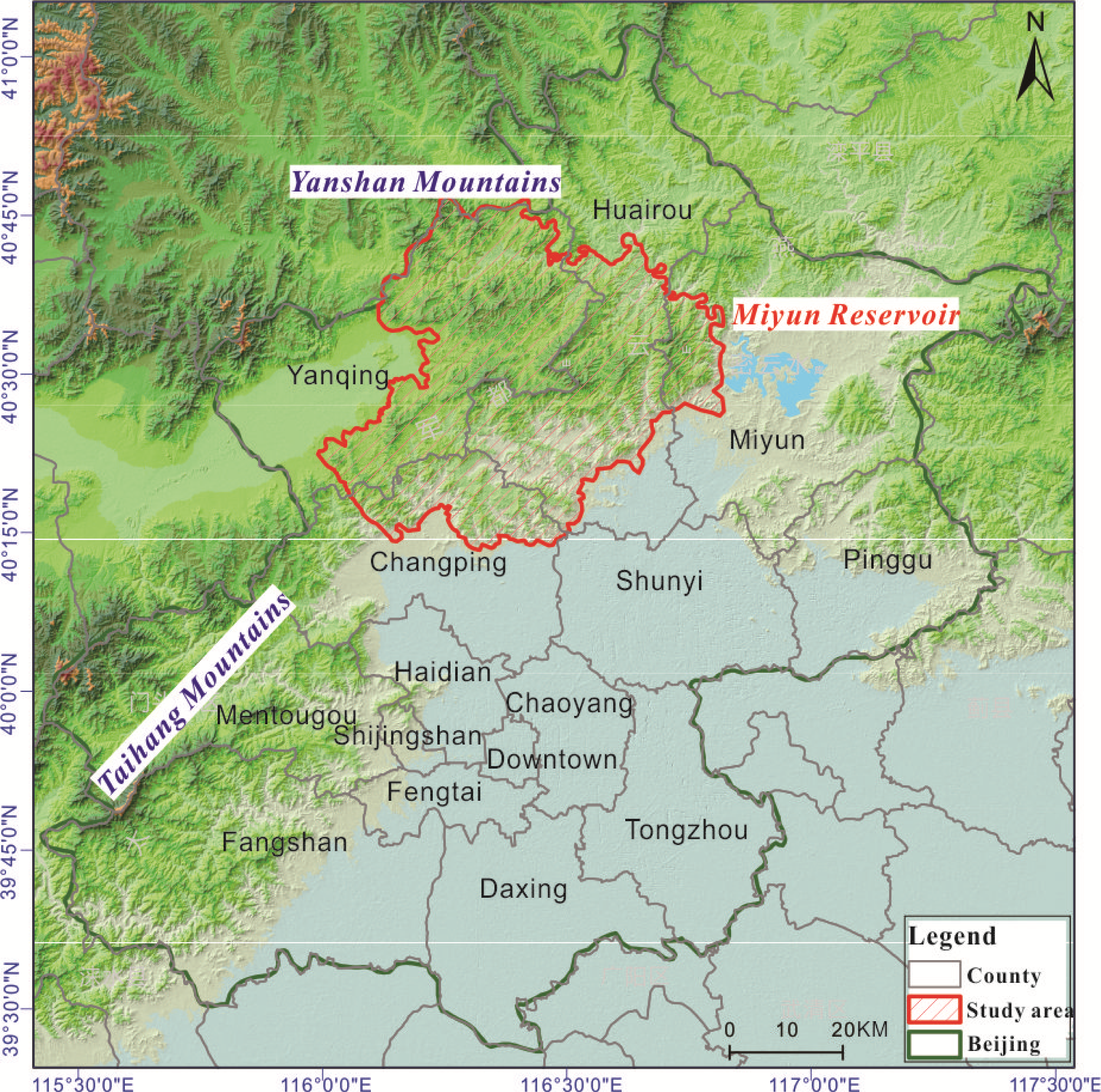
2.1. Study Area
2.2. Data Acquisition and Processing
2.2.1. Satellite Image Data and DEM
2.2.2. Field Sampling Data
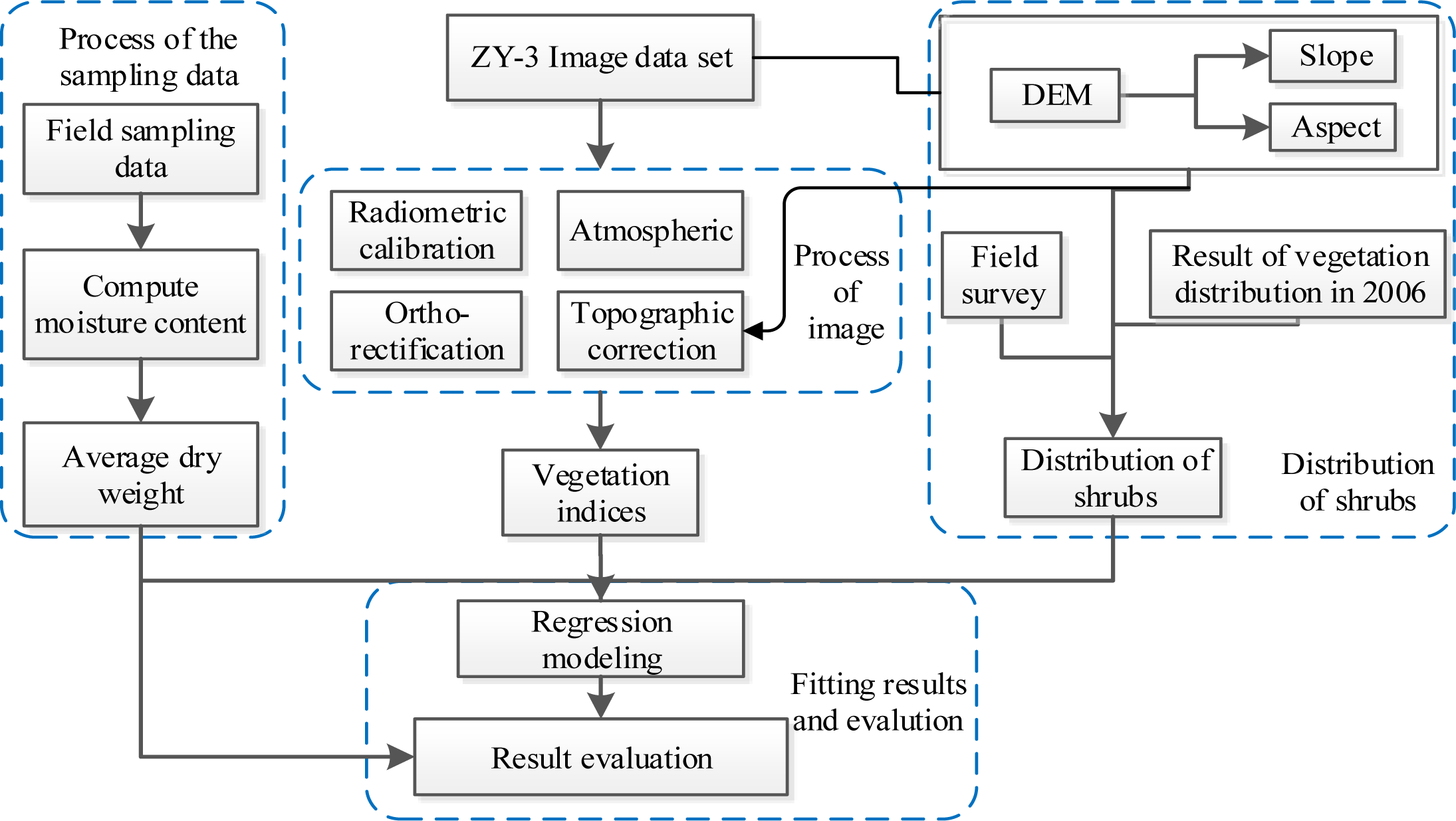
2.2.3. Data Processing
2.3. Methods
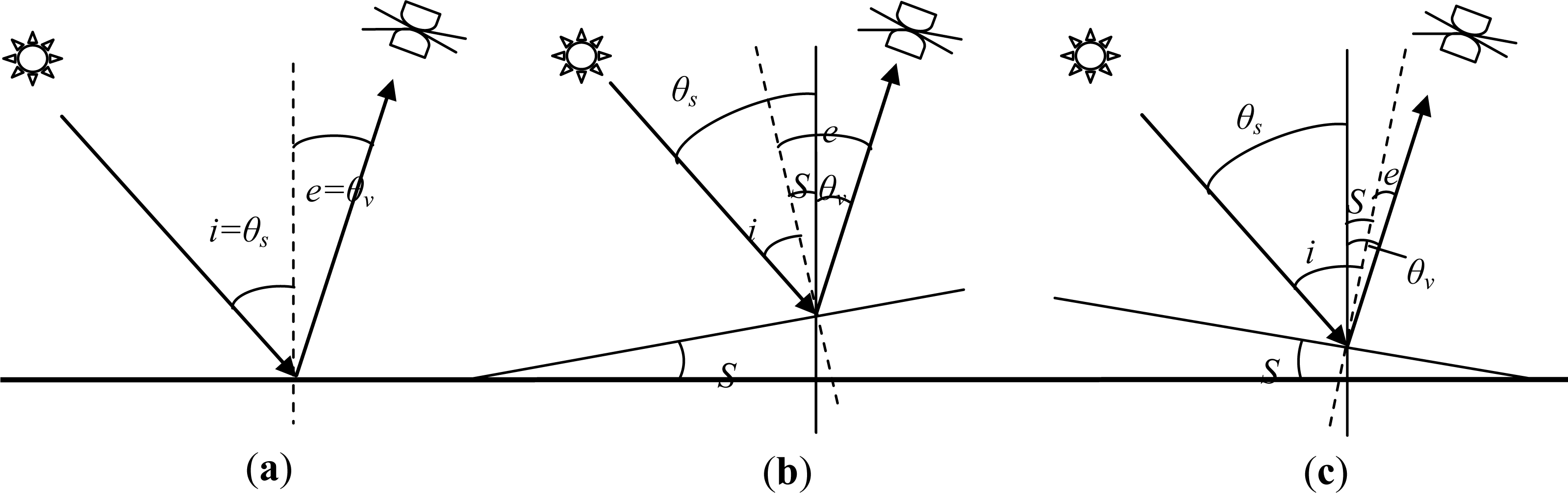
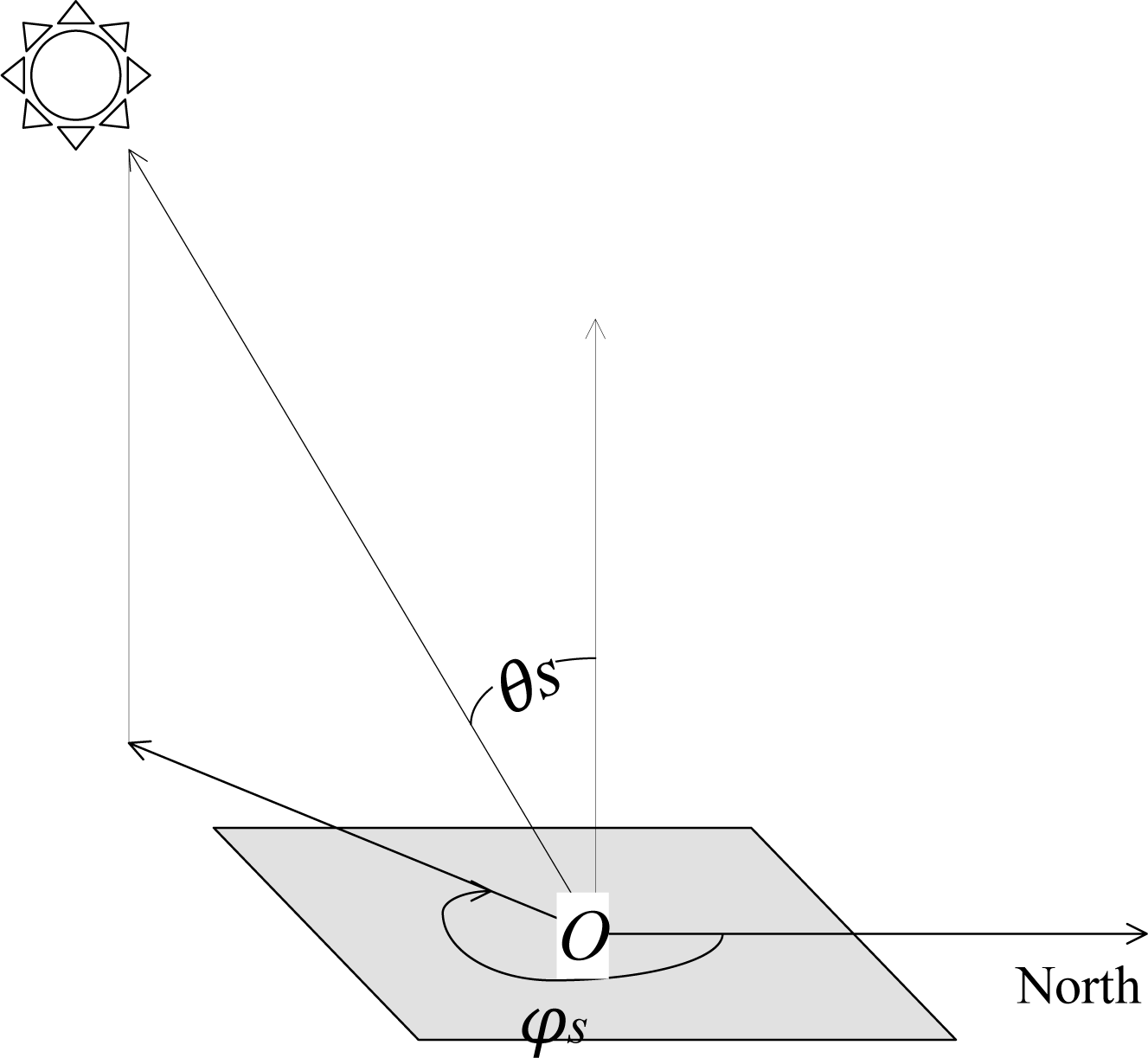
2.3.1. Topographic Correction Models
| Topographic Correction Models | Expression | Presenter | Transformation Expression | |
|---|---|---|---|---|
| 1 | Cosine | Teillet [7] | ||
| 2 | C-HuangWei | HuangWei et al. [9] | ||
| 3 | SCS+C | Soenen et al. [11] | ||
| 4 | Minnaert | Smith et al. [12] | ||
| 5 | Minnaert+SCS | Reeder [13] |
2.3.2. Biomass Estimation
3. Result
3.1. Comparison of Different Topographic Correction Models
3.1.1. Visual Inspection
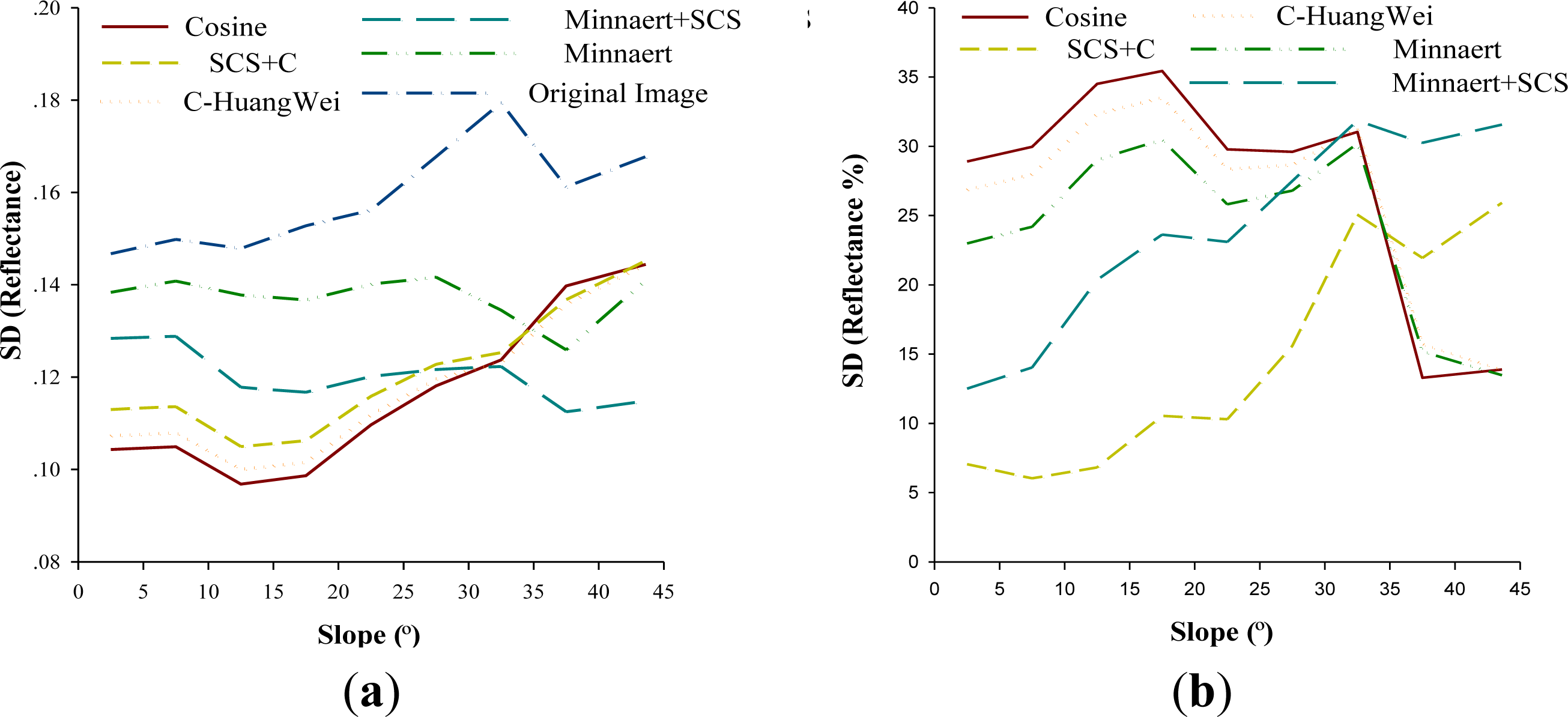
3.1.2. Statistical Analysis
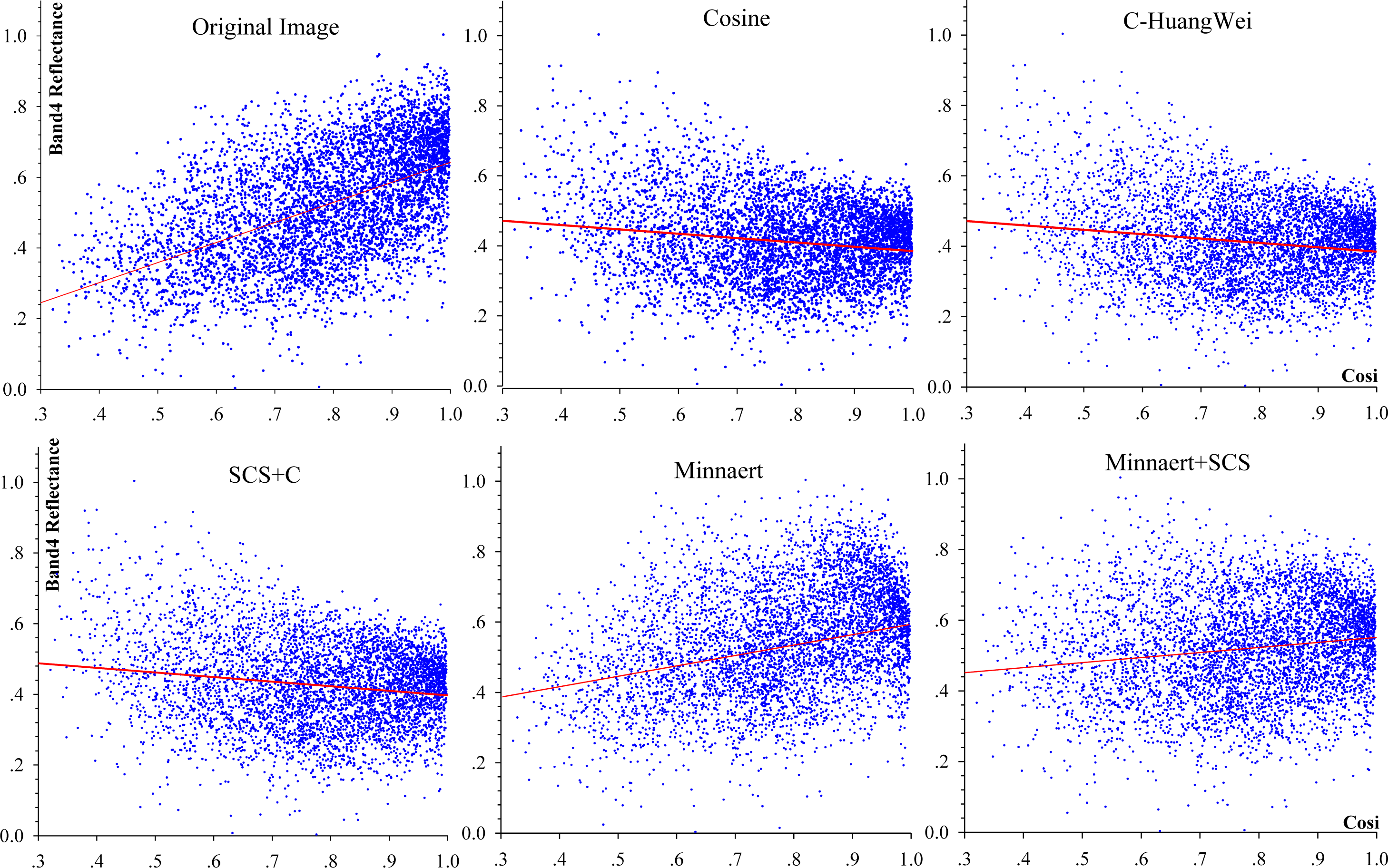
3.1.3. Correlation Analysis
3.2. Effects on Biomass Estimation
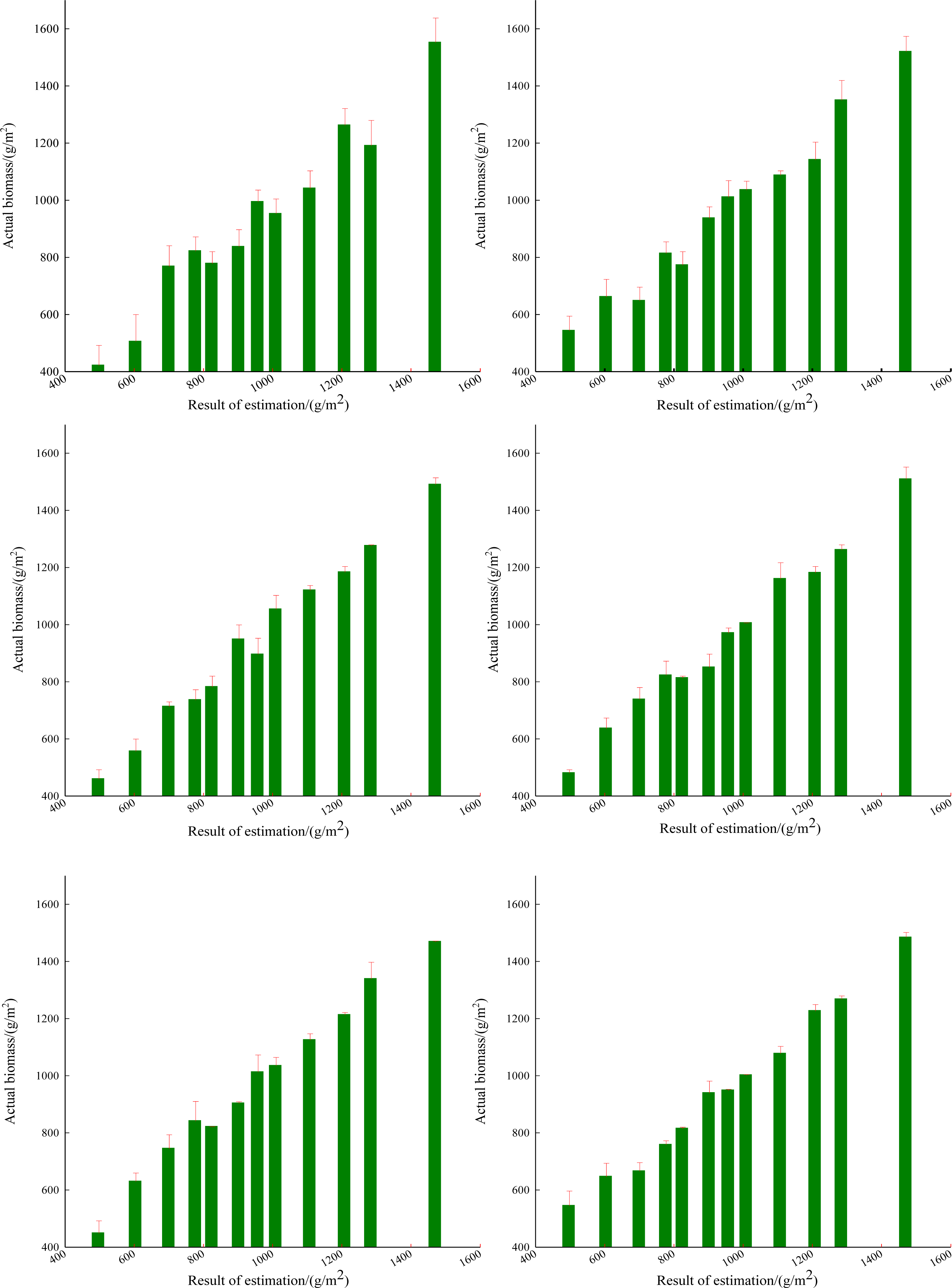
3.2.1. Fitting Results of Biomass
3.2.2. Effects on Biomass Estimation
4. Discussion
5. Conclusions
- (1)
- The topographic correction model based on Lambertian reflection theory tends to cause excessive correction due to the sky diffuse reflection and the surrounding terrain. The models based on non-Lambertian reflection assumption yield better correction results. Visual comparison, statistical analysis and correlation analysis show that the Minnaert+SCS model can effectively weaken the influence of terrain relief on pixels in ZY-3 satellite multispectral images, and restore a true reflectance of the pixels in the relief area.
- (2)
- The precision of the regression fitting between spectral vegetation indices and shrub leaf biomass is improved after topographic correction, as well as the determination coefficient R2. All the above shows that the topographic correction on ZY-3 satellite data is able to improve the estimation of shrub leaf biomass to a certain extent. In addition, results based on non-Lambertian reflection models are superior to those based on Lambertian reflection models. Furthermore, with the Minnaert+SCS model, the biomass regression fitting result has the R2 of 0.869, and the SD is reduced to 58.4 g/m2, which suggests that in areas of topographic relief, topographic correction is indispensable to the biomass estimation based on vegetation indices.
- (3)
- Further research should be carried out with imagery acquired from different sensors and solar zenith angles, to examine the performances of the methods under different illumination criteria. Moreover, how the accuracy of the DEM affects the results of topographic correction of ZY-3 imagery should also be investigated in future studies.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Du, N.; Zhang, X.R.; Wang, W.; Chen, H.; Tan, X.F.; Wang, R.Q.; Guo, W.H. Foliar phenotypic plasticity of a warm-temperate shrub, vitex negundo var. heterophylla, to different light environments in the field. Acta Ecol. Sin 2011, 31, 6049–6059. (In Chinese) [Google Scholar]
- Yin, Z.F.; Ouyang, H.; Xu, X.L.; Song, M.H.; Duan, D.Y.; Zhang, X.Z. Water and heat balance and water use of shrub grassland and crop fields in Lhasa River Valley. Acta Geogr. Sin 2009, 64, 303–314. (In Chinese) [Google Scholar]
- Estornell, J.; Ruiz, L.A.; Velázquez-Martí, B.; Hermosilla, T. Estimation of biomass and volume of shrub vegetation using LiDAR and spectral data in a Mediterranean environment. Biomass Bioenergy 2012, 46, 710–721. [Google Scholar]
- Estornell, J.; Ruiz, L.A.; Velázquez-Martí, B.; Fernández-Sarría, A. Estimation of shrub biomass by airborne LiDAR data in small forest stands. For. Ecol. Manag 2011, 262, 1697–1703. [Google Scholar]
- Gao, Y.N.; Zhang, W.C. A simple empirical topographic correction method for ETM+ imagery. Int. J. Remote Sens 2009, 30, 2259–2275. [Google Scholar]
- Gao, Y.N.; Zhang, W.C. Comparison test and research progress of topographic correction on remotely sensed data. Geogr. Res 2008, 27, 467–477. [Google Scholar]
- Teillet, P.M.; Guindon, B.; Goodenough, D.G. On the slope-aspect correction of multispectral scanner data. Can. J. Remote Sens 1982, 8, 84–106. [Google Scholar]
- Gao, Y.N.; Zhang, W.C. Simplification and modification of a physical topographic correction algorithm for remotely sensed data. Acta Geodaet. Cartogr. Sin 2008, 37, 89–94. (In Chinese) [Google Scholar]
- Huang, W.; Zhang, L.P.; Li, P.X. An improved topographic correction approach for satellite image. J. Image Graph 2005, 10, 1124–1128. [Google Scholar]
- Gu, D.; Gillespie, A. Topographic normalization of landsat TM images of forest based on subpixel Sun-Canopy-Sensor geometry. Remote Sens. Environ 1998, 64, 166–175. [Google Scholar]
- Soenen, S.A.; Peddle, D.R.; Coburn, C.A. SCS+C: A modified Sun-Canopy-Sensor topographic correction in forested terrain. IEEE Trans. Geosci. Remote Sens 2005, 43, 2148–2159. [Google Scholar]
- Smith, J.A.; Lin, T.L.; Ranson, K.J. The Lambertian assumption and Landsat data. Photogramm. Eng. Remote Sens 1980, 46, 1183–1189. [Google Scholar]
- Reeder, D.H. Topographic Correction of Satellite Images: Theory and Application; Dartmouth College: Hanover, NH, USA, 2002. [Google Scholar]
- Stijn, H.; Emilio, C. Evaluation of different topographic correction methods for Landsat imagery. Int. J. Appl. Earth Observ. Geoinf 2011, 13, 691–700. [Google Scholar]
- Shi, D.; Yan, G.J.; Mu, X.H. Optical remote sensing image apparent radiance topographic correction physical model. J. Remote Sens 2009, 6, 1030–1046. [Google Scholar]
- Ediriweera, S.; Pathirana, S.; Danaher, T.; Nichols, D.; Moffiet, T. Evaluation of different topographic corrections for Landsat TM data by prediction of foliage projective cover (FPC) in topographically complex landscapes. Remote Sens 2013, 5, 6767–6789. [Google Scholar]
- Vincini, M.; Reeder, D.; Frazzi, E. An Empirical Topographic Normalization Method for Forest TM Data. In Proceedings of the 2002 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Toronto, Canada, 24–28 June 2002; Volume 4, pp. 2091–2093.
- Civco, D.L. Topographic normalization of Landsat thematic mapper digital magery. Photogram. Eng. Remote Sens 1989, 55, 1303–1309. [Google Scholar]
- Dymond, J.R.; Shepherd, J.D. Correction of the topographic effect in remote sensing. IEEE Trans. Geosci. Remote Sens 1999, 37, 2618–2620. [Google Scholar]
- Ekstrand, S. Landsat TM-based forest damage assessment: Correction for topographic effects. Photogram. Eng. Remote Sens 1996, 62, 51–161. [Google Scholar]
- Richter, R.; Kellenberger, T.; Kaufmann, H. Comparison of topographic correction methods. Remote Sens 2009, 1, 184–196. [Google Scholar]
- Law, K.H.; Nichol, J. Topographic Correction for Differential Illumination Effects on IKONOS Satellite Imagery. In Proceedings of the 10th Congress of International Society for Photogrammetry and Remote Sensing, Istanbul, Turkey, 12–23 July 2004; Volume 35, p. 6.
- Gao, M.L.; Zhao, W.J.; Gong, Z.N.; He, X.H. The study of vegetation biomass inversion based on the HJ satellite data in Yellow River wetland. Acta Ecol. Sin 2013, 33, 542–553. (In Chinese) [Google Scholar]
- Li, X.; Yeh, A.; Liu, K.; Wang, S.G. Inventory of mangrove wetlands in the Pearl River Estuary of China using remote sensing. J. Geogr. Sci 2006, 16, 155–164. [Google Scholar]
- Li, S.; Zhang, Z.L.; Zhou, D.M. An estimation of aboveground vegetation biomass in a national natural reserve using remote sensing. Acta Ecol. Sin 2011, 30, 278–290. [Google Scholar]
- Guo, Z.F.; Chi, H.; Sun, G.Q. Estimating forest aboveground biomass using HJ-1 Satellite CCD and ICESat GLAS waveform data. Sci. China: Earth Sci 2010, 53, 16–25. [Google Scholar]
- Anaya, J.A.; Chuvieco, E.; Palacios-Orueta, A. Aboveground biomass assessment in Colombia: A remote sensing approach. For. Ecol. Manag 2009, 257, 1237–1246. [Google Scholar]
- Deering, D.W.; Haas, R.H.; Rouse, J.W.; Schell, J.A. Monitoring the Vernal Advancement of Retrogradation of Natural Vegetation; Final Report 1974; NASA/GSFC: Greenbelt, MD, USA, 1974. [Google Scholar]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ 1994, 48, 119–126. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ 1996, 58, 289–298. [Google Scholar]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ 2004, 90, 337–352. [Google Scholar]
- Chen, J. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens 1996, 22, 229–242. [Google Scholar]
- Roujean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ 1995, 51, 375–384. [Google Scholar]
- Crippen, R.E. Calculating the vegetation index faster. Remote Sens. Environ 1990, 34, 71–73. [Google Scholar]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ 1996, 55, 95–107. [Google Scholar]
- Goel, N.S.; Qin, W.H. Influences of canopy architecture on relationships between various vegetation indices and LAI and FPAR: A computer simulation. Remote Sens. Rev 1994, 10, 309–347. [Google Scholar]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ 2000, 76, 156–172. [Google Scholar]
- Holben, B.N.; Justice, C.O. The topographic effect on spectral response from Nadir-Pointing sensors. Photogram. Eng. Remote Sens 1980, 46, 1191–1200. [Google Scholar]
- Lu, D.S.; Ge, H.; He, S.Z.; Xu, A.J.; Zhou, G.M.; Du, H.Q. Pixel-based Minnaert correction method for reducing topographic effects on a Landsat 7 ETM+ image. Photogram. Eng. Remote Sens 2008, 74, 1343–1350. [Google Scholar]
- Conese, C.; Gilabert, M.A.; Maselli, F.; Bottai, L. Topographic normalization of TM scenes through the use of an atmospheric correction method and digital terrain models. Photogram. Eng. Remote Sens 1993, 59, 1745–1753. [Google Scholar]
- Wu, J.D.; Marvin, E.B.; Wang, D.; Steven, M.M. A comparison of illumination geometry-based methods for topographic correction of QuickBird images of an undulant area. ISPRS J. Photogram. Remote Sens 2008, 63, 223–236. [Google Scholar]

| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Solar azimuth angle | 60.784798° | Atmosphere model | Mid-Latitude Summer |
| Solar zenith angle | 148.091629° | Aerosol model | Rural |
| Latitude | 40.571969° | Water column multiplier | 1.00 |
| Longitude | 116.632222° | Visibility | 35 km |
| Parameters | Band1 | Band2 | Band3 | Band4 |
|---|---|---|---|---|
| C(SCS+C) | 1.4144 | 0.6041 | 0.6314 | 0.4405 |
| k(Minnaert) | 0.3956 | 0.5620 | 0.5518 | 0.6196 |
| k(Minnaert+SCS) | 0.4281 | 0.6348 | 0.6223 | 0.7061 |
| Vegetation Index | Full Name * | Expression | Presenter |
|---|---|---|---|
| NDVI | Normalized Difference Vegetation Index | Deering et al. [28] | |
| MSAVI | Modified Soil Adjusted Vegetation Index | Qi et al. [29] | |
| GNDVI | Green Normalized Difference Vegetation Index | Gitelson et al. [30] | |
| MTVI2 | Modified Triangular Vegetation Index 2 | Haboudane [31] | |
| MSR | Modified Simple Ratio Vegetation Index | Chen et al. [32] | |
| RDVI | Ratio Difference Vegetation Index | Roujean et al. [33] | |
| IPVI | Infrared Percentage Vegetation Index | Crippen et al. [34] | |
| OSAVI | Optimized Soil Adjusted Vegetation Index | Rondeaux et al. [35] | |
| NLI | Non-Linear Index | Goel et al. [36] | |
| TVI | Triangular Vegetation Index | Broge et al. [37] |
| % Reduction in SD | ||||
|---|---|---|---|---|
| Band 1 | Band 2 | Band 3 | Band 4 | |
| Cosine | −12.6 | 2.1 | −13.5 | 27.4 |
| C-HuangWei | −11.0 | −31.2 | −12.4 | 26.5 |
| SCS+C | −7.9 | 12.6 | 16.1 | 24.2 |
| Minnaert | −13.6 | 9.8 | 19.0 | 13.7 |
| Minnaert+SCS | −1.9 | 12.6 | 16.2 | 23.9 |
| Correction Model | R2 | Expression of Fitting Line |
|---|---|---|
| Original Image | 0.306 | y = 0.5673x + 0.0753 |
| Cosine | 0.0580 | y = −0.1825x + 0.5412 |
| C-HuangWei | 0.0264 | y = −0.1239x + 0.5086 |
| SCS+C | 0.0253 | y = −0.1216x + 0.5068 |
| Minnaert | 0.0263 | y = 0.1425x + 0.4073 |
| Minnaert+SCS | 0.0246 | y = 0.1179x + 0.4210 |
| Model | Expression | R2 | SE(g/m2) | Sig. | F |
|---|---|---|---|---|---|
| Original image | Y = −204.847 + 1209.428MTVI2-2405.185RDVI + 47.623TVI + 1338.759MSR + 1742.851NLI + 2482.307GNDVI | 0.756 | 88.5 | * | 9.312 |
| Cosine | Y = −268.452 + 1094.142MTVI2-1922.190RDVI + 64.352TVI + 1097.733MSR − 1048.229NLI + 1862.554GNDVI | 0.787 | 86.4 | * | 8.799 |
| C-HuangWei | Y = −229.937 + 1109.368MTVI2-2192.665RDVI + 59.320TVI + 1400.529MSR − 1558.106NLI + 2056.861GNDVI | 0.773 | 84.0 | * | 8.752 |
| SCS+C | Y = −238.902 + 1320.922MTVI2-2106.025RDVI + 50.221TVI + 1128.092MSR − 1615.210NLI + 2102.425GNDVI | 0.790 | 82.3 | * | 9.017 |
| Minnaert | Y = −302.228 + 1529.474MTVI2-2351.601RDVI + 38.944TVI + 1037.805MSR − 2209.750NLI + 1083.262GNDVI | 0.854 | 76.2 | ** | 9.362 |
| Minnaert+SCS | Y = −217.032 + 1604.227MTVI2-2409.825RDVI + 40.352TVI + 1099.027MSR − 2128.104NLI + 1166.460GNDVI | 0.869 | 72.7 | ** | 9.401 |
| Correction Model | SD | Maximum Error |
|---|---|---|
| Original Image | 74.1 | 99.6 |
| Cosine | 72.0 | 100.2 |
| C-HuangWei | 71.3 | 96.8 |
| SCS+C | 68.9 | 93.1 |
| Minnaert | 62.7 | 84.2 |
| Minnaert+SCS | 58.4 | 64.7 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gao, M.-L.; Zhao, W.-J.; Gong, Z.-N.; Gong, H.-L.; Chen, Z.; Tang, X.-M. Topographic Correction of ZY-3 Satellite Images and Its Effects on Estimation of Shrub Leaf Biomass in Mountainous Areas. Remote Sens. 2014, 6, 2745-2764. https://doi.org/10.3390/rs6042745
Gao M-L, Zhao W-J, Gong Z-N, Gong H-L, Chen Z, Tang X-M. Topographic Correction of ZY-3 Satellite Images and Its Effects on Estimation of Shrub Leaf Biomass in Mountainous Areas. Remote Sensing. 2014; 6(4):2745-2764. https://doi.org/10.3390/rs6042745
Chicago/Turabian StyleGao, Ming-Liang, Wen-Ji Zhao, Zhao-Ning Gong, Hui-Li Gong, Zheng Chen, and Xin-Ming Tang. 2014. "Topographic Correction of ZY-3 Satellite Images and Its Effects on Estimation of Shrub Leaf Biomass in Mountainous Areas" Remote Sensing 6, no. 4: 2745-2764. https://doi.org/10.3390/rs6042745
APA StyleGao, M.-L., Zhao, W.-J., Gong, Z.-N., Gong, H.-L., Chen, Z., & Tang, X.-M. (2014). Topographic Correction of ZY-3 Satellite Images and Its Effects on Estimation of Shrub Leaf Biomass in Mountainous Areas. Remote Sensing, 6(4), 2745-2764. https://doi.org/10.3390/rs6042745






