Modeling Species Distribution Using Niche-Based Proxies Derived from Composite Bioclimatic Variables and MODIS NDVI
Abstract
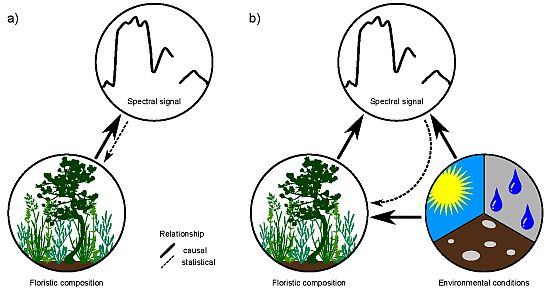
:1. Introduction
2. Material and Methods
2.1. Study Area
2.2. Floristic Data
2.3. Bioclimate Variables
2.4. MODIS-NDVI Time Series
2.4. Statistical Analyses
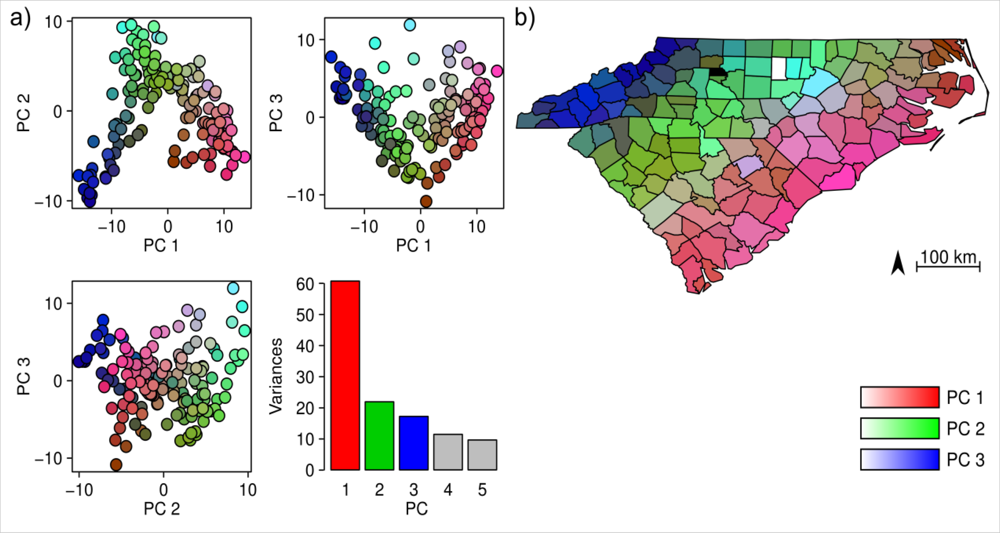
3. Results
4. Discussion
4.1. Floristic Patterns along the Climatic Gradients
4.2. Climatic Influences on NDVI
4.3. Relationship between Floristic Patterns and NDVI Time Series
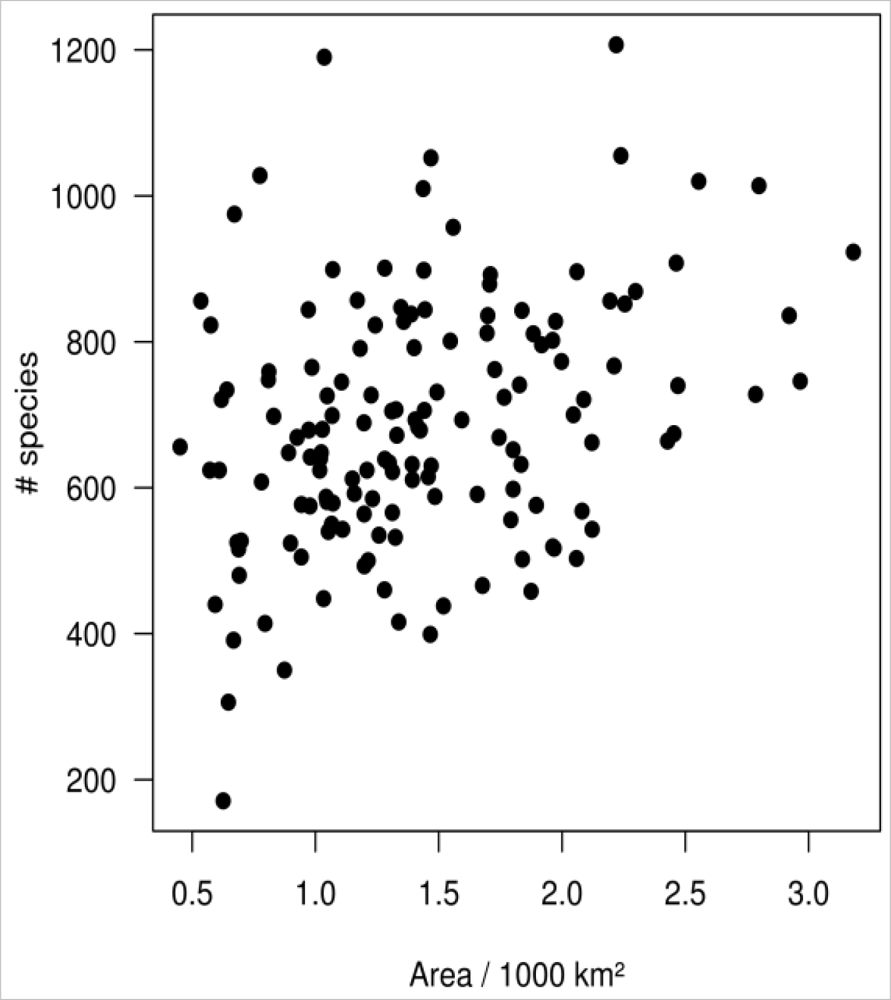
4.4. Spatial Autocorrelation and Area Effect
4.5. Model Output Deviates from Realized Niche
4.6. Theoretical Limitations of the Approach
5. Conclusions
Acknowledgments
References
- Ustin, S.L.; Roberts, D.A.; Gamon, J.A. Using imaging spectroscopy to study ecosystem processes and properties. BioScience 2004, 53, 523–534. [Google Scholar]
- Kokaly, R.F.; Asner, G.P.; Ollinger, S.V.; Martin, M.E.; Wessman, C.A. Characterizing canopy biochemistry from imaging spectroscopy and its application to ecosystem studies. Remote Sens. Environ 2009, 113, S78–S91. [Google Scholar]
- He, K.S.; Rocchini, D.; Neteler, M.; Nagendra, H. Benefits of hyperspectral remote sensing for tracking plant invasions. Divers. Distrib 2011, 17, 381–392. [Google Scholar]
- Castro-Esau, K.L.; Sánchez-Azofeifa, G.A.; Rivard, B.; Wright, S.J.; Quesada, M. Variability in leaf optical properties of mesoamerican trees and the potential for species classification. Am. J. Bot 2006, 93, 517–530. [Google Scholar]
- Price, J. How unique are spectral signatures? Remote Sens. Environ 1994, 49, 181–186. [Google Scholar]
- Feilhauer, H.; Faude, U.; Schmidtlein, S. Combining Isomap ordination and imaging spectroscopy to map continuous floristic gradients in a heterogeneous landscape. Remote Sens. Environ 2011, 115, 2513–2524. [Google Scholar]
- Asner, G.P.; Martin, R.E.; Tupayachi, R.; Emerson, R.; Martinez, P.; Sinca, F.; Powell, G.V.N.; Wright, S.J.; Lugo, A.E. Taxonomy and remote sensing of leaf mass per area (LMA) in humid tropical forests. Ecol. Appl 2011, 21, 85–98. [Google Scholar]
- Huntley, B.; Berry, P.M.; Cramer, W.; McDonald, A.P. Modeling present and potential future ranges of some European higher plants using climate response surfaces. J. Biogeogr 1995, 22, 967–1001. [Google Scholar]
- Pearson, R.G.; Dawson, T.E.; Liu, C. Modelling species distributions in Britain: A hierarchical integration of climate and land-cover data. Ecography 2004, 27, 285–298. [Google Scholar]
- Austin, M.P.; Cunningham, R.B.; Fleming, P.M. New approaches to direct gradient analysis using environmental scalars and statistical curve-fitting procedures. Vegetatio 1984, 55, 11–27. [Google Scholar]
- Austin, M.P.; Gaywood, M.J. Current problems of environmental gradients and species response curves in relation to continuum theory. J. Veg. Sci 1994, 5, 473–482. [Google Scholar]
- Guisan, A.; Zimmermann, N.E. Predictive habitat distribution models in ecology. Ecol. Model 2000, 135, 147–186. [Google Scholar]
- Guisan, A.; Thuiller, W. Predicting species distributions: Offering more than simple habitat models. Ecol. Lett 2005, 8, 993–1009. [Google Scholar]
- Hutchinson, G.E. Concluding remarks. Cold Spring Harbor Symposium on Quantitative Biology 1957, 22, 415–457. [Google Scholar]
- Guisan, A.; Weiss, S.B.; Weiss, A.D. GLM versus CCA spatial modeling of plant species distribution. Plant Ecol 1999, 143, 107–122. [Google Scholar]
- Lassueur, T.; Joost, S.; Randin, C.F. Very high resolution digital elevation models: Do they improve models of plant species distribution? Ecol. Model 2006, 198, 139–153. [Google Scholar]
- Berry, P.M.; Dawson, T.P.; Harrison, P.A.; Pearson, R.G. Modelling potential impacts of climate change on the bioclimatic envelope of species in Britain and Ireland. Glob. Ecol. Biogeogr 2002, 11, 453–462. [Google Scholar]
- Pearson, R.G.; Dawson, T.P. Predicting the impacts of climate change on the distribution of species: are bioclimate envelope models useful? Glob. Ecol. Biogeogr 2003, 12, 361–371. [Google Scholar]
- Heikkinen, R.K.; Luoto, M.; Araújo, M.B.; Virkkala, R.; Thuiller, W.; Sykes, M.T. Methods and uncertainties in bioclimatic envelope modelling under climate change. Progr. Phys. Geogr 2006, 30, 751–777. [Google Scholar]
- Fairbanks, D.H.K.; McGwire, K.C. Patterns of floristic richness in vegetation communities of California: Regional scale analysis with multi-temporal NDVI. Glob. Ecol. Biogeogr 2004, 13, 221–235. [Google Scholar]
- He, K.S.; Zhang, J.; Zhang, R. Linking variability in species composition and MODIS NDVI based on beta diversity measurements. Acta Oecol 2009, 35, 14–21. [Google Scholar]
- Morisette, J.T.; Jarnevich, C.S.; Ullah, A.; Cai, W.J.; Pedelty, J.A.; Gentle, J.E.; Stohlgren, T.J.; Schnase, J.L. A tamarisk habitat suitability map for the continental United States. Front. Ecol. Environ 2006, 4, 11–17. [Google Scholar]
- McPherson, J.M.; Jetz, W. Effects of species’ ecology on the accuracy of distribution models. Ecography 2007, 30, 135–151. [Google Scholar]
- Zimmermann, N.E.; Edwards, T.C.; Moisen, G.G.; Frescino, T.S.; Blackard, J.A. Remote sensing-based predictors improve distribution models of rare, early successional and broadleaf tree species in Utah. J. Appl. Ecol 2007, 44, 1057–1067. [Google Scholar]
- Buermann, W.; Saatchi, S.; Smith, T.B.; Zutta, B.R.; Chaves, J.A.; Mila, B.; Graham, C.H. Predicting species distributions across the Amazonian and Andean regions using remote sensing data. J. Biogeogr 2008, 35, 1160–1176. [Google Scholar]
- Hassan, Q.K.; Bourque, C.P.-A. Potential species distribution of Balsam Fir based on the integration of biophysical variables derived with remote sensing and process-based methods. Remote Sens 2009, 1, 393–407. [Google Scholar]
- Peterson, A.T.; Nakazawa, Y. Environmental data sets matter in ecological niche modelling: An example with Solenopsis invicta and Solenopsis richteri. Glob. Ecol. Biogeogr 2008, 17, 135–144. [Google Scholar]
- Prates-Clark, C.D.; Saatchi, S.S.; Agosti, D. Predicting geographical distribution models of high-value timber trees in the Amazon Basin using remotely sensed data. Ecol. Model 2008, 211, 309–323. [Google Scholar]
- Morán-Ordóñez, A.; Suárez-Seoane, S.; Elith, J.; Calvo, L.; de Luis, E. Satellite surface reflectance improves habitat distribution mapping: A case study on heath and shrub formations in the Cantabrian Mountains (NW Spain). Divers. Distrib 2012, 18, 588–602. [Google Scholar]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol 2005, 25, 1965–1978. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ 1979, 8, 127–150. [Google Scholar]
- Tucker, C.J.; Sellers, P.J. Satellite remote sensing for primary production. Int. J. Remote Sens 1986, 7, 1395–1416. [Google Scholar]
- He, K.; Zhang, J. Testing the correlation between species diversity and productivity among global ecoregions, biomes, and biogeographical realms. Ecol. Inform 2009, 4, 93–98. [Google Scholar]
- Tucker, C.J.; Vanpraet, C.; Boerwinkel, E.; Gaston, A. Satellite remote sensing of total dry matter production in the Senegalese Sahel. Remote Sens. Environ 1983, 13, 461–474. [Google Scholar]
- Gleason, H.A. The individualistic concept of the plant association. Bull. Torrey Bot. Club 1926, 53, 7–26. [Google Scholar]
- McIntosh, R.P.; Gleason, H.A. “Individualistic Ecologist” 1882–1975: His contributions to ecological theory. Bull. Torrey Bot. Club 1975, 102, 253–273. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intel. Lab. Syst 2001, 58, 109–130. [Google Scholar]
- Asner, G.P.; Martin, R.E. Spectral and chemical analysis of tropical forests: Scaling from leaf to canopy levels. Remote Sen. Environ 2008, 112, 3958–3970. [Google Scholar]
- Coops, N.C.; Smith, M.L.; Martin, M.E.; Ollinger, S.V. Prediction of Eucalypt foliage nitrogen content from satellite-derived hyperspectral data. IEEE Trans. Geosci. Remote Sens 2003, 41, 1338–1346. [Google Scholar]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and Partial Least Squares regression. Remote Sens. Environ 2003, 86, 542–553. [Google Scholar]
- Kooistra, L.; Salas, E.A.L.; Clevers, J.; Wehrens, R.; Leuven, R.; Nienhuis, P.H.; Buydens, L.M.C. Exploring field vegetation reflectance as an indicator of soil contamination in river floodplains. Environ. Poll 2004, 127, 281–290. [Google Scholar]
- Ollinger, S.V.; Smith, M.L.; Martin, M.E.; Hallett, R.A.; Goodale, C.L.; Aber, J.D. Regional variation in foliar chemistry and N cycling among forests of diverse history and composition. Ecology 2002, 83, 339–355. [Google Scholar]
- Schmidtlein, S.; Feilhauer, H.; Bruelheide, H. Mapping plant strategy types using remote sensing. J. Veg. Sci 2012, 23, 395–405. [Google Scholar]
- Martens, M.; Martens, H. Modified Jack-knife estimation of parameter uncertainty in bilinear modelling by partial least squares regression (PLSR). Food Qual. Pref 2000, 11, 5–16. [Google Scholar]
- Goward, S.N.; Tucker, C.J.; Dye, D.G. North American vegetation patterns observed with the NOAA-7 advanced very high resolution radiometer. Vegetatio 1985, 64, 3–14. [Google Scholar]
- Zhang, X.; Friedl, L.; Schaaf, M.A.; Strahler, A.H. Climate controls on vegetation phenological patterns in northern mid- and high latitudes inferred from MODIS data. Glob. Change Biol 2004, 10, 1133–1145. [Google Scholar]
- Wang, J.; Rich, P.M.; Price, K.P. Temporal responses of NDVI to precipitation and temperature in the central Great Plains, USA. Int. J. Remote Sens 2003, 24, 2345–2364. [Google Scholar]
- Sun, D.; Kafatos, M. Note on the NDVI-LST relationship and the use of temperature-related drought indices over North America. Geophys. Res. Lett 2007, 34, L24406. [Google Scholar]
- Gillespie, T.W. Predicting woody-plant species richness in tropical dry forests: A case study from South Florida, USA. Ecol. Appl 2005, 15, 2737. [Google Scholar]
- Malo, A.R.; Nicholson, S.E. A study of rainfall and vegetation dynamics in the African Sahel using normalized difference vegetation index. J. Arid Environ 1990, 19, 1–24. [Google Scholar]
- Farrar, T.J.; Nicholson, S.E.; Lare, A.R. The influences of soil type on the relationships between NDVI, rainfall, and soil moisture in semiarid Botswana. II. NDVI response to soil moisture. Remote Sens. Environ 1994, 50, 121–133. [Google Scholar]
- Yang, Y.; Yang, L.; Merchant, J.W. An assessment of AVHRR/NDVI–ecoclimatological relations in Nebraska, USA. Int. J. Remote Sens 1997, 18, 2161–2180. [Google Scholar]
- Schultz, P.A.; Halpert, M.S. Global correlation of temperature, NDVI and precipitation. Adv. Space Res 1993, 13, 277–280. [Google Scholar]
- Easterling, D.R.; Peterson, T.C.; Karl, T.R. On the development and use of homogenized climate datasets. J. Clim 1997, 9, 1429–1434. [Google Scholar]
- Landsberg, H.E. The Urban Climate; International Geophysical Series; Academic Press: New York, NY, USA, 1981; Volume 28, p. 275. [Google Scholar]
- Kukla, G.; Gavin, J.; Karl, T.R. Urban warming. J. Climate Appl. Meteor 1986, 25, 1265–1270. [Google Scholar]
- Karl, T.R.; Jones, P.D.; Knight, R.W.; Kukla, G.; Plummer, N.; Razuvayev, V.; Gallo, K.P.; Lindseay, J.; Charlson, R.J.; Peterson, T.C. A new perspective on recent global warming. Bull. Am. Meteorol. Soc 1993, 74, 1007–1023. [Google Scholar]
- Gallo, K.P.; Easterling, D.R.; Peterson, T.C. The influence of land use land cover on climatological values of the diurnal temperature range. J. Clim 1996, 9, 2941–2944. [Google Scholar]
- Geerts, B. Empirical estimation of the monthly-mean daily temperature range. Theor. Appl. Climatol 2003, 74, 145–165. [Google Scholar]
- Sun, D.; Pinker, R.T.; Kafatos, M. Diurnal temperature range over the United States: A satellite view. Geophys. Res. Lett 2006, 33, L05705. [Google Scholar]
- Armitage, R.P.; Kent, M.; Weaver, R.E. Identification of the spectral characteristics of British semi-natural upland vegetation using direct ordination: A case study from Dartmoor, UK. Int. J. Remote Sens 2004, 25, 3369–3388. [Google Scholar]
- Schmidtlein, S.; Zimmermann, P.; Schüpferling, R.; Weiß, C. Mapping the floristic continuum: Ordination space position estimated from imaging spectroscopy. J. Veg. Sci 2007, 18, 131–140. [Google Scholar]
- Feilhauer, H.; Oerke, E.C.; Schmidtlein, S. Quantifying empirical relations between planted species mixtures and canopy reflectance with PROTEST. Remote Sens. Environ 2010, 114, 1513–1521. [Google Scholar]
- Guisan, A.; Lehmann, A.; Ferrier, S.; Aspinall, R.; Overton, R.; Austin, M.P.; Hastie, T. Making better biogeographic predictions of species distribution. J. Appl. Ecol 2006, 43, 386–392. [Google Scholar]
- Kissling, W.D.; Carl, G. Spatial autocorrelation and the selection of simultaneous autoregressive models. Glob. Ecol. Biogeogr 2008, 17, 59–71. [Google Scholar]
- Legendre, P. Spatial autocorrelation: Trouble or new paradigm? Ecology 1993, 74, 1659–1673. [Google Scholar]
- Diniz-Filho, J.A.F.; Bini, L.M.; Hawkins, B.A. Spatial autocorrelation and red herrings in geographical ecology. Glob. Ecol. Biogeogr 2003, 12, 53–64. [Google Scholar]
- Dormann, C. Effects of incorporating spatial autocorrelation into the analysis of species distribution data. Ecography 2007, 16, 129–138. [Google Scholar]
- Barthlott, W.; Hostert, A.; Kier, G.; Küper, W.; Kreft, H.; Mutke, J.; Rafiqpoor, M.D.; Sommer, J.H. Geographic patterns of vascular plant diversity at continental to global scales. Erdkunde 2007, 61, 305–315. [Google Scholar]
- Kier, G.; Mutke, J.; Dinerstein, E.; Ricketts, T.H.; Kuper, W.; Kreft, H.; Barthlott, W. Global patterns of plant diversity and floristic knowledge. J. Biogeogr 2005, 32, 1107–1116. [Google Scholar]
- Pulliam, H.R. On the relationship between niche and distribution. Ecol. Lett 2000, 3, 349–361. [Google Scholar]
- Andrew, M.E.; Ustin, S.L. The role of environmental context in mapping invasive plants with hyperspectral image data. Remote Sens. Environ 2008, 112, 4301–4317. [Google Scholar]
- Underwood, E.; Ustin, S.; Dipietro, D. Mapping non-native plants using hyperspectral imagery. Remote Sens. Environ 2003, 86, 150–161. [Google Scholar]
- Araújo, M.B.; Guisan, A. Five (or so) challenges for species distribution modelling. J. Biogeogr 2006, 33, 1677–1688. [Google Scholar]





| Variable | Description | Unit |
|---|---|---|
| Tma | Annual mean temperature | °C |
| DRm | Mean diurnal temperature range (mean of monthly (max temp - min temp)) | °C |
| TS | Temperature Seasonality (standard deviation of temperatures) | °C |
| Tmaxwm | Maximum temperature of the warmest month | °C |
| Tmincm | Minimum temperature of the coldest month | °C |
| TRa | Temperature annual range (Tmaxwm − Tmincm) | °C |
| I | Isothermality (DRm/TRa) | - |
| Tmwtq | Mean temperature of wettest quarter | °C |
| Tmdq | Mean temperature of driest quarter | °C |
| Tmwq | Mean temperature of warmest quarter | °C |
| Tmcq | Mean temperature of coldest quarter | °C |
| Pa | Annual precipitation | mm |
| Pwtm | Precipitation of the wettest month | mm |
| Pdm | Precipitation of the driest month | mm |
| PS | Precipitation seasonality (coefficient of variation) | mm−1 |
| Pwtq | Precipitation of the wettest quarter | mm |
| Pdq | Precipitation of the driest quarter | mm |
| Pwm | Precipitation of the warmest quarter | mm |
| Pcq | Precipitation of the coldest quarter | mm |
| Tma | Pa | DRm | |
|---|---|---|---|
| PC1 | 0.89*** | −0.31*** | −0.30*** |
| PC2 | 0.29*** | −0.66*** | 0.40*** |
| PC3 | −0.17* | 0.19* | 0.04ns |
Share and Cite
Feilhauer, H.; He, K.S.; Rocchini, D. Modeling Species Distribution Using Niche-Based Proxies Derived from Composite Bioclimatic Variables and MODIS NDVI. Remote Sens. 2012, 4, 2057-2075. https://doi.org/10.3390/rs4072057
Feilhauer H, He KS, Rocchini D. Modeling Species Distribution Using Niche-Based Proxies Derived from Composite Bioclimatic Variables and MODIS NDVI. Remote Sensing. 2012; 4(7):2057-2075. https://doi.org/10.3390/rs4072057
Chicago/Turabian StyleFeilhauer, Hannes, Kate S. He, and Duccio Rocchini. 2012. "Modeling Species Distribution Using Niche-Based Proxies Derived from Composite Bioclimatic Variables and MODIS NDVI" Remote Sensing 4, no. 7: 2057-2075. https://doi.org/10.3390/rs4072057
APA StyleFeilhauer, H., He, K. S., & Rocchini, D. (2012). Modeling Species Distribution Using Niche-Based Proxies Derived from Composite Bioclimatic Variables and MODIS NDVI. Remote Sensing, 4(7), 2057-2075. https://doi.org/10.3390/rs4072057