Application of Semi-Automated Filter to Improve Waveform Lidar Sub-Canopy Elevation Model
Abstract
:1. Introduction
2. Materials and Methods
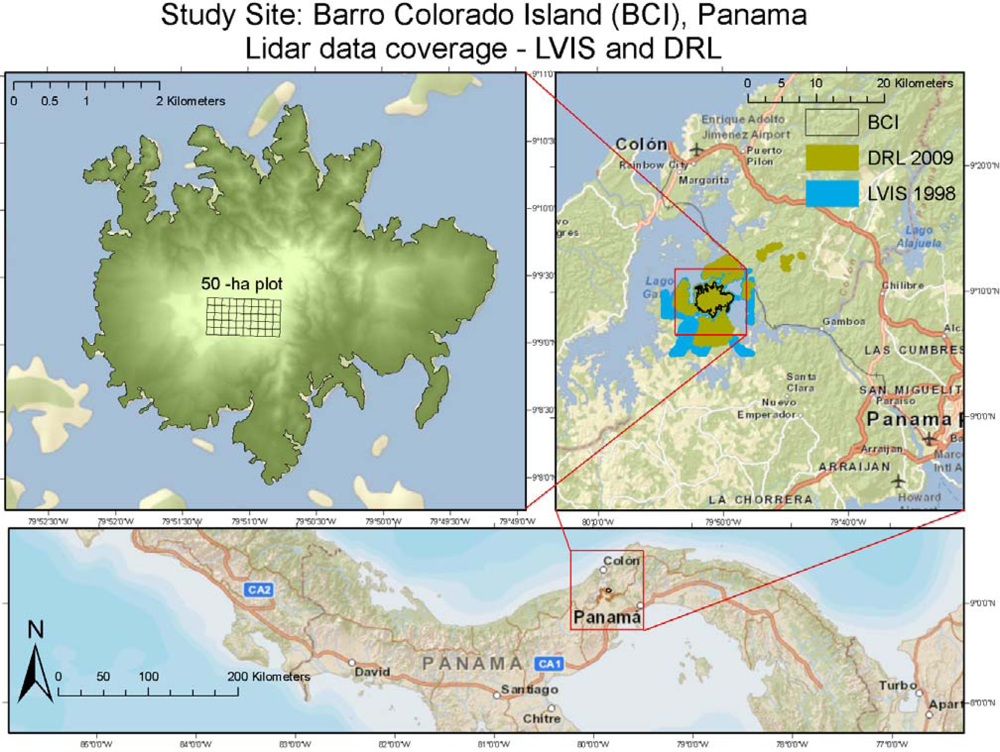
2.1. Study Area and Field Data
2.2. Lidar Data
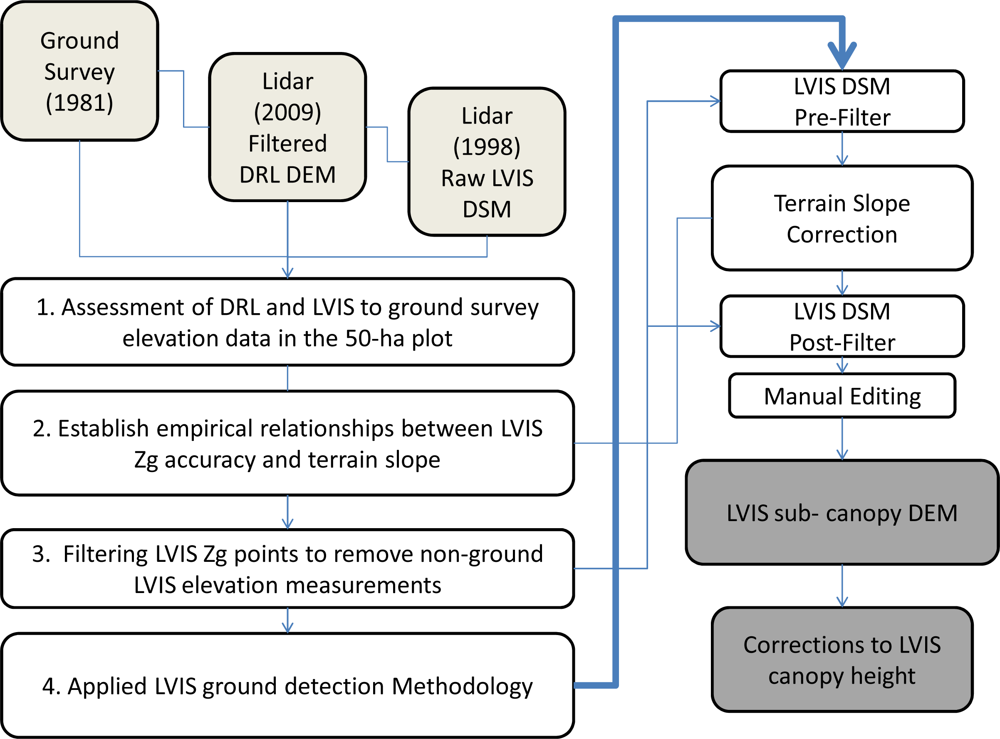
2.3. Methodology
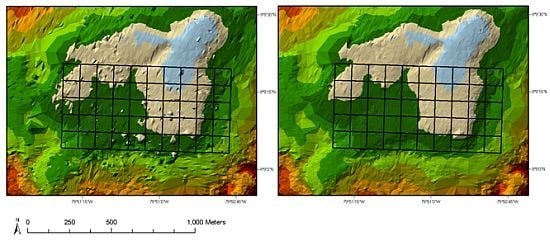
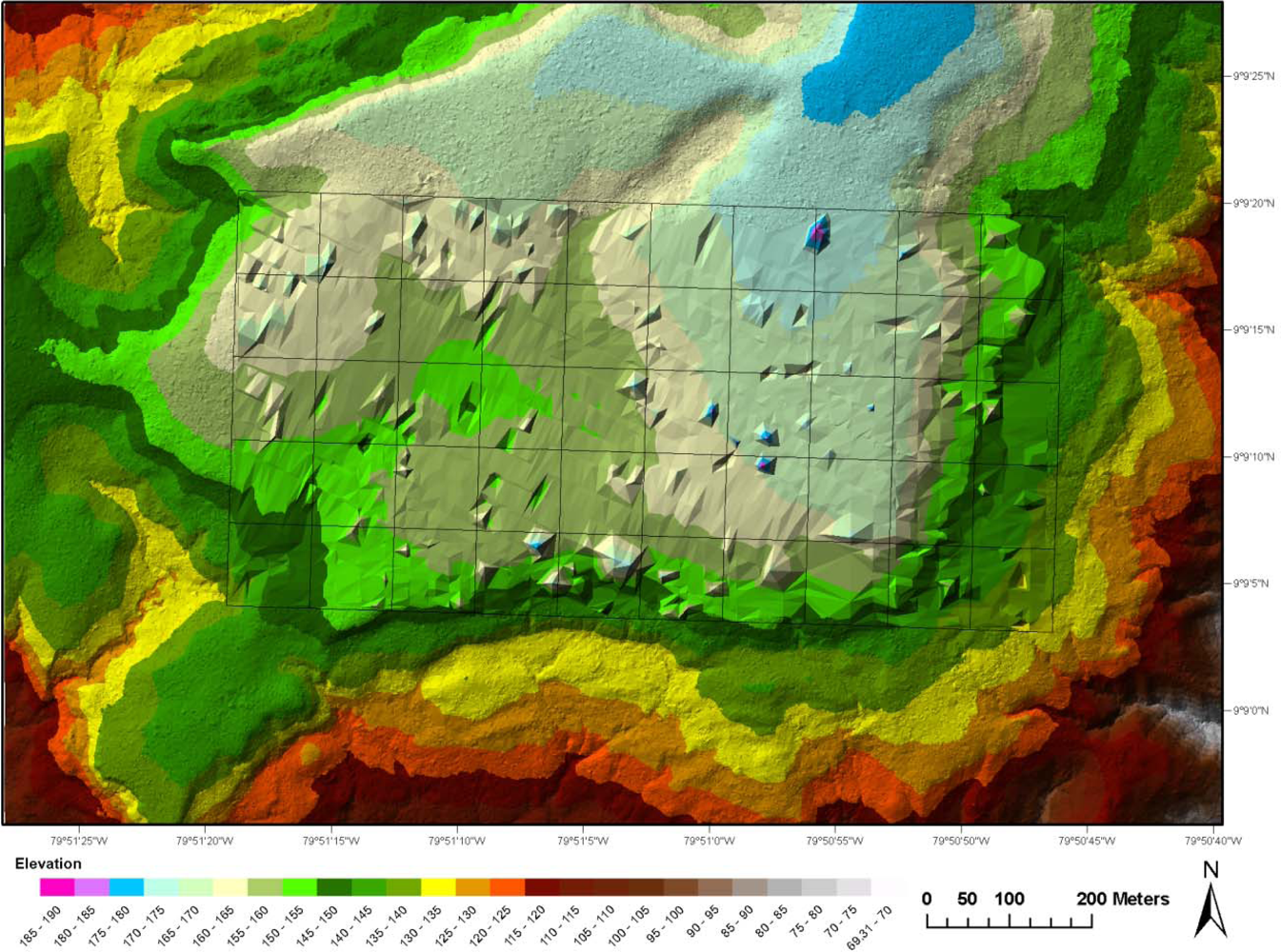
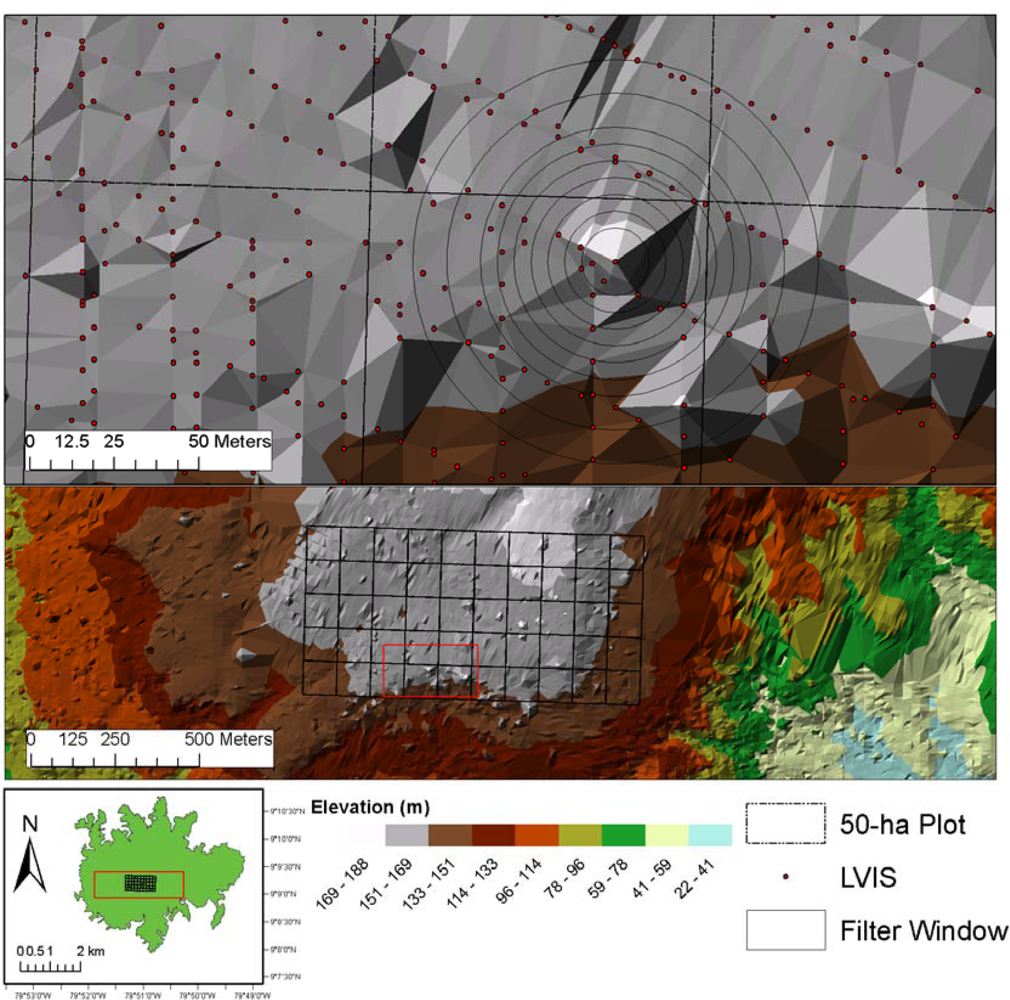
2.3.1. Assessment of DRL and LVIS to Ground Survey Elevations in the 50-ha Plot
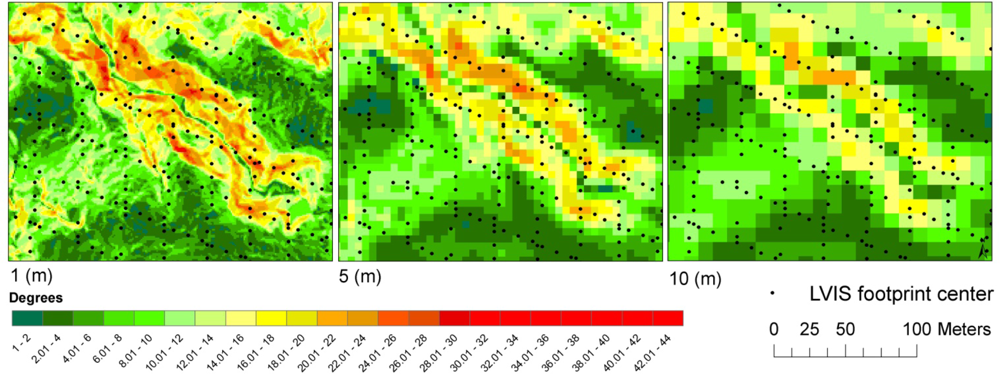
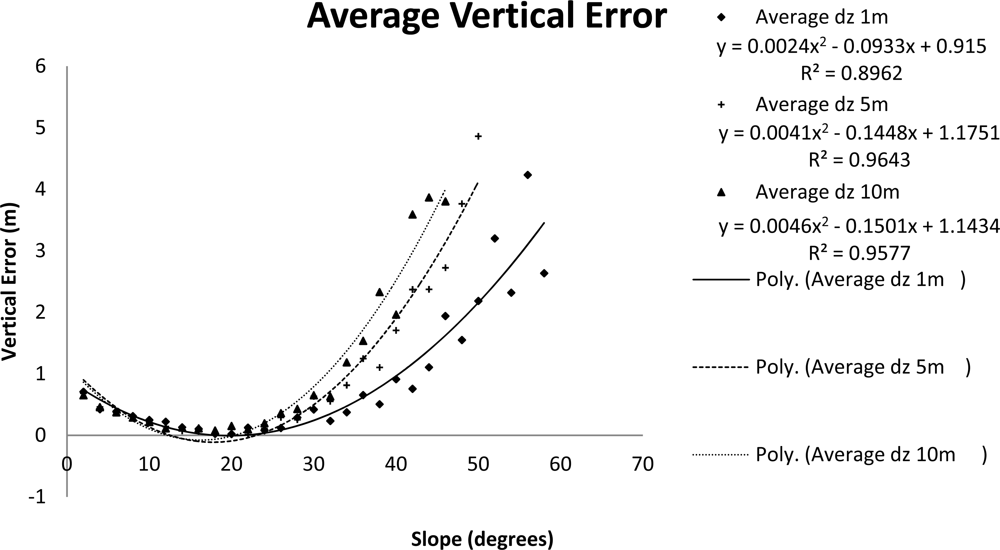
2.3.2. Establishing Empirical Relationships between LFL Zg Accuracy and Terrain Slope and Applying Slope Dependent Elevation Adjustments
2.3.3. Filtering LVIS Zg Points to Remove Non-Ground LVIS Elevation Measurements
2.3.4. Applied LVIS Ground Detection Methodology
3. Results and Discussion
3.1. Assessment of DRL and LVIS to Ground Survey Elevations in the 50-ha Plot
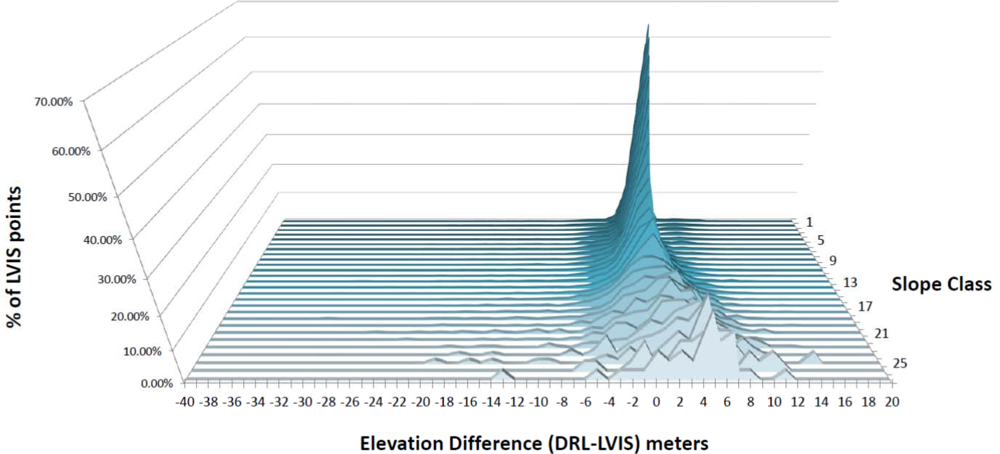
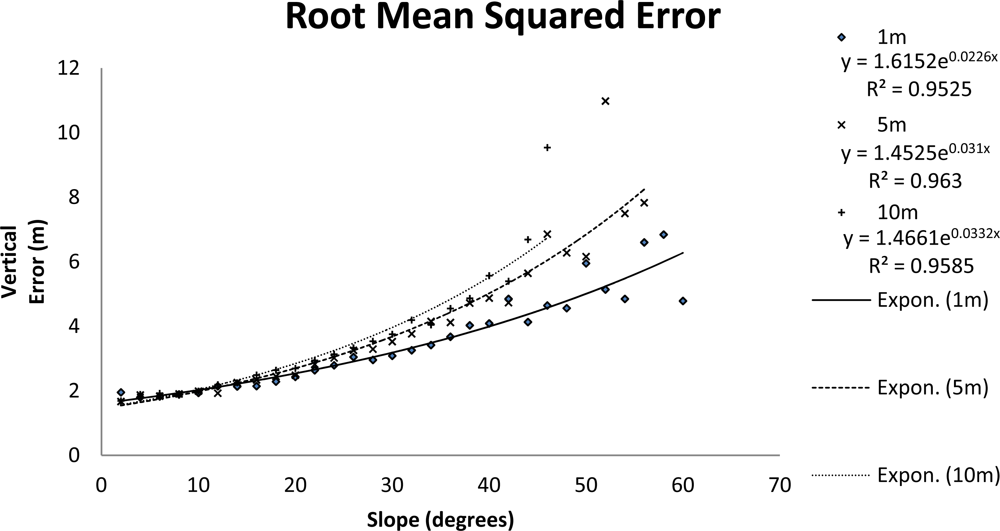
3.2. Establishing Empirical Relationships between Terrain Slope and LVIS LFL Zg Vertical Accuracy
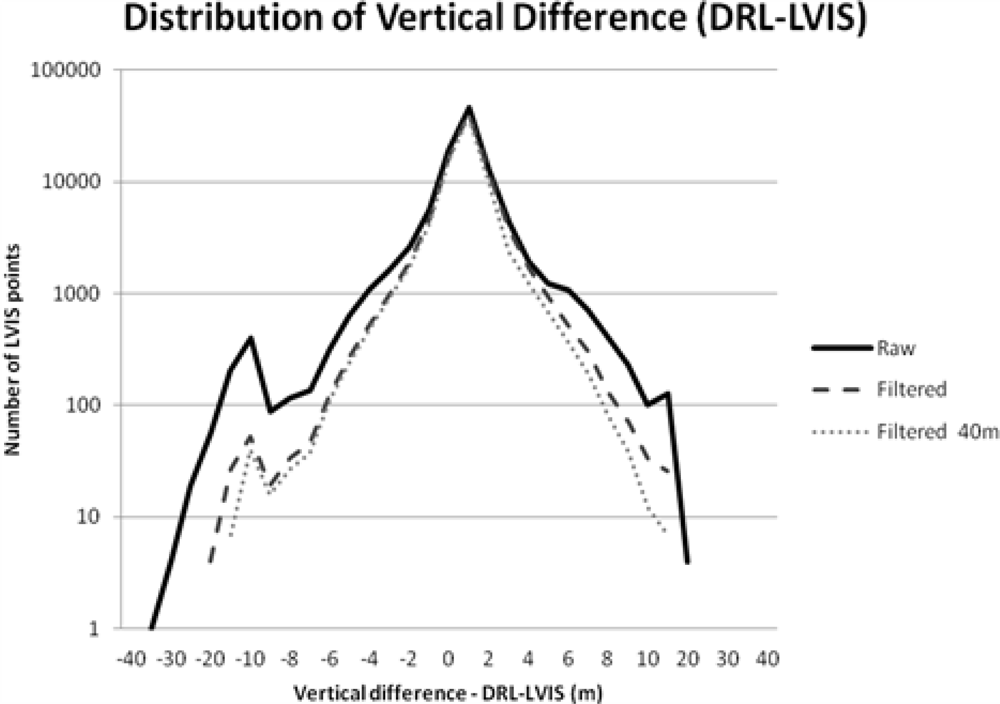
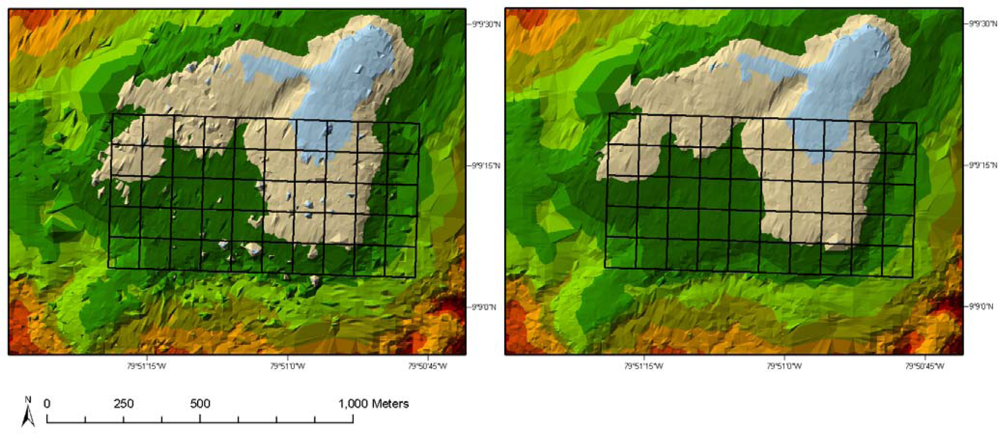
3.3. Filtering of LVIS Zg Elevation Data
4. Conclusions
Acknowledgments
References
- Ranson, K.J.; Sun, G. Mapping biomass of a northern forest using multifrequency SAR data. IEEE Trans. Geosci. Remote Sens 1994, 32, 388–396. [Google Scholar]
- Imhoff, M.L. Radar backscatter and biomass saturation: Ramifications for global biomass inventory. IEEE Trans. Geosci. Remote Sens 1995, 33, 511–518. [Google Scholar]
- Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: Making redd a reality. Environ. Res. Lett 2007, 2, 045023. [Google Scholar]
- Asner, G.; Mascaro, J.; Muller-Landau, H.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; Hall, J.; van Breugel, M. A universal airborne lidar approach for tropical forest carbon mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar remote sensing for ecosystem studies. BioScience 2002, 52, 19–30. [Google Scholar]
- Turner, W.; Spector, S.; Gardiner, N.; Fladeland, M.; Sterling, E.; Steininger, M. Remote sensing for biodiversity science and conservation. Trends Ecol. Evol 2003, 18, 306–314. [Google Scholar]
- Blair, J.B.; Rabine, D.L.; Hofton, M.A. The laser vegetation imaging sensor: A medium-altitude, digitisation-only, airborne laser altimeter for mapping vegetation and topography. ISPRS J. Photogramm 1999, 54, 115–122. [Google Scholar]
- Sheng, Y. Quantifying the size of a lidar footprint: A set of generalized equations. IEEE Geosci. Remote Sens. Lett 2008, 5, 419–422. [Google Scholar]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci 2011, 108, 9899–9904. [Google Scholar]
- Lefsky, M.A. A global forest canopy height map from the moderate resolution imaging spectroradiometer and the geoscience laser altimeter system. Geophys. Res. Lett 2010, 37, L15401. [Google Scholar]
- Simard, M.; Zhang, K.; Rivera-Monroy, V.H.; Ross, M.S.; Ruiz, P.L.; Castaneda-Moya, E.; Twilley, R.R.; Rodriguez, E. Mapping height and biomass of mangrove forests in everglades national park with srtm elevation data. Photogramm. Eng. Remote Sensing 2006, 72, 299–311. [Google Scholar]
- Harding, D.J.; Carabajal, C.C. IceSat waveform measurements of within-footprint topographic relief and vegetation vertical structure. Geophys. Res. Lett 2005, 32, L21S10. [Google Scholar]
- Lefsky, M.A.; Keller, M.; Pang, Y.; De Camargo, P.B.; Hunter, M.O. Revised method for forest canopy height estimation from geoscience laser altimeter system waveforms. J. Appl. Remote Sens 2007, 1, 013537–013518. [Google Scholar]
- Carabajal, C.C.; Harding, D.J.; Suchdeo, V.P. IceSat Lidar and Global Digital Elevation Models: Applications to DesDyni. Proceedings of 2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 1907–1910.
- Chen, Q. Assessment of terrain elevation derived from satellite laser altimetry over mountainous forest areas using airborne lidar data. ISPRS J. Photogramm 2010, 65, 111–122. [Google Scholar]
- Dubayah, R.O.; Drake, J.B. Lidar remote sensing for forestry. J. For 2000, 98, 44–46. [Google Scholar]
- Clark, M.L.; Clark, D.B.; Roberts, D.A. Small-footprint lidar estimation of sub-canopy elevation and tree height in a tropical rain forest landscape. Remote Sens. Environ 2004, 91, 68–89. [Google Scholar]
- Asner, G.P.; Hughes, R.F.; Vitousek, P.M.; Knapp, D.E.; Kennedy-Bowdoin, T.; Boardman, J.; Martin, R.E.; Eastwood, M.; Green, R.O. Invasive plants transform the three-dimensional structure of rain forests. Proc. Natl. Acad. Sci 2008, 105, 4519–4523. [Google Scholar]
- Kellner, J.R.; Clark, D.B.; Hubbell, S.P. Pervasive canopy dynamics produce short-term stability in a tropical rain forest landscape. Ecol. Lett 2009, 12, 155–164. [Google Scholar]
- King, D.A. Allometry and life history of tropical trees. J. Trop. Ecol 1996, 12, 25–44. [Google Scholar]
- Drake, J.B.; Knox, R.G.; Dubayah, R.O.; Clark, D.B.; Condit, R.; Blair, J.B.; Hofton, M. Above-ground biomass estimation in closed canopy neotropical forests using lidar remote sensing: Factors affecting the generality of relationships. Global Ecol. Biogeogr 2003, 12, 147–159. [Google Scholar]
- Dubayah, R.; Prince, S.; Jaja, J.; Blair, J.B.; Bufton, J.L.; Knox, R.; Luthcke, S.B.; Clark, D.B.; Weishampel, J.F. The Vegetation Canopy Lidar Mission. Proceedings of Land Satellite Information in the Next Decade II: Sources and Applications, Washington, DC, USA, 2–5 December 1997; pp. 2–5.
- Hofton, M.A.; Rocchio, L.E.; Blair, J.B.; Dubayah, R. Validation of vegetation canopy lidar sub-canopy topography measurements for a dense tropical forest. J. Geodynam 2002, 34, 491–502. [Google Scholar]
- Zhang, K.; Chen, S.-C.; Whitman, D.; Shyu, M.-L.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne lidar data. IEEE Trans. Geosci. Remote Sens 2003, 41, 872–882. [Google Scholar]
- Zhang, K.; Whitman, D. Comparison of three algorithms for filtering airborne lidar data. Photogramm. Eng. Remote Sensing 2005, 71, 313–324. [Google Scholar]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm 2004, 59, 85–101. [Google Scholar]
- Flood, M. Lidar activities and research priorities in the commercial sector. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci 2001, 34, 3–8. [Google Scholar]
- Drake, J.B.; Dubayah, R.O.; Knox, R.G.; Clark, D.B.; Blair, J.B. Sensitivity of large-footprint lidar to canopy structure and biomass in a neotropical rainforest. Remote Sens. Environ 2002, 81, 378–392. [Google Scholar]
- Drake, J.B.; Dubayah, R.O.; Clark, D.B.; Knox, R.G.; Blair, J.B.; Hofton, M.A.; Chazdon, R.L.; Weishampel, J.F.; Prince, S. Estimation of tropical forest structural characteristics using large-footprint lidar. Remote Sens. Environ 2002, 79, 305–319. [Google Scholar]
- Weishampel, J.F.; Blair, J.B.; Knox, R.G.; Dubayah, R.; Clark, D.B. Volumetric lidar return patterns from an old-growth tropical rainforest canopy. Int. J. Remote Sens 2000, 21, 409–415. [Google Scholar]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. Lidar remote sensing of forest structure. Progr. Phys. Geogr 2003, 27, 88–106. [Google Scholar]
- Clark, D.B.; Clark, D.A. Landscape-scale variation in forest structure and biomass in a tropical rain forest. For. Ecol. Manage 2000, 137, 185–198. [Google Scholar]
- Croat, T.B. Flora of Barro Colorado Island; Stanford University Press: Stanford, CA, USA, 1978. [Google Scholar]
- Condit, R. Research in large, long-term tropical forest plots. Trends Ecol. Evol 1995, 10, 18–22. [Google Scholar]
- Condit, R. Tropical Forest Census Plots: Methods and Results from Barro Colorado Island, Panama and a Comparison with Other Plots; Springer: Berlin, Germany, 1998. [Google Scholar]
- Ahmed, R.; Siqueira, P.; Bergen, K.; Chapman, B.; Hensley, S. A Biomass Estimate over the Harvard Forest Using Field Measurements with Radar and Lidar Data. Proceedings of 2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 4768–4771.
- Hubbell, S.P.; Foster, R.B.; O’Brien, S.T.; Harms, K.E.; Condit, R.; Wechsler, B.; Wright, S.J.; de Lao, S.L. Light-gap disturbances, recruitment limitation, and tree diversity in a neotropical forest. Science 1999, 283, 554–557. [Google Scholar]
- Gale, N. The relationship between canopy gaps and topography in a western ecuadorian rain forest1. Biotropica 2000, 32, 653–661. [Google Scholar]
- Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint lidar and hyperspectral sensors. Remote Sens. Environ 2011, 115, 2931–2942. [Google Scholar]
- Raupach, M.R. Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Bound.-Lay. Meteorol 1994, 71, 211–216. [Google Scholar]
- Montgomery, R.A.; Chazdon, R.L. Forest structure, canopy architecture, and light transmittance in tropical wet forests. Ecology 2001, 82, 2707–2718. [Google Scholar]
- Hinsley, S.A.; Hill, R.A.; Gaveau, D.L.A.; Bellamy, P.E. Quantifying woodland structure and habitat quality for birds using airborne laser scanning. Functional Ecology 2002, 16, 851–857. [Google Scholar]
- Birnbaum, P. Canopy surface topography in a French guiana forest and the folded forest theory. Plant Ecology 2001, 153, 293–300. [Google Scholar]
- Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sens. Environ 2005, 96, 375–398. [Google Scholar]
- Hyde, P.; Dubayah, R.; Peterson, B.; Blair, J.B.; Hofton, M.; Hunsaker, C.; Knox, R.; Walker, W. Mapping forest structure for wildlife habitat analysis using waveform lidar: Validation of montane ecosystems. Remote Sens. Environ 2005, 96, 427–437. [Google Scholar]
- Clark, D.B.; Read, J.M.; Clark, M.L.; Cruz, A.M.; Dotti, M.F.; Clark, D.A. Application of 1-m and 4-m resolution satellite data to studies of tree demography, stand structure and land-use classification in tropical rain forest landscapes. Ecol. Appl 2004, 14, 61–74. [Google Scholar]
- West, G.B.; Enquist, B.J.; Brown, J.H. A general quantitative theory of forest structure and dynamics. Proc. Natl. Acad. Sci 2009, 106, 7040–7045. [Google Scholar]
| Low Point Filter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Filtering Iteration | Routine | From | To | Search for | Vertical Threshold (m) | Search Radius (m) | Limit STDEV | Z-Tolerance |
| 1 | ClassifyLow | LVIS_GRND | LVIS_ZG | single point | 2 | 15 | NA | NA |
| 2 | ClassifyLow | LVIS_GRND | LVIS_ZG | single point | 3 | 20 | NA | NA |
| 3 | ClassifyLow | LVIS_GRND | LVIS_ZG | single point | 3 | 25 | NA | NA |
| 4 | ClassifyLow | LVIS_GRND | LVIS_ZG | single point | 3 | 30 | NA | NA |
| 5 | ClassifyLow | LVIS_GRND | LVIS_ZG | single point | 3.5 | 35 | NA | NA |
| 6 | ClassifyLow | LVIS_GRND | LVIS_ZG | group of points | 2 | 15 | NA | NA |
| 7 | ClassifyLow | LVIS_GRND | LVIS_ZG | group of points | 3 | 20 | NA | NA |
| 8 | ClassifyBelow | LVIS_GRND | LVIS_ZG | single point | 3 | NA | 3 | 5 |
| 9 | ClassifyBelow | LVIS_GRND | LVIS_ZG | single point | 4 | NA | 4 | 4 |
| High Point Filter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Filtering Iteration | Routine | From | To | Search for | Vertical Threshold (m) | Search Radius (m) | Points Required | Limit STDEV |
| 1 | ClassifyAir | LVIS_GRND | LVIS_ZG | single point | 2 | 10 | 3 | 1 |
| 2 | ClassifyAir | LVIS_GRND | LVIS_ZG | single point | 3 | 15 | 3 | 1.5 |
| 3 | ClassifyAir | LVIS_GRND | LVIS_ZG | single point | 3 | 20 | 3 | 1.5 |
| 4 | ClassifyAir | LVIS_GRND | LVIS_ZG | single point | 3 | 25 | 4 | 2 |
| 5 | ClassifyAir | LVIS_GRND | LVIS_ZG | single point | 3.5 | 30 | 5 | 2.5 |
| 6 | ClassifyAir | LVIS_GRND | LVIS_ZG | group of points | 2 | 40 | 7 | 2 |
| 7 | ClassifyAir | LVIS_GRND | LVIS_ZG | group of points | 3 | 50 | 15 | 2 |
| 8 | ClassifyAir | LVIS_GRND | LVIS_ZG | single point | 3 | 60 | 20 | 1.5 |
| Iteration | Total Points | Points Removed | % Removed | DRL-Zg | Minimum Change | Maximum | Ave Abs Change Value | RMS | STDEV |
|---|---|---|---|---|---|---|---|---|---|
| Filtered Interior −40 m | 76,056 | 21,984 | 22.42% | 0.33 | −18.26 | 13.57 | 0.986 | 1.505 | 1.469 |
| Filtered Interior −20 m | 81,315 | 16,725 | 17.06% | 0.36 | −18.26 | 13.57 | 1.006 | 1.533 | 1.490 |
| Filtering/Manual Editing | 86,363 | 11,677 | 11.91% | 0.44 | −18.98 | 14.90 | 1.049 | 1.580 | 1.517 |
| Filtered -> Slope | 86,397 | 11,643 | 11.88% | 0.13 | −21.33 | 14.97 | 0.997 | 1.610 | 1.605 |
| Corrected ->Filter | |||||||||
| Slope Corrected -> Filtered | 86,498 | 11,542 | 11.77% | 0.14 | −22.66 | 14.93 | 1.002 | 1.617 | 1.612 |
| Automatic Filtering | 86,806 | 11,234 | 11.46% | 0.42 | −21.06 | 14.90 | 1.067 | 1.645 | 1.589 |
| Manual Editing | 96,144 | 1,896 | 1.93% | 0.34 | −30.76 | 16.38 | 1.193 | 1.928 | 1.898 |
| Raw Interior (−20 m) | 92,074 | 5,966 | 6.09% | 0.22 | −35.68 | 16.38 | 1.289 | 2.309 | 2.298 |
| Raw Interior (−40 m) | 86,063 | 11,977 | 12.22% | 0.18 | −35.68 | 15.04 | 1.277 | 2.314 | 2.307 |
| Raw (Slope Corrected) | 97,788 | 252 | 0.26% | 0.00 | −35.85 | 16.33 | 1.273 | 2.318 | 2.318 |
| Raw | 98,040 | 0 | 0.00% | 0.28 | −35.68 | 16.38 | 1.325 | 2.329 | 2.312 |
Share and Cite
Fricker, G.A.; Saatchi, S.S.; Meyer, V.; Gillespie, T.W.; Sheng, Y. Application of Semi-Automated Filter to Improve Waveform Lidar Sub-Canopy Elevation Model. Remote Sens. 2012, 4, 1494-1518. https://doi.org/10.3390/rs4061494
Fricker GA, Saatchi SS, Meyer V, Gillespie TW, Sheng Y. Application of Semi-Automated Filter to Improve Waveform Lidar Sub-Canopy Elevation Model. Remote Sensing. 2012; 4(6):1494-1518. https://doi.org/10.3390/rs4061494
Chicago/Turabian StyleFricker, Geoffrey A., Sassan S. Saatchi, Victoria Meyer, Thomas W. Gillespie, and Yongwei Sheng. 2012. "Application of Semi-Automated Filter to Improve Waveform Lidar Sub-Canopy Elevation Model" Remote Sensing 4, no. 6: 1494-1518. https://doi.org/10.3390/rs4061494