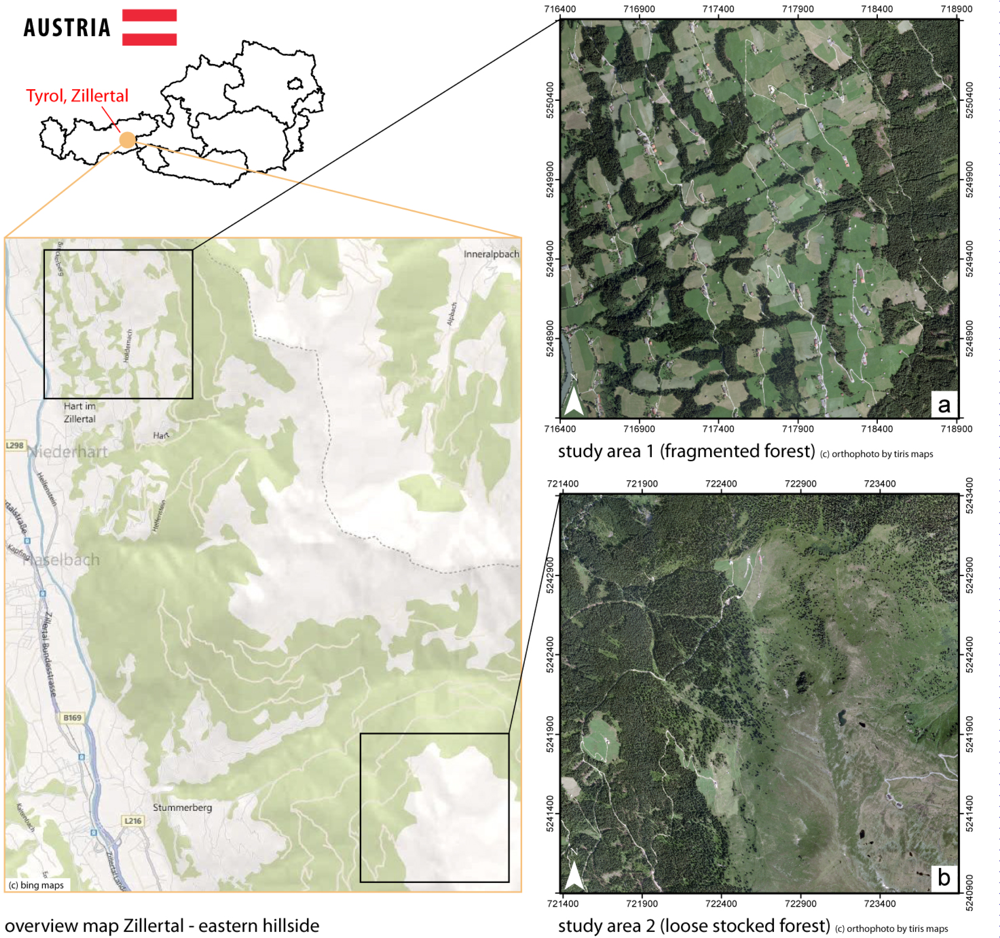
1. Introduction
In recent years, the increasing use of forest products derived from airborne laser scanning (ALS) data as well as many ongoing projects related to this topic show the high demand for this research field. Different products like, e.g., estimated tree heights [
1–
3], growing stock estimations [
4,
5], or forest structure analyses [
6,
7] are of interest for a broad field of applications and users (e.g., forestry, biologists, risk management for natural hazards). An overview of current methods for extracting forest parameters from ALS is given in Hyyppä
et al. [
8]. The results determined from these applications are highly dependent on the fundamental input parameters’ size and position of the delineated forest areas. The delineation of these areas is therefore a crucial task. The size of forested areas is also of interest for governmental authorities (e.g., taxation, financial support of the European Commission) and, in a broader sense, for politics (e.g., greenhouse gases, Kyoto protocol).
The delineation of forests has a long tradition in remote sensing. In the past, mainly aerial images were used for a manual or semi-automated extraction of forested areas. Shadow effects limit this task, particularly for detecting small forest clearings and the exact delineation of forest borders. Additionally, the quality of the results of a manual delineation is subjective and variable between analysts and may lead to inhomogeneous, maybe even incorrect datasets. In particular, in loosely stocked areas, the delineated results show low quality. To classify an area as forest or non-forest, different national forest definitions are available [
9], beside a global definition of the Food and Agriculture Organization of the United Nations (FAO) [
10,
11]. To delineate forested areas, an exact geometric forest definition is required. Unfortunately, the current forest definitions are imprecise in most cases. For example, the criterion of crown coverage (CC) is fundamental and mandatory. With regard to the forest definition given by European Commission, the criterion of minimum area is the second important criterion. CC, also known as vertical canopy coverage [
12], or forest canopy cover, is defined as the proportion of the forest floor covered by the vertical projection of the tree crowns [
13]. Most of the common forest definitions lack precise geometric descriptions for calculating CC (e.g., the reference size and shape for which the amount of projected crown area is calculated). Therefore, the results of current forest delineations are often not comparable and make the CC a doubtful criterion. In recent years, fully automated methods for a forest delineation, based on aerial images or ALS data, have been proposed. They can overcome the limitations of manual delineation in most instances and produce user independent results in short evaluation times.
Radoux
et al. [
14], for example, use different very high resolution multispectral satellite images to delineate forest stands in Belgium. They use an automatic segmentation to delineate homogeneous land cover objects, based on the orthorectified images from IKONOS-2 and SPOT-5. Unfortunately, no criteria of a forest definition are treated.
Mustonen
et al. [
15] evaluate the applicability of a canopy height model (CHM), derived from ALS data, for an automatic segmentation of forest stands in Finland. Additionally, they evaluate a segmentation based on the CHM combined with aerial images. For the delineation of stands based on the CHM, the height information of forest stands is used as a fundamental input. The authors mention that the use of other parameters, such as number of stems per hectare or canopy cover, both derived from ALS, could be an improvement. However, the method of Mustonen
et al. [
15] focuses on delineating forest stands inside forested areas.
Wang
et al. [
16,
17] use aerial images together with ALS data for the automatic delineation of forested areas in Switzerland. They use a green vegetation index, derived from the red and green spatial bands of orthophotos, in combination with a height thresholded canopy height model (CHM), derived from ALS data, to classify forest candidate pixels from the images. In a next step, they apply an image segmentation to find homogeneous, independent regions. By checking the curvature of each segment based on the CHM, forested areas are found. Unfortunately, Wang
et al. do not treat the criterion of CC, which is a mandatory criterion in the Swiss forest definition [
18].
Straub
et al. [
19] delineate forested areas in Germany, based on the normalized digital surface model (nDSM) derived from ALS data. Furthermore, they use point density maps to derive a normalized image, which is thresholded to find areas (pixels) covered by vegetation. Based on these areas, they classify into forest vegetation and non-forest vegetation. For this classification, the criteria height, CC, area and width are used. The reference areas for checking the CC criterion are extracted by intersecting vegetation pixels above 3 m with a grid of 20 × 20 m. In the resulting, individually shaped areas, pixels lower than 5 m in the nDSM are summed. The relation between reference area and summed pixels represents the amount of CC. Regions with a CC value greater than 50% are connected and checked against the minimum area criterion of 1,000 m
2. Finally, the minimum width is checked by “skeletonization” and by analyzing profiles of the resulting areas. Unfortunately, Straub
et al. [
19] do not explain why they use a square shaped grid with a grid size of 20 × 20 m for checking the CC criterion. As discussed in Eysn
et al. [
20], different settings for the grid size lead to different results.
As summarized in the three examples from Finland, Switzerland and Germany, forest is delineated with different methods and parameter settings from ALS data and orthophotos. This is critical because delineation results based on different definitions need to be compared. For example, the Global Forest Resources Assessment (FRA) is based on data (e.g., the amount of forested areas) that countries provide to the FAO in response to a common questionnaire every 5 to 10 years. The FAO analyzes this information and presents the current status of the world’s forest resources and their changes over time [
21]. Because taxation is also strongly related to the amount of forested areas, a clear forest definition and consequently technically correct forest delineation are crucial.
In the approach here presented, the forested areas are automatically delineated, based on ALS data and considering the forest definition of the Austrian national forest inventory (NFI). As shown in Eysn
et al. [
20], different settings for reference size and shape within the CC calculation process lead to different delineation results. Therefore, the focus is laid on implementing the criterion of CC in a comprehensible, geometrically clearly defined way to be able to produce comparable delineation results. The used forest definition is mainly based on the five criteria (1) minimum tree height (2) minimum CC (3) minimum forest area (4) minimum forest area width and (5) land use [
22]. In the approach here presented, criteria one to four are treated.
The remaining parts of this paper are organized as follows: Section 2 describes the selected study areas and the used data. Section 3 describes the methodology and implementation, whereas results are presented and discussed in Section 4. Finally, concluding remarks are given in Section 5. This special issue paper is based on two conference papers by Eysn
et al. [
20,
23].
3. Methods
The delineation of forested areas is commonly a large area application. Performing this task on a pure pointcloud basis would be very extensive because of the large amount of data, which arises when working with high-density laser point data. Therefore, the focus of this work was to develop a method based on the rasterized ALS data. In addition to the ALS point clouds, most of these base products, such as DTM and the digital surface model (DSM), are available with a spatial resolution of 1 × 1 m for all federal states in Austria.
As described in Section 1, only the geometrical criteria of the Austrian NFI (min. area, min. height, min. width and min. crown coverage) are used for the delineation of forested areas. Land use criteria are not considered in this study. It has to be clarified that land use and legal restrictions are in most cases not deducible from ALS data. Other data sources, such as the cadastre, are needed to gather this information. From a hierarchical point of view, the four geometrical criteria of the Austrian NFI have equal rights. To apply these criteria to remote sensed data, a hierarchy has to be defined with respect to a processing chain. For instance, it would make no sense to check the minimum forested area if there is no potential area detected yet. In this approach, the hierarchy is defined as follows: (1) min. height, (2) min. CC, (3) min. area and (4) min. width, whereas (3) and (4) are checked in an iterative process.
3.1. Derived Base Products
In a preliminary working process, two base products were calculated from the pointcloud. The first one is the nDSM, which is derived by subtracting the DTM from the DSM. The nDSM, also known as CHM, is a very suitable product for the delineation of forested areas because it directly shows object heights (e.g., tree heights). In order to process the DSM, a land-cover-dependent derivation approach, described in Hollaus
et al. [
26], was chosen. This approach makes use of the strengths of different algorithms for generating the final DSM by using surface roughness information to combine two DSMs, which are calculated based (i) on the highest echo within a raster cell and (ii) on moving least squares interpolation (
i.e., moving planes interpolation). The second base product is a slope adaptive echo ratio (sER) map, which is calculated, based on the 3D point cloud using FE and LE ALS data. As described in Höfle
et al. [
27,
28], the sER is defined as the ratio between the number of neighboring echoes in a fixed search distance of 1.0 m measured in 3D (a sphere) and all echoes located within the same search distance in 2D (a cylinder). The sER is a measure for local transparency and roughness of the top-most surface and is well suited for the elimination of artificial objects in the forest delineation process (see Section 3.2). The base products derived have a spatial resolution of 1 × 1 m
2 and have been processed consistently for all study areas using the OPALS software [
29].
3.2. Removing Artificial Objects
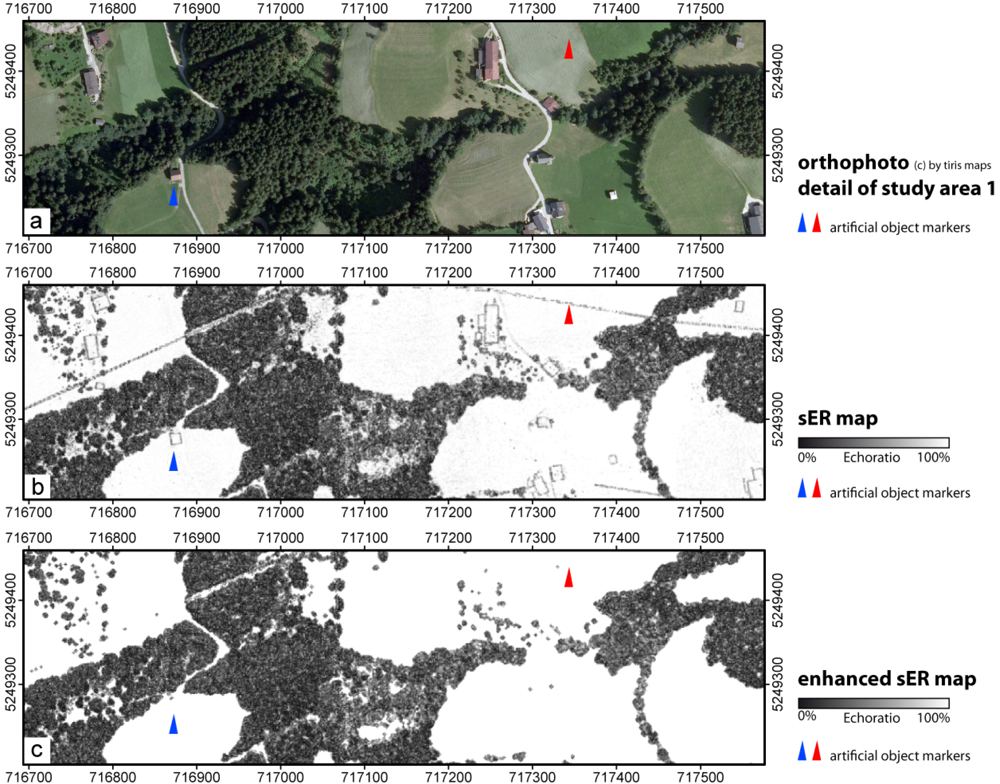
Since all elevated objects, e.g., buildings, forests, power lines and cable cars, are present in the nDSM, a pre-processing step is required to extract a vegetation mask that includes potential forested areas. As shown in previous studies [
27,
30], the sER can be used to differentiate between buildings and forested areas. A sER value of 100% means that the echoes within the 2D search radius describe a planar surface (e.g., roofs), whereas a sER value lower than 100% means that the echoes are vertically distributed within the 2D search area, thus indicating penetrable objects,
i.e., forests. A specialty of the sER is that the outer edges of buildings as well as power lines appear as pixel lines with values lower than 100% in the sER maps (see figure in Section 4.2). This is the case because echoes that are vertically distributed on walls of buildings and in the area of power lines wrongly indicate penetrable objects. Therefore, an empirically determined threshold of 85% is applied to the sER map for eliminating artificial objects. Furthermore, morphological operations (opening, closing) are applied to remove the remaining building borders and power lines. The resulting vegetation mask provides a fundamental input for the delineation of forested areas.
3.3. Minimum Height Criterion
The minimum height criterion is not well defined in the Austrian NFI, since it is dependent on an “in situ reachable tree height”. Depending on this in situ reachable tree height, which obviously has to be defined by user-dependent expert knowledge, the minimum tree height can be set to 2–7 m. Reachable tree heights cannot be obtained from ALS data directly. However, as the goal of this approach is a user independent result, a minimum tree height of 2.0 m is used for the automatic delineation process. The minimum height criterion is applied by height thresholding the nDSM within the vegetation mask.
3.4. Minimum Crown Coverage Criterion
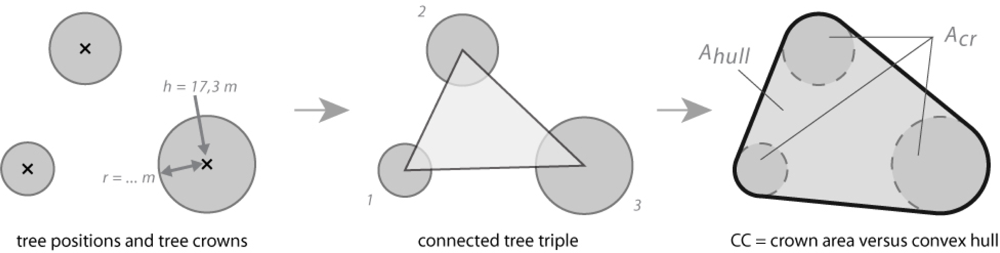
The parameter CC defines the vertically projected crown area of trees within a certain reference area. Current automatic methods for calculating CC maps are commonly based on a moving window approach. The kernel size of the moving window, which defines the reference area, is a fundamental parameter. Since there is no exact definition of the size and the shape of the reference area available in the NFI, different results are derived if different kernel sizes and shapes (e.g., square, circle) are applied [
21]. Another limitation of the moving window approach is that smoothing effects occur at the border of a forest and at small clearings. To overcome these limitations, a new unambiguous approach for determining CC is presented. The method developed aims to define the criterion of CC with a clear geometrical definition, which is based on ALS and NFI data. The basic idea is to express CC as a relation between the sum of the crown areas of three neighboring trees and the area of their convex hull (
Figure 2).
3.4.1. Potential Tree Positions
The potential tree positions are detected with a local maxima filter applied to the nDSM. A circular kernel with an empirically determined size of 5 × 5 m [
23] is used to determine potential tree positions. The chosen properties of the local maxima filter are optimized for trees at the timberline, because those areas are the most critical ones for the CC criterion. The detected positions are restricted, to be found within valid areas of the vegetation mask, as well as within valid areas of the height-thresholded nDSM.
3.4.2. Tree Crown Estimation
The crown radii
Ri are assessed using the following empirical function, describing the relationship between tree height and crown radius:
The input parameters for this function are the tree heights
ti (z-value of the nDSM at the detected potential tree position) and the elevation of the tree
ei (z-value of the DTM at the detected potential tree position). The coefficients
a,
b and
c are calibrated, based on sample crowns. For this calibration the following two possibilities are investigated:
Measurements of crown radii from the NFI are used for the calibration. For this study the function was calibrated for trees near the timberline. Tree crowns, tree heights and elevations of sample trees, measured within multiple field campaigns of the Austrian NFI (Section 2.3), are used to calibrate the coefficients
a,
b and
c in
Equation (1). The calibrated function is applied to the detected tree positions to estimate the crowns for all trees within the study areas.
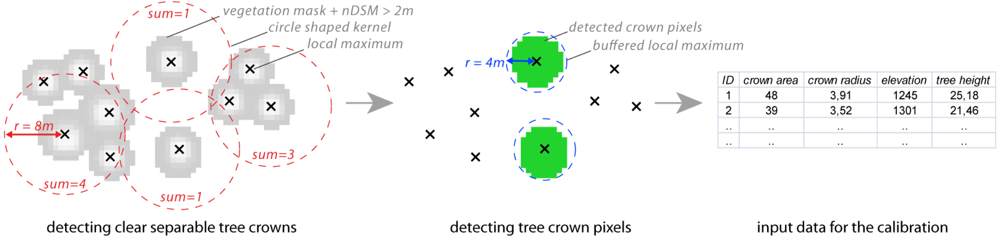
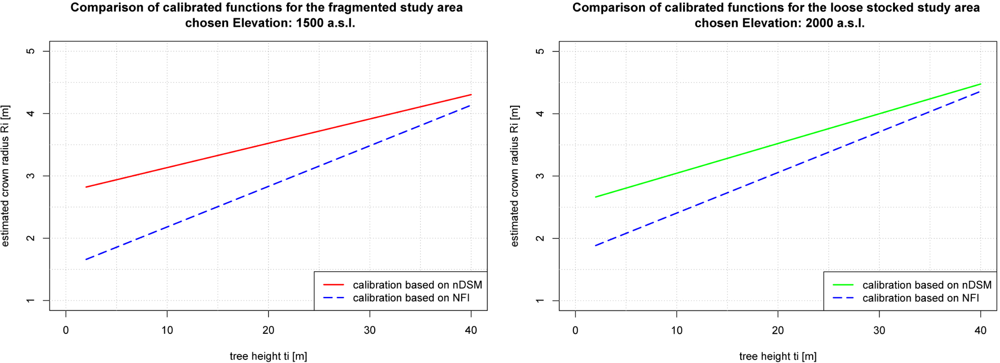
Clearly separable tree crown samples are automatically extracted from the nDSM to calibrate the function. The main idea is to extract only trees which are located at least 8 m away from any other detected tree. The distance of 8 m is empirically determined for the study areas and represents the largest tree crown diameter found in the study areas. Based on the tree crowns of those filtered trees the function is locally calibrated (
Figure 3). The sample trees are detected with a moving window approach, based on a binary raster map of the local maxima. Pixels in the resulting map, where the sum of all pixels within a circular kernel with a radius of 8 m is one, provide positions of trees with a clear, separable crown. The broadest crown diameter is found by applying the NFI calibrated function to the detected local maxima. The positions found are buffered by half of the previously-used kernel size and are intersected with the height thresholded nDSM (nDSM ≥ 2 m) and the vegetation mask. The resulting binary map shows the crown pixels of the identified sample trees. For each tree, the crown area is extracted from the map, and furthermore the average crown radius is derived. Additionally, the tree height and elevation of each sample tree is extracted from the nDSM and the DTM respectively at the position of the corresponding local maximum. For each study area the coefficients of
Equation (1) are estimated by solving the system of linear equations based on the crown radii provided, tree heights and elevations of the sample trees. Finally, for each study area the locally calibrated function is applied to derive the crown radii for all trees.
To validate the estimated crowns for both possibilities, the derived crown areas are compared to the source map. The source map for the calculations is the height-thresholded nDSM (nDSM > 2 m) intersected with the vegetation map. In the source map, all pixels fulfilling the selected threshold are assumed to represent a crown pixel. For each study area the sum of these pixels represents the amount of land covered by tree crowns. To perform a clear validation of the estimated tree crowns, only crown pixels from detected trees should be investigated; otherwise crown pixels of non-detected trees or artificial objects such as buildings and power lines would distort the validation. For that reason the detected local maxima positions are buffered by half of the biggest tree crown diameter found in the study areas to limit the crown pixel to the tree crowns that are represented by detected local maxima. These remaining crown pixels are summed and represent the reference crown area. Furthermore, the areas of the estimated crowns are also summed for each study area and calibration method and compared with the reference crown area.
3.4.3. Tree Triples
To connect three neighboring trees, a Delaunay triangulation is applied to the previously-detected tree positions. Since the nearest neighbor graph is a subgraph of the Delaunay triangulation, the three closest standing trees are connected and the minimum inner angles of the triangles are maximized to provide non-sharp-angled triangles, if possible. Further details on Delaunay triangulations can be found in Fortune [
31] or Isenburg
et al. [
32]. The Delaunay triangulation is calculated using libraries of the software CGAL [
33].
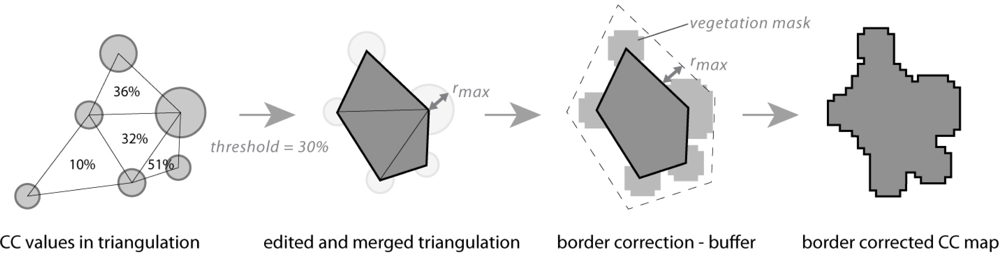
3.4.4. CC Calculation
In a next step, the sum of the crown areas A
cr of three neighboring trees and the area of their convex hull A
hull is calculated for each tree triple. For this purpose, a tool was implemented in Python [
34], which imports a triangulation, calculates the parameters A
cr and A
hull and returns the CC value for each tree triple. For overlapping tree crowns within a tree triple, the area of the union of crowns is used for A
cr. The derived CC values are assigned to their associated triangles. In a next step, the selected CC threshold of 30% is applied to the triangulation and triangles, which do not fulfill the threshold, are removed. As the exported result is an edited triangulation with triangles fulfilling the CC criterion, the borderlines of the derived map represent the tree stem axes and not the convex hulls of the tree triples (
Figure 4). For this reason, a borderline correction is applied by buffering the resulting map by the maximum available crown radius found in the study area. In order to prevent an overestimation of the derived potential forest mask, the buffered area is intersected with the vegetation mask and the resulting areas are added to the valid areas of the edited triangulation. The result of these calculations is a potential forest mask that considers the minimum height criterion as well as the minimum CC criterion.
3.5. Minimum Area Criterion
The minimum area criterion is applied by using standard GIS-queries. The areas of all valid polygons are calculated for the potential forest mask fulfilling the height- and CC-criterion. Firstly, gaps within polygons are checked. If the gap is smaller than 500 m2, the gap is filled. Secondly, the polygons themselves are checked. All polygons that do not fulfill the minimum area criterion of 500 m2 are erased.
3.6. Minimum Width Criterion
The minimum width criterion of 10 m is applied by using morphologic operations (open, close) based on the intermediate result fulfilling the criteria height, CC and area. For this operation, a circular kernel with a radius of 5 pixels (pixel size 1 × 1 m) is used to eliminate narrow forested areas that do not fulfill the criterion. This operation is also related to the area criterion, because the removal of narrow areas leads to changes of the forested areas. Therefore, an iterative process of checking minimum area and width is applied.
3.7. Validation
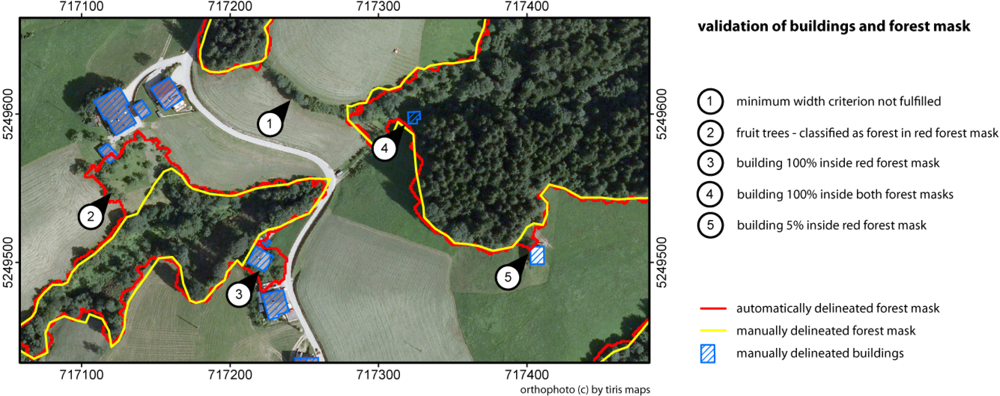
The validation of the final forest mask is performed for the study area 1 (fragmented forest) by comparing the automatically-delineated mask to a reference mask. The reference mask is manually interpreted, based on an orthophoto, using the criteria of the Austrian NFI. The orthophoto was acquired in July 2009 and has a spatial resolution of 0.2 m.
To validate the automatically delineated forest mask with respect to the footprint areas of buildings covered by the forest mask, a building layer is created by manually delineating buildings, based on an orthophoto. Because the acquisition date of the orthophoto differs from the acquisition date of the ALS data, the delineated buildings might be incorrect, or even incomplete, as a result of changes. Therefore, the sER map was used as an additional input within the delineation process to update the building polygons, as necessary. Buildings within densely forested areas might be overgrown and therefore not visible in the orthophoto or sER map. To acquire information about such buildings, the cadastre is used as a third input to gain completeness. For both study areas, the delineated building polygons are intersected with the final forest mask. The remaining building polygons are analyzed.
5. Conclusions
The results of the approach here presented show the high potential of an automatic delineation of forested areas, based on airborne laser scanning and national forest inventory data. The method presented delivers repeatable and objective results. Compared to a manually delineated reference mask, the method presented delivers a Kappa of 0.92 for the fragmented study area. The overall accuracy of 96% obtained shows good agreement with the overall accuracy of 97% obtained by Straub
et al. [
19]. The applied workflow considers the four geometrical criteria of the Austrian national forest inventory. Therefore, the criterion of land use and other special restrictions need to be considered in further investigations. The criterion of land use could be investigated by a combination of high-resolution aerial images or with a cadastre. The ‘tree triples’ approach provides a clearly defined reference size for calculating the crown coverage and overcomes limitations such as smoothing effects or dependency of the kernel size and shape of the moving window approach, especially in loosely stocked forests. The crown coverage value is calculated for each tree triple independently and therefore an interaction with neighboring triples is not considered. A possible improvement of the method presented would be to intersect the triangles of a triangulation of tree positions with a map of the estimated tree crowns. The area of interest for the crown coverage calculation of each triple would then be the triangle connecting three trees, and not the convex hull of the estimated crowns. Since fragments of artificial objects may remain in the vegetation mask, further steps need to be done for the elimination of these fragments. In addition, buildings that have been removed in the vegetation mask may be considered fully or partly as forest if they are surrounded by trees. For example, infrastructure GIS layers or the cadastre could be a sufficient input to tackle these issues. The local maxima detection could be improved, especially for dense forests, by applying a more complex detection method [
35–
37]. The estimation of tree crowns based on the tree height shows consistent results, especially at the upper timberline. The estimation of crowns could be improved by a local calibrated function for mixed and deciduous forests. This could be achieved by using a tree species map, e.g., derived from full-waveform airborne laser scanning data as presented by Hollaus
et al. [
30]. Further investigations in optimizing the local calibration of the function based on the normalized digital surface model need to be done. A different approach for assessing the tree crowns could be based on a segmentation of the crowns, e.g., based on the normalized digital surface model [
38–
40]. However, acquiring reference measurements from field data for large areas as well as the manual orthophoto interpretation is still challenging. Therefore, the reliable and fully automatic method presented for delineating forested areas from airborne laser scanning data provides a beneficial tool for operational applications. Finally, we recommend extending the available forest definitions with clear geometric definitions of the parameter crown coverage. In particular, the reference area is often missing in current forest definitions. Due to the new possibilities that are provided by airborne laser scanning data, such geometric definitions can be easily considered within the forest area delineation workflow.