Energy-Aware Adaptive Weighted Grid Clustering Algorithm for Renewable Wireless Sensor Networks
Abstract
1. Introduction
2. Related Work
3. The Preliminary Description of the Problem
3.1. Problem Formulation
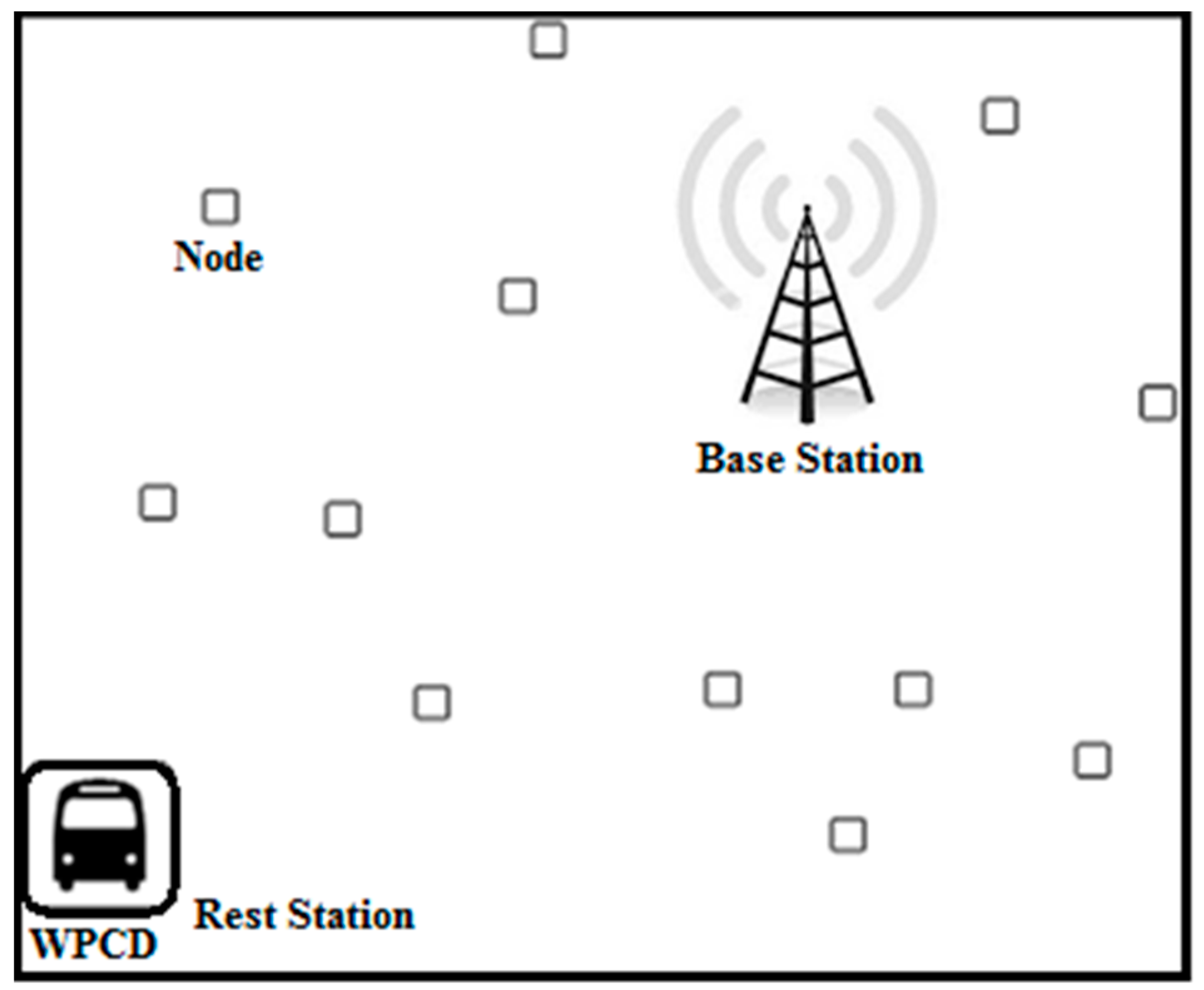
3.2. System Model
- The energy of each node remains equal both at the beginning and at the end of one renewable cycle during the time of τ.
- To make a node operational, the energy of the node is never less than the Emin.
- The WPCD starts its journey from a RS and arrives at node i on the prescribed path using the shortest path algorithm.
- During time τi, the WPCD charges the battery of node i remotely via wireless power transfer technology.
- Then, the WPCD revolves towards the next node to supply power. Finally, it takes a vacation at the RS until the start of the next cycle. Vacation time denoted as τvac, helps the WPCD to energize its battery for the next charge cycle whereas τ is the complete time required for one charge cycle.
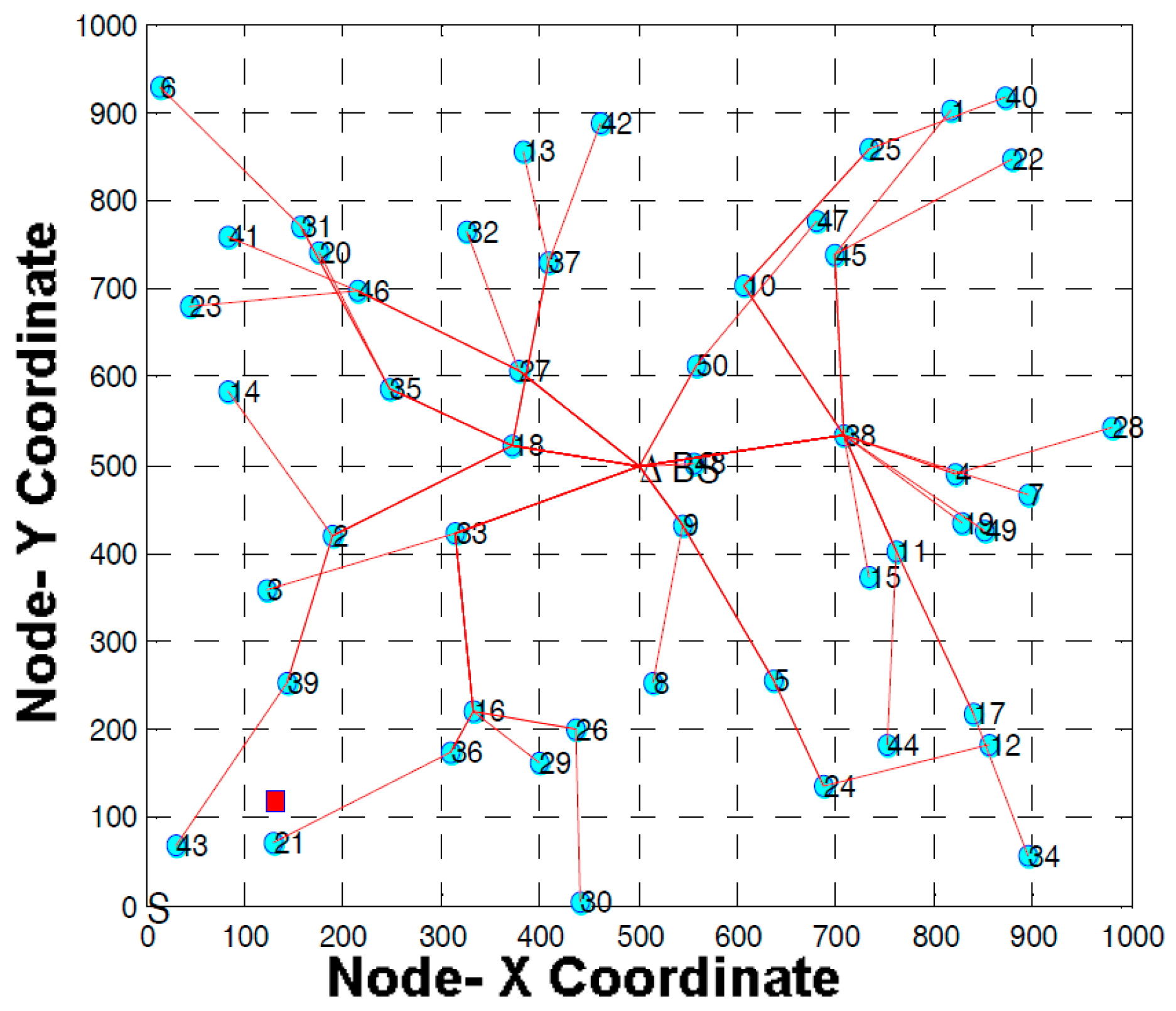
4. Proposed Travelling Path for the WPCD
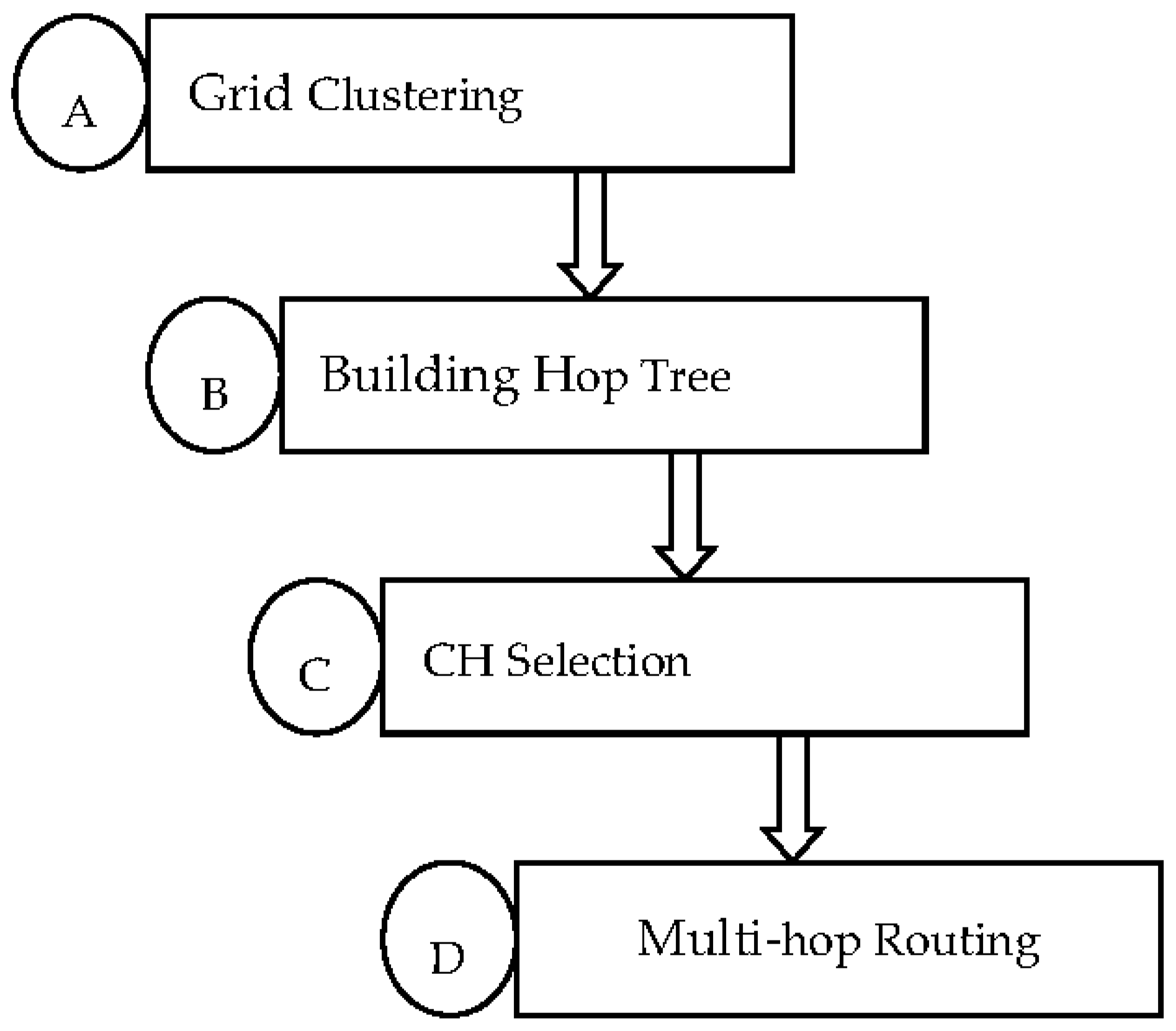
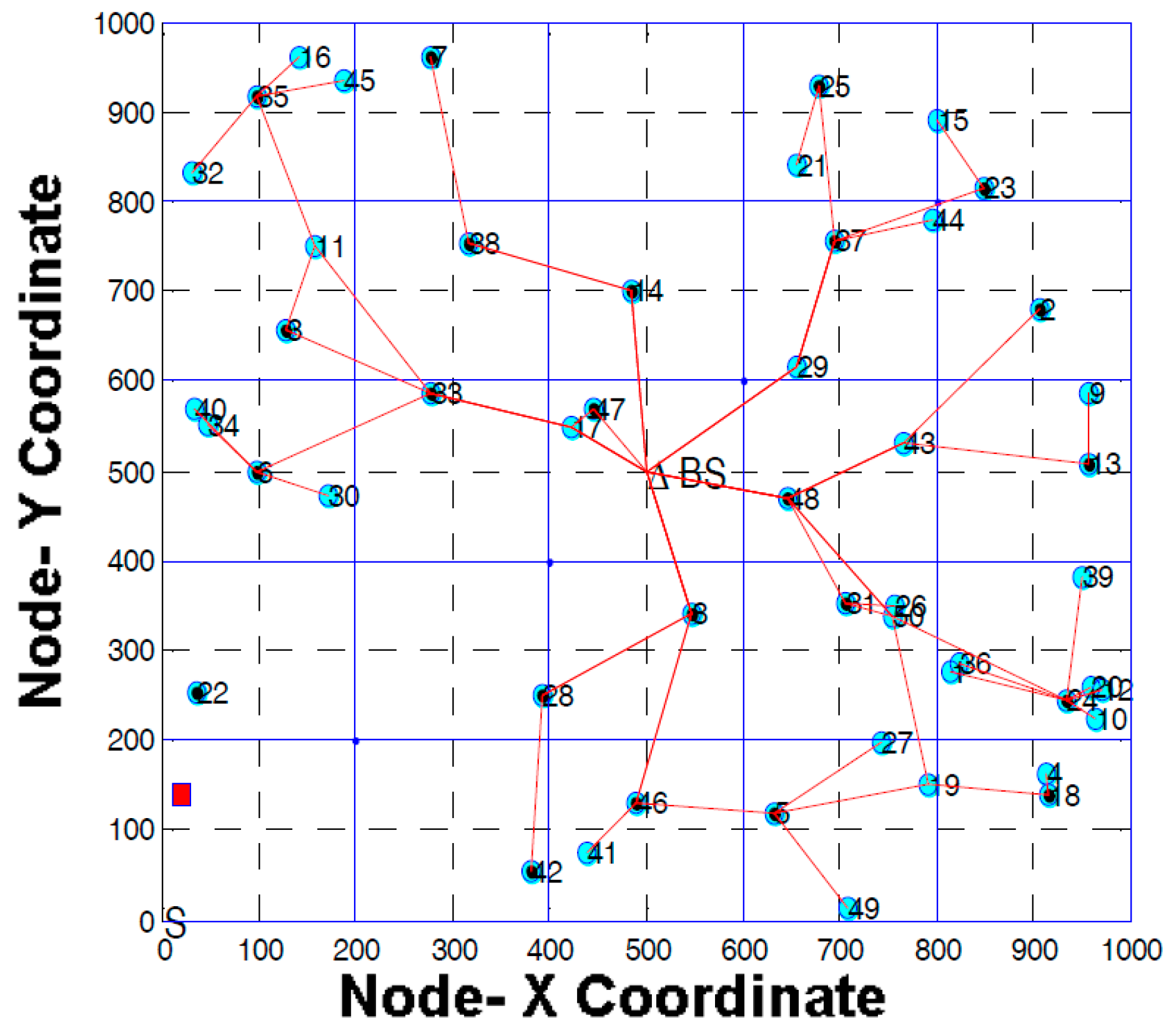
5. Weighted Grid Clustering Algorithm
5.1. Weighted Grid Clustering
- A CH saves energy and space by creating only one routing table for all nodes rather than making an individual routing table for each node as in single-hop routing.
- A CH schedules the activities for all nodes in its specified region. These activities are maintained by broadcasting a message to all the member nodes. This message contains different schedules in which nodes can perform their operations (sending/receiving) with the CH and other nodes as well. After that, nodes can turn on their sleep mode.
5.2. Construction of the Hop Tree
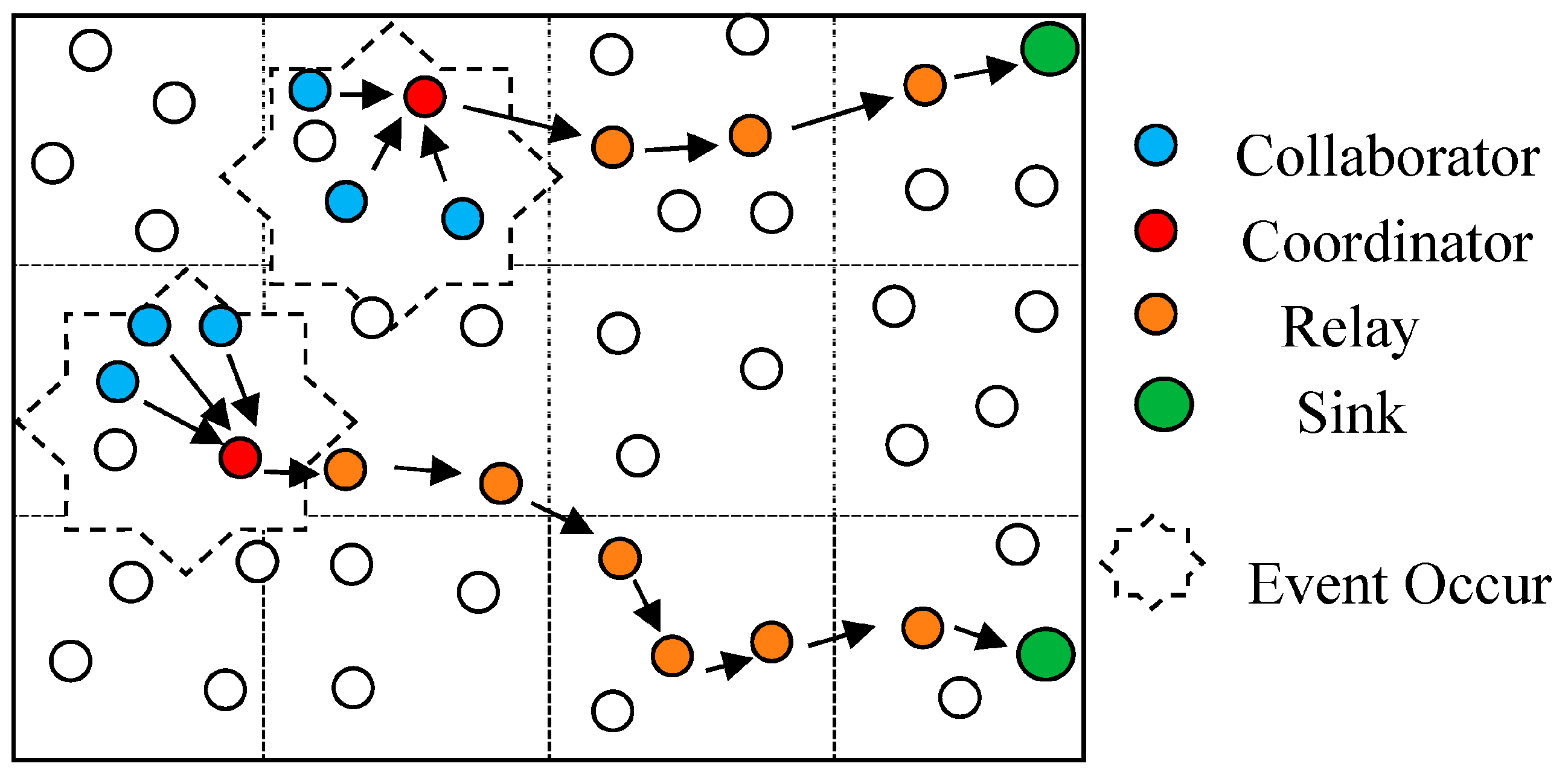
- Sink: A node which is responsible for accumulating data from the following defined coordinator and collaborator nodes.
- Relay: These nodes receive data from the coordinator and forward it to the sink.
- Collaborator: If there is some data from any node, then these nodes are responsible for sending this data towards the coordinator.
- Coordinator: This node accumulates all the data from the collaborator and sends the result towards the sink. These roles of the sensor nodes are shown in Figure 3.
| Algorithm 1. Building of the Hop Tree |
|
5.3. Selection of Cluster Heads
| Algorithm 2. Selection of a Cluster Head among Clusters |
|
5.4. Multi-Hop Routing
- Inter cluster data routing
- Intra cluster data routing
| Algorithm 3. Multi-hop routing and Hop Tree update |
|
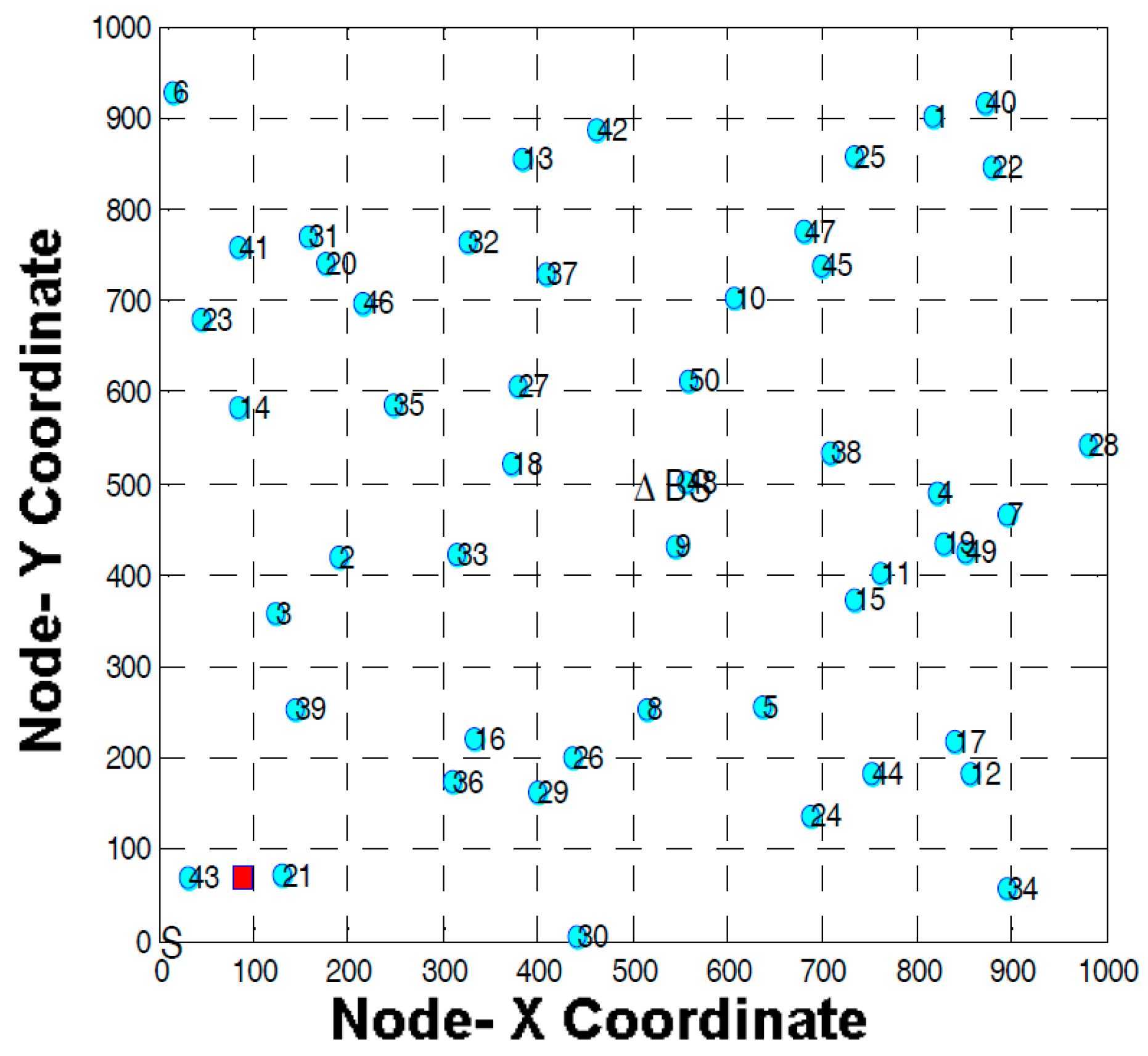
6. Simulation and Performance Assessment
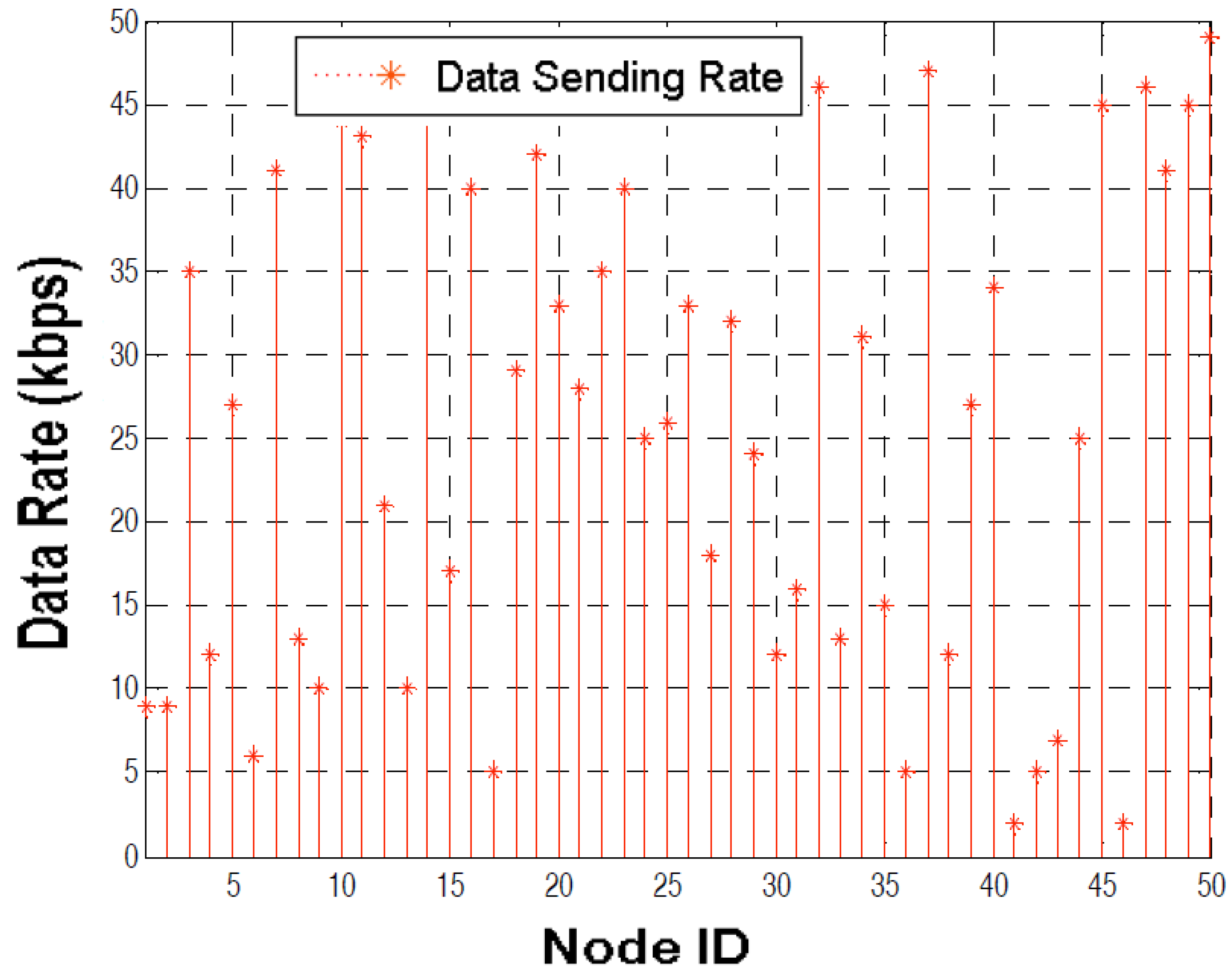
6.1. Simulation Environment
- Emax = 1.2 × 2.5 × 3600 seconds = 10,800 J = 10.8 kj
- Emin = 0.05 × Emax = 540 J = 0.54 kj
- Different types of routing scenario (single-hop and grid clustering)
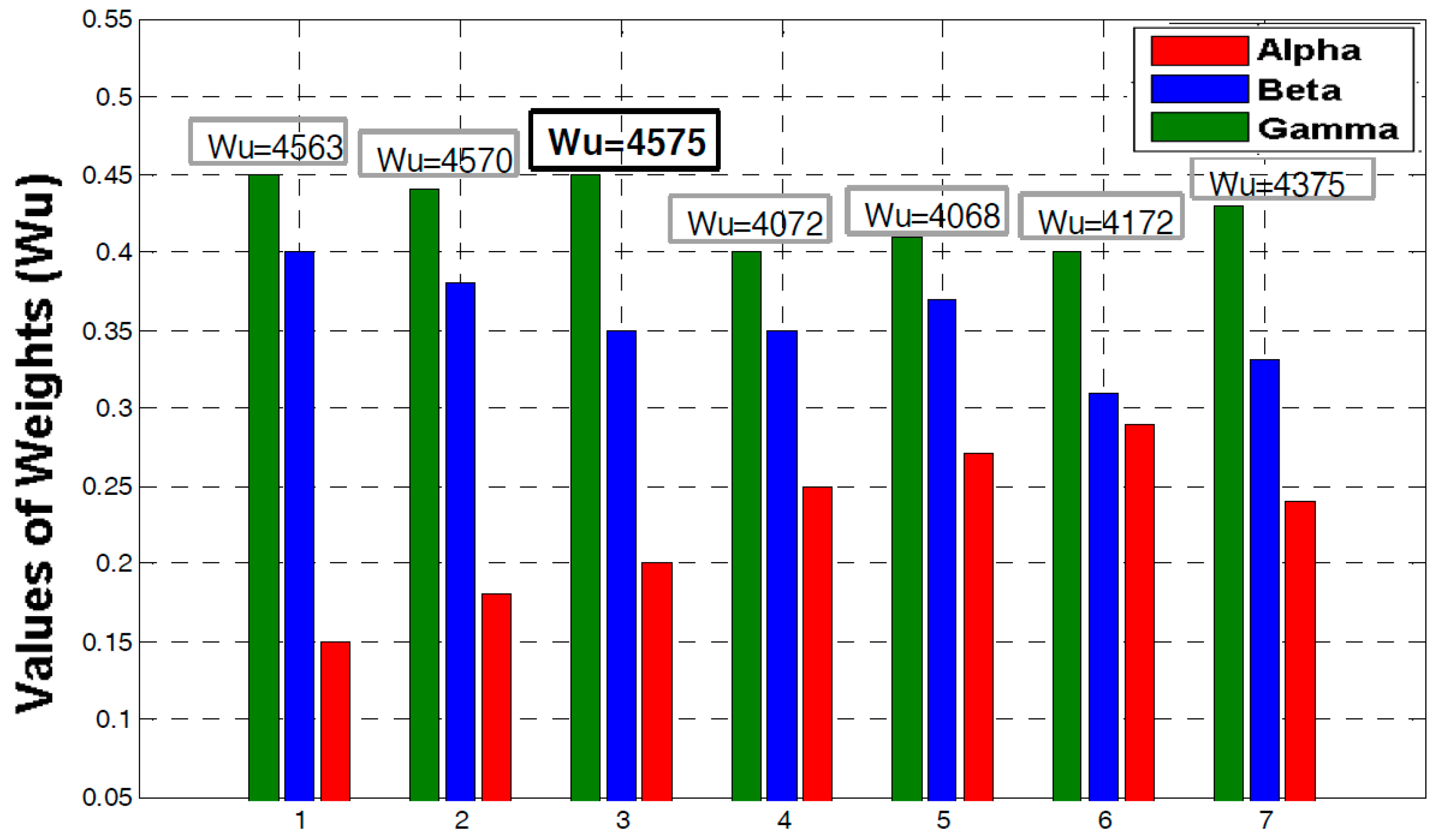
- Diverse values of weighted parameters (α, β and γ are shown in Figure 4)
- Different locations of deployed nodes (11 different cases to compute the mean and variance)
- Considering the special situations of nodes (busy nodes, CH nodes and idle nodes)
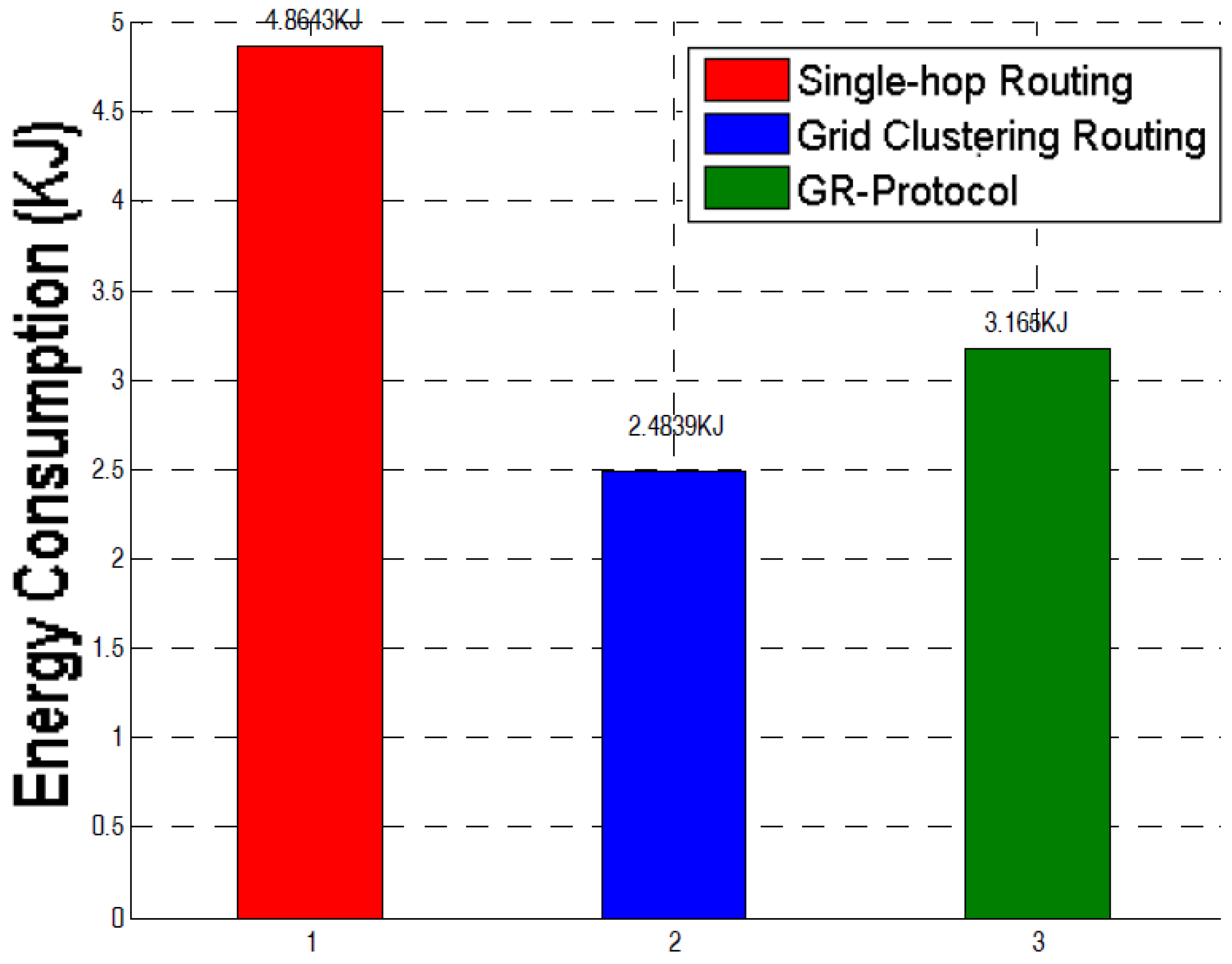
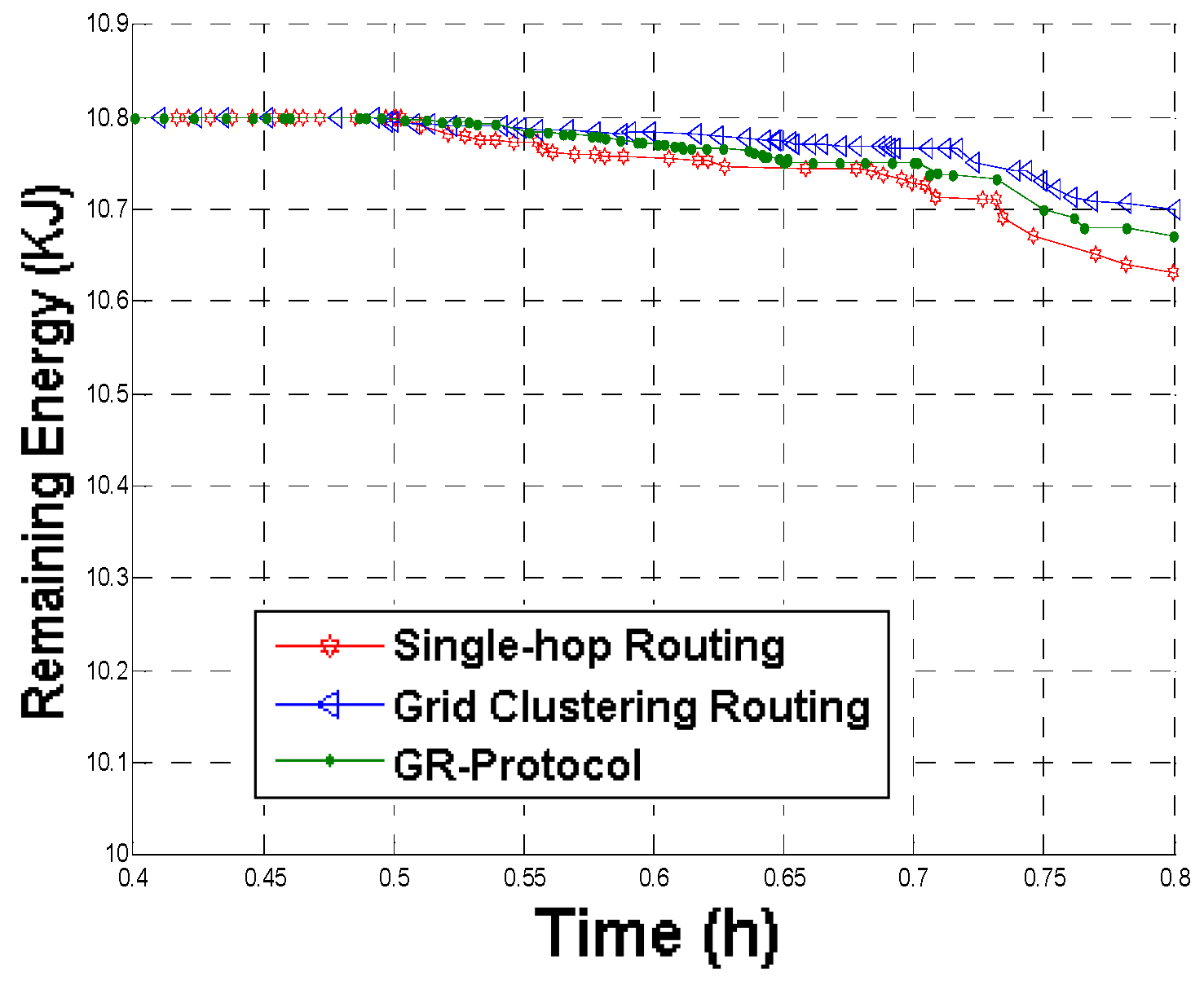
6.2. Results
6.3. Comparative Graphs
7. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mahamuni, C. A military surveillance system based on wireless sensor networks with extended coverage life. In Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, India, 22–24 December 2016. [Google Scholar]
- Luo, H.; Wu, K.; Guo, Z.; Gu, L.; Ni, L. Ship Detection with Wireless Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 1336–1343. [Google Scholar] [CrossRef]
- Ramar, R.; Shanmugasundaram, R. Connected k-Coverage Topology Control for Area Monitoring in Wireless Sensor Networks. Wirel. Pers. Commun. 2015, 84, 1051–1067. [Google Scholar] [CrossRef]
- Yaakob, N.; Khalil, I. A Novel Congestion Avoidance Technique for Simultaneous Real-Time Medical Data Transmission. IEEE J. Biomed. Health Inform. 2016, 20, 669–681. [Google Scholar] [CrossRef] [PubMed]
- Risodkar, Y.; Pawar, A. A survey: Structural health monitoring of bridge using WSN. In Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, India, 22–24 December 2016. [Google Scholar]
- Lazarescu, M. Design of a WSN Platform for Long-Term Environmental Monitoring for IoT Applications. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 45–54. [Google Scholar] [CrossRef]
- Figueiredo, C.M.; Nakamura, E.F.; Ribas, A.D.; de Souza, T.R.; Barreto, R.S. Assessing the communication performance of wireless sensor networks in rainforests. In Proceedings of the 2009 2nd IFIP Wireless Days (WD), Paris, France, 15–17 December 2009; pp. 1–6. [Google Scholar]
- Lara-Cueva, R.; Gordillo, R.; Valencia, L.; Benitez, D. Determining the Main CSMA Parameters for Adequate Performance of WSN for Real-Time Volcano Monitoring System Applications. IEEE Sens. J. 2017, 17, 1493–1502. [Google Scholar] [CrossRef]
- Rotariu, C.; Bozomitu, R.; Cehan, V.; Pasarica, A.; Costin, H. A wireless sensor network for remote monitoring of bioimpedance. In Proceedings of the 2015 38th International Spring Seminar on Electronics Technology (ISSE), Eger, Hungary, 6–10 May 2015. [Google Scholar]
- Wang, P.; Hou, H.; He, X.; Wang, C.; Xu, T.; Li, Y. Survey on Application of Wireless Sensor Network in Smart grid. Procedia Comput. Sci. 2015, 52, 1212–1217. [Google Scholar] [CrossRef]
- Li, R.; Asaeda, H.; Li, J.; Fu, X. A Distributed Authentication and Authorization Scheme for In-Network Big Data Sharing. Digit. Commun. Netw. 2017. [Google Scholar] [CrossRef]
- Razzaque, M.; Dobson, S. Energy-Efficient Sensing in Wireless Sensor Networks Using Compressed Sensing. Sensors 2014, 14, 2822–2859. [Google Scholar] [CrossRef] [PubMed]
- Zaman, N.; Jung, L.T.; Yasin, M. Enhancing Energy Efficiency of Wireless Sensor Network through the Design of Energy Efficient Routing Protocol. J. Sens. 2016, 2016, 1–16. [Google Scholar] [CrossRef]
- Chang, J.H.; Tassiulas, L. Energy conserving routing in wireless ad-hoc networks. In Proceedings of the Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies, INFOCOM ’05, Tel Aviv, Israel, 26–30 March 2000; pp. 22–31. [Google Scholar]
- Li, Q.; Aslam, J.; Rus, D. Online power-aware routing in wireless Ad-hoc networks. In Proceedings of the 7th Annual International Conference on Mobile Computing and Networking, MobiCom ’01, Rome, Italy, 16–21 July 2001; pp. 97–107. [Google Scholar]
- Fan, K.-W.; Zheng, Z.; Sinha, P. Steady and fair rate allocation for rechargeable sensors in perpetual sensor networks. In Proceedings of the 6th ACM conference on Embedded network sensor systems, SenSys ’08, Raleigh, NC, USA, 5–7 November 2008; pp. 239–252. [Google Scholar]
- Meninger, S.; Mur-Miranda, J.; Amirtharajah, R.; Chandrakasan, A.; Lang, J. Vibration-to-electric energy conversion. IEEE Trans. VLSI Syst. 2001, 9, 64–76. [Google Scholar] [CrossRef]
- Kansal, A.; Potter, D.; Srivastava, M.B. Performance aware tasking for environmentally powered sensor networks. In Proceedings of the Joint International Conference on Measurement and Modeling of Computer Systems—SIGMETRICS 2004/Performance 2004, New York, NY, USA, 10–14 June 2004. [Google Scholar]
- Park, C.; Chou, P. AmbiMax: Autonomous Energy Harvesting Platform for Multi-Supply Wireless Sensor Nodes. In Proceedings of the 2006 3rd Annual IEEE Communications Society on Sensor and Ad Hoc Communications and Networks, Reston, VA, USA, 25–28 September 2006. [Google Scholar]
- Tong, B.; Li, Z.; Wang, G.; Zhang, W. On-Demand Node Reclamation and Replacement for Guaranteed Area Coverage in Long-Lived Sensor Networks. In Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering; Quality of Service in Heterogeneous Networks; Springer: Berlin/Heidelberg, Germany, 2009; pp. 148–166. [Google Scholar]
- Tong, B.; Wang, G.; Zhang, W.; Wang, C. Node Reclamation and Replacement for Long-lived Sensor Networks. In Proceedings of the 2009 6th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, Rome, Italy, 22–26 June 2009. [Google Scholar]
- Yang, J.; Ozel, O.; Ulukus, S. Broadcasting with an Energy Harvesting Rechargeable Transmitter. IEEE Trans. Wirel. Commun. 2012, 11, 571–583. [Google Scholar] [CrossRef]
- Klues, K.; Hackmann, G.; Chipara, O.; Lu, C. A component-based architecture for power-efficient media access control in wireless sensor networks. In Proceedings of the 5th International Conference on Embedded Networked Sensor Systems—SenSys ’07, Sydney, Australia, 6–9 November 2007. [Google Scholar]
- Yang, Y.; Wang, C. Wireless Rechargeable Sensor Networks; SpringerBriefs in Electrical and Computer Engineering; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljacic, M. Wireless Power Transfer via Strongly Coupled Magnetic Resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- André, K.; Moffatt, R.; Marin, S. Simultaneous mid-range power transfer to multiple devices. Appl. Phys. Lett. 2010, 96, 044102. [Google Scholar]
- Hassan, M.; Zawawi, A. Wireless power transfer (Wireless lighting). In Proceedings of the 2015 5th International Conference on Information & Communication Technology and Accessibility (ICTA), Marrakech, Morocco, 21–23 December 2015. [Google Scholar]
- Chen, S.-H.; Cheng, Y.-C.; Lee, C.-H.; Wang, S.-P.; Chen, H.-Y.; Chen, T.-Y.; Wei, H.-W.; Shih, W.-K. Extending sensor network lifetime via wireless charging vehicle with an efficient routing protocol. In Proceedings of the SoutheastCon 2016, Norfolk, VA, USA, 30 March–3 April 2016. [Google Scholar]
- Rahimi, M.; Shah, H.; Sukhatme, G.; Heideman, J.; Estrin, D. Studying the feasibility of energy harvesting in a mobile sensor network. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No. 03CH37422), Taipei, Taiwan, 14–19 September 2003. [Google Scholar]
- Shi, Y.; Xie, L.; Hou, Y.T.; Sherali, H.D. On renewable sensor networks with wireless energy transfer. In Proceedings of the IEEE INFOCOM 2011, Shanghai, China, 10–15 April 2011. [Google Scholar]
- Shi, L.; Han, J.; Han, D.; Ding, X.; Wei, Z. The dynamic routing algorithm for renewable wireless sensor networks with wireless power transfer. Comput. Netw. 2014, 74, 34–52. [Google Scholar] [CrossRef]
- Fu, L.; He, L.; Cheng, P.; Gu, Y.; Pan, J.; Chen, J. ESync: Energy Synchronized Mobile Charging in Rechargeable Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2015, 65, 7415–7431. [Google Scholar] [CrossRef]
- Li, S.; Mi, C.C. Wireless Power Transfer for Electric Vehicle Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 4–17. [Google Scholar]
- Chen, S.-H.; Chen, T.-Y.; Cheng, Y.-C.; Wei, H.-W.; Hsu, T.-S.; Shih, W.-K. Developing a user-friendly sensor network simulator to imitate wireless charging vehicle behaviors. In Proceedings of the 2016 International Conference on Computing, Networking and Communications (ICNC), Kauai, HI, USA, 15–18 February 2016. [Google Scholar]
- WiPower | Qualcomm. 2017. Available online: https://www.qualcomm.com/products/wipower (accessed on 5 August 2017).
- Xie, L.; Shi, Y.; Hou, Y.T.; Lou, W.; Sherali, H.D.; Midkiff, S.F. On renewable sensor networks with wireless energy transfer: The multi-node case. In Proceedings of the 2012 9th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Seoul, Korea, 18–21 June 2012. [Google Scholar]
- Kumar, K.S.; Amutha, R. An Algorithm for Energy Efficient Cooperative Communication in Wireless Sensor Networks. KSII Trans. Internet Inf. Syst. 2016, 10, 3080–3099. [Google Scholar]
- Zhuang, Y.; Pan, J.; Wu, G. Energy-optimal grid-based clustering in wireless microsensor networks with data aggregation. Int. J. Parallel Emergent Distrib. Syst. 2010, 25, 531–550. [Google Scholar] [CrossRef]
- Nakade, V.; Chavhan, N. Review on DRINA: An Energy Efficient Routing Approach for Wireless Sensor Networks. In Proceedings of the 2015 Fifth International Conference on Communication Systems and Network Technologies, Gwalior, India, 4–6 April 2015. [Google Scholar]
- MATLAB R2015a Free Download. Download Latest Free Software. [Online]. Available online: https://www.mathworks.com/products.html?s_tid=gn_ps (accessed on 1 September 2016).
- Reddy, T.B. Linden’s Handbook of Batteries, 4th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Rout, R.R.; Krishna, M.S.; Gupta, S. Markov Decision Process-Based Switching Algorithm for Sustainable Rechargeable Wireless Sensor Networks. IEEE Sens. J. 2016, 16, 2788–2797. [Google Scholar] [CrossRef]
- Sun, P.; Li, G.; Wang, F. An Adaptive Back-Off Mechanism for Wireless Sensor Networks. Future Internet 2017, 9, 19. [Google Scholar] [CrossRef]


| Notation | Detail Description of the Notations |
|---|---|
| WPCD | wireless portable charging device |
| RS | rest station |
| BS | base station |
| N | number of nodes in the wireless sensor networks |
| P | path of travel for WPCD |
| Ƥ | the whole set of traveling path for WPCD |
| ACK | route formation acknowledgment message |
| ρ | the coefficient of energy consumption for receiving the data |
| Tm | the whole set of time instances in considering m phase |
| U | the full transfer rate of WPCD |
| V | revolving speed of WPCD |
| ai | time to approach node i by WPCD in the first charge cycle |
| Cij or CiB | energy consumption coefficient for sending data from node i to j and base station alternatively |
| Dij | located distance between node i and j |
| Dp | moving distance for the prescribed path P |
| DTSP | shortest traveled distance in a charge cycle |
| Emax | the maximum energy of a node’s battery |
| Emin | the minimum energy of a node’s battery |
| ei(t) | the energy of sensor node at time t |
| gij(t) or giB(t) | the coefficient for flow rate from node i to j base station respectively |
| Ri | the rate of gathering data by monitoring the environment |
| Ui | power transfer rate at node i in the first charge cycle |
| πi | ith node visited by the WPCD |
| τ | complete time spent by the WPCD in a charge cycle |
| τi | time used by the WPCD to charge the battery of node i |
| τ0 | a time when WPCD is not transferring power to any node |
| τvac | vacation time (time for WPCD to be charge itself) |
| τp | time to travel of WPCD for a path P |
| τTSP | minimum moving time of WPCD in the charge cycle |
| Parameters | Assumed Values |
|---|---|
| Number of nodes | 50 |
| Length | 1000 m |
| Width | 1000 m |
| Emax | 10,800 J |
| Emin | 540 J |
| ρ | 5 × 10−8 J/b |
| Location of BS | [500, 500] m |
| Location of WPCD | [0,0] |
| Speed of WPCD | 5 m/s |
| U | 5 W |
| Antenna | Omni-directional |
| Path Loss | Log Normal Shadowing |
| Routing | Grid-based clustering, Single-hop, GR-Protocol |
| Simulation run time | Almost 1 h |
| Communication radius | 100 m |
| Voltage of battery (NiMH) | 1.2 V |
| Electricity quantity of battery (NiMH) | 2.5 Ah |
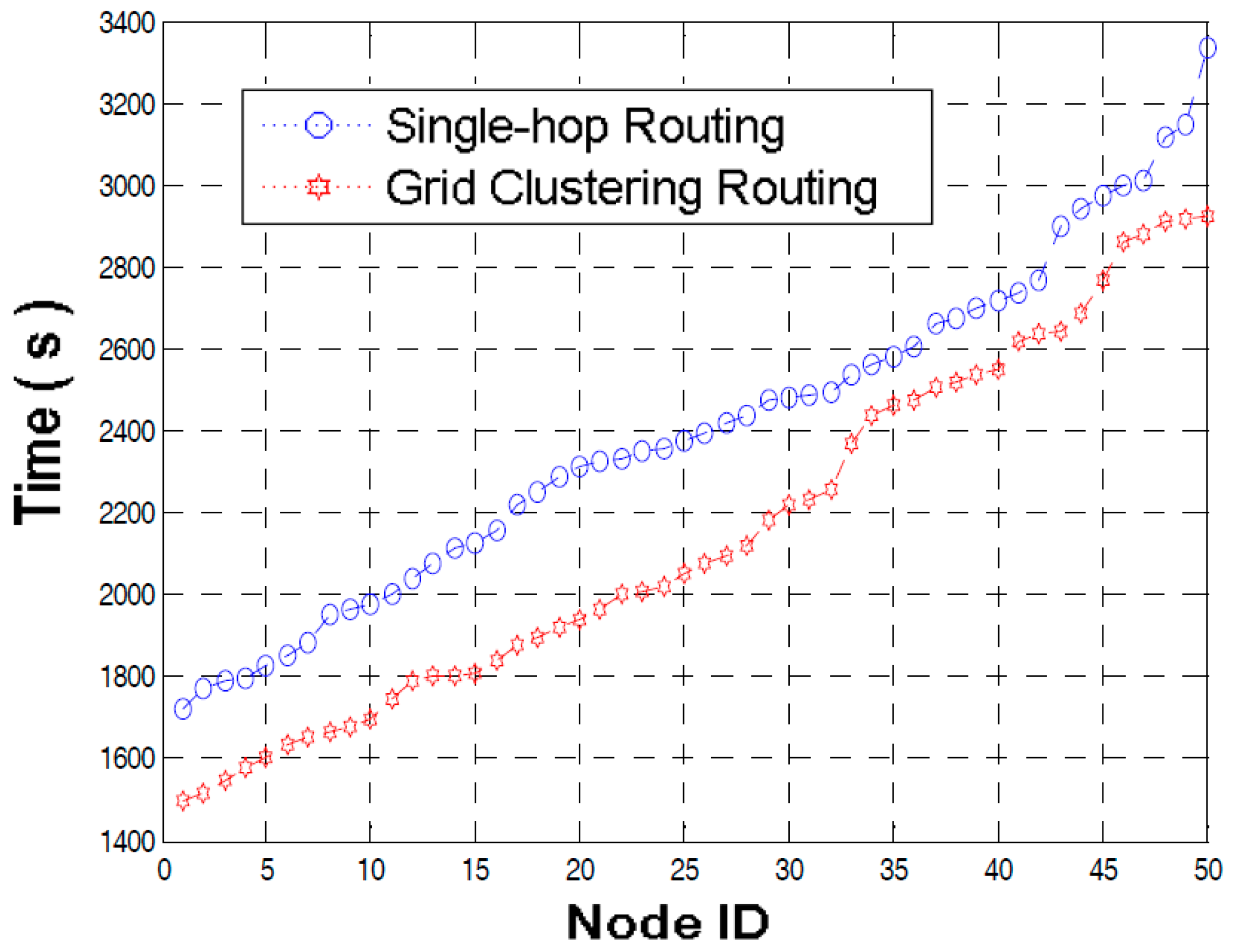
| Node | Node Location (m) (x, y) | Arriving Time of WPCD (s) | Node’s Minimal Energy ei(ai) kj | Node Location (m) (x, y) | Arriving Time of WPCD (s) | Node’s Minimal Energy ei(ai) kj |
|---|---|---|---|---|---|---|
| Single-hop Routing | Single-hop Routing | Single-hop Routing | Grid Clustering Routing | Grid Clustering Routing | Grid Clustering Routing | |
| 1 | (816.9, 901.8) | 1757.1 | 10.6 | (816.9, 901.8) | 1498.9 | 10.8 |
| 2 | (189.5, 419.5) | 1821.9 | 10.5 | (189.5, 419.5) | 1515.4 | 10.8 |
| 3 | (123.7, 358.1) | 1849.2 | 10.7 | (123.7, 358.1) | 1547.1 | 10.8 |
| 4 | (821.0, 489.0) | 1873.9 | 10.7 | (821.0, 489.0) | 1576.1 | 10.8 |
| 5 | (637.9, 256.0) | 1894.8 | 10.6 | (637.9, 256.0) | 1605.5 | 10.8 |
| 6 | (16.1, 929.2) | 1908.7 | 10.7 | (16.1, 929.2) | 1635.7 | 10.8 |
| 7 | (896.0, 466.7) | 1951.8 | 10.7 | (896.0, 466.7) | 1650.4 | 10.8 |
| 8 | (515.3, 254.0) | 1969.8 | 10.7 | (515.3, 254.0) | 1662.1 | 10.8 |
| 9 | (544.5, 431.2) | 1995.9 | 10.7 | (544.5, 431.2) | 1674.4 | 10.8 |
| 10 | (606.4, 702.5) | 2014.4 | 10.7 | (606.4, 702.5) | 1698.2 | 10.8 |
| 11 | (760.4, 402.3) | 2056.3 | 10.7 | (760.4, 402.3) | 1747.4 | 10.8 |
| 12 | (855.3, 181.8) | 2098.6 | 10.4 | (855.3, 181.8) | 1789.6 | 10.8 |
| 13 | (382.9, 856.2) | 2134.0 | 10.4 | (382.9, 856.2) | 1799.6 | 10.8 |
| 14 | (84.6, 584.2) | 2146.2 | 10.7 | (84.6, 584.2) | 1803.3 | 10.8 |
| 15 | (733.9, 373.5) | 2159.6 | 10.7 | (733.9, 373.5) | 1809.5 | 10.8 |
| 16 | (733.9, 373.6) | 2175.5 | 10.7 | (733.9, 373.6) | 1838.0 | 10.8 |
| 17 | (839.7, 219.0) | 2229.5 | 10.5 | (839.7, 219.0) | 1874.3 | 10.8 |
| 18 | (371.7, 522.2) | 2250.5 | 10.7 | (371.7, 522.2) | 1897.5 | 10.7 |
| 19 | (828.2, 433.4) | 2275.9 | 10.7 | (828.2, 433.4) | 1919.7 | 10.8 |
| 20 | (176.5, 741.3) | 2303.5 | 10.7 | (176.5, 741.3) | 1939.6 | 10.8 |
| Single-Hop Routing | Grid Clustering Routing | |
|---|---|---|
| Total Distance covered by WPCD | 6502.826120 (m) | 6761.404616 (m) |
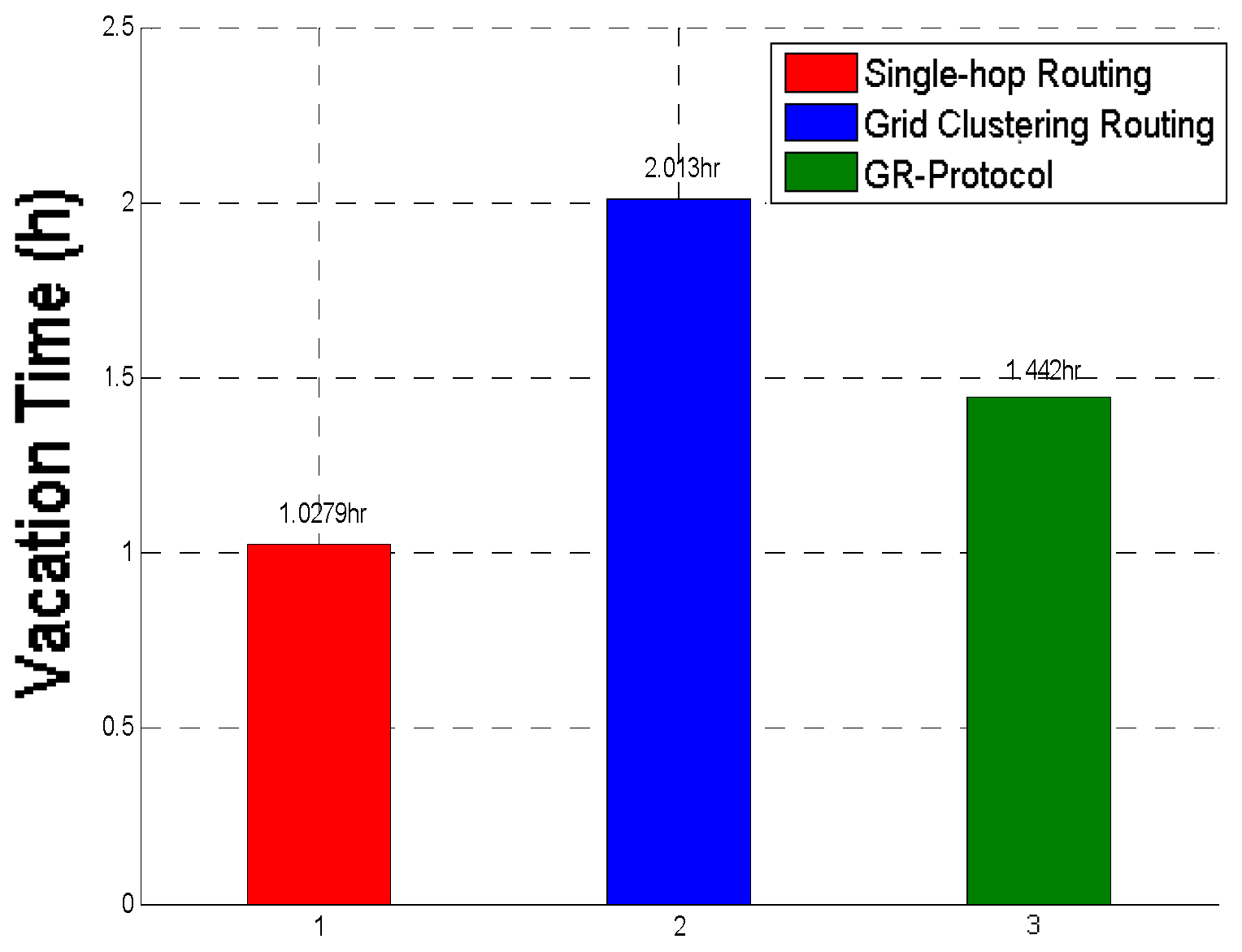
| Traveling Time for WPCD by Physical Path P | 1300.565224 (s) | 1352.280923 (s) |
| Overall Time consumed in the renewable charge cycle | 1666.658984 (s) | 1393.098968 (s) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aslam, N.; Xia, K.; Haider, M.T.; Hadi, M.U. Energy-Aware Adaptive Weighted Grid Clustering Algorithm for Renewable Wireless Sensor Networks. Future Internet 2017, 9, 54. https://doi.org/10.3390/fi9040054
Aslam N, Xia K, Haider MT, Hadi MU. Energy-Aware Adaptive Weighted Grid Clustering Algorithm for Renewable Wireless Sensor Networks. Future Internet. 2017; 9(4):54. https://doi.org/10.3390/fi9040054
Chicago/Turabian StyleAslam, Nelofar, Kewen Xia, Muhammad Tafseer Haider, and Muhammad Usman Hadi. 2017. "Energy-Aware Adaptive Weighted Grid Clustering Algorithm for Renewable Wireless Sensor Networks" Future Internet 9, no. 4: 54. https://doi.org/10.3390/fi9040054
APA StyleAslam, N., Xia, K., Haider, M. T., & Hadi, M. U. (2017). Energy-Aware Adaptive Weighted Grid Clustering Algorithm for Renewable Wireless Sensor Networks. Future Internet, 9(4), 54. https://doi.org/10.3390/fi9040054







