A Robust Image Watermarking Scheme Based on SVD in the Spatial Domain
Abstract
:1. Introduction
2. Background
2.1. Singular Value Decomposition (SVD)
2.2. Arnold Transform
3. SVD-Based Watermarking and Its Impact on the Spatial Domain
3.1. SVD-Based Watermarking
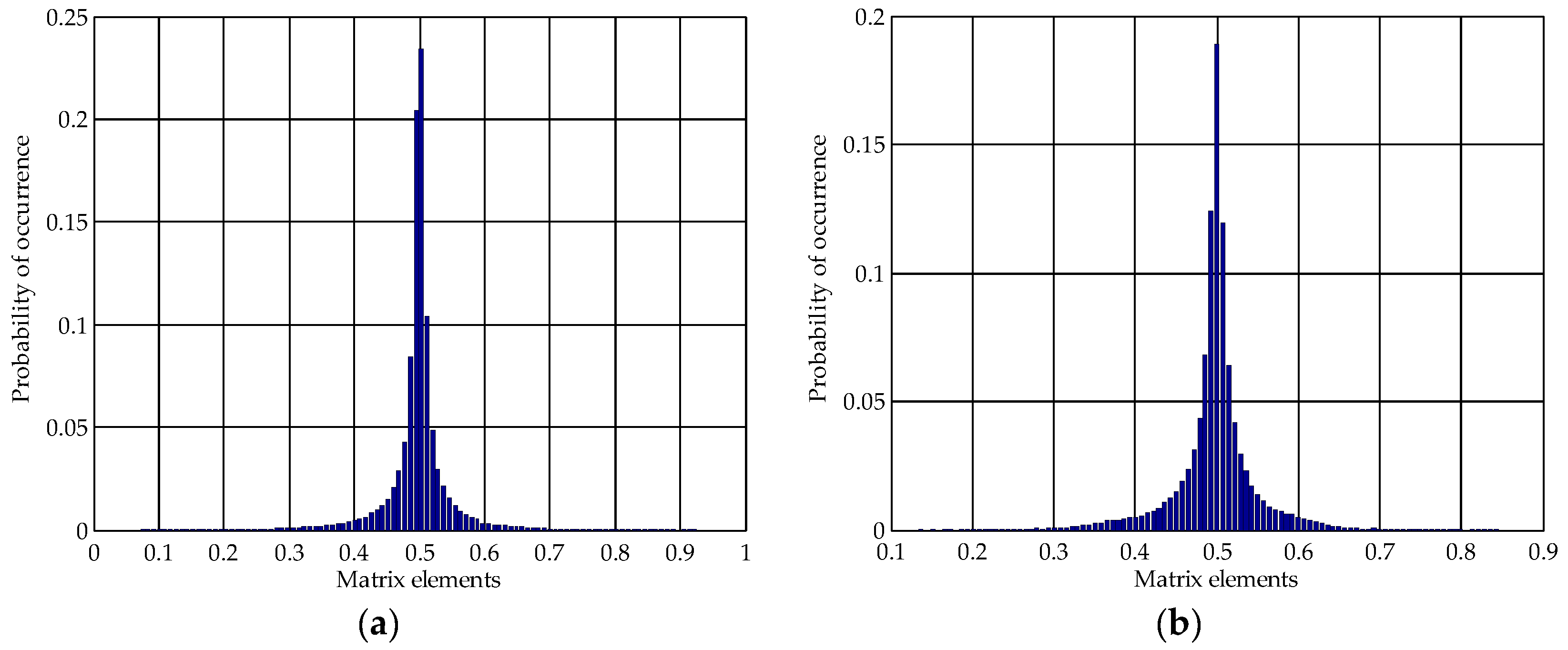
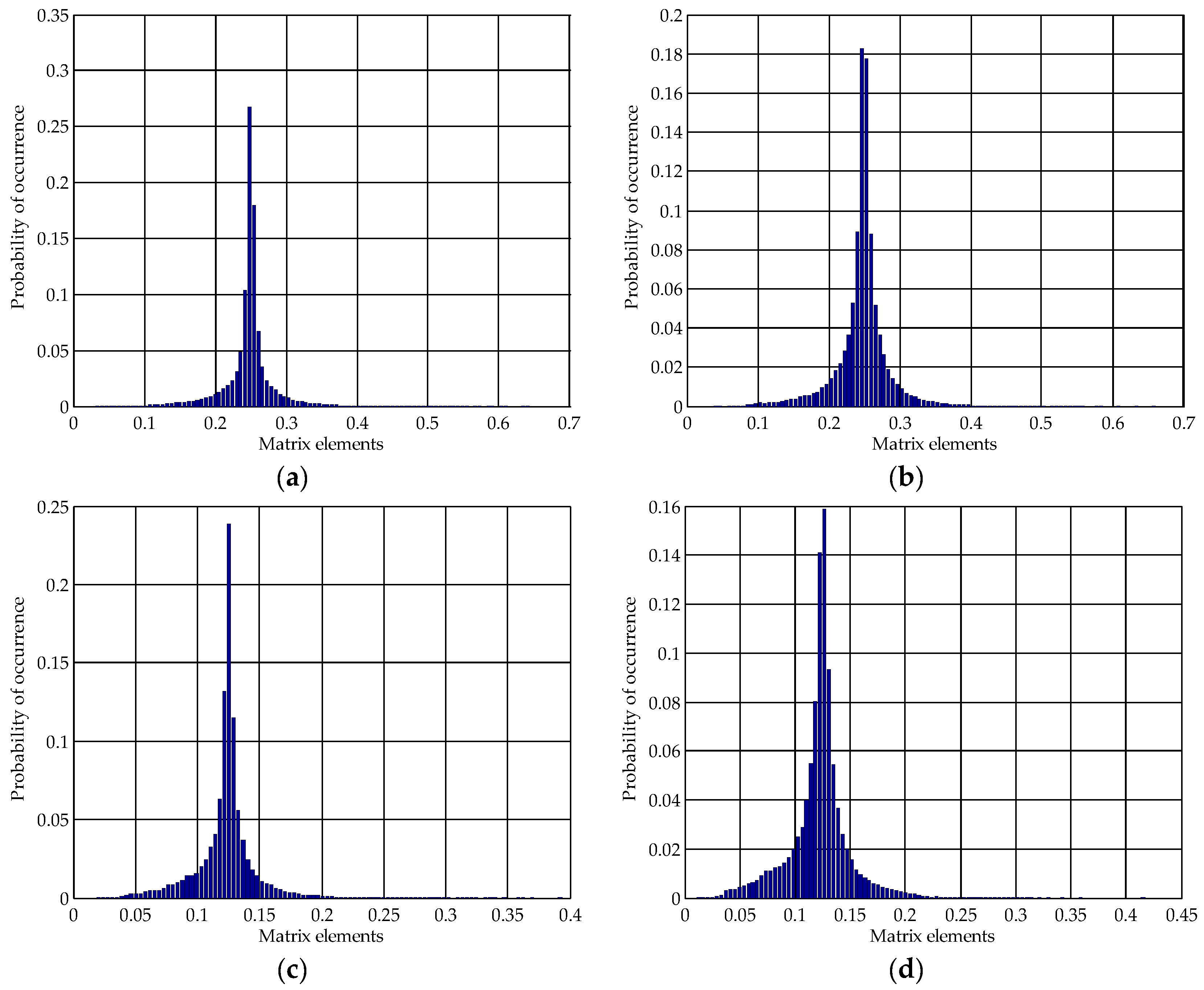
3.2. The Impact of SVD-Based Watermarking on the Pixel Values in the Spatial Domain
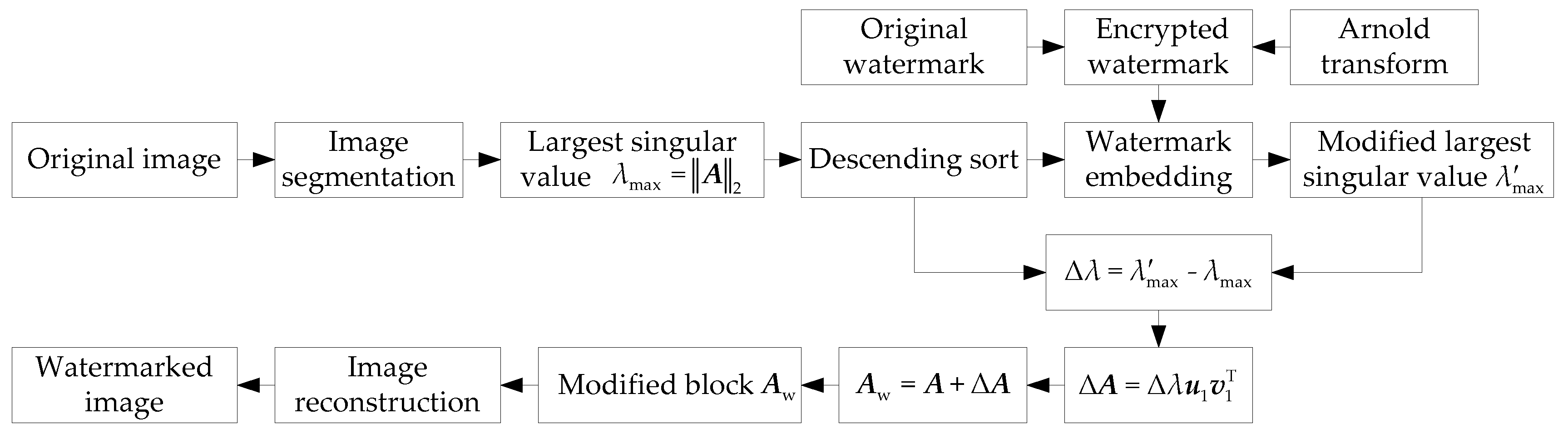
4. The Proposed Scheme
4.1. Watermark Embedding
4.2. Watermark Extraction
5. Experimental Results and Performance Analysis
5.1. Imperceptibility Test
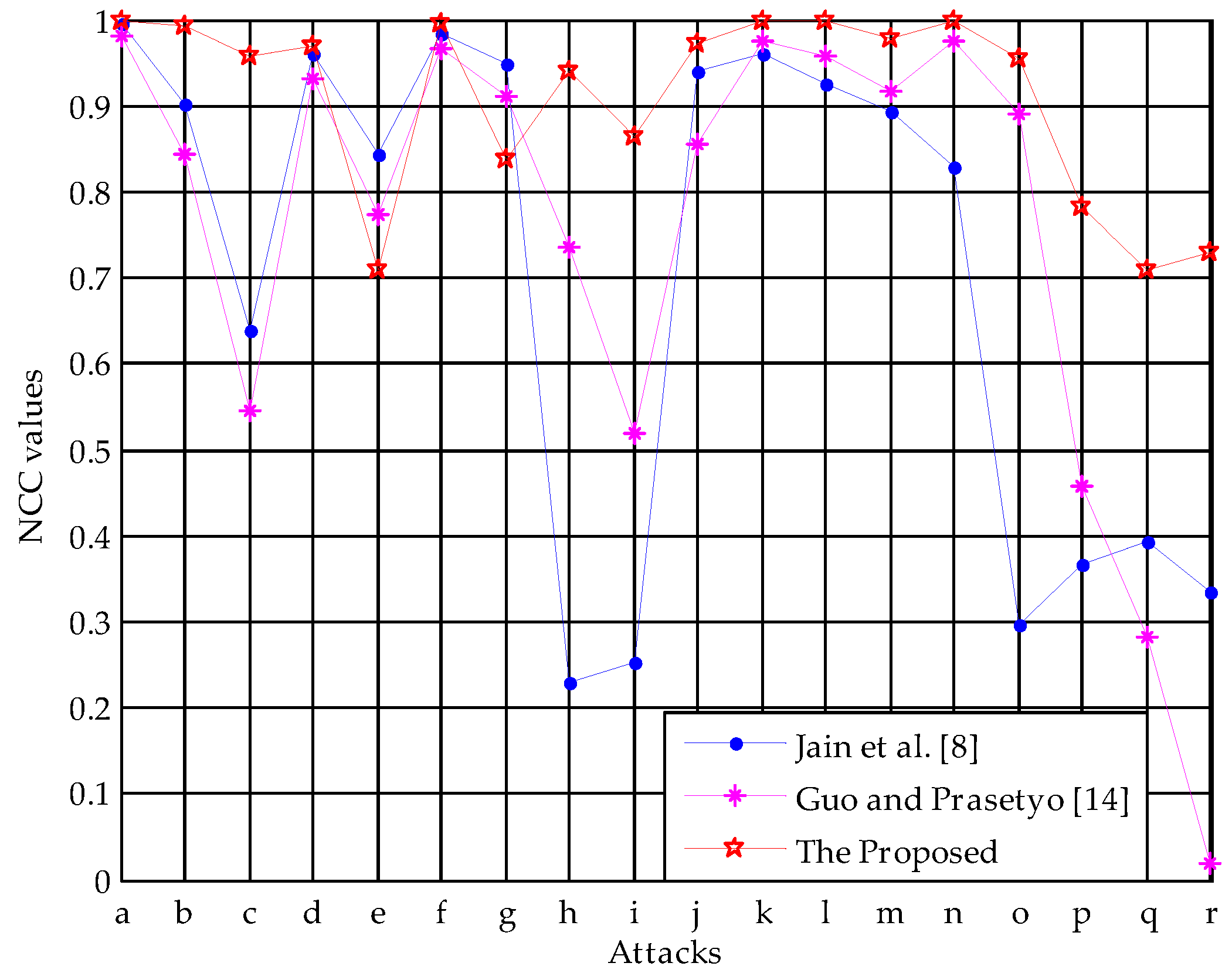
5.2. Robustness Test
5.3. Performance Comparisons
5.4. Algorithmic Complexity Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hai, T.; Li, C.M.; Zain, J.M.; Abdalla, A.N. Robust image watermarking theories and techniques: A review. J. Appl. Res. Technol. 2014, 12, 122–138. [Google Scholar]
- Nyeem, H.; Boles, W.; Boyd, C. Digital image watermarking: Its formal model, fundamental properties and possible attacks. EURASIP J. Adv. Signal Process. 2014, 1, 1–22. [Google Scholar] [CrossRef]
- Su, Q.T.; Wang, G.; Jia, S.L.; Zhang, X.F.; Liu, Q.M.; Liu, X.X. Embedding color image watermark in color image based on two-level DCT. Signal Image Video Process. 2015, 9, 991–1007. [Google Scholar] [CrossRef]
- Keshavarzian, R.; Aghagolzadeh, A. ROI based robust and secure image watermarking using DWT and Arnold map. AEU Int. J. Electron. Commun. 2016, 70, 278–288. [Google Scholar] [CrossRef]
- Liu, R.Z.; Tan, T.N. An SVD-based watermarking scheme for protecting rightful ownership. IEEE Trans. Multimed. 2002, 4, 121–128. [Google Scholar]
- Zhang, X.P.; Li, K. Comments on “An SVD-based watermarking scheme for protecting rightful ownership”. IEEE Trans. Multimed. 2005, 7, 593–594. [Google Scholar] [CrossRef]
- Rykaczewski, R. Comments on “An SVD-based watermarking scheme for protecting rightful ownership”. IEEE Trans. Multimed. 2007, 9, 421–423. [Google Scholar] [CrossRef]
- Jain, C.; Arora, S.; Panigrahi, P.K. A reliable SVD based watermarking scheme. Comput. Sci. 2008. [Google Scholar]
- Lai, C.C.; Tsai, C.C. Digital image watermarking using discrete wavelet transform and singular value decomposition. IEEE Trans. Instrum. Meas. 2010, 59, 3060–3063. [Google Scholar] [CrossRef]
- Gupta, A.K.; Raval, M.S. A robust and secure watermarking scheme based on singular values replacement. Sadhana 2012, 37, 425–440. [Google Scholar] [CrossRef]
- Fazli, S.; Moeini, M. A robust image watermarking method based on DWT, DCT, and SVD using a new technique for correction of main geometric attacks. Opt. Int. J. Light Electron. Opt. 2016, 127, 964–972. [Google Scholar] [CrossRef]
- Makbol, N.M.; Khoo, B.E. Robust blind image watermarking scheme based on redundant discrete wavelet transform and singular value decomposition. AEU Int. J. Electron. Commun. 2013, 67, 102–112. [Google Scholar] [CrossRef]
- Guo, J.M.; Prasetyo, H. Security analyses of the watermarking scheme based on redundant discrete wavelet transform and singular value decomposition. AEU Int. J. Electron. Commun. 2014, 68, 816–834. [Google Scholar] [CrossRef]
- Guo, J.M.; Prasetyo, H. False-positive-free SVD-based image watermarking. J. Vis. Commun. Image Represent. 2014, 25, 1149–1163. [Google Scholar] [CrossRef]
- Ranade, A.; Mahabalarao, S.S.; Kale, S. A variation on SVD based image compression. Image Vision Comput. 2007, 25, 771–777. [Google Scholar] [CrossRef]
- Singh, D.; Singh, S.K. DWT-SVD and DCT based robust and blind watermarking scheme for copyright protection. Multimed. Tools Appl. 2017, 76, 13001–13024. [Google Scholar] [CrossRef]
- Lai, C.C. A digital watermarking scheme based on singular value decomposition and tiny genetic algorithm. Digit. Signal Process. 2011, 21, 522–527. [Google Scholar] [CrossRef]
- Mishra, A.; Agarwal, C.; Sharma, A.; Bedi, P. Optimized gray-scale image watermarking using DWT-SVD and firefly algorithm. Expert Syst. Appl. 2014, 41, 7858–7867. [Google Scholar] [CrossRef]
- Yang, X.S. Multiobjective firefly algorithm for continuous optimization. Eng. Comput. 2013, 29, 175–184. [Google Scholar] [CrossRef]
- Yavuz, E.; Telatar, Z. Comments on “A digital watermarking scheme based on singular value decomposition and tiny genetic algorithm”. Digit. Signal Process. 2013, 23, 1335–1336. [Google Scholar] [CrossRef]
- Ali, M.; Ahn, C.W. Comments on “Optimized gray-scale image watermarking using DWT-SVD and firefly algorithm”. Expert Syst. Appl. 2015, 42, 2392–2394. [Google Scholar] [CrossRef]
- Ansari, I.A.; Pant, M.; Ahn, C.W. Robust and false positive free watermarking in IWT domain using SVD and ABC. Eng. Appl. Artif. Intell. 2016, 49, 114–125. [Google Scholar] [CrossRef]
- Su, Q.T.; Niu, Y.G.; Wang, Q.J.; Sheng, G.R. A blind color image watermarking based on DC component in the spatial domain. Opt. Int. J. Light Electron. Opt. 2013, 124, 6255–6260. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.Y.; Zhou, X. Fragile watermarking for image authentication using the characteristic of SVD. Algorithms 2017, 10, 27. [Google Scholar] [CrossRef]
- Marini, E.; Autrusseau, F.; Callet, P.L.; Campisi, P. Evaluation of standard watermarking techniques. In Proceedings of the SPIE Conference on Security, Steganography, and Watermarking of Multimedia Contents IX, San Jose, CA, USA, 26 February 2007; Volume 6505, pp. 1–10. [Google Scholar]



| Quantization Step | ||||||||
|---|---|---|---|---|---|---|---|---|
| Lena | SSIM | 1 | 1 | 0.9991 | 0.9974 | 0.9917 | 0.9707 | 0.9226 |
| NCC | 0.5014 | 0.4841 | 1 | 1 | 1 | 1 | 1 | |
| Barbara | SSIM | 1 | 1 | 0.9994 | 0.9983 | 0.9941 | 0.9793 | 0.9422 |
| NCC | 0.4883 | 0.5021 | 1 | 1 | 1 | 1 | 1 | |
| Baboon | SSIM | 1 | 1 | 0.9996 | 0.9987 | 0.9957 | 0.9844 | 0.9532 |
| NCC | 0.4910 | 0.5193 | 1 | 1 | 1 | 1 | 1 | |
| Image | PSNR (dB) | SSIM |
|---|---|---|
| Lena | 49.07 | 0.9946 |
| Barbara | 48.99 | 0.9963 |
| Boat | 49.09 | 0.9936 |
| Airplane | 49.13 | 0.9926 |
| Peppers | 49.28 | 0.9951 |
| Baboon | 49.06 | 0.9975 |
| Clock | 48.51 | 0.9890 |
| Average | 49.02 | 0.9941 |
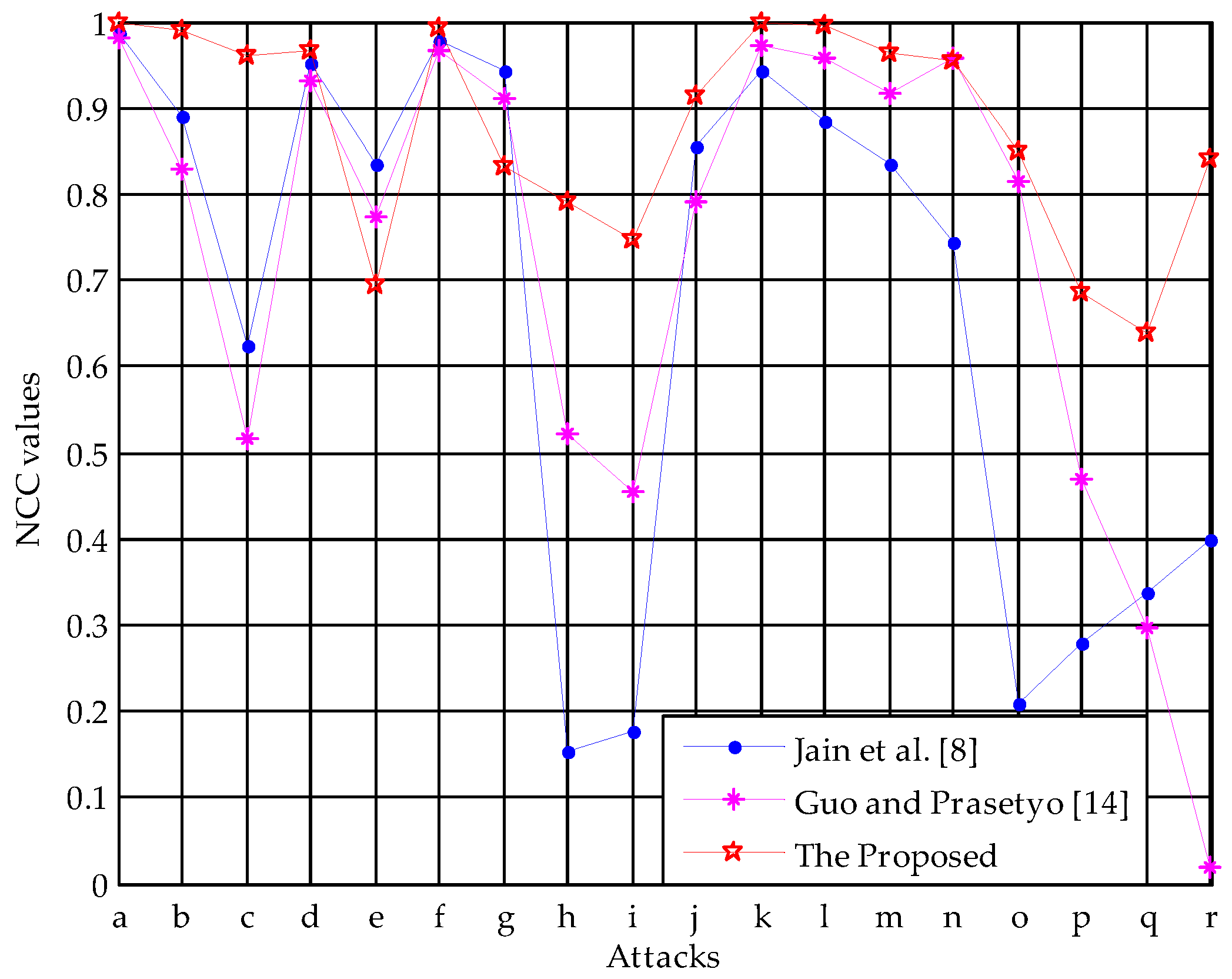
| Attack | Jain et al. [8] | Guo and Prasetyo [14] | The Proposed |
|---|---|---|---|
| PSNR (dB) | 21.10 | 39.26 | 49.07 |
| No Attack | 0.9948 | 0.9814 | 1 |
| Salt and Pepper Noise (0.001) | 0.9033 | 0.8442 | 0.9923 |
| Salt and Pepper Noise (0.005) | 0.6383 | 0.5441 | 0.9566 |
| Gaussian Noise (0, 0.0001) | 0.9598 | 0.9308 | 0.9693 |
| Gaussian Noise (0, 0.0005) | 0.8426 | 0.7737 | 0.7099 |
| Speckle Noise (0.0001) | 0.9845 | 0.9660 | 0.9944 |
| Speckle Noise (0.0005) | 0.9474 | 0.9098 | 0.8379 |
| Median Filter (3 × 3) | 0.2306 | 0.7351 | 0.9386 |
| Average Filter (3 × 3) | 0.2535 | 0.5192 | 0.8641 |
| Image Sharpening | 0.9411 | 0.8545 | 0.9724 |
| JPEG (Q = 90) | 0.9591 | 0.9743 | 1 |
| JPEG (Q = 80) | 0.9244 | 0.9565 | 0.9986 |
| JPEG (Q = 70) | 0.8930 | 0.9176 | 0.9793 |
| Rescaling (2, 0.5) | 0.8276 | 0.9743 | 1 |
| Rescaling (0.5, 2) | 0.2966 | 0.8904 | 0.9538 |
| Cropping (top 25%) | 0.3679 | 0.4581 | 0.7828 |
| Cropping (middle 25%) | 0.3923 | 0.2812 | 0.7083 |
| Cropping (right 25%) | 0.3351 | 0.0202 | 0.7297 |
| Attack | Jain et al. [8] | Guo and Prasetyo [14] | The Proposed |
|---|---|---|---|
| PSNR (dB) | 21.14 | 39.26 | 48.99 |
| No Attack | 0.9882 | 0.9803 | 1 |
| Salt and Pepper Noise (0.001) | 0.8918 | 0.8290 | 0.9910 |
| Salt and Pepper Noise (0.005) | 0.6257 | 0.5150 | 0.9595 |
| Gaussian Noise (0, 0.0001) | 0.9524 | 0.9300 | 0.9663 |
| Gaussian Noise (0, 0.0005) | 0.8347 | 0.7731 | 0.6936 |
| Speckle Noise (0.0001) | 0.9783 | 0.9657 | 0.9939 |
| Speckle Noise (0.0005) | 0.9430 | 0.9118 | 0.8316 |
| Median Filter (3 × 3) | 0.1548 | 0.5221 | 0.7897 |
| Average Filter (3 × 3) | 0.1756 | 0.4552 | 0.7469 |
| Image Sharpening | 0.8547 | 0.7921 | 0.9138 |
| JPEG (Q = 90) | 0.9425 | 0.9733 | 1 |
| JPEG (Q = 80) | 0.8853 | 0.9566 | 0.9952 |
| JPEG (Q = 70) | 0.8340 | 0.9168 | 0.9621 |
| Rescaling (2, 0.5) | 0.7447 | 0.9582 | 0.9552 |
| Rescaling (0.5, 2) | 0.2080 | 0.8135 | 0.8497 |
| Cropping (top 25%) | 0.2802 | 0.4705 | 0.6848 |
| Cropping (middle 25%) | 0.3387 | 0.2955 | 0.6393 |
| Cropping (right 25%) | 0.3987 | 0.0192 | 0.8414 |
| Computational Time (s) | Jain et al. [8] | Guo and Prasetyo [14] | The Proposed | |
|---|---|---|---|---|
| SVD Domain | Spatial Domain | |||
| Embedding Time | 0.4337 | 0.4721 | 0.8509 | 0.3536 |
| Extraction Time | 0.2973 | 0.2805 | 0.2295 | 0.1901 |
| Total Time | 0.7310 | 0.7526 | 1.0804 | 0.5437 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wang, C.; Zhou, X. A Robust Image Watermarking Scheme Based on SVD in the Spatial Domain. Future Internet 2017, 9, 45. https://doi.org/10.3390/fi9030045
Zhang H, Wang C, Zhou X. A Robust Image Watermarking Scheme Based on SVD in the Spatial Domain. Future Internet. 2017; 9(3):45. https://doi.org/10.3390/fi9030045
Chicago/Turabian StyleZhang, Heng, Chengyou Wang, and Xiao Zhou. 2017. "A Robust Image Watermarking Scheme Based on SVD in the Spatial Domain" Future Internet 9, no. 3: 45. https://doi.org/10.3390/fi9030045







