Robust Image Embedded Watermarking Using DCT and Listless SPIHT

Abstract

This paper presents a DCT-based (DCT: discrete cosine transform) listless set partitioning in hierarchical trees (SPIHT) digital watermarking technique that is robust against several common attacks such as cropping, filtering, sharpening, noise, inversion, contrast manipulation, and compression. The proposed technique is made further robust by the incorporation of the Chinese remainder theorem (CRT) encryption technique. Our scheme is compared with the recently proposed CRT-based DCT technique, CRT-based spatial domain watermarking, and DCT-based inter block correlation techniques. Extensive simulation experiments show better robustness in common image manipulations and, at the same time, the proposed technique successfully makes the watermark perceptually invisible. A better Tamper Assessment Function (TAF) value of 2–15% and a better Normalized Correlation (NC) is achieved compared to some of the above techniques. In particular, the proposed technique shows better robustness on compression attacks at moderate to higher compression ratios. It is possible to maintain the imperceptibility and low TAF for various values by doubling the capacity of the watermark.

1. Introduction

With the rapid growth in technology, the internet has become the most popular channel for every user to download digital multimedia data like images and videos. Since the environment of internet is open, this data can easily be tampered with or manipulated, for which data integrity must be ensured. Digital watermarking is a common technique that used to verify this integrity. The watermarking technique consists of three parts, namely: (i) the watermark; (ii) the embedding stage, and; (iii) the verification stage. In the embedding stage the algorithm incorporates the watermark into the host image. However, the algorithm extracts and authenticates the watermark in the verification stage. The goal of image authentication is to verify the originality of the host image by detecting malicious manipulations. There are two essential requirements for image watermarking. One is invisibility, i.e., the visual quality of the watermarked images should not be destroyed by embedding the watermark. The other is robustness, i.e., the watermark should be able to resist attacks, even if the attacks are deliberately made [1].

Digital watermarking techniques are performed in the spatial domain [2] and in the transformed domain [3,4,5,6,7]. The transformed domain is more robust and operates more imperceptibility than the spatial domain [8,9]. In the transform domain DCT make use of energy distribution properties and human visual system scheme for embedding the watermark [10]. Blind watermarking schemes with interesting results havebeen proposed in [11,12]. Some of the other transformed-domain watermarking schemes have been proposed in [13,14,15,16,17]. SVD (singular value decomposition) is also used in watermarking where the properties of U coefficients (after SVD decomposition) modification cause less degradation of image quality [17,18,19,20,21,22]. Some of the watermarking techniques using the Ridgelet transform are also proposed [23,24].

The CRT-based scheme, which provides robustness against some common image processing manipulations, is proposed in [25,26]. Digital watermarking is also performed using segmentation of DCT blocks [27]. Each DC coefficient is extracted and stored in a matrix before processing, making it expensive in terms of memory requirement [28]. Hsu and Wu [6] used middle DCT coefficients for embedding watermark. The algorithm is not very robust against JPEG compression.

Watermarking schemes can be implemented in VLSI (very large scale integration) chips. Hardware implementation in consumer electronic devices such as digital camera, PDAs, and mobile devices requires low power, high reliability, real-time performance and easy integration. For example, viability of integration of watermarking chips in any digital camera or JPEG codec. Several issues related to hardware implementation of several watermarking algorithms for images and videos have been reported by Kougianos et al. [29]. DCT domain watermarking is popular for hardware implementation because there are a number of fast algorithms exists [30,31,32,33,34]: 8 × 8 DCT is mostly used for hardware implementation; 4 × 4 DCT provides less computation at a cost of less energy compaction.

SPIHT [35] is a benchmark algorithm for the compression of still images and videos in an embedded fashion. It has precise rate control, i.e., the user can set any target bit rate (compression ratio) to reconstruct the compressed images. However, SPIHT uses an auxiliary list, which causes a lot of memory management problem for hardware realization. To overcome this listless SPIHT has been proposed which does not make use of auxiliary lists [36]. The state information that keeps track of set partitions is held in a state marker table in the memory. This algorithm takes less memory and is easy to implement in hardware compared to a conventional JPEG.

Recently, CRT-based watermarking with some results has been reported in [25,26]. CRT provides additional security, for example, in selecting a set of relatively prime numbers £ = {P₁, P₂, … Pr}, a large integer K can be represented by a set of smaller integers {k₁, k₂…. k_n}. It is extremely difficult to get back the K value without the knowledge of £. This fact provides additional security. Further, CRT is based on simultaneous congruence of modular arithmetic and computationally efficient. This motivates the authors to combine listless SPIHT with CRT techniques in a blind watermarking scheme to provide added security and robustness against compression attacks. To the best of the authors’ knowledge there is no such work proposed in the literature that combines listless SPIHT with CRT in blind watermarking schemes.

The proposed method exhibits superior performance in terms of PSNR (peak signal to noise ratio)/structural similarity (SSIM) and tamper assessment function (TAF) over most of the recently proposed schemes in literature. Good TAF (in %) and Normalized Correlation (NC) values are also obtained for most of the common attacks such as cropping, tampering, noise addition, brightening, sharpening and compression. Attacks such as scaling, rotation, filtering and geometric transformation are not considered in this paper.

The rest of the paper is organized as follows: Related works are presented in Section 2. Section 3 discusses the implementation of embedding and the extraction aspect of the proposed scheme. Comparison results are presented in Section 4. Finally, in Section 5 the conclusion and future research direction have been made.

2. Related Work

SPIHT is a tree-based image compression algorithm. It scans the transformed coefficients in a depth first search. Set partitioning embedded block (SPECK) is block based image compression algorithm [37]. However, it scans the coefficients using a breadth-first approach. The listless variants of SPIHT and SPECK are called Listless SPIHT (i.e., NLS) and Listless SPECK (LSK), respectively [36,38]. These listless algorithms have been proposed to overcome the memory management problems associated with SPIHT and SPECK. Listless SPIHT and LSK can compress images from a lossy to a lossless format. These algorithms generate a bit string in order of importance. That means that the lower part of the bit string contains more information of the image than higher part of the bit string. The user can truncate at any point of the compressed bit string to reconstruct an image, which is a compressed representation of the original image. However, none of these algorithms are used in image/video watermarking schemes in the literature. Most of the works in literature use JPEG/JPEG 2000 for compression of the watermarked images. Compression using listless SPIHT and LSK has superior performance than JPEG and is highly competitive with JPEG 2000 [38]. JPEG 2000 is computationally intensive because of context modelling and adaptive arithmetic coding. Listless SPIHT and LSK are much less complex and take less memory for compression and reconstruction. The authors considered a modified listless SPIHT for compression of the watermarked image from lossy to lossless, because compression is considered as one of the attacks in the watermarking scheme [39,40].

CRT-based encryption technique provides additional security and robustness against the existing schemes. Patra et al. proposed DCT-based CRT techniques that provide better robustness against various attacks [25,26]. In order to achieve the merit of both CRT and listless SPIHT, we proposed a blind watermarking scheme which uses modified listless SPIHT (NLS) that combines with DCT coefficients and CRT encryption technique.

3. Proposed Scheme

The block diagram of the proposed scheme is shown in Figure 1. The uniqueness of the scheme is that the key is generated randomly during embedding process instead of using a known key for embedding in comparison to other methods. The generated key is required to send to the receiver for watermark extraction.

The embedding and extraction technique of the proposed method is based on combining the CRT technique in the DCT domain. The listless SPIHT compression scheme is used to generate an embedded compressed bit string which can be used for storage and/or transmission. This method added the flexibility to compress losslessly or lossy by setting a target bit rate. In addition, better security and better robustness is achieved during the extraction phase. We have presented the detailed algorithm for embedding and extraction in the following subsections.

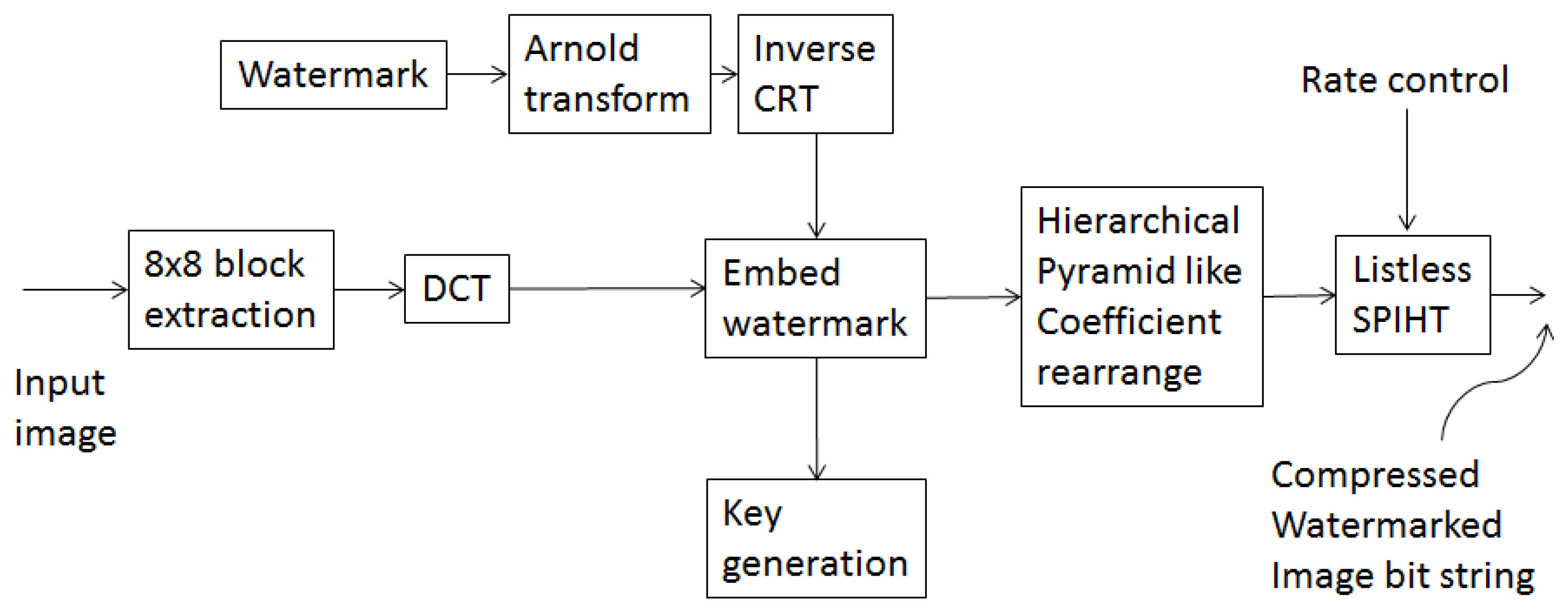
3.1. Embedding Procedure

The following steps describe the watermark embedding procedure on the host image.

Step-1 Partition of blocks

The host image is taken as a grayscale image and watermark is a binary image. Initially, the host image is divided into blocks of 8 × 8 pixels. The single watermark bit is then embedded in a single block selected. Then the blocks are chosen as random.

Step-2 Selection of DCT coefficients

In order to improve robustness, the preferred choice is to embed the watermark into the most significant coefficients. However, it will degrade the quality of the watermark. If insignificant coefficients are used for embedding, the watermark may be lost during lossy compression. Since proposed scheme use block size 8 × 8 pixels, the resulting DCT block is also of the same size. This gives a total of 64 DCT coefficients. We have included both DC and low-frequency AC coefficients for embedding in order to achieve trade-off between quality and robustness. The DC component and the remaining 63 low-frequency AC components are selected as the possible locations for embedding the watermark bits in the DCT domain.

Step-3 Zigzag scanning of the DCT coefficients

After zigzagging the DCT coefficients, one value must be selected. During that selection, randomizing the coefficients is done using a pseudo random generator. Using randomization technique, security and authentication aspects will increase as the value is changing for every execution. During randomization, one of the selected coefficients is chosen and its index is stored as a secret key whenever we execute the code. This feature adds more security to the data while embedding the procedure.

Step-4 Arnold transform

This is a digital scrambling algorithm to randomize the bits of the watermark. It improves the robustness of the digital watermark. In order to increase the security and robustness of watermark, we use Torus automorphism (TA), which could disperse a watermark equally and randomly [41]. Applying TA for scrambling the binary watermark before embedding offers cryptographic protection against intentional reconstruction of watermark [39]. Further, the key utilized in the TA permutation procedure for scrambling the watermark is also required during the inverse TA permutation (descrambling) procedure. The TA permutation procedure is based on the following equation [39].

$$\left(\begin{array}{l}i*\\ j*\end{array}\right)=\left(\begin{array}{cc}1& 1\\ k& k+1\end{array}\right)\times \left(\begin{array}{l}i\\ j\end{array}\right)\mathrm{mod}m,$$

(1)

Equation (1) indicates that each pixel of the watermark pattern at coordinate $(i,j)$ will move to $(i*,j*)$. The $k$ and $m$ are the key parameters given by the user.

Step-5 Embedding the watermark bits

After dividing 8 × 8 blocks, one watermark bit gets embedded in each of the block. Considering one block at a time, the procedure for embedding the watermark bits is listed as follows:

• Randomly select an 8 × 8 block from host image and apply DCT to the block.
• Randomly select a watermark bit from the watermark image in order to embed into the block.
• Randomly select a DCT coefficient (DC or one of the AC components) to embed the watermark bit. Let its value be denoted as $\vartheta$.
• Let P₁ and P₂ be the pair-wise co-prime numbers used in CRT (say, P₁ = 38 and P₂ = 107) for the DC coefficient. For an AC coefficient, let the values of P₁ = 38 and P₂ = 55.
• Find E₁ and E₂ by applying the inverse CRT to $\vartheta$. Let the absolute difference between E₁ and E₂ value be $\prime z\prime$.
• Determine the value D = max(P₁,P₂) – 1.
• The required condition for embedding watermark bit ‘1’, is

  $$z\ge D/u,$$

  (2)

  where $u=2$ if $\vartheta$ is DC coefficient, otherwise, $u=3$. Apply CRT to modify $\vartheta$. If the condition is not satisfied, then $\vartheta$ is modified in step of 8 until the required condition in Equation (2) is satisfied.
• The required condition for embedding watermark bit ‘0’ is

  $$z<D/u,$$

  (3)
• Apply CRT to modify $\vartheta$. If the condition in Equation (3) is not satisfied, then $\vartheta$ is modified in step 8 until the required condition is satisfied.
• Reconstruct DCT block with the modified DCT coefficient $\widehat{\vartheta }$ and apply inverse DCT to the block to construct the watermarked image block.
• Repeat the steps (represented in bullet form) 1–9 for all the remaining blocks until all the watermark bits are embedded.

Note that the range of possible values for DC and the AC coefficients are not the same. The range of the DC coefficient is from values 0 to 2040, while for AC coefficients, it will be from the −1020 to +1020 in monochrome images. According to CRT, the product of the pair-wise co-prime numbers (also called the dynamic range) must be greater than the largest possible number [25]. The block diagram for embedding procedure is shown in Figure 1.

Step-6 Hierarchical Pyramid-like coefficient arrangement:

Figure 2 shows an arrangement of the DCT coefficients in a hierarchical pyramid structure. The coefficients in each 8 × 8 block are arranged in a parent-child relationship. The parent of a coefficient $i$ is $\lfloor \frac{i}{4}\rfloor$ for $4\le i\le 63$, while the set of four children associated with $j^{th}$ coefficient is $\{4j,4j+1,4j+2,4j+3\}$ for $0\le j\le 15$. The DC coefficient indexed as 0 is the root of the tree, which has only three children, e.g., 1, 2 and 3. The offspring corresponds to direct descendent in the same spatial location in the next finer band of pyramid. A tree corresponds to a node having 4 children which always form a group of 2 × 2 adjacent pixels. In the bottom part of the Figure 2, arrows indicate the same indexed coefficients of other blocks those are grouped together so as to form an overall 3-level pyramid structure.

Step-7 Listless SPIHT compression algorithm

SPIHT is the benchmark algorithm for compression of still images. It makes use of ordered auxiliary lists to encode significant information in a bit plane manner. The movement of list nodes, addition of new nodes to the list and deletion of a node from the list while processing the ordered bit planes in SPIHT causes a lot of memory management problems. To overcome this listless variant of SPIHT, called NLS is proposed in [36]. NLS reduces memory management problem by using state table markers for encoding coefficients. Further, NLS need less dynamic memory storage for the image. The proposed watermark algorithm makes use of modified NLS for compressing the image form lossy to lossless. Precise rate control can be achieved while compression is lossy. The modified NLS is similar to NLS except that the refinement pass is executed prior to sorting pass. This ensures better compression performance in modified NLS.

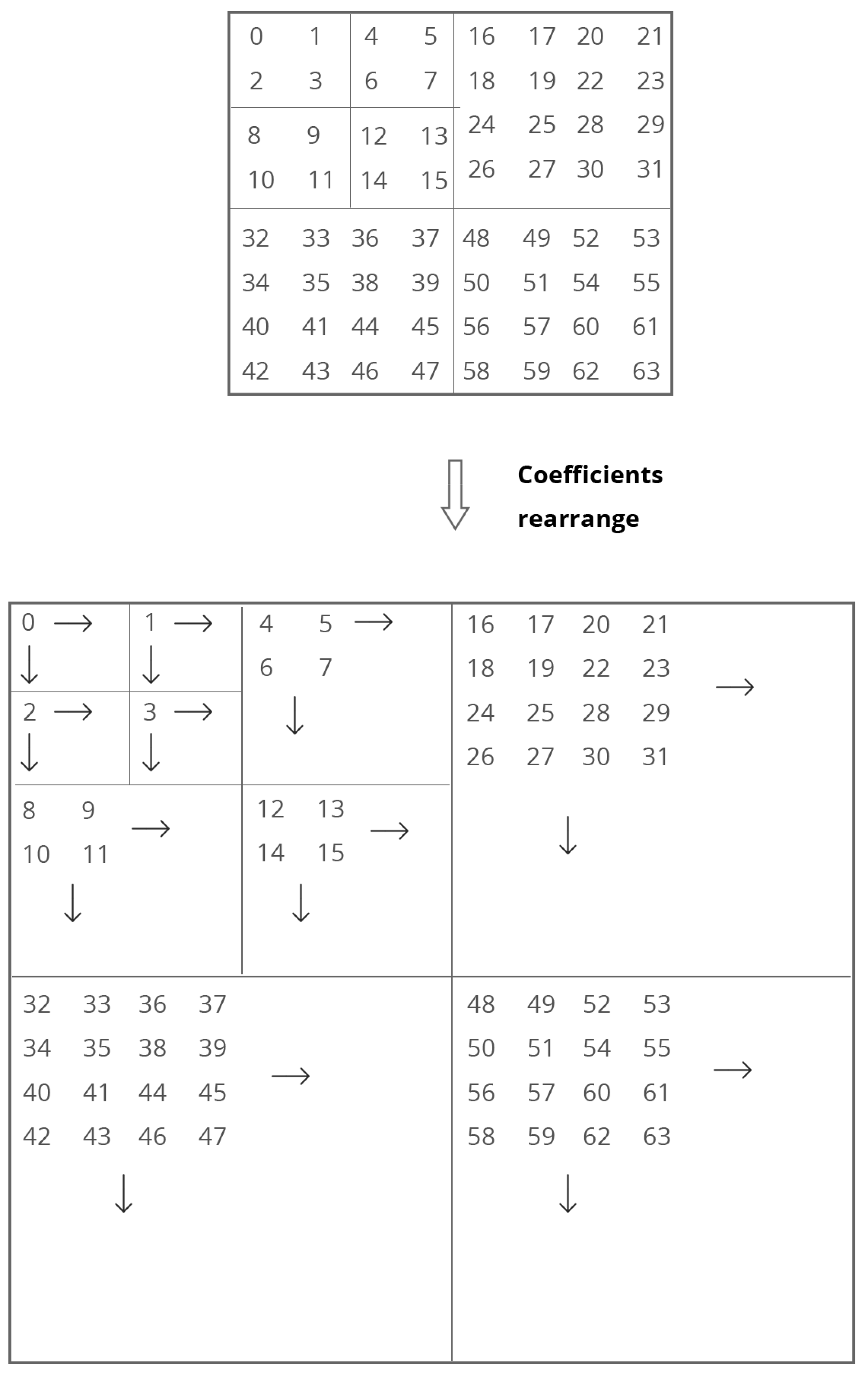
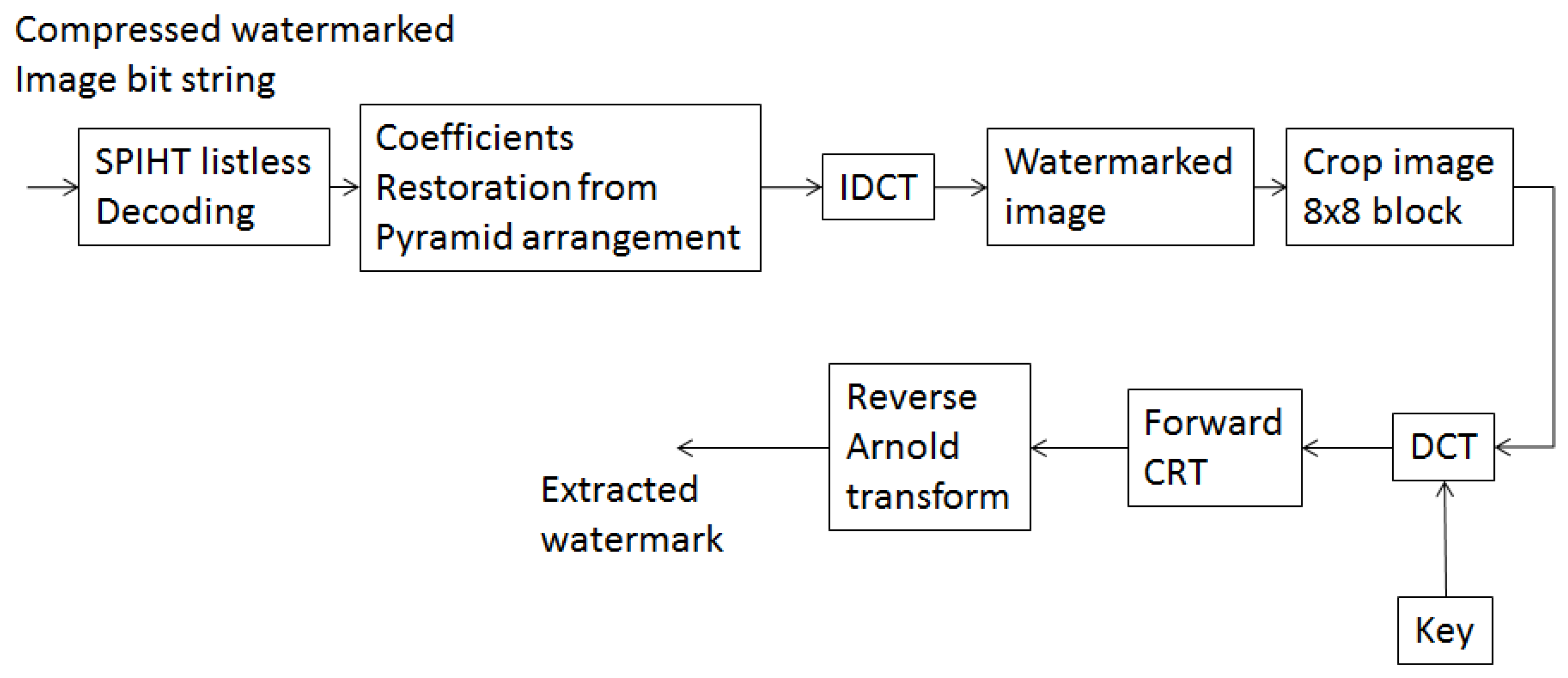
3.2. Extraction Procedure

The procedure of extraction is the reverse of embedding procedure. Figure 3 shows the extraction process. The detailed of watermark extraction process is outlined as follows:

Step-1 Listless SPIHT decoding

SPIHT decodes the image form the compressed bit string. It follows the exact reverse process that the SPIHT encoder does [36,37].

Step-2 Coefficient restoration algorithm

This process restore the coefficients back into the original position, i.e., individual 8 × 8 blocks of coefficients that has been arranged into hierarchical manner before SPIHT encoding.

Step-3 IDCT

Inverse DCT is applied in to all the 8 × 8 blocks to find the image pixels and merge all 8 × 8 block to construct a large compressed decoded watermarked image (512 × 512 in this case).

Step-4 Extraction of watermark

For this, following information must be known to get the watermark extracted from the watermarked image: (i) Image which is watermarked; (ii) Size of watermark; (iii) Watermark Key; and (iv) Pair-wise numbers of co-prime P₁ and P₂.

With knowledge of the watermark key, the DCT coefficient that is embedded with watermark information $\widehat{\vartheta }$ is extracted. Thus, with values of P₁, P₂ and $\widehat{\vartheta }$, the E₁, E₂ are determined. Next, using a CRT scheme, a comparison is made between the $z$ and D. If $z\ge D/u,$ the bit 1 would be extracted, otherwise the bit 0 would be get extracted. The scale factor $u$ is then set to 2 for the coefficient of DC, otherwise it is get set to 3. Thus, the above steps were then repeated until every block consecutively to get all watermark bits extracted.

In order to improve robustness, the preferred choice is to embed the watermark into the most significant coefficients. However, it will degrade the quality of the watermark. If insignificant coefficients are used for embedding, the watermark may have been lost during lossy compression. Since the proposed scheme use block-size 8 × 8 pixels, the resulting DCT block is also of same size. This gives a total of 64 DCT coefficients.

3.3. Secret Keys

Secrete keys are vital for the proposed algorithm to implement embedding and extraction procedures. Three keys are utilized and these should be preserved well for watermark extraction and verification. These are:

• The parameters for Torus automorphism permutation: The disarrangement parameters $k$ and $m$ obtained in Equation (1) are necessary when reconstructing the watermark pattern.
• The record number of the selected block has to be preserved.
• The embedding position of the watermark bits, i.e., the DCT coefficients and their positions have to be preserved.
• Co-prime numbers used in CRT.

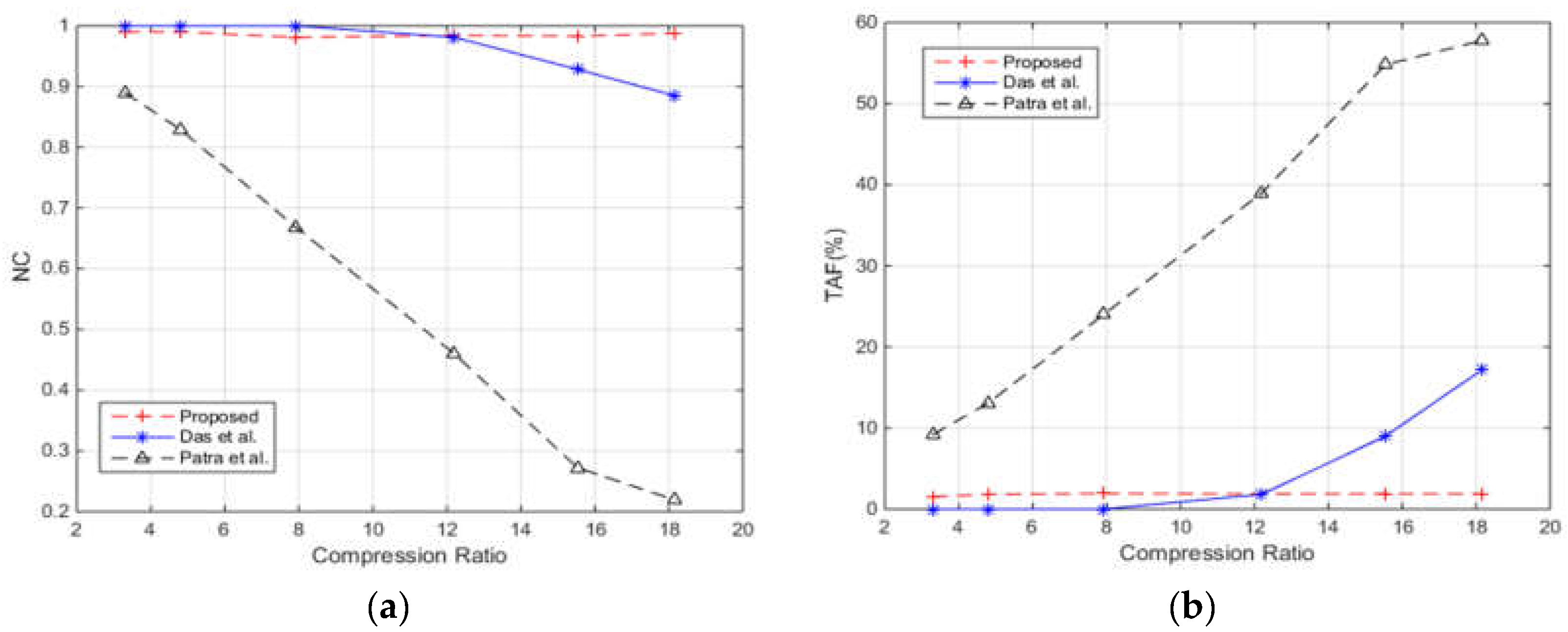
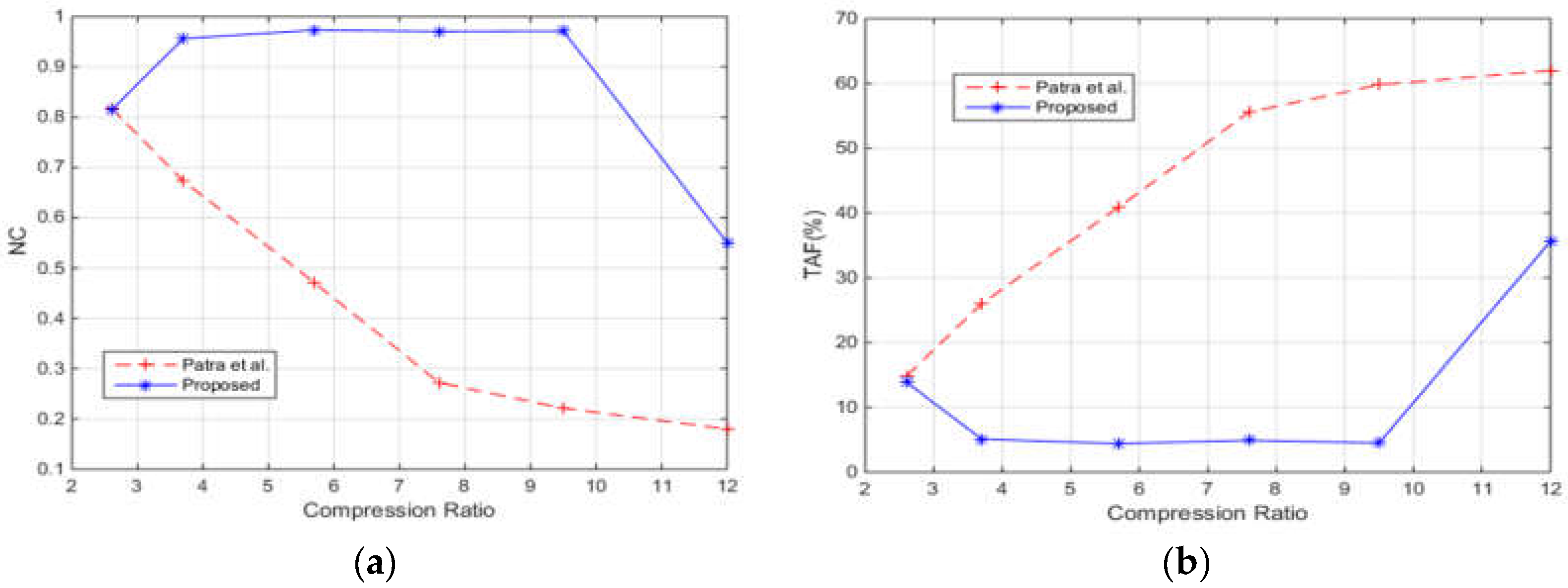
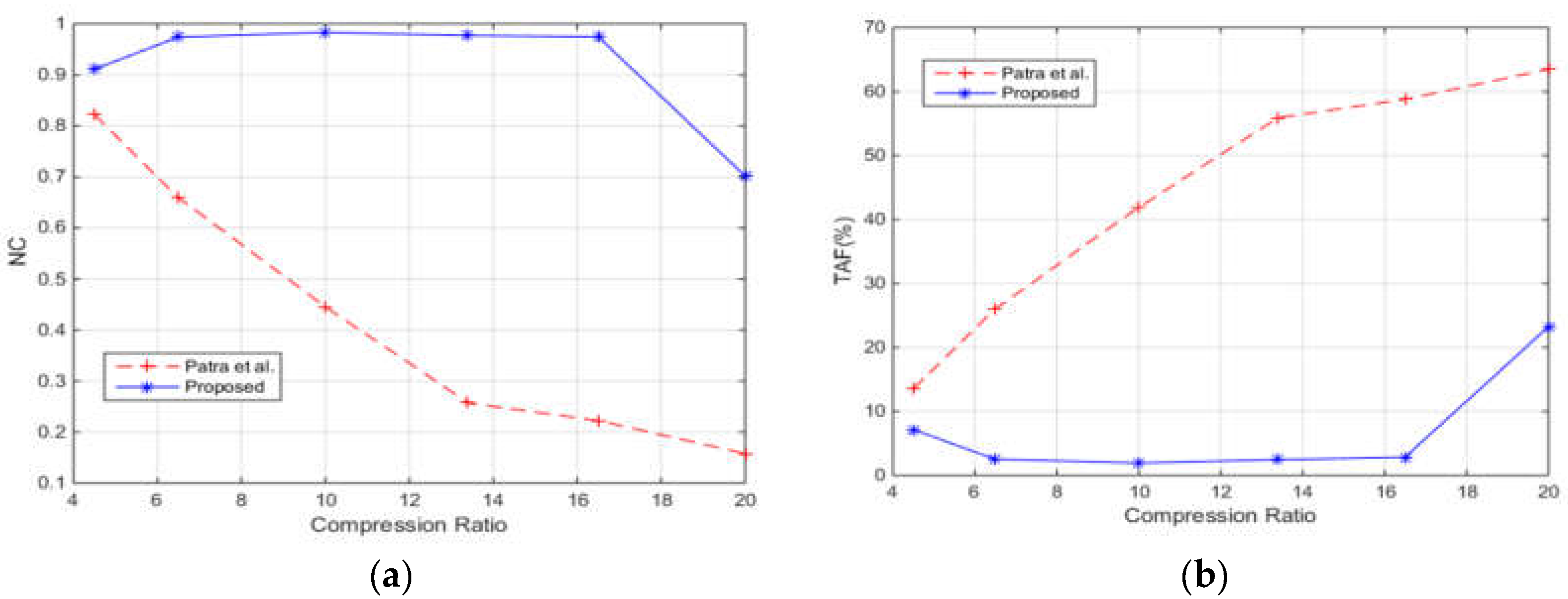
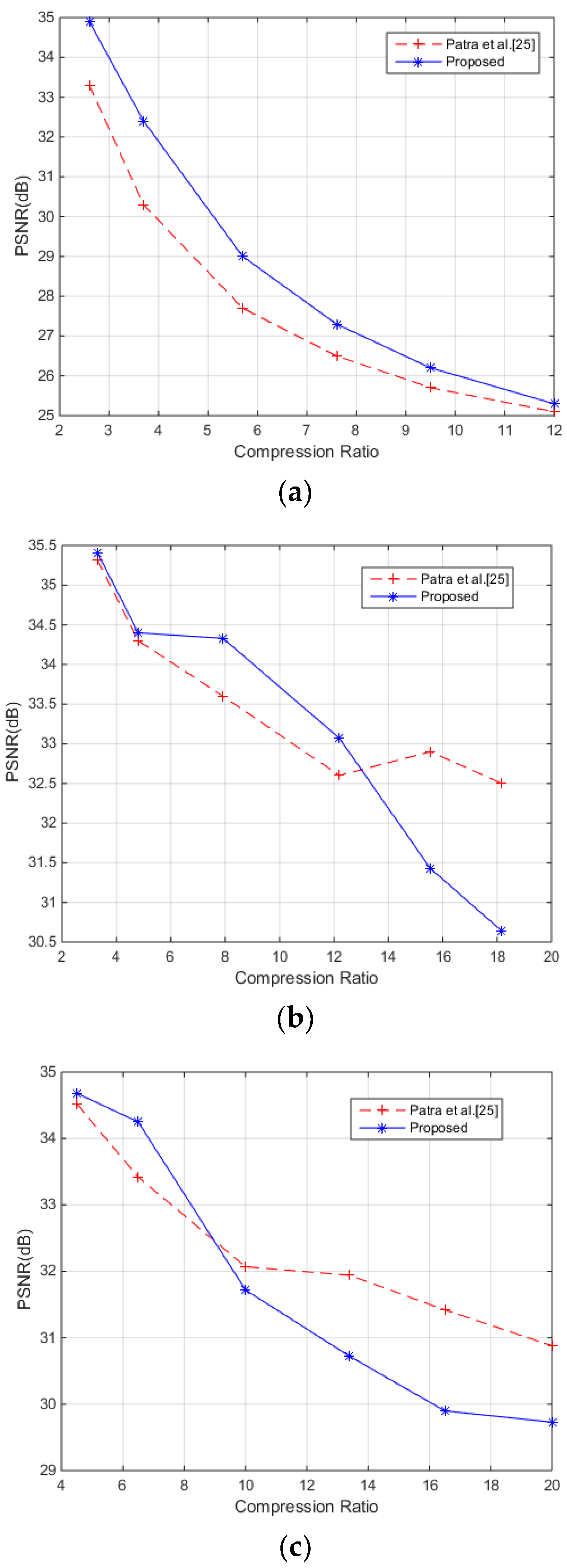
4. Simulation Results and Analysis

The experiments have been conducted on test images of size 512 × 512 pixels. MATLAB 14.1 tool is used for experiments on an Intel core i5 processor, 2.6 GHz CPU and 6 GB RAM. The watermark used in the experiment is a binary image of 62 × 64 pixels. In order to validate the objective judgement of the extracting fidelity, the performance comparison of the proposed method is compared with other schemes in terms of PSNR, Tamper assessment function (TAF) and Normalized Correlation (NC). For a watermark of size $m\times n$, the TAF in percentage is defined as:

$$\mathrm{TAF}(\%)=\frac{1}{mn}\left[{\displaystyle \sum _{i=0}^m{\displaystyle \sum _{j=0}^{n}w(i,j)\oplus \overline{w}(i,j)}}\right]\times 100,$$

(4)

and, Normalized Correlation (NC) is defined as:

$$\mathrm{NC}=\frac{{\displaystyle \sum _{i=0}^m{\displaystyle \sum _{j=0}^{n}w(i,j)\times \overline{w}(i,j)}}}{{\displaystyle \sum _{i=0}^m{\displaystyle \sum _{j=0}^n{[w(i,j)]}^2}}},$$

(5)

where $w(i,j)$ and $\overline{w}(i,j)$ represent the original and extracted watermarks at position $(i,j)$, respectively; and, $\oplus$ is exclusive or operation. TAF represents the number of bits of the extracted watermark that are different from the original watermark. The acceptance level of TAF is usually 20% as the extracted watermark is not recognizable beyond this value. Similarly, the NC value is 1 for highest-quality watermark and 0 for lowest-quality watermark. Watermark having NC below 0.3–0.4 is not recognizable.

PSNR is a quantitative measure of image quality between original host image and watermarked image. The value of PSNR usually ranges between 20 dB (low quality) and 40 dB (high quality). For 8-bit grayscale images PSNR is given as:

$$\mathrm{PSNR}(\mathrm{dB})=10 {\log }_{10}\left[\frac{{255}^2}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$MN$}\right.{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{[X(i,j)-\overline{X}(i,j)]}^2}}}\right],$$

(6)

where $X$ represents the host image, and $\overline{X}$ represents the watermarked image. $M\times N$ represents the size of the two images.

Structural similarity (SSIM) index is used for measuring similarity between two images. SSIM is designed to improve on traditional methods such as PSNR, which has been proven to be inconsistent with human visual perception. The measure between two images $X$ and $\overline{X}$ of same size $M\times N$ is given by:

$$\mathrm{SSIM}=\frac{(2{\mu }_x{\mu }_{\overline{x}}+c_1)(2{\sigma }_{x\overline{x}}+c_2)}{({\mu }_x^2+{\mu }_{\overline{x}}^2+c_1)({\sigma }_x^2+{\sigma }_{\overline{x}}^2+c_2)},$$

(7)

where ${\mu }_x$ and ${\sigma }_x^2$ are the average and variance of image $X$ respectively, ${\mu }_{\overline{x}}$ and ${\sigma }_{\overline{x}}^2$ are the average and variance of watermarked image $\overline{X}$ respectively. ${\sigma }_{x\overline{x}}$ is the covariance. $c_1$ and $c_2$ are two variables to stabilize the denominator. Its range is from 0 to 1. If two images are perfectly matched, SSIM = 1.

The performance comparison is carried out considering the following performance criteria:

• Quality of the watermarked images.
• Robustness of the scheme against common attacks such as compression, crop, histogram manipulation, auto contrast, noise, inversion and filtering.

4.1. Quality of the Watermarked Images

Table 1. PSNR (Peak signal to noise ratio), structural similarity (SSIM), tamper assessment function (TAF), and Normalized Correlation (NC) performance on the Lena Image’; SPIHT: set partitioning in hierarchical trees; LSK: Listless SPECK. Bolded numbers indicate improvement in results.

Image	Bit Rate (bpp)	Algorithm	PSNR (dB)	SSIM	NC	TAF (%)
Lena	0.25	SPIHT [35]	31.24	0.9075	0.1317	65.15
		LSK [38]	30.93	0.8974	0.3032	52.75
		Proposed	30.93	0.8982	0.3201	51.61
	0.5	SPIHT	31.10	0.9167	0.9848	1.71
		LSK	31.31	0.9301	0.9828	2.04
		Proposed	31.36	0.9292	0.9848	1.86
	1.0	SPIHT	33.87	0.9600	0.9801	1.84
		LSK	34.02	0.9621	0.9797	1.91
		Proposed	34.13	0.9617	0.9804	1.94
	1.5	SPIHT	34.35	0.9658	0.9227	6.14
		LSK	34.76	0.9677	0.9180	6.52
		Proposed	34.40	0.9676	0.9149	6.32
	2.0	SPIHT	34.83	0.9686	0.9298	5.56
		LSK	34.76	0.9677	0.9180	6.52
		Proposed	34.90	0.9693	0.9257	5.26
	2.5	SPIHT	35.41	0.9738	0.9510	4.00
		LSK	35.33	0.9733	0.9517	4.08
		Proposed	35.44	0.9740	0.9598	4.07
	3.0	SPIHT	35.65	0.9724	0.9490	4.08
		LSK	35.52	0.9744	0.9480	4.28
		Proposed	35.65	0.9739	0.9558	3.27
	Lossless	SPIHT	35.83	0.9762	0.9841	1.36
		LSK	35.68	0.9754	0.9747	2.24
		Proposed	36.00	0.9750	0.9831	1.36

,

Table 2. PSNR, SSIM, TAF and NC performance on the Barbara Image.

Image	Bit Rate (bpp)	Algorithm	PSNR (dB)	SSIM	NC	TAF (%)
Barbara	0.25	SPIHT [35]	26.92	0.8454	0.0300	72.93
		LSK [38]	27.26	0.8749	0.0527	71.27
		Proposed	27.25	0.8730	0.0700	70.33
	0.5	SPIHT	29.42	0.9106	0.3788	47.58
		LSK	29.03	0.9047	0.7539	19.63
		Proposed	28.97	0.9034	0.7762	17.94
	1.0	SPIHT	31.48	0.9474	0.9784	3.09
		LSK	32.16	0.9572	0.9673	3.57
		Proposed	32.25	0.9572	0.9737	3.27
	1.5	SPIHT	34.27	0.9714	0.9737	2.84
		LSK	34.43	0.9731	0.9689	3.25
		Proposed	34.50	0.9731	0.9659	3.57
	2.0	SPIHT	34.77	0.9774	0.9034	7.68
		LSK	34.78	0.9775	0.8974	8.19
		Proposed	34.83	0.9784	0.9045	7.38
	2.5	SPIHT	35.52	0.9801	0.9355	5.56
		LSK	35.25	0.9800	0.9136	6.98
		Proposed	35.54	0.9804	0.9416	5.26
	3.0	SPIHT	35.77	0.9821	0.9521	4.15
		LSK	35.66	0.9830	0.9477	4.41
		Proposed	35.86	0.9824	0.9440	4.73
	Lossless	SPIHT	36.06	0.9822	0.9791	2.04
		LSK	35.66	0.9814	0.9443	4.58
		Proposed	36.24	0.9827	0.9770	2.19

and

Table 3. PSNR, SSIM, TAF and NC performance on the Boat Image.

Image	Bit Rate (bpp)	Algorithm	PSNR (dB)	SSIM	NC	TAF (%)
Boat	0.25	SPIHT [35]	29.34	0.9066	0.078	69.70
		LSK [38]	29.20	0.9024	0.1425	64.76
		Proposed	29.21	0.9036	0.1610	63.43
	0.5	SPIHT	29.61	0.9085	0.9814	2.31
		LSK	30.04	0.9244	0.9791	2.41
		Proposed	30.10	0.9241	0.9801	2.41
	1.0	SPIHT	33.20	0.9599	0.9801	2.31
		LSK	33.42	0.9660	0.9743	2.64
		Proposed	33.44	0.9641	0.9757	2.36
	1.5	SPIHT	34.22	0.9648	0.9119	6.95
		LSK	34.32	0.9655	0.9088	7.15
		Proposed	34.34	0.9690	0.9136	6.75
	2.0	SPIHT	34.87	0.9693	0.9055	7.40
		LSK	34.80	0.9702	0.9058	7.56
		Proposed	34.94	0.9709	0.9099	7.18
	2.5	SPIHT	35.53	0.9732	0.9440	4.81
		LSK	35.44	0.9745	0.9470	4.41
		Proposed	35.52	0.9751	0.9456	4.51
	3.0	SPIHT	35.70	0.9758	0.9564	3.48
		LSK	35.60	0.9738	0.9396	4.88
		Proposed	35.75	0.9756	0.9537	3.88
	Lossless	SPIHT	35.92	0.9758	0.9804	1.89
		LSK	35.78	0.9747	0.9656	2.79
		Proposed	36.10	0.9760	0.9811	1.73

shows the compression performance comparison on the watermarked images for Lena, Barbara, and Boat images, respectively, using SPIHT, LSK and the proposed algorithm. The PSNR and SSIM performance is quite satisfactory below a BR (bit rate) of 0.25 bits per pixel (bpp). The corresponding compression ratio (CR) can be found using the formula CR = 8/BR, (i.e., CR = 32:1). The TAF (in %) and NC values are also listed. It can be noted from the Table 1, Table 2 and Table 3 that the extracted watermark using all the three algorithms are not recognizable above a BR of 0.25 bpp. As we increase the bit rate, the quality of the watermark and watermarked images is also improved. It can be seen from the Table 1, Table 2 and Table 3 that the proposed scheme provides better watermark quality and better compressed image quality at lossless compression mode for Lena, Barbara and Boat images. In lossy compression mode, our proposed scheme is highly competitive (with respect to watermarked image and the quality of extracted watermark) with SPIHT and LSK in most of the BR. A comparison of the extracted watermark quality is figured out in the Figure 4, Figure 5 and Figure 6 for Lena, Mandrill, and Boat images. For the Lena image (Figure 4), the proposed scheme outperforms NC and TAF values compared to the work by Patra et al. [25] at all compression ratios. Additionally, our scheme outperforms Das et al. [40] above 12:1 compression ratios. The similar improvements are also observed for Mandrill and Boat images in Figure 5 and Figure 6, respectively. We have not shown the comparison of TAF and NC values for Mandrill and Boat images due to unavailability of experimental datum by Das et al. [40]. Figure 7 shows the PSNR vs. Compression ratio for Mandrill, Lena, and Boat images. It is observed that for Mandrill image, our scheme outperforms the scheme by Patra et al. [25] in all CRs, i.e., the quality of the watermarked image is better using our scheme. However, a similar trend is not visualized in Lena and Boat images for all CRs. This is because our scheme provides better robustness and compression performance for texture images than smooth images.

Comparison of TAF and NC values on JPEG compression attacks:

4.2. Robustness after Different Attacks

Table 4. Simulation results of common image processing attacks.

Attacks	Crop	Noise (Impulse)	Sharpen	Invert	Histogram Equalize
Attacked Images
PSNR (dB)	35.8	35.9	37.9	35.9	34.9
Extracted Watermark
NC	0.7158	0.7208	0.5034	0.9771	0.5415
Attacks	Crop (top left)	Crop (top right)	Crop (bottom left)	Crop (bottom right)	Auto contrast
Attacked Images
PSNR (dB)	35.8	35.8	35.84	35.86	35.82
Extracted Watermark
NC	0.7316	0.7269	0.7411	0.7316	0.9838

shows the quality of the extracted watermark after some conventional attacks such as cropping, addition of noise, sharpening, inversion, histogram equalization and auto contrast operations. It observed that the proposed method could able to extract a good quality watermark in all cases. Image inversion and auto contrast operation give better quality watermark with an NC value close to 1. Acceptable quality watermark is also obtained in cropping attack, masking face with a black box, cropping a quarter part of the image on any direction, noise and sharpen operations. Similar acceptable quality watermark can also be obtained by masking the image with a white box. The PSNR values indicate the extracted quality of the watermarked images. PSNR values of 35–36 dB indicate good quality watermarked images are also obtained in most of the attacks.

A comparison of quality of the watermark (NC values) for different attacks is shown in

Table 5. NC comparison of extracted watermark after common attacks.

Scheme	Crop	Noise	Sharpen	Invert	Histogram Equalize	Crop (Bottom Left)
Patra et al. [39]
NC	0.7650	0.9970	0.3798	0.1563	0.1344	0.7529
Patra et al. [25]
NC	0.7097	0.7012	0.4997	0.9413	0.5371	0.7417
Proposed
NC	0.7158	0.7208	0.5034	0.9771	0.5415	0.7411

. The comparison is made with recent CRT-based algorithms by Patra et al. in [25,26]. It can be seen that there is a significant improvement in the quality of the watermark in invert, sharpen, histogram equalization and cropping attacks using the proposed scheme. There is also a noticeable improvement in cropping, sharpening, invert, histogram equalization attacks compared to Patra et al. [26]. Further, the proposed scheme shows some improvement for all the mentioned attacks compared to the scheme by Patra et al. [25].

5. Conclusions

A new approach for authentication and copyright protection based on DCT and listless SPIHT is proposed in this paper. The proposed method exhibit improved security and robustness due to incorporation of CRT for modifying the coefficients. The coefficient to be modified is selected randomly for every block. The average PSNR performance for compression is better compared to other CRT-based algorithms. Satisfactory TAF and NC values for watermark are obtained on a compression ratio up to 25:1 in most of the images, which is not possible in other schemes. Some major image attacks such as brightening, sharpening, noise, cropping, and inversion in the proposed scheme exhibit better resistance to the DCT-based CRT scheme. The overall complexity of the proposed scheme is less complex because CRT involves only modular operations for computation along with low-complexity listless SPIHT. Further research will involve implementing the proposed scheme on video watermarking.