Security Enhancement for Data Migration in the Cloud
Abstract
:1. Introduction
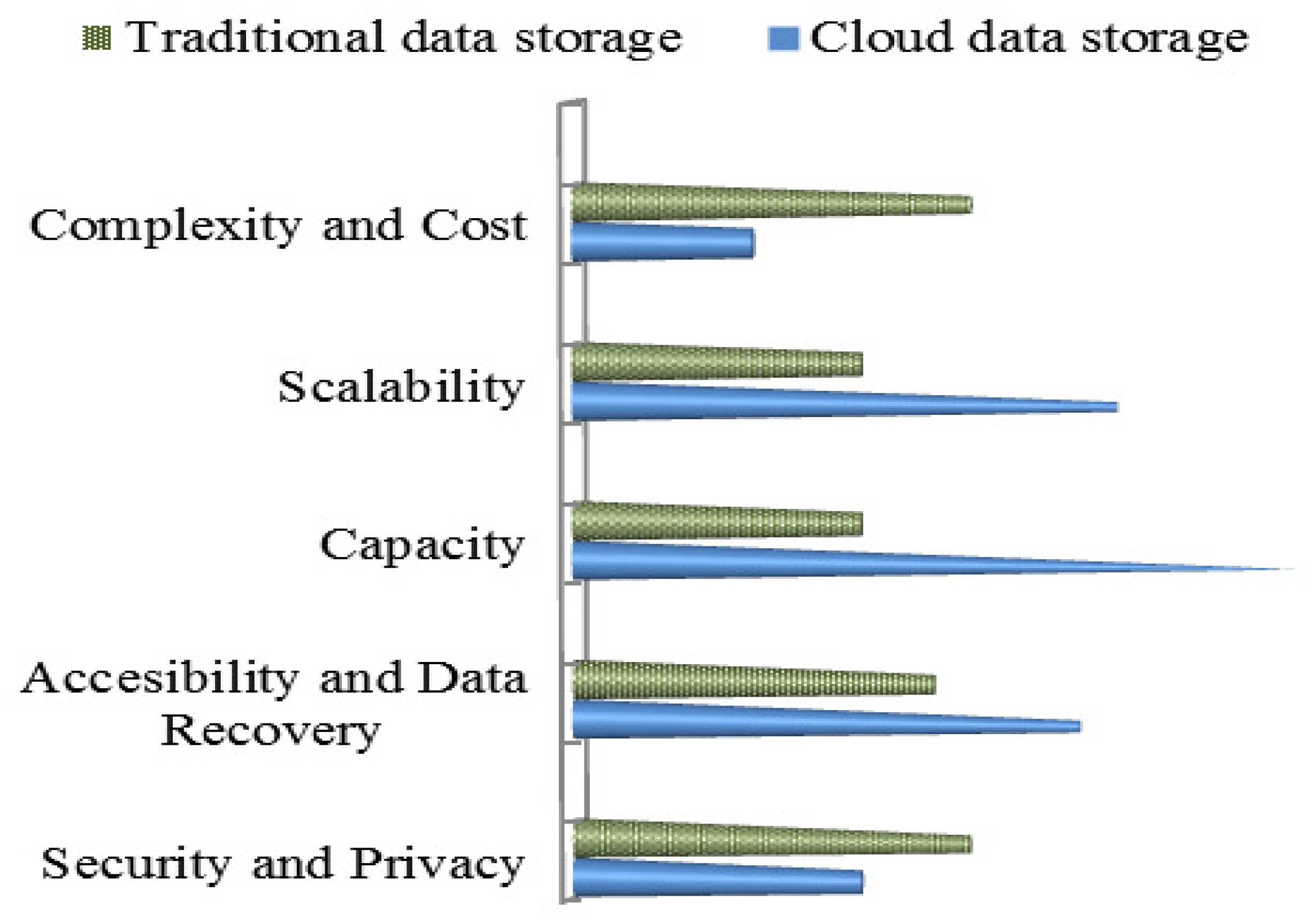
1.1. Cloud Data Storage versus Traditional Data Storage
1.1.1. Lower Complexity and Costs
1.1.2. Scalability and Capacity
1.1.3. Archival and Disaster Recovery Purposes
1.1.4. Greater Accessibility and Reliability
1.2. Cloud Storage Security and Privacy Threats
2. Background Preliminaries
2.1. Cryptographic Algorithms
2.1.1. Symmetric-Key Algorithm Also Known as Secret Key Encryption
2.1.2. Asymmetric-Key Algorithm or Public-Key Encryption
2.1.3. Hashing Algorithms, Also Called One-Way Encryption
2.2. Data Masking or Obfuscation
- the Unmasked e-mail address is: [email protected];
- masking result: [email protected].
2.3. Information Dispersal Algorithm
3. Existing Solutions and Prior Works
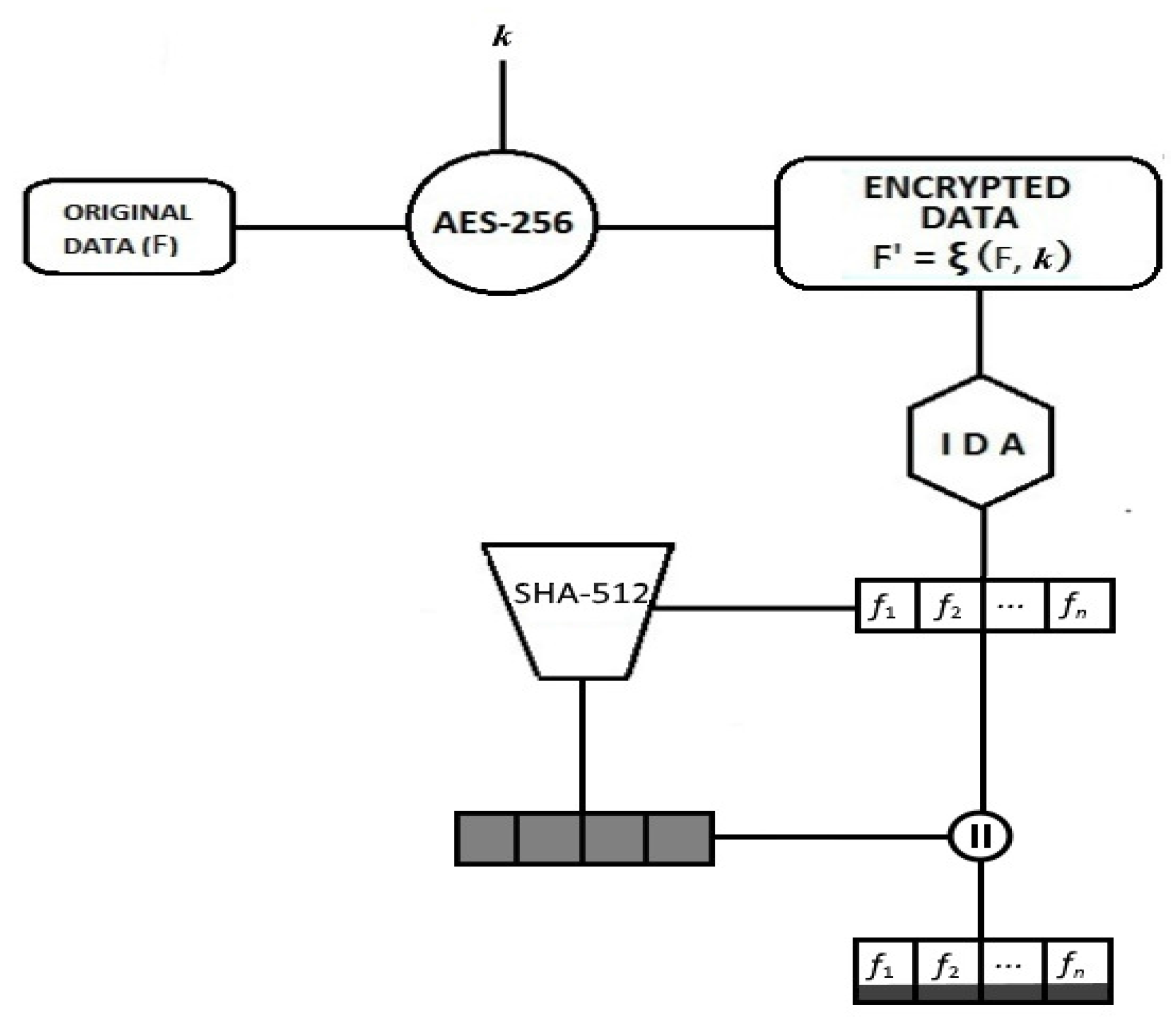
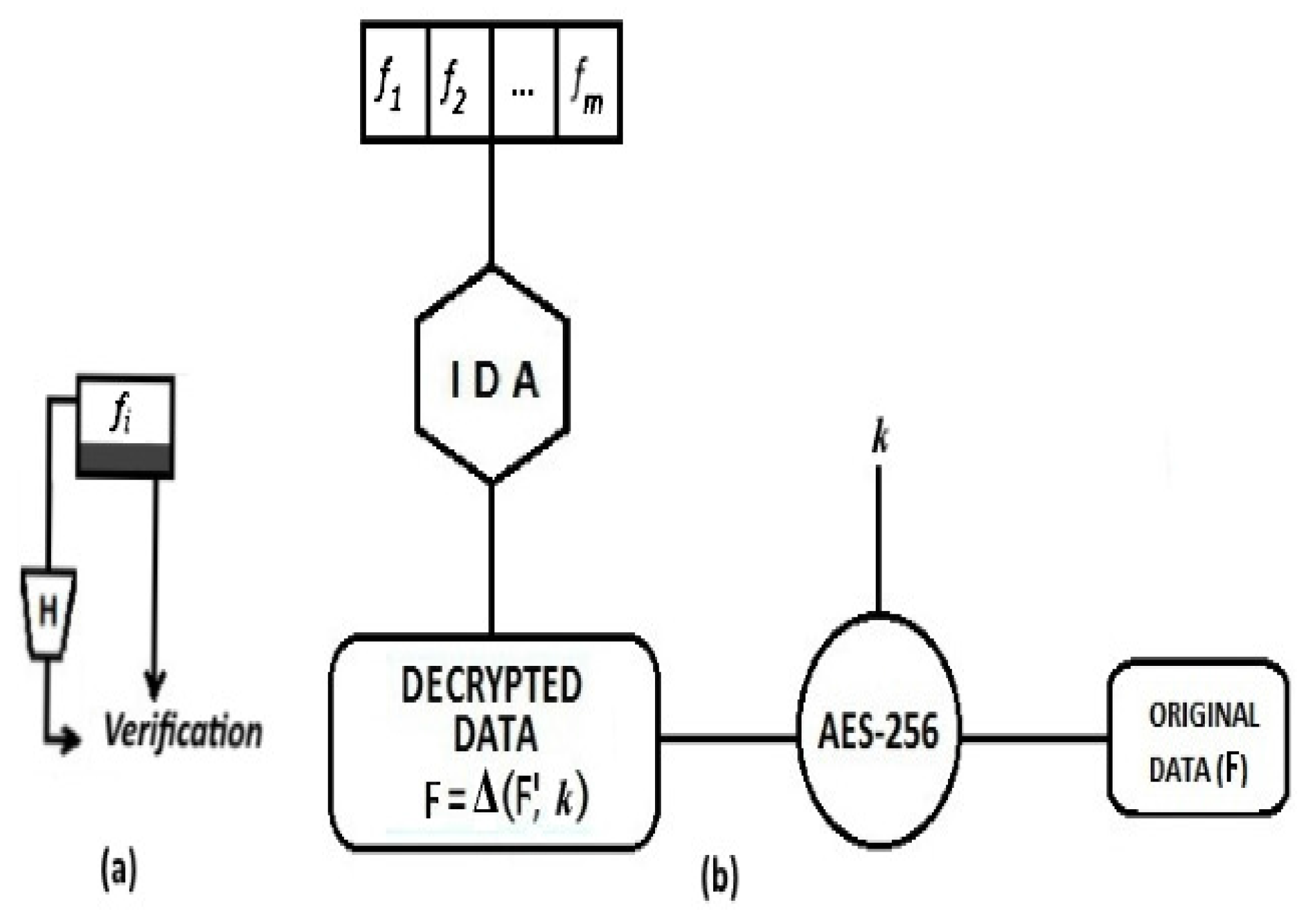
4. Proposed Model
4.1. Overview of the Encoding Process
4.2. Overview of the Decoding Process
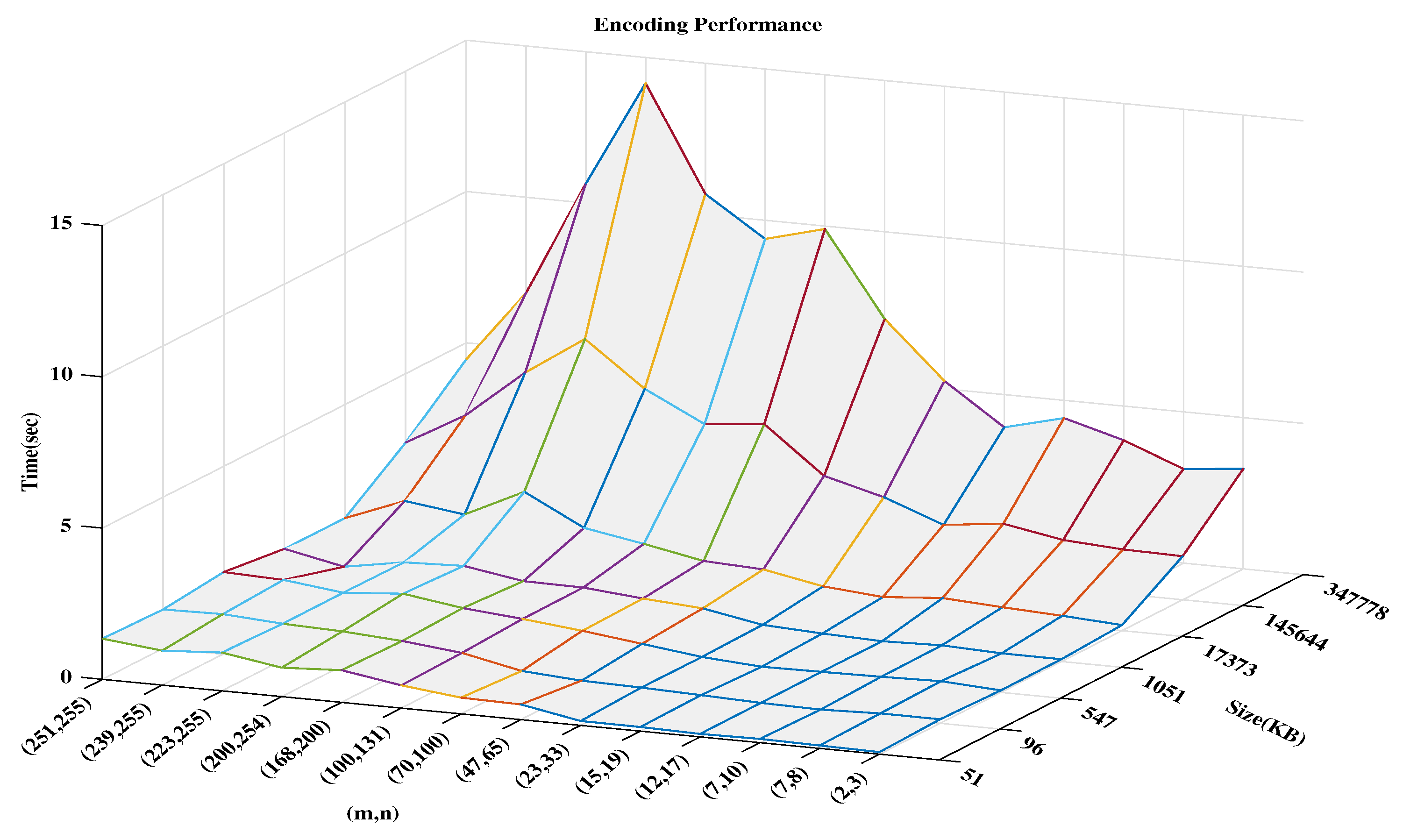
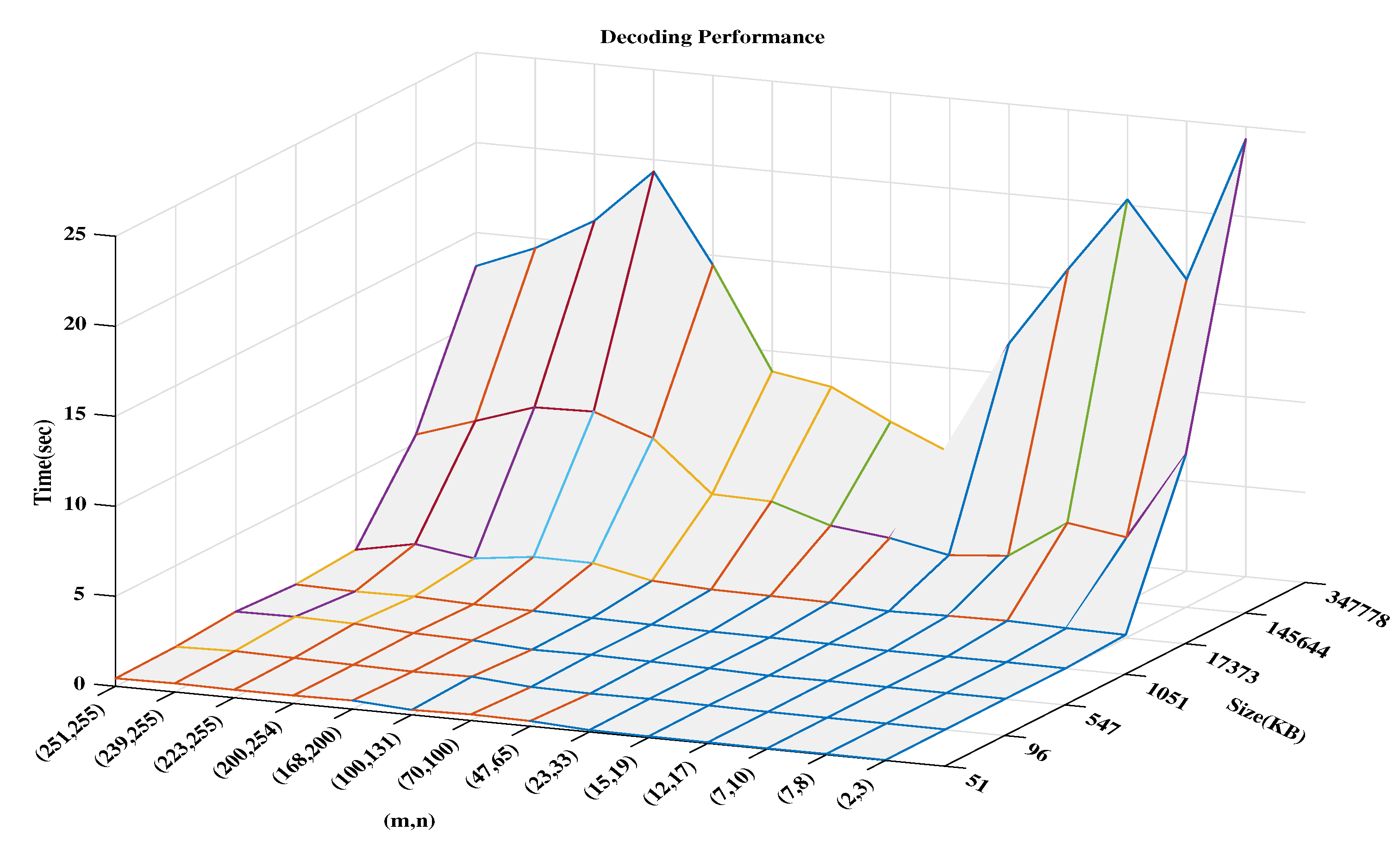
5. Experimental And Result Evaluations
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- NIST, Cloud Computing Program–29 July 2016: Cloud Computing. Available online: https://www.nist.gov/programs-projects/cloud-computing (accessed on 13 January 2017).
- Wolfgang, G. Cost Reduction Remains Chief Reason to Adopt Cloud, Confusion Still Apparent. Available online: http://www.tomsitpro.com/articles/cloud_survey-kpmg-tech_adoption-provider-it_security,1-803.html (accessed on 7 January 2017).
- Cloud Computing. Available online: https://en.wikipedia.org/wiki/Cloud_computing#Security_and_privacy (accessed on 8 February 2017).
- Press Releases. Cloud Storage Security Challenges. Available online: https://www.nasuni.com/news/26-top_5_security_challenges_of_cloud_storage/ (accessed on 5 April 2017).
- Stallings, W. Cryptography and Network Security Principles and Practices, 6th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Mask Sensitive Data. Available online: https://dataapps.io/redact.html (accessed on 12 January 2017).
- Sarada, G.; Abitha, N.; Manikandan, G.; Sairam, N. A few new approaches for data masking. In Proceedings of the 2015 International Conference on Circuit, Power and Computing Technologies, Nagercoil, India, 19–20 March 2015. [Google Scholar]
- Rabin, M.O. Efficient dispersal of information for security, load balancing, and fault tolerance. J. ACM 1989, 36, 335–348. [Google Scholar] [CrossRef]
- Li, M. On the Confidentiality of Information Dispersal Algorithms and Their Erasure Codes. arXiv, 2013; arXiv:1206.4123v2. [Google Scholar]
- Jaeger, B. Security as a Service Working Group, Defined Categories of Security as a Service (Preview)—Continuous Monitoring as a Service. Cloud Security Alliance 2016. Available online: https://downloads.cloudsecurityalliance.org/assets/research/security-as-a-service/csa-categories-securities-prep.pdf (accessed on 10 August 2016).
- Wall, M. Can We Trust Cloud Providers to Keep Our Data Safe? Available online: http://www.bbc.com/news/business-36151754 (accessed on 29 April 2016).
- White Paper. Securing Sensitive Data within Amazon Web Services Ec2 and Ebs: Challenges and the Solutions to Protecting Data within the AWS Cloud. Copyright 2013 Vormetric. Available online: http://go.thalesesecurity.com/rs/480-LWA-970/images/wp-securing-data-within-AWS.pdf (accessed on 29 April 2016).
- Rancourt, C. Celebrities Hacked: Are Your Personal Photos Safe in the Cloud? Available online: http://www.nextadvisor.com/blog/2014/09/02/celebrities-hacked-personal-photos-cloud-safe/ (accessed on 13 January 2017).
- Ahmadi, M.; Moghaddam, F.F.; Jam, A.J.; Gholizadeh, S.; Eslami, M. A 3-level re-encryption model to ensure data protection in cloud computing environments. In Proceedings of the IEEE Conference on System, Process & Control, Kuala Lumpur, Malaysia, 12–14 December 2014. [Google Scholar]
- Surv, N.; Wanve, B.; Kamble, R.; Patil, S.; Katti, J. Framework for client side aes encryption technique in cloud computing. In Proceedings of the IEEE International Advance Computing Conference, Banglore, India, 12–13 June 2015; pp. 525–528. [Google Scholar]
- Singh, S.; Kumar, V. Secured user’s authentication and private data storage-access scheme in cloud computing using elliptic curve cryptography. In Proceedings of the 2015 2nd International Conference on Computing for Sustainable Global Development, New Delhi, India, 11–13 March 2015. [Google Scholar]
- Raj, G.; Kesireddi, R.C.; Gupta, S. Enhancement of security mechanism for confidential data using aes-128, 192 and 256 bit encryption in cloud. In Proceedings of the 2015 1st International Conference on Next Generation Computing Technologies, Dehradun, India, 4–5 September 2015. [Google Scholar]
- Arockiam, L.; Monikandan, S. Efficient cloud storage confidentiality to ensure data security. In Proceedings of the International Conference on Computer Communication and Informatics, Coimbatore, India, 3–5 January 2014; pp. 1–5. [Google Scholar]
- Suthar, K.; Patel, J. EncryScation: A novel framework for cloud iaas, daas security using encryption and obfuscation techniques. In Proceedings of the 2015 5th Nirma University International Conference on Engineering (NUiCONE), Ahmedabad, India, 26–28 November 2015. [Google Scholar]
- Mar, K.K.; Law, C.Y.; Chin, V. Secure personal cloud storage. In Proceedings of the 10th International Conference for Internet Technology and Secured Transactions (ICITST-2015), London, UK, 14–16 December 2015. [Google Scholar]
- Zhang, X.; Wang, H. A study of the use of idas in cloud storage. Int. J. Future Comput. Commun. 2013, 2, 67. [Google Scholar] [CrossRef]
- Rich, S.; Gellman, B. NSA Seeks to Build Quantum Computer That Could Crack Most Types of Encryption. Available online: https://www.washingtonpost.com/world/national-security/nsa-seeks-to-build-quantum-computer-that-could-crack-most-types-of-encryption/2014/01/02/8fff297e-7195-11e3-8def-a33011492df2_story.html?utm_term=.217ad6b56479 (accessed on 14 July 2016).
- Balamurugan, S.; Sathyanarayana, S.; Manikandasaran, S.S. ESSAO: Enhanced security service algorithm using data obfuscation technique to protect data in public cloud storage. Indian J. Sci. Technol. 2016, 9. [Google Scholar] [CrossRef]
- Smith, C. PointThe Year of BYOE (Bring Your Own Encryption). Available online: https://cipherpoint.com/2014/06/2014-the-year-of-byoe-bring-your-own-encryption/ (accessed on 15 June 2016).
- Finite Field. Available online: https://en.wikipedia.org/wiki/Finite_field (accessed on 8 February 2017).
- Minowa, T.; Takahashi, T. Secure Distributed Storage for Bulk Data; Springer: Berlin/Heidelberg, Germany, 2012; pp. 566–575. [Google Scholar]
- Rubenking, N.J. The Best Encryption Software of 2017. Available online: http://www.pcmag.com/article/347066/the-best-encryption-software-of-2016 (accessed on 5 June 2017).
- Mishra, B.; Jena, D. Securing files in the cloud. In Proceedings of the 2016 IEEE International Conference on Cloud Computing in Emerging Markets, Bangalore, India, 19–21 October 2016. [Google Scholar]
| Notations | Description |
|---|---|
| F | Original data |
| Encrypted data | |
| Slices set | |
| Encoded set | |
| Slice data file | |
| Encryption, Decryption | |
| Encryption key | |
| Hash value using SHA-512 | |
| || | Concatenation |
| Encrypted file length | |
| n | total number of slices |
| m | number of symbols/bytes required to reconstruct |
| Slice data file length |
| Procedure |
|---|
| Input: Original data F; key , Threshold |
| Output: |
| (Note that is the encryption algorithm, is the hashing algorithm) |
| compute the encrypted version of the original data file F using under κ |
| := with F and |
| Let be the slicing algorithm that return a vector under the threshold (m,n) |
| := with and n |
| set indexCount to 1 |
| set := new initial list |
| for each in do |
| set call with |
| concatenate the data with the corresponding hash value |
| set |
| Append to the concatenated data |
| increment indexCount |
| return: |
| end procedure. |
| Procedure |
|---|
| Input: vector H; key ,value m |
| Output: Original data F |
| (Note that is the encryption algorithm, is the hashing algorithm) |
| let integrityCheck function checks the integrity of a particular data |
| set indexCount to 1 |
| set := new initial list |
| for each in H do |
| if integrityCheck with then |
| deconcatenate from |
| compute ;= - |
| else |
| compute |
| Append to the deconcatenated data |
| set := |
| Let be the slicing algorithm that return a vector under m |
| Reconstruct using |
| := with |
| Compute the decrypted version of F using under κ |
| F:= with and |
| return: F |
| end procedure |
| Process | Duration |
|---|---|
| Encryption | 0.367 |
| Slicing-IDA | 1.125 |
| Hashing and Concatenation | 0.474 |
| Verification | 1.453 |
| Reconstruction-IDA | 1.157 |
| Decryption | 0.297 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ngnie Sighom, J.R.; Zhang, P.; You, L. Security Enhancement for Data Migration in the Cloud. Future Internet 2017, 9, 23. https://doi.org/10.3390/fi9030023
Ngnie Sighom JR, Zhang P, You L. Security Enhancement for Data Migration in the Cloud. Future Internet. 2017; 9(3):23. https://doi.org/10.3390/fi9030023
Chicago/Turabian StyleNgnie Sighom, Jean Raphael, Pin Zhang, and Lin You. 2017. "Security Enhancement for Data Migration in the Cloud" Future Internet 9, no. 3: 23. https://doi.org/10.3390/fi9030023





