Feature-Based Image Watermarking Algorithm Using SVD and APBT for Copyright Protection
Abstract
:1. Introduction
2. Related Work
2.1. Digital Watermarking
2.2. APBT
2.3. SIFT Algorithm
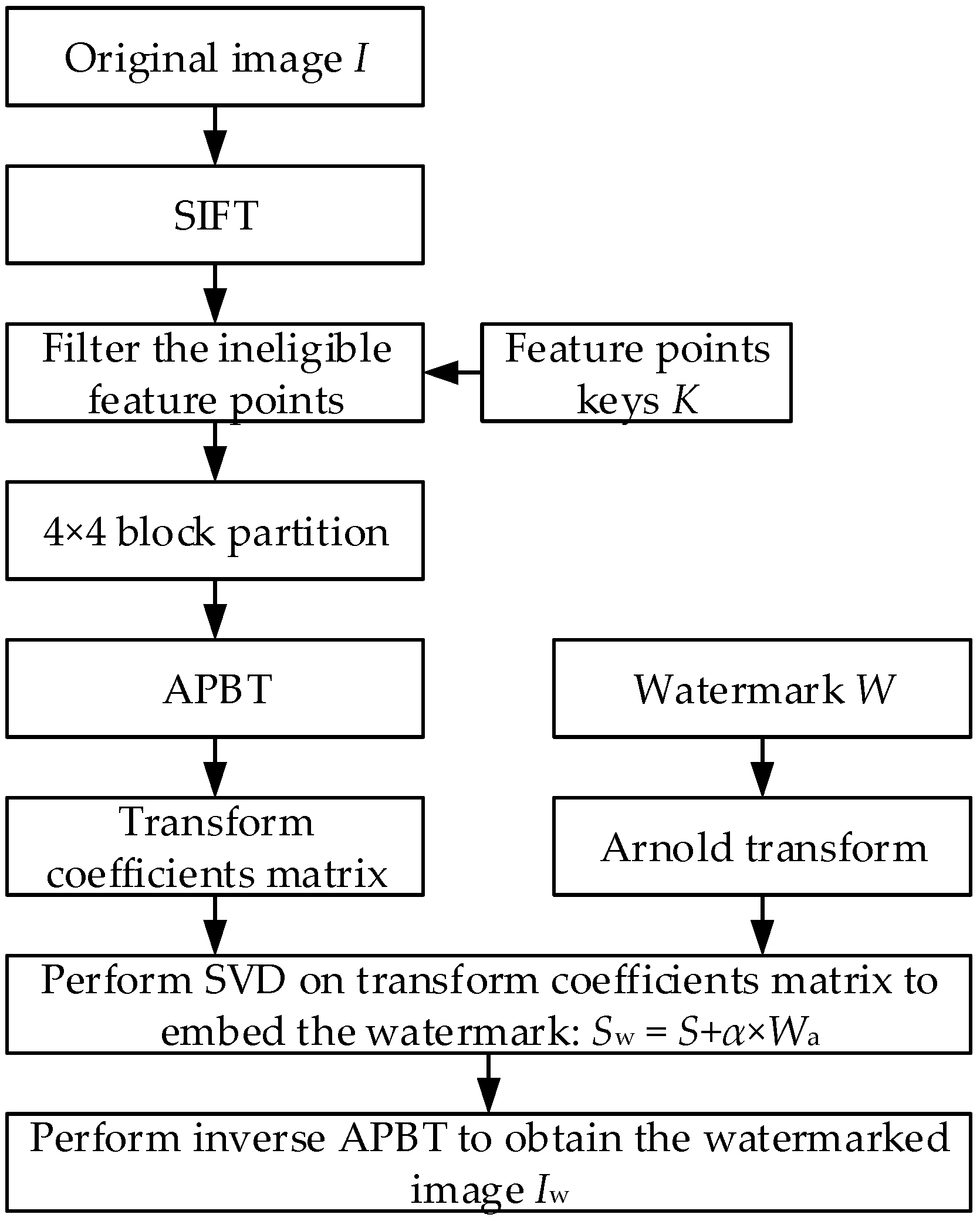
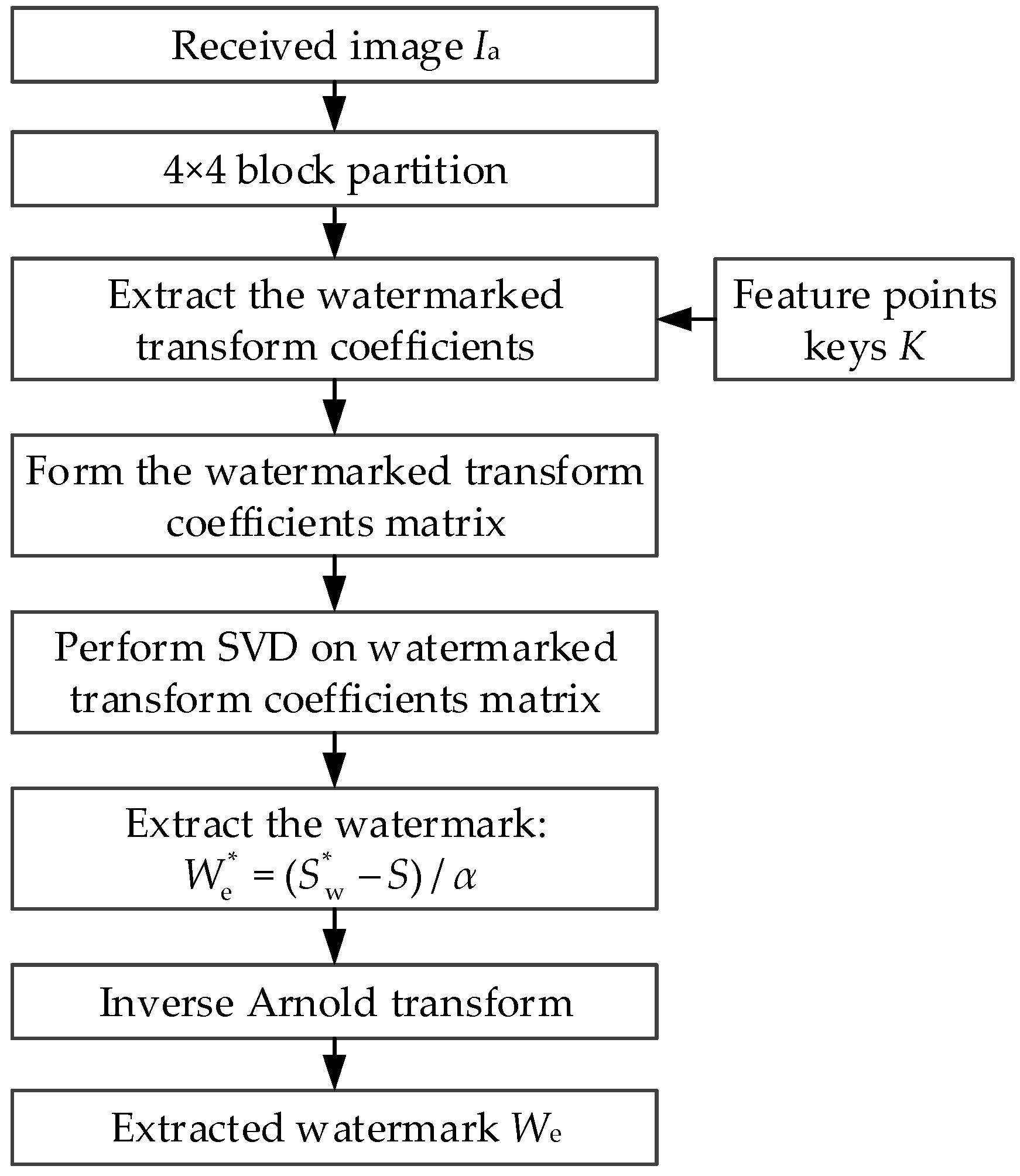
3. The Proposed Algorithm
3.1. Preparation before Embedding
3.2. Watermark Embedding
3.3. Watermarking Extraction
4. Experimental Results and Comparative Analyses
4.1. Performance Evaluation Indexes
4.2. Performance Comparisons
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Skodras, A.; Christopoulos, C.; Ebrahimi, T. The JPEG 2000 still image compression standard. IEEE Signal Process. Mag. 2001, 18, 36–58. [Google Scholar] [CrossRef]
- Lou, D.C.; Liu, J.L. Fault resilient and compression tolerant digital signature for image authentication. IEEE Trans. Consum. Electron. 2000, 46, 31–39. [Google Scholar]
- Langelaar, G.C.; Setywan, I.; Lagendijk, R.L. Watermarking digital image and video data. IEEE Signal Process. Mag. 2000, 17, 20–46. [Google Scholar] [CrossRef]
- Van Schyndel, R.G.; Tirkel, A.Z.; Osborne, C.F. A digital watermark. In Proceedings of the 1st IEEE International Conference on Image Processing, Austin, TX, USA, 13–16 November 1994; pp. 86–90. [Google Scholar]
- Mishra, A.; Agarwal, C.; Sharma, A.; Bedi, P. Optimized gray-scale image watermarking using DWT-SVD and Firefly algorithm. Expert Syst. Appl. 2014, 41, 7858–7867. [Google Scholar] [CrossRef]
- Sakthivel, S.M.; Ravi Sankar, A. A real time watermarking of grayscale images without altering its content. In Proceedings of the International Conference on VLSI Systems, Architecture, Technology and Applications, Bengaluru, India, 8–10 January 2015; pp. 1–6. [Google Scholar]
- Jin, X.Z. A digital watermarking algorithm based on wavelet transform and Arnold. In Proceedings of the International Conference on Computer Science and Service System, Nanjing, China, 27–29 June 2011; pp. 3806–3809. [Google Scholar]
- An, Z.Y.; Liu, H.Y. Research on digital watermark technology based on LSB algorithm. In Proceedings of the 4th International Conference on Computational and Information Sciences, Chongqing, China, 17–19 August 2012; pp. 207–210. [Google Scholar]
- Qi, X.J.; Xin, X. A singular-value-based semi-fragile watermarking scheme for image content authentication with tamper localization. J. Vis. Commun. Image Represent. 2015, 30, 312–327. [Google Scholar] [CrossRef]
- Makbol, N.M.; Khoo, B.E. Robust blind image watermarking scheme based on redundant discrete wavelet transform and singular value decomposition. AEU—Int. J. Electron. Commun. 2013, 67, 102–112. [Google Scholar] [CrossRef]
- Pujara, C.; Bhardwaj, A.; Gadre, V.M.; Khire, S. Secure watermarking in fractional wavelet domains. IETE J. Res. 2007, 53, 573–580. [Google Scholar] [CrossRef]
- Rasti, P.; Samiei, S.; Agoyi, M.; Escalera, S.; Anbarjafari, G. Robust non-blind color video watermarking using QR decomposition and entropy analysis. J. Vis. Commun. Image Represent. 2016, 38, 838–847. [Google Scholar] [CrossRef]
- Cheng, M.Z.; Yan, L.; Zhou, Y.J.; Min, L. A combined DWT and DCT watermarking scheme optimized using genetic algorithm. J. Multimed. 2013, 8, 299–305. [Google Scholar]
- Guo, J.T.; Zheng, P.J.; Huang, J.W. Secure watermarking scheme against watermark attacks in the encrypted domain. J. Vis. Commun. Image Represent. 2015, 30, 125–135. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Chang, C.C.; Yang, X.Q. A reversible image authentication scheme based on fragile watermarking in discrete wavelet transform domain. AEU—Int. J. Electron. Commun. 2016, 70, 1055–1061. [Google Scholar] [CrossRef]
- Martino, F.D.; Sessa, S. Fragile watermarking tamper detection with images compressed by fuzzy transform. Inf. Sci. 2012, 195, 62–90. [Google Scholar] [CrossRef]
- Lin, C.S.; Tsay, J.J. A passive approach for effective detection and localization of region level video forgery with spatio-temproal coherence analysis. Dig. Investig. 2014, 11, 120–140. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the 7th IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar]
- Mikolajczyk, K.; Schmid, C. A performance evaluation of local descriptors. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 18–20 June 2003; Volume 2, pp. 257–263. [Google Scholar]
- Lee, H.; Kim, H.; Lee, H. Robust image watermarking using local invariant features. Opt. Eng. 2006, 45, 535–545. [Google Scholar]
- Lyu, W.L.; Chang, C.C.; Nguyen, T.S.; Lin, C.C. Image watermarking scheme based on scale-invariant feature transform. KSII Trans. Int. Inf. Syst. 2014, 8, 3591–3606. [Google Scholar]
- Thorat, C.G.; Jadhav, B.D. A blind digital watermark technique for color image based on integer wavelet transform and SIFT. Proced. Comput. Sci. 2010, 2, 236–241. [Google Scholar] [CrossRef]
- Luo, H.J.; Sun, X.M.; Yang, H.F.; Xia, Z.H. A robust image watermarking based on image restoration using SIFT. Radioengineering 2011, 20, 525–532. [Google Scholar]
- Pham, V.Q.; Miyaki, T.; Yamasaki, T.; Aizawa, K. Geometrically invariant object-based watermarking using SIFT feature. In Proceedings of the 14th IEEE International Conference on Image Processing, San Antonio, TX, USA, 16–19 September 2007; Volume 5, pp. 473–476. [Google Scholar]
- Zhang, L.; Tang, B. A combination of feature-points-based and SVD-based image watermarking algorithm. In Proceedings of the International Conference on Industrial Control and Electronics Engineering, Xi’an, China, 23–25 August 2012; pp. 1092–1095. [Google Scholar]
- Hou, Z.X.; Wang, C.Y.; Yang, A.P. All phase biorthogonal transform and its application in JPEG-like image compression. Signal Process. Image Commun. 2009, 24, 791–802. [Google Scholar] [CrossRef]
- Yang, F.F.; Wang, C.Y.; Huang, W.; Zhou, X. Embedding binary watermark in DC components of all phase discrete cosine biorthogonal transform. Int. J. Secur. Appl. 2015, 9, 125–136. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Babaud, J.; Witkin, A.P.; Baudin, M.; Duda, R.O. Uniqueness of the Gaussian kernel for scale-space filtering. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Jain, C.; Arora, S.; Panigrahi, P.K. A reliable SVD based watermarking scheme. Comput. Sci. arXiv 2008. Available online: https://arxiv.org/pdf/0808.0309.pdf (accessed on 18 April 2017).
- Zhang, Z.; Wang, C.Y.; Zhou, X. Image watermarking scheme based on DWT-DCT and SSVD. Int. J. Secur. Appl. 2016, 10, 191–206. [Google Scholar]
- Fzali, S.; Moeini, M. A robust image watermarking method based on DWT, DCT, and SVD using a new technique for correction of main geometric attacks. Optik 2016, 127, 964–972. [Google Scholar] [CrossRef]








| Images | PSNR | NC | BER | |
|---|---|---|---|---|
| Airplane | w1 | 90.56 | 0.9994 | 0.0008 |
| w2 | 93.28 | 0.9961 | 0.0137 | |
| Baboon | w1 | 79.31 | 0.9683 | 0.0156 |
| w2 | 89.76 | 0.9043 | 0.0068 | |
| Barbara | w1 | 91.18 | 0.9648 | 0.0176 |
| w2 | 90.27 | 0.8681 | 0.0447 | |
| Bank | w1 | 82.92 | 0.9577 | 0.0195 |
| w2 | 91.18 | 0.9137 | 0.0317 | |
| Elaine | w1 | 74.59 | 0.9401 | 0.0225 |
| w2 | 77.68 | 0.7354 | 0.0680 | |
| Barche | w1 | 79.55 | 0.9542 | 0.0195 |
| w2 | 92.32 | 0.8772 | 0.0391 | |
| Milkdrop | w1 | 78.12 | 0.9225 | 0.0273 |
| w2 | 81.05 | 0.7129 | 0.0653 | |
| Panzer | w1 | 78.85 | 0.9683 | 0.0146 |
| w2 | 85.78 | 0.8803 | 0.0389 | |
| Announcer | w1 | 76.48 | 0.8121 | 0.0957 |
| w2 | 85.50 | 0.8973 | 0.0376 | |
| Vogue | w1 | 77.78 | 0.7928 | 0.0969 |
| w2 | 83.29 | 0.8515 | 0.0434 | |
| Cablecar | w1 | 86.30 | 0.8577 | 0.0770 |
| w2 | 90.28 | 0.9044 | 0.0342 | |
| Canyon | w1 | 85.98 | 0.8299 | 0.0784 |
| w2 | 93.29 | 0.8918 | 0.0400 | |
| Clown | w1 | 81.42 | 0.8208 | 0.1056 |
| w2 | 87.69 | 0.8281 | 0.0489 | |
| Cornfield | w1 | 86.63 | 0.8618 | 0.0853 |
| w2 | 84.19 | 0.8949 | 0.0365 | |
| Frog | w1 | 82.54 | 0.8270 | 0.0842 |
| w2 | 85.07 | 0.8820 | 0.0430 | |
| Fruits | w1 | 75.17 | 0.8879 | 0.0784 |
| w2 | 81.49 | 0.9217 | 0.0291 | |
| Different Indexes | Jain et al. [30] | Zhang et al. [31] | Fzali and Moeini [32] | APDCBT |
|---|---|---|---|---|
| PSNR (dB) | 20.98 | 39.75 | 56.42 | 90.56 |
| Execution Time (s) | 1.10 | 2.43 | 3.46 | 6.07 |
| Gaussian Noise (0, 0.01) | 0.9695 | 0.8016 | 0.9897 | 0.9983 |
| Salt and Pepper Noise (0.01) | 0.9157 | 0.8925 | 0.9842 | 0.9923 |
| JPEG Compression (QF = 50) | 0.9877 | 0.9850 | 0.9865 | 0.9830 |
| JPEG Compression (QF = 100) | 0.9960 | 0.9984 | 0.9999 | 0.9838 |
| Sparse Region Cropping (100 × 100) | 0.8236 | 0.9236 | 0.9999 | 0.9841 |
| Sparse Region Cropping (256 × 256) | - | 0.8187 | 0.9602 | 0.9821 |
| Dense Region Cropping (100 × 100) | 0.6589 | 0.9255 | 0.9804 | 0.9847 |
| Dense Region Cropping (256 × 256) | - | 0.8182 | 0.9682 | 0.9881 |
| Combination of Attacks | BER | NC |
|---|---|---|
| 1 | 0.0008 | 0.9994 |
| 2 and 4 | 0.0061 | 0.9945 |
| 2 and 5 | 0.0039 | 0.9974 |
| 2 and 6 | 0.0049 | 0.9991 |
| 3 and 4 | 0.0046 | 0.9949 |
| 3 and 5 | 0.0049 | 0.9949 |
| 3 and 6 | 0.0081 | 0.9915 |
| 4 and 5 | 0.0088 | 0.9838 |
| 4 and 6 | 0.0120 | 0.9847 |
| 2, 4, and 5 | 0.0046 | 0.9991 |
| 2, 4, and 6 | 0.0046 | 0.9993 |
| 3, 4, and 5 | 0.0061 | 0.9889 |
| 3, 4, and 6 | 0.0066 | 0.9915 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, C.; Wang, X.; Wang, M. Feature-Based Image Watermarking Algorithm Using SVD and APBT for Copyright Protection. Future Internet 2017, 9, 13. https://doi.org/10.3390/fi9020013
Zhang Y, Wang C, Wang X, Wang M. Feature-Based Image Watermarking Algorithm Using SVD and APBT for Copyright Protection. Future Internet. 2017; 9(2):13. https://doi.org/10.3390/fi9020013
Chicago/Turabian StyleZhang, Yunpeng, Chengyou Wang, Xiaoli Wang, and Min Wang. 2017. "Feature-Based Image Watermarking Algorithm Using SVD and APBT for Copyright Protection" Future Internet 9, no. 2: 13. https://doi.org/10.3390/fi9020013
APA StyleZhang, Y., Wang, C., Wang, X., & Wang, M. (2017). Feature-Based Image Watermarking Algorithm Using SVD and APBT for Copyright Protection. Future Internet, 9(2), 13. https://doi.org/10.3390/fi9020013







