2. Results and Discussion
Ferromagnetic materials can be magnetized by the Earth’s magnetic field. Because their magnetic permeability is much higher than that of air, their presence creates a path of low reluctance, distorting lines of geomagnetic flux. Furthermore, most ferromagnetic elements have their own residual magnetism, which in effect causes them to act like a magnetic dipole. Thus, there are two sources of magnetization of a given ferromagnetic object—remanent magnetization and magnetization by external magnetic field such as earth magnetic field. Most ferromagnetic objects will disturb the surrounding magnetic field with both of these effects. Actual distinction between the sources of object magnetization, which in turn cause surrounding field perturbations, is unimportant from the detection and localization point of view. For the study of these disturbances, an XY scanning system was designed and built, with a single, tri-axial magnetoresistive Honeywell HMR2300 sensor (
Figure 1). The sensor has a resolution of 7 nT and measuring range of ±200 µT, which is sufficient to measure weak magnetic fields.
During the measurements, no additional fields have been applied. Therefore only background disturbances were measured, mainly disturbances of the natural Earth’s magnetic field. Scanning probe system transit along parallel lines with a given interval (20 mm), setting the measuring plane (200 mm × 200 mm). Unlike other existing magneto-vision systems, application of tri-axial sensor enabled gathering information about the magnetic induction vector value and its direction with respect to each measurement point in the scanning plane, not only its absolute value, or value of only one component, as is the case with most Hall effect systems.
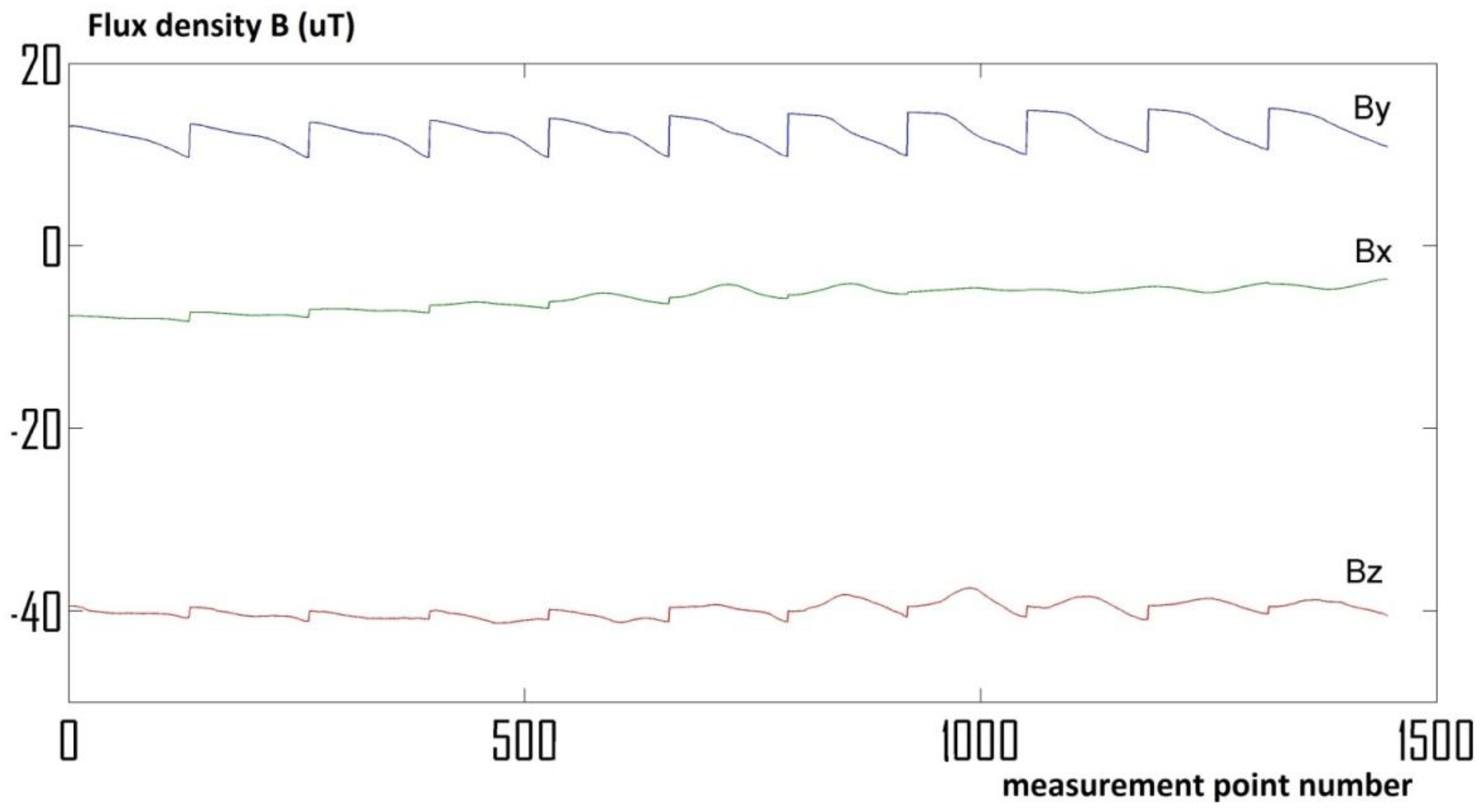
Measurement results are gathered in the form of three signals, proportional to the induction vector components in measurement points (
Figure 2). Raw data are enough to calculate the value and direction of the magnetic induction vectors in all measurement points. By subtraction of the relatively constant Earth’s magnetic field, vectors of additional magnetic disturbances can be visualized (
Figure 3). Visualization of the distribution of the magnetic induction vector absolute values, interpolated to 1000 × 1000 points resolution, is also possible (
Figure 4).
Figure 1.
Schematic block diagram of the measuring system: HMR 2300—magnetoresistive sensor, Sample—investigated object, Sm—stepper motors, C—motor controllers, MI 3.8.9—trajectory generator, Ps—power supply, PC—controlling and image processing computer.
Figure 1.
Schematic block diagram of the measuring system: HMR 2300—magnetoresistive sensor, Sample—investigated object, Sm—stepper motors, C—motor controllers, MI 3.8.9—trajectory generator, Ps—power supply, PC—controlling and image processing computer.
Figure 2.
Raw measurements data collected using the magnetovision scanning system.
Figure 2.
Raw measurements data collected using the magnetovision scanning system.
Since the magnetoresistive sensor measures only the value of the three components of the flux density vector at a point in which it is physically located, a separation of distortion generated by a sample object from the background is problematic. The simplest laboratory solution is the differential measurement by measurement without the test object and subtracting the result from the measurement with an object. This method gives the best results, allowing precise separation of magnetic induction distribution of the background and the object, which allows for low-level noise in the magnetovision image. However, this method is possible only in certain conditions, where it is possible to make measurements with an object and without, in the same plane. For this reason, a method of differential measurement was developed, minimizing the impact of the background to the measurement results. With this method, both the Earth’s magnetic field as well as the other sources of background can be filtered out. In its basic form, a differential measurement is the measurement in two parallel planes, at the height x above the test object, and x + h, where h is the distance between the planes of measurement, and then subtracting the results.
Figure 3.
Visualization of induction vectors value and direction on measurement lines for simple dipole sample, with magnetic background removed. Additional disturbances of the magnetic field can be clearly seen.
Figure 3.
Visualization of induction vectors value and direction on measurement lines for simple dipole sample, with magnetic background removed. Additional disturbances of the magnetic field can be clearly seen.
Figure 4.
Visualization of the distribution of the magnetic induction vector absolute values, with the magnetic background intact. In addition to positive and negative disturbances, the Earth’s magnetic field can be seen.
Figure 4.
Visualization of the distribution of the magnetic induction vector absolute values, with the magnetic background intact. In addition to positive and negative disturbances, the Earth’s magnetic field can be seen.
Distribution of flux density lines near a ferromagnetic object placed in the Earth’s magnetic field is similar to a magnetic dipole field distribution. In particular, the magnetic flux density can be described as a dipole magnetic field characterized by a magnetic dipole moment
. Induction of the magnetic field on the axis of the magnet, in a vacuum, at a distance
x from its center is expressed by the formula:
where:
—magnetic dipole moment (Am
2);
magnetic permeability of vacuum;
—induction replacement constant (Tm
3)
Since the value of the flux density
B is reduced in proportion to the cube of the distance from the source, if
a ≈
x, distortion
caused by the object in the first measurement plane will be up to 8 times greater than the
in the second plane. If, however, other sources of magnetic field are at a significantly greater distance
y >>
x from the first measurement plane, their influence
on the value of magnetic induction in the planes
P1 and
P2 will be similar. Therefore:
where:
—result of flux density measurement in plane
P1;
—result of flux density measurement in plane
P2;
,
—Background magnetic induction values in
P1,
P2 planes. Assuming:
,
. Then:
As a result it is therefore possible to get a rough magnetovision image of the sample located a short distance from the sensor by subtracting the results of a measurement in the plane P2 from the results in the plane P1. Differential bi-plane measurement gives the absolute value of the difference in magnetic induction value between the measurement planes.
A similar method to compensate for the impact of background on the measurement result is the gradient measurement used in astrophysics and geology (e.g., in gradiometers). In the generalization it is based on the measurement of the magnetic field or gravity values at different levels and the field gradient designation on that basis. Use of this method also yields good results, but the images obtained are distinctly different than those obtained by the differential method. They allow us to distinguish between positive and negative areas of magnetic disturbance relative to the Earth’s field, but the bi-plane measurement gives a better picture of the silhouette of the hidden object.
3. Experimental Section
Measurements were carried out on a test stand setup described in previous chapter. For the purpose of the study, a steel cylinder, 70 mm in diameter and 20 mm in height was used as a sample object. Such element can simulate landmine for tests [
5]. Distance between measurement planes for the differential method was set to
h = 50mm.
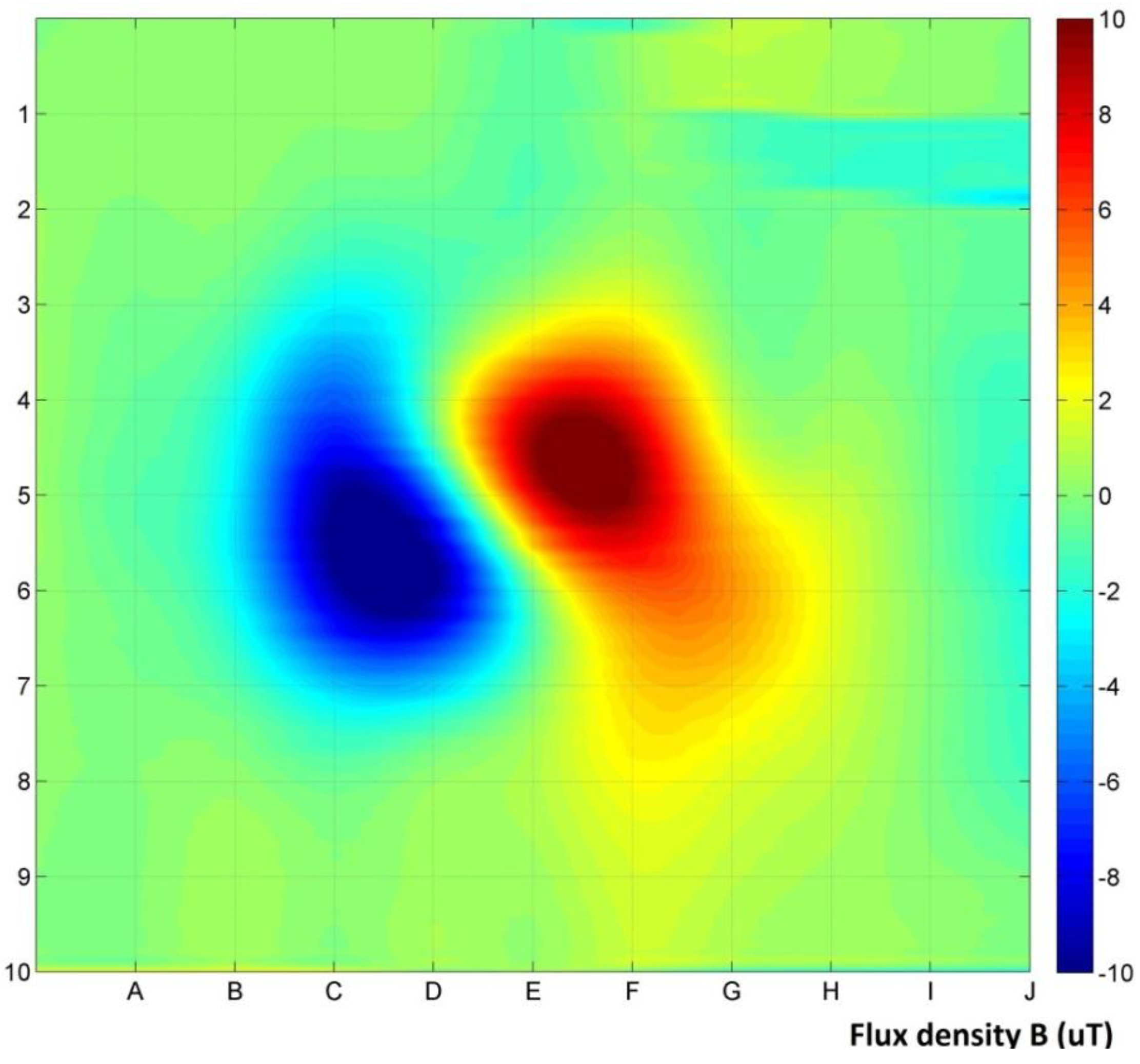
Figure 5 shows the gradient measurement results of the sample, with removing the influence of background magnetic field. Results exhibit a distinct difference between the positive and negative areas of magnetic disturbance. Distance of the sample from the plane of the measurement was
x = 100 mm.
Figure 6 shows a magnetovision image obtained by differential bi-plane measurement within 100 mm of the sample. Minimization of the background impact on the result is clearly visible. It is also clear, that this method provides the easiest way for localization of the sample, using the reference grid.
Figure 5.
Gradient measurement results, 100 mm distance from the sample.
Figure 5.
Gradient measurement results, 100 mm distance from the sample.
Figure 6.
Differential bi-plane measurement within 100 mm of the sample.
Figure 6.
Differential bi-plane measurement within 100 mm of the sample.
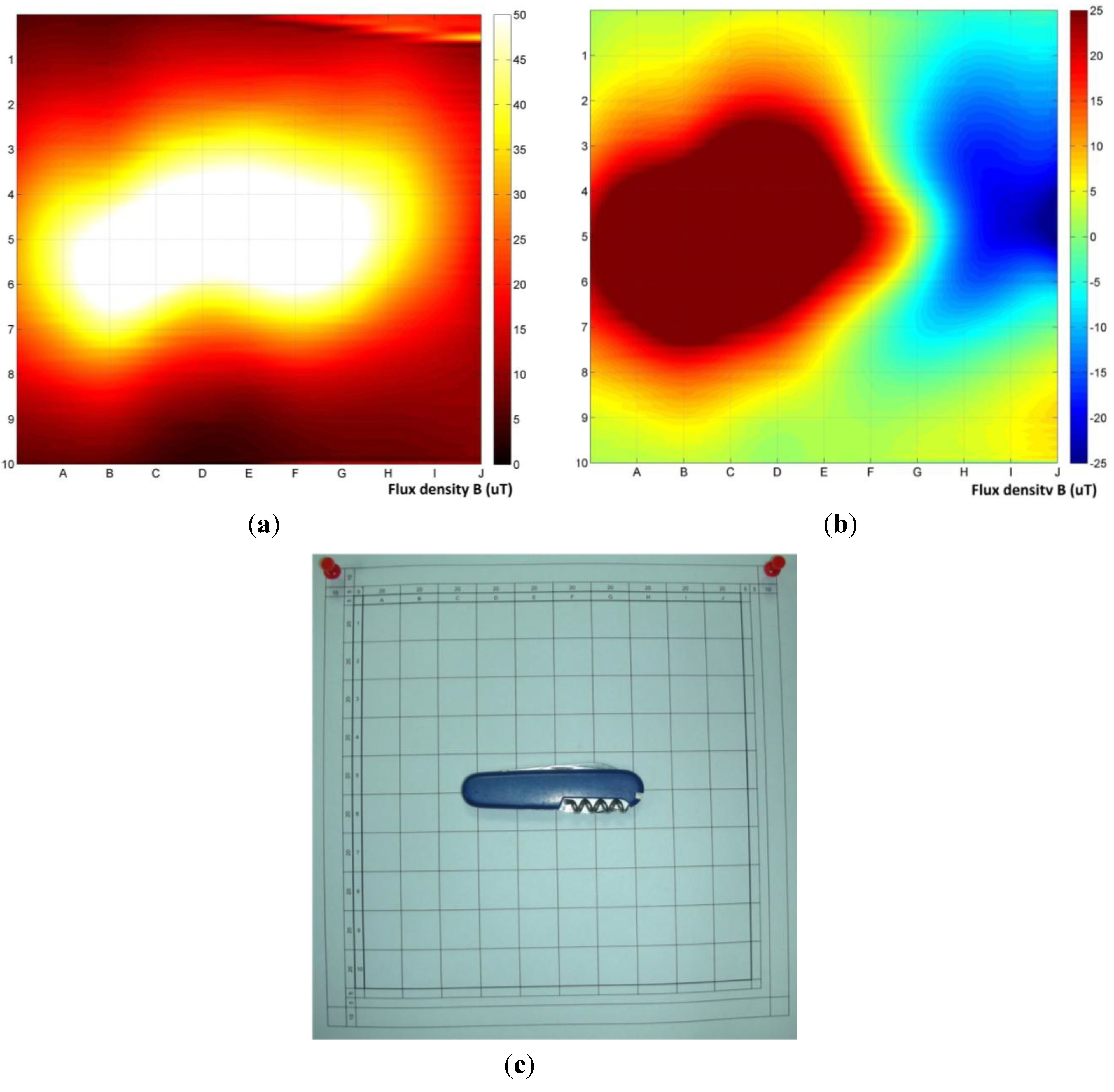
Figure 7 shows the results of the application of the developed method of measurements to determine the location of a sample, relative to the measurement plane. In addition, the comparison of the results of the differential bi-planar (
Figure 7a) and gradient (
Figure 7b) methods was performed. The object subjected to the test was a standard Swiss army knife, which is a very complex object from magnetic signature point of view. The distance of the first plane from the object was 50 mm. Bi-plane differential measurement results are shown in
Figure 7a, whereas gradient measurement without removing the influence of the background is shown in
Figure 7b. The position of sample on the reference grid is shown in
Figure 7c. Results of up to 60 μT were obtained for absolute value of the disorders (
Figure 7a) and −15–40 μT for the measurement of the background gradient (
Figure 7b)
Figure 7.
Measurement of the position of dangerous object (Swiss army knife): (a) biplane differential measurement; (b) gradient measurement without background separation; (c) a photograph of the actual position within 100 mm of the sample.
Figure 7.
Measurement of the position of dangerous object (Swiss army knife): (a) biplane differential measurement; (b) gradient measurement without background separation; (c) a photograph of the actual position within 100 mm of the sample.
Figure 8 shows the results of the application of the developed method of measurements to determine the location of a sample, relative to the measurement plane. The object subjected to the test was buried under the 50 mm layer of soil. The distance of the measurement plane from the ground level was also 50 mm. For such a small distance, single plane measurement was enough to determine the position of sample. Part of the conducted experiments was to find the sample hidden from the operator, using only this method. Results of up to ±15 μT were obtained for absolute value of the disorders relative to the background gradient. Based on the results, the location and size of the object can be determined, which is very useful from practical point of view.
Figure 8.
Application of the developed method of measurements to determine the location of a buried sample: (a) Comparison of the actual sample position (red circle); and (b) measurements results.
Figure 8.
Application of the developed method of measurements to determine the location of a buried sample: (a) Comparison of the actual sample position (red circle); and (b) measurements results.