Dielectric and Elastic Characterization of Nonlinear Heterogeneous Materials
Abstract
:1. Introduction
2. Introductory Remarks on Linear and Nonlinear Dielectric Homogenization
2.1. Two-phases materials
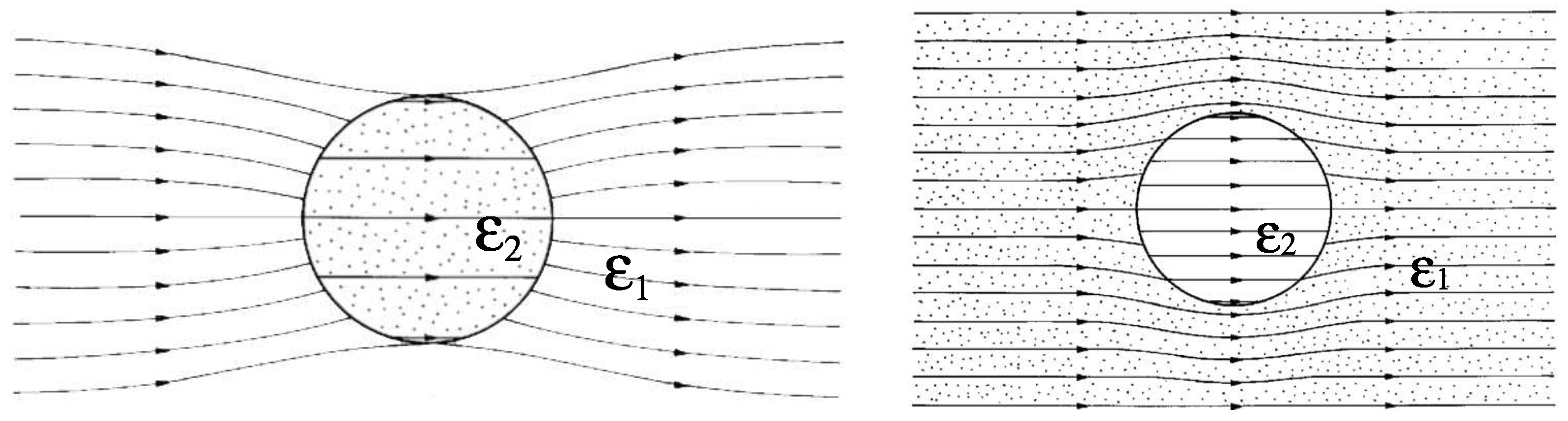
2.2. Three-phases materials
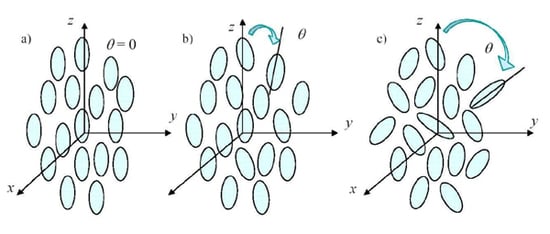
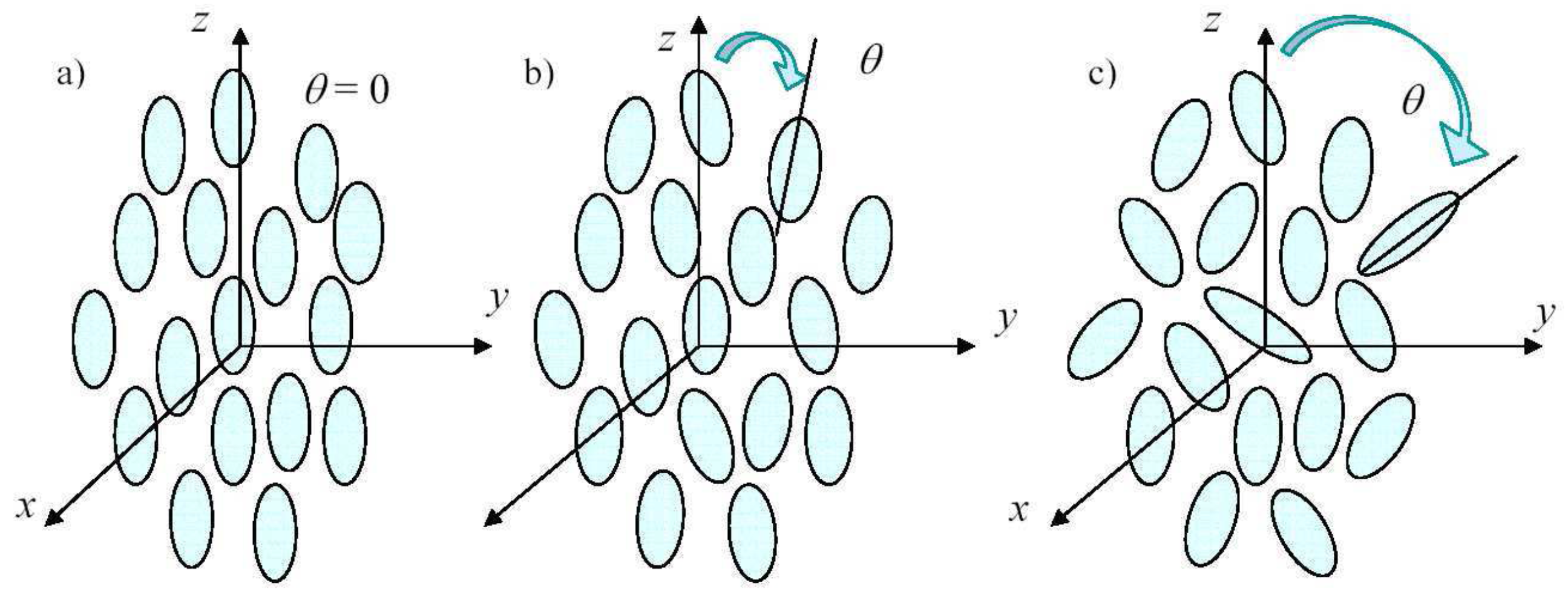
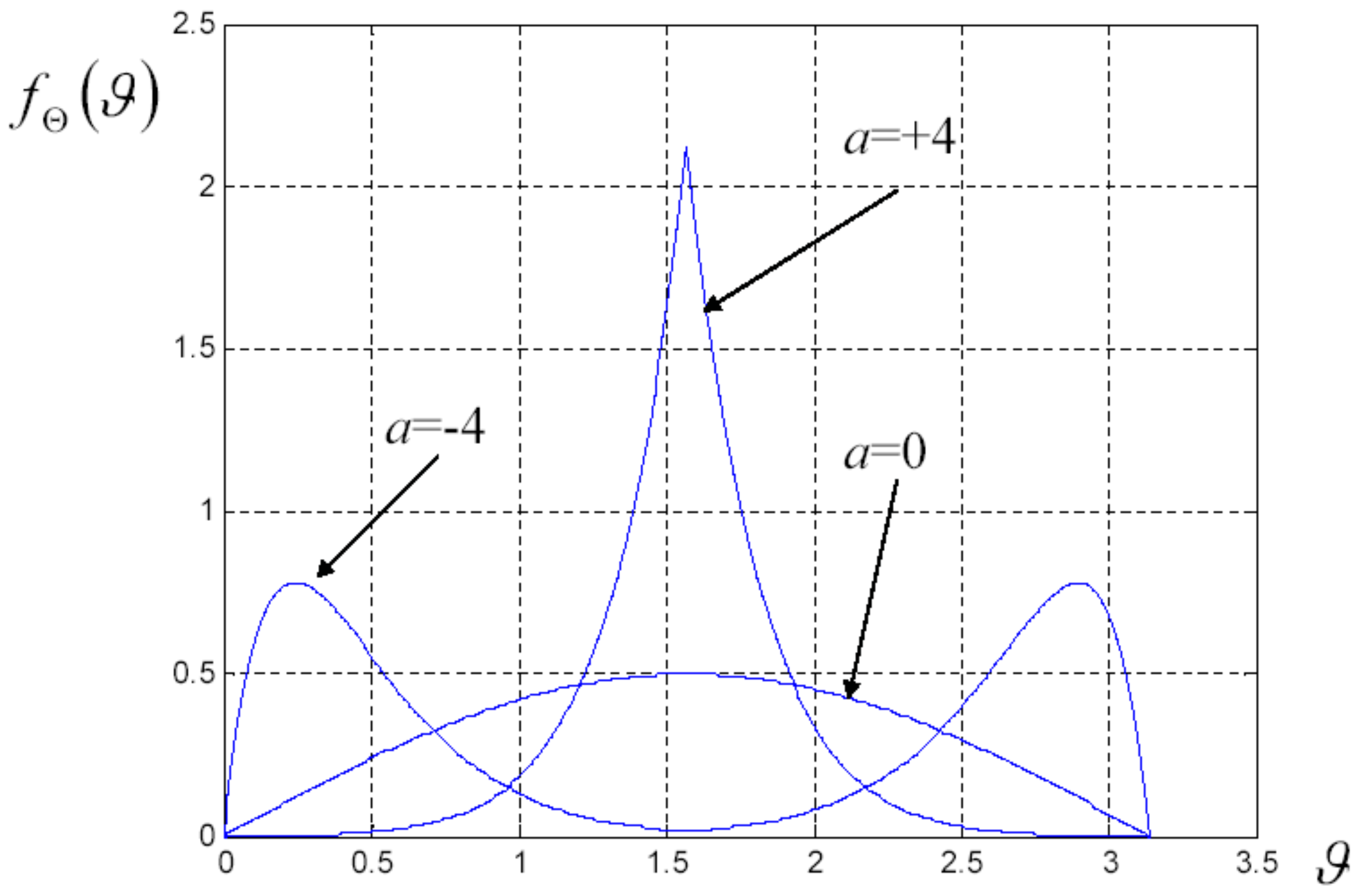
3. Nonlinear Electric Homogenization for Pseudo-Oriented Ellipsoids
4. Field Perturbation Due to One Single Nonlinear Ellipsoidal Inclusion in a Uniform Field
5. Average Electric Field Inside a Single Pseudo-Random Oriented Inclusion
6. Averaging Process in a Dilute Mixture
7. Example of Application
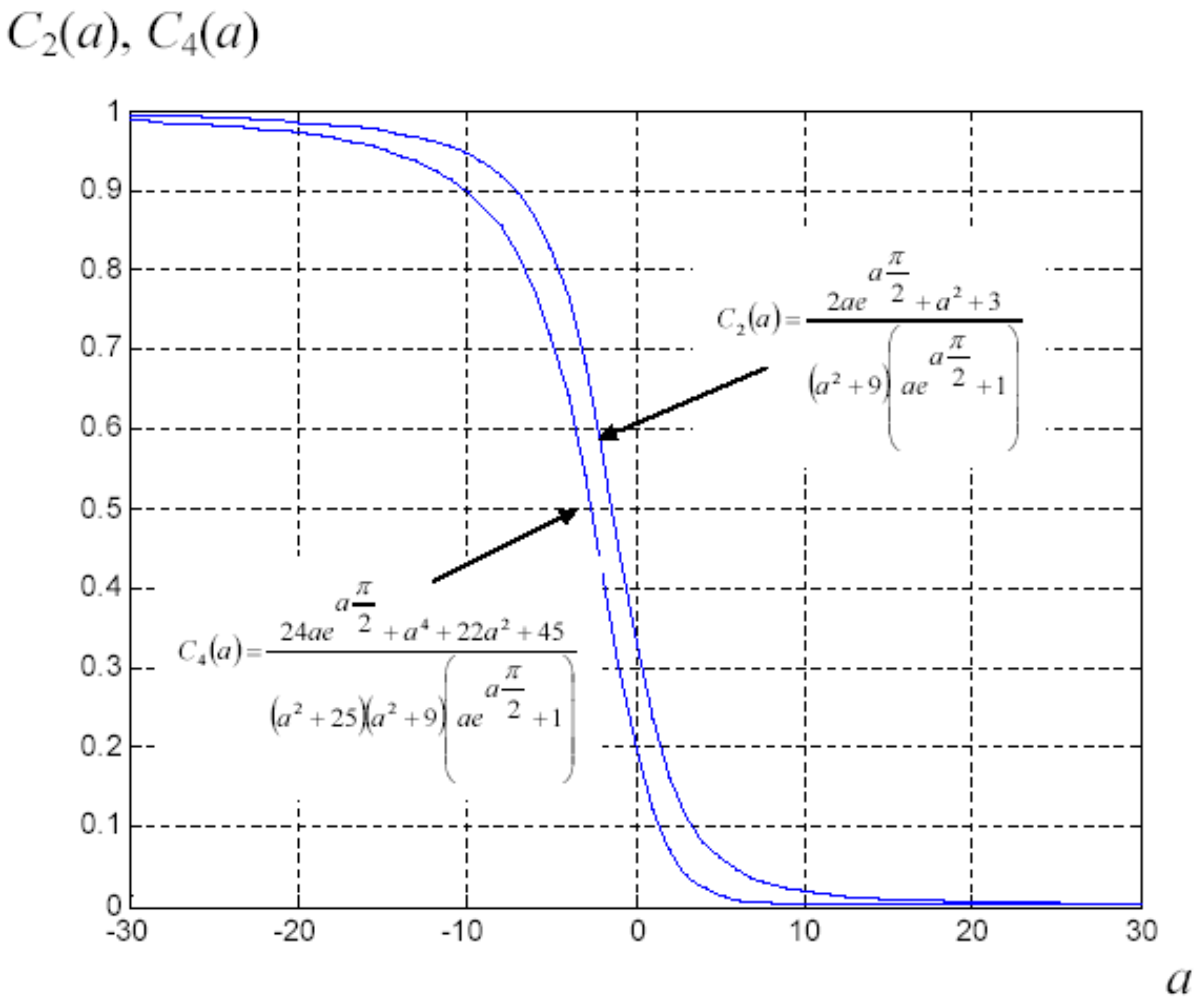
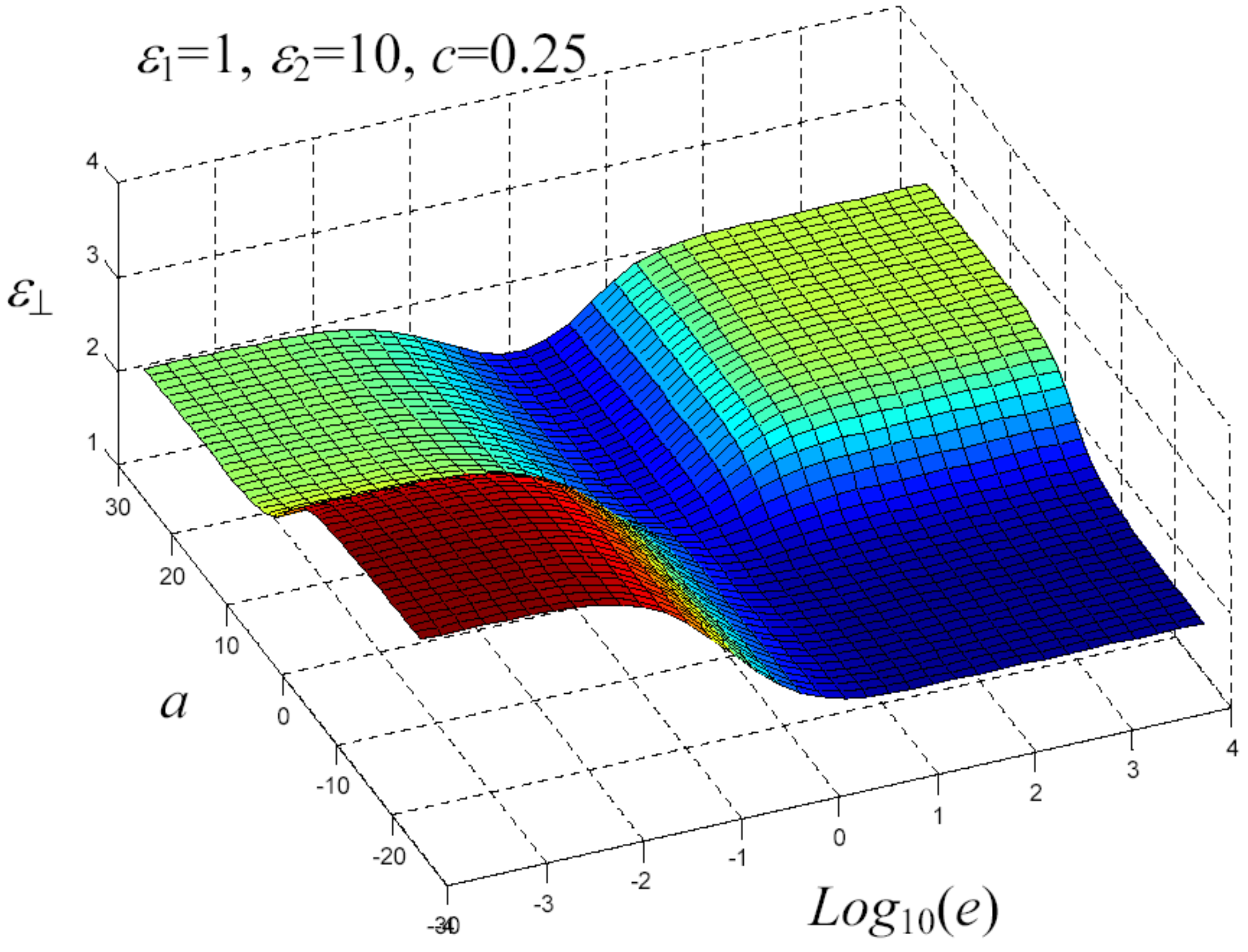
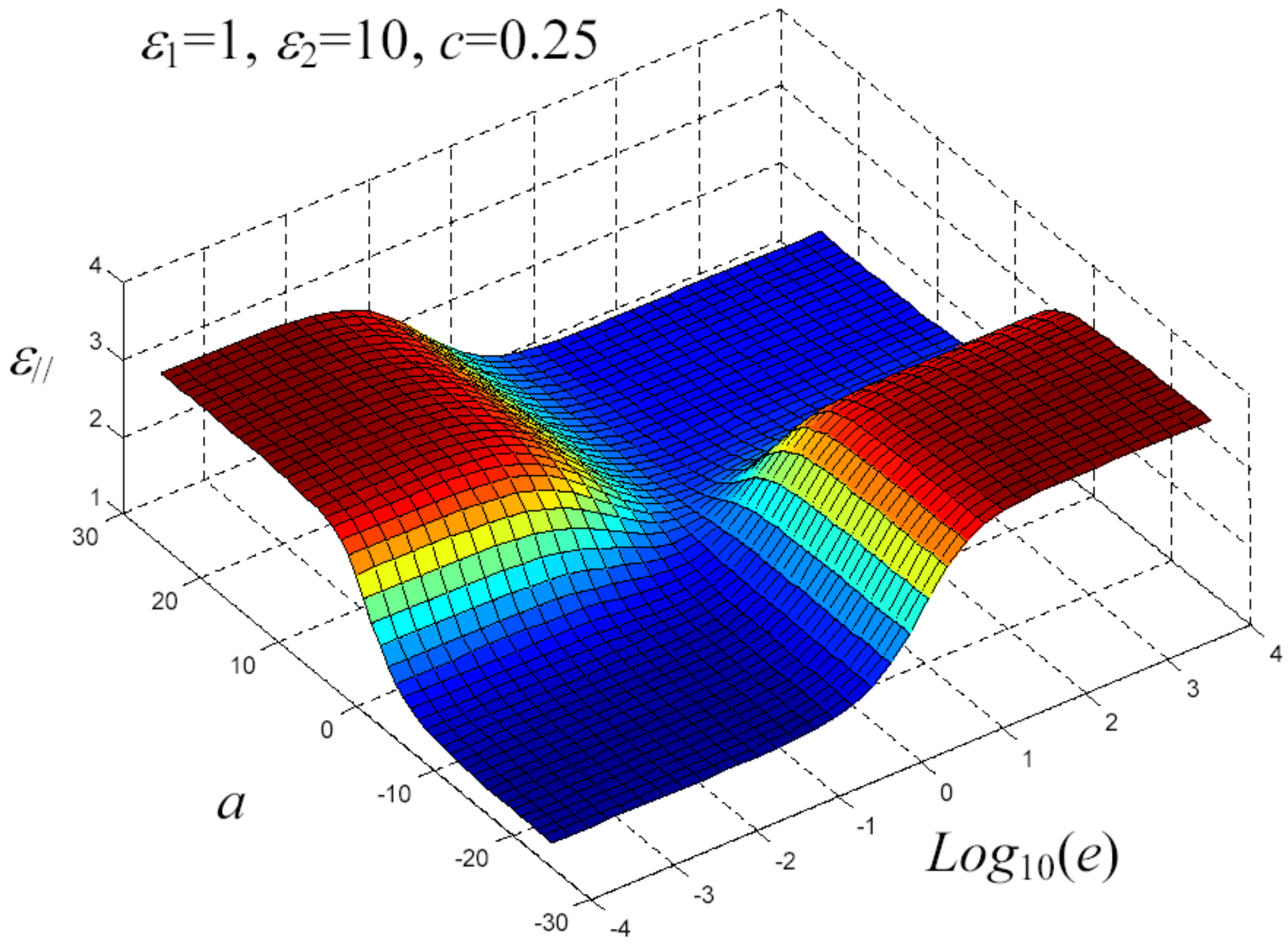
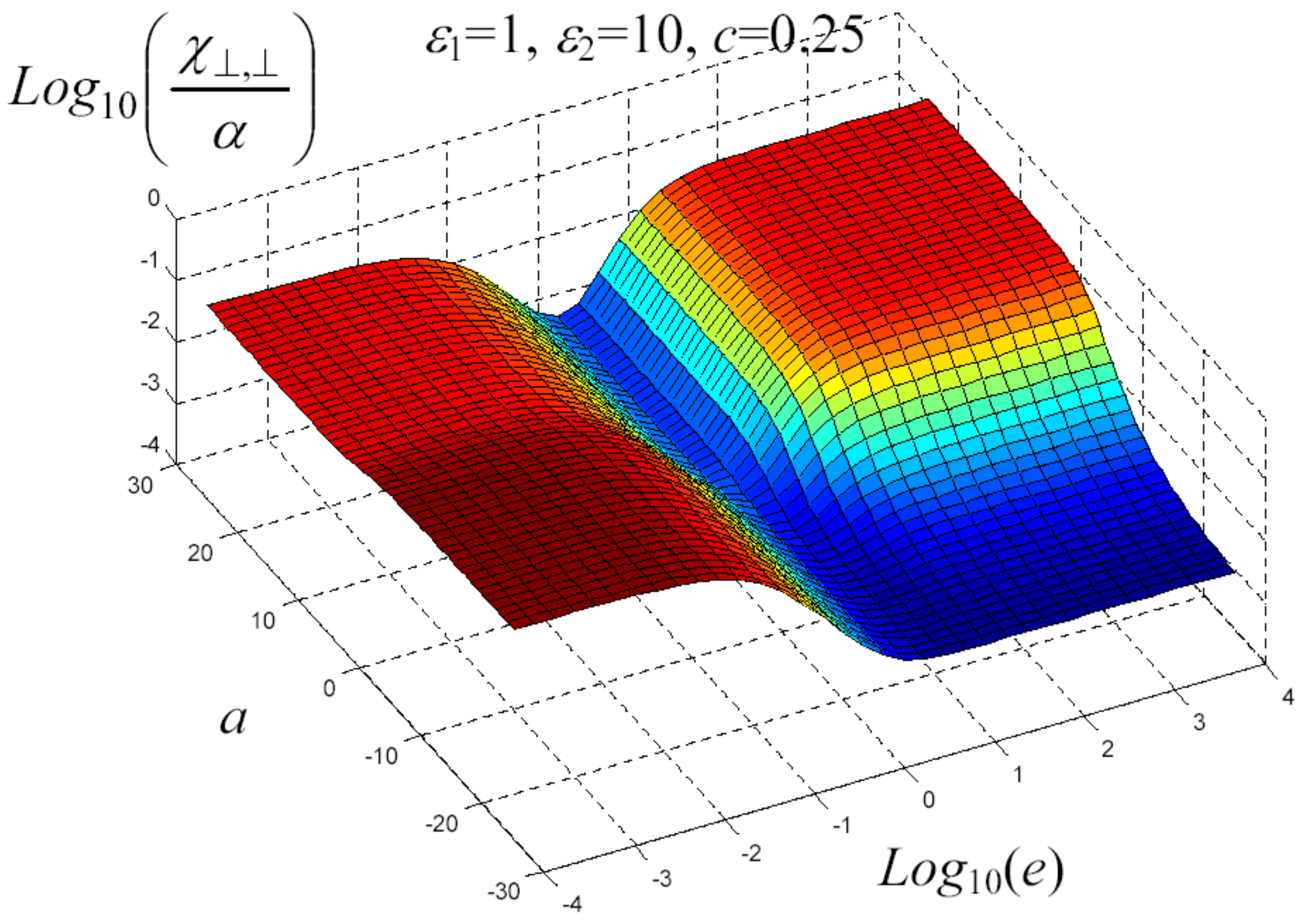
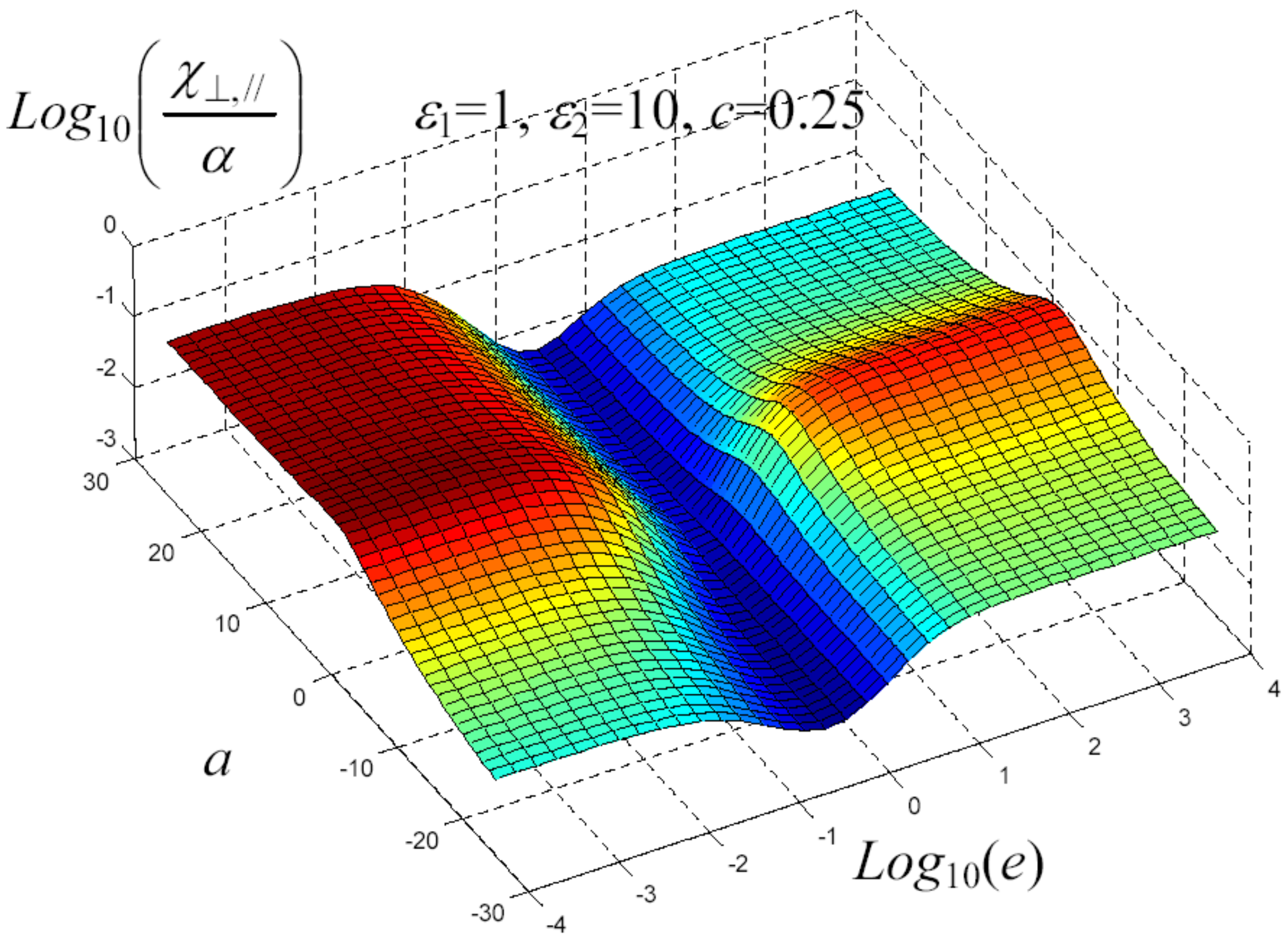
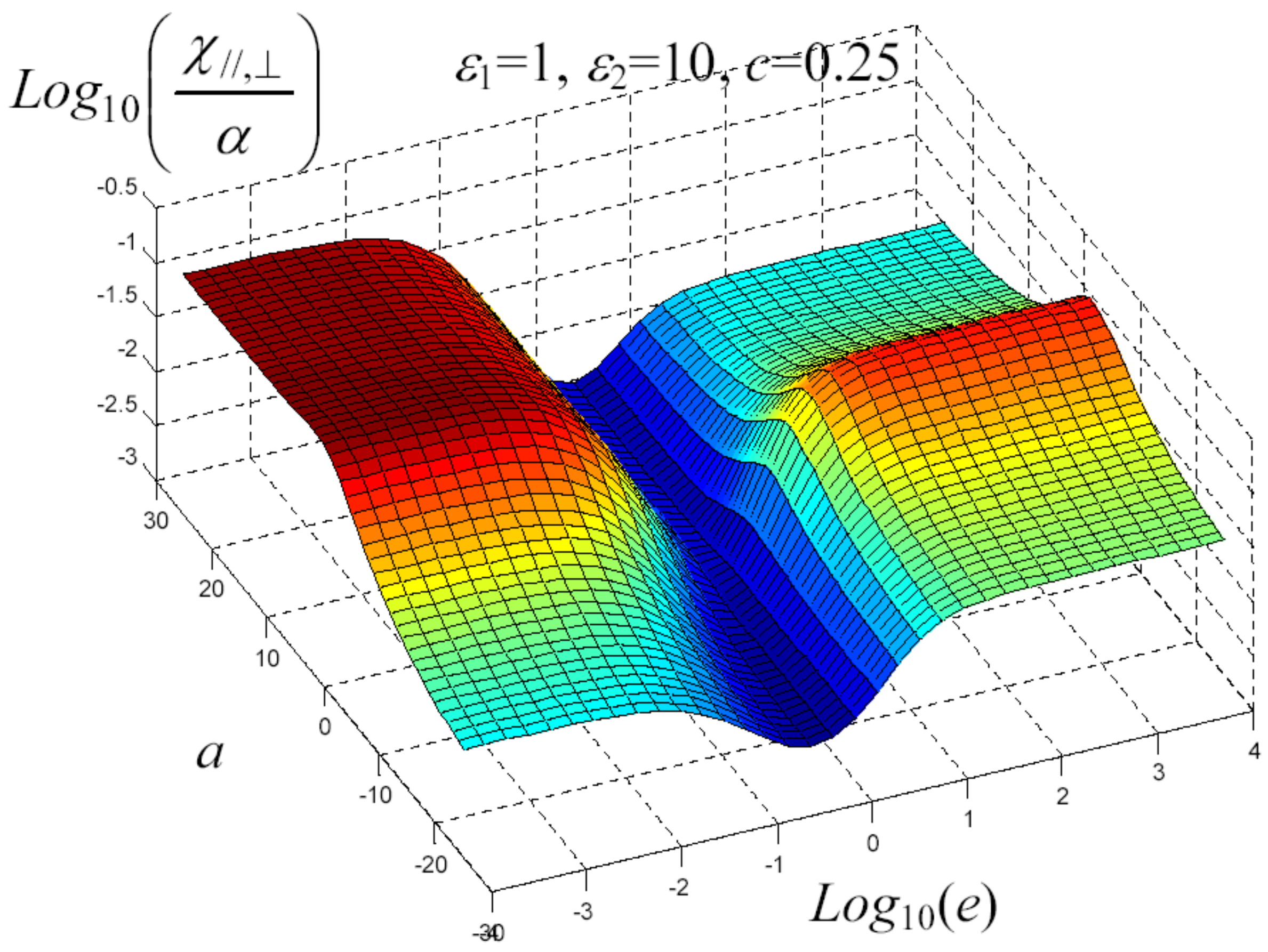
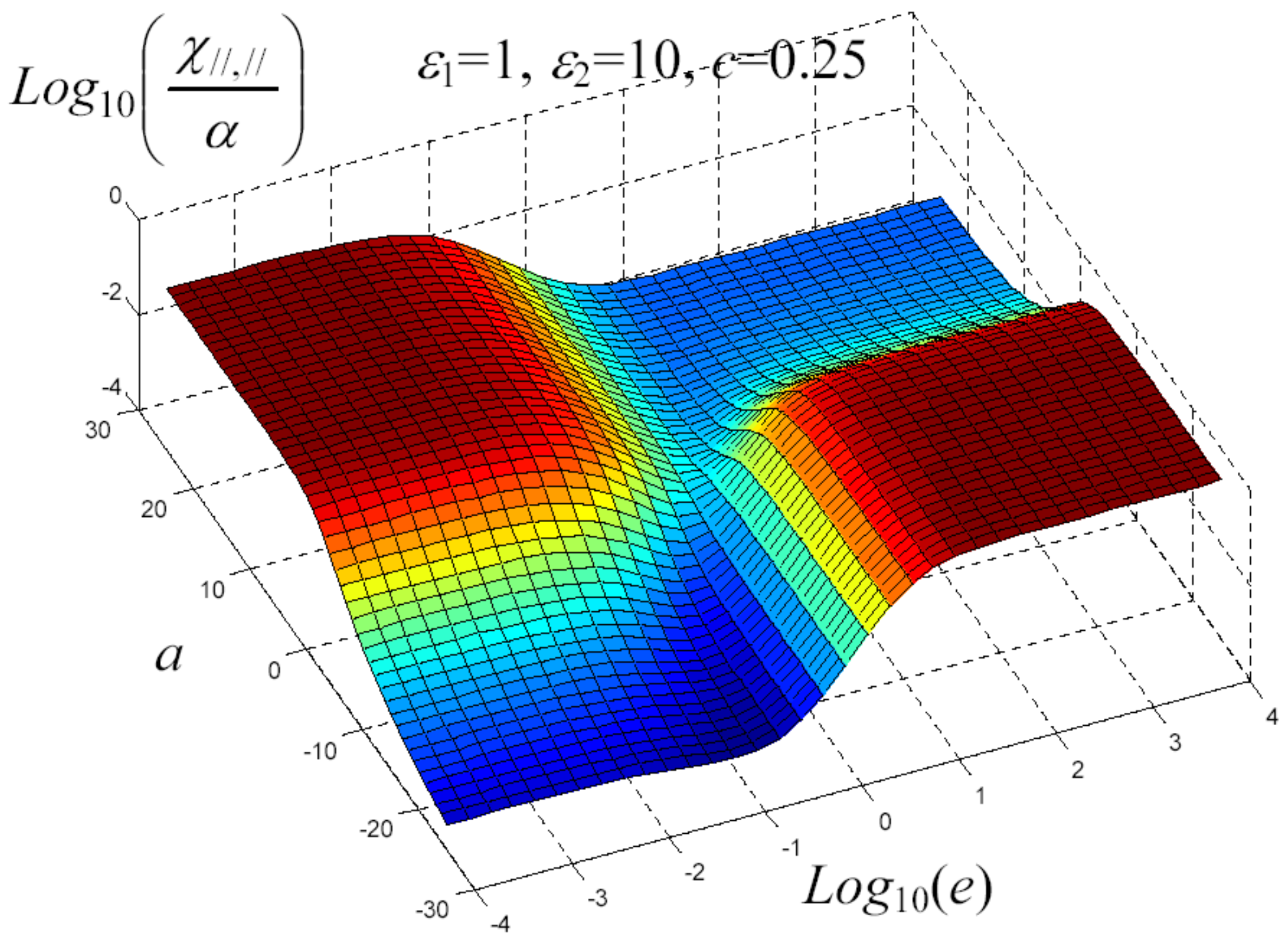
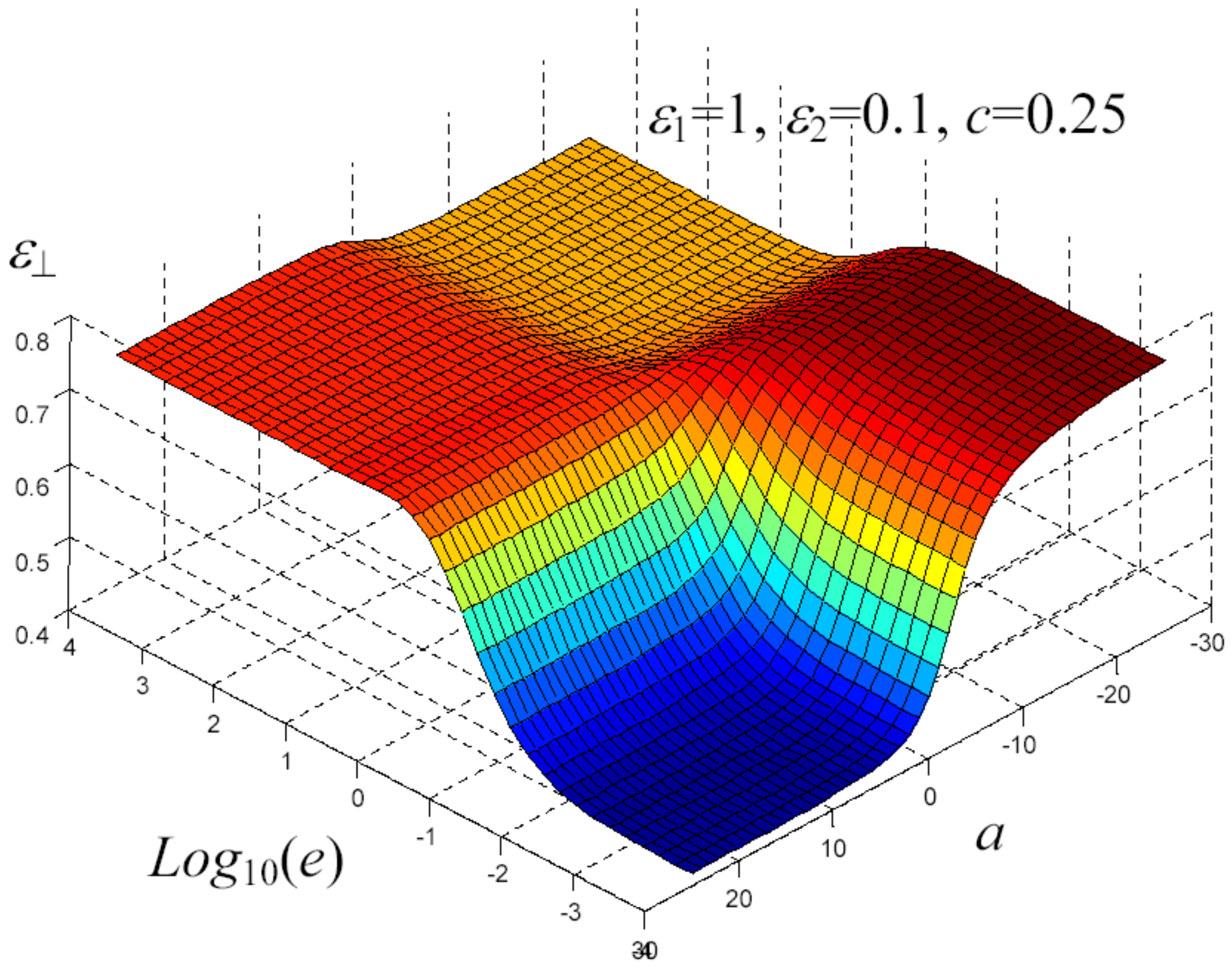
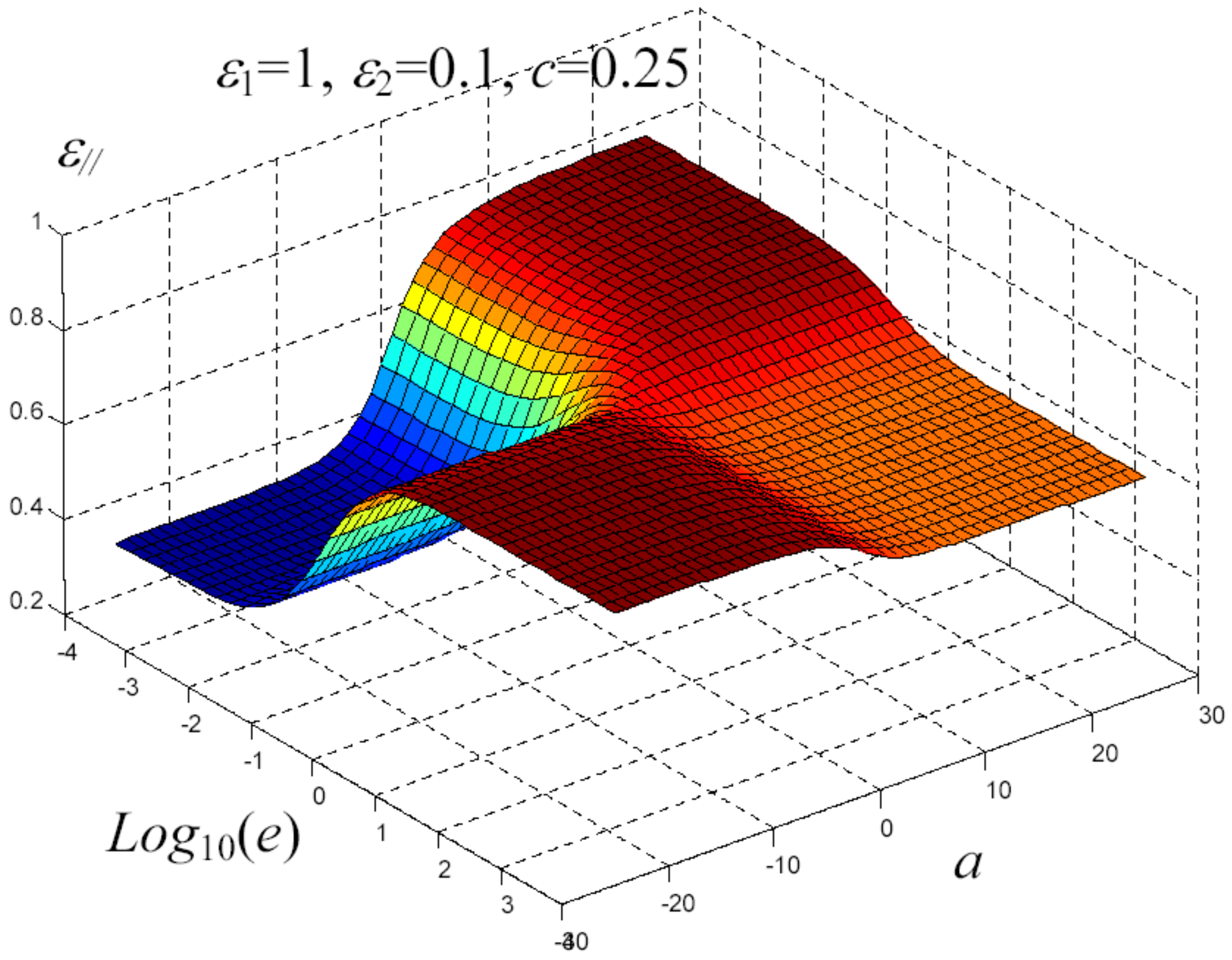
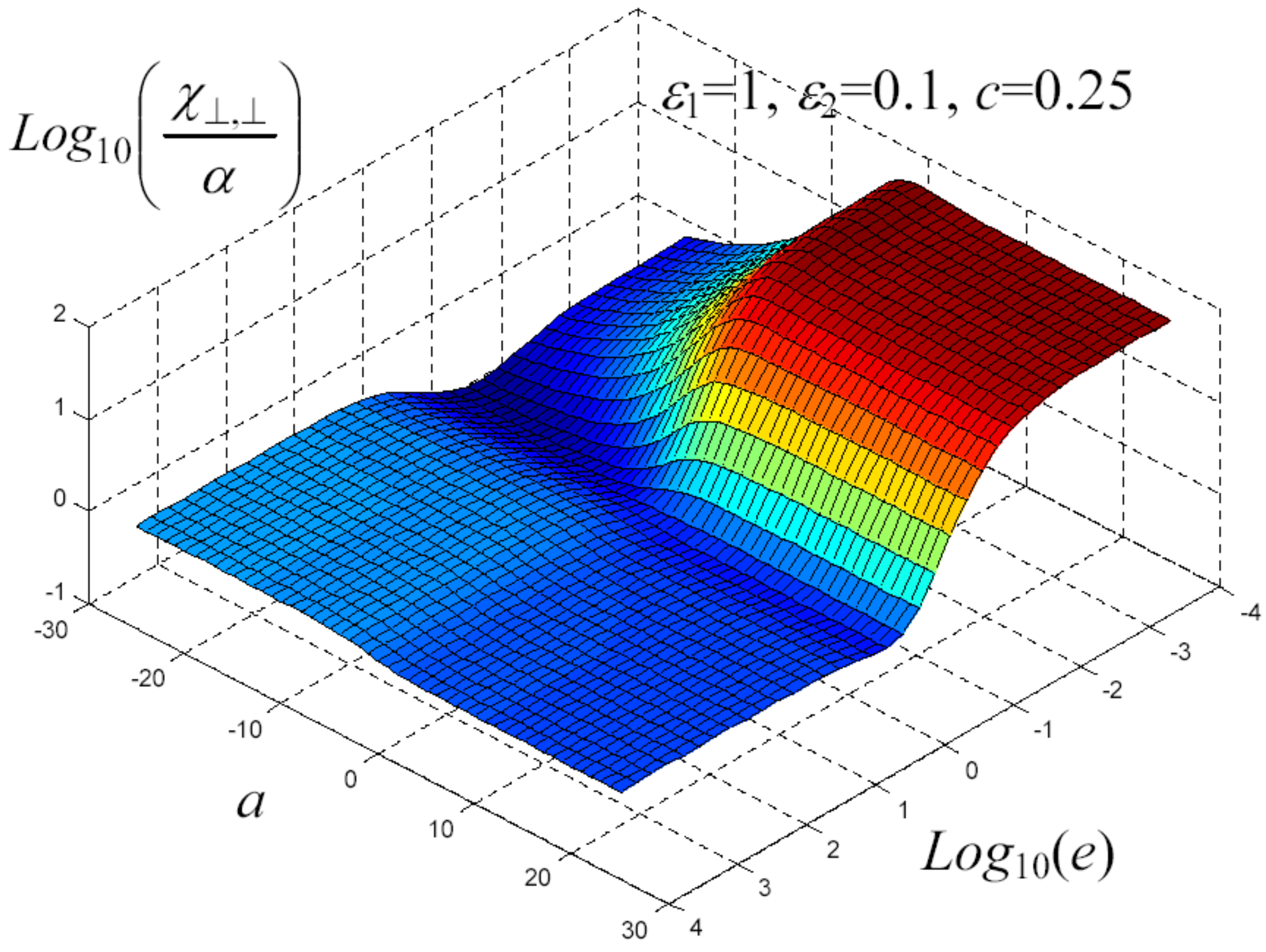
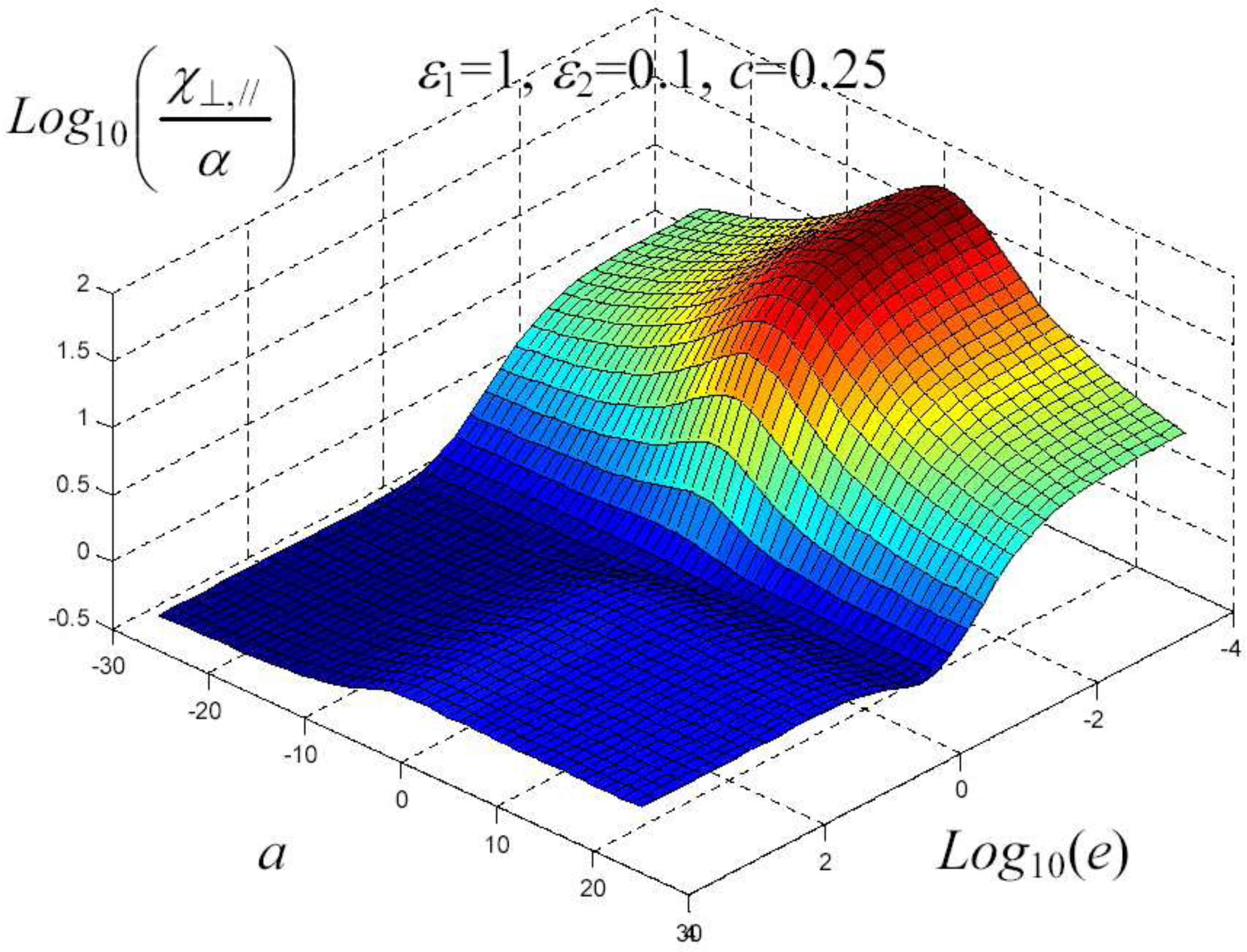
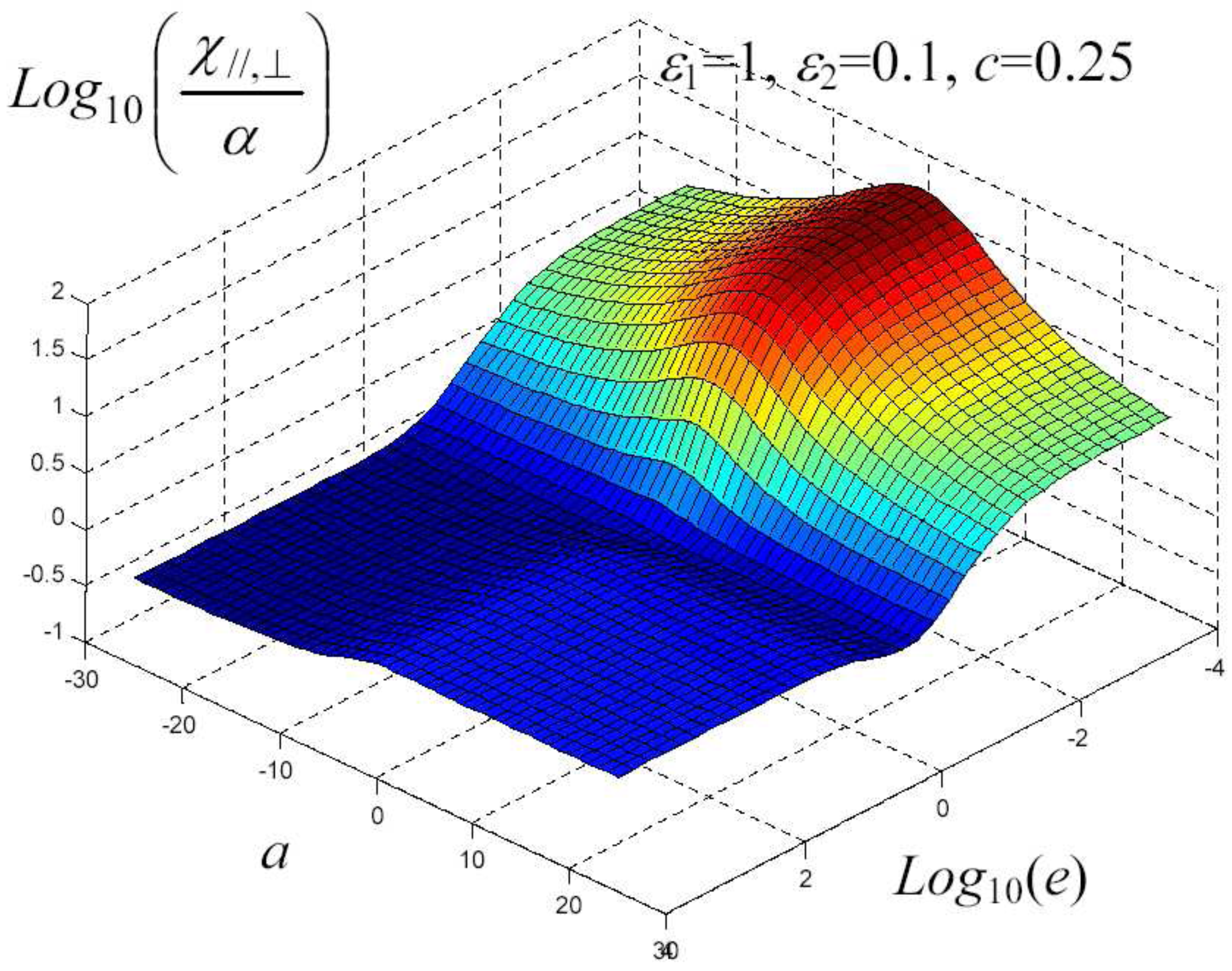
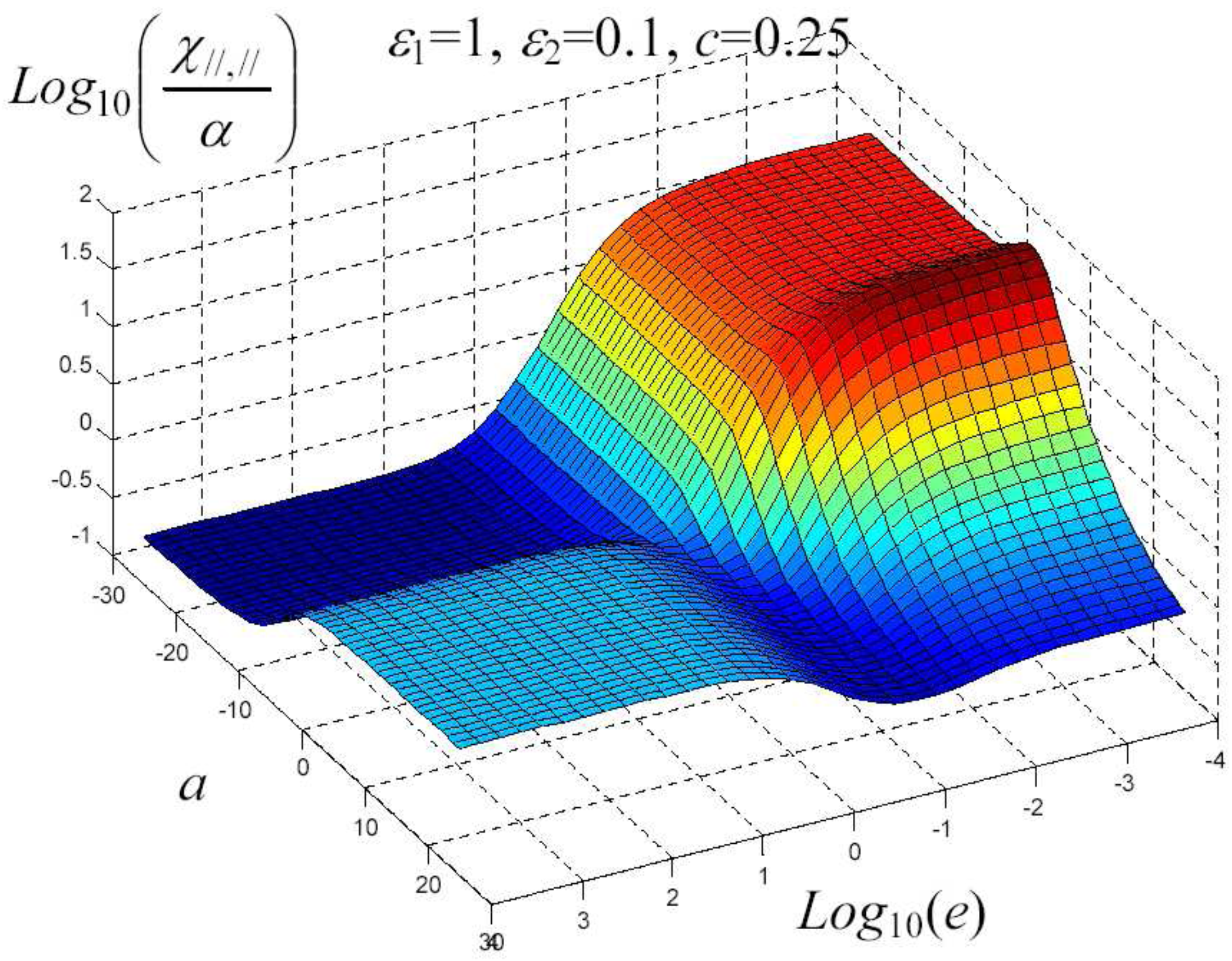
8. Nonlinear Elastic Homogenization
- those having both physical and geometrical linearity;
- those which are physically nonlinear but geometrically linear;
- those linear physically but nonlinear geometrically;
- those nonlinear both physically and geometrically.
9. Nonlinear Elastic Constitutive Equations
- and , in order to preserve the symmetry of the stress tensor and of the strain tensor;
- , derived by the existence of an elastic energy density (Green hypothesis).
9.1. Cauchy elasticity
9.2. Green elasticity
10. Eshelby Theory for Nonlinear Inhomogeneities
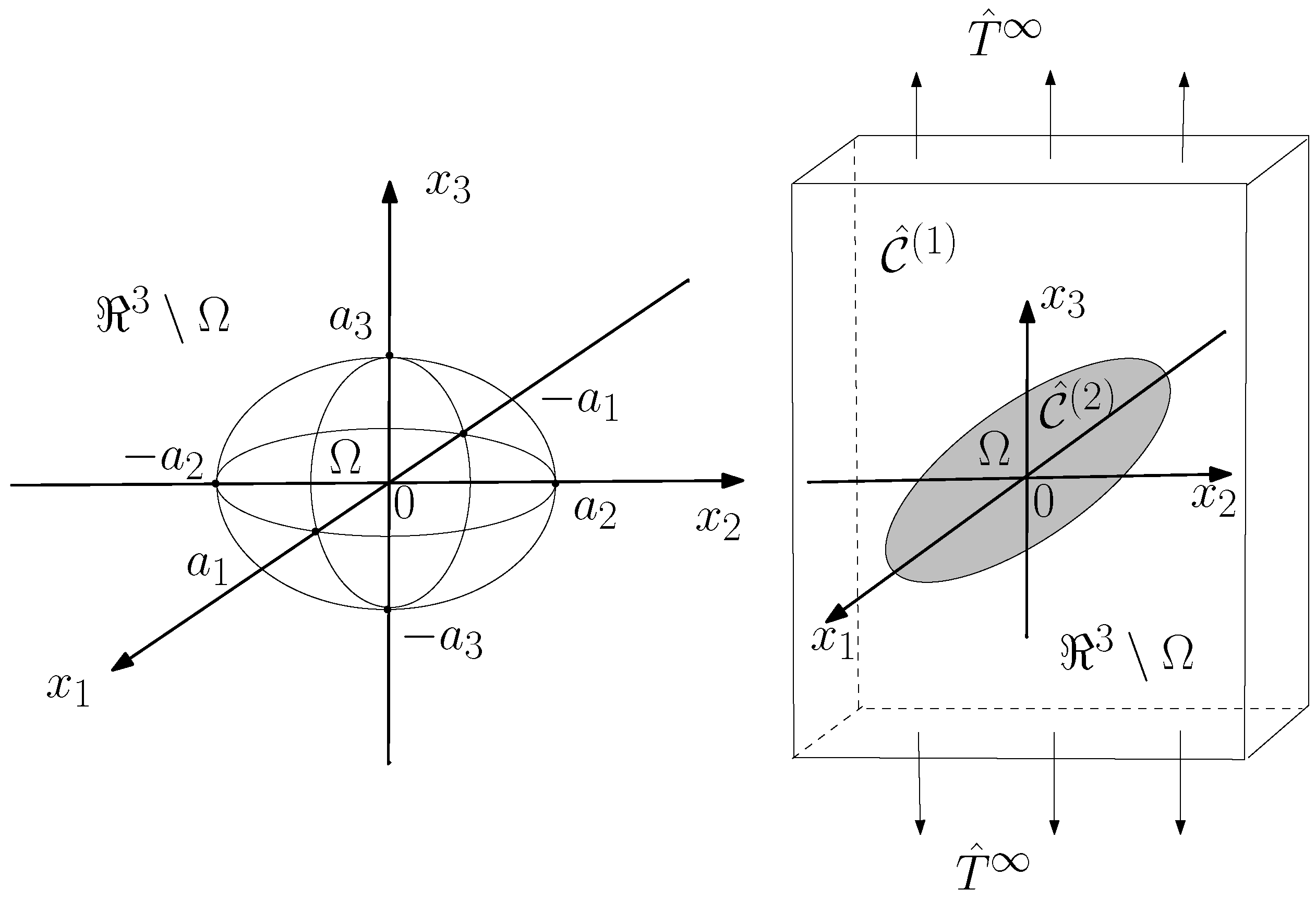
10.1. Nonlinear Eshelby theory within green elasticity
11. Elastic Dispersion of Nonlinear Spherical Inhomogeneities
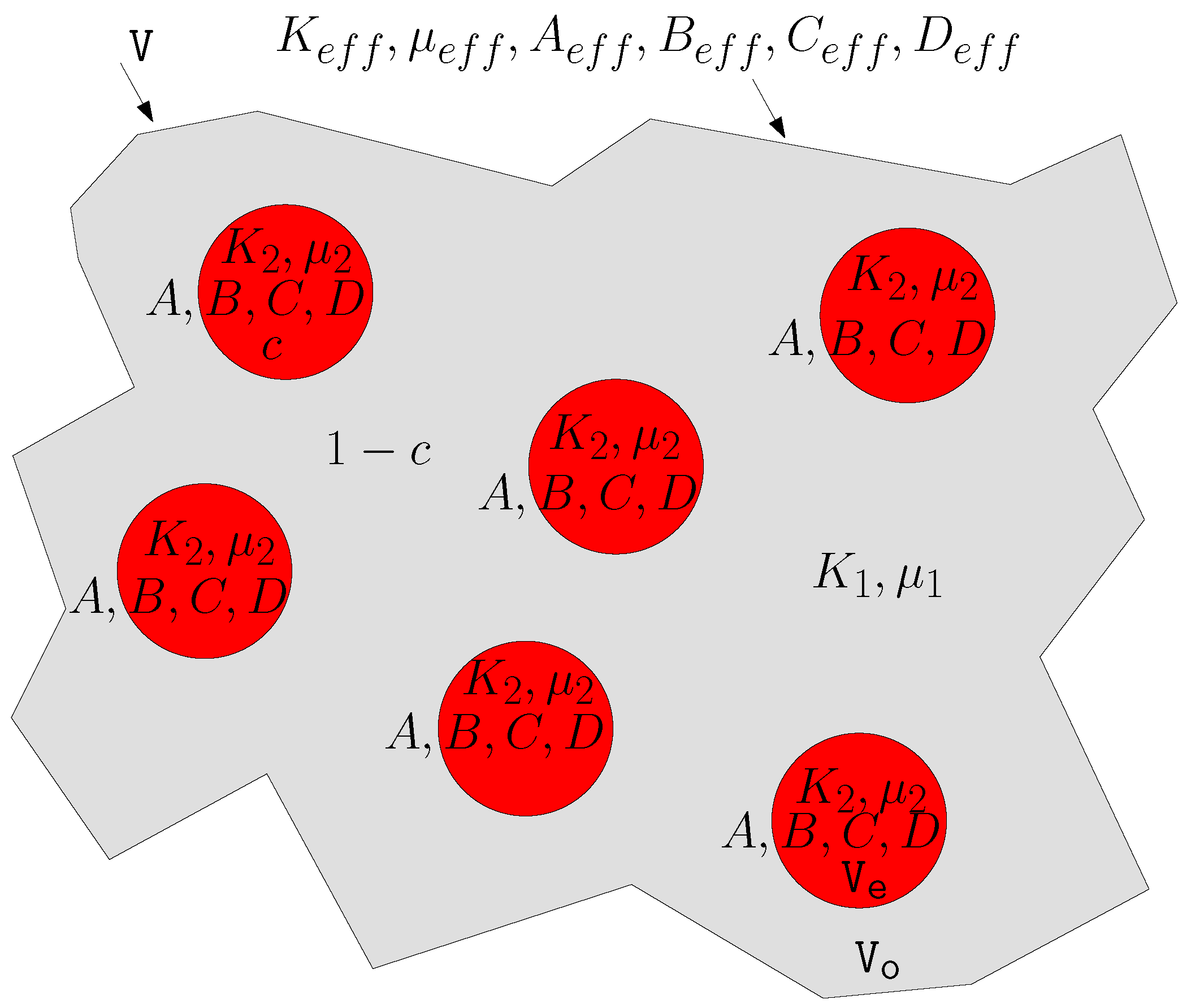
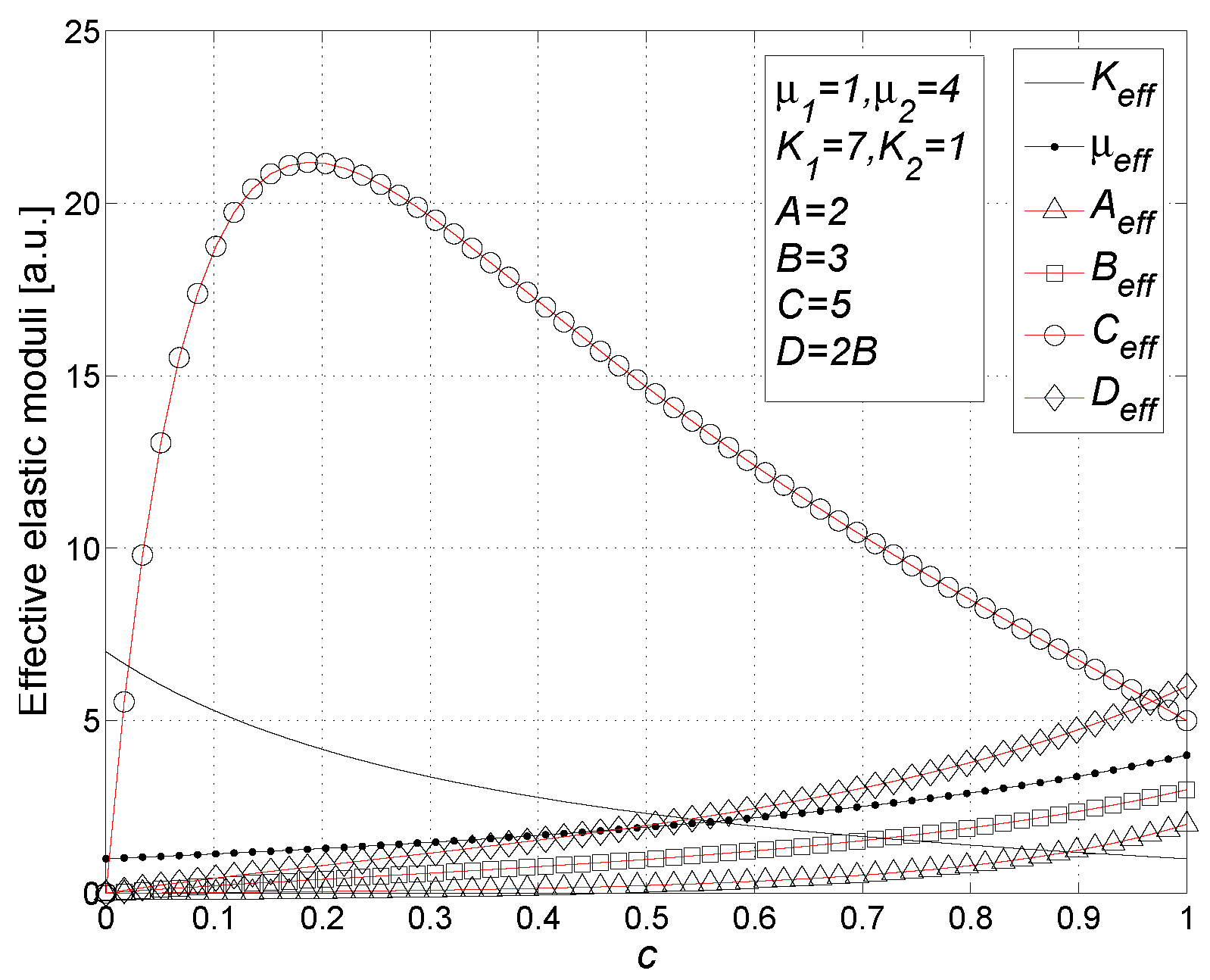
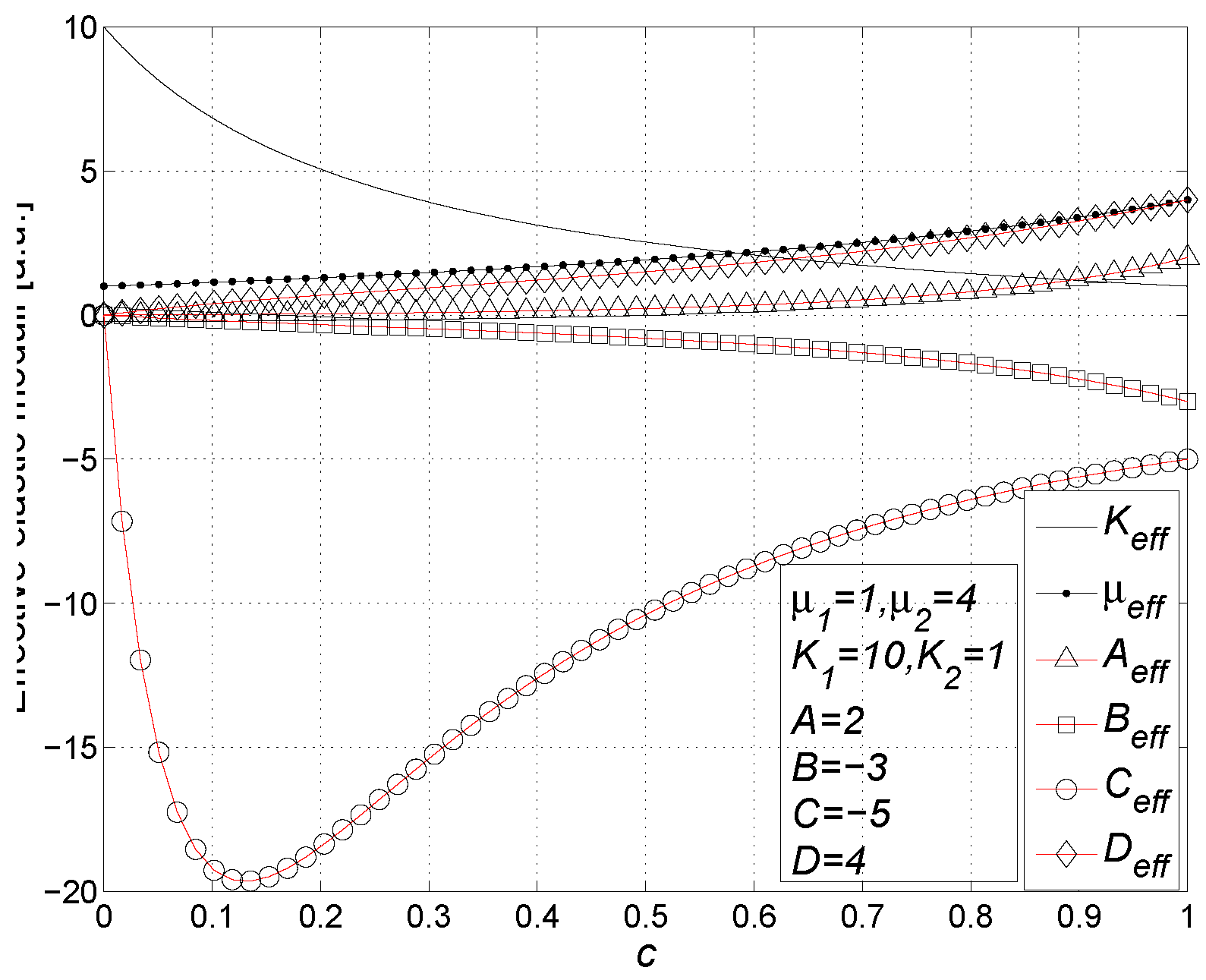
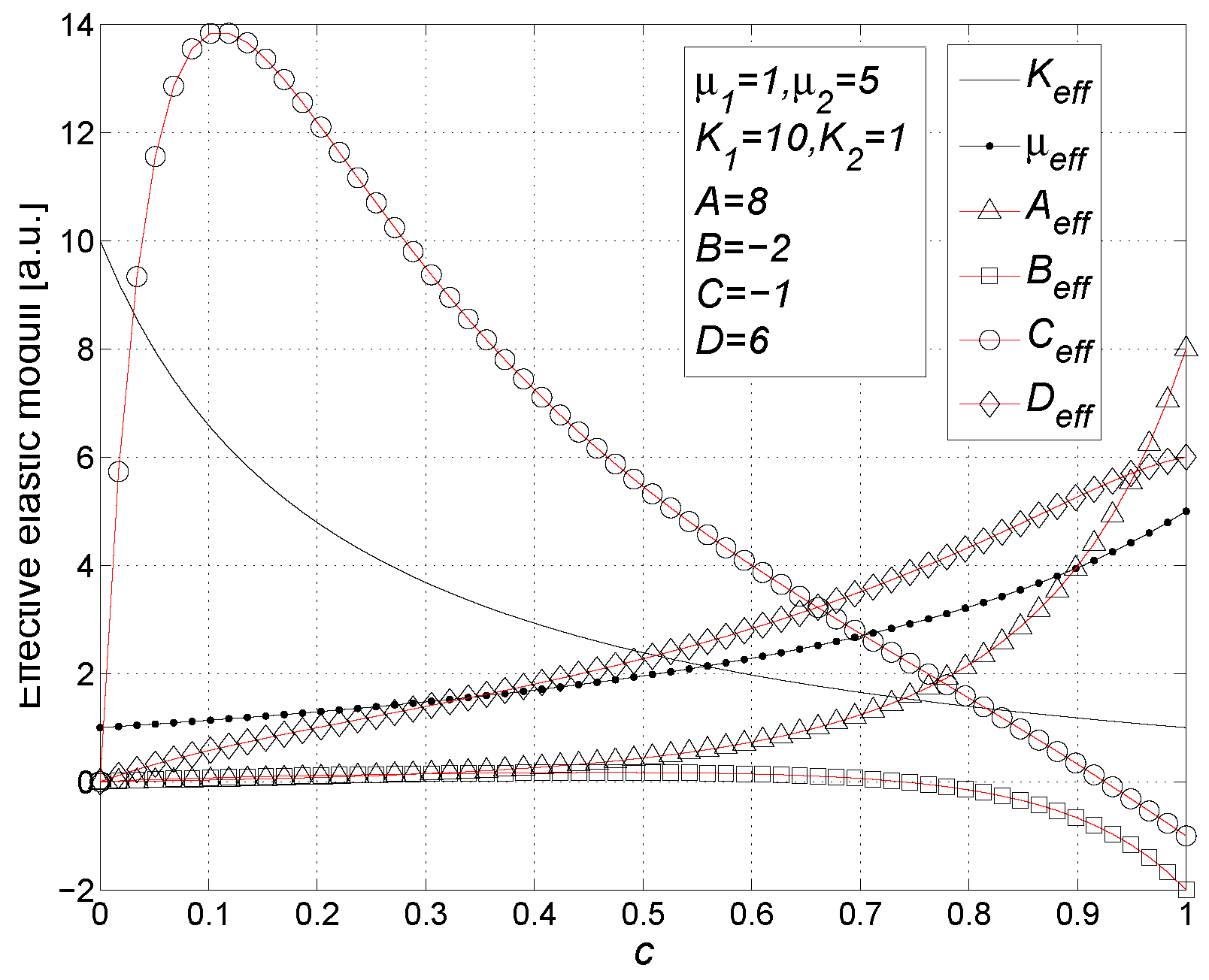
11.1. Results
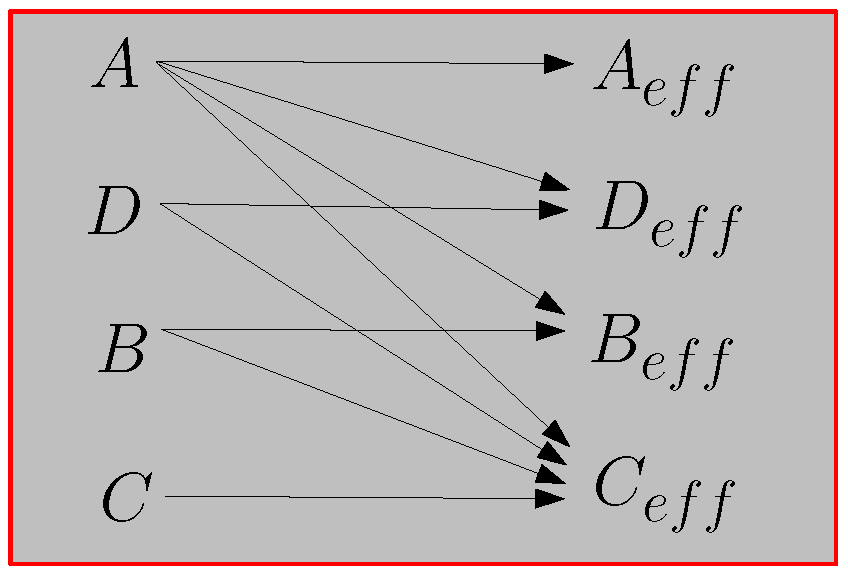
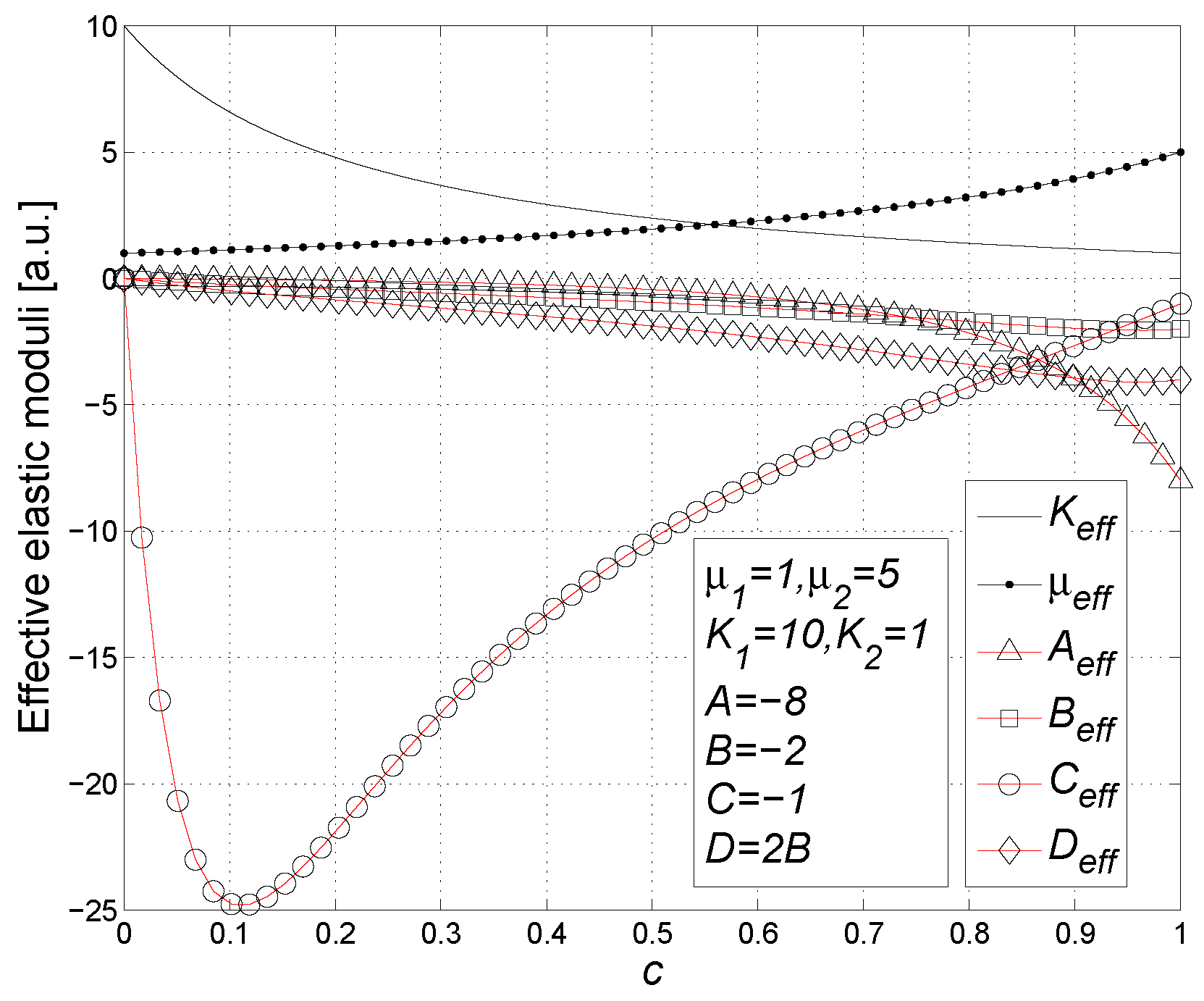
- The nonlinear elastic moduli A, B, C and D influence the effective nonlinear moduli of the composite material following the universal scheme showed in Figure 19. Therefore, there is a complicated mixing of the nonlinear elastic modes induced by the heterogeneity of the structure. The results for the nonlinear effective parameters, obtained with a single coefficient (A, B, C or D) different from zero, are reported in Appendix B, in form of series expansions in the volume fraction up to the first order. They are coherent with the scheme shown in Figure 19.
- 3.
- If the linear elastic moduli of the matrix and of the spheres are the very same ( and ), we simply obtain , and the following special set of results for the nonlinear componentsIt means that the nonlinearity of the overall system is simply proportional to the nonlinearity of the spheres.
- 4.
- We have developed our procedure under the hypothesis of Cauchy nonlinear elasticity for the spheres embedded in the linear matrix. If we let we move from the Cauchy elasticity to the Green elasticity, assuming the existence of a strain energy function for the inhomogeneities. It is important to remark that the following property holds: if then the relation is true for the effective nonlinear moduli. It can be verified by direct calculation and it means that our approach is perfectly consistent with the energy balance of the composite material. In other words, we have verified that if a strain energy function exists for the embedded spheres, then an overall strain energy function exists for the whole composite structure.
- 5.
- If we consider the special value of the Poisson ratio (both for the matrix and the spheres) and different values for the Young moduli , we obtain another interesting result: the effective Poisson ratio assume the same value , the effective Young modulus assumes the valueand the effective nonlinear elastic moduli can be calculated as followswhere the symbol X represents any modulus A, B, C or D (the four effective parameters exhibit the same behavior). Therefore, we can say that the special value uncouples the behavior of the nonlinear elastic modes (described at the point 2), generating a direct correspondence among the nonlinear moduli of the spheres and the effective nonlinear moduli. Furthermore, if we add the condition , we get back to the point 3. The special value for the Poisson ratio comes out in several issues considering a dispersion of spheres. For example, for linear porous materials (with spherical pores) and for linear dispersions of rigid spheres the value is a fixed points for the Poisson ratio: if , then we have for all spheres concentrations [33,100]. Moreover, there is another interesting behavior of the effective Poisson ratio for high volume fraction of pores or rigid spheres: in both cases for the effective Poisson ratio converges to the fixed value , irrespective of the matrix Poisson ratio [33,100,101,102].
- 6.
- Finally, we analyze the properties of the dispersion when incompressible material is utilized for the embedded spheres: the constitutive relation Equation (102) describes an incompressible medium in the limit (or, equivalently, since ); by inverting Equation (102), writing the strain tensor in terms of the stress tensor and performing such a limit, we obtain (up to the second order)which describes a nonlinear isotropic and incompressible material. We remark that only the nonlinear modulus A intervenes in defining such a constitutive equation and that Equation (144) imposes , as requested by the incompressibility. In this limiting condition, as for the effective linear moduli, we observe that Equation (136) for remains unchanged and Equation (137) leads toOn the other hand, the nonlinear elastic moduli have been eventually found aswhereOne can observe that, as expected, the effective nonlinear elastic moduli depend only on the modulus A describing the nonlinearity of the spheres, as shown in Equation (144). Moreover, we remark that a single modulus A for the spheres can generate four different effective nonlinear moduli, as predicted by the scheme in Figure 19.
12. Elastic Dispersion of Parallel Nonlinear Cylindrical Inhomogeneities
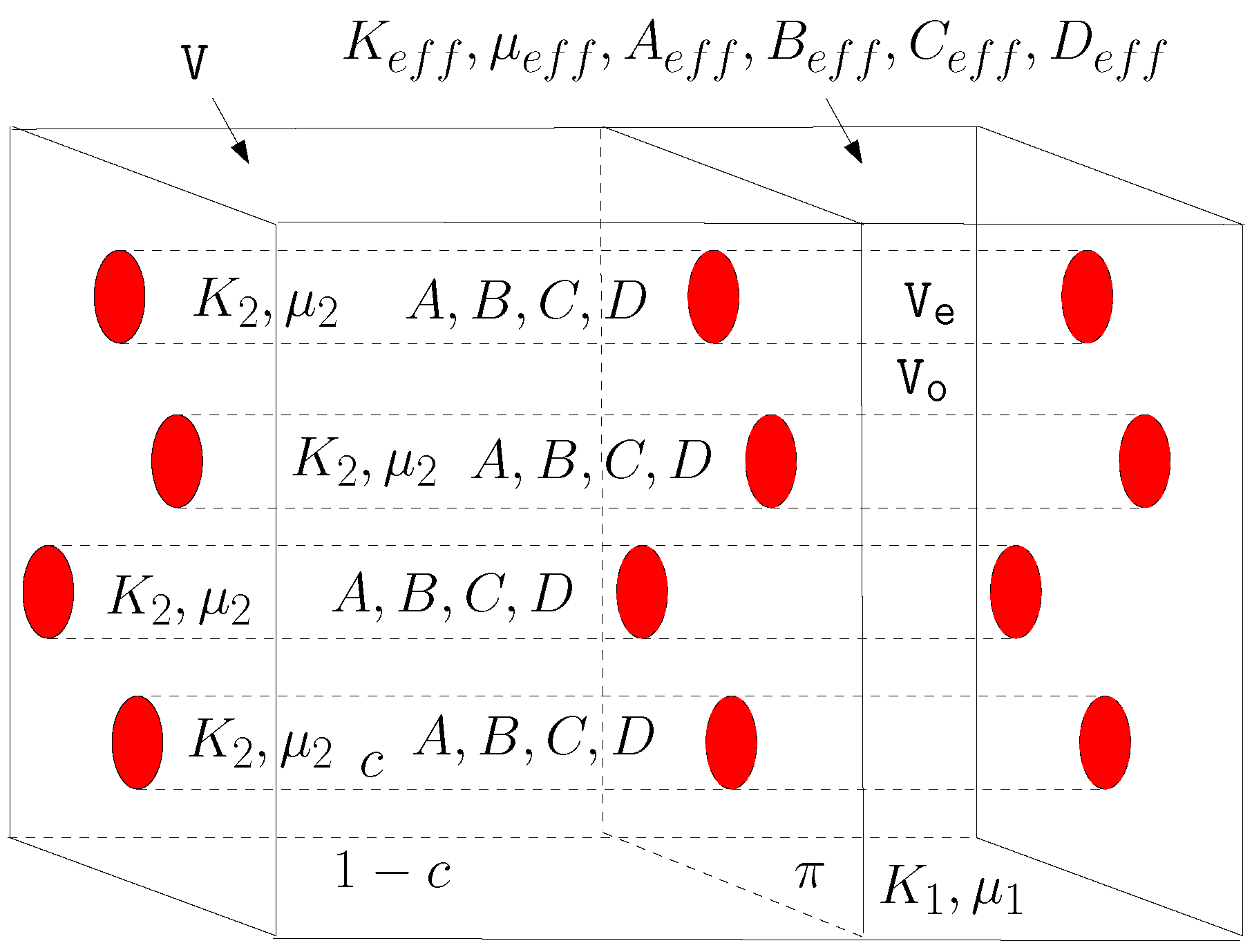
12.1. Results
13. Conclusions
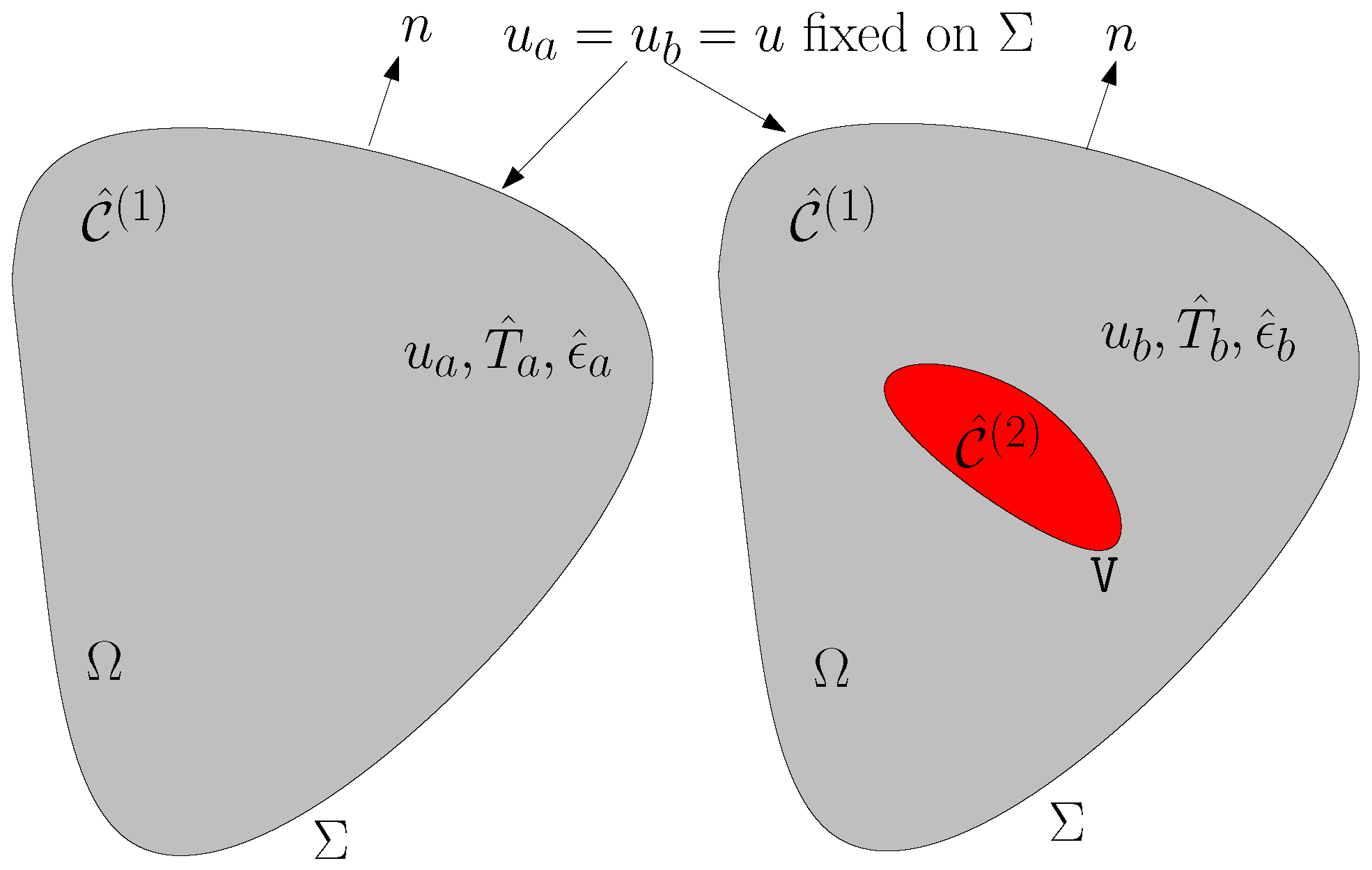
Appendix A Symmetry and Positive Definiteness of the Tensor
Concept of inclusion
Concept of inhomogeneity

Lemma: The tensor is symmetric
Lemma: The tensor is positive definite
Appendix B First Order Expansions for a Dispersion of Spheres
Appendix C First Order Expansions for a Dispersion of Cylinders
Acknowledgements
References and Notes
- Torquato, S. Exact expression for the effective elastic tensor of disordered composites. Phys. Rev. Lett. 1997, 79, 681–684. [Google Scholar] [CrossRef]
- Stroud, D.; Hui, P.M. Nonlinear susceptibilities of granular matter. Phys. Rev. B 1988, 37, 8719–8724. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the effective magnetic permeability of multiphase materials. J. Appl. Phys. 1962, 33, 3125–3131. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids. 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Brown, W.F. Solid mixture permittivities. J. Chem. Phys. 1955, 23, 1514–1517. [Google Scholar] [CrossRef]
- Torquato, S. Effective stiffness tensor of composite media-I. Exact series expansions. J. Mech. Phys. Solids 1997, 45, 1421–1448. [Google Scholar] [CrossRef]
- Torquato, S. Effective stiffness tensor of composite media-II. Applications to isotropic dispersions. J. Mech. Phys. Solids 1998, 46, 1411–1440. [Google Scholar] [CrossRef]
- Bianco, B.; Parodi, M. A unifying approach for obtaining closed-form expressions of mixtures permittivities. J. Electrostat. 1984, 15, 183–195. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Clarendon: Oxford, UK, 1881. [Google Scholar]
- Brosseau, C. Modelling and simulation of dielectric heterostructures: A physical survey from an historical perspective. J. Phys. D: Appl. Phys. 2006, 39, 1277–1294. [Google Scholar] [CrossRef]
- Fricke, H. The Maxwell-Wagner dispersion in a suspension of ellipsoids. J. Phys. Chem. 1953, 57, 934–937. [Google Scholar] [CrossRef]
- Fricke, H. A mathematical treatment of the electric conductivity and capacity of disperse systems. Phys. Rev. 1924, 24, 575–587. [Google Scholar] [CrossRef]
- Sihvola, A.; Kong, J.A. Effective permittivity of dielectric mixtures. IEEE Trans. Geosci. Remo. Sen. 1988, 26, 420–429. [Google Scholar] [CrossRef]
- Sihvola, A. Electromagnetic Mixing Formulas and Applications; The Institution of Electrical Engineers: London, UK, 1999. [Google Scholar]
- Van Beek, L.K.H. Dielectric behaviour of heterogeneous systems. In Progress in Dielectric; Heywood: London, UK, 1967; Volume 7, pp. 71–114. [Google Scholar]
- Bruggeman, D.A.G. Dielektrizitatskonstanten und Leitfahigkeiten der Mishkorper aus isotropen Substanzen. Ann. Phys. (Leipzig) 1935, 24, 636–664. [Google Scholar] [CrossRef]
- Giordano, S. Effective medium theory for dispersions of dielectric ellipsoids. J. Electrostat. 2003, 58, 59–76. [Google Scholar] [CrossRef]
- Bianco, B.; Chiabrera, A.; Giordano, S.D.C.-E.L.F. Characterization of random mixtures of piecewise non-linear media. Bioelectromagnetics 2000, 21, 145–149. [Google Scholar] [CrossRef]
- Bianco, B.; Giordano, S. Electrical characterization of linear and non-linear random networks and mixtures. Int. J. Circuit Theor. Appl. 2003, 31, 199–218. [Google Scholar] [CrossRef]
- Giordano, S. Disordered lattice networks: General theory and simulations. Int. J. Circuit Theor. Appl. 2005, 33, 519–540. [Google Scholar] [CrossRef]
- Giordano, S. Two-dimensional disordered lattice networks with substrate. Physica A 2007, 375, 726–740. [Google Scholar] [CrossRef]
- Giordano, S. Relation between microscopic and macroscopic mechanical properties in random mixtures of elastic media. J. Eng. Mater. Technol. ASME 2007, 129, 453–461. [Google Scholar] [CrossRef]
- Goncharenko, A.V.; Popelnukh, V.V.; Venger, E.F. Effect of weak nonsphericity on linear and nonlinear optical properties of small particle composites. J. Phys. D: Appl. Phys. 2002, 35, 1833–1838. [Google Scholar] [CrossRef]
- Lakhtakia, A.; Mackay, T.G. Size–dependent Bruggeman approach for dielectric–magnetic composite materials. AEU Int. J. Electron. Commun. 2005, 59, 348–351. [Google Scholar] [CrossRef]
- Mackay, T.G. Homogenization giving rise to unusual metamaterials. In Proc. SPIE, Denver, CO, USA, 12 August 2004; Lakhtakia, A., Maksimenko, S.A., Eds.; Vol. 5509, pp. 34–45.
- Zharov, A.A.; Shadrivov, I.V.; Kivshar, Y.S. Nonlinear properties of left-handed metamaterials. Phys. Rev. Lett. 2003, 91, 37401:1–37401:4. [Google Scholar] [CrossRef] [PubMed]
- Giordano, S.; Rocchia, W. Shape dependent effects of dielectrically nonlinear inclusions in heterogeneous media. J. Appl. Phys. 2005, 98, 104101:1–104101:10. [Google Scholar] [CrossRef]
- Walpole, L.J. Elastic behaviour of composite materials: theoretical foundations. Adv. Appl. Mech. 1981, 11, 169–242. [Google Scholar]
- Christensen, R.M. Mechanics of Composite Materials; Dover Publication Inc.: New York, NY, USA, 2005. [Google Scholar]
- Hashin, Z. Analysis of composite materials–A survey. J. Appl. Mech. 1983, 50, 481–505. [Google Scholar] [CrossRef]
- Norris, N. A differential scheme for the effective moduli of composites. Mech. Mater. 1985, 4, 1–16. [Google Scholar] [CrossRef]
- McLaughlin, R. A study of the differential scheme for composite materials. Int. J. Eng. Sci. 1977, 15, 237–244. [Google Scholar] [CrossRef]
- Giordano, S. Differential schemes for the elastic characterisation of dispersions of randomly oriented ellipsoids. Eur. J. Mech. A-Solid. 2003, 22, 885–902. [Google Scholar] [CrossRef]
- Kachanov, M.; Sevostianov, I. On quantitative characterization of microstructures and effective properties. Int. J. Solids Struct. 2005, 42, 309–336. [Google Scholar] [CrossRef]
- Markov, K.Z.; Preziozi, L. (Eds.) Heterogeneous Media: Micromechanics Modeling Methods and Simulations; Birkhauser: Boston, MA, USA, 2000.
- Kachanov, M. Effective elastic properties of cracked solids: critical review of some basic concepts. Appl. Mech. Rev. 1992, 45, 305–336. [Google Scholar] [CrossRef]
- Giordano, S.; Colombo, L. Effects of the orientational distribution of cracks in solids. Phys. Rev. Lett. 2007, 98, 055503:1–055503:4. [Google Scholar] [CrossRef] [PubMed]
- Giordano, S.; Colombo, L. Effects of the orientational distribution of cracks in isotropic solids. Eng. Frac. Mech. 2007, 74, 1983–2003. [Google Scholar] [CrossRef]
- Zanda, G. Electromagnetic Properties of Linear and Nonlinear Composite Materials. Master Degree Thesis, University of Cagliari, Italy, 2008. [Google Scholar]
- Leung, K.M. Optical bistability in the scattering and absorption of light from nonlinear microparticles. Phys. Rev. A 1986, 33, 2461–2464. [Google Scholar] [CrossRef] [PubMed]
- Haus, J.W.; Inguva, R.; Bowden, C.M. Effective-medium theory for nonlinear ellipsoidal composites. Phys. Rev. A 1989, 40, 5729–5734. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, G.S.; Gupta, S.D. T-Matrix approach to the nonlinear susceptibilities of heterogeneous media. Phys. Rev. A 1988, 38, 5678–5687. [Google Scholar] [CrossRef] [PubMed]
- Stratton, J.A. Electromagnetic Theory; Mc Graw Hill: New York, NY, USA, 1941. [Google Scholar]
- Giordano, S.; Palla, P.L.; Colombo, L. Effective permittivity of materials containing graded ellipsoidal inclusions. Eur. Phys. J. B 2008, 66, 29–35. [Google Scholar] [CrossRef]
- Goncharenko, A.V. Optical properties of core-shell particle composites. I. Linear response. Chem. Phys. Lett. 2004, 386, 25–31. [Google Scholar] [CrossRef]
- Goncharenko, A.V. Optical properties of core-shell particle composites. II. Nonlinear response. Chem. Phys. Lett. 2007, 439, 121–126. [Google Scholar] [CrossRef]
- Chen, G.Q.; Wu, Y.M. Effective dielectric response of nonlinear composites of coated metal inclusions. Chin. Phys. Lett. 2007, 24, 1724–1728. [Google Scholar]
- Pinchuk, A. Optical bistability in nonlinear composites with coated ellipsoidal nanoparticles. J. Phys. D: Appl. Phys. 2003, 36, 460–464. [Google Scholar] [CrossRef]
- Gu, L.; Gao, L. Optical bistability of a nondilute suspension of nonlinear coated particles. Physica B 2005, 368, 279–286. [Google Scholar] [CrossRef]
- Park, J.; Lu, W. Orientation of core-shell nanoparticles in an electric field. Appl. Phys. Lett. 2007, 91, 053113:1–053113:3. [Google Scholar] [CrossRef]
- Yu, K.W.; Hui, P.M.; Stroud, D. Effective dielectric response of nonlinear composites. Phys. Rev. B 1993, 47, 14150–14156. [Google Scholar] [CrossRef]
- Bergman, D.J.; Levy, O.; Stroud, D. Theory of optical bistability in a weakly nonlinear composite medium. Phys. Rev. B 1994, 49, 129–134. [Google Scholar] [CrossRef]
- Levy, O.; Bergman, D.J.; Stroud, D. Harmonic generation, induced nonlinearity, and optical bistability in nonlinear composites. Phys. Rev. E 1995, 52, 3184–3194. [Google Scholar] [CrossRef]
- Hui, P.M.; Cheung, P.; Stroud, D. Theory of third harmonic generation in random composites of nonlinear dielectrics. J. Appl. Phys. 1998, 84, 3451–3458. [Google Scholar] [CrossRef]
- Hui, P.M.; Xu, C.; Stroud, D. Second-harmonic generation for a dilute suspension of coated particles. Phys. Rev. B 2004, 69, 014203:1–014203:7. [Google Scholar] [CrossRef]
- Wei, E.B.; Wu, Z.K. The Nonlinear effective dielectric response of graded composites. J. Phys.: Condens. Matter 2004, 16, 5377–5386. [Google Scholar] [CrossRef]
- De Gennes, P.G. The Physics of Liquid Crystals; Clarendon: Oxford, UK, 1974. [Google Scholar]
- Chandrasekhar, S. Liquid Crystals; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Nagatani, T. Effective permittivity in random anisotropic media. J. Appl. Phys. 1980, 51, 4944–4949. [Google Scholar] [CrossRef]
- Shafiro, B.; Kachanov, M. Anisotropic effective conductivity of materials with nonrandomly oriented inclusions of diverse ellipsoidal shapes. J. Appl. Phys. 2000, 87, 8561–8569. [Google Scholar] [CrossRef]
- Giordano, S. Order and disorder in heterogeneous material microstructure: electric and elastic characterization of dispersions of pseudo oriented spheroids. Int. J. Eng. Sci. 2005, 43, 1033–1058. [Google Scholar] [CrossRef]
- Giordano, S. Equivalent permittivity tensor in anisotropic random media. J. Electrostat. 2006, 64, 655–663. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Pergamon: Oxford, UK, 1960. [Google Scholar]
- Castañeda, P.P.; Suquet, P. Nonlinear composites. Adv. Appl. Mech. 1998, 34, 171–302. [Google Scholar]
- Talbot, D.R.S.; Willis, J.R. Variational principles for inhomogeneous nonlinear media. J. Appl. Math. 1985, 35, 39–54. [Google Scholar]
- Talbot, D.R.S.; Willis, J.R. Bounds and self-consistent estimates for the overall properties of nonlinear composites. J. Appl. Math. 1987, 39, 215–240. [Google Scholar] [CrossRef]
- Castañeda, P.P. The effective mechanical properties of nonlinear isotropic composites. J. Mech. Phys. Solids 1991, 39, 45–71. [Google Scholar] [CrossRef]
- Castañeda, P.P. Bounds and estimates for the properties of nonlinear heterogeneous systems. Philos. Trans. R. Soc. London A 1992, 340, 531–567. [Google Scholar] [CrossRef]
- Castañeda, P.P. A new variational principle and its application to nonlinear heterogeneous systems. J. Appl. Math. 1992, 52, 1321–1341. [Google Scholar] [CrossRef]
- Castañeda, P.P. Exact second-order estimates for the effective mechanical properties of nonlinear composite materials. J. Mech. Phys. Solids 1996, 44, 827–862. [Google Scholar] [CrossRef]
- Suquet, P. Overall potentials and extremal surfaces of power law or ideally plastic composites. J. Mech. Phys. Solids 1993, 41, 981–1002. [Google Scholar] [CrossRef]
- Talbot, D.R.S.; Willis, J.R. Some explicit bounds for the overall behaviour of nonlinear composites. Int. J. Solids Struct. 1992, 29, 1981–1987. [Google Scholar] [CrossRef]
- Beran, M.J. Use of the variational approach to determine bounds for the effective permittivity of random media. Il Nuovo Cimento 1965, 38, 771–782. [Google Scholar] [CrossRef]
- Catheline, S.; Gennisson, J.L.; Fink, M. Measurement of elastic nonlinearity of soft solid with transient elastography. J. Acoust. Soc. Am. 2003, 114, 3087–3091. [Google Scholar] [CrossRef] [PubMed]
- Catheline, S.; Gennisson, J.L.; Tanter, M.; Fink, M. Observation of shock transverse waves in elastic media. Phys. Rev. Lett. 2003, 91, 164301:1–164301:4. [Google Scholar] [CrossRef] [PubMed]
- Buehler, M.J.; Abraham, F.F.; Gao, H. Hyperelasticity governs dynamic fracture at a critical length scale. Nature 2003, 426, 141–146. [Google Scholar] [CrossRef] [PubMed]
- Buehler, M.J.; Gao, H. Dynamical fracture instabilities due to local hyperelasticity at crack tips. Nature 2006, 439, 307–310. [Google Scholar] [CrossRef] [PubMed]
- Holỳ, V.; Springholz, G.; Pinczolits, M.; Bauer, G. Strain induced vertical and lateral correlations in quantum dot superlattices. Phys. Rev. Lett. 1999, 83, 356–359. [Google Scholar] [CrossRef]
- Schmidbauer, M.; Seydmohamadi, Sh.; Grigoriev, D.; Wang, Zh.M.; Mazur, Yu.I.; Schäfer, P.; Hanke, M.; Khler, R.; Salamo, G.J. Controlling Planar and Vertical Ordering in Three-Dimensional (In,Ga)As Quantum Dot Lattices by GaAs Surface Orientation. Phys. Rev. Lett. 2006, 96, 066108:1–066108:4. [Google Scholar] [CrossRef] [PubMed]
- Mattoni, A.; Colombo, L.; Cleri, F. Atomistic study of the interaction between a microcrack and a hard inclusion in β-SiC. Phys. Rev. B 2004, 70, 094108:1–094108:10. [Google Scholar] [CrossRef]
- Atkin, R.J.; Fox, N. An Introduction to the Theory of Elasticity; Dover Publication Inc.: New York, NY, USA, 1980. [Google Scholar]
- Novozhilov, V.V. Foundations of the Nonlinear Theory of Elasticity; Dover Publication Inc.: New York, NY, USA, 1999. [Google Scholar]
- Ballabh, T.K.; Paul, M.; Middya, T.R.; Basu, A.N. Theoretical multiple-scattering calculation of nonlinear elastic constants of disordered solids. Phys. Rev. B 1992, 45, 2761–2771. [Google Scholar] [CrossRef]
- Mura, T. Micromechanics of Defects in Solids; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Dover Publication Inc.: New York, NY, USA, 2002. [Google Scholar]
- Landau, L.D.; Lifschitz, E.M. Theory of Elasticity, Course of Theoretical Physics, Vol. 7, 3rd ed.; Butterworth Heinemann: Oxford, UK, 1986. [Google Scholar]
- Sekoyan, S.S. Higher-order moduli of elasticity for an isotropic elastic body. Int. Appl. Mech. 1974, 10, 1259–1262. [Google Scholar] [CrossRef]
- Hiki, Y. Higher order elastic constants of solids. Ann. Rev. Mater. Sci. 1981, 11, 51–73. [Google Scholar] [CrossRef]
- Hughes, D.S.; Kelly, J.L. Second-order elastic deformation of solids. Phys. Rev. 1953, 92, 1145–1149. [Google Scholar] [CrossRef]
- Bateman, T.; Mason, W.P.; McSkimin, H.J. Third-order elastic moduli of germanium. J. Appl. Phys. 1961, 32, 928–936. [Google Scholar] [CrossRef]
- Cain, T.; Ray, J.R. Third-order elastic constants from molecular dynamics: Theory and an example calculation. Phys. Rev. B 1988, 38, 7940–7946. [Google Scholar] [CrossRef]
- Zhao, J.; Winey, J.M.; Gupta, Y.M. First-principles calculations of second- and third-order elastic constants for single crystals of arbitrary symmetry. Phys. Rev. B 2007, 75, 094105:1–094105:7. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion and related problems. Proc. R. Soc. London Ser. A 1957, A241, 376–396. [Google Scholar] [CrossRef]
- Eshelby, J.D. The elastic field outside an ellipsoidal inclusion. Proc. R. Soc. London Ser. A 1959, A252, 561–569. [Google Scholar] [CrossRef]
- Sevostianov, I.; Vakulenko, A. Inclusion with non-linear properties in elastic medium. Int. J. Fracture 2000, 107, 9–14. [Google Scholar]
- Tsvelodub, I.Yu. Determination of the strength characteristics of a physically nonlinear inclusion in a linearly elastic medium. J. Appl. Mech. Tech. Phys. 2000, 41, 734–739. [Google Scholar]
- Tsvelodub, I.Yu. Physically nonlinear ellipsoidal inclusion in a linearly elastic medium. J. Appl. Mech. Tech. Phys. 2004, 45, 69–75. [Google Scholar] [CrossRef]
- Giordano, S.; Colombo, L.; Palla, P.L. Nonlinear elastic Landau coefficients in heterogeneous materials. Europhys. Lett. 2008, 83, 66003:1–66003:5. [Google Scholar] [CrossRef]
- Giordano, S.; Palla, P.L.; Colombo, L. Nonlinear elasticity of composite materials. Eur. Phys. J. B 2009, 68, 89–101. [Google Scholar] [CrossRef]
- Christensen, R.M. Effective properties of composite materials containing voids. Proc. R. Soc. London, Ser. A 1993, 440, 461–473. [Google Scholar] [CrossRef]
- Zimmerman, R.W. Elastic moduli of a solid containing spherical inclusions. Mech. Mater. 1991, 12, 17–24. [Google Scholar] [CrossRef]
- Zimmerman, R.W. Behaviour of the poisson ratio of a two-phase composite materials in the high-concentration limit. Appl. Mech. Rev. 1994, 47, 38–44. [Google Scholar] [CrossRef]
- Thorpe, M.F.; Sen, P.N. Elastic moduli of two dimensional composite continua with elliptical inclusions. J. Acoust. Soc. Am. 1985, 77, 1674–1680. [Google Scholar] [CrossRef]
- Hill, R. Theory of mechanical properties of fibre-strengthened materials: I. Elastic behaviour. J. Mech. Phys. Solids 1964, 12, 199–212. [Google Scholar] [CrossRef]
- Hill, R. Theory of mechanical properties of fibre-strengthened materials: II. Inelastic behaviour. J. Mech. Phys. Solids 1964, 12, 213–218. [Google Scholar] [CrossRef]
- Hill, R. Theory of mechanical properties of fibre-strengthened materials: III. Self-consistent model. J. Mech. Phys. Solids 1965, 13, 189–198. [Google Scholar] [CrossRef]
- Snyder, K.A.; Garboczi, E.J. The elastic moduli of simple two-dimensional isotropic composites: Computer simulation and effective medium theory. J. Appl. Phys. 1992, 72, 5948–5955. [Google Scholar] [CrossRef]
© 2009 by the authors. Licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Giordano, S. Dielectric and Elastic Characterization of Nonlinear Heterogeneous Materials. Materials 2009, 2, 1417-1479. https://doi.org/10.3390/ma2041417
Giordano S. Dielectric and Elastic Characterization of Nonlinear Heterogeneous Materials. Materials. 2009; 2(4):1417-1479. https://doi.org/10.3390/ma2041417
Chicago/Turabian StyleGiordano, Stefano. 2009. "Dielectric and Elastic Characterization of Nonlinear Heterogeneous Materials" Materials 2, no. 4: 1417-1479. https://doi.org/10.3390/ma2041417