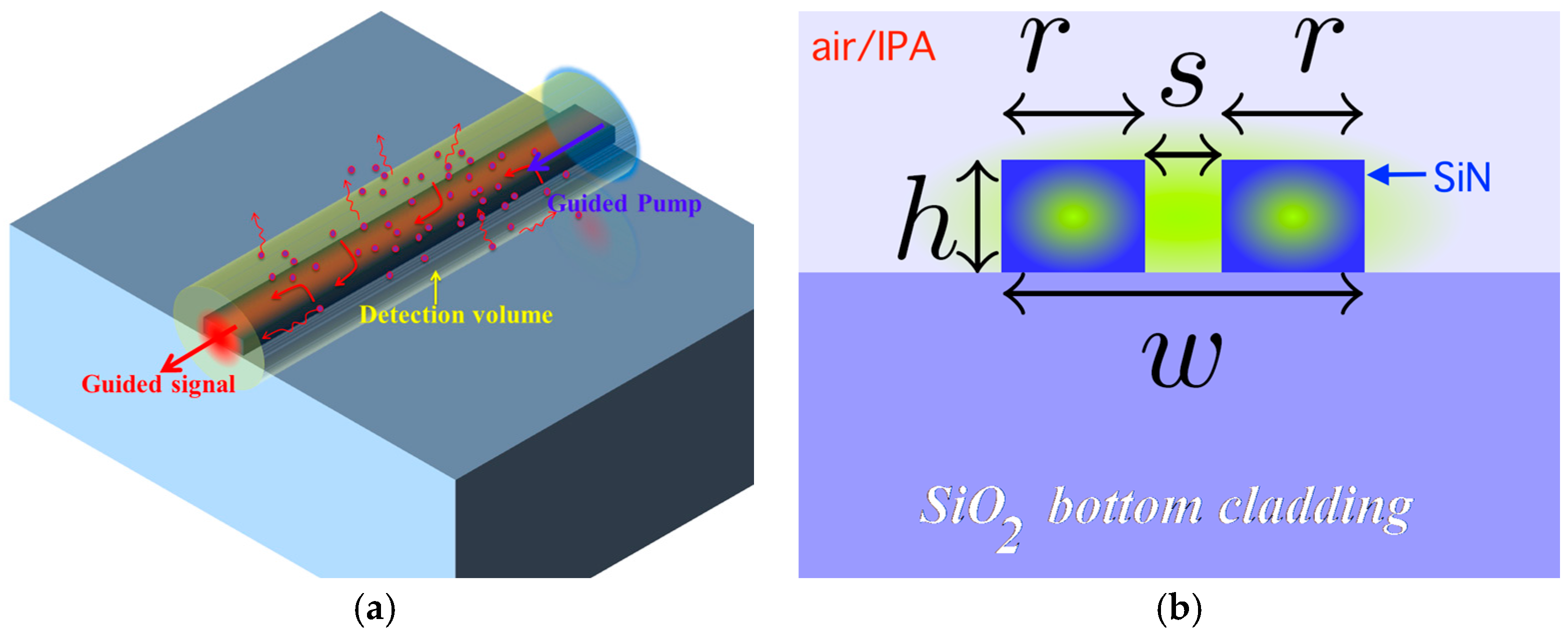
In this section, we detail experiments performed in order to pinpoint the origin of the WGBL and suggest a mitigation strategy based on the design of the optical mode. In
Section 2.1, we describe a typical spectrum and identify several features of the WGBL originating from the SiN waveguides deposited using a plasma enhanced plasma chemical vapor deposition (PECVD) method and fabricated using fluorine based chemistry, as reported in [
13] and subsequently used for the NWERS experiments [
2,
3,
4,
6,
7]. We decompose the WGBL spectrum into a component dominant at low vibrational frequencies, henceforth referred to as a low-frequency dominant component (LFDC), and other components consisting of various peaks due to specific molecular vibrations in the core.
Section 2.2 is dedicated to demonstrating that the WGBL is dominated by the signal from the core, followed by
Section 2.3 where we determine the strength of WGBL relative to that of Iso-Propyl Alcohol (IPA), a standard analyte used in on-chip evanescent Raman spectroscopy. In
Section 2.4 we focus on the study of the origin of the LFDC and discuss the dependence of this component on the excitation wavelength and input power to rule out the possibility that this feature originates from fluorescence or nonlinearities in the waveguide. In
Section 2.5 we propose and demonstrate that the WGBL can be reduced by using slotted waveguides and quasi-transverse-magnetic (TM) modes. A mathematical model to calculate the contribution from the core material relative to the top cladding is developed in the
Appendix A and used throughout the article. Unless otherwise stated, the measurements are done with the setup detailed in [
2,
4], which is also briefly discussed in the Methods section. The PECVD SiN waveguide used in the current experimental studies has also been reported in [
13] and is also briefly described in Methods section.
2.1. Different Raman Features in the WGBL
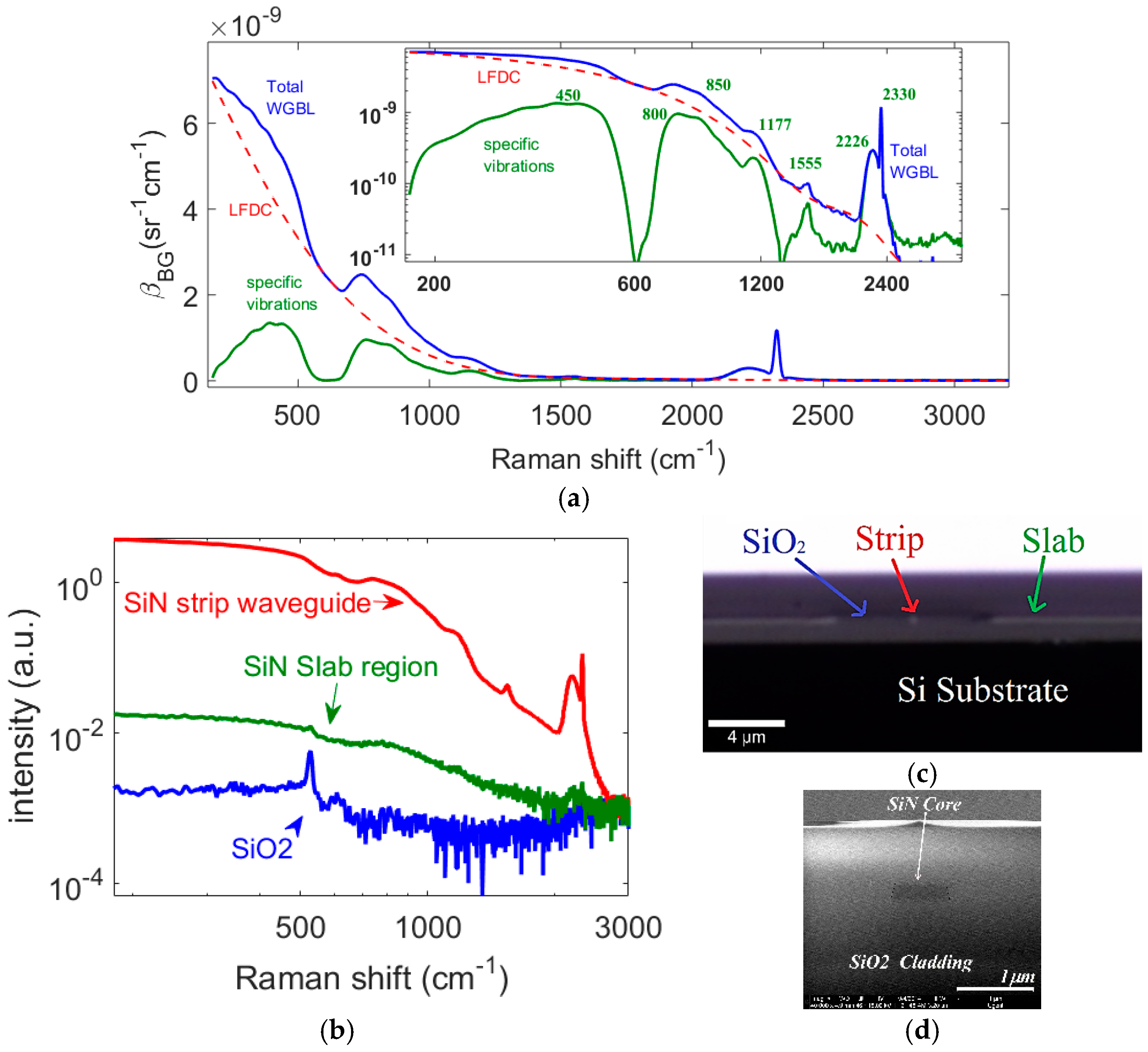
In
Figure 2a we display the WGBL intensity expressed in terms of the units of Raman efficiency,
βBG (see
Appendix A for details), from an air-cladded, 0.7 cm long, 700 nm wide PECVD SiN strip waveguide measured using excitation and collection from the fundamental quasi-transverse electric (TE) mode collected using a setup that collects co-propagating spontaneous Raman signals coupled with the waveguide mode (see
Section 4). The WGBL consists of a component that is monotonically decreasing with wavenumber shift and a combination of several convolved peaks. The earlier component, depicted by the red dashed line in
Figure 2a, is referred to as the low-frequency dominant component (LFDC). These features, particularly the LFDC, are more distinguishable in logarithmic scale showing the WGBL intensity in the full dynamic range of the spectrometer. The LFDC is discussed in Second 2.4. In this paper we approximate LFDC with a 5th order polynomial using an asymmetric cost function [
11].
In order to separate several peaks contained in the WGBL and identify their origin, we subtract the LFDC from the total WGBL. The subtracted spectrum is also shown in
Figure 1a with a solid green line. The subtracted spectrum consists of features that have also been observed in the infrared absorption spectrum measured for silicon-nitride thin-films [
14,
15,
16]. The major peaks centered around 450, 800, 850, 1175, 1555, and 2226 cm
−1 are assigned, respectively, to Si breathing, Si-O bending, Si-N stretching, N-H bending, N-H
2 bending, Si-H rocking and Si-H stretching [
14,
15,
16]. The peaks due to hydrogen are suggestive of an incomplete reaction of hydrogen-rich silane, ammonia, and H
2 during plasma enhanced chemical vapor deposition (PECVD). The strong narrowband peak at 2330 cm
−1 is assigned to the interstitial N
2 (typical diluent) incorporated in the core during the deposition process, as also reported in the deposition of GaN and ZnO [
17].
At this point, it is instructive to look at the z-scan data of the SiN-SiO-Si stack presented in [
18], which also suggests that several peaks are indeed due to the SiN rich waveguide core. To further corroborate the statement that the background peaks indeed originate from the SiN-rich core material and not SiO
2 cladding, we measured the Raman spectrum of the stack at several locations of the waveguide cross-section depicted in
Figure 2c,d using a confocal microscope (see Methods for the description of the measurement parameters).
Figure 2b plots the confocal Raman spectra of the SiN-rich waveguide core material obtained by coupling the light into the strip waveguide, along with the confocal Raman signal obtained from the SiO
2 cladding. The confocal spectrum from the strip waveguide, as well as from the slab region, feature most of the distinct features of the WGBL measured using the conventional NWERS setup, while most of these features are absent in the Raman spectrum of the SiO
2 cladding. However, due to waveguide enhancement, the contribution from the strip waveguide is larger by more than two orders of magnitude compared to that of the slab region because of diffraction. All of these spectra are taken under similar experimental conditions including integration time and pump power. Hence, relative amplitudes from each location are indicative of their relative contributions for the WGBL. Thus, we conclude that the peaks contained in WGBL mainly consist of Raman peaks originating from the vibrations of several chemical bonds in the SiN waveguide core material and impurities incorporated therein during the deposition of the core material. This observation emphasizes the importance of the optimization of the deposition method in order to avoid incomplete reaction and the incorporation of the associated reaction products in the core.
Having confirmed that the origin of the several peaks observed in WGBL are from the core, next, we study the relative contributions of the core and cladding material for the LFDC. To this end, as shown in
Figure 3a,b, we collect the WGBL spectra from waveguides with SiO
2 as bottom and top cladding with different widths, namely
w = 500 nm and
w = 800 nm, and two orthogonal excitation and collection polarizations (quasi-TE and quasi-TM) that interact very differently with the cladding material [
3]. We normalize these spectra with the peak at 2330 cm
−1, as we know that it originates from the core. This normalization using an intrinsic peak allows us to get rid of the experimental differences, for example, that might occur due to differences of coupling and waveguide losses which vary from one measurement to another. In addition, assuming that the waveguide loss spectra for different Stokes shift is the same for these different cases, the use of a peak known to originate from the core renders the measured spectra relative to the contribution from the core for each of the different cases. As shown in
Figure 3a,b, for a given polarization, we observe that except for a monotonously increasing amplitude difference between the two waveguide geometries, which culminates at about 0.8 dB at 200 cm
−1, there is no significant difference in the spectra. We ascribe this difference to substrate leakage which monotonously increases for the longer wavelength for the smaller waveguide [
13], particularly in the coupling section terminating at 220 nm.
On the ground of these arguments, and other experiments to be described in the next section, we can conclude that the SiO
2 cladding does not have a significant contribution to the observed WGBL. In the
Appendix A, we develop a theoretical model assuming that the WGBL is primarily due to core material. In the next section, we investigate the implications of this model in more detail with the aid of some experiments which further corroborate the conclusion derived here.
2.2. Dominant Source of the WGBL
In order to study the properties of the WGBL with the knowledge of the reference Raman signal from an analyte drop-casted as the top cladding, we quantify the signal-to-background ratio (SBR),
RS/B =
Cs/CB as the ratio between the signal counts
Cs from the top-cladding and WGBL counts
CB from the core measured at a given wavenumber. The implicit assumptions that are needed to treat the SBR
RS/B as a parameter of investigation are detailed in the
Appendix A. Besides comparing the strength of the WGBL relative to a known analyte, the rationale for taking this ratio is to remove any common-mode signal variations across different measurements, such as differences in the coupling losses, waveguide losses, etc. In the present study,
RS/B is the ratio between the average signal counts of the 819 cm
−1 Raman peak from the IPA upper-cladding and the average background signal evaluated at 819 cm
−1. We investigate how
RS/B varies with waveguide length, waveguide width and mode polarization. This study will allow us to corroborate the suggestion from
Section 2.1 that a significant amount of the WGBL, including the LFDC depicted by the red dashed line in
Figure 2a, originates from the waveguide core.
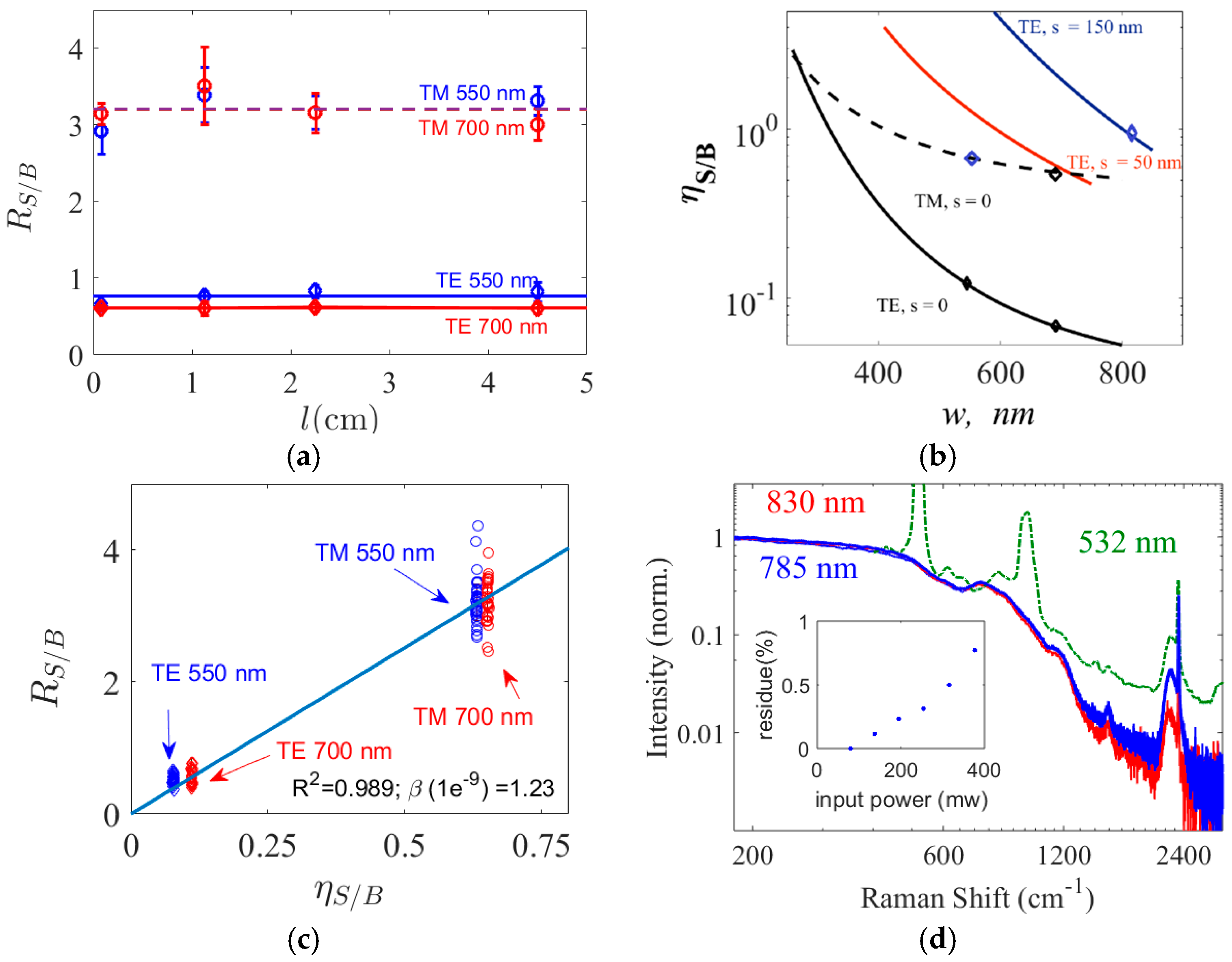
In
Figure 4a the dependence of
RS/B on waveguide length
l is experimentally investigated for the two fundamental modes for the strip waveguides of thickness
h = 220 nm and widths
w = 700 nm and
w = 550 nm. The experimental values are extracted from three chips measured three times. Two major conclusions can be drawn from
Figure 4a. Firstly, the WGBL depends in a similar manner on waveguide length as does the Raman signal from the analyte. Secondly, we can conclude that the most significant contribution for the WGBL comes from the core of the waveguide, since the corresponding photon count ratio
RS/B is lower for the TE mode compared to the TM mode. It results from the fact that the confinement factor for the core (hence the corresponding photon counts contribution) is higher for the TE mode than for the TM mode for the given geometry of our waveguides where
h ≪
w [
3]. To further validate this statement, we calculate a parameter called
core-to-cladding conversion ratio (CCR)
ηS/B. The CCR
ηS/B is the ratio between the theoretical specific conversion efficiencies between the core and the top-cladding assuming the WGBL originates predominantly from the core, and is given by Equation (A8) in the
Appendix A. The values of
ηS/B calculated using COMSOL finite elements mode solver using this model are shown in
Figure 4b for different waveguide geometries. As displayed in
Figure 4b, a higher
RS/B is expected for the TM mode compared to that of the TE mode for both waveguides studied. Furthermore, as shown in
Figure 4c, a linear fit between
ηS/B and
RS/B for both TE and TM modes and both waveguide geometries with goodness of fit
R2 = 0. 989 demonstrates a proportional relationship between
ηS/B and
RS/B. This is expected from Equation (A9), and indicates several assumptions made in the model are practically valid. As remarked in the
Appendix A in the context of Equation (A9), the proportionality constant between
RS/B and
ηS/B is the ratio between the scattering efficiencies (the product of the scattering particle number density and the scattering cross-section) of the WGBL and the signal. Hence, the data shown in
Figure 4c can be used to calculate the background scattering efficiency
βBG relative to the top cladding scattering efficiency. This will be discussed next.
2.3. Determination of the Scattering Efficiency of the WGBL
Since the product of the concentration of pure IPA and the cross section of its 819 cm
−1 line is known (
βs,819 =
ρs σs,819 = 6.22 × 10
−9 sr
−1·cm
−1) [
2], the Raman scattering efficiency of the WGBL
βBG,819 can be calculated to be
βBG,819 = 1.2 ± 0.1 × 10
−9 sr
−1·cm
−1 using the slope of the line fitting the data and Equation (A9). This value is about six times smaller than the value for pure IPA. Once
βBG is determined at one frequency, one can extrapolate the efficiency values to the entire Stokes region of interest by using a measured spectrum of the WGBL. The entire spectrum of the background efficiency, based on our measurement, is shown in
Figure 2a. For an arbitrary analyte with a different cross-section or concentration (scattering efficiency), the value of the WGBL efficiency
βBG given in
Figure 2a can be used to predict the signal-to-background ratio
RS/B, or the corresponding SNR. In the last statement, we have implicitly assumed that all the features of the
βBG spectrum, including the LFDC, behave like a Raman signal. Next, we present some experimental observations and theoretical considerations, which show that this is indeed the case.
2.4. Low Frequency Dominant Component of the WGBL
In this section we focus on the study of the LFDC component of the WGBL that was shown with a red dashed line in
Figure 2a. Generally, a broadband background emission in a Raman measurement is associated with auto-fluorescence arising from the electronic transitions of the material itself. The intensity of fluorescence depends strongly on the pump wavelength, while the spectral shape, plotted as a function of wavelength, does not change. Therefore, if plotted in
wavenumber shifts with respect to different pump wavelengths, one observes a substantial change in the emission spectrum. A common strategy to discern fluorescence from Raman scattering, therefore, is to excite the material with wavelengths that differ by some significant amount (>500 cm
−1 in wavenumbers) and then observe if the emission spectra in wavenumber shifts has changed. A significant difference in the spectrum means that the emission is primarily due to fluorescence. A Raman spectrum does not change since the Stokes spectrum shifts with the pump wavelength.
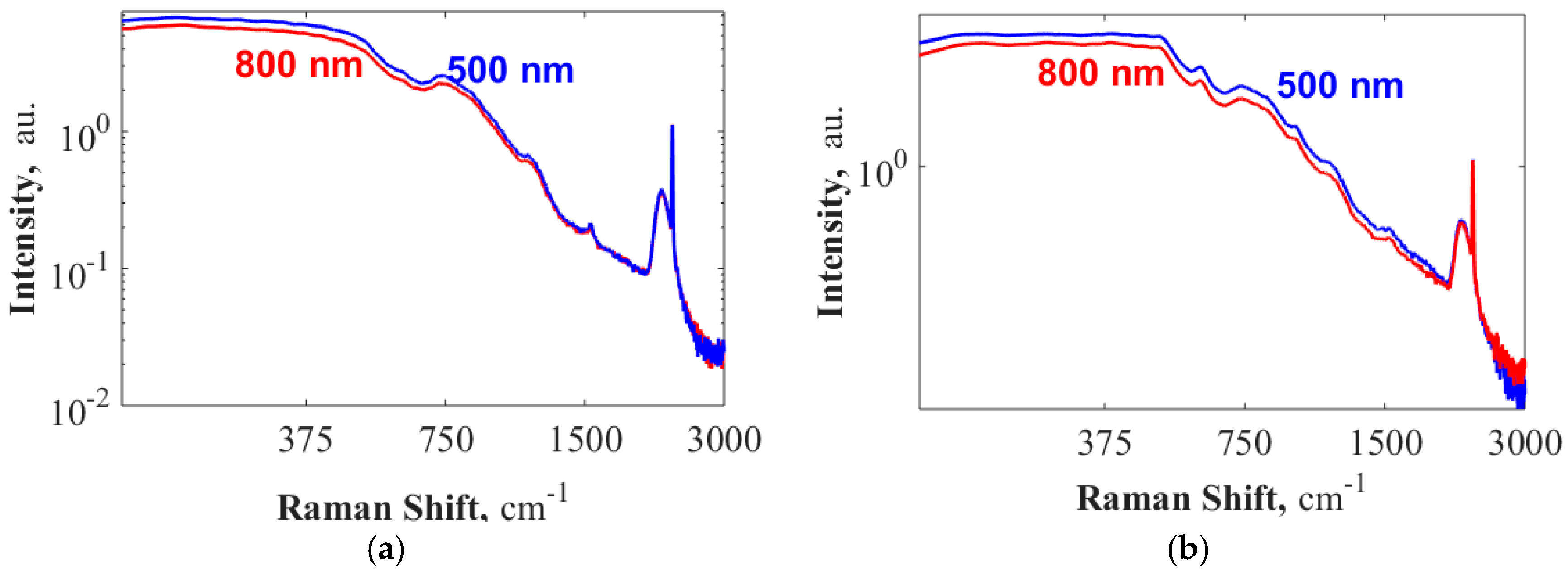
In
Figure 4d, we show the WGBL (normalized to the maximum) generated by the fundamental TE mode of a 700 nm wide strip waveguide when excited at 785 nm and 830 nm wavelengths. The pump at 830 nm corresponds to about 690 cm
−1 difference in wavenumbers compared to a pump at 785 nm. We observe a negligible difference in the spectra. A small difference that is observed is attributed to the difference in the quantum efficiency of the detectors for the two spectra in absolute wavelengths. The quantum efficiency of silicon detectors in the spectrometer at the Raman peak of 2330 cm
−1 is lower for the 785 nm pump and even more so for 830 nm pump, as Si has a band-gap near to 1.14 eV (1087 nm). In
Figure 4d, we also plot the spectrum obtained from a confocal Raman microscope using an excitation at 532 nm during a z-scan of the waveguide stack Si-SiO-SiN as reported in [
18]. This spectrum is collected at the z-value corresponding to the strongest signal from the peak at 2330 cm
−1 that originates from the interstitial N
2 in the core material. The spectrum amplitude is normalized to the same scale for comparison. Apart from the peaks at 520 and 960 cm
−1 ascribed to Si [
18], which is unavoidable in a z-scan from the top of the material stack, there is no significant difference in the WGBL spectra. Thus, based on these measurements, we conclude that the WGBL spectra do not differ significantly over a pump wavelength spectral range between 532 and 830 nm. This conclusion excludes the possibility that a significant contribution of the LFDC originates from fluorescence of the waveguide material and indicates that it is due to Raman scattering.
However, a spectrum of emission due to a non-linear process, such as a
χ3 process, may also be invariant to the pump wavelength to a certain degree. In order to rule out the possibility that the origin of the WGBL is a nonlinear process, we varied the pump power from 60 to 380 mW, (with ~8 dB in-coupling losses). In
Figure 4d we have plotted all the WGBL spectra obtained from a strip waveguide of
w = 700 nm and
h = 220 nm for different input pump powers in blue (corresponding to a 785 nm pump wavelength). The normalized spectra show no visible difference. In order to quantify the variation of the total spectral shape for different input powers, we implemented a least-square algorithm that finds a normalization scalar
that rescales the entire spectrum
Si(
ν) to a reference spectrum obtained using 60 mW input pump power
S60(
ν) such that the residue
is minimized. The rescaling of spectra using
ensures that any difference in the entire spectral shape is quantified as
Resi. In the inset of
Figure 4d, the corresponding mean-squared error (
Resi) is shown. The
Resi is less than 1% for the whole spectral range and all the input powers investigated. From this result we conclude that the shape of the WGBL does not depend on the input pump power level. The small and monotonic increase of the residue with the pump power can be attributed to the shot noise and the fluctuations of the input laser, which increases with the input power. If the WGBL originated from a non-linear process, the shape of the silicon nitride spectra should have been significantly influenced by the input power during the 6-fold increase in the waveguide power [
19] thereby increasing the
Resi quite significantly.
In conclusion, in this section we ruled out the possibility that the LFDC observed at low wavenumbers in the WGBL is due to auto-fluorescence or any non-linear process. It is hence likely that it originates from a Raman scattering process occurring in the SiN core. Such broadband Raman scattering has been ascribed to breaking of momentum selection rules due to disorder in the amorphous material, and photon-phonon coupling due to thermal fluctuations [
20,
21,
22]. A detailed study of the behavior of such a Raman scattering process in a guiding structure is outside the scope of this paper. The important conclusion from this section is that the LFDC efficiency spectrum
βBG calculated in
Section 2.3 can be treated like a Raman spectrum. This conclusion is used in the next section to propose and demonstrate a mitigation strategy.
2.5. Mitigation Strategies
In
Section 2.2, a parameter called core-to-cladding conversion ratio (CCR)
ηS/B was introduced using Equation (A8) in order to quantify the contribution of the waveguide core for the WGBL in comparison to the analyte signal from the top cladding. This parameter is plotted in
Figure 4b for a core thickness
h of 220 nm as a function of waveguide width for the TE mode of a slot waveguide (
s = 150 nm) and both for fundamental TE and TM modes for strip waveguides. Evidently, the CCR
ηS/B can be used to select the optimal mode and optimal waveguide design for high signal and low background, as the signal to background counts ratio (SBR)
RS/B is proportional to the CCR. For example, from
Figure 4b, we expect high signal counts to background counts ratio (SBR)
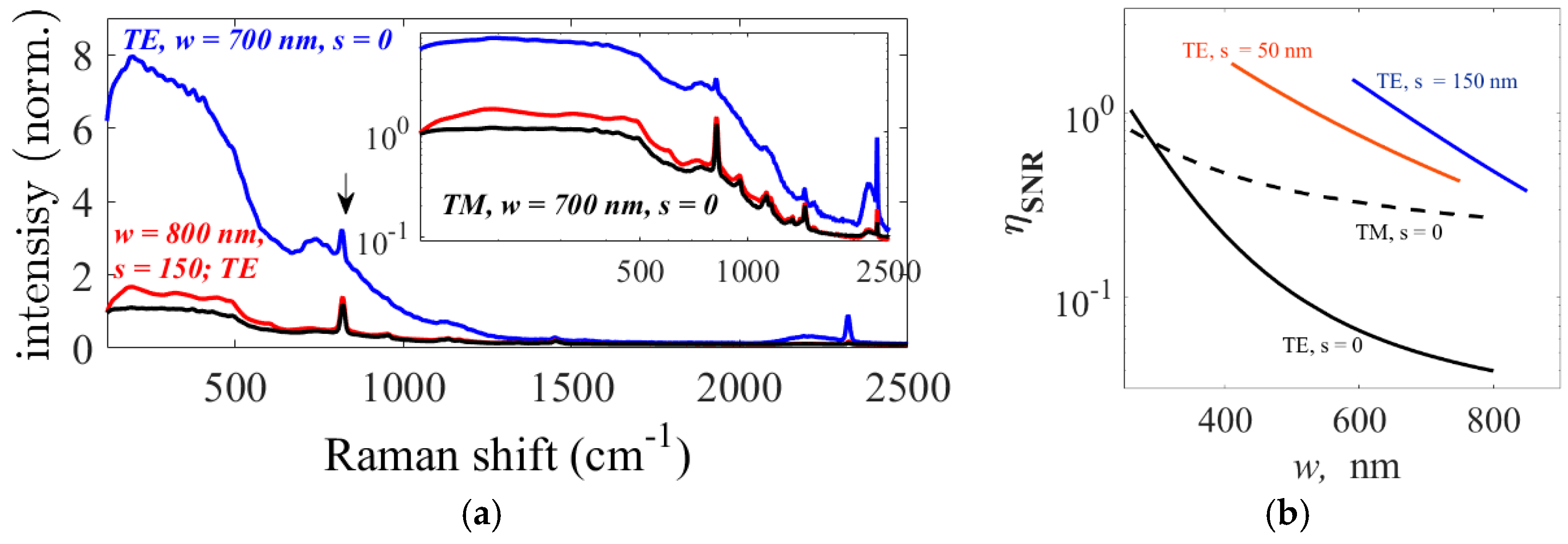
RS/B, for slotted waveguides compared to strip waveguides if both waveguides are excited using the fundamental TE mode. Similarly, the SBR for slotted waveguide is comparable to that of the fundamental TM mode in a strip waveguide. This is observed experimentally as already demonstrated in
Figure 3a and further illustrated using their respective spectra in
Figure 5a.
Although the CCR
ηS/B is useful in determining the relative strength of the signal compared to the WGBL, it is not an accurate design parameter for optimization of the actual SNR. Standard deviation of the photon count fluctuation (shot-noise) due to the WGBL is actually proportional to the square root of the WGBL counts, since the photon count follows Poisson statistics. Hence, a more relevant design parameter is,
SNR-equivalent efficiency ηSNR defined as:
Here, the numerator integral is evaluated in the top-cladding region where the analyte is located while the integral in the denominator is evaluated in the core region, which has been demonstrated to be the main source of the WGBL. Several quantities used in Equation (1) are further clarified in the
Appendix A. The SNR-equivalent efficiency
ηSNR is independent of analyte specific variables, such as analyte cross-section or density, and experiment specific variables, such as detector sensitivity. It is exclusively a function of the electromagnetic mode field distribution.
Figure 5b shows the
ηSNR calculated using Equation (1) for slot (
s = 150 nm) and strip silicon nitride waveguides of various widths. Notice that one may derive a wrong conclusion if CCR
ηS/B is used instead of
ηSNR for design of the waveguide to minimize the SNR, as CCR does not account for the signal enhancement parameterized by
ηs in Equation (1).
2.6. Remarks on the Wavelength Dependence of Several Experimental and Theoretical Parameters
In this paper, the influence of wavelength dependence of coupling efficiency, scattering efficiency, signal-to-noise ratio, and attenuation has been ignored. This leads to a negligible error in the conclusions and analyses we have presented for Stokes shifts <3000 cm
−1 and waveguide widths >300 nm with cut-off wavelength >1030 nm (Raman shift ~3000 cm
−1). As discussed in
Section 2.1, substrate leakage at longer wavelengths contributes to a signal difference <1 dB for the largest Raman shift we have discussed, i.e., 3000 cm
−1 [
13]. Furthermore, ignoring Stokes shifts in the numerical model leads to a maximum of about 20% error (for Stokes shifts <3000 cm
−1), which is comparable to the experimental error [
3]. In addition, the setup used for the measurements described in this paper uses an achromatic lens to collect the Raman signal, hence there is negligible wavelength dependence of coupling of waveguide signal to the spectrometer. Consequently, the influence of wavelength dependence on these several factors has been ignored in this paper. An accurate determination of these influences may be needed if waveguide widths smaller than 300 nm or Stokes shifts much larger than 3000 cm
−1 are of concern.